-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Theoretical and Mathematical Physics
p-ISSN: 2167-6844 e-ISSN: 2167-6852
2012; 2(3): 41-50
doi:10.5923/j.ijtmp.20120203.04
Deformed Quantum Field Theory, Thermodynamics at Low and High Energies, and Gravity. II. Deformation Parameter
A.E. Shalyt-Margolin
National Centre of Particles and High Enerоgy Physics, Bogdanovich Str. 153, Minsk, 220040, Belarus
Correspondence to: A.E. Shalyt-Margolin, National Centre of Particles and High Enerоgy Physics, Bogdanovich Str. 153, Minsk, 220040, Belarus.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
The principal objective of this paper is to show that deformation of the General Relativity within the scope of both the Generalized Uncertainty Principle (UV-cutoff) and the Extended Uncertainty Principle (IR-cutoff) in the cases when the corresponding gravitational equations have a thermodynamic interpretation may be studied in terms of a small parameter introduced in previous works of the author. From this viewpoint the parameter is though to be universal. Consideration is given to the possibility for extension of the obtained results to more general cases. Possible generalization of the uncertainty relation for the pair (cosmological constant, space-time volume), where the cosmological constant is regarded as a dynamic quantity at high and low energies, is analyzed. This paper is devoted to the 70-th Anniversary of Professor Nikolai Maksimovich Shumeiko, Director of the Belarusian Particles and High Energy Physics National Centre.
Keywords: Quantum Field Theory with UV ,IR Cutoff, Gravitational Thermodynamics, Deformed Gravity
Cite this paper: A.E. Shalyt-Margolin, Deformed Quantum Field Theory, Thermodynamics at Low and High Energies, and Gravity. II. Deformation Parameter, International Journal of Theoretical and Mathematical Physics, Vol. 2 No. 3, 2012, pp. 41-50. doi: 10.5923/j.ijtmp.20120203.04.
Article Outline
1. Introduction
- In the last decade numerous works devoted to a Quantum Field Theory (QFT) at Planck’s scale[1–3] have been published (of course, the author has no pretensions of being exhaustive in his references). This interest stems from the facts that (i) at these scales it is expected to reveal the effects of a Quantum Gravity (QG), and this still unresolved theory is intriguing all the researchers engaged in the field of theoretical physics; (ii) modern accelerators, in particular LHC, have the capacity of achieving the energies at which some QG effects may be exhibited.Now it is clear that Quantum Field Theory (QFT) at Planck’s scales, and possibly at very large scales as well, undergoes changes associated with the appearance of additional parameters related to (i) a minimal length (on the order of the Planck’s length) and (ii)a minimum momentum. As this takes place, the corresponding parameters are naturally considered as deformation parameters, i.e. the related quantum theories are considered as a high-energy deformation (at Planck’s scales) and a low-energy deformation (IR-cutoff), respectively, of the well-known quantum field theory, the latter being introduced in the corresponding high- and low-energy limits and exact to a high level. The deformation is understood as an extension of a particular theory by inclusion of one or several additional parameters in such a way that the initial theory appears in the limiting transition [4].Most natural approach to the introduction of the above- mentioned parameters is to treat a quantum field theory with the Generalized Uncertainty Principle (GUP)[5–15] and with the Extended Uncertainty Principle (EUP), respectively [12– 15]. In the case of GUP we easily obtain a minimal length on the order of the Planck’s
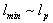 and the corresponding high-energy deformation of well-known QFT–QFT with GUP. It should be noted that QFT with GUP at Planck’s scales (Early Universe) is attested in many works (for example[5–11])). Even if we disregard the works devoted to a string theory, still remaining a tentative one, GUP is quite naturally derived from the gedanken experiment[6–9].On the other hand, GUP has no way in the spaces with large length scales (for example (A)dS). For such spaces, e.g., in[12,14] the Extended Uncertainty Principle has been introduced (find its exact definition below) giving an absolute minimum in the uncertainty of the momentum.The problem is to find whether there are cases when the deformations generated by GUP and EUP are defined by the same parameter. By author’s opinion this is the case for Gravity modified (deformed) within GUP and EUP, when the corresponding initial theory has a "thermodynamic interpretation"[16–21]. Specifically, the deformation parameter
and the corresponding high-energy deformation of well-known QFT–QFT with GUP. It should be noted that QFT with GUP at Planck’s scales (Early Universe) is attested in many works (for example[5–11])). Even if we disregard the works devoted to a string theory, still remaining a tentative one, GUP is quite naturally derived from the gedanken experiment[6–9].On the other hand, GUP has no way in the spaces with large length scales (for example (A)dS). For such spaces, e.g., in[12,14] the Extended Uncertainty Principle has been introduced (find its exact definition below) giving an absolute minimum in the uncertainty of the momentum.The problem is to find whether there are cases when the deformations generated by GUP and EUP are defined by the same parameter. By author’s opinion this is the case for Gravity modified (deformed) within GUP and EUP, when the corresponding initial theory has a "thermodynamic interpretation"[16–21]. Specifically, the deformation parameter 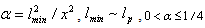 where x is the measuring scale, introduced by the author in a series of works[22–32] meets the above requirements.Note that this parameter has been introduced to study the deformation of QFT at Planck’s scale, although the deformation per se, associated with a high-energy modification of the density matrix, was "minimal" in that it presented no noncommutativity operators related to different spatial coordinates
where x is the measuring scale, introduced by the author in a series of works[22–32] meets the above requirements.Note that this parameter has been introduced to study the deformation of QFT at Planck’s scale, although the deformation per se, associated with a high-energy modification of the density matrix, was "minimal" in that it presented no noncommutativity operators related to different spatial coordinates 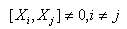 | (1) |
 (vacuum energy density), GUP is studied for the pair (
(vacuum energy density), GUP is studied for the pair ( )[33,34], where
)[33,34], where  – is the "space-time volume". In this Section consideration is given to the possible existence of EUP for this pair, i.e. to a possible extension of the Uncertainty Principle to the pair in the IR region, and hence to the possible substantiation of the proper (coincident with the experimental) value for
– is the "space-time volume". In this Section consideration is given to the possible existence of EUP for this pair, i.e. to a possible extension of the Uncertainty Principle to the pair in the IR region, and hence to the possible substantiation of the proper (coincident with the experimental) value for  . In Section 4 the results of Section 2 are applied to Einstein’s Equations for space with horizon and to Friedmann’s Equations. It is demonstrated that in both cases their deformation (in the first case within GUP and in the second case within EUP) may be interpreted with the use of the same small dimensionless parameter having a known variability domain.And, finally, in Section 5 the problems of further investigations are discussed, some final comments are given.
. In Section 4 the results of Section 2 are applied to Einstein’s Equations for space with horizon and to Friedmann’s Equations. It is demonstrated that in both cases their deformation (in the first case within GUP and in the second case within EUP) may be interpreted with the use of the same small dimensionless parameter having a known variability domain.And, finally, in Section 5 the problems of further investigations are discussed, some final comments are given.2. Universal Deformation Parameter in Gravitational Thermodynamics with GUP and EUP
- In this Section the Gravitational Thermodynamics (GT) is understood as thermodynamics of spaces with horizon[18, 20].
2.1. Gravitational Thermodynamics with GUP
- We use the notation and principal results from[14]. So, GUP is of the form
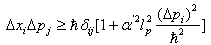 | (2) |
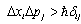 , we have
, we have 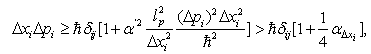 | (3) |
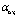 – parameter
– parameter 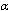 corresponding to
corresponding to 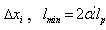 . Besides, as distinct from[14], for the dimensionless factor in GUP, instead of
. Besides, as distinct from[14], for the dimensionless factor in GUP, instead of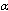 , we use
, we use 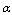 to avoid confusion with the deformation parameter.In this terms the uncertainty in moment is given by the nonstrict inequality
to avoid confusion with the deformation parameter.In this terms the uncertainty in moment is given by the nonstrict inequality 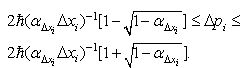 | (4) |
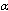 one can derive exact expressions. Indeed, in terms of
one can derive exact expressions. Indeed, in terms of 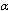 the GUP-modification (or rather GUP-deformation)is easily obtained for the Hawking temperature[36–39,14,15] that has been computed in the asymptotically flat
the GUP-modification (or rather GUP-deformation)is easily obtained for the Hawking temperature[36–39,14,15] that has been computed in the asymptotically flat 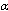 - dimensional space for a Schwarzshild black hole with a metric given by
- dimensional space for a Schwarzshild black hole with a metric given by 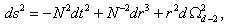 | (5) |
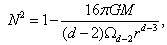 | (6) |
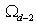 is the area of the unit sphere
is the area of the unit sphere 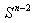 , and
, and 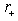 is the uncertainty in the emitted particle position by the Hawking effect, expressed as
is the uncertainty in the emitted particle position by the Hawking effect, expressed as 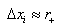 | (7) |
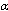 arises naturally. Actually, modification of the Hawking temperature is of the form, see formula (10) in[14]
arises naturally. Actually, modification of the Hawking temperature is of the form, see formula (10) in[14] 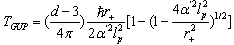 | (8) |
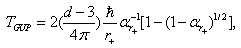 | (9) |
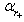 - parameter
- parameter 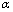 associated with
associated with 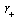 . It is clear that
. It is clear that 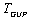 is actually the deformation
is actually the deformation 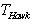 – black hole temperature for a semiclassical case[40]. In such a manner compared to
– black hole temperature for a semiclassical case[40]. In such a manner compared to 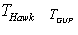 is additionally dependent only on the dimensionless small deformation parameter
is additionally dependent only on the dimensionless small deformation parameter 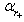 .The dependence of the black hole entropy on
.The dependence of the black hole entropy on 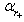 may be derived in a similar way. For a semiclassical approximation of the Bekenstein-Hawking formula[41,40]
may be derived in a similar way. For a semiclassical approximation of the Bekenstein-Hawking formula[41,40]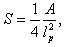 | (10) |
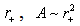 and (10) is clearly of the form
and (10) is clearly of the form 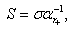 | (11) |
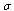 is some dimensionless denumerable factor. The general formula for quantum corrections [38] given as
is some dimensionless denumerable factor. The general formula for quantum corrections [38] given as 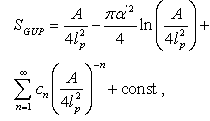 | (12) |
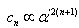 can always be computed to any desired order of accuracy[38], may be also written in the general case as a Laurent series in terms of
can always be computed to any desired order of accuracy[38], may be also written in the general case as a Laurent series in terms of 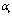
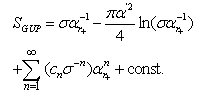 | (13) |
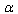 is referred to as
is referred to as 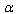 -representation.
-representation. 2. Gravitational Thermodynamics with EUP
- Let us consider QFT with EUP[14]. In this case we obtain QFT with
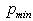 . Obviously, there is no minimal length
. Obviously, there is no minimal length 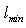 in QFT with EUP whatsoever but we assume that QFT with GUP is valid. At the present time for such an assumption we can find solid argumentation[6–9]. As will be shown later, in this case the fundamental quantities may be also expressed in terms of
in QFT with EUP whatsoever but we assume that QFT with GUP is valid. At the present time for such an assumption we can find solid argumentation[6–9]. As will be shown later, in this case the fundamental quantities may be also expressed in terms of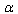 . Hereinafter we use a small dimensionless parameter
. Hereinafter we use a small dimensionless parameter 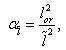 | (14) |
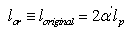 ,
,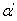 –dimensionless constant on the order of unity from GUP (2), and it is suggested that
–dimensionless constant on the order of unity from GUP (2), and it is suggested that 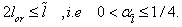 | (15) |
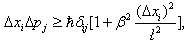 | (16) |
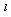 is the characteristic, large length scale
is the characteristic, large length scale 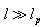 and
and 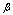 is a dimensionless real constant on the order of unity[14]. From EUP there is an absolute minimum in the momentum uncertainty:
is a dimensionless real constant on the order of unity[14]. From EUP there is an absolute minimum in the momentum uncertainty: 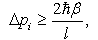 | (17) |
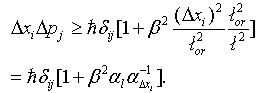 | (18) |
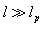
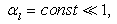 | (19) |
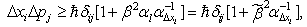 | (20) |
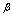 is redetermined as
is redetermined as 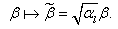 | (21) |
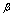 may be left as it is, whereas
may be left as it is, whereas 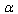 may be redetermined because
may be redetermined because 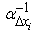 in (18),(20) is not a small parameter. In consequence we can redeterminate
in (18),(20) is not a small parameter. In consequence we can redeterminate 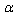 as
as 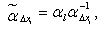 | (22) |
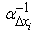 is now a small parameter.Owing to such a duality, EUP (16), (18) may be rewritten in terms of a new small parameter
is now a small parameter.Owing to such a duality, EUP (16), (18) may be rewritten in terms of a new small parameter 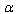 similar to
similar to 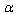 as follows:
as follows: 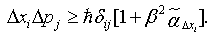 | (23) |
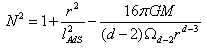 | (24) |
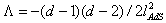 .Therewith the
.Therewith the 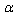 -representation of the Hawking temperature
-representation of the Hawking temperature 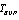 [14] (formula (15)) takes the form
[14] (formula (15)) takes the form 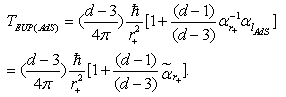 | (25) |
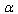 - representation of the Hawking temperature for a Schwarzshild-AdS black hole and for a combined case ((formula (28) from the[14])) of GUP and EUP – (GEUP)
- representation of the Hawking temperature for a Schwarzshild-AdS black hole and for a combined case ((formula (28) from the[14])) of GUP and EUP – (GEUP) 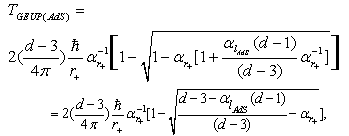 | (26) |
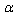 .Similarly, we can obtain the
.Similarly, we can obtain the  -representation for the corresponding value of
-representation for the corresponding value of  ((formula (32) from[14]) in the de Sitter (dS) space by the substitution
((formula (32) from[14]) in the de Sitter (dS) space by the substitution 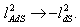 Note that, as it has been indicated in[33, 34],
Note that, as it has been indicated in[33, 34], 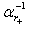 has one more interesting feature
has one more interesting feature 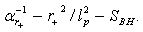 | (27) |
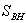 is the Bekenstein-Hawking semiclassical black hole entropy with the characteristic linear size
is the Bekenstein-Hawking semiclassical black hole entropy with the characteristic linear size 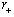 . For example, in the spherically symmetric case
. For example, in the spherically symmetric case 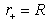 - radius of the corresponding sphere with the surface areaA, and
- radius of the corresponding sphere with the surface areaA, and 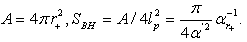 | (28) |
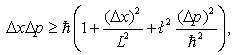 | (29) |
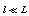 and
and 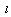 defines the limit of the UV-cutoff (not being such up to a constant factor as in the case of GUP).Then a minimal length is determined as
defines the limit of the UV-cutoff (not being such up to a constant factor as in the case of GUP).Then a minimal length is determined as 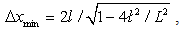 , whereas
, whereas 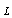 defines the limit for IR-cutoff i. e. we have a minimum momentum
defines the limit for IR-cutoff i. e. we have a minimum momentum 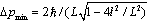 .And using the Euclidian action formalism by Gibbons and Hawking[42], in[15] the corresponding correction of the Hawking temperature for an ordinary(not A(dS)) Schwarzshild-black hole is computed. This correction is given as
.And using the Euclidian action formalism by Gibbons and Hawking[42], in[15] the corresponding correction of the Hawking temperature for an ordinary(not A(dS)) Schwarzshild-black hole is computed. This correction is given as 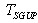 . In the notation of this work
. In the notation of this work 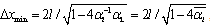 ,where
,where 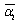 –small parameter introduced in conformity with (22). We can easily obtain the
–small parameter introduced in conformity with (22). We can easily obtain the 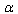 -representation for
-representation for 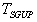 that is completely similar to the
that is completely similar to the 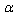 -representation of
-representation of 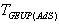 .It should be noted that in the realistic theories
.It should be noted that in the realistic theories 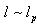 , and it is obvious that
, and it is obvious that 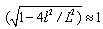 . Thus,
. Thus, 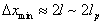 and hence in this case we get a minimal length that is much the same (to within
and hence in this case we get a minimal length that is much the same (to within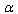 ) as in the case of GUP. It is seen that, with due regard for the requirement
) as in the case of GUP. It is seen that, with due regard for the requirement 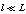 ,
, 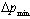 is derived close (to within
is derived close (to within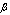 ) to
) to 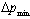 (17) in a theory with EUP.The question arises as to what for all these manipulations with writing and rewriting of the already derived expressions in the
(17) in a theory with EUP.The question arises as to what for all these manipulations with writing and rewriting of the already derived expressions in the 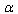 -representation are necessary.1. Owing to this procedure, we can draw the conclusion that all the quantities within the scope of the stated problem are dependent on one and the same deformation parameter
-representation are necessary.1. Owing to this procedure, we can draw the conclusion that all the quantities within the scope of the stated problem are dependent on one and the same deformation parameter 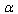 that is small, dimensionless (discrete in the case of GUP), and varying over the given interval. And, provided the infrared cutoff l is defined, we have
that is small, dimensionless (discrete in the case of GUP), and varying over the given interval. And, provided the infrared cutoff l is defined, we have 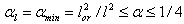 and
and 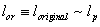 .If we primordially consider a theory with GUP only, then
.If we primordially consider a theory with GUP only, then 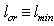 . But in the arbitrary case it is required that
. But in the arbitrary case it is required that 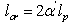 , where
, where 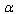 is a certain dimensionless constant on the order of unity.The property of discreteness is retained for
is a certain dimensionless constant on the order of unity.The property of discreteness is retained for 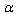 in the cases when only GUP (without generalizations)is valid because in this case the length seems to be quantized, the lengths being considered from
in the cases when only GUP (without generalizations)is valid because in this case the length seems to be quantized, the lengths being considered from 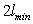 rather than from
rather than from 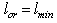 as a singularity arises otherwise[23–30].2. Actually, all the quantities may be represented as a Laurent series in terms of
as a singularity arises otherwise[23–30].2. Actually, all the quantities may be represented as a Laurent series in terms of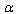 , and a solution of the problem at hand may be understood as finding of the members in this series.3. When the problem has separate solutions for the cases including the UV- and IR-cutoffs, we can consider expansion in each of the cases in terms of their own small parameters:
, and a solution of the problem at hand may be understood as finding of the members in this series.3. When the problem has separate solutions for the cases including the UV- and IR-cutoffs, we can consider expansion in each of the cases in terms of their own small parameters: 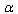 in the case of UV-cutoff and
in the case of UV-cutoff and 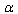 in the case of IR-cutoff, where
in the case of IR-cutoff, where 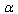 is a duality of
is a duality of 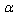
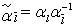 ,
,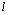 determines, to within a factor on the order of unity, the characteristic system’s size, and
determines, to within a factor on the order of unity, the characteristic system’s size, and 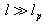 .
.3. The Cosmological Constant Problem and QFT with GUP and SGUP
- In this section it is assumed that
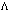 may be varying in time. Generally speaking,
may be varying in time. Generally speaking, 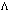 is referred to as a constant just because it is such in the equations, where it occurs: Einstein equations[43]. But in the last few years the dominating point of view has been that
is referred to as a constant just because it is such in the equations, where it occurs: Einstein equations[43]. But in the last few years the dominating point of view has been that 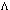 is actually a dynamic quantity, now weakly dependent on time[44–46]. It is assumed therewith that, despite the present-day smallness of
is actually a dynamic quantity, now weakly dependent on time[44–46]. It is assumed therewith that, despite the present-day smallness of 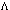 or even its equality to zero, nothing points to the fact that this situation was characteristics for the early Universe as well. Some recent results[47–50] are rather important pointing to a potentially dynamic character of
or even its equality to zero, nothing points to the fact that this situation was characteristics for the early Universe as well. Some recent results[47–50] are rather important pointing to a potentially dynamic character of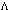 . Specifically, of great interest is the Uncertainty Principle derived in these works for the pair of conjugate variables
. Specifically, of great interest is the Uncertainty Principle derived in these works for the pair of conjugate variables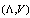 :
: 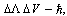 | (30) |
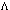 is the vacuum energy density (cosmological constant). It is a dynamic value fluctuating around zero;
is the vacuum energy density (cosmological constant). It is a dynamic value fluctuating around zero; 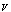 is the space-time volume. Here the volume of space-time
is the space-time volume. Here the volume of space-time 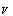 results from the Einstein-Hilbert action
results from the Einstein-Hilbert action 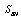 [48]:
[48]: 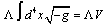 | (31) |
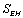 . In this case the notion of conjugation is well-defined, but approximate, as implied by the expansion about the static Fubini–Study metric (Section 6.1 of [47]). Unfortunately, in the proof per se (30), relying on the procedure with a non-linear and non-local Wheeler– de-Witt-like equation of the background-independent Matrix theory, some unconvincing arguments are used, making it insufficiently rigorous (Appendix 3 of[47]). But, without doubt, this proof has a significant result, though failing to clear up the situation.In [33, 34, 51] the Heisenberg Uncertainty Relation for the pair
. In this case the notion of conjugation is well-defined, but approximate, as implied by the expansion about the static Fubini–Study metric (Section 6.1 of [47]). Unfortunately, in the proof per se (30), relying on the procedure with a non-linear and non-local Wheeler– de-Witt-like equation of the background-independent Matrix theory, some unconvincing arguments are used, making it insufficiently rigorous (Appendix 3 of[47]). But, without doubt, this proof has a significant result, though failing to clear up the situation.In [33, 34, 51] the Heisenberg Uncertainty Relation for the pair 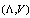 (30) has been generalized to GUP
(30) has been generalized to GUP 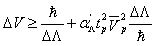 | (32) |
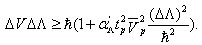 | (33) |
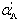 is a new constant and
is a new constant and 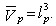 In the case of UV - limit:
In the case of UV - limit: 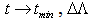 becomes significant
becomes significant 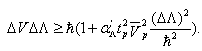 | (34) |
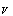 – spatial part of
– spatial part of 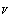 The existence of
The existence of 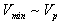 directly follows from GUP for the pair
directly follows from GUP for the pair 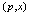 (2) and GUP for the pair
(2) and GUP for the pair 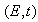 [24,30] as well as from solutions of the quadratic inequalities(32),(33).So, (32) is nothing else but
[24,30] as well as from solutions of the quadratic inequalities(32),(33).So, (32) is nothing else but 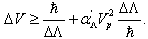 | (35) |
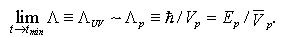 | (36) |
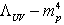 , in agreement with the value obtained using a standard (i.e. without super-symmetry and the like) quantum field theory[52,53]. Despite the fact that
, in agreement with the value obtained using a standard (i.e. without super-symmetry and the like) quantum field theory[52,53]. Despite the fact that 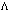 at Planck’s scales (referred to as
at Planck’s scales (referred to as 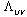 ) is also a dynamic quantity, it is not directly related to the familiar
) is also a dynamic quantity, it is not directly related to the familiar 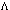 because the latter, as opposed to the first one, is derived from Einstein’s equations
because the latter, as opposed to the first one, is derived from Einstein’s equations 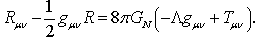 | (37) |
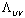 may be considered as some high-energy generalization (deformation) of the conventional cosmological constant in the low-energy limit.The problem is whether a correct generalization of GUP for the pair
may be considered as some high-energy generalization (deformation) of the conventional cosmological constant in the low-energy limit.The problem is whether a correct generalization of GUP for the pair 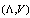 (33) to the Symmetric Generalized Uncertainty Principle (SGUP) of the form given by (29) is possible. If the answer is positive, a theory also includes
(33) to the Symmetric Generalized Uncertainty Principle (SGUP) of the form given by (29) is possible. If the answer is positive, a theory also includes 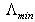 that may be referred to as
that may be referred to as 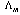 in similarity with
in similarity with 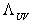 . Then, similar to Т (29), an additional term defining the IR-cutoff must be of the form
. Then, similar to Т (29), an additional term defining the IR-cutoff must be of the form 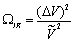 | (38) |
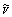 - certain space-time volume effectively specifying the IR-limit of the observable part of the Universe with the spatial part
- certain space-time volume effectively specifying the IR-limit of the observable part of the Universe with the spatial part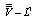 ;
; 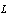 – radius of the observable part of the Universe. Now it is known that
– radius of the observable part of the Universe. Now it is known that 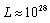 . Clearly, the introduction of an additional term of the form (38) into the right-hand side of (33) leads to
. Clearly, the introduction of an additional term of the form (38) into the right-hand side of (33) leads to  and might lead to the value of
and might lead to the value of 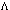 close to the experimental value
close to the experimental value 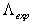 [54]. Note that the Holographic Principle[55–61] used to the Universe as a whole[61] gives
[54]. Note that the Holographic Principle[55–61] used to the Universe as a whole[61] gives 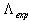 [60]. In[62,63,33,34] it has been demonstrated that the
[60]. In[62,63,33,34] it has been demonstrated that the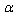 –representation (
–representation (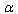 –deformation) of QFT with GUP plays a significant role. In particular, consider
–deformation) of QFT with GUP plays a significant role. In particular, consider 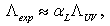 | (39) |
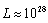 .(39) is like (22). But the Holographic Principle imposes strict restrictions on the number of degrees of freedom in the Universe, and hence for us it is important to study the inferences of introducing the additional term of the form (38) in (33).
.(39) is like (22). But the Holographic Principle imposes strict restrictions on the number of degrees of freedom in the Universe, and hence for us it is important to study the inferences of introducing the additional term of the form (38) in (33).4. GUP, EUP, and General Relativity Deformation
- In this Section we use the previously obtained results for some cases of high- energy and low-energy deformation of GR. Specifically, we demonstrate that in the cases when the Thermodynamics Approach[16–21] is applicable to the General Relativity the deformation of GR with GUP and EUP may be a natural result of the
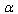 -representation.
-representation.4.1. 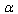 –Representation of Einstein’s Equations for Space with Horizon
–Representation of Einstein’s Equations for Space with Horizon
- Let us consider
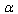 -representation and high energy
-representation and high energy 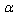 - deformation of the Einstein’s field equations for the specific cases of horizon spaces (the point (c) of Section 4). In so doing the results of the survey work ([20] p.p.41,42)are used. Then, specifically, for a static, spherically symmetric horizon in space-time described by the metric
- deformation of the Einstein’s field equations for the specific cases of horizon spaces (the point (c) of Section 4). In so doing the results of the survey work ([20] p.p.41,42)are used. Then, specifically, for a static, spherically symmetric horizon in space-time described by the metric 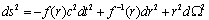 | (40) |
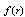 , at
, at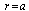 .It is known that for horizon spaces one can introduce the temperature that can be identified with an analytic continuation to imaginary time. In the case under consideration ([20], eq.(116))
.It is known that for horizon spaces one can introduce the temperature that can be identified with an analytic continuation to imaginary time. In the case under consideration ([20], eq.(116))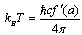 | (41) |
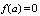 and
and 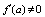 must be fulfilled. Then at the horizon
must be fulfilled. Then at the horizon 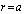 Einstein’s field equations
Einstein’s field equations 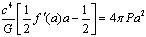 | (42) |
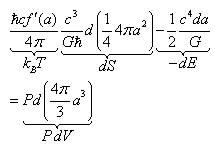 | (43) |
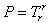 is the trace of the momentum-energy tensor and radial pressure. In the last equation
is the trace of the momentum-energy tensor and radial pressure. In the last equation 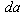 arises in the infinitesimal consideration of Einstein’s equations when studying two horizons distinguished by this infinitesimal quantity
arises in the infinitesimal consideration of Einstein’s equations when studying two horizons distinguished by this infinitesimal quantity 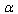 and
and 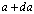 ([20] formula (118)).Now we consider (43) in a new notation, expressing
([20] formula (118)).Now we consider (43) in a new notation, expressing 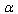 in terms of the corresponding deformation parameter
in terms of the corresponding deformation parameter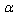 . Hereinafter in this Section we write
. Hereinafter in this Section we write 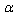 instead of
instead of 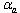 as we consider the same
as we consider the same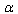 . Then we have
. Then we have 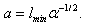 | (44) |
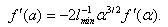 | (45) |
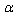 –representation" the following:
–representation" the following: 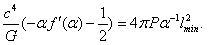 | (46) |
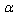 , we get
, we get 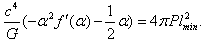 | (47) |
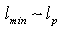 (that is just the case if the Generalized Uncertainty Principle (GUP) is satisfied), we have
(that is just the case if the Generalized Uncertainty Principle (GUP) is satisfied), we have 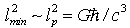 . When selecting a system of units, where
. When selecting a system of units, where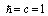 , we arrive at
, we arrive at 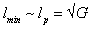 , and then (46) is of the form
, and then (46) is of the form 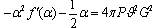 | (48) |
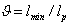 . L. h. s. of (48) is dependent on
. L. h. s. of (48) is dependent on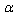 . Because of this, r. h. s. of (48) must be dependent on
. Because of this, r. h. s. of (48) must be dependent on 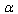 as well, i. e.
as well, i. e. 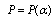 . Analysis of
. Analysis of 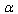 -Representation of Einstein’s Equations Now let us get back to (43). In[20] the low-energy case has been considered, for which ([20] p.42 formula (120))
-Representation of Einstein’s Equations Now let us get back to (43). In[20] the low-energy case has been considered, for which ([20] p.42 formula (120)) 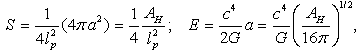 | (49) |
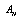 is the horizon area. In our notation (49) may be rewritten as
is the horizon area. In our notation (49) may be rewritten as 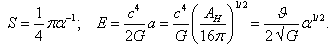 | (50) |
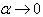 (LE), B)
(LE), B) 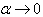 (HE)C)
(HE)C) 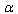 complies with the familiar scales and energies.The case of C) is of no particular importance as it may be considered within the scope of the conventional General Relativity.Indeed, in point A)
complies with the familiar scales and energies.The case of C) is of no particular importance as it may be considered within the scope of the conventional General Relativity.Indeed, in point A) 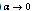 is not actually an exact limit as a real scale of the Universe (Infrared (IR)-cutoff
is not actually an exact limit as a real scale of the Universe (Infrared (IR)-cutoff 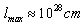 ), and then
), and then 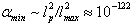 In this way A) is replaced by A1)
In this way A) is replaced by A1) 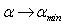 . In any case at low energies the second term in the left-hand side (48) may be neglected in the infrared limit. Consequently, at low energies (48) is written as
. In any case at low energies the second term in the left-hand side (48) may be neglected in the infrared limit. Consequently, at low energies (48) is written as 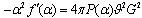 | (51) |
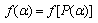 satisfying(51). In this case formulae (49) are valid as at low energies a semiclassical approximation is true. But from (51)it follows that
satisfying(51). In this case formulae (49) are valid as at low energies a semiclassical approximation is true. But from (51)it follows that 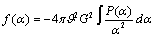 | (52) |
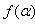 , we can obtain
, we can obtain 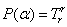 Possible High Energy
Possible High Energy 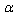 -Deformation of General Relativity Let us consider the high-energy case B). Here two variants are possible. I. First variant. In this case it is assumed that in the high-energy (Ultraviolet (UV))limit the thermodynamic identity (43) is retained but now all the quantities involved in this identity become
-Deformation of General Relativity Let us consider the high-energy case B). Here two variants are possible. I. First variant. In this case it is assumed that in the high-energy (Ultraviolet (UV))limit the thermodynamic identity (43) is retained but now all the quantities involved in this identity become 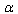 -deformed. This means that they appear in the
-deformed. This means that they appear in the 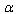 -representation with quantum corrections and are considered at high values of the parameter
-representation with quantum corrections and are considered at high values of the parameter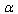 , i.e. at
, i.e. at 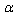 close to 1/4. In particular, the temperature T from equation (43) is changed by
close to 1/4. In particular, the temperature T from equation (43) is changed by 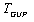 (9), the entropy S from the same equation given by semiclassical formula (49) is changed by
(9), the entropy S from the same equation given by semiclassical formula (49) is changed by 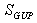 (13), and so forth:
(13), and so forth: 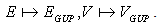 .Then the high-energy
.Then the high-energy 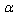 -deformation of equation (43) takes the form
-deformation of equation (43) takes the form 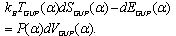 | (53) |
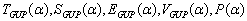 and expanding them into a Laurent series in terms of
and expanding them into a Laurent series in terms of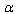 , close to high values of
, close to high values of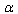 , specifically close to
, specifically close to 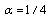 , we can derive a solution for the high energy
, we can derive a solution for the high energy 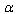 -deformation of general relativity (53) as a function of
-deformation of general relativity (53) as a function of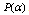 . As this takes place, provided at high energies the generalization of (43) to (53) is possible, we can have the high-energy
. As this takes place, provided at high energies the generalization of (43) to (53) is possible, we can have the high-energy 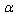 -deformation of the metric. Actually, as from (43) it follows that
-deformation of the metric. Actually, as from (43) it follows that 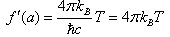 | (54) |
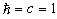 ), we get
), we get 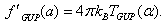 | (55) |
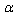 -representation. This means that, when
-representation. This means that, when 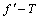 , we have
, we have 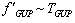 with the same factor of proportionality. In this case the function
with the same factor of proportionality. In this case the function 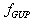 determining the high-energy
determining the high-energy 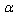 -deformation of the spherically symmetric metric may be in fact derived by the expansion of
-deformation of the spherically symmetric metric may be in fact derived by the expansion of 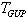 , that is known from (9), into a Laurent series in terms of
, that is known from (9), into a Laurent series in terms of 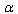 close to high values of
close to high values of 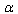 (specifically close to
(specifically close to 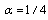 ), and by the subsequent integration.It might be well to remark on the following.1.1 As on going to high energies we use (GUP),
), and by the subsequent integration.It might be well to remark on the following.1.1 As on going to high energies we use (GUP), 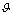 from equation (48)is expressed in terms of
from equation (48)is expressed in terms of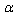 –dimensionless constant from GUP (2):
–dimensionless constant from GUP (2): 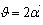 1.2 Of course, in all the formulae including
1.2 Of course, in all the formulae including 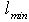 this quantity must be changed by
this quantity must be changed by 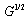 and hence
and hence 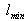 by
by 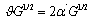 1.3 As noted in the end of subsection 6.1, and in this case also knowing all the high-energy deformed quantities
1.3 As noted in the end of subsection 6.1, and in this case also knowing all the high-energy deformed quantities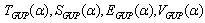 , we can find
, we can find 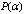 at
at 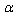 close to 1/4.1.4 Here it is implicitly understood that the Ultraviolet limit of Einstein’s equations is independent of the starting horizon space. This assumption is quite reasonable. Because of this, we use the well-known formulae for the modification of thermodynamics and statistical mechanics of black holes in the presence of GUP[36–39,14,15].1.5 The use of the thermodynamic identity (53) for the description of the high energy deformation in General Relativity implies that on going to the UV-limit of Einstein’s equations for horizon spaces in the thermodynamic representation (consideration) we are trying to remain within the scope of equilibrium statistical mechanics[64] (equilibrium thermodynamics)[65]. However, such an assumption seems to be too strong. But some grounds to think so may be found as well. Among other things, of interest is the result from[36] that GUP may prevent black holes from their total evaporation. In this case the Planck’s remnants of black holes will be stable, and when they are considered, in some approximation the equilibrium thermodynamics should be valid. At the same time, by author’s opinion these arguments are rather weak to think that the quantum gravitational effects in this context have been described only within the scope of equilibrium thermodynamics[65].According to the remark of 4.1.5, it is assumed that the interpretation of Einstein’s equations as a thermodynamic identity (43) is not retained on going to high energies (UV–limit), i.e. at
close to 1/4.1.4 Here it is implicitly understood that the Ultraviolet limit of Einstein’s equations is independent of the starting horizon space. This assumption is quite reasonable. Because of this, we use the well-known formulae for the modification of thermodynamics and statistical mechanics of black holes in the presence of GUP[36–39,14,15].1.5 The use of the thermodynamic identity (53) for the description of the high energy deformation in General Relativity implies that on going to the UV-limit of Einstein’s equations for horizon spaces in the thermodynamic representation (consideration) we are trying to remain within the scope of equilibrium statistical mechanics[64] (equilibrium thermodynamics)[65]. However, such an assumption seems to be too strong. But some grounds to think so may be found as well. Among other things, of interest is the result from[36] that GUP may prevent black holes from their total evaporation. In this case the Planck’s remnants of black holes will be stable, and when they are considered, in some approximation the equilibrium thermodynamics should be valid. At the same time, by author’s opinion these arguments are rather weak to think that the quantum gravitational effects in this context have been described only within the scope of equilibrium thermodynamics[65].According to the remark of 4.1.5, it is assumed that the interpretation of Einstein’s equations as a thermodynamic identity (43) is not retained on going to high energies (UV–limit), i.e. at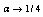 , and the situation is adequately described exclusively by non-equilibrium thermodynamics [65,66]. Naturally, the question arises: which of the additional terms introduced in (43) at high energies may be leading to such a description?In the[51,33] it has been shown that in case the cosmological term
, and the situation is adequately described exclusively by non-equilibrium thermodynamics [65,66]. Naturally, the question arises: which of the additional terms introduced in (43) at high energies may be leading to such a description?In the[51,33] it has been shown that in case the cosmological term 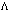 is a dynamic quantity, it is small at low energies and may be sufficiently large at high energies. In the right-hand side of (48) in the
is a dynamic quantity, it is small at low energies and may be sufficiently large at high energies. In the right-hand side of (48) in the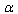 –representation the additional term
–representation the additional term 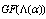 is introduced:
is introduced: 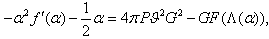 | (56) |
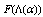 we denote the term including
we denote the term including 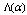 as a factor. Then its inclusion in the low-energy case (42)(or in the
as a factor. Then its inclusion in the low-energy case (42)(or in the 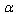 -representation (48)) has actually no effect on the thermodynamic identity (43)validity, and consideration within the scope of equilibrium thermodynamics still holds true. It is well known that this is not the case at high energies as the
-representation (48)) has actually no effect on the thermodynamic identity (43)validity, and consideration within the scope of equilibrium thermodynamics still holds true. It is well known that this is not the case at high energies as the 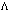 -term may contribute significantly to make the "process" non-equilibrium in the end[65,66].Is this the only cause for violation of the thermodynamic identity (43) as an interpretation of the high-energy generalization of Einstein’s equations? Further investigations are required to answer this question.
-term may contribute significantly to make the "process" non-equilibrium in the end[65,66].Is this the only cause for violation of the thermodynamic identity (43) as an interpretation of the high-energy generalization of Einstein’s equations? Further investigations are required to answer this question.4.2.α–Representation for Friedmann Equations with GUP and EUP
- Thermodynamic interpretation of Section 4 has been also developed for Friedmann Equations (FEs) of the Friedmann- Robertson-Walker (FRW) Universe in[21]. In the process it is taken into consideration that in the FRW space-time, where the metric is given by the formula
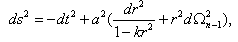 | (57) |
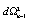 denotes a line element of the (
denotes a line element of the (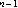 )-dimensional unit sphere,
)-dimensional unit sphere, 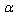 is the scale factor, kis the spatial curvature constant, there is a dynamic apparent horizon, the radius of which is as follows:
is the scale factor, kis the spatial curvature constant, there is a dynamic apparent horizon, the radius of which is as follows: 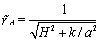 | (58) |
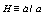 is the Hubble parameter.FEs in[21] have been derived proceeding from the assumption that apparent horizon is endowed with the associated entropy and temperature such the event horizon in the black hole case
is the Hubble parameter.FEs in[21] have been derived proceeding from the assumption that apparent horizon is endowed with the associated entropy and temperature such the event horizon in the black hole case 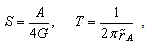 | (59) |
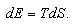 | (60) |
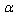 –representation. For simplicity, let us consider the case
–representation. For simplicity, let us consider the case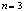 .Then for GUP the formula (26) from[67] takes the form
.Then for GUP the formula (26) from[67] takes the form 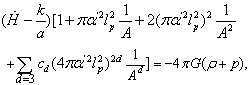 | (61) |
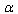 –representation its form is more elegant
–representation its form is more elegant 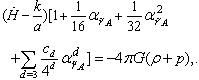 | (62) |
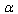 –representation of the second Friedmann Equation (formula (27) from [67])
–representation of the second Friedmann Equation (formula (27) from [67]) 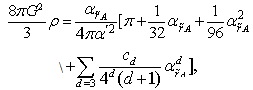 | (63) |
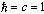 .It is obvious that therewith familiar FEs appear at low energies, i.e. at
.It is obvious that therewith familiar FEs appear at low energies, i.e. at 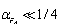 .In the nontrivial high-energy case one can obtain the solution for FE and, in particular
.In the nontrivial high-energy case one can obtain the solution for FE and, in particular 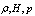 as a series in terms of
as a series in terms of 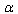 close to 1/4.In the case of EUP the
close to 1/4.In the case of EUP the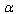 –representation of the deformed FE[67] seems to be even simpler. Specifically, using (18) – (23), one can derive deformed first Friedmann equation of the form
–representation of the deformed FE[67] seems to be even simpler. Specifically, using (18) – (23), one can derive deformed first Friedmann equation of the form 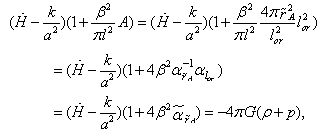 | (64) |
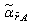 is small.In a similar way we can obtain the
is small.In a similar way we can obtain the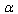 –representation of the EUP-deformation for the second Friedmann equation.
–representation of the EUP-deformation for the second Friedmann equation.5. Some Comments and Problems of Interest
- In this Section some comments are given and some problems are stated.С1. The Laurent series expansion in terms of
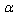 is asymmetric for UV and IR cutoffs. Indeed, as in the general case the variability domain
is asymmetric for UV and IR cutoffs. Indeed, as in the general case the variability domain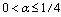 , in the UV-cutoff when
, in the UV-cutoff when 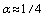 the contribution is made by
the contribution is made by 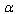 -terms both with positive and with negative powers, while in the IR-cutoff (
-terms both with positive and with negative powers, while in the IR-cutoff (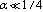 ) only the
) only the 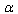 -terms with negative powers will be significant.C2. The external constant
-terms with negative powers will be significant.C2. The external constant 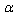 in the cases, where
in the cases, where 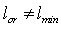 (EUP or SGUP is the case), is not found in the final expressions, being reduced due to the substitution of (22).Several questions remain to be answered and necessitate further investigations.Q1) How far the
(EUP or SGUP is the case), is not found in the final expressions, being reduced due to the substitution of (22).Several questions remain to be answered and necessitate further investigations.Q1) How far the 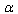 -representation may be extended for the General Relativity? As shown in this work, such a representation exists for the General Relativity at High and Low Energies when the Thermodynamic Approach[16–21] is applicable or, that is the same, the Thermodynamic Interpretation is the case. It is interesting whether the extension of the
-representation may be extended for the General Relativity? As shown in this work, such a representation exists for the General Relativity at High and Low Energies when the Thermodynamic Approach[16–21] is applicable or, that is the same, the Thermodynamic Interpretation is the case. It is interesting whether the extension of the 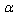 -representation to the general case both at High and Low Energies is possible. The problem is whether, in some or other way, the general case may be reduced to the well-known ones.Q2) Considering Q1), for High Energy the problem is whether there is an effective description of the space-time foam [68–70] in terms of
-representation to the general case both at High and Low Energies is possible. The problem is whether, in some or other way, the general case may be reduced to the well-known ones.Q2) Considering Q1), for High Energy the problem is whether there is an effective description of the space-time foam [68–70] in terms of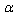 . The results of[71] suggest that such a description should be existent.Q3) Proceeding from the results of E. Verlinde[72], the problem is whether the High-Energy deformation of the Entropic Force is obtainable. Provided the answer of Q1) positive, the problem concerns the form of this deformation in terms of
. The results of[71] suggest that such a description should be existent.Q3) Proceeding from the results of E. Verlinde[72], the problem is whether the High-Energy deformation of the Entropic Force is obtainable. Provided the answer of Q1) positive, the problem concerns the form of this deformation in terms of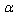 : we must find its
: we must find its 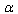 -representation.Note that the notion of Entropic Force, however, without the introduction of the term per se has been proposed by T. Padmanabhan in Conclusion of his paper[73] earlier than by E. Verlinde.
-representation.Note that the notion of Entropic Force, however, without the introduction of the term per se has been proposed by T. Padmanabhan in Conclusion of his paper[73] earlier than by E. Verlinde.6. Conclusions
- The essence of the principal result obtained in this work may be stated as follows. In the cases when Einstein equations have an explicit thermodynamic interpretation, their limiting transition to UV and IR cutoffs may be described within the scope of the same dimensionless deformation parameter that is naturally introduced in a quantum field theory with the fundamental length. In the case the problems stated in the previous Section will be solved positively, the small dimensionless discrete parameter
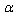 must be at once introduced in Нigh-Energy Thermodynamics and Gravity, without its appearance in the low-energy limit at the scales under study. At the same time, at large scales GR has not been subjected to verification too [74]. The availability of Dark Matter and Dark Energy is a strong motivation for the IR-modification of GR [75–77]. The deformation of the General Relativity due to EUP seems to be one of the IR-modifications of Gravity possible. In this case an analysis of such a deformation in terms of the parameter
must be at once introduced in Нigh-Energy Thermodynamics and Gravity, without its appearance in the low-energy limit at the scales under study. At the same time, at large scales GR has not been subjected to verification too [74]. The availability of Dark Matter and Dark Energy is a strong motivation for the IR-modification of GR [75–77]. The deformation of the General Relativity due to EUP seems to be one of the IR-modifications of Gravity possible. In this case an analysis of such a deformation in terms of the parameter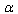 , of the corresponding variability domain, and the like may be important for studies of the IR-modified (IR-deformed) General Relativity.
, of the corresponding variability domain, and the like may be important for studies of the IR-modified (IR-deformed) General Relativity.Acknowledgments
- I am grateful to Prof. Sabine Hossenfelder (Stockholm, Sweden) for the information about a number of interesting works in the field of physics at Planck’s scales and for her support that has stimulated my research efforts. Besides, I would like to thank Prof. Rong-Jia Yang (Baoding, China) for his support.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML