Wladimir Belayev
Center for Relativity and Astrophysics, 185 Box, 194358, Saint-Petersburg, Russia
Correspondence to: Wladimir Belayev, Center for Relativity and Astrophysics, 185 Box, 194358, Saint-Petersburg, Russia.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
We consider variation of energy of the light-like particle in the pseudo-Riemann space-time, find lagrangian, canonical momenta and forces. Equations of the critical curve are obtained by the nonzero energy integral variation in accordance with principles of the calculus of variations in mechanics. This method is compared with the Fermat's principle for the stationary gravity field. The produced equations are solved for the metrics of Schwarzschild, FLRW model for the flat space and Gödel. For these spaces effective mass of light-like particle is established. Relativistic analogue of inertial mass for photon is determined in central gravity field in empty space.
Keywords:
variational methods, energy integral, light-like particle, canonical momenta and forces, Fermat's principle
Cite this paper: Wladimir Belayev, Application of Lagrange Mechanics for Analysis of the Light-Like Particle Motion in Pseudo-Riemann Space, International Journal of Theoretical and Mathematical Physics, Vol. 2 No. 2, 2012, pp. 10-15. doi: 10.5923/j.ijtmp.20120202.03.
1. Introduction
One of postulates of general relativity is claim that in gravity field in the absence of other forces the word lines of the material particles and the light rays are geodesics. In differential geometry a geodesic line in case of not null path is defined as a curve, whose tangent vector is parallel propagated along itself[1]. The differential equations of geodesic can be found also by the variation method as a path of extremal length with the aid of the virtual displacements of coordinates 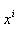 on a small quantity
on a small quantity 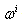 . When we add variation to coordinate of the material particle, the time-like interval slow changes, though that leaves it time-like.Finding of the differential equations of the null geodesic, corresponding to the light ray motion, by calculus of variations is described in[2]. In space-time with metrical coefficients
. When we add variation to coordinate of the material particle, the time-like interval slow changes, though that leaves it time-like.Finding of the differential equations of the null geodesic, corresponding to the light ray motion, by calculus of variations is described in[2]. In space-time with metrical coefficients 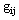 it is considered variation of the first integral of these equations
it is considered variation of the first integral of these equations 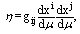 | (1) |
where µ is affine parameter. Deriving variation for extremum determination we must admit arbitrary small displacements of coordinates. The variation of integral of 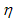 expanded in multiple Taylor series is written as (see eq2) where
expanded in multiple Taylor series is written as (see eq2) where 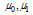 are values of the affine parameter in points, which are linked by found geodesic. The sum of terms containing variations
are values of the affine parameter in points, which are linked by found geodesic. The sum of terms containing variations 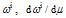 in first power is equated to null. Under condition
in first power is equated to null. Under condition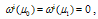 this leads to the geodesic equations in form
this leads to the geodesic equations in form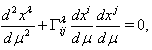 | (3) |
where 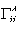 are Christoffel symbols: Here a comma denotes partial differentiation.The other terms of series in (2), containing variations of coordinates and their derivatives by
are Christoffel symbols: Here a comma denotes partial differentiation.The other terms of series in (2), containing variations of coordinates and their derivatives by 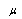 in more high powers or their products and being able to have nonzero values, don't take into account. Thus such method admits violation of the condition
in more high powers or their products and being able to have nonzero values, don't take into account. Thus such method admits violation of the condition 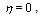 which means that with certain coordinates variations the interval a prior becomes time-like or space-like. Since this interval accords with the light ray motion, one leads to the Lorentz-invariance violation in locality, namely, anisotropies.It is shown for the massive particle[5] that a fundamental space-time discreteness need not contradict Lorentz invariance, and causal set's discreteness is in fact locally Lorentz invariant. The possibility of Lorentz symmetry break for the photon in vacuum by effects from the Plank scale is studied in[3,4]. However, experiments[6] show exceptionally high precision of constancy of the light speed confirmed a Lorentz symmetry in locality, and astrophysical tests don't detect isotropic Lorentz violation[4].In the method of calculus of variations in the large[7] ones are considered as possible paths along the manifold disregarding kind of interval, not as the trajectories of physical particles. This approach exceeds the limits of classical variational principle in mechanics, according as which virtual motions of the system are compared with cinematically possible motions.
which means that with certain coordinates variations the interval a prior becomes time-like or space-like. Since this interval accords with the light ray motion, one leads to the Lorentz-invariance violation in locality, namely, anisotropies.It is shown for the massive particle[5] that a fundamental space-time discreteness need not contradict Lorentz invariance, and causal set's discreteness is in fact locally Lorentz invariant. The possibility of Lorentz symmetry break for the photon in vacuum by effects from the Plank scale is studied in[3,4]. However, experiments[6] show exceptionally high precision of constancy of the light speed confirmed a Lorentz symmetry in locality, and astrophysical tests don't detect isotropic Lorentz violation[4].In the method of calculus of variations in the large[7] ones are considered as possible paths along the manifold disregarding kind of interval, not as the trajectories of physical particles. This approach exceeds the limits of classical variational principle in mechanics, according as which virtual motions of the system are compared with cinematically possible motions.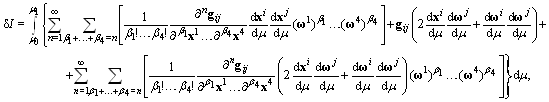 | (2) |
Approximating time-like interval conforming in general relativity to the material particle motion between fixed points to null leads in physical sense to unlimited increase of its momentum, and the space-like interval doesn't conform to move of any object. In this connection it should pay attention on speculation that discreteness at the Planck scale reveals maximum value of momentum for the fundamental particles [8].The geodesic line must be extremal[1], and the test particle moves along it only in the absence of non-gravity forces. Should photon have some rest mass variations of its path don't give different kinds of intervals, but this assumption doesn't confirm by experiments[9]. We examine choosing of energy so in order that application of variational principle to its integral for deriving of the isotropic critical curves equations would not lead to considering non-null paths.
2. Definition of Energy and Its Variation
The interval in pseudo-Riemann space-time with metrical coefficients 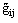 :
: 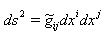 | (5) |
after substitutions 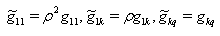 | (6) |
is rewritten in form  | (7) |
Here,  is some quantity, which is assumed to be equal 1. Putting down
is some quantity, which is assumed to be equal 1. Putting down  as time, coordinates with indexes
as time, coordinates with indexes  as space coordinates and considering
as space coordinates and considering 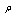 as energy of light-like particle with
as energy of light-like particle with 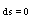 [10] we present it as
[10] we present it as 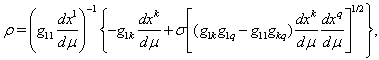 | (8) |
where 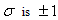 .Indexes except
.Indexes except 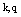 take values 1 to 4. With denotation of the velocity four-vector components as
take values 1 to 4. With denotation of the velocity four-vector components as 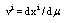 energy variation will be
energy variation will be 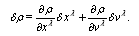 | (9) |
After substitution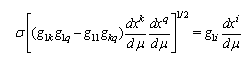 | (10) |
the partial derivatives withresect to coordinates are writtens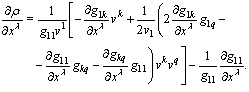 | (11) |
This expression is reduced to 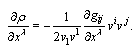 | (12) |
The partial derivatives with respect to components of the velocity four-vector are 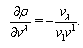 | (13) |
For the particle, moving in empty space, lagrangian is taken in form 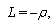 | (14) |
and conforms to relation[11]: 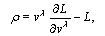 | (15) |
which is integral of the motion. Obtained derivatives give the canonical momenta 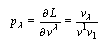 | (16) |
and forces 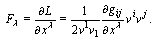 | (17) |
Components of the associated vector of the canonical momenta are 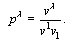 | (18) |
Units is chosen so that a light velocity constant is 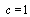 . Components of energy-momentum four-vector of photon in Minkowski space are proportional to four-velocities:
. Components of energy-momentum four-vector of photon in Minkowski space are proportional to four-velocities: 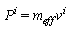 with coefficient of proportionality
with coefficient of proportionality 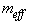 , which is effective mass. It is represented as
, which is effective mass. It is represented as 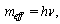 | (19) |
where h is Planck constant and v is frequency of photon. Normalized effective mass of light-like particle in pseudo-Riemannian space-time is defined as coefficient of proportionality between components of the vectors of canonical momenta and the four-velocities with raised indices. It becomes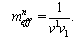 | (20) |
With coefficient of normalization 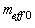 it can be expressed in terms of effective mass as
it can be expressed in terms of effective mass as 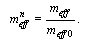 | (21) |
3. Equations of Isotropic Critical Curve
Motion equations are found from variation of energy integral 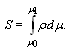 | (22) |
Energy 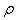 is non-zero, its variations leave interval to be light-like, and application of standard variational procedure yields Euler-Lagrange equations
is non-zero, its variations leave interval to be light-like, and application of standard variational procedure yields Euler-Lagrange equations 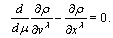 | (23) |
Critical curve equations are obtained by substitution of partial derivatives (12) and (13) in these equations. For derivative of the first component of four-velocity vector we have 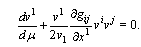 | (24) |
For finding of other three equations of motion the second term of (23) is presented in form 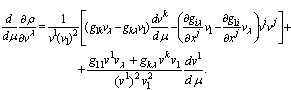 | (25) |
Replacement of derivative 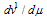 here on its expression, obtained from (24), and substitution found terms in Euler- Lagrange equations gives
here on its expression, obtained from (24), and substitution found terms in Euler- Lagrange equations gives 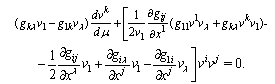 | (26) |
These equations contain accelerations corresponded to the space coordinates and describe coupled with (24) the motion of the test light-like particle along critical curve. They don't coincide to usual form (3) of the null geodesics equations.Let us clear whether proposed variational method conforms to Fermat's principle for stationary gravity field[1], which is formulated as follows 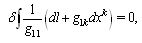 | (27) |
where 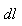 is element of spatial distance along the ray
is element of spatial distance along the ray 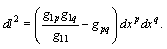 | (28) |
Denoting 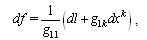 | (29) |
and comparing this expression with (8) we write 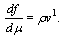 | (30) |
Therefore, variation (27) is equivalent to variation of integral 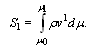 | (31) |
The Euler-Lagrange equation, corresponded to the time coordinate, will be 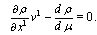 | (32) |
Since metrical coefficients in case of the stationary field doesn't depend on the time, we have 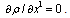 The value of
The value of 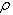 is constant. Thus, expression (32) is idential equation.Equations for the space coordinates are follows:
is constant. Thus, expression (32) is idential equation.Equations for the space coordinates are follows: 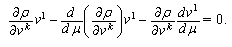 | (33) |
We condition by appropriate choice of the affine parameter 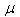 the constant value of
the constant value of 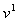 . Then, the third term in the left part of equations will be vanishing and they shall be identical to (23).For the static gravity field the Fermat's principle gives solution, which conforms to geodesics[12].
. Then, the third term in the left part of equations will be vanishing and they shall be identical to (23).For the static gravity field the Fermat's principle gives solution, which conforms to geodesics[12].
4. Photon's Dynamics in Schwarzschild Space-Time
A centrally symmetric gravity field in the free space is described by the Schwarzschild metric. At spherical coordinates 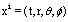 its line element is
its line element is 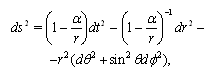 | (34) |
where 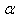 is constant.For this space we find equations of the critical curve of the integral energy
is constant.For this space we find equations of the critical curve of the integral energy 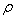 . The canonical momenta (16) for the cyclic coordinates
. The canonical momenta (16) for the cyclic coordinates 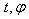 are the constants of motion
are the constants of motion 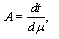 | (35) |
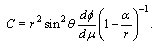 | (36) |
Equations (26) for coordinates 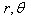 give
give 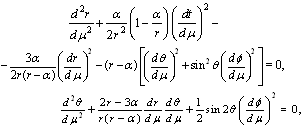 | (38) |
Metric (34) for the isotropic curve yields 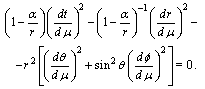 | (39) |
Assuming that 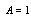 and considering motion in plane
and considering motion in plane 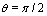 we write derivatives of the cyclic coordinates
we write derivatives of the cyclic coordinates 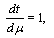 | (40) |
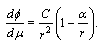 | (41) |
Substituting these values in equation (39) we find 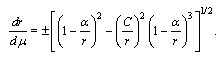 | (42) |
Found velocities coincide with solutions of the null geodesic equations for the Schwarzschild space-time[2] to within parameter of differentiation 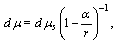 | (43) |
where 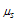 corresponds to geodesic equations.The canonical momenta (16) and forces (17) are
corresponds to geodesic equations.The canonical momenta (16) and forces (17) are 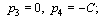 | (44) |
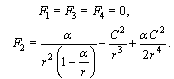 | (45) |
Nonzero components of vector of the canonical momenta with raised indices are 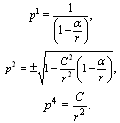 | (46) |
It follows from Eq. (20) that normalized effective mass of photon in the central gravity field changes as 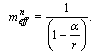 | (47) |
A nonzero component of vector of the canonical forces with raised indices is 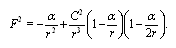 | (48) |
In so far as with gravitational constant G and mass M the Newtonian limit of gravity theory requires 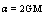 , the first term of
, the first term of 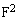 yields twice gravity force. One conforms to the light deflection in central gravity field [13], which is twice value being given by the gravity theory.Substituting components of the velocity four-vector in Eq. (37) we obtain radial the acceleration
yields twice gravity force. One conforms to the light deflection in central gravity field [13], which is twice value being given by the gravity theory.Substituting components of the velocity four-vector in Eq. (37) we obtain radial the acceleration 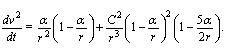 | (49) |
A second Newton Law states that massive body under action of the force 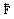 experiences acceleration
experiences acceleration 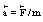 , where m is its inertial mass. By analogy normalized inertial mass of photon is found as ratio of the canonical force F2 to the radial acceleration
, where m is its inertial mass. By analogy normalized inertial mass of photon is found as ratio of the canonical force F2 to the radial acceleration 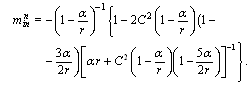 | (50) |
With rα≥α2,C2, this yields 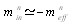 . Thus, excepting area, where signs of F2 and
. Thus, excepting area, where signs of F2 and 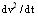 are identical or one of these quantities is equal to 0, inertial mass of photon is negative, i. e. it experiences antigravirational influence[14].
are identical or one of these quantities is equal to 0, inertial mass of photon is negative, i. e. it experiences antigravirational influence[14].
5. Extremal Isotropic Curves in FLRW Space-Time
The FLRW cosmological model for the flat space with rectangular coordinates 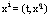 is described by metric
is described by metric 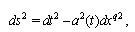 | (51) |
where 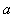 is the length scale factor.Equation (24) gives
is the length scale factor.Equation (24) gives 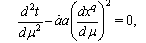 | (52) |
where overdot denotes derivative with respect to time. The Euler-Lagrange equations for the cyclic coordinates 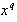 yield constants of motion
yield constants of motion 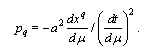 | (53) |
Having extracted derivatives with respect to the space-like coordinates from this equation and substituting them in (52) we obtain 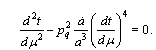 | (54) |
This equation has solution, which with denotation 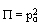 is written in form
is written in form 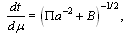 | (55) |
where 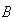 is constant. Substitution found first component of the four-velocity vector in equation (53) gives
is constant. Substitution found first component of the four-velocity vector in equation (53) gives 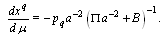 | (56) |
The condition, following from Eq. (51): 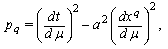 | (57) |
corresponds to isotropic curve. It yields 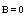 and components of the four-velocity vector turn out to
and components of the four-velocity vector turn out to 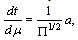 | (58) |
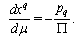 | (59) |
They conform to solution of equations of the null geodesics for the FLRW space-time[2].The canonical momenta of the light-like particle are 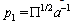 | (60) |
and constant 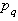 . The canonical forces are
. The canonical forces are 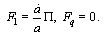 | (61) |
Their associated values is written as 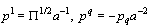 | (62) |
and 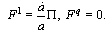 | (63) |
Normalized effective mass of the photon in the flat space is 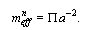 | (64) |
Assumed that at present time t0 the length scale factor is 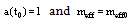 we obtain, taking into account Eq. (21), follows:
we obtain, taking into account Eq. (21), follows: 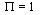 | (65) |
and 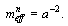 | (66) |
6. Extremal Isotropic Curves in Gödel Space-Time
The stationary solution of the Einstein's field equation with cosmological constant found by Gödel describes gravity field of the rotating uniform dust matter. With coordinates 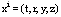 the line element is written in form
the line element is written in form 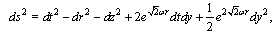 | (67) |
where 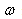 is constant.The canonical momenta (16) for cyclic coordinates
is constant.The canonical momenta (16) for cyclic coordinates 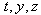 are the constants of motion. They are written in form
are the constants of motion. They are written in form 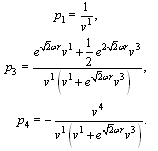 | (68) |
These equations with following from Eq. (67) condition 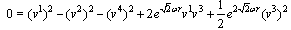 | (69) |
yield components of the four-velocity vector: 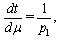 | (70) |
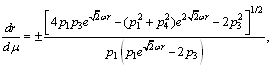 | (71) |
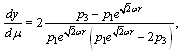 | (72) |
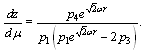 | (73) |
With 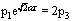 the singularity takes place.The obtained equations differ from the solution of the null geodesics equations in the Gödel 's space-time[15].The canonical momentum corresponding to coordinate
the singularity takes place.The obtained equations differ from the solution of the null geodesics equations in the Gödel 's space-time[15].The canonical momentum corresponding to coordinate 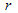 is
is 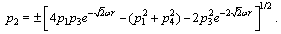 | (74) |
Canonical forces have values 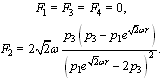 | (75) |
Associated canonical momentum and forces are 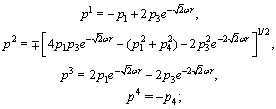 | (76) |
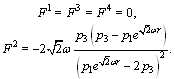 | (77) |
Normalized effective mass of the light-like particle in the Gödel space-time is 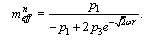 | (78) |
7. Conclusions
The proposed form of energy allows applying of the Lagrange's mechanics for analysis of the light-like particle motion. Considered procedure of production of the motion equations by variation of the energy integral conforms to principles of the calculus of variations in the classic mechanics in accordance with which the motion variations must be cinematically admissible for the system. The virtual displacements of coordinates retain path of the light-like particle to be null in the pseudo-Riemann space-time, i.e. not lead to the Lorentz-invariance violation in locality. For the stationary gravity field the equations, obtained by this method, agrees with result given by the Fermat's principle. Their solutions for the Schwarzschild metric being static and for the Friedmann-Lemaitre-Robertson-Walker metric for the flat space coincide with solutions of the null geodesics equations to within appropriate parameter. For the Gödel 's space-time these solutions are different.Normalized effective mass of light-like particle is defined as coefficient of proportionality between canonical momenta and components of four-velocity vector. Analog of 's inertial mass for photon in Schwarzschild's space-time has negative value for newtonian limit of gravity.
ACKNOWLEDGEMENTS
I acknowledge J. Foukzon, I. Sivcov and A. Beshenkov for useful discussion.
References
| [1] | L.D. Landau and E.M. Lifshitz, Classical Theory of Fields, Fourth Revised English Edition, Oxford: Pergamon, 1975. |
| [2] | G.C. McVittie, General Relativity and Cosmology, London, Chapman and Hall Ltd., 1956. |
| [3] | A. Kostelecky and A. Pickering, Vacuum Photon Splitting in Lorentz-Violating Quantum Electrodynamics, Phys. Rev. Lett. 91 (2003) 031801, hep-ph/0212382; T. Jacobson, S. Liberati, D. Mattingly, F.W. Stecker, New limits on Planck scale Lorentz violation in QED, Phys.Rev.Lett. 93 (2004) 021101, astro-ph/0309681. |
| [4] | A. Kostelecky, M. Mewes, Astrophysical Tests of Lorentz and CPT Violation with Photons, Astrophys.J.689 (2008) L1-L4, arXiv:0809.2846. |
| [5] | F. Dowker, J. Henson, R. D. Sorkin, Quantum Gravity Phenomenology, Lorentz Invariance and Discreteness, Mod. Phys.Lett. A19 (2004) 1829-1840, gr-qc/0311055; L. Bombelli, J. Henson, R. D. Sorkin, Discreteness without symmetry breaking: a theorem, gr-qc/0605006. |
| [6] | H. Mueller et al. Relativity tests by complementary rotating Michelson-Morley experiments, Phys.Rev.Lett. 99 (2007) 050401, arXiv: 0706.2031; P. L. Stanwix et al. Improved test of Lorentz Invariance in Electrodynamics using Rotating Cryogenic Sapphire Oscillators, Phys.Rev. D74 (2006) 081101, gr-qc/0609072; Antonini et al. Test of constancy of speed of light with rotating cryogenic optical resonators, Phys. Rev. A. 71 (2005) 050101. |
| [7] | M. Morse, The Calculus of Variations in the Large, Colloquium Publications of the American Mathematical Society, vol. 18. New York, 1934. |
| [8] | G. Amelino-Camelia, Doubly Special Relativity, Nature 418 (2002) 34-35, gr-qc/0207049; J. Magueijo and L. Smolin, Lorentz invariance with an invariant energy scale, Phys. Rev. Lett. 88 (2002) 190403, hep-th/0112090. |
| [9] | A.S. Goldhaber and M.M. Nieto, Photon and Graviton Mass Limits, ArXiv:0809.1003. |
| [10] | W.B. Belayev, Variation of the light-like particle energy and its critical curve equations, arXiv:0806.3350. |
| [11] | L.D. Landau and E.M. Lifshitz, Vol. 1. Mechanics, 3ed., Oxford: Pergamon, 1976. |
| [12] | W. Pauli, Theory of relativity, Dover Publications, Inc., 1981. |
| [13] | A. Einstein, Die Grundlage der allgemainen Relativitätstheorie, Ann. Phys. 49 (1916) 769-822. |
| [14] | W.B. Belayev, Effective and Inertial Masses of a Photon Near a Blac Hole for a Family of Envelope Orbits, Wolfram Demonstrations Project, 2011, http://demonstrations.wolfram. com/EffectiveAndInertialMassesOfAPhotonNearABlackHoleForAFamilyO/. |
| [15] | G. Dautcourt, M. Abdel-Megied, Revisiting the Light Cone of the Gödel Universe, Class.Quant.Grav. 23 (2006) 1269-1288, gr-qc/0511015; G. Dautcourt, The lightcone of Gödel-like spacetimes, Class.Quant.Grav.27 (2010) 225024, arXiv: 1009.5231. |

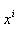 on a small quantity
on a small quantity 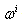 . When we add variation to coordinate of the material particle, the time-like interval slow changes, though that leaves it time-like.Finding of the differential equations of the null geodesic, corresponding to the light ray motion, by calculus of variations is described in[2]. In space-time with metrical coefficients
. When we add variation to coordinate of the material particle, the time-like interval slow changes, though that leaves it time-like.Finding of the differential equations of the null geodesic, corresponding to the light ray motion, by calculus of variations is described in[2]. In space-time with metrical coefficients 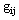 it is considered variation of the first integral of these equations
it is considered variation of the first integral of these equations 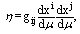
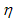 expanded in multiple Taylor series is written as (see eq2) where
expanded in multiple Taylor series is written as (see eq2) where 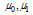 are values of the affine parameter in points, which are linked by found geodesic. The sum of terms containing variations
are values of the affine parameter in points, which are linked by found geodesic. The sum of terms containing variations 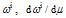 in first power is equated to null. Under condition
in first power is equated to null. Under condition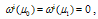 this leads to the geodesic equations in form
this leads to the geodesic equations in form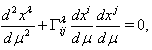
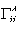 are Christoffel symbols: Here a comma denotes partial differentiation.The other terms of series in (2), containing variations of coordinates and their derivatives by
are Christoffel symbols: Here a comma denotes partial differentiation.The other terms of series in (2), containing variations of coordinates and their derivatives by 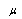 in more high powers or their products and being able to have nonzero values, don't take into account. Thus such method admits violation of the condition
in more high powers or their products and being able to have nonzero values, don't take into account. Thus such method admits violation of the condition 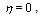 which means that with certain coordinates variations the interval a prior becomes time-like or space-like. Since this interval accords with the light ray motion, one leads to the Lorentz-invariance violation in locality, namely, anisotropies.It is shown for the massive particle[5] that a fundamental space-time discreteness need not contradict Lorentz invariance, and causal set's discreteness is in fact locally Lorentz invariant. The possibility of Lorentz symmetry break for the photon in vacuum by effects from the Plank scale is studied in[3,4]. However, experiments[6] show exceptionally high precision of constancy of the light speed confirmed a Lorentz symmetry in locality, and astrophysical tests don't detect isotropic Lorentz violation[4].In the method of calculus of variations in the large[7] ones are considered as possible paths along the manifold disregarding kind of interval, not as the trajectories of physical particles. This approach exceeds the limits of classical variational principle in mechanics, according as which virtual motions of the system are compared with cinematically possible motions.
which means that with certain coordinates variations the interval a prior becomes time-like or space-like. Since this interval accords with the light ray motion, one leads to the Lorentz-invariance violation in locality, namely, anisotropies.It is shown for the massive particle[5] that a fundamental space-time discreteness need not contradict Lorentz invariance, and causal set's discreteness is in fact locally Lorentz invariant. The possibility of Lorentz symmetry break for the photon in vacuum by effects from the Plank scale is studied in[3,4]. However, experiments[6] show exceptionally high precision of constancy of the light speed confirmed a Lorentz symmetry in locality, and astrophysical tests don't detect isotropic Lorentz violation[4].In the method of calculus of variations in the large[7] ones are considered as possible paths along the manifold disregarding kind of interval, not as the trajectories of physical particles. This approach exceeds the limits of classical variational principle in mechanics, according as which virtual motions of the system are compared with cinematically possible motions.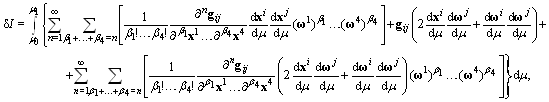
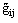 :
: 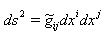
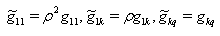
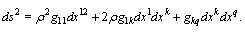
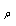 is some quantity, which is assumed to be equal 1. Putting down
is some quantity, which is assumed to be equal 1. Putting down 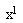 as time, coordinates with indexes
as time, coordinates with indexes 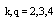 as space coordinates and considering
as space coordinates and considering 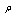 as energy of light-like particle with
as energy of light-like particle with 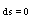 [10] we present it as
[10] we present it as 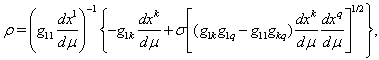
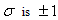 .Indexes except
.Indexes except 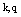 take values 1 to 4. With denotation of the velocity four-vector components as
take values 1 to 4. With denotation of the velocity four-vector components as 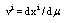 energy variation will be
energy variation will be 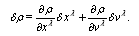
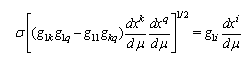
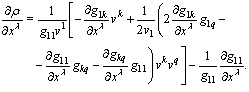
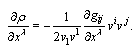
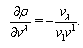
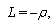
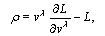
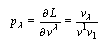
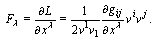
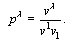
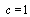 . Components of energy-momentum four-vector of photon in Minkowski space are proportional to four-velocities:
. Components of energy-momentum four-vector of photon in Minkowski space are proportional to four-velocities: 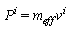 with coefficient of proportionality
with coefficient of proportionality 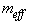 , which is effective mass. It is represented as
, which is effective mass. It is represented as 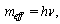
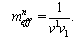
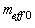 it can be expressed in terms of effective mass as
it can be expressed in terms of effective mass as 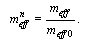
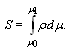
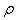 is non-zero, its variations leave interval to be light-like, and application of standard variational procedure yields Euler-Lagrange equations
is non-zero, its variations leave interval to be light-like, and application of standard variational procedure yields Euler-Lagrange equations 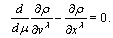
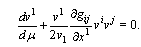
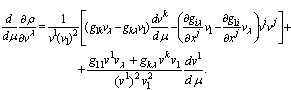
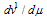 here on its expression, obtained from (24), and substitution found terms in Euler- Lagrange equations gives
here on its expression, obtained from (24), and substitution found terms in Euler- Lagrange equations gives 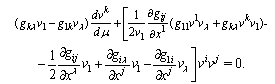
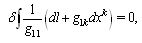
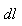 is element of spatial distance along the ray
is element of spatial distance along the ray 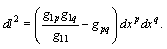
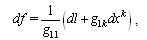
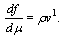
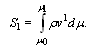
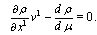
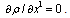 The value of
The value of 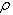 is constant. Thus, expression (32) is idential equation.Equations for the space coordinates are follows:
is constant. Thus, expression (32) is idential equation.Equations for the space coordinates are follows: 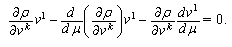
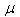 the constant value of
the constant value of 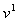 . Then, the third term in the left part of equations will be vanishing and they shall be identical to (23).For the static gravity field the Fermat's principle gives solution, which conforms to geodesics[12].
. Then, the third term in the left part of equations will be vanishing and they shall be identical to (23).For the static gravity field the Fermat's principle gives solution, which conforms to geodesics[12].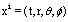 its line element is
its line element is 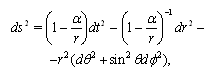
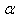 is constant.For this space we find equations of the critical curve of the integral energy
is constant.For this space we find equations of the critical curve of the integral energy 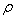 . The canonical momenta (16) for the cyclic coordinates
. The canonical momenta (16) for the cyclic coordinates 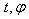 are the constants of motion
are the constants of motion 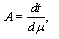
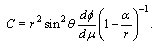
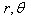 give
give 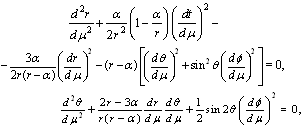
 and considering motion in plane
and considering motion in plane  we write derivatives of the cyclic coordinates
we write derivatives of the cyclic coordinates 
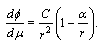
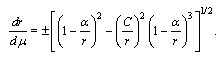
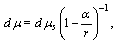
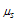 corresponds to geodesic equations.The canonical momenta (16) and forces (17) are
corresponds to geodesic equations.The canonical momenta (16) and forces (17) are 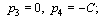
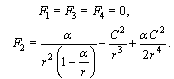
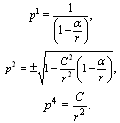
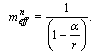
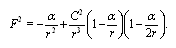
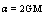 , the first term of
, the first term of 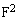 yields twice gravity force. One conforms to the light deflection in central gravity field [13], which is twice value being given by the gravity theory.Substituting components of the velocity four-vector in Eq. (37) we obtain radial the acceleration
yields twice gravity force. One conforms to the light deflection in central gravity field [13], which is twice value being given by the gravity theory.Substituting components of the velocity four-vector in Eq. (37) we obtain radial the acceleration 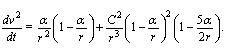
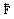 experiences acceleration
experiences acceleration 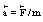 , where m is its inertial mass. By analogy normalized inertial mass of photon is found as ratio of the canonical force F2 to the radial acceleration
, where m is its inertial mass. By analogy normalized inertial mass of photon is found as ratio of the canonical force F2 to the radial acceleration 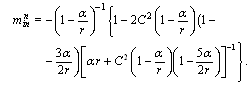
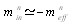 . Thus, excepting area, where signs of F2 and
. Thus, excepting area, where signs of F2 and 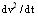 are identical or one of these quantities is equal to 0, inertial mass of photon is negative, i. e. it experiences antigravirational influence[14].
are identical or one of these quantities is equal to 0, inertial mass of photon is negative, i. e. it experiences antigravirational influence[14].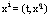 is described by metric
is described by metric 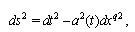
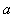 is the length scale factor.Equation (24) gives
is the length scale factor.Equation (24) gives 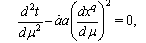
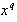 yield constants of motion
yield constants of motion 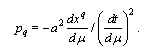
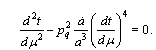
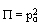 is written in form
is written in form 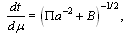
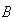 is constant. Substitution found first component of the four-velocity vector in equation (53) gives
is constant. Substitution found first component of the four-velocity vector in equation (53) gives 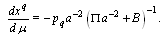
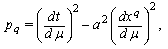
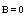 and components of the four-velocity vector turn out to
and components of the four-velocity vector turn out to 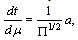
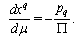
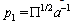
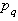 . The canonical forces are
. The canonical forces are 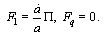
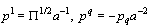
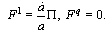
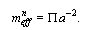
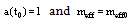 we obtain, taking into account Eq. (21), follows:
we obtain, taking into account Eq. (21), follows: 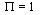
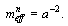
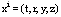 the line element is written in form
the line element is written in form 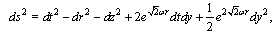
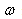 is constant.The canonical momenta (16) for cyclic coordinates
is constant.The canonical momenta (16) for cyclic coordinates 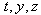 are the constants of motion. They are written in form
are the constants of motion. They are written in form 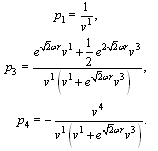
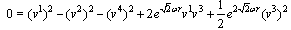
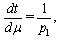
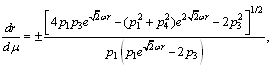
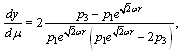
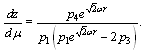
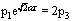 the singularity takes place.The obtained equations differ from the solution of the null geodesics equations in the Gödel 's space-time[15].The canonical momentum corresponding to coordinate
the singularity takes place.The obtained equations differ from the solution of the null geodesics equations in the Gödel 's space-time[15].The canonical momentum corresponding to coordinate 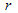 is
is 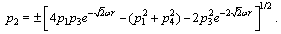
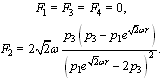
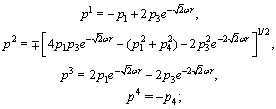
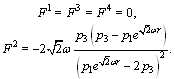
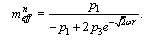
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML