Esam A. Gomaa
Chemistry Department, Faculty of Science, Mansoura University,35516-Mansoura, Egypt
Correspondence to: Esam A. Gomaa , Chemistry Department, Faculty of Science, Mansoura University,35516-Mansoura, Egypt.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The microscopic charging (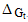 charging), ion-dipole (
charging), ion-dipole (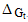 ion-dipole) and ion-induced dipole (
ion-dipole) and ion-induced dipole (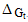 ion-induced dipole) free energies of transfer for some ions from methanol to mixed methanol (MeOH)-dimethylformamide (DMFA) solvents were calculated. These ions are potassium, rubidium and cesium. These theoretical free energies were compared with that of experimental values and the difference excess free energies of solvation were discussed. I t was observed that the excess free energies for all ions are positive and follow the following order:
ion-induced dipole) free energies of transfer for some ions from methanol to mixed methanol (MeOH)-dimethylformamide (DMFA) solvents were calculated. These ions are potassium, rubidium and cesium. These theoretical free energies were compared with that of experimental values and the difference excess free energies of solvation were discussed. I t was observed that the excess free energies for all ions are positive and follow the following order: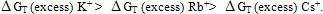 Indicating more solvation behaviour by increasing the percentage of DMFA in the mixed solvents due to more attraction of these ions in the range rich in DMFA
Indicating more solvation behaviour by increasing the percentage of DMFA in the mixed solvents due to more attraction of these ions in the range rich in DMFA
Keywords:
Microscopic free energy, potassium,robedium, cesium,excess free energy, organic solvents
1. Calculations and Results
The electrostatic free energies of transfer  is known as the microscopic free energies of interaction[1]. The solvation free energies of ions is important in the applications of all fields,chemistry,physics and theoretical sciencesto obtain the corresponding energies of salts.Also chemical reactions can be theoreticaly expected to happen by knowing the free energy values for reactants and products. When we know the free energies of the ions we can easily obtain that for any simple, heavy element, lanthanide and actinide salts,which facilitate the explanation of different reactions.The salvation free energy of an ion has been formulated by number of authors cited by Covington[1] as a composite of neutral and electrostatic contribution.A neutral part may be considered to be equivalent to the salvation energy of uncharged molecules analogous to the ion in structure and size. The electrostatic contribution of the free energy is not exact evaluated before.In this work we did simple view to evaluate the electrostatic free energies and compare it with the available experimental values done by using the asymmetric Ph4AsPh4B (tetraphenylarsonium tetraphenylborate) assumption for evaluating single ion thermodynamics[Popovych...][2].Transfer values are the difference in the thermodynamic functions in solvents or mixed solvents and that of methanol as reference solvent. The electrostatic microscopic free energies of transfer is composite of energy contributions from charging a sphere, ion induced dipole, ion induced dipole/and the ion quadrupole interactions. The last one the ion-quadrupole interaction are very small that can be neglected[1]. The charging of sphere can be calculated by using Born equation[2]. Other microscopic terms may be evaluated according to Buckingham model[3]. The neutral free energy is almost the same for ions that having the same electronic shells. But the microscopic free energies are only different and need evaluation.
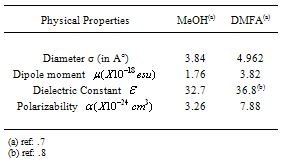
is known as the microscopic free energies of interaction[1]. The solvation free energies of ions is important in the applications of all fields,chemistry,physics and theoretical sciencesto obtain the corresponding energies of salts.Also chemical reactions can be theoreticaly expected to happen by knowing the free energy values for reactants and products. When we know the free energies of the ions we can easily obtain that for any simple, heavy element, lanthanide and actinide salts,which facilitate the explanation of different reactions.The salvation free energy of an ion has been formulated by number of authors cited by Covington[1] as a composite of neutral and electrostatic contribution.A neutral part may be considered to be equivalent to the salvation energy of uncharged molecules analogous to the ion in structure and size. The electrostatic contribution of the free energy is not exact evaluated before.In this work we did simple view to evaluate the electrostatic free energies and compare it with the available experimental values done by using the asymmetric Ph4AsPh4B (tetraphenylarsonium tetraphenylborate) assumption for evaluating single ion thermodynamics[Popovych...][2].Transfer values are the difference in the thermodynamic functions in solvents or mixed solvents and that of methanol as reference solvent. The electrostatic microscopic free energies of transfer is composite of energy contributions from charging a sphere, ion induced dipole, ion induced dipole/and the ion quadrupole interactions. The last one the ion-quadrupole interaction are very small that can be neglected[1]. The charging of sphere can be calculated by using Born equation[2]. Other microscopic terms may be evaluated according to Buckingham model[3]. The neutral free energy is almost the same for ions that having the same electronic shells. But the microscopic free energies are only different and need evaluation.Table (1): Physical Parameters of MeOH and DMFA at 298.15 K.
 |
| |
|
2. Individual Microscopic Energies
The individual microscopic interaction energies are given below for positive ions K+, Rb+ and Cs+. 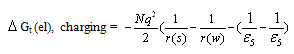 | (1) |
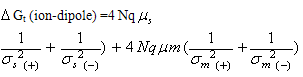 | (2) |
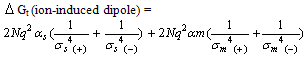 | (3) |
N is the avogadro's number, q the effective charge density, 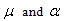 are the dipole moment and polarizability,
are the dipole moment and polarizability, 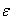 the dielectric constant, r the radius and σ is the interaction diameter. Small and m denote mixed solvent and methanol, respectively. For the two oppositely charged ions of the same size, the energy contributions of ion-quadrupole interactions are equal but have opposite signs, so that on addition of them these energy terms cancel out[4]. Therefore the electrostatic free energy terms can be considered as the sum for all the microscopic free energies in pure solvents.
the dielectric constant, r the radius and σ is the interaction diameter. Small and m denote mixed solvent and methanol, respectively. For the two oppositely charged ions of the same size, the energy contributions of ion-quadrupole interactions are equal but have opposite signs, so that on addition of them these energy terms cancel out[4]. Therefore the electrostatic free energy terms can be considered as the sum for all the microscopic free energies in pure solvents. 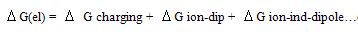 | (4) |
3. Discussion
In binary solvents, it is expected that the solvent composition of the ions is different from the composition of the bulk solution. The greater the dipole moment of a molecule, the better the chance for this molecule to be at the vicinity of the ion. In binary solvents, the solvent composition described as the mole fraction of first solvent in the mixtures, Xs1 in the vicinity of the ion, owing to the dipole effect is estimated by[5, 6]. 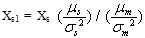 | (5) |
Where Xs is the mole fraction of methanol. A similar affect may be expected for ion-induced-dipole interaction such that the mole fraction thus influenced by: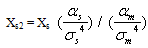 | (6) |
For mixed solvents the electrostic energies becomes: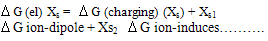 | (7) |
Equation 7…………………………..equal equation. 8: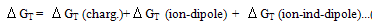 | (8) |
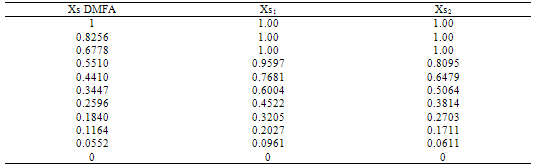
Table (2). Parameters Xs1 and Xs2 for mixed MeOH-DMFA solvents at 298.15 K.
 |
| |
|
The physical parameters of DMFA and MeOH are shown in Table (1). The Xs1 and Xs2 calculated are cited in Table (2). All the solvated radii are taken from ref.8, the dielectric constants & dipole moments were calculated by summing the multiplication of each property by the mole fraction of each solvent in the binary mixture.Table (3). Microscopic free energies of solvation of potassium ion and its excess solvation free energies in mixed MeOH-DMFA solvents at 298.15 K (in K.J/mole).
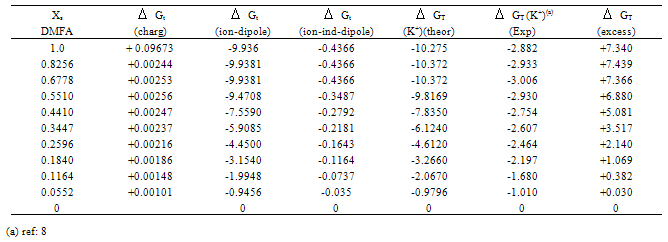 |
| |
|
Table (4). Microscopic free energies of solvation for rubidium ion and its excess solvation free energies in mixed MeOH. DMFA solvents at 298.15 K (in KJ/mole).
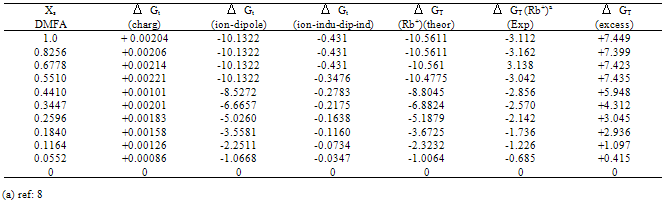 |
| |
|
Table (5). Microscopic free energies of solvation for cesium ion and its excess solvation free energies in mixed MeOH-DMFA solvents at 298.15 K (in KJ/mole).
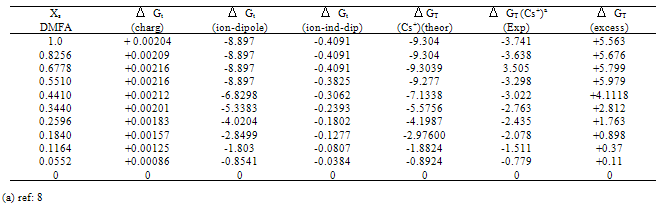 |
| |
|
4. Conclusions
All the calculated microscopic free energies for the ions under consideration were calculated and listed in Tables 3, 4 and 5. The total microscopic free energies calculated were compared with the experimental values taken from ref. 8 and the excess values were evaluated by applying equation[9-15]. 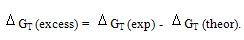 It observed from Tables 3, 4 & 5 that the excess free energies for all ions are positive and follow the following order:
It observed from Tables 3, 4 & 5 that the excess free energies for all ions are positive and follow the following order: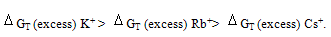 Indicating more solvation behaviour by increasing the percentage of DMFA in the mixed solvents due to more attraction of these ions in the range rich in DMFA. It was also concluded that the excess energies lie in the range between 90 to 94% as calculated from the references aboveref .2. This great part of the free energies is the neutral contribution which can be evaluated experimentally of calculated theoretically. Therefore on using such this work the electrostatic free energies can be calculated. On adding the neutral free energies to it we can obtain the whole free energies of solvation
Indicating more solvation behaviour by increasing the percentage of DMFA in the mixed solvents due to more attraction of these ions in the range rich in DMFA. It was also concluded that the excess energies lie in the range between 90 to 94% as calculated from the references aboveref .2. This great part of the free energies is the neutral contribution which can be evaluated experimentally of calculated theoretically. Therefore on using such this work the electrostatic free energies can be calculated. On adding the neutral free energies to it we can obtain the whole free energies of solvation
References
| [1] | A. K. Covington and T. Dickinson, "Physical chemistry of organic solvent systems", Plenum Press, New York (1973). |
| [2] | O. Popovych, and R. P. T. Tomkins, "Non aqueous solution Chemistry", John Wiley & Sons, Inc., New York (1981). |
| [3] | Y. Marcus, "Ion properties", Marcel Dekker, New York (1997). |
| [4] | J. I. Kim, "The Ph4AsPh4B assumption for single ion thermodynamics and its asymmetric partition to cation and anion", Bull. Soc. Chim. Belg., 95(1986) 435-446. |
| [5] | J. I. Kim and E. A. Gomaa, "Preferential solvation of single ions: The Ph4AsPh4B assumption for single ion thermodynamics in mixed dimethylsulfoxide-water solvents", Bull. Soc. Chim. Belg., 90(1981) 391-410 . |
| [6] | J. I. Kim, A. Cecal, H. J. Born and E. A. Gomaa, "Preferential solvation of single ions: a critical study of Ph4AsPh4B assumption for single ion thermodynamics in mixed aqueous-acetonitrile and aqueous- N-N-dimethyl formamide solvents", Z. Phys. Chem. Neue Folge, 110(1978)209-227. |
| [7] | Esam A. Gomaa, "Transfer free energies of ions from water to N, N-dimethylformamide and its aqueous mixtures based on Ph4AsPh4B and Ph4SbBPh4 assumption", Thermochem. Acta, 142(1989). 19-27 . |
| [8] | Esam A. Gomaa, "Solvation free energies of K+, Rb+ and Cs+ ions in methanol-NN-dimethylformamide mixtures", Croatica Chemica Acta, 62(1989) 475-480 . |
| [9] | Gy.Takli,”Evaluation of individual ionic partial molar volumes in aqueous solutions”J.Chem.Thermodynamics,40(2008)770-776. |
| [10] | Yizhak Marcus,”On the preferential salvation of drugs and PAHs in binary solvent mixtures”,Journal Molecular Liquids,140(2008)61-67. |
| [11] | K.Rajagopal,S.Edwin Gladson,” Partial molar and partial compressibility of four homologous alpha amino acids in aqueous sodium fluoride solutions at different temperatures.”, J.Chem.Thermodynamics,43(2011)852-867. |
| [12] | Ewa Kamenska-Piotrowice,Janusz Stangret,Joanna Szymanska-Cybulska,” Solvation of cobalt(II) and trifluoromethanesulfonate ions in N,N-dimethylformamide-methanol mixed solvents,studied by means of FT-IR spectroscopy.”,Spectrochimica Acta,Part A,60(2007),1-8. |
| [13] | E.A.Gomaa and B.M.Al-Jahdali,”Association of Cu(NO3)2 eith Kryptofix-221 in mixed (MeOH-DMF) solvents at different temperatures.”,American Journal of Fluid Dynamics, 12 (2011) 4-8. |
| [14] | Nagah A.El-Shishtawi,Maany a.Hammada and Esam A.Gomaa,” Inflence of peranent magnet on the association constants of FeCl3 + 10% PVA(polyvinyl alcohol)in 50% ethanol-water solutions conductometrically at 298.15K using new equation for 1:3 asymmetric electrolytes.”, Physical Chemistry, 1(2011) 14-16. |
| [15] | E.A.Gomaa,”Solvation parameters of lead acetate in mixed, N,N-dimethylformamide–water mixtures at 298.15K.”, Analele Universitate din Bucuresti-Chimie,vol.19 (2010) 45-48. |

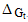 charging), ion-dipole (
charging), ion-dipole (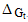 ion-dipole) and ion-induced dipole (
ion-dipole) and ion-induced dipole (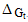 ion-induced dipole) free energies of transfer for some ions from methanol to mixed methanol (MeOH)-dimethylformamide (DMFA) solvents were calculated. These ions are potassium, rubidium and cesium. These theoretical free energies were compared with that of experimental values and the difference excess free energies of solvation were discussed. I t was observed that the excess free energies for all ions are positive and follow the following order:
ion-induced dipole) free energies of transfer for some ions from methanol to mixed methanol (MeOH)-dimethylformamide (DMFA) solvents were calculated. These ions are potassium, rubidium and cesium. These theoretical free energies were compared with that of experimental values and the difference excess free energies of solvation were discussed. I t was observed that the excess free energies for all ions are positive and follow the following order: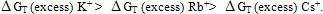 Indicating more solvation behaviour by increasing the percentage of DMFA in the mixed solvents due to more attraction of these ions in the range rich in DMFA
Indicating more solvation behaviour by increasing the percentage of DMFA in the mixed solvents due to more attraction of these ions in the range rich in DMFA
 is known as the microscopic free energies of interaction[1]. The solvation free energies of ions is important in the applications of all fields,chemistry,physics and theoretical sciencesto obtain the corresponding energies of salts.Also chemical reactions can be theoreticaly expected to happen by knowing the free energy values for reactants and products. When we know the free energies of the ions we can easily obtain that for any simple, heavy element, lanthanide and actinide salts,which facilitate the explanation of different reactions.The salvation free energy of an ion has been formulated by number of authors cited by Covington[1] as a composite of neutral and electrostatic contribution.A neutral part may be considered to be equivalent to the salvation energy of uncharged molecules analogous to the ion in structure and size. The electrostatic contribution of the free energy is not exact evaluated before.In this work we did simple view to evaluate the electrostatic free energies and compare it with the available experimental values done by using the asymmetric Ph4AsPh4B (tetraphenylarsonium tetraphenylborate) assumption for evaluating single ion thermodynamics[Popovych...][2].Transfer values are the difference in the thermodynamic functions in solvents or mixed solvents and that of methanol as reference solvent. The electrostatic microscopic free energies of transfer is composite of energy contributions from charging a sphere, ion induced dipole, ion induced dipole/and the ion quadrupole interactions. The last one the ion-quadrupole interaction are very small that can be neglected[1]. The charging of sphere can be calculated by using Born equation[2]. Other microscopic terms may be evaluated according to Buckingham model[3]. The neutral free energy is almost the same for ions that having the same electronic shells. But the microscopic free energies are only different and need evaluation.
is known as the microscopic free energies of interaction[1]. The solvation free energies of ions is important in the applications of all fields,chemistry,physics and theoretical sciencesto obtain the corresponding energies of salts.Also chemical reactions can be theoreticaly expected to happen by knowing the free energy values for reactants and products. When we know the free energies of the ions we can easily obtain that for any simple, heavy element, lanthanide and actinide salts,which facilitate the explanation of different reactions.The salvation free energy of an ion has been formulated by number of authors cited by Covington[1] as a composite of neutral and electrostatic contribution.A neutral part may be considered to be equivalent to the salvation energy of uncharged molecules analogous to the ion in structure and size. The electrostatic contribution of the free energy is not exact evaluated before.In this work we did simple view to evaluate the electrostatic free energies and compare it with the available experimental values done by using the asymmetric Ph4AsPh4B (tetraphenylarsonium tetraphenylborate) assumption for evaluating single ion thermodynamics[Popovych...][2].Transfer values are the difference in the thermodynamic functions in solvents or mixed solvents and that of methanol as reference solvent. The electrostatic microscopic free energies of transfer is composite of energy contributions from charging a sphere, ion induced dipole, ion induced dipole/and the ion quadrupole interactions. The last one the ion-quadrupole interaction are very small that can be neglected[1]. The charging of sphere can be calculated by using Born equation[2]. Other microscopic terms may be evaluated according to Buckingham model[3]. The neutral free energy is almost the same for ions that having the same electronic shells. But the microscopic free energies are only different and need evaluation.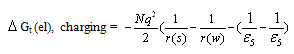
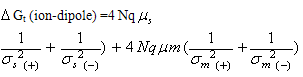
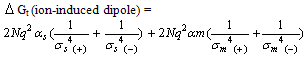
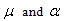 are the dipole moment and polarizability,
are the dipole moment and polarizability, 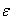 the dielectric constant, r the radius and σ is the interaction diameter. Small and m denote mixed solvent and methanol, respectively. For the two oppositely charged ions of the same size, the energy contributions of ion-quadrupole interactions are equal but have opposite signs, so that on addition of them these energy terms cancel out[4]. Therefore the electrostatic free energy terms can be considered as the sum for all the microscopic free energies in pure solvents.
the dielectric constant, r the radius and σ is the interaction diameter. Small and m denote mixed solvent and methanol, respectively. For the two oppositely charged ions of the same size, the energy contributions of ion-quadrupole interactions are equal but have opposite signs, so that on addition of them these energy terms cancel out[4]. Therefore the electrostatic free energy terms can be considered as the sum for all the microscopic free energies in pure solvents. 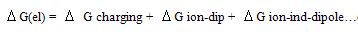
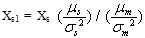
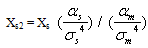
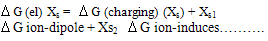
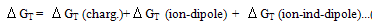
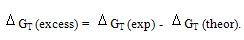 It observed from Tables 3, 4 & 5 that the excess free energies for all ions are positive and follow the following order:
It observed from Tables 3, 4 & 5 that the excess free energies for all ions are positive and follow the following order: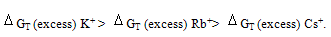 Indicating more solvation behaviour by increasing the percentage of DMFA in the mixed solvents due to more attraction of these ions in the range rich in DMFA. It was also concluded that the excess energies lie in the range between 90 to 94% as calculated from the references aboveref .2. This great part of the free energies is the neutral contribution which can be evaluated experimentally of calculated theoretically. Therefore on using such this work the electrostatic free energies can be calculated. On adding the neutral free energies to it we can obtain the whole free energies of solvation
Indicating more solvation behaviour by increasing the percentage of DMFA in the mixed solvents due to more attraction of these ions in the range rich in DMFA. It was also concluded that the excess energies lie in the range between 90 to 94% as calculated from the references aboveref .2. This great part of the free energies is the neutral contribution which can be evaluated experimentally of calculated theoretically. Therefore on using such this work the electrostatic free energies can be calculated. On adding the neutral free energies to it we can obtain the whole free energies of solvation Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML



