Yuriy N Zayko
P. A. Stolypin’s Volga Regional Institute of State Service, Saratov, 410031, Russia
Correspondence to: Yuriy N Zayko, P. A. Stolypin’s Volga Regional Institute of State Service, Saratov, 410031, Russia.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
This article is a continuation of the previous author's article on the same problem[1]. Here choice of metrics discusses in detail, so as another possible metrics, like generalization of the Schwarzschild metric of massive body due to radiation of electromagnetic wave. A problem of lowering the initially spherical symmetry to axial one in solution’s level for Einstein-Maxwell (or Maxwell) equations due to fixation of z-axis of coordinate system and its recovery with the help of zero-modes is discussed. Localized solutions of the Einstein-Maxwell equations (geons) are discussed, too.
Keywords:
Metric, Zero Modes, Geon, Radiation
Cite this paper: Yuriy N Zayko, Explicit Solutions of the Maxwell-Einstein Equations.II, International Journal of Theoretical and Mathematical Physics, Vol. 1 No. 1, 2011, pp. 17-21. doi: 10.5923/j.ijtmp.20110101.03.
1. Introduction
Present article is a continuation of previous author’s work[1], devoted to treating of peculiarities of electromagnetic wave’s (EMW) propagation in Universe under influence of its own gravitation field. For this purpose we take the coupled Maxwell-Einstein equations as basic ones. Main attention isn’t paid to discussion of the results of[1], but investigation of some intelligent questions such as methodology of treating, etc. There are following questions:- metric, used in[1] and other possible metrics;- localized domains of electromagnetic and gravitation energy – geons[2], and others. Problem of angular dependence of spherical EMW (SEMW) is discussed, too.
2. Metric, Used in[1]
Let us remember a problem[1]. The initial basic equations in[1] are the coupled Einstein’s equations of gravity and Maxwell’s equations for EMW without the sources[3]: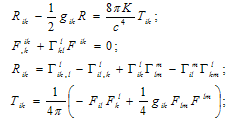 | (1) |
Here R – trace of Ricci’s tensor Rik: R = Rii , gik – metric tensor; Tik and Fik– tensor of energy-momentum and electromagnetic one; Гikl – Christoffel’s symbols; с – light speed in vacuum, K – gravitation constant; indices i, k, l take values 0, 1, 2, 3; repeated indices mean summation; comma means usual, i.e. non-covariant derivative[1]. Let us find a solution of (1) which corresponds to existence of spherical light wave at r → ∞. For this we use an expression for interval just as in well-known Schwarzschild problem[1]: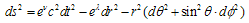 | (2) |
ν = ν(t, r, θ), λ = λ(t, r, θ); x0 =ct, t –time; x1= r, x2 = θ, x3 = φ – spherical co-ordinates. SEMW is characterized by frequency ω and moment momentum vector М. Let us choose z - axis of the co-ordinate system in direction perpendicular to M. It simplifies a treating because the dependence of azimuthal angle φ in (1) may be omitted. For the variables’ splitting an additional condition was used in[1]: λ =α(r, t) + β(θ), ν = -α(r, t)+β(θ). After variables’ separation equations (1) were solved in a usual way, i.e. energy-momentum tensor Tik was expressed through Ricci’s one, or finally through metric tensor gik. From the other hand, we used similar representation of Tik through components of electromagnetic field tensor Fik. If one strictly follows this procedure he falls in contradiction – left and right parts of resulting equations have different dependence of polar angle θ. This contradiction could be partially eliminated when Tik is averaging on time interval greater than wave period. The whole elimination of this contradiction could be achieved when one takes the differences of abovementioned values. After this procedure is completed than expressions for the coefficients in (2) looks as follows: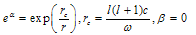 | (3) |
Here l – is a whole nonnegative number which determines orbital angular moment-momentum of SEMW, ω – is a frequency of SEMW at infinity.
3. Zero Modes
Solutions of the Maxwell equation which was used in[1]1 obey degeneration, connecting with arbitrariness of z – axis’ direction of co-ordinate system. If direction of z – axis is fixed the initial spherical symmetry of problem is lowered. As was shown in quantum field theory2 [4] if one tries to fulfil quasi-classic quantization near these solutions then so-called “zero modes” arise. They describe quantum transitions between degenerate states. Zero modes always arise when static solution with continuous group of symmetry, having translation invariance, for example, is quantized[4].Zero modes in our problem are arising due to fact that all directions of z – axis are equivalent: all solutions corresponding to its different directions are possible and have the same energy. In order to eliminate zero modes, one must explicitly take into account the transitions between degenerate states. For the simplicity one can do this in quantum description. A simplification of problem is connected with fact that angular behavior of photon wave function is just the same as for classical EMW. Let us calculate the probability of transition from the state with orbital quantum number l, which angular behavior is described by Pl (cos(θ)) in co-ordinate system with given axis z, to the state with the same quantum number in co-ordinate system with axis z’ deviating from z on angle Δθ. In this latter co-ordinate system angular behavior of wave function describes as Pl (cos(θ+Δθ))3. Let us expand Pl (cos(θ+Δθ)) in series on Legendre polinoms Pl k (cos(θ)):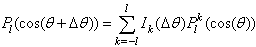 | (4) |
The amplitude of transition probability Ik (Δθ) one can find with the help of adding theorem for spherical functions[6]: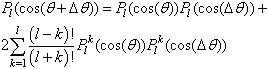 | (5) |
Due to orthogonality of joined Legendre polinoms[6], we receive: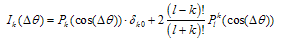 | (6) |
where δkl – Kroneker’s symbol. Interested probabilities look as follows: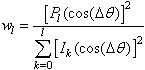 | (7) |
Denominator in (7) arises because joined Legendre polinoms are orthogonal, but not-orthonormal set of functions. Quantity wl is a “fraction” of function Pl (cos(θ+Δθ)) in initial function Pl (cos(θ)). Figure 1 represents results of calculation wl (Δθ) for different l: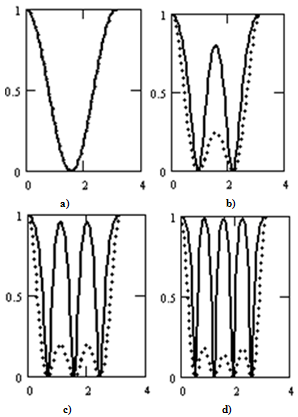 | Figure 1. Plot of wl(Δθ) |
Ordinata: points – (Pl (cos(θ)))2, solid curve – wl (Δθ); Abscissa: angles θ and Δθ from 0 to π; a) l = 1 (curves coincide), b) l = 2, c) l = 3, d) l = 4.These results show that angle region Δθс, where fraction of “shifted” harmonic Pl (cos(θ+Δθ)) in the “basic” one Pl (cos(θ)) is significant, is comparable with scale θc of angular dependence of Pl (cos(θ)), which has order of value 1/l. This can be assigned to effect of zero modes, because both abovementioned harmonics have the same energy. Of course, this effect vanishes when direction of z axis is fixed physically, for instance, with the help of external field4.
4. Another Metrics
Abovementioned metric was received mainly with the help of Maxwell equations only. Einstein equations play minimal role which consists of assertion that R00 = R11, while values of Ricci’s tensor do not have matter. This corresponds to problem under consideration which is to find curvature of space-time metric produced by EMW only without any massive body. That is why final result does not depend on EMW amplitude. Amplitude dependence arises in another problem concerning with treating of metric produced by massive irradiative body, i.e. additions to Schwarzschild metric. We present this result below. Our treating is based on results of[1].Let us equal expressions for T00 obtained from Einstein equations omitting part depending on polar angle θ5, and that one from Maxwell equations for SEMW of TM-type: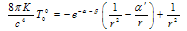 | (8) |
We used here components of tensor of electromagnetic field F01 = Ψ(r,t)·Φ(θ). Last equation in (8) can be simplified with the help of function f(r,t), which is described by equation[1]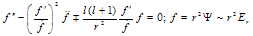 | (9) |
Signs ± correspond to converging and diverging SEMW, Er – radial component of electrical field of SEMW. If we put f(z,t) = G(z)e±iωt, | z | = ωr/c, ω – frequency, then we receive equation for G(z) in complex plane z: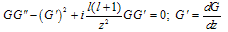 | (10) |
which will be used below. Resulting equation for metric looks as follows: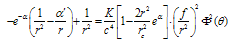 | (11) |
It is obvious from (11) that we meet discrepancy mentioned earlier which isn’t overwhelmed with the help of subtracting procedure like in[1]. Perhaps, taking into account results of Paragraph 2 we can implement averaging procedure to energy-momentum tensor of EMW not only in time as earlier, but in angle θ too. Finally we find an equation for metric which slightly differs from (11): Φ2(θ) in right hand side of (11) will be absent. This equation has a solution which defines metric differing from that which was received in[1].Equation which is leading from (11) if average on θ is completed looks as follows: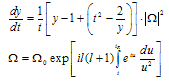 | (12) |
Here y = e –α, t = 1/x = rc / r, Ω = G·(Γ)½, Γ = 4K/c4rc2, tR =rc/R, R – radius of photosphere. Boundary condition for (12) is y(t=0) = 1, i.e. metric at infinity (x → ∞) is flat. In order to receive (12) we use a solution of (10)[1]:which corresponds to spherical wave at infinity. Finally an equation (12) looks as follows: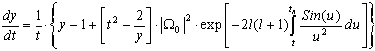 | (13) |
If EMW is absent equation (13) has well-known solution which is corresponding to Schwarzschild metric: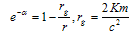 Here m is a mass of body which plays role of source of gravitation field. One can omits t2 << 2/y in equation (13) at large distance r >> rc Let us evaluate order of magnitude of value |Ω0|2, which is connected with energy flow density of radiation from massive stellar body. Note that electromagnetic field of star treated as field of spherical radiator can be replaced by field of elementary electrical dipole at large distance[7]. Taking it into account one can connect radial component Er of EMW and star luminosity L and find an expression for |Ω0|2
Here m is a mass of body which plays role of source of gravitation field. One can omits t2 << 2/y in equation (13) at large distance r >> rc Let us evaluate order of magnitude of value |Ω0|2, which is connected with energy flow density of radiation from massive stellar body. Note that electromagnetic field of star treated as field of spherical radiator can be replaced by field of elementary electrical dipole at large distance[7]. Taking it into account one can connect radial component Er of EMW and star luminosity L and find an expression for |Ω0|2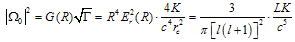 | (14) |
Substitution values for L = 4(1032 ÷ 1035) J/s 6 (in visible and roentgen parts of spectrum) in (14) leads to evaluation for |Ω0|2 ≈ (10-20 ÷ 10-17 )/[l(l+1)]2. If we put R = 30Rc7, where Rc = 6.96·10-8 m is radius of the Sun then we receive value for tR ≈ 7.63l (l+1)·(10-19 ÷ 10-22) in different parts of spectral diapason.It is hard to receive any valuable quantitative result due to variation in values for different parts in equation (13). But one can treat an asymptotic behavior of (13) in limit t << 1(r >> rc). Expanding integrand in (13) on u, one can turn this equation to known form[9]. Final expression for metric looks as follows: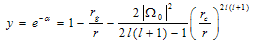 | (15) |
It is obvious from (15) that corrections to Schwarzschild metric, which is described by first two members in (15) due to stellar radiation, are extremely small in the frame of known Universe. Nonetheless, this result has principal significance8. To receive space-time metric at the vicinity of massive dipole (multi-pole in general case) radiator one have to replace in (14) star luminosity L to intensity I of dipole (multi-pole) radiation[3].
5. Geons
Einstein-Maxwell equations predict possibility of geons, which were described as “meta-stable complexes of energy of electromagnetic or gravitation waves, tightly binding by their own gravitation attraction”[2]. Geon is essentially non-linear object whose existence is obliged to nonlinearity of Einstein, or Maxwell-Einstein equations. Meaning of Tik used in[1] eliminating its self- nonlinearity doesn’t influence on intrinsic non-linearity of Einstein’s equations. Thus there exist their solutions of this type amongst others. To find them explicitly let us remember some results of[1]. Solution of the equation (1) for TM-type wave in plane of complex variable z looks as follows 9 f(z,t) = G(z)e±iωt, | z | = ωr/c, ω – frequency; f = r2Ψ(r,t), F01 = Ψ(r,t)·Φ(θ), Φ(θ) describes angle part of solution. Behavior of G(z) is described by equation (10). Rigorous solution G for boundary condition G ~ eiz at infinity looks as follows: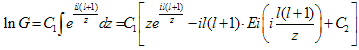 | (16) |
Ei(x) – integral exponent, C1 = i and C2– are constants. For localized solutions of equation (1) one have to put constant C1<0 in (16). Then asymptotic behavior of this solution will be: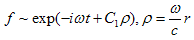 | (17) |
Metric for solutions of this type is just the same as one received in[1] for solutions of wave type (3). It follows from (17) that electrical charge of geon is equal zero.
6. Conclusions
At present time a lot of explicit solutions of Einstein’s equations was found and its number is still growing10. There are many catalogues of these solutions[10]. It is very problematic task to find unknown solution. Nevertheless, let us quote[10] with reference to W. Kinnersley[11]:“Back in 1975 Kinnersley wrote: “Most of the known exact solutions11 describe situations which are frankly unphysical, and these do have a tendency to distract attention from the more useful ones. But the situation is also partially the fault of those of us who work in this field. We toss in null currents, macroscopic neutrino fields and tachyons for the sake of greater ‘generality’; we seem to take delight at the invention of confusing anti-intuitive notation; and when all is done we leave our newborn metric wobbling on its vierbein without any visible means of interpretation12.” Not much has changed since then”. In the present article quite different physical approach is used. Those solutions which have no physical interpretation probably have minimal interest not due to their mistakenness but senselessness. Thus, solutions of Rainich type[12], probably do not realize for reasons which were outlined by L. Witten[13,14]13. Methods used in this article are not so rigorous as those which are used in[10], for instance. But this is not a reason to reject them. We hope that further treating of problems outlined in the present article will lead to their improvement. Results obtained in present article permit to fill gaps in applications of general relativity, such as corrections to the Schwarzschild metric due to radiation of massive body. It was shown that averaging of energy-momentum tensor Tik in right-hand side of the Maxwell-Einstein equations can be ground due to taking into account restrictions imposed on these ones. Let us speak some words about geons, which were described previously by J.A. Wheeler[2], as irradiative objects with huge amount of mass (~ 1042 g[15]). Radiation of geons is corresponding to complex value of constant C1 (see Paragraph 5) with Im (C1) ≠ 0. This condition leads to vanishing such irradiative objects, due to loss of their energy-mass, so only non-irradiative objects with Im (C1) = 0 can be observed after long period of existence. These objects can be detected by scattering light, or other particles, only due to its gravitation field14 In all other aspects geons stay “invisible”. This permits to consider geons as potential candidates for sources of so-called “dark mass” in the Universe.
ACKNOWLEDGMENTS
Author expresses his thanks to prof. M.V. Davidovich for discussions.
Notes
1. So as all similar solutions, which can be found in scientific literature (see[5], for example). As a consequence, field distribution in spheroidal electromagnetic resonator has axial symmetry.2. This effect takes place in classical electrodynamics, or mechanics, too, when theory of perturbations is performing. 3. Pl are Legendre polinoms, Plk - are joined Legendre polinoms.4. This result is self-interesting, because it explains abovementioned results of classical electrodynamics (see footnote 1). 5. This part contains derivatives β(θ) only, which equal zero[1].6. For stars in main sequence L=106Lc, Lc=4•1026J/s – Sun’s luminosity. For supernova L=109Lc [8].7. For stats in main sequence.8. So as, for instance, Nordström-Reissner metric.9. Equation (9) for f(z, t) is presented earlier.10. Approximately with rate 100 per year[10].11. Of Einstein equations12. In spite of this was sentenced in 1975 present situation unlikely be changed because it has its origin in human nature which stay permanent during millen-niums.13. Another reason of Rainich’s solutions absence in reality is that gravitation field in Einstein equation is not self-produced[14].14. This is a subject of separate treating[16].
References
| [1] | Y. N. Zayko. “Explicit Solutions of the Maxwell-Einstein Equations”, International Journal of Theoretical and Mathematical Physics, 2011, 1(1), 1-6 |
| [2] | Ch. W. Misner, J.A. Wheeler. “Classical Physics as Geometry”, J. Ann. of Phys., 2, № 6, 525 (1957) |
| [3] | L.D. Landau, E.M. Lifshits. Course of Theoretical Physics, Vol. 5. Theory of Fields, Nauka, Moscow (1967).-460 p |
| [4] | R. Rajaraman. An Introduction to Solitons and Instantons in Quantum Field Theory,. North-Holland Publishing Company, Amsterdam-NY-Oxford (1982) |
| [5] | V.V. Nikolsky, T.I. Nikolskaya. Electrodynamics and radio-wave propagation. Nauka, Moscow, (1989), 544 p |
| [6] | G. Arfken. Mathematical Methods for Physicists, Academic Press, NY and London |
| [7] | G.T. Markov, A.F. Chaplin. An Exсitation of Electromagnetic Waves. Energy, Moscow (1966).- 376 p |
| [8] | А.V. Tutukov. “Stars”, Physical Encyclopedia: in 5 vol., Moscow: Soviet Encyclopedia Publishing, 1990, V. 2 – 704 p., pp. 687-688 |
| [9] | E. Kamke. Gewöhnliche Differentialgleichungen. Leipzig, 1959 |
| [10] | D. Kramer, H. Stephani, M. Maccallum, H. Herlt, Exact Solutions of the Einstein Field Equations,; ed. E. Schmutzer.-Berlin, 1980 |
| [11] | Kinnersley, W. (1975). Recent progress in exact solutions, in: Shaviv, G., and Rosen, J. (Ed.). General Relativity and Gravitation (Proceedings of GR7, Tel-Aviv 1974), Wiley, New York, London |
| [12] | G.Y. Rainich. Electrodynamics in the General Relativity Theory, Trans. Am. Math. Soc. 1925, V. 27, pp. 106-136 |
| [13] | L. Witten. Initial Value Problem of the Einstein-Maxwell Field, Phys. Rev. 1960, V. 120, # 2, pp. 635-640 |
| [14] | J. Weber. “Gravitation and Light”, in Gravitation and Relativity, ed. by H.-Y. Chiu and W.F. Hoffman, W.A. Benjamin, Inc.- 1964 |
| [15] | J. A. Wheeler, “Neutrinos, Gravitation and Geometry”, Bologna, 1960 |
| [16] | Y. N. Zayko. “Mass-less Particles’ Behavior in Gravitation Fields”, to be published |

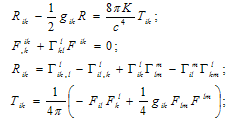
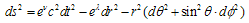
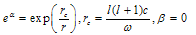
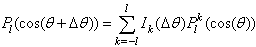
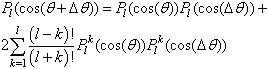
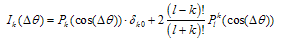
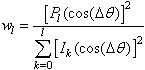

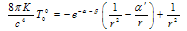
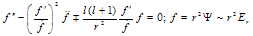
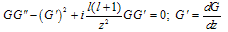
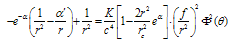
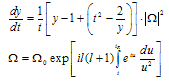
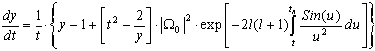
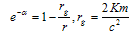 Here m is a mass of body which plays role of source of gravitation field. One can omits t2 << 2/y in equation (13) at large distance r >> rc Let us evaluate order of magnitude of value |Ω0|2, which is connected with energy flow density of radiation from massive stellar body. Note that electromagnetic field of star treated as field of spherical radiator can be replaced by field of elementary electrical dipole at large distance[7]. Taking it into account one can connect radial component Er of EMW and star luminosity L and find an expression for |Ω0|2
Here m is a mass of body which plays role of source of gravitation field. One can omits t2 << 2/y in equation (13) at large distance r >> rc Let us evaluate order of magnitude of value |Ω0|2, which is connected with energy flow density of radiation from massive stellar body. Note that electromagnetic field of star treated as field of spherical radiator can be replaced by field of elementary electrical dipole at large distance[7]. Taking it into account one can connect radial component Er of EMW and star luminosity L and find an expression for |Ω0|2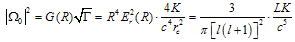
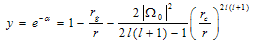
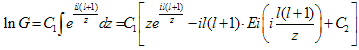
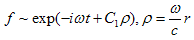
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML