Yuriy N. Zayko
Department of Applied Informatics and Information Technologies in Control, P.A. Stolypin’s Volga Regional Institute of State Service, Saratov, 410031, Russia
Correspondence to: Yuriy N. Zayko , Department of Applied Informatics and Information Technologies in Control, P.A. Stolypin’s Volga Regional Institute of State Service, Saratov, 410031, Russia.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
This article concerns the effect of gravitation field of the spherical electro-magnetic wave (EMW) on its propagation in vacuum. For this it was received a solution of the coupled Maxwell-Einstein equations. It is shown that in addition with traveling wave EMW at а great distance some new solution of so-called instanton type exists. It describes the process of quantum tunneling between degenerate states corresponding to convergent and divergent spherical waves in quasi-classical approximation. It is shown that these solutions for zero moment momentum describe fields of point-like charges – electric e and magnetic g. Symmetry of Maxwell equations with respect to group U(1) of dual transformations: (E+iH) → (E+iH)eiα, (E and H are electric and magnetic fields, α – is real parameter) is valid for generalized charge e + ig, which is transformed in the same manner. Spontaneous breaking of symmetry of this group, which is characterized tgα = - g/e, leads to arising mass-less particles (photons?) due to Goldstone theorem. This also leads to the fact that magnetic charges cannot be detected in Nature.
Keywords:
Gravitation, Electromagnetic Wave, Metrics, Instanton, Monopole
Cite this paper:
Yuriy N. Zayko , "Explicit Solutions of Maxwell-Einstein Equations", International Journal of Theoretical and Mathematical Physics, Vol. 1 No. 1, 2011, pp. 12-16. doi: 10.5923/j.ijtmp.20110101.02.
1. Introduction
The geometry of space-time is judged on light beam behavior[1]. It is commonly supposed that the form of light waves which is corresponding to these beams does not matter. It is shown below that it is not true, i.e. geometry will be different for plane and spherical waves, for example. The reason is connected with the gravitational field of spherical electromagnetic wave (SEMW). Indeed, beams normal to the front of SEMW are not parallel one to another and so their contribution to gravitational field is nonzero in general case. An expression for corresponding metric is presented in[2] for the case of week field. In the present article this effect is treated for the gravitational field of SEMW of arbitrary value. At the same time, beams normal to the front of plane electromagnetic (PEMW) wave are parallel one to another and do not have gravitational effect[2], so the corresponding metric is flat.
2. Basic Equations
Let us choose coupled Einstein’s equation of gravity and Maxwell’s equations of electromagnetic field in vacuum as basic ones[1,2]: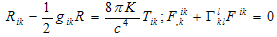 | (1) |
Here R – trace of Ricci’s tensor Rik: R = Rii , gik – metric tensor; Tik and Fik– tensor of energy-momentum and electromagnetic one; Гikl – Christoffel’s symbols; с – light speed in vacuum, K – gravitation constant; indices i, k, l take values 0, 1, 2, 3; repeated indices mean summation; comma means usual, i.e. non-covariant derivative[1]. Let us find a solution of (1) which corresponds to existence of spherical light wave at r → ∞. For this we use an expression for interval just as in well-known Schwarzschild problem[1]: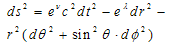 | (2) |
ν = ν(t, r, θ), λ = λ(t, r, θ); x0 =ct, t –time; x1= r, x2 = θ, x3 = φ – spherical co-ordinates. SEMW is characterized by frequency ω and moment momentum vector М. Let us choose z - axis of the co-ordinate system in direction perpendicular to M. It simplifies a treating because the dependence of azimuth angle φ in (1) may be omitted. Second equation in (1) may be transformed to[1]: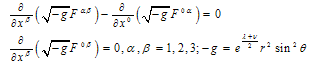 | (3) |
where α =1, 2 correspond for the SEMW of TM - type, and α=3 – for SEMW of TE-type. Below we restrict ourselves with the case of TM – type1, for which nonzero components of vector-potential and electromagnetic tensor are only А1, А2 and: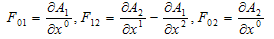 | (4) |
We use the Hamilton calibration А0 = 0. For variables’ separation we assume an additional condition: λ =α(r, t)+β(θ), ν = -α(r, t)+β(θ). Substitution of (4) into (3) gives us two equations for the components А1 and А2: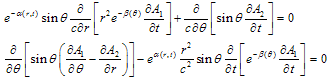 | (5) |
First equation in (3) follows from (5). If we take a derivative of the first equation in (5) on r and second – on ct, then we exclude A2 from the equations. Representing F01 = Ψ(r,t)·Φ(θ), we receive equations for Ψ(r,t) and Φ(θ):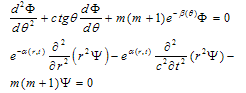 | (6) |
It leads from (6) that for β → 0 Φ(cosθ) = Pm(cosθ), where Pm (cosθ) – Legendre polinomial, and m is nonnegative integer[3,4].
3. Tensor of Energy-Momentum
Energy-momentum tensor’s components Tki may be expressed by the components of metric tensor gki with the help of Einstein’s equation of gravity [1]: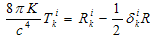 | (7) |
where δki – unit 4-tensor, and R – is a trace of tensor Rik. The details of calculations one can find in[1], for example. Besides Christoffel’s symbols presented in[1], we need some additional ones; a symbol ~ means a derivative by the angle θ :A result looks as follows: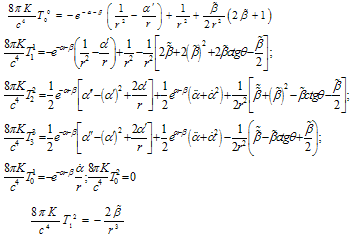 | (8) |
Let us express components of the energy-momentum tensor Tki from the Maxwell equation’s solutions Tik = (-FilFkl + δikFlmFlm/4)/4π[1]: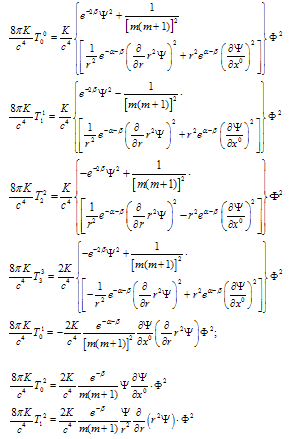 | (8a) |
One must assume the right-hand sides of (8а) in a sense of mean-time values, but this procedure could be implemented in any stage of calculations.
4. Solution of the Equations
If one subtracts the second equation from the first, and the fourth from the third in (8a) and equals their results to the same ones in (8) he came to the following equations: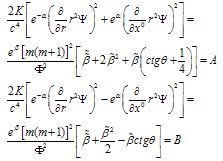 | (9) |
The constants А and В are the integrals for the equations (6). The equation which is led from the expressions for T01 in (8) and (8a) after time-meaning procedure looks as follows: Average in time T02 gives identity.Note that average procedure does not change the equations (9).Second equation in (6) describes plane running wave at r → ∞, what leads to the condition В = 0. If one expresses eα from the second equation (9) with the help of solutions of wave equation and substitutes it to the second equation (6), then he receives an equation: 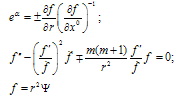 | (10) |
Prime means the derivative on x1 = r and point – on x0, respectively; signs “±” correspond to convergent and divergent waves. A boundary condition for this equation is the presence of plane running wave at r → ∞. The solutions of (6), corresponding to the first equation in (9) one can treat in pseudo-Euclead space which metric follows from the Minkowski space’s metric with substitution time co-ordinate x0 to “time” co-ordinate –iy0 in pseudo-Euclead space. At the same time one can introduce pseudo-Euclead action Λ, which is connected with the action S in Minkowski’s space as follows Λ = iS , i = (-1)½. It is known [5] that localized solutions of Euclead field equations with finite Euclead action are instantons. An instantons of classical field equations in Minkowski’s space describe in quasi-classical limit tunneling between degenerate classical states, which are convergent and divergent SEMW. This procedure turns second hyperbolic equation in (6) to the elliptic one. If one suppose its finiteness at r → ∞ then he receives a condition А = 0 from the first equation (9). This provides second equation (6) looks as follows: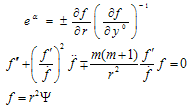 | (11) |
Here prime still means a derivative on x1 = r, and point – on y0. Right hand sides of the equations (9) determine functions β(θ). It is obvious from (9) that constant β(θ) = β0 is its solution. We consider below the case β0 = 0 2. This case is characterized by angle dependence of the SEMW field closely like to one in flat Galileo space-time.Let us treat solutions of equations (10) and (11). A solution of (10) in complex plane z looks as follows: f(z,t) = F(z)e±iωt, | z | = ωr/c, ω – frequency. For the F(z) we have an equation: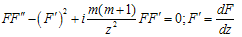 | (12) |
Its solution with abovementioned boundary condition: F ~ eiz at z → ∞ looks as follows: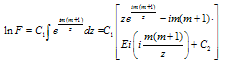 | (13) |
Ei(x) – is an integral exponent, C1 = i and C2 are constants. The value of eα=F'(z)/iF(z) in (10), which determines the metric one can receive with the help of the Dalembert-Euler formulas [6]: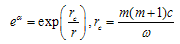 | (14) |
Analogously, solutions of (11) looks as follows: f(z, y0) = F(z)e±ωτ, z = ωr/c, y0 = cτ. Substituting this in (11) one can receive an equation for F(z):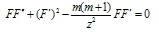 | (15) |
Prime means derivative on z. Its solution finite at z → ∞ looks as follows: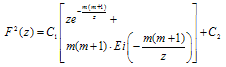 | (16) |
С1,2 are constants. A corresponding metric coefficient in (10) looks as follows (С2 = 0):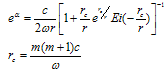 | (17) |
Action for (16) in distorted space-time looks as follows[1]: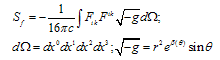 | (18) |
Corresponding action in pseudo-Euclead space is Λ = iSf , dx0 = -idy0. Taking into account norm integral for Φ(θ)[3], one can receive (for β = 0):Constant С1 > 0, because Λ > 0. Figure. 1 shows the dependence Λ(r0) versus instanton’s size r0 :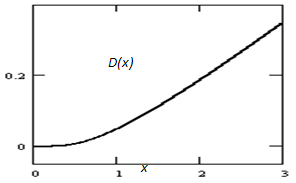 | Figure 1. Pseudo-Euclead action Λ versus instanton’s size r0. D(x) = Λ(x) /(С1/4с) -dimensionless action; x = r0 /rc – -dimensionless distance; m = 1. |
Let us treat geodesic’s behavior. An interval (2) for spherically symmetry of SEMW looks as follows ( dθ = dφ = 0):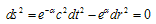 | (20) |
Taking into account value eα = exp(rc/r), one can receive an equation for geodesic lines: 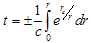 | (21) |
Figure. 2 shows its solutions. 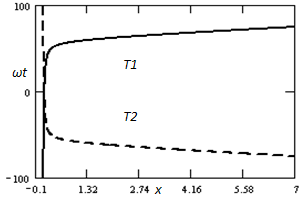 | Figure 2. Geodesic lines (light beams trajectories). Ti = ωt, x = r /rc; i = 1(solid curves) corresponds to sign “+”, i = 2 (dashed curves) corresponds to sign ““ in (21); m = 1. An ordinate axis has an abscissa х = - 0.1. |
Assuming that function under integral has a singularity at r = 0 low limit 0 of this integral is replaced by some little value b ≠ 0, which is going to 0 after evaluation. In case shown on Figure. 2 b = 0.15. This determines behavior of the curves on figure. Derivatives dr/dt on both branches of “light cone” become zero at r = 0, what is result of space-time distortion due to self-gravitational field of SEMW. From the point of view of distant observer light beam needs infinite time in order to achieve point r = 0 if value of m ≠ 0. It is so because integral (21) diverges and two branches (21) go to infinity for b→ 0. The geodesic lines in case m = 0 looks as follows: t = ± r / c. As it follows from above space-time geometry corresponding to SEMW differs from the one of flat space-time corresponding to PEMW. Besides that, instanton solutions of (1) brings new sight on the process of transformation of convergent SEMW to divergent one. Indeed, convergent SEMW with m ≠ 0 becomes divergent one during finite time only if it transfers to instanton state3 at some r0 with finite probability ~ exp(-2Λ0 / ћ) (ћ is a Planck constant, Λ0 = Λ(r0)) and vice versa. It means in turn that no information from sphere of radius r0 can be transferred from the past to future. Value of r0 is not determined by theory.
5. Solutions with m = 0
Let us treat solutions of Maxwell-Einstein equations, or more precisely of Maxwell ones, which is corresponding to value m = 0. As it may be shown they have a form (in TM-case):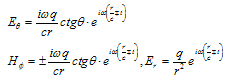 | (22) |
q is a constant, signs ± in the exponent correspond to convergent and divergent waves. In TE-case corresponding solutions have similar form with the substitution E → -H, H → E[7]. These solutions usually are out of consideration in traditional electrodynamics due to their singularity at the polar axis. More over, there exists a rigorous theorem[4] which declares that Maxwell equations in vacuum have only trivial, i.e. zero solutions with irradiative boundary conditions, so constant q must has zero value in (22). But if we consider static case ω = 0, we find immediately that last equation in (22) describes an electrical field of point-like charge q = e in vacuum4. This feature of Maxwell equations is seeming strange but it is in correspondence with the Einstein’s point of view: ”I feel that it is a delusion to think of the electrons and the fields as two physically different, independent entities. Since neither can exist without the other, there is only one reality to be described, which happens to have two different aspects; and the theory ought to recognize this from the start instead of doing things twice” (cited in [8, p.32]). It does not contradict the essence of problem, because charge and fluid densities (but not charge) stay zero. Problems which are generated by the solutions (22) are connecting with their interpretation. In the case of TE-waves that solutions describe a well-known P.A.M. Dirac’s monopole. It is interesting, that in this case problems are overwhelmed, or bypassed, with the assumption that these hypothetical objects exist in the outer regions of the Universe and are still unavailable for detecting[9].Let us prove that within Einstein’s conception absence of monopoles in Nature is principal and is connected with zero photon mass. Transformation concerned earlier E → -H, H → E is a special case of Maxwell vacuum equations’ invariance with respect of continuous group of “dual symmetry” U(1): (E+iH) → (E+iH)eiα, where α – is a real parameter (dual phase)[9]. In the case of traditional electrodynamics zero photon mass is leading from calibration invariance of the Lagrangian of interaction[10]. In our case “charges” q are intrinsic characteristics of electromagnetic field and calibration group does not matter for description of their interaction, because the interaction is absent. Dual group plays its role in proof of zero value of photon mass. Symmetry of dual group is valid for “charges” q in (22) too. They transform as follows: (e + ig) → (e + ig)eiα where e denotes value of electrical “charge” and g does the same for magnetic one. Zero value of magnetic “charge” is connected with spontaneous breaking of dual group’s symmetry, what is characterizing with tg α = -g/e. According to Goldstone’s theorem this leads to arising of particles, which mass is equal zero – photons. It is shown in quantum theory that tg α ≈ -137n/2, n- is integer, and α ≈ -π/2 5
6. Conclusions
The conclusion that gravity of SEMW is connected with only its anisotropic, i.e. non-spherical part was known earlier[2]. In[2] a case of week gravitation fields of finite light beams is treated. One can receive a distribution of beams velocities near the basic beam which speed is taking as 1. First of all, one needs an expression for the interval ds near basic beam, passing along x axis[2]: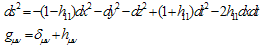 | (23) |
Here hμν is additions to the Galileo metric tensor δμν of flat space-time. For light beams ds2 = 0. Dividing ds2 in (23) on dt2 one can receive an equation for speeds of probe beams near basic one:This in turn can be presented as follows: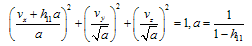 | (25) |
One can see from (25) that spherical symmetry in probe beams’ speed distribution takes place only if h11 = 0, what corresponds to the absence of gravity.The main result of present article is that Universe looks like as real channels of information, i.e. channels with noises, which need infinite time in order to transfer information completely.
ACKNOWLEDGMENTS
Author would like to thanks prof. S.A. Smolyansky and prof. M.V. Davidovich for discussions.
Notes
1. A solution for the SEMW of TE – type does not need separate treating because Maxwell-Einstein equations are invariant with the transformation Е → -Н, Н → Е, (so as Maxwell ones ) due to invariance of energy-momentum tensor Тik2. In case β ≠ 0, corresponding to flat-less metric at infinity one has a condition for m: m(m+1)e-β = k(k+1), where k is nonnegative integer. A solution of this equation is m = k = 0 or random β. This corresponds to effective value rc = 0.3. Instantons reconstruct the symmetry of time inversion, i.e. t → -t, of the equations (6), what is violated for its solution (13). 4. Or magnetic field of point-like magnetic charge q = g for dual-transformed analog of (22)5.As is shown in author’s article[11], there was another mass-less “particle”, corresponding to this violation of symmetry. Equation of motion for this “particle” looks as follows: αt + v·grad α= 0, v is a speed of energy propagation of electro-magnetic wave, α is so-called “dual phase”, mentioned above. More over, field E + iH ((22) and its dual transformed analog) corresponds to radiation of dion, hypothetical particle which has both electric and magnetic charge, placed in the point r = 0.
References
| [1] | L.D. Landau, E.M. Lifshits. Course of Theoretical Physics, Vol. 5. Theory of Fields, Nauka, Moscow (1967).-460 p |
| [2] | R.C. Tolman. Relativity Thermodynamics and Cosmology, Clarendon Press, Oxford (1969) |
| [3] | G. Arfken. Mathematical Methods for Physicists, Academic Press, NY and London |
| [4] | G.T. Markov, A.F. Chaplin. An Exсitation of Electromagnetic Waves. Energy, Moscow (1966).- 376 p |
| [5] | R. Rajaraman. An Introduction to Solitons and Instantons in Quantum Field Theory. North-Holland Publishing Company, Amsterdam-NY-Oxford (1982) |
| [6] | М.А. Lavrent’ev, B.V. Shabat. Methods of complex variables theory. Nauka, Мoscow (1958).- 678 p |
| [7] | V.V. Nikolsky, T.I. Nikolskaya. Electrodynamics and radio-wave propagation. Nauka, Moscow, (1989), 544 p |
| [8] | Carver A. Mead. Collective Electrodynamics I, in book “Feynmann and Computation. Exploring the Limits of Computers. Ed. By A.J.G. Hey, Perseus Books, Reading, Massachusetts, (1998).- 438 p. http://www.aw.com/gb /abp/ |
| [9] | A. D. Dolgov Magnetic monopole// Physical Encyclopedia: in 5 vol., Moscow: Soviet Encyclopedia Publishing, 1990, V. 2, pp. 687-688 |
| [10] | V.B. Berestetsky. Problems in Physics of Elementary Particles. Nauka, Moscow, (1979).- 256 p |
| [11] | Y. N. Zayko Dynamics of dual phase. – To be published |

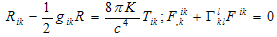
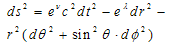
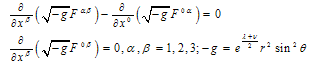
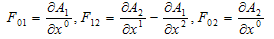
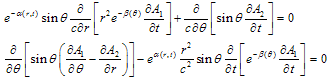
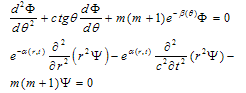
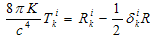
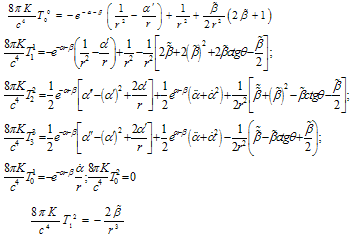
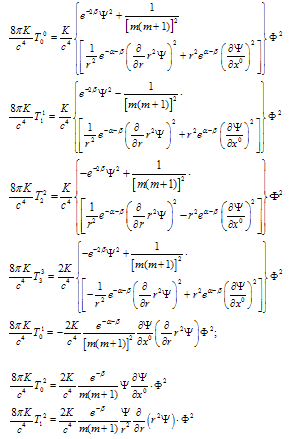
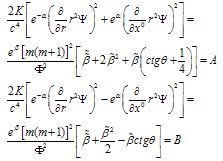
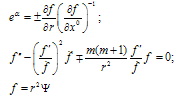
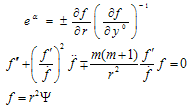
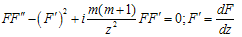
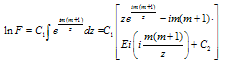
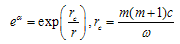
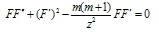
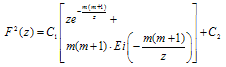
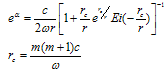
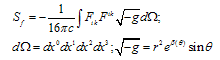

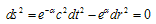
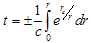
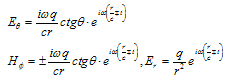
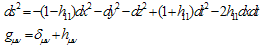
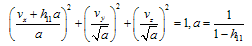
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML