-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Theoretical and Mathematical Physics
p-ISSN: 2167-6844 e-ISSN: 2167-6852
2011; 1(1): 1-11
doi: 10.5923/j.ijtmp.20110101.01
Quantum Theory at Planck Scale, Dynamical Cosmological Term and Deformed Gravity
A. E. Shalyt-Margolin
National Centre of Particles and High Energy Physics, Bogdanovich Str. 153, Minsk, 220040, Belarus
Correspondence to: A. E. Shalyt-Margolin , National Centre of Particles and High Energy Physics, Bogdanovich Str. 153, Minsk, 220040, Belarus.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
The dark energy problem is analyzed from the viewpoint of the time-varying cosmological term. It is demonstrated that, at least within the scope of the holographic principle, an experimental value of the vacuum energy density may be derived and may be tested quite well with a new small parameter arising in a quantum theory with the fundamental length on the order of Planck’s length. Besides, within a theory proclaiming the existence of such fundamental length a high-energy deformation of the General Relativity for the space with horizon has been constructed. The obtained results have been applied to solving of the dark energy problem, making it possible to frame the following hypothesis: a dynamic cosmological term is a measure of deviation from a thermodynamic identity (the first law of thermodynamics) of the high-energy (Planck’s) deformation of Einstein equations for horizon spaces in their thermodynamic interpretation.
Keywords: Dark Energy, Fundamental Length, Deformation Parameter
Cite this paper: A. E. Shalyt-Margolin , "Quantum Theory at Planck Scale, Dynamical Cosmological Term and Deformed Gravity", International Journal of Theoretical and Mathematical Physics, Vol. 1 No. 1, 2011, pp. 1-11. doi: 10.5923/j.ijtmp.20110101.01.
Article Outline
1. Introduction
- The cosmological constant
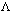 is presently the most probable candidate for a role of dark energy. However, more and more researchers arrive at the idea that
is presently the most probable candidate for a role of dark energy. However, more and more researchers arrive at the idea that 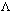 is a dynamic quantity
is a dynamic quantity 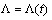 [1–3] rather than a constant. The idea is also supported by the inflation models pointing to the fact that in the early Universe the quantity was enormous[4], whereas this is evidently not so for the present-day Universe. If this is really the case, we have to appreciate time variations of this quantity and to realize why its current value conforms to the observable. It should be recalled that in the initial calculations of
[1–3] rather than a constant. The idea is also supported by the inflation models pointing to the fact that in the early Universe the quantity was enormous[4], whereas this is evidently not so for the present-day Universe. If this is really the case, we have to appreciate time variations of this quantity and to realize why its current value conforms to the observable. It should be recalled that in the initial calculations of 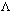 with the use of a quantum field theory (QFT) it was cut-off at large (Planck) momenta[5,6] and, actually, implicitly it was QFT with the fundamental length on the order of Planck’s
with the use of a quantum field theory (QFT) it was cut-off at large (Planck) momenta[5,6] and, actually, implicitly it was QFT with the fundamental length on the order of Planck’s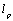 . On the other hand, in the last decade numerous works devoted to a Quantum Field Theory (QFT) at Planck’s scale[7–9] have been published(of course, the author has no pretensions of being exhaustive in his references). This interest stems from the facts that (i) at these scales it is expected to reveal the effects of a Quantum Gravity (QG), and this still unresolved theory is intriguing all the researchers engaged in the field of theoretical physics; (ii) modern accelerators, in particular LHC, have the capacity of achieving the energies at which some QG effects may be exhibited.Planck’s scales undergoes changes associated with the appearance of additional parameters related to a minimal length (on the order of the Planck’s length). As this takes place, the corresponding parameters are naturally considered as deformation parameters, i.e. the related quantum theories are considered as a high-energy deformation (at Planck’s scales) of the well-known quantum field theory. The deformation is understood as an extension of a particular theory by inclusion of one or several additional parameters in such a way that the initial theory appears in the limiting transition[10].The present work is a natural continuation of the previous papers of the author. The idea that a quantum theory at the Planck scales must involve the fundamental length has been put forward in the works devoted to a string theory fairly a long time ago[11]. But since it is still considered to be a tentative theory, some other indications have been required. Fortunately, by the present time numerous publications have suggested the appearance of the fundamental length in the Early Universe with the use of various approaches[12–15]. Of particular importance is the work[12], where on the basis of a simple gedanken experiment it is demonstrated that, with regard to the gravitational interactions (Planck’s scales) exhibited in the Early Universe only, the Heisenberg Uncertainty Principle should be extended to the Generalized Uncertainty Principle[11–15]that in turn is bound to bring forth the fundamental length on the order of Planck’s length. The advent of novel theories in physics of the Early Universe is associated with the introduction of new parameters, i.e. with a deformation of the well-known theories. Of course, in this case Heisenberg Algebra is subjected to the corresponding deformation too. Such a deformation may be based on the Generalized Uncertainty Principle (GUP)[16–18] as well as on the density matrix deformation[19–29]. At the same time, the above-mentioned new deformation parameters so far have not appeared in gravity despite the idea that they should. The situation is that no evident efforts have been undertaken to develop the high-energy (Planck’s scale) gravity deformations including the deformation parameters introduced in a Quantum Theory of the Early Universe. In this paper, with GUP held true, the possibility for the high-energy gravity deformation is considered for a specific case of Einstein’s equations. As this takes place, the parameter
. On the other hand, in the last decade numerous works devoted to a Quantum Field Theory (QFT) at Planck’s scale[7–9] have been published(of course, the author has no pretensions of being exhaustive in his references). This interest stems from the facts that (i) at these scales it is expected to reveal the effects of a Quantum Gravity (QG), and this still unresolved theory is intriguing all the researchers engaged in the field of theoretical physics; (ii) modern accelerators, in particular LHC, have the capacity of achieving the energies at which some QG effects may be exhibited.Planck’s scales undergoes changes associated with the appearance of additional parameters related to a minimal length (on the order of the Planck’s length). As this takes place, the corresponding parameters are naturally considered as deformation parameters, i.e. the related quantum theories are considered as a high-energy deformation (at Planck’s scales) of the well-known quantum field theory. The deformation is understood as an extension of a particular theory by inclusion of one or several additional parameters in such a way that the initial theory appears in the limiting transition[10].The present work is a natural continuation of the previous papers of the author. The idea that a quantum theory at the Planck scales must involve the fundamental length has been put forward in the works devoted to a string theory fairly a long time ago[11]. But since it is still considered to be a tentative theory, some other indications have been required. Fortunately, by the present time numerous publications have suggested the appearance of the fundamental length in the Early Universe with the use of various approaches[12–15]. Of particular importance is the work[12], where on the basis of a simple gedanken experiment it is demonstrated that, with regard to the gravitational interactions (Planck’s scales) exhibited in the Early Universe only, the Heisenberg Uncertainty Principle should be extended to the Generalized Uncertainty Principle[11–15]that in turn is bound to bring forth the fundamental length on the order of Planck’s length. The advent of novel theories in physics of the Early Universe is associated with the introduction of new parameters, i.e. with a deformation of the well-known theories. Of course, in this case Heisenberg Algebra is subjected to the corresponding deformation too. Such a deformation may be based on the Generalized Uncertainty Principle (GUP)[16–18] as well as on the density matrix deformation[19–29]. At the same time, the above-mentioned new deformation parameters so far have not appeared in gravity despite the idea that they should. The situation is that no evident efforts have been undertaken to develop the high-energy (Planck’s scale) gravity deformations including the deformation parameters introduced in a Quantum Theory of the Early Universe. In this paper, with GUP held true, the possibility for the high-energy gravity deformation is considered for a specific case of Einstein’s equations. As this takes place, the parameter 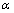 appearing in the Quantum Field Theory (QFT) with the UV cut off (fundamental length) produced by the density matrix deformation is used. There is no discrepancy of any kind as the deformation parameter in the GUP- produced Heisenberg algebra deformation is quite naturally expressed in terms of
appearing in the Quantum Field Theory (QFT) with the UV cut off (fundamental length) produced by the density matrix deformation is used. There is no discrepancy of any kind as the deformation parameter in the GUP- produced Heisenberg algebra deformation is quite naturally expressed in terms of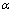 , and this will be shown later (Section 3). Besides, by its nature,
, and this will be shown later (Section 3). Besides, by its nature, 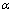 is better applicable to study the high-energy deformation of General Relativity because it is small, dimensionless (making series expansion more natural), and the corresponding representation of the Einstein’s equations in its terms or its deformation appear simple. Structurally, the paper is as follows. Section 2 presents a short discussion o the notion of a dynamic cosmological term and also the general problem statement associated with its connection to the dark energy problem. In Section 3 the approaches to the deformation of a quantum theory at the Planck scales are briefly reviewed. In Section 4 the possibilities for derivation of a modern value of the dark energy in the assumption of the existing dynamic cosmological term
is better applicable to study the high-energy deformation of General Relativity because it is small, dimensionless (making series expansion more natural), and the corresponding representation of the Einstein’s equations in its terms or its deformation appear simple. Structurally, the paper is as follows. Section 2 presents a short discussion o the notion of a dynamic cosmological term and also the general problem statement associated with its connection to the dark energy problem. In Section 3 the approaches to the deformation of a quantum theory at the Planck scales are briefly reviewed. In Section 4 the possibilities for derivation of a modern value of the dark energy in the assumption of the existing dynamic cosmological term 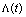 are analyzed using the standard approach to the cosmological constant
are analyzed using the standard approach to the cosmological constant  [5,6]. It is shown that only the validity of the holographic principle gives the required result. This Section is mainly based on the author’s results[30,31]. In Section 5 it is shown how to interpret quantum corrections for the thermodynamic characteristics of black holes considering the deformation of a theory with the fundamental length[31]. Essentially new results are presented in Sections 5 and thermodynamic description of the General Relativity is used. The possibility for the high energy deformation of Einstein’s equations is discussed within the scope of both equilibrium thermodynamics and non-equilibrium thermodynamics. In the latter case the approach is contemplated only in terms of a nature of the cosmological term. Moreover, in this case a more precise definition for the dependence of this term on the deformation parameter is possible. In Section 7 the derived results are applied to solve the dark energy problem. Based on the results obtained, in Conclusion the following hypothesis is framed: a dynamic cosmological term is a measure of deviation from the thermodynamic identity (the first law of thermodynamics) of the high-energy (Planck’s) deformation of Einstein equations for horizon spaces in their thermodynamic interpretation.
[5,6]. It is shown that only the validity of the holographic principle gives the required result. This Section is mainly based on the author’s results[30,31]. In Section 5 it is shown how to interpret quantum corrections for the thermodynamic characteristics of black holes considering the deformation of a theory with the fundamental length[31]. Essentially new results are presented in Sections 5 and thermodynamic description of the General Relativity is used. The possibility for the high energy deformation of Einstein’s equations is discussed within the scope of both equilibrium thermodynamics and non-equilibrium thermodynamics. In the latter case the approach is contemplated only in terms of a nature of the cosmological term. Moreover, in this case a more precise definition for the dependence of this term on the deformation parameter is possible. In Section 7 the derived results are applied to solve the dark energy problem. Based on the results obtained, in Conclusion the following hypothesis is framed: a dynamic cosmological term is a measure of deviation from the thermodynamic identity (the first law of thermodynamics) of the high-energy (Planck’s) deformation of Einstein equations for horizon spaces in their thermodynamic interpretation. 2. Dark Energy and Dynamical Cosmological Term
- The dark matter problem[32], along with the dark energy problem[33], is presently the basic problem in modern fundamental physics, astrophysics, and cosmology. Whereas for a nature of the first real hypotheses have been accepted already[34], the dark energy still remains enigmatic[35–38]. But it is the opinion of most researchers that dark energy represents the energy of the cosmic vacuum, its density being associated with the cosmological term
 in Einstein’s equation[5,6,39]. In this respect an important reservation must be made – the point is that most common is the term cosmological constant. Actually, due to the Bianchi identities[40]
in Einstein’s equation[5,6,39]. In this respect an important reservation must be made – the point is that most common is the term cosmological constant. Actually, due to the Bianchi identities[40] 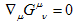 | (1) |
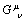 – Einstein equations
– Einstein equations 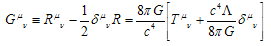 | (2) |
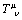 (energy-momentum density tensor) remains covariantly valid
(energy-momentum density tensor) remains covariantly valid 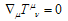 | (3) |
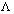 is a constant. But, as has been rightly noted in several publications (e.g.,[1–3]), conservation laws (3) are only regulating the energy-momentum exchange between the field sources and gravitational field and are liable to be violated if an independent energy source is existent in the Universe. Such a source may be associated with a time-varying cosmological term. So, in this case it is reasonable to consider
is a constant. But, as has been rightly noted in several publications (e.g.,[1–3]), conservation laws (3) are only regulating the energy-momentum exchange between the field sources and gravitational field and are liable to be violated if an independent energy source is existent in the Universe. Such a source may be associated with a time-varying cosmological term. So, in this case it is reasonable to consider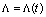 .Then the Bianchi identity (1) is replaced by the "generalized Bianchi identity"[2]
.Then the Bianchi identity (1) is replaced by the "generalized Bianchi identity"[2] 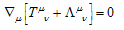 | (4) |
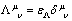 is some energy-momentum tensor (referred to as the dark energy-momentum tensor [2]) related to the cosmological term, where
is some energy-momentum tensor (referred to as the dark energy-momentum tensor [2]) related to the cosmological term, where 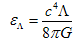 | (5) |
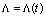 and different relationships between
and different relationships between 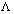 and
and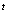 . Rather detailed references to such models have been made in the thesiswork[41]. Of interest is the problem: how can we obtain the observable value of
. Rather detailed references to such models have been made in the thesiswork[41]. Of interest is the problem: how can we obtain the observable value of 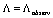 knowing that
knowing that 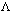 is dependent on .
is dependent on . 3. Quantum Theory at Planck’s Scale and Universal Deformation Parameter
- In the last twenty years the researchers have come to the understanding that studies of the Early Universe physics (extremely high – Planck’s energies) necessitate changes in the fundamental physical theories, specifically quantum mechanics and quantum field theory. Inevitably a fundamental length should be involved in these theories[14–17]. This idea has been first suggested by a string theory[11]. But it is still considered to be a tentative theory without the experimental status and merely an attractive model. However, the fundamental length has been involved subsequently in more simple and natural considerations[12]. The main approach to framing of Quantum Mechanics with fundamental length (QMFL) and Quantum Field Theory with fundamental length (QFTFL) (or with Ultraviolet (UV) cutoff) is that associated with the Generalized Uncertainty Principle (GUP)[11–18]:
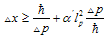 | (6) |
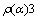 and deformation parameter (additional parameter)
and deformation parameter (additional parameter) 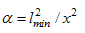 | (7) |
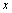 is the measuring scale,
is the measuring scale, 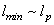 and
and 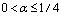 [19–25]. The explicit form of the above-mentioned deformation gives the exponential ansatz
[19–25]. The explicit form of the above-mentioned deformation gives the exponential ansatz 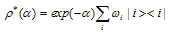 | (8) |
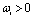 are independent of
are independent of 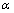 and their sum is equal to 1. In the corresponding deformed Quantum Theory (denoted as
and their sum is equal to 1. In the corresponding deformed Quantum Theory (denoted as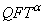 ) for average values we have
) for average values we have 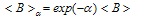 | (9) |
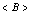 - average in well-known QFT[24,25]. All the variables associated with the considered
- average in well-known QFT[24,25]. All the variables associated with the considered 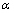 - deformed quantum field theory are hereinafter marked with the upper index
- deformed quantum field theory are hereinafter marked with the upper index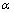 . Note that the deformation parameter
. Note that the deformation parameter 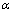 is absolutely naturally represented as a ratio between the squared UV and IR limits
is absolutely naturally represented as a ratio between the squared UV and IR limits 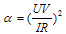 | (10) |
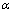 -deformation of QFT has been formed. By “minimal” it is meant that no space-time noncommutativity was required, i.e. there was no requirement for noncommutative operators associated with different spatial coordinates
-deformation of QFT has been formed. By “minimal” it is meant that no space-time noncommutativity was required, i.e. there was no requirement for noncommutative operators associated with different spatial coordinates 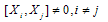 | (11) |
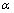 -deformation of QFT –
-deformation of QFT – 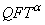 [19-28] to some new deformation
[19-28] to some new deformation 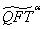 compatible with GUP, as it has been noted in[29]. We can easily show that QFT parameter of deformations associated with GUP may be expressed in terms of the parameter
compatible with GUP, as it has been noted in[29]. We can easily show that QFT parameter of deformations associated with GUP may be expressed in terms of the parameter 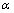 that has been introduced in the approach associated with the density matrix deformation[30,31]. Here the notation of[42] is used. Then
that has been introduced in the approach associated with the density matrix deformation[30,31]. Here the notation of[42] is used. Then 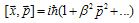 | (12) |
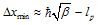 | (13) |
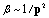 , and for
, and for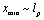 ,
, 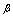 corresponding to
corresponding to 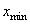 is nothing else but
is nothing else but 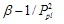 | (14) |
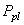 is Planck’s momentum:
is Planck’s momentum: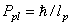 . In this way
. In this way 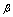 is changing over the following interval:
is changing over the following interval: 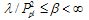 | (15) |
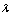 is a numerical factor and the second member in (12) is accurately reproduced in momentum representation (up to the numerical factor) by
is a numerical factor and the second member in (12) is accurately reproduced in momentum representation (up to the numerical factor) by 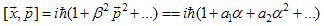 | (16) |
4. Dynamical Cosmological Term and Its Modern Value
- As is known, a direct calculation of the vacuum energy density
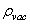 results in the value that is higher than the experimental one by a factor of
results in the value that is higher than the experimental one by a factor of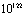 . According to the typical reasoning that is already “canonical” we have[5,6,43]:
. According to the typical reasoning that is already “canonical” we have[5,6,43]: 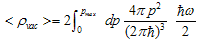 | (17) |
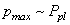 is the momentum cut-off at Planck scales, because the General Relativity is valid right up to the Planck scales. Proceeding from
is the momentum cut-off at Planck scales, because the General Relativity is valid right up to the Planck scales. Proceeding from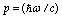 , we can obtain[43]
, we can obtain[43]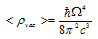 | (18) |
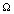 is given by
is given by 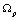 , where
, where 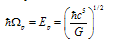 | (19) |
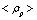 is higher than the observable value
is higher than the observable value 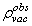 [6,43] approximately by a factor of
[6,43] approximately by a factor of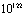 . Yet, taking the cosmological term as a dynamic quantity, we can write (17) as
. Yet, taking the cosmological term as a dynamic quantity, we can write (17) as 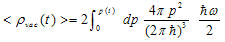 | (20) |
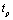 , turns to (17) as follows:
, turns to (17) as follows: 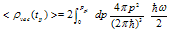 | (21) |
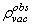 is sooner determined by low momenta and energies (corresponding to large scales) and also by the infrared limit that is given by a radius of the measurable part of the Universe
is sooner determined by low momenta and energies (corresponding to large scales) and also by the infrared limit that is given by a radius of the measurable part of the Universe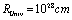 . For such momenta by the uncertainty principle (17) we have
. For such momenta by the uncertainty principle (17) we have 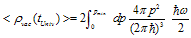 | (22) |
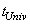 –Universe life-time,
–Universe life-time, 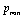 –"minimal" momentum.As
–"minimal" momentum.As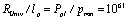 , then by analogy (18)and in the infrared limit
, then by analogy (18)and in the infrared limit 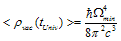 | (23) |
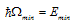 | (24) |
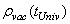 is lower than
is lower than 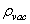 calculated from(17) by a factor of
calculated from(17) by a factor of 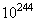 rather than by a factor of
rather than by a factor of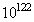 . This result is easily obtained using the Uncertainty Principle for the pair of conjugate variables
. This result is easily obtained using the Uncertainty Principle for the pair of conjugate variables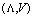 ,[44–47]:
,[44–47]: 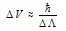 | (25) |
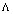 is the dynamic cosmological term,
is the dynamic cosmological term, 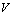 is the space-time volume. And
is the space-time volume. And 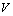 results from the Einstein- Hilbert action
results from the Einstein- Hilbert action 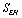 [45]:
[45]: 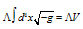 | (26) |
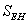 . In[30,31] the Uncertainty Principle (25) has been generalized at Planck scales up to the Generalized Uncertainty Principle
. In[30,31] the Uncertainty Principle (25) has been generalized at Planck scales up to the Generalized Uncertainty Principle 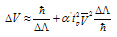 | (27) |
 - spatial part
- spatial part  that, as is assumed, may be extracted explicitly.(27) is of interest from the viewpoint of two limits[30,31]:1) IR - limit:
that, as is assumed, may be extracted explicitly.(27) is of interest from the viewpoint of two limits[30,31]:1) IR - limit: 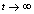 2) UV - limit:
2) UV - limit: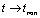 . In the case of IR-limit we have large volumes
. In the case of IR-limit we have large volumes 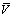 and
and 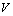 at low
at low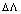 . Because of this, the main contribution on the right-hand side of (27) is made by the first term, as great
. Because of this, the main contribution on the right-hand side of (27) is made by the first term, as great 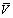 in the second term is damped by small
in the second term is damped by small 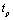 and
and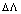 . Thus, we derive at
. Thus, we derive at 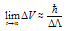 | (28) |
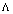 is a dynamic value fluctuating around zero. And for the case 2)
is a dynamic value fluctuating around zero. And for the case 2) 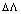 becomes significant
becomes significant 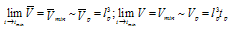 | (29) |
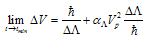 | (30) |
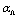 absorbs all the above-mentioned proportionality coefficients. For (30),
absorbs all the above-mentioned proportionality coefficients. For (30),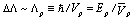 .It is easily seen that in this case
.It is easily seen that in this case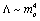 , in agreement with the value obtained using a standard (i.e. without super-symmetry and the like) quantum field theory[6,5]. Despite the fact that at Planck’s scales (referred to as
, in agreement with the value obtained using a standard (i.e. without super-symmetry and the like) quantum field theory[6,5]. Despite the fact that at Planck’s scales (referred to as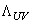 ) (30) is also a dynamic quantity, it is not directly related to well-known
) (30) is also a dynamic quantity, it is not directly related to well-known 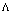 (25),(28) (called
(25),(28) (called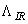 ) because the latter, as opposed to the first one, is derived from Einstein’s equations
) because the latter, as opposed to the first one, is derived from Einstein’s equations 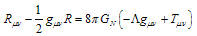 | (31) |
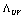 may be considered as some high-energy generalization of the conventional cosmological constant, leading to
may be considered as some high-energy generalization of the conventional cosmological constant, leading to 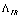 in the low-energy limit. As
in the low-energy limit. As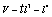 , where
, where 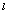 -characteristic linear dimension
-characteristic linear dimension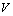 , it is directly inferred that in the infrared region calculated for
, it is directly inferred that in the infrared region calculated for 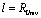 is lower than
is lower than 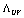 in
in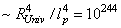 , that is in a perfect agreement with the result obtained by the direct calculations at the beginning of this Section. In other words, a quantum field theory with UV-cutoff in the assumption that is a dynamic quantity gives no correct value for
, that is in a perfect agreement with the result obtained by the direct calculations at the beginning of this Section. In other words, a quantum field theory with UV-cutoff in the assumption that is a dynamic quantity gives no correct value for 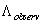 as well. In this way, similar to[48,49], we obtain
as well. In this way, similar to[48,49], we obtain 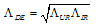 | (32) |
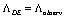 – cosmological term corresponding to the observable value. Now we demonstrate that the Holographic Principle[50–53] is helpful in the solution of this problem, the deformation parameter
– cosmological term corresponding to the observable value. Now we demonstrate that the Holographic Principle[50–53] is helpful in the solution of this problem, the deformation parameter 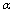 (7)”testing” variations of
(7)”testing” variations of 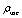 in time and hence playing the critical role. In terms of the deformation parameter , the principal values of the Vacuum Energy Problem may be simply and clearly defined. Let us begin with the Schwarzschild black holes, whose semiclassical entropy is given by
in time and hence playing the critical role. In terms of the deformation parameter , the principal values of the Vacuum Energy Problem may be simply and clearly defined. Let us begin with the Schwarzschild black holes, whose semiclassical entropy is given by 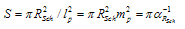 | (33) |
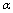
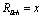 is the measuring scale and
is the measuring scale and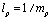 . Here
. Here 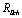 is the adequate Schwarzschild radius, and
is the adequate Schwarzschild radius, and 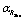 is the value of
is the value of 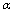 associated with this radius. Then, as it has been pointed out in [55], in case the Fischler - Susskind cosmic holographic conjecture[56] is valid, the entropy of the Universe is limited by its "surface" measured in Planck units[55]:
associated with this radius. Then, as it has been pointed out in [55], in case the Fischler - Susskind cosmic holographic conjecture[56] is valid, the entropy of the Universe is limited by its "surface" measured in Planck units[55]: 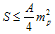 | (34) |
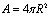 is defined in terms of the apparent (Hubble) horizon
is defined in terms of the apparent (Hubble) horizon 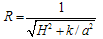 | (35) |
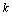 and scale
and scale 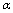 factors. Again, interpreting from (35) as a measuring scale, we directly obtain(34) in terms of :
factors. Again, interpreting from (35) as a measuring scale, we directly obtain(34) in terms of : 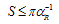 | (36) |
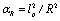 . Therefore, the average entropy density may be found as
. Therefore, the average entropy density may be found as 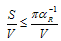 | (37) |
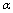 parameter one can easily estimate the upper limit for the energy density of the Universe (denoted here by
parameter one can easily estimate the upper limit for the energy density of the Universe (denoted here by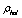 ):
): 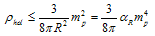 | (38) |
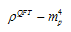 | (39) |
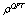 we denote the energy vacuum density calculated from well-known QFT (without UV cutoff)[5]. Obviously, as
we denote the energy vacuum density calculated from well-known QFT (without UV cutoff)[5]. Obviously, as 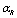 for
for 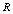 determined by (35) is very small, actually approximating zero,
determined by (35) is very small, actually approximating zero, 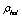 is by several orders of magnitude smaller than the value expected in QFT –
is by several orders of magnitude smaller than the value expected in QFT –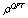 .Since
.Since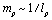 , the right-hand side of (38) is actually nothing else but the energy density in Holographic Dark Energy Models[57–60]. Thus, in Holographic Dark Energy Models the principal quantity, holographic energy density
, the right-hand side of (38) is actually nothing else but the energy density in Holographic Dark Energy Models[57–60]. Thus, in Holographic Dark Energy Models the principal quantity, holographic energy density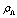 , may be estimated in terms of the deformation parameter
, may be estimated in terms of the deformation parameter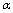 .In fact, the upper limit of the right-hand side of (38) is attainable, as it has been indicated in[55]. The "overestimation" value of
.In fact, the upper limit of the right-hand side of (38) is attainable, as it has been indicated in[55]. The "overestimation" value of 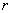 for the energy density
for the energy density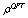 , compared to
, compared to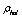 , may be determined as
, may be determined as 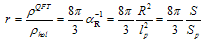 | (40) |
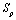 is the entropy of the Plank mass and length for the Schwarzschild black hole. It is clear that due to smallness of
is the entropy of the Plank mass and length for the Schwarzschild black hole. It is clear that due to smallness of 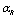 the value of
the value of 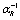 is on the contrary too large. It may be easily calculated (e.g., see[55])
is on the contrary too large. It may be easily calculated (e.g., see[55]) 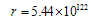 | (41) |
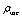 is involved in
is involved in 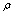 as a term
as a term 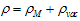 | (42) |
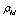 - average matter density, in case of
- average matter density, in case of 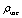 we can arrive to the same upper limit (right-hand side of the formula (38)) as for
we can arrive to the same upper limit (right-hand side of the formula (38)) as for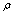 .Average values of any quantity in QFT with UV-cutoff may be expended in terms of the small parameter
.Average values of any quantity in QFT with UV-cutoff may be expended in terms of the small parameter 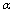 (Section 3). Specifically, for the vacuum energy density
(Section 3). Specifically, for the vacuum energy density 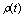 in the most general case we have
in the most general case we have 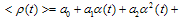 | (43) |
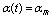 :
: 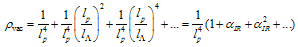 | (44) |
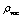 is understood as the quantity calculated for
is understood as the quantity calculated for 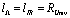 and
and 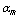 corresponds to
corresponds to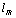 .But as shown previously, if the holographic principle is valid, this expansion has a more exact form
.But as shown previously, if the holographic principle is valid, this expansion has a more exact form  | (45) |
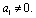
5. Gravitational Thermodynamics in Low and High Energy and Deformed Quantum Theory
- In the last decade a number of very interesting works have been published. We can primary name the works[61–70], where gravitation, at least for the в spaces with horizon, is directly associated with thermodynamics and the results obtained demonstrate a holographic character of gravitation. Of the greatest significance is a pioneer work[54]. For black holes the association has been first revealed in[71,72], where related the black-hole event horizon temperature to the surface gravitation. In[69], has shown that this relation is not accidental and may be generalized for the spaces with horizon. As all the foregoing results have been obtained in a semiclassical approximation, i.e. for sufficiently low energies, the problem arises: how these results are modified when going to higher energies. In the context of this paper, the problem may be stated as follows: since we have some infra- red (IR) cutoff
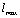 and ultraviolet (UV) cutoff
and ultraviolet (UV) cutoff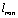 , we naturally have a problem how the above-mentioned results on Gravitational Thermodynamics are changed for
, we naturally have a problem how the above-mentioned results on Gravitational Thermodynamics are changed for 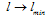 | (46) |
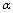 (33), (10) that in the accepted notation is of the form
(33), (10) that in the accepted notation is of the form 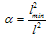 | (47) |
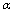 arises naturally. Indeed, modification of the Hawking temperature is of the following form[73,75,78]:
arises naturally. Indeed, modification of the Hawking temperature is of the following form[73,75,78]: 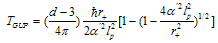 | (48) |
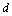 is the space-time dimension, and
is the space-time dimension, and 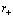 is the uncertainty in the emitted particle position by the Hawking effect, expressed as
is the uncertainty in the emitted particle position by the Hawking effect, expressed as 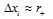 | (49) |
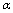 – dimensionless constant from GUP. But as we have
– dimensionless constant from GUP. But as we have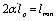 , in terms of
, in terms of 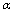 (48) may be written in a natural way as follows:
(48) may be written in a natural way as follows: 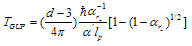 | (50) |
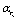 - parameter
- parameter 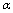 associated with the IR-cutoff
associated with the IR-cutoff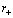 . In such a manner
. In such a manner 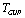 is only dependent on the constants including the fundamental ones and on the deformation parameter
is only dependent on the constants including the fundamental ones and on the deformation parameter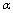 .The dependence of the black hole entropy on
.The dependence of the black hole entropy on 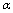 may be derived in a similar way. For a semiclassical approximation of the Bekenstein-Hawking formula[71,72]
may be derived in a similar way. For a semiclassical approximation of the Bekenstein-Hawking formula[71,72] 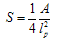 | (51) |
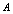 – surface area of the event horizon, provided the horizon event has radius
– surface area of the event horizon, provided the horizon event has radius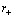 , then
, then 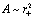 and (51) is clearly of the form
and (51) is clearly of the form 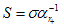 | (52) |
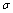 is some dimensionless denumerable factor. The general formula for quantum corrections[77] given as
is some dimensionless denumerable factor. The general formula for quantum corrections[77] given as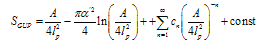 | (53) |
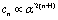 can always be computed to any desired order of accuracy[77], may be also written as a power series in
can always be computed to any desired order of accuracy[77], may be also written as a power series in 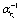 (or Laurent series in
(or Laurent series in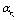 )
) 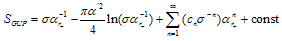 | (54) |
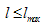 | (55) |
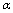 should be exhibited.Quite recently, in a series of papers, and specifically in[61–67], it has been shown that Einstein equations may be derived from the surface term of the GR Lagrangian, in fact containing the same information as the bulk term.It should be noted that Einstein’s equations[at least for space with horizon] may be obtained from the proportionality of the entropy and horizon area together with the fundamental thermodynamic relation connecting heat, entropy, and temperature[54]. In fact[61–68], this approach has been extended and complemented by the demonstration of holographicity for the gravitational action (see also[69]).And in the case of Einstein-Hilbert gravity, it is possible to interpret Einstein’s equations as the thermodynamic identity[70]:
should be exhibited.Quite recently, in a series of papers, and specifically in[61–67], it has been shown that Einstein equations may be derived from the surface term of the GR Lagrangian, in fact containing the same information as the bulk term.It should be noted that Einstein’s equations[at least for space with horizon] may be obtained from the proportionality of the entropy and horizon area together with the fundamental thermodynamic relation connecting heat, entropy, and temperature[54]. In fact[61–68], this approach has been extended and complemented by the demonstration of holographicity for the gravitational action (see also[69]).And in the case of Einstein-Hilbert gravity, it is possible to interpret Einstein’s equations as the thermodynamic identity[70]: 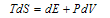 | (56) |
 , all the corresponding results should be modified (deformed) to meet the following requirements: (a) to be clearly dependent on the deformation parameter at high energies; (b) to be duplicated, with high precision, at low energies due to the suitable limiting transition. The problem may be more specific. As, according to[54, 69,70] and some other works, gravitation is greatly determined by thermodynamics, and at high energies the latter is a "deformation of the classical thermodynamics". Here "high- energy deformation of thermodynamics" is understood as some (meanwhile unknown) deformation of thermodynamics in high energies. This theory is still unframed, though several of its elements
, all the corresponding results should be modified (deformed) to meet the following requirements: (a) to be clearly dependent on the deformation parameter at high energies; (b) to be duplicated, with high precision, at low energies due to the suitable limiting transition. The problem may be more specific. As, according to[54, 69,70] and some other works, gravitation is greatly determined by thermodynamics, and at high energies the latter is a "deformation of the classical thermodynamics". Here "high- energy deformation of thermodynamics" is understood as some (meanwhile unknown) deformation of thermodynamics in high energies. This theory is still unframed, though several of its elements  and the like[73–80] are known already. It is interesting whether gravitation at high energies (or what is the same, quantum gravity or Planck scale) is being determined by the corresponding deformed thermodynamics. The formulae (50) and (54) are elements of the high-energy
and the like[73–80] are known already. It is interesting whether gravitation at high energies (or what is the same, quantum gravity or Planck scale) is being determined by the corresponding deformed thermodynamics. The formulae (50) and (54) are elements of the high-energy  -deformation in thermodynamics, a general pattern of which still remains to be formed. Obviously, these formulae should be involved in the general pattern giving better insight into the quantum gravity, as they are applicable to black mini-holes (Planck black holes) which may be a significant element of such a pattern. But what about other elements of this pattern? How can we generalize the results[54,69,70]when the IR-cutoff tends to the UV- cutoff (formula (46))? What are modifications of the thermodynamic identity (56) in a high-energy deformed thermodynamics and how is it applied in high-energy (quantum) gravity? By authors opinion, the methods developed to solve the problem of point (c) and elucidation of other above- mentioned problems may form the basis for a new approach to solution of the quantum gravity problem. And one of the keys to the quantum gravity problem is a better insight into the high-energy thermodynamics.
-deformation in thermodynamics, a general pattern of which still remains to be formed. Obviously, these formulae should be involved in the general pattern giving better insight into the quantum gravity, as they are applicable to black mini-holes (Planck black holes) which may be a significant element of such a pattern. But what about other elements of this pattern? How can we generalize the results[54,69,70]when the IR-cutoff tends to the UV- cutoff (formula (46))? What are modifications of the thermodynamic identity (56) in a high-energy deformed thermodynamics and how is it applied in high-energy (quantum) gravity? By authors opinion, the methods developed to solve the problem of point (c) and elucidation of other above- mentioned problems may form the basis for a new approach to solution of the quantum gravity problem. And one of the keys to the quantum gravity problem is a better insight into the high-energy thermodynamics. 6.α–Representation of Einstein’s Equations
- Let us consider
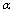 -representation and high energy
-representation and high energy 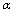 -deformation of the Einstein’s field equations for the specific cases of horizon spaces (the point (c) of Section 4). In so doing the results of the survey work[81] are used. Then, specifically, for a static, spherically symmetric horizon in space-time described by the metric
-deformation of the Einstein’s field equations for the specific cases of horizon spaces (the point (c) of Section 4). In so doing the results of the survey work[81] are used. Then, specifically, for a static, spherically symmetric horizon in space-time described by the metric 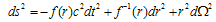 | (57) |
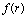 , at
, at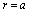 .It is known that for horizon spaces one can introduce the temperature that can be identified with an analytic continuation to imaginary time. In the case under consideration ([81], eq.(116))
.It is known that for horizon spaces one can introduce the temperature that can be identified with an analytic continuation to imaginary time. In the case under consideration ([81], eq.(116)) 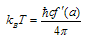 | (58) |
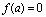 and
and 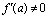 must be fulfilled. Then at the horizon
must be fulfilled. Then at the horizon 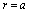 Einstein’s field equations
Einstein’s field equations 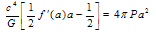 | (59) |
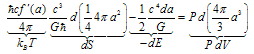 | (60) |
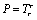 is the trace of the momentum-energy tensor and radial pressure. In the last equation arises in the infinitesimal consideration of Einstein’s equations when studying two horizons distinguished by this infinitesimal quantity
is the trace of the momentum-energy tensor and radial pressure. In the last equation arises in the infinitesimal consideration of Einstein’s equations when studying two horizons distinguished by this infinitesimal quantity 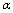 and
and 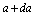 ([81] formula (118)).Now we consider (60) in new notation expressing
([81] formula (118)).Now we consider (60) in new notation expressing 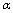 in terms of the corresponding deformation parameter
in terms of the corresponding deformation parameter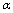 . Then we have
. Then we have 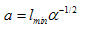 | (61) |
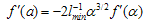 | (62) |
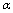 - representation" the following:
- representation" the following: 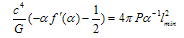 | (63) |
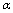 , we get
, we get 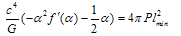 | (64) |
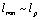 (that is just the case if the Generalized Uncertainty Principle (GUP) is satisfied), we have
(that is just the case if the Generalized Uncertainty Principle (GUP) is satisfied), we have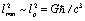 . When selecting a system of units, where
. When selecting a system of units, where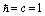 , we arrive at
, we arrive at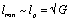 , and then (63) is of the form
, and then (63) is of the form 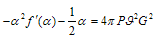 | (65) |
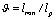 . L.h.s. of (65) is dependent on
. L.h.s. of (65) is dependent on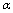 . Because of this, r.h.s. of (65) must be dependent on
. Because of this, r.h.s. of (65) must be dependent on 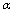 as well, i. e. . Analysis of
as well, i. e. . Analysis of 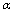 -Representation of Einstein’s Equations Now let us get back to (60). In[81] the low-energy case has been considered, for which ([81] formula (120))
-Representation of Einstein’s Equations Now let us get back to (60). In[81] the low-energy case has been considered, for which ([81] formula (120)) 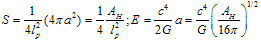 | (66) |
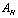 is the horizon area. In our notation (66) may be rewritten as
is the horizon area. In our notation (66) may be rewritten as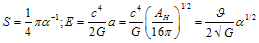 | (67) |
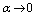 (LE), B)
(LE), B)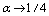 (HE), C)
(HE), C) 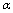 complies with the familiar scales and energies. The case of C) is of no particular importance as it may be considered within the scope of the conventional General Relativity. Indeed, in point A)
complies with the familiar scales and energies. The case of C) is of no particular importance as it may be considered within the scope of the conventional General Relativity. Indeed, in point A) 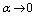 is not actually an exact limit as a real scale of the Universe (Infrared (IR) - cutoff
is not actually an exact limit as a real scale of the Universe (Infrared (IR) - cutoff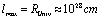 ), and then In this way A) is replaced by A1)
), and then In this way A) is replaced by A1)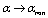 . In any case at low energies the second term in the left-hand side (65) may be neglected in the infrared limit. Consequently, at low energies (65) is written as
. In any case at low energies the second term in the left-hand side (65) may be neglected in the infrared limit. Consequently, at low energies (65) is written as 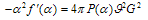 | (68) |
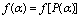 satisfying (68). In this case formulae (66) are valid as at low energies a semiclassical approximation is true. But from (68) it follows that
satisfying (68). In this case formulae (66) are valid as at low energies a semiclassical approximation is true. But from (68) it follows that 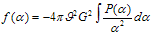 | (69) |
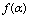 , we can obtain
, we can obtain 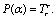 But it is noteworthy that, when studying the infrared modified gravity[82-84], we have to make corrections for the considerations of point A1).
But it is noteworthy that, when studying the infrared modified gravity[82-84], we have to make corrections for the considerations of point A1). 7. Possible High Energy α-Deformation of General Relativity
- Let us consider the high-energy case B). Here two variants are possible. I. First variantIn this case it is assumed that in the high-energy (Ultraviolet (UV)) limit the thermodynamic identity (60) (or that is the same (56) is retained but now all the quantities involved in this identity become -deformed. This means that they appear in the
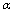 -representation with quantum corrections and are considered at high values of the parameter
-representation with quantum corrections and are considered at high values of the parameter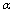 , i.e. at
, i.e. at 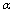 close to 1/4. In particular, the temperature
close to 1/4. In particular, the temperature 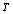 from equation (60) is changed by
from equation (60) is changed by 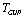 (50), the entropy
(50), the entropy 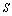 from the same equation given by semiclassical formula (66) is changed by
from the same equation given by semiclassical formula (66) is changed by 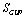 (54), and so forth:
(54), and so forth: 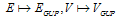 Then the high-energy
Then the high-energy 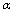 -deformation of equation (60) takes the form
-deformation of equation (60) takes the form 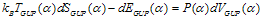 | (70) |
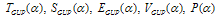 and expanding them into a Laurent series in terms of
and expanding them into a Laurent series in terms of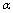 , close to high values of
, close to high values of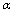 , specifically close to
, specifically close to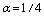 , we can derive a solution for the high energy
, we can derive a solution for the high energy 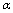 -deformation of general relativity (70) as a function of
-deformation of general relativity (70) as a function of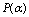 . As this takes place, provided at high energies the generalization of (60) to (70)is possible, we can have the high-energy
. As this takes place, provided at high energies the generalization of (60) to (70)is possible, we can have the high-energy 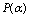 -deformation of the metric. Actually, as from (60) it follows that
-deformation of the metric. Actually, as from (60) it follows that 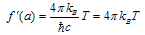 | (71) |
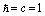 ), we get
), we get 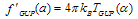 | (72) |
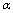 -representation. This means that, when
-representation. This means that, when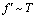 , we have
, we have 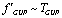 with the same factor of proportionality. In this case the function
with the same factor of proportionality. In this case the function 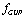 determining the high-energy
determining the high-energy 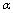 -deformation of the spherically symmetric metric may be in fact derived by the expansion of
-deformation of the spherically symmetric metric may be in fact derived by the expansion of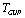 , that is known from (50), into a Laurent series in terms of
, that is known from (50), into a Laurent series in terms of 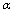 close to high values of
close to high values of 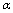 (specifically close to
(specifically close to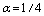 ), and by the subsequent integration. It might be well to remark on the following. 7.1 As on going to high energies we use (GUP),
), and by the subsequent integration. It might be well to remark on the following. 7.1 As on going to high energies we use (GUP), 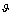 from equation (65) is expressed in terms of
from equation (65) is expressed in terms of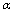 –dimensionless constant from GUP (6), (50):
–dimensionless constant from GUP (6), (50):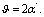 7.2 Of course, in all the formulae including
7.2 Of course, in all the formulae including 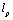 this quantity must be changed by
this quantity must be changed by 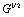 and hence
and hence 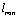 by
by 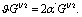 7.3 As noted in the end of subsection 6.1, and in this case also knowing all the high-energy deformed quantities
7.3 As noted in the end of subsection 6.1, and in this case also knowing all the high-energy deformed quantities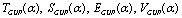 , we can find
, we can find 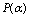 at
at 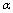 close to 1/4. 7.4 Here it is implicitly understood that the Ultraviolet limit of Einstein’s equations is independent of the starting horizon space. This assumption is quite reasonable. Because of this, we use the well-known formulae for the modification of thermodynamics and statistical mechanics of black holes in the presence of GUP[73–80]7.5 The use of the thermodynamic identity (70) for the description of the high energy deformation in General Relativity implies that on going to the UV-limit of Einstein’s equations for horizon spaces in the thermodynamic representation (consideration) we are trying to remain within the scope of equilibrium statistical mechanics[85] (equilibrium thermodynamics)[86]. However, such an assumption seems to be too strong. But some grounds to think so may be found as well. Among other things, of interest is the result from[73] that GUP may prevent black holes from their total evaporation. In this case the Planck’s remnants of black holes will be stable, and when they are considered, in some approximation the equilibrium thermodynamics should be valid. At the same time, by author’s opinion these arguments are rather weak to think that the quantum gravitational effects in this context have been described only within the scope of equilibrium thermodynamics[86].II. Second variantAccording to the remark of .5, it is assumed that the interpretation of Einstein’s equations as a thermodynamic identity (60) is not retained on going to high energies (UV–limit), i.e. at
close to 1/4. 7.4 Here it is implicitly understood that the Ultraviolet limit of Einstein’s equations is independent of the starting horizon space. This assumption is quite reasonable. Because of this, we use the well-known formulae for the modification of thermodynamics and statistical mechanics of black holes in the presence of GUP[73–80]7.5 The use of the thermodynamic identity (70) for the description of the high energy deformation in General Relativity implies that on going to the UV-limit of Einstein’s equations for horizon spaces in the thermodynamic representation (consideration) we are trying to remain within the scope of equilibrium statistical mechanics[85] (equilibrium thermodynamics)[86]. However, such an assumption seems to be too strong. But some grounds to think so may be found as well. Among other things, of interest is the result from[73] that GUP may prevent black holes from their total evaporation. In this case the Planck’s remnants of black holes will be stable, and when they are considered, in some approximation the equilibrium thermodynamics should be valid. At the same time, by author’s opinion these arguments are rather weak to think that the quantum gravitational effects in this context have been described only within the scope of equilibrium thermodynamics[86].II. Second variantAccording to the remark of .5, it is assumed that the interpretation of Einstein’s equations as a thermodynamic identity (60) is not retained on going to high energies (UV–limit), i.e. at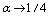 , and the situation is adequately described exclusively by non-equilibrium thermodynamics[86,87]. Naturally, the question arises: which of the additional terms introduced in (60) at high energies may be leading to such a description?In the[30,31] it has been shown that in case the cosmological term
, and the situation is adequately described exclusively by non-equilibrium thermodynamics[86,87]. Naturally, the question arises: which of the additional terms introduced in (60) at high energies may be leading to such a description?In the[30,31] it has been shown that in case the cosmological term 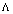 is a dynamic quantity, it is small at low energies and may be sufficiently large at high energies. In the right-hand side of (65) in the
is a dynamic quantity, it is small at low energies and may be sufficiently large at high energies. In the right-hand side of (65) in the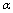 –representation the additional term
–representation the additional term 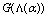 is introduced:
is introduced: 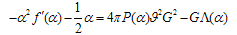 | (73) |
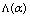 is the cosmological term depending from
is the cosmological term depending from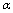 . Then its inclusion in the low-energy case (59)(or in the
. Then its inclusion in the low-energy case (59)(or in the 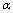 - representation (65)) has actually no effect on the thermodynamic identity (60) validity, and consideration within the scope of equilibrium thermodynamics still holds true. It is well known that this is not the case at high energies as the
- representation (65)) has actually no effect on the thermodynamic identity (60) validity, and consideration within the scope of equilibrium thermodynamics still holds true. It is well known that this is not the case at high energies as the 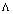 -term may contribute significantly to make the "process" non-equilibrium in the end[86,87].Is this the only cause for violation of the thermodynamic identity (60) as an interpretation of the high-energy generalization of Einstein’s equations? Further investigations are required to answer this question.
-term may contribute significantly to make the "process" non-equilibrium in the end[86,87].Is this the only cause for violation of the thermodynamic identity (60) as an interpretation of the high-energy generalization of Einstein’s equations? Further investigations are required to answer this question. 8. Conclusions
- Thus, this work presents an analysis of the dark energy problem on the assumption that it is the time-varying vacuum energy, that conforms to the dynamic cosmological term
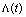 . Note that the question of the explicit relationship between
. Note that the question of the explicit relationship between 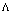 and
and 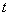 is not touched, we have rather studied the problem of deriving the currently observable value for
is not touched, we have rather studied the problem of deriving the currently observable value for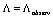 . As such a consideration inevitably involves the physics of the early Universe (Planck scales) and hence QFT with the fundamental length (on the order of Planck’s
. As such a consideration inevitably involves the physics of the early Universe (Planck scales) and hence QFT with the fundamental length (on the order of Planck’s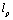 ), it is associated with new parameters (deformation parameters) and, in the limiting transition to low-energy, QFT with the fundamental length turns to well-known QFT (without cutoff). By the author’s opinion,
), it is associated with new parameters (deformation parameters) and, in the limiting transition to low-energy, QFT with the fundamental length turns to well-known QFT (without cutoff). By the author’s opinion, 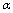 (7) is the most optimal of the deformation parameters from the standpoint of the problems considered in this work.The results obtained in Sections 6 and 7 enable framing of the following hypothesis:a dynamic cosmological term is a measure of deviation from the thermodynamic identity (the first law of thermodynamics) of the high-energy (Planck’s) deformation of Einstein equations for horizon spaces in their thermodynamic interpretation.The dynamic cosmological term correlates well with inflation models[4] as the latter require a very high at the early stages of the Universe, and this is distinct from
(7) is the most optimal of the deformation parameters from the standpoint of the problems considered in this work.The results obtained in Sections 6 and 7 enable framing of the following hypothesis:a dynamic cosmological term is a measure of deviation from the thermodynamic identity (the first law of thermodynamics) of the high-energy (Planck’s) deformation of Einstein equations for horizon spaces in their thermodynamic interpretation.The dynamic cosmological term correlates well with inflation models[4] as the latter require a very high at the early stages of the Universe, and this is distinct from 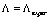 in the modern period. Of great interest is the recent work[89], where a mechanism of the vacuum energy decay in the de Sitter space is established to support a dynamic nature of
in the modern period. Of great interest is the recent work[89], where a mechanism of the vacuum energy decay in the de Sitter space is established to support a dynamic nature of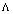 . This work is a step to the incorporation of deformation parameters involved in a quantum field theory at Planck’s scales into the high-energy deformation of the General Relativity (GR). The corresponding calculations with the adequate interpretation must follow next. It is interesting to consider the high energy
. This work is a step to the incorporation of deformation parameters involved in a quantum field theory at Planck’s scales into the high-energy deformation of the General Relativity (GR). The corresponding calculations with the adequate interpretation must follow next. It is interesting to consider the high energy 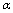 -deformation of GR in a more general case. The problem is how far a thermodynamic interpretation of Einstein’s equations may be extended? We should remember that, as all the deformations considered involve a minimal length at the Planck level
-deformation of GR in a more general case. The problem is how far a thermodynamic interpretation of Einstein’s equations may be extended? We should remember that, as all the deformations considered involve a minimal length at the Planck level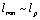 , a minimal three-dimensional volume should also be the case
, a minimal three-dimensional volume should also be the case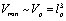 . And this is of particular importance for high energy thermodynamics (some indications to this fact have been demonstrated in[30,31]).
. And this is of particular importance for high energy thermodynamics (some indications to this fact have been demonstrated in[30,31]).  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML