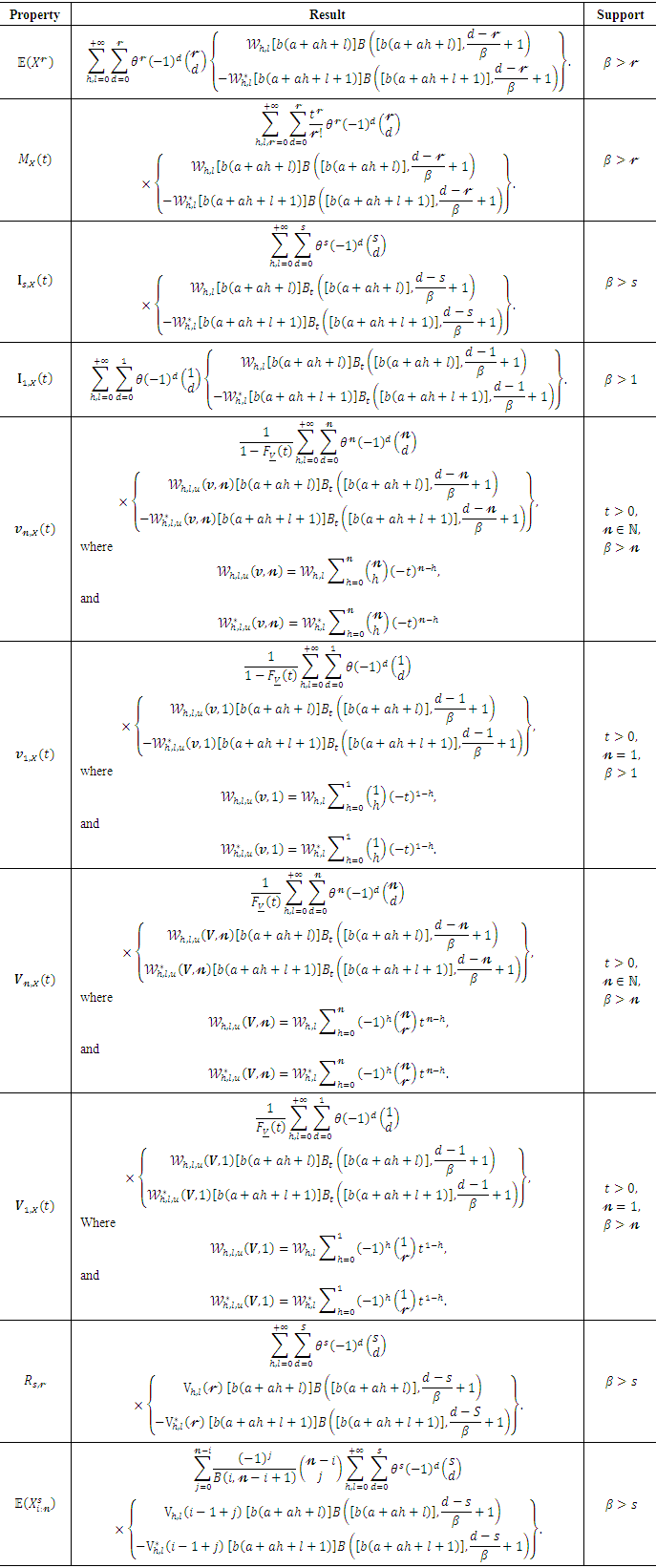| [1] | Ali, M.M.; Mikhail, N.N.; Haq, M.S. (1978). A class of bivariate distributions including the bivariate logistic. J. Multivar. Anal, 8, 405–412. |
| [2] | Alizadeh, M., Jamal, F., Yousof, H. M., Khanahmadi, M. and Hamedani, G. G. (2020a). Flexible Weibull generated family of distributions: characterizations, mathematical properties and applications. University Politehnica of Bucharest Scientific Bulletin-Series A-Applied Mathematics and Physics, 82(1), 145-150. |
| [3] | Alizadeh, M., Yousof, H. M., Jahanshahi, S. M. A., Najibi, S. M. and Hamedani, G. G. (2020b). The transmuted odd log-logistic-G family of distributions. Journal of Statistics and Management Systems, 23(4), 1-27. |
| [4] | Altun, E., Yousof, H. M. and Hamedani, G. G. (2018). A new log-location regression model with influence diagnostics and residual analysis. Facta Universitatis, Series: Mathematics and Informatics, 33(3), 417-449. |
| [5] | Altun, E., Yousof, H. M. and Hamedani, G. G. (2021). The Gudermannian generated family of distributions with characterizations, regression models and applications, Studia Scientiarum Mathematicarum Hungarica, forthcoming. |
| [6] | Aryal, G. R. and Yousof, H. M. (2017). The exponentiated generalized-G Poisson family of distributions. Economic Quality Control, 32(1), 1-17. |
| [7] | Balakrishnan, N.; Lai, C.D. (2009). Continuous Bivariate Distributions; Springer Science & Business Media: Berlin/Heidelberg, Germany. |
| [8] | Brito, E., Cordeiro, G. M., Yousof, H. M., Alizadeh, M. and Silva, G. O. (2017). Topp-Leone Odd Log-Logistic Family of Distributions, Journal of Statistical Computation and Simulation, 87(15), 3040–3058. |
| [9] | Chesneau, C. and Yousof, H. M. (2021). On a special generalized mixture class of probabilistic models. Journal of Nonlinear Modeling and Analysis, 3(1), 71-92. |
| [10] | Cordeiro, G. M., Ortega, E. M. and Popovic, B. V. (2015). The gamma-Lomax distribution. Journal of Statistical computation and Simulation, 85(2), 305-319. |
| [11] | Cordeiro, G. M., Yousof, H. M., Ramires, T. G. and Ortega, E. M. M. (2018). The Burr XII system of densities: properties, regression model and applications. Journal of Statistical Computation and Simulation, 88(3), 432-456. |
| [12] | El-Morshedy, M., Alshammari, F. S., Hamed, Y. S., Eliwa, M. S., Yousof, H. M. (2021). A New Family of Continuous Probability Distributions. Entropy, 23, 194. https://doi.org/10.3390/e23020194. |
| [13] | Eugene, N., Lee, C. and Famoye, F. (2002). Beta-normal distribution and its applications. Commun. Stat. Theory Methods, 31, 497-512. |
| [14] | Falgore, J. Y. (2020). The Zubair-inverse lomax distribution with applications. Asian Journal of Probability and Statistics, 1-14. |
| [15] | Farlie, D.J.G. (1960). The performance of some correlation coefficients for a general bivariate distribution. Biometrika, 47, 307–323. |
| [16] | Gumbel, E.J. (1960). Bivariate exponential distributions. J. Am. Stat. Assoc., 55, 698–707. |
| [17] | Gumbel, E.J. (1961). Bivariate logistic distributions. J. Am. Stat. Assoc., 56, 335–349. |
| [18] | Gupta, R. C., Gupta, P. L. and Gupta, R. D. (1998). Modeling failure time data by Lehman alternatives. Communications in Statistics-Theory and methods, 27(4), 887-904. |
| [19] | Hamedani, G. G. Rasekhi, M., Najib, S. M., Yousof, H. M. and Alizadeh, M., (2019). Type II general exponential class of distributions. Pak. J. Stat. Oper. Res., XV (2), 503-523. |
| [20] | Hamedani, G. G. Yousof, H. M., Rasekhi, M., Alizadeh, M., Najibi, S. M. (2017). Type I general exponential class of distributions. Pak. J. Stat. Oper. Res., XIV (1), 39-55. |
| [21] | Hamedani, G. G., Altun, E, Korkmaz, M. C., Yousof, H. M. and Butt, N. S. (2018). A new extended G family of continuous distributions with mathematical properties, characterizations and regression modeling. Pak. J. Stat. Oper. Res., 14(3), 737-758. |
| [22] | Johnson, N.L.; Kotz, S. (1975). On some generalized Farlie-Gumbel-Morgenstern distributions. Commun. Stat. Theory, 4, 415–427. |
| [23] | Johnson, N.L.; Kotz, S. (1977). On some generalized Farlie-Gumbel-Morgenstern distributions-II: Regression, correlation and further generalizations. Commun. Stat. Theory, 6, 485–496. |
| [24] | Karamikabir, H., Afshari, M., Yousof, H. M., Alizadeh, M. and Hamedani, G. (2020). The Weibull Topp-Leone Generated Family of Distributions: Statistical Properties and Applications. Journal of The Iranian Statistical Society, 19(1), 121-161. |
| [25] | Korkmaz, M. C. Yousof, H. M. and Hamedani G. G. (2018a). The exponential Lindley odd log-logistic G family: properties, characterizations and applications. Journal of Statistical Theory and Applications, 17(3), 554 - 571. |
| [26] | Korkmaz, M. Ç., Altun, E., Yousof, H. M. and Hamedani, G. G. (2020). The Hjorth's IDB Generator of Distributions: Properties, Characterizations, Regression Modeling and Applications. Journal of Statistical Theory and Applications, 19(1), 59-74. |
| [27] | Korkmaz, M. C., Yousof, H. M., Hamedani G. G. and Ali, M. M. (2018b). The Marshall–Olkin generalized G Poisson family of distributions, Pakistan Journal of Statistics, 34(3), 251-267. |
| [28] | Lemonte, A. J. and Cordeiro, G. M. (2013). An extended Lomax distribution. Statistics, 47(4), 800-816. |
| [29] | Lomax, K.S. (1954). Business failures: Another example of the analysis of failure data, Journal of the American Statistical Association, 49, 847-852. |
| [30] | Mansour, M., Yousof, H. M., Shehata, W. A. M. and Ibrahim, M. (2020). A new two parameter Burr XII distribution: properties, copula, different estimation methods and modeling acute bone cancer data, Journal of Nonlinear Science and Applications, 13, 223–238. |
| [31] | Marshall, A. W. and Olkin, I. (1997). A new method for adding a parameter to a family of distributions with application to the Exponential and Weibull families. Biometrika, 84, 641-652. |
| [32] | Marzouk, W., Jamal, F. and Ahmed, A. E. (2019). The Generalized Odd Lomax Generated Family of Distributions with Applications. Gazi University Journal of Science, 32(2), 737-755. |
| [33] | Merovci, F., Alizadeh, M., Yousof, H. M. and Hamedani G. G. (2017). The exponentiated transmuted-G family of distributions: theory and applications, Communications in Statistics-Theory and Methods, 46(21), 10800-10822. |
| [34] | Merovci, F., Yousof, H. M. and Hamedani, G. G. (2020). The Poisson Topp Leone Generator of Distributions for Lifetime Data: Theory, Characterizations and Applications. Pakistan Journal of Statistics and Operation Research, 16(2), 343-355. |
| [35] | Mead, M. E. (2016). On five-parameter Lomax distribution: properties and applications. Pakistan Journal of Statistics and Operation Research, 185-199. |
| [36] | Morgenstern, D. (1956). Einfache beispiele zweidimensionaler verteilungen. Mitteilingsbl. Math. Stat., 8, 234–235. |
| [37] | Murthy, D.N.P.; Xie, M.; Jiang, R. (2004). Weibull Models; John Wiley & Sons: Hoboken, NJ, USA. |
| [38] | Nascimento, A. D. C., Silva, K. F., Cordeiro, G. M., Alizadeh, M. and Yousof, H. M. (2019). The odd Nadarajah-Haghighi family of distributions: properties and applications. Studia Scientiarum Mathematicarum Hungarica, 56(2), 1-26. |
| [39] | Nelsen, R.B. (2007). An Introduction to Copulas; Springer Science & Business Media: Berlin/Heidelberg, Germany. |
| [40] | Nofal, Z. M., Afify, A. Z., Yousof, H. M. and Cordeiro, G. M. (2017). The generalized transmuted-G family of distributions. Communications in Statistics-Theory and Method, 46, 4119-4136. |
| [41] | Oguntunde, P. E., Khaleel, M. A., Ahmed, M. T., Adejumo, A. O. and Odetunmibi, O. A. (2017). A new generalization of the Lomax distribution with increasing, decreasing, and constant failure rate. Modelling and Simulation in Engineering, 2017. |
| [42] | Pougaza, D.B.; Djafari, M.A. (2010). Maximum entropies copulas. In Proceedings of the 30th international workshop on Bayesian inference and maximum Entropy methods in Science and Engineering, Chamonix, France, 4–9 July 2010; pp. 329–336. |
| [43] | Rezaei, S., B. B. Sadr, M. Alizadeh, and S. Nadarajah. (2017). Topp-Leone generated family of distributions: Properties and applications. Communications in Statistics: Theory and Methods 46 (6), 2893–2909. |
| [44] | Yousof, H. M., Afify, A. Z., Alizadeh, M., Butt, N. S., Hamedani, G. G. and Ali, M. M. (2015). The transmuted exponentiated generalized-G family of distributions, Pak. J. Stat. Oper. Res., 11, 441-464. |
| [45] | Yousof, H. M., Afify, A. Z., Hamedani, G. G. and Aryal, G. (2017a). The Burr X generator of distributions for lifetime data. Journal of Statistical Theory and Applications, 16, 288–305. |
| [46] | Yousof, H. M., Alizadeh, M., Jahanshahi, S. M. A., Ramires, T. G., Ghosh, I. and Hamedani, G. G. (2017b). The transmuted Topp-Leone G family of distributions: theory, characterizations and applications. Journal of Data Science, 15(4), 723-740. |
| [47] | Yousof, H. M., Altun, E., Ramires, T. G., Alizadeh, M. and Rasekhi, M. (2018). A new family of distributions with properties, regression models and applications, Journal of Statistics and Management Systems, 21(1), 163-188. |
| [48] | Yousof, H. M., Mansoor, M. Alizadeh, M., Afify, A. Z., Ghosh, I. and Afify, A. Z. (2020). The Weibull-G Poisson family for analyzing lifetime data. Pak. J. Stat. Oper. Res., 16 (1), 131-148. |



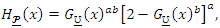
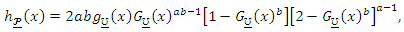
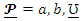 refers to the parameters vector of the new family and
refers to the parameters vector of the new family and 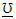 refers to the parameters vector of any base-line model. For
refers to the parameters vector of any base-line model. For 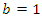 , the TLG-G family reduces to the one-parameter Topp Leone G (TL-G) family. Suppose that
, the TLG-G family reduces to the one-parameter Topp Leone G (TL-G) family. Suppose that 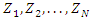 be an independent and identically random variables (iid RVs) with common CDF follows the TLG-G family and
be an independent and identically random variables (iid RVs) with common CDF follows the TLG-G family and 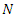 be RV with probability mass function
be RV with probability mass function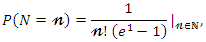 defining
defining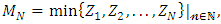 then
then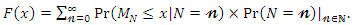
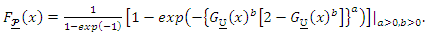
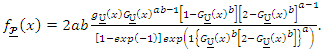
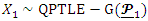 and
and 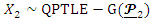 . Then depending on the continuous marginals
. Then depending on the continuous marginals 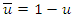 and
and 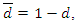 the Clayton copula can be expressed as
the Clayton copula can be expressed as 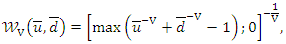 where
where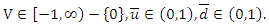 Let
Let 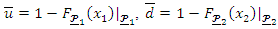 and
and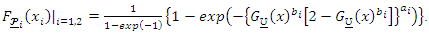 Then, the BQPTLG-G type distribution can be obtained from
Then, the BQPTLG-G type distribution can be obtained from 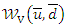 . A straightforward multivariate extension via Clayton copula can be derived.
. A straightforward multivariate extension via Clayton copula can be derived.  and
and 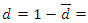
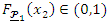 as follows
as follows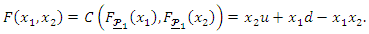
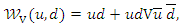 where the continuous marginal function
where the continuous marginal function 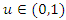 ,
, 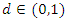 and
and 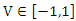 where
where 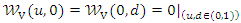 , which under the grounded minimum condition and
, which under the grounded minimum condition and 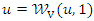 and
and 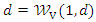 under the grounded maximum condition. Clearly, the grounded minimum (maximum) conditions are valid for any copula. Setting
under the grounded maximum condition. Clearly, the grounded minimum (maximum) conditions are valid for any copula. Setting 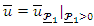 and
and 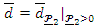 . Then, we have
. Then, we have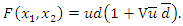 Then, the joint PDF can be expressed as
Then, the joint PDF can be expressed as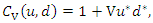 where
where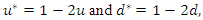 or
or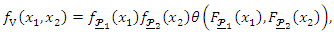 where the two function
where the two function 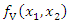 and
and 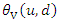 are PDFs corresponding to the joint CDFs
are PDFs corresponding to the joint CDFs 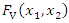 and
and 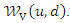
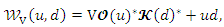 with
with 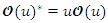 and
and 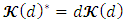 where
where 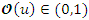 and
and 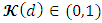 are two continuous functions where
are two continuous functions where 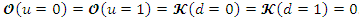 . Then, let
. Then, let 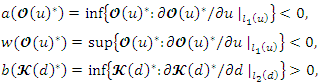 and
and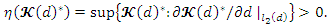 Then, for
Then, for 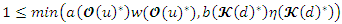 we have
we have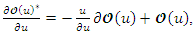 where
where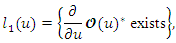 and
and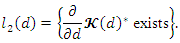 The following four types can be derived and considered:Type I:The new bivariate version via modified FGMC type I can written as
The following four types can be derived and considered:Type I:The new bivariate version via modified FGMC type I can written as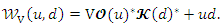 Type II: Consider
Type II: Consider 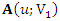 and
and 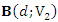 which satisfy the above conditions where
which satisfy the above conditions where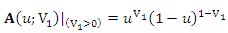 and
and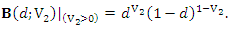 Then, the corresponding bivariate version (modified FGMC Type II) can be derived from
Then, the corresponding bivariate version (modified FGMC Type II) can be derived from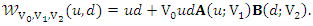 Type III: Let
Type III: Let 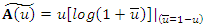 and
and 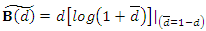 . Then, the associated CDF of the BQPTLG-G-FGM (modified FGMC type III) as
. Then, the associated CDF of the BQPTLG-G-FGM (modified FGMC type III) as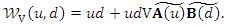 Type IV: Using the quantile concept, the CDF of the BQPTLG-G-FGM (modified FGMC type IV) model can be obtained using
Type IV: Using the quantile concept, the CDF of the BQPTLG-G-FGM (modified FGMC type IV) model can be obtained using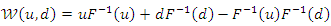 where
where 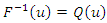 and
and 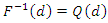 .
.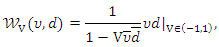 the corresponding joint PDF of the Archimedean Ali-Mikhail-Haq copula can be express as
the corresponding joint PDF of the Archimedean Ali-Mikhail-Haq copula can be express as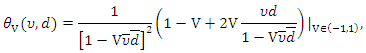 then for any
then for any 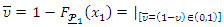 and
and 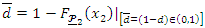 we have
we have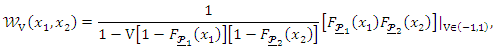 and
and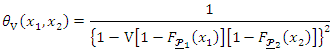
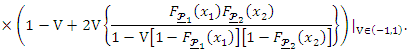
 where
where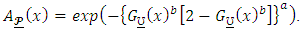 Then,
Then,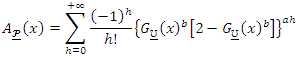 Compiling the expansion of
Compiling the expansion of 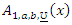 in to (5), we have
in to (5), we have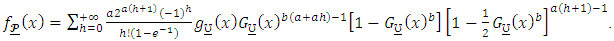
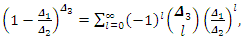
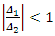 and
and 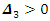 real non-integer. Using (7), the QPTLG-G class in (6) can be written as
real non-integer. Using (7), the QPTLG-G class in (6) can be written as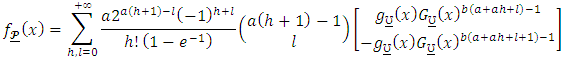 Which can be summarized as
Which can be summarized as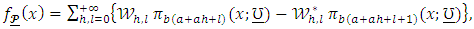
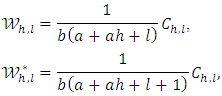 and
and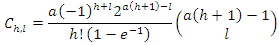 and
and 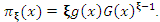 Equation (8) reveals that the density of the QPTLG-G family can then be expressed as a linear representation of exp-G PDFs. Also, the CDF of the QPTLG-G family can also be expressed as a mixture of exp-G CDFs. By integrating (8), we have
Equation (8) reveals that the density of the QPTLG-G family can then be expressed as a linear representation of exp-G PDFs. Also, the CDF of the QPTLG-G family can also be expressed as a mixture of exp-G CDFs. By integrating (8), we have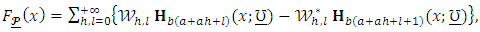
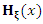 is the CDF of the exp-G family with power parameter
is the CDF of the exp-G family with power parameter 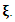
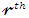 ordinary moment of
ordinary moment of 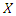 where
where 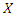 follows QPTLG-G family with parameters
follows QPTLG-G family with parameters 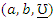 is given by
is given by 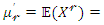
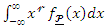 . Then we obtain
. Then we obtain 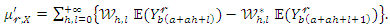
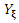 denotes the density of the exp-G model with power parameter
denotes the density of the exp-G model with power parameter 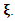 The expected value
The expected value 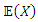 can be derived from when
can be derived from when 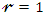 in (10). The integrations in
in (10). The integrations in 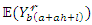 and
and 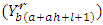 can be computed numerically for most parent distributions. The
can be computed numerically for most parent distributions. The 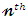 central moment of
central moment of 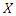 , variance
, variance 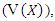 skewness
skewness 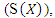 kurtosis
kurtosis 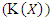 and dispersion index
and dispersion index 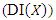 measures can be derived using well-known relationships. The
measures can be derived using well-known relationships. The 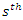 incomplete moment, say
incomplete moment, say 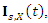 of
of 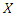 can be expressed from (9) as
can be expressed from (9) as 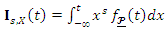 . Then
. Then 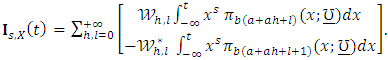
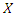 are given by
are given by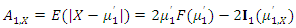 and
and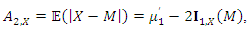 respectively, where
respectively, where 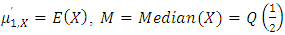 is the median,
is the median, 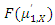 is obtained from (4) and
is obtained from (4) and 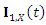 is the first incomplete moment given by (11) with
is the first incomplete moment given by (11) with 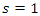 as
as 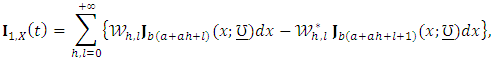 where
where 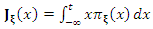 is the first incomplete moment of the exp-G distribution. The moment generating function
is the first incomplete moment of the exp-G distribution. The moment generating function 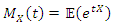 of
of 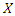 can be derived as
can be derived as 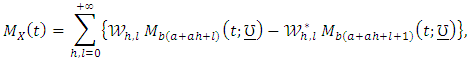 where
where 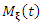 is the moment generating function of
is the moment generating function of 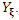
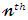 moment of the residual life, say
moment of the residual life, say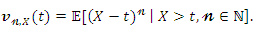 Then, the
Then, the 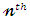 moment of the residual life of
moment of the residual life of 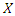 can be given as
can be given as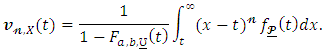 Therefore, using (8) we have
Therefore, using (8) we have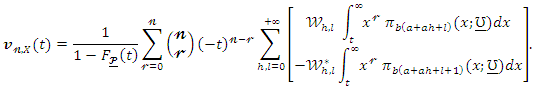 The life expectation can then be defined by
The life expectation can then be defined by 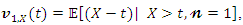 which represents the expected additional life length for a unit which is alive at age
which represents the expected additional life length for a unit which is alive at age 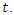 The MRL of
The MRL of 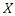 can be obtained by setting
can be obtained by setting 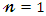 in the last equation.
in the last equation. 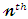 moment of the reversed residual life, say
moment of the reversed residual life, say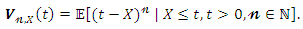 The
The 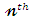 moment of the reversed residual life of
moment of the reversed residual life of 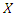 can be given as
can be given as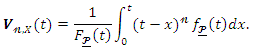 Then, the
Then, the 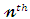 moment of the reversed residual life of
moment of the reversed residual life of 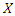 becomes
becomes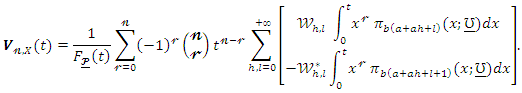 The mean inactivity time (MIT) is given by
The mean inactivity time (MIT) is given by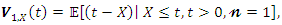 and it refers to the waiting time elapsed since the failure of an item on condition that this failure had occurred in
and it refers to the waiting time elapsed since the failure of an item on condition that this failure had occurred in 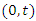 .
. PWM of
PWM of 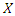 following the QPTLG-G family, say
following the QPTLG-G family, say 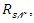 is formally defined by
is formally defined by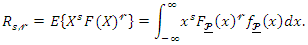 Using equations (4) and (5), we can write
Using equations (4) and (5), we can write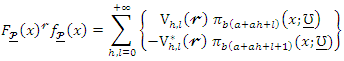 where
where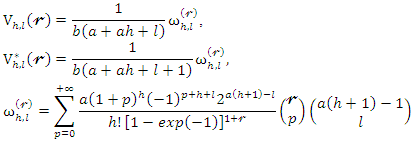 and
and 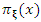 is defined above. Then, the
is defined above. Then, the 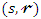 th PWM of
th PWM of 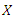 can be expressed as
can be expressed as 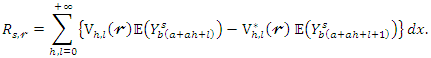
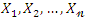 be a random sample from the QPTLG-G family of distributions and let
be a random sample from the QPTLG-G family of distributions and let 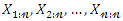 be the corresponding order statistics. The PDF of
be the corresponding order statistics. The PDF of 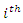 order statistic, say
order statistic, say 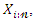 can be written as
can be written as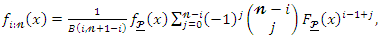
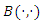 is the beta function. Substituting (4) and (5) in equation (12) and using a power series expansion, we get
is the beta function. Substituting (4) and (5) in equation (12) and using a power series expansion, we get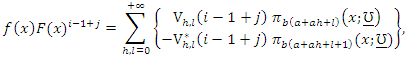 where
where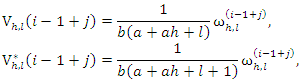 and
and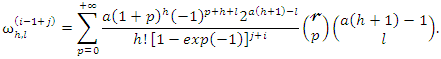 Then, the PDF of
Then, the PDF of 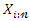 can be written as
can be written as 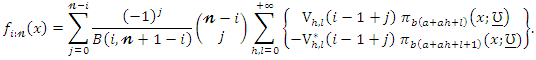 Then, the density function of the QPTLG-G order statistics is a mixture of exp-G PDFs. Based on the last result, we note that the main properties of
Then, the density function of the QPTLG-G order statistics is a mixture of exp-G PDFs. Based on the last result, we note that the main properties of 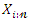 follow from those properties of
follow from those properties of 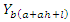 and
and 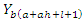 . For example, the
. For example, the 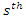 moments of
moments of 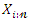 can be expressed as
can be expressed as 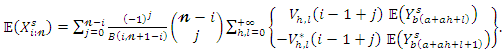
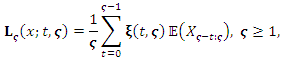 where
where 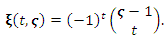
 be a random variable having the exp-L distribution with power parameter
be a random variable having the exp-L distribution with power parameter  Then the CDF of the exp-L model can be expressed as
Then the CDF of the exp-L model can be expressed as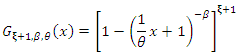 Then, the
Then, the 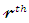 ordinary moment of
ordinary moment of 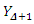 is given by
is given by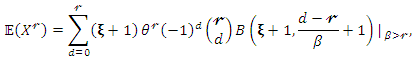 where
where 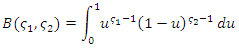 is the complete beta function. Theorem 2:Let
is the complete beta function. Theorem 2:Let  be a random variable having the exp-L distribution with power parameter
be a random variable having the exp-L distribution with power parameter  Then, the
Then, the  incomplete moment of
incomplete moment of 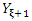 is given by
is given by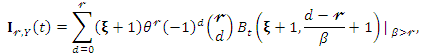 where
where 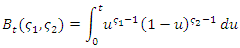 is the incomplete beta function.
is the incomplete beta function. be a random sample from the QPTLG-G distribution with parameters
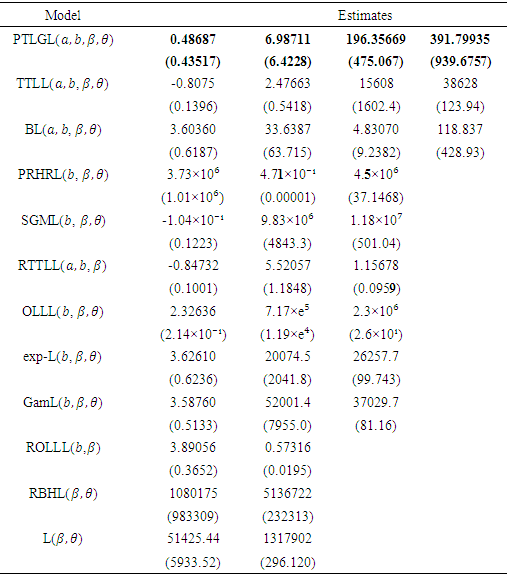
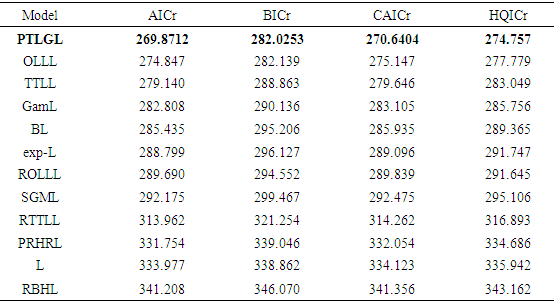
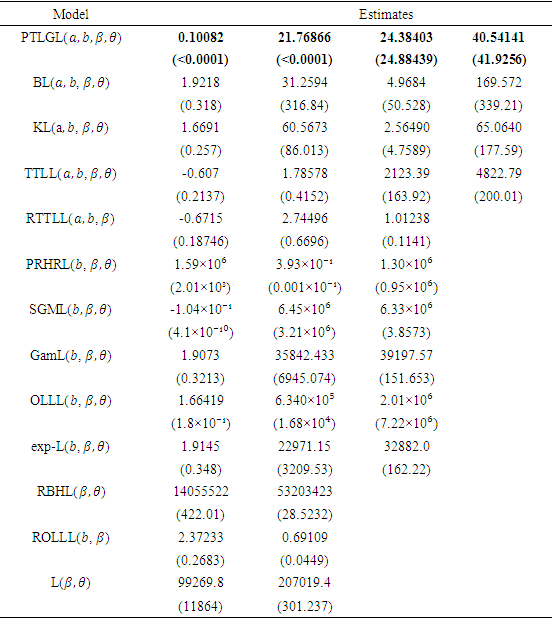
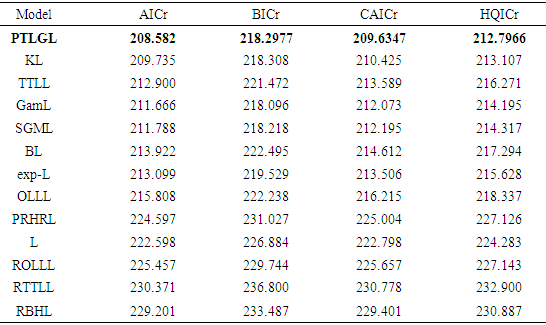
be a random sample from the QPTLG-G distribution with parameters 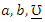 . For determining the maximum likelihood estimators (MLEs) of
. For determining the maximum likelihood estimators (MLEs) of 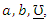 we have the log-likelihood function
we have the log-likelihood function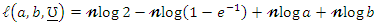
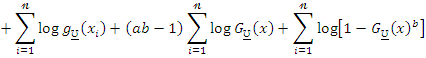
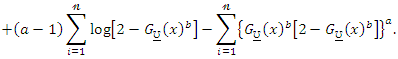 The components of the score vector are
The components of the score vector are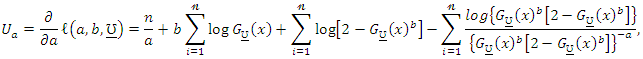
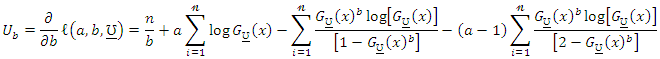
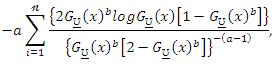 and
and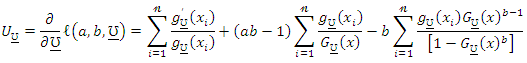
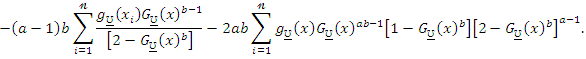 Setting the nonlinear system of equations
Setting the nonlinear system of equations 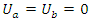 and
and 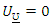 and solving them simultaneously yields the MLE. To solve these equations, it is usually more convenient to use nonlinear optimization methods such as the quasi-Newton algorithm to numerically maximize
and solving them simultaneously yields the MLE. To solve these equations, it is usually more convenient to use nonlinear optimization methods such as the quasi-Newton algorithm to numerically maximize 
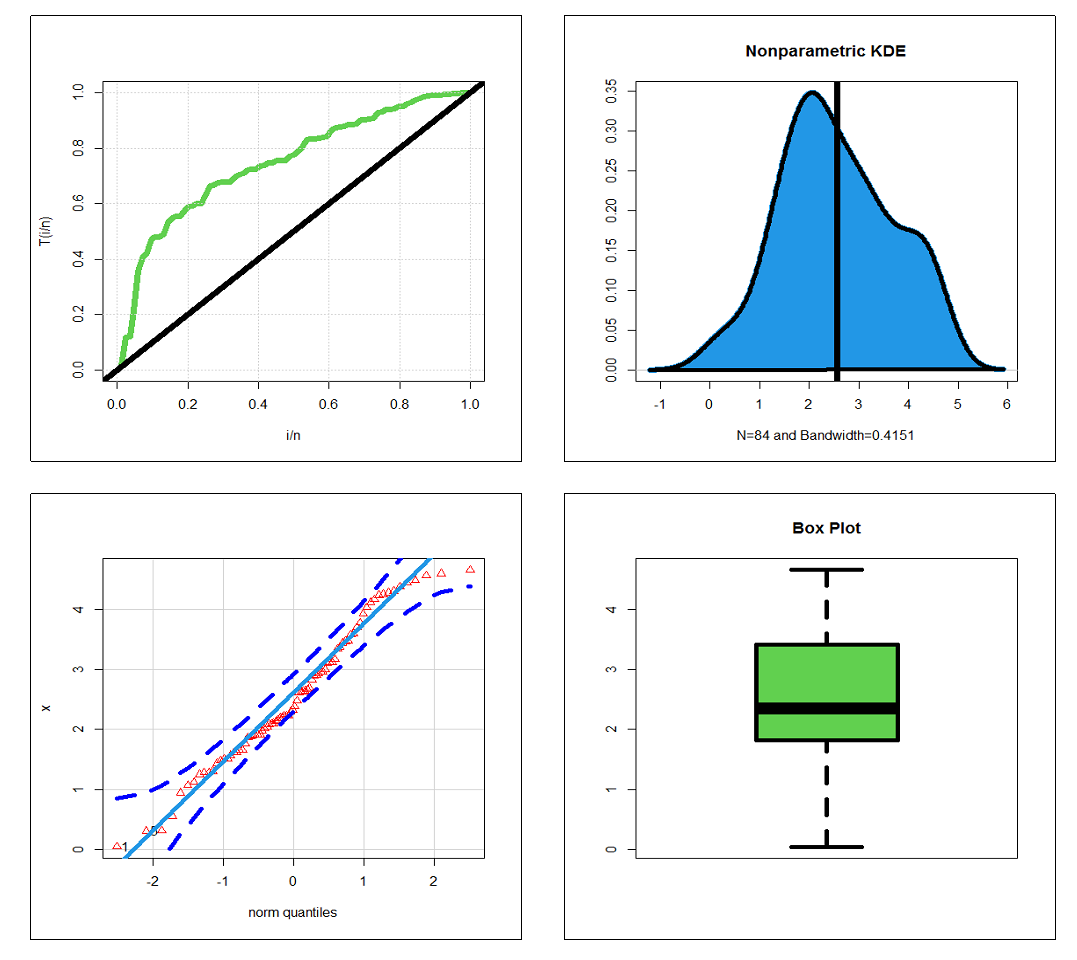
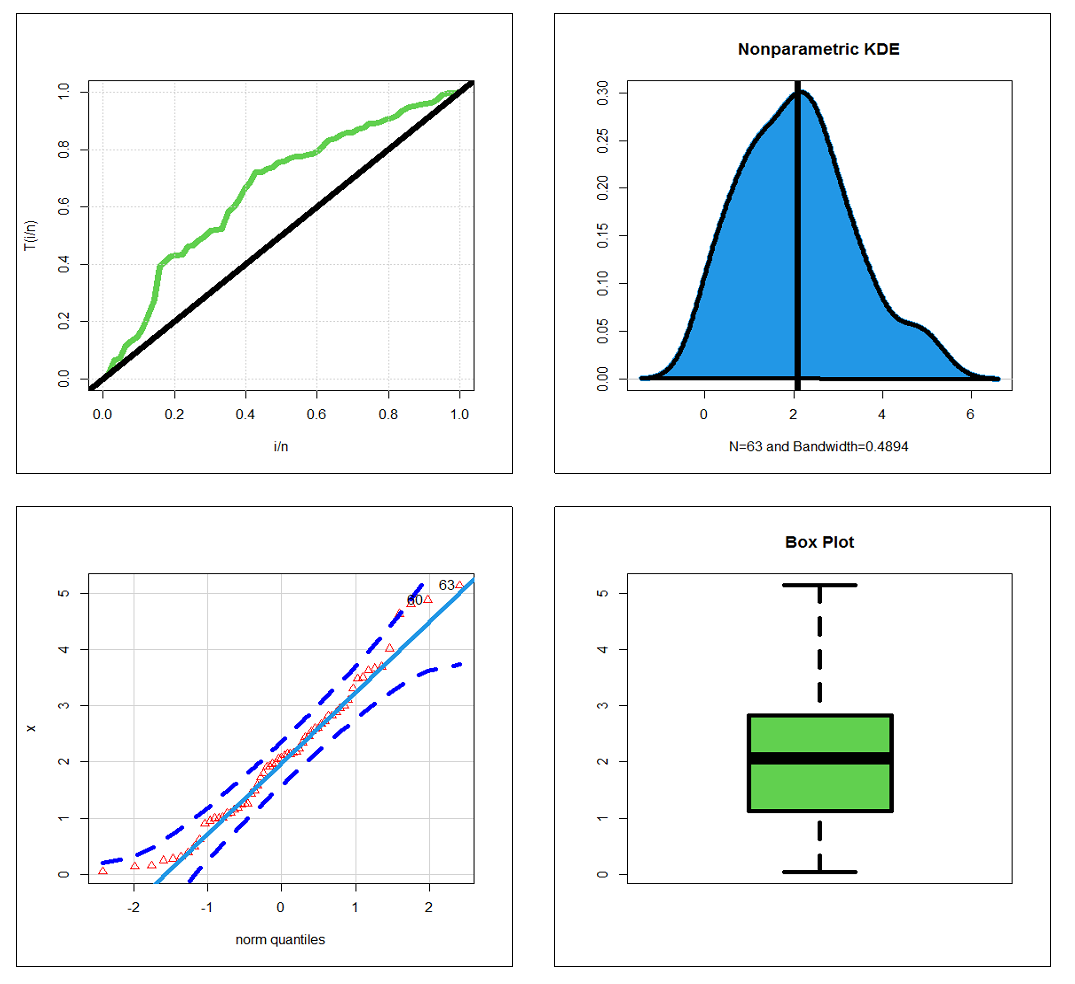
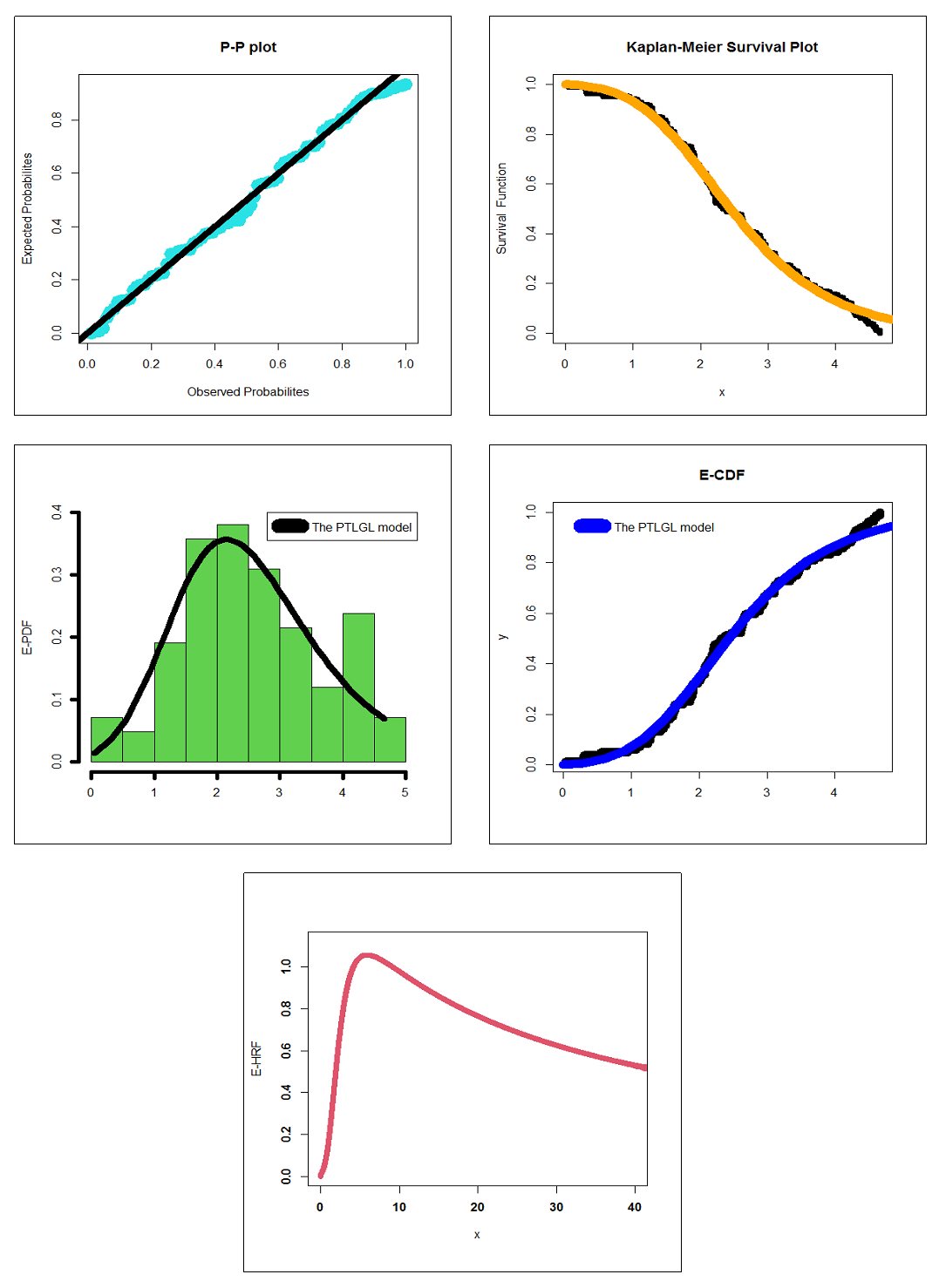
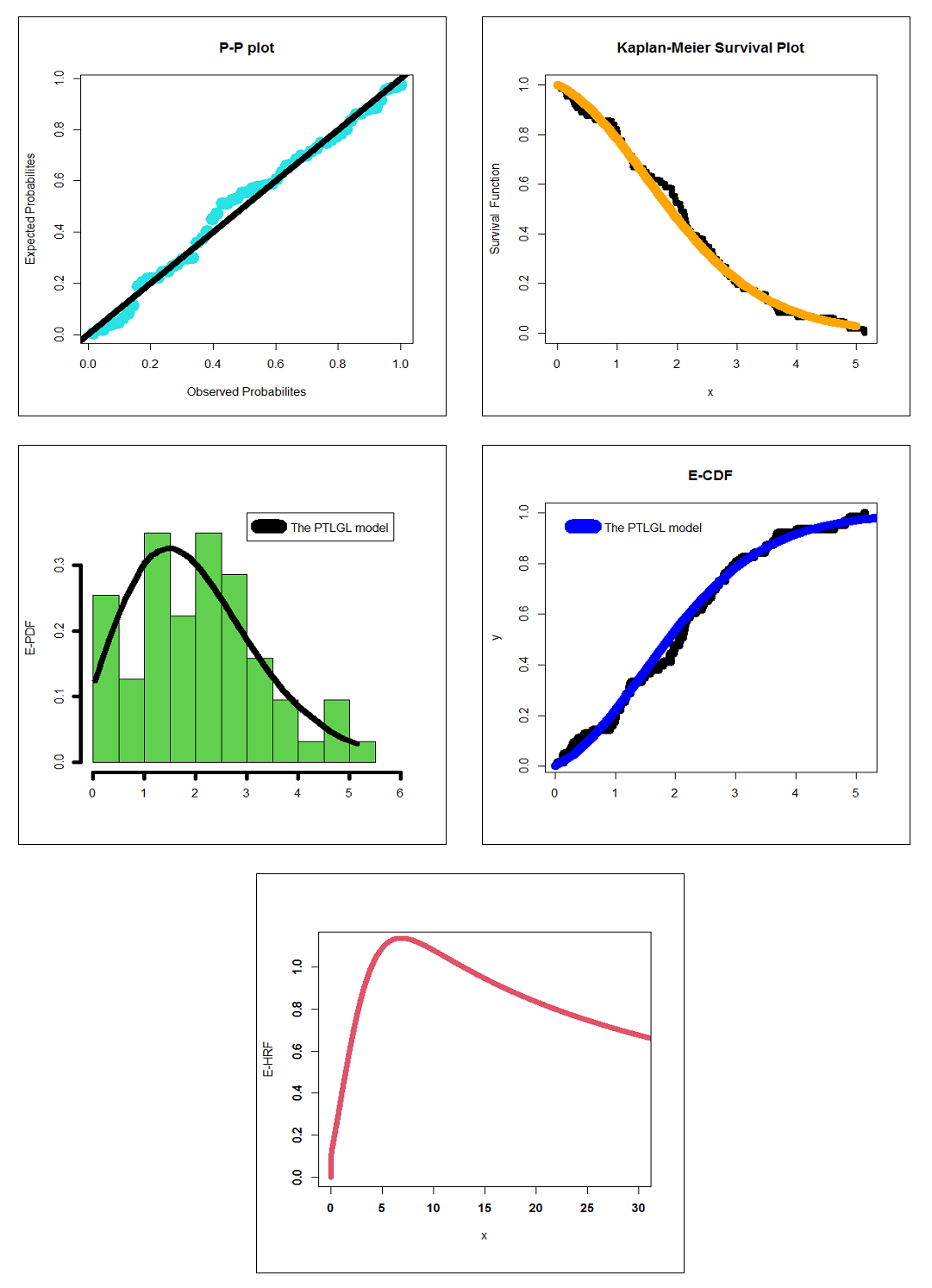
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML