-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Probability and Statistics
p-ISSN: 2168-4871 e-ISSN: 2168-4863
2021; 10(2): 27-45
doi:10.5923/j.ijps.20211002.01
Received: May 8, 2021; Accepted: Jun. 2, 2021; Published: Jun. 15, 2021

Berry-Esseen Type Bound in Partially Linear Regression Model under Mixing Sequences
Sallieu Kabay Samura
Department of Mathematics and Statistics, Fourah Bay College, University of Sierra Leone, Sierra Leone
Correspondence to: Sallieu Kabay Samura , Department of Mathematics and Statistics, Fourah Bay College, University of Sierra Leone, Sierra Leone.
| Email: |  |
Copyright © 2021 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

It is well-known that the confidence intervals of 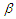 and
and 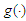 in partially linear regression model lie in the limit distributions of their estimators. However the accuracy of the confidence intervals depends on how fast the theoretical distributions of the estimators converge to their limits. As a results, Berry-Esseen type bounds can be used to assess the accuracy. The aim of this paper is to study the Barry-Esseen type bounds for the estimators of
in partially linear regression model lie in the limit distributions of their estimators. However the accuracy of the confidence intervals depends on how fast the theoretical distributions of the estimators converge to their limits. As a results, Berry-Esseen type bounds can be used to assess the accuracy. The aim of this paper is to study the Barry-Esseen type bounds for the estimators of 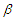 and
and 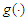 in the partially linear regression model with
in the partially linear regression model with 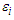 satisfying
satisfying 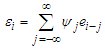 with
with 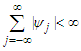 and
and 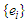 being stationary
being stationary 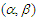 -mixing random variables. By choosing suitable weighted functions, the Berry-Esseen type bounds for the estimators
-mixing random variables. By choosing suitable weighted functions, the Berry-Esseen type bounds for the estimators 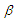 and
and 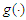 can achieve
can achieve 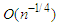 and
and 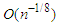 respectively. Simulation studies are conducted to demonstrate the performance of the proposed procedure.
respectively. Simulation studies are conducted to demonstrate the performance of the proposed procedure.
Keywords:
Partially linear model, Berry-esseen bound, 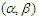 -mixing sequence
-mixing sequence
Cite this paper: Sallieu Kabay Samura , Berry-Esseen Type Bound in Partially Linear Regression Model under Mixing Sequences, International Journal of Probability and Statistics , Vol. 10 No. 2, 2021, pp. 27-45. doi: 10.5923/j.ijps.20211002.01.
Article Outline
1. Introduction
- Partially linear regression model is a combination of linear and nonparametric parts in which the relationship between the response and some explanatory variables are linear whereas the other predictors are emerged in the model in unspecified association form. Opsomer and Ruppert (1999) argued for the advantage of partially linear regression model, including that there is less worry of overfitting, that they are more easily interpretable, and that the estimator is more efficient for the parametric components. Also, various estimation and variable selection methods for the partially linear regression model have been developed which we refer to, Horowitz (2009), Liu et al. (2011), Roozbeh et al. (2012), Amini and Roozbeh (2016), Roozbeh and Arashi (2016), Roozbeh (2018) and Amini and Roozbeh (2019) to mention a few.Since its introduction by Engle et al. (1986), partially linear regression models have been studied by many authors. For example, Heckman (1986), Rice (1986), Chen (1988) and Speckman (1988) studied the consistency properties of the estimator of
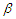 under different assumptions. Schick (1996) and Liang and Härdle (1997) extended the root n consistency and asymptotic results for the case of heteroscedasticity. Härdle et al. (2000) provided a good comprehensive reference of the partially linear model. Chen et al. (1998) and Gao et al. (1994) established the strong consistency and asymptotic normality, respectively, for the least squares estimators and weighted least-squares estimator (WLSE, for short) of
under different assumptions. Schick (1996) and Liang and Härdle (1997) extended the root n consistency and asymptotic results for the case of heteroscedasticity. Härdle et al. (2000) provided a good comprehensive reference of the partially linear model. Chen et al. (1998) and Gao et al. (1994) established the strong consistency and asymptotic normality, respectively, for the least squares estimators and weighted least-squares estimator (WLSE, for short) of 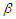 based on nonparametric estimates
based on nonparametric estimates 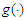 and
and 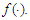 You et al. (2007) further studied the model and developed an inferential procedure which includes a test of heteroscedasticity, a two-step estimator of
You et al. (2007) further studied the model and developed an inferential procedure which includes a test of heteroscedasticity, a two-step estimator of 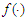 , mean square errors of
, mean square errors of 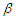 and
and 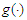 and a bootstrap goodness of fit test. If
and a bootstrap goodness of fit test. If 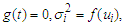 then the model boils down to the heteroscedastic linear model, whose asymptotic properties of the WLSE of
then the model boils down to the heteroscedastic linear model, whose asymptotic properties of the WLSE of 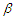 were studied by Carroll (1982), Robinson (1987) and Carroll and Härdle (1989), respectively.In this paper, we will further study the limit behaviors of the estimators in the partially linear regression model under
were studied by Carroll (1982), Robinson (1987) and Carroll and Härdle (1989), respectively.In this paper, we will further study the limit behaviors of the estimators in the partially linear regression model under 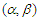 -mixing random variables, the concept of which was first introduced by Bradley (1985) as follows.Let
-mixing random variables, the concept of which was first introduced by Bradley (1985) as follows.Let  be a sequence of random variables defined on a fixed probability space
be a sequence of random variables defined on a fixed probability space 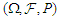 . Denote
. Denote 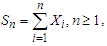 and
and 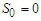 . Let
. Let 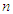 and
and 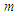 be positive integers. Write
be positive integers. Write 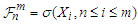 . Given
. Given 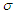 -algebras
-algebras 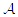 and
and 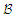 in
in 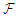 , let
, let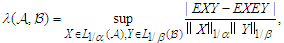 where
where 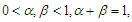 and
and 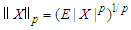 . Define the
. Define the 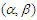 -mixing coefficients by
-mixing coefficients by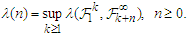 Definition 1.1. A sequence
Definition 1.1. A sequence 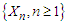 of random variable is said to be
of random variable is said to be 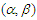 -mixing if
-mixing if 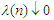 as
as 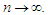 Since the concept of
Since the concept of 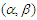 -mixing was introduced by Bradley (1985), many limit theorems were established. Bradley (1985) discussed central limit theorems under absolute regularity for
-mixing was introduced by Bradley (1985), many limit theorems were established. Bradley (1985) discussed central limit theorems under absolute regularity for 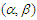 -mixing sequences. Shao (1993) established limit theorems of
-mixing sequences. Shao (1993) established limit theorems of 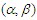 -mixing sequences; Cai (1991) obtained strong consistency and rates for recursive nonparametric conditional probability density estimators under
-mixing sequences; Cai (1991) obtained strong consistency and rates for recursive nonparametric conditional probability density estimators under 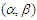 -mixing conditions; Lu and Lin (1997) gave the bounds of covariance of
-mixing conditions; Lu and Lin (1997) gave the bounds of covariance of 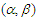 -mixing sequences; Shen and Zhang (2011) studied some convergence theorems for
-mixing sequences; Shen and Zhang (2011) studied some convergence theorems for 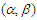 -mixing random variables, and obtained some new strong laws of large numbers for weighted sums of
-mixing random variables, and obtained some new strong laws of large numbers for weighted sums of 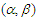 -mixing random variables; Gao (2016) investigated the
-mixing random variables; Gao (2016) investigated the 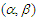 -mixing sequences which are stochastically dominated, and presented some strong stability; Yu (2016) showed the Resenthal-type inequality of the
-mixing sequences which are stochastically dominated, and presented some strong stability; Yu (2016) showed the Resenthal-type inequality of the 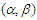 -mixing sequences, and investigated the strong convergence theorems.The aim of this paper is to further study the Barry-Esseen type bounds for the estimators of
-mixing sequences, and investigated the strong convergence theorems.The aim of this paper is to further study the Barry-Esseen type bounds for the estimators of 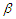 and
and 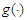 in the partially linear regression model (2.1) with
in the partially linear regression model (2.1) with 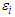 satisfying
satisfying 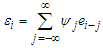 with
with 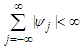 and
and 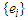 being stationary
being stationary 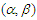 -mixing random variables. By choosing suitable weighted functions, the Berry-Esseen type bounds for the estimators
-mixing random variables. By choosing suitable weighted functions, the Berry-Esseen type bounds for the estimators 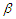 and
and 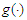 can achieve
can achieve 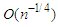 and
and 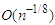 respectively.This work is organised as follows: In Section 2, we recall the partially linear regression model and construct the partial least squares estimator for both the parametric and non-parametric components. The main results and numerical analysis (simulations and real data) are presented in Section 3. The proofs of the main results are provided in Section 4.Throughout this paper, the symbols
respectively.This work is organised as follows: In Section 2, we recall the partially linear regression model and construct the partial least squares estimator for both the parametric and non-parametric components. The main results and numerical analysis (simulations and real data) are presented in Section 3. The proofs of the main results are provided in Section 4.Throughout this paper, the symbols 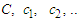 denote positive constants whose values may be different in different places. Let
denote positive constants whose values may be different in different places. Let 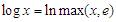 and
and 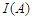 be the indicator function of the set
be the indicator function of the set 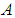 . Let
. Let 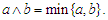
2. Model and Estimation
- Consider the following partially linear regression model:
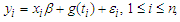 | (2.1) |
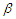 is an unknown parameter of interest,
is an unknown parameter of interest, 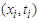 are nonrandom design points,
are nonrandom design points, 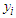 are the response variables,
are the response variables, 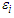 are random errors,
are random errors, 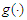 is an unknown functions defined on closed interval [0,1].If
is an unknown functions defined on closed interval [0,1].If 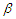 is the true parameter, then model (2.1) is reduced to a nonparametric regression model
is the true parameter, then model (2.1) is reduced to a nonparametric regression model 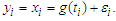 Since
Since 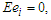 we have
we have 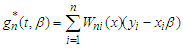 . Using the least squares method, we obtain
. Using the least squares method, we obtain 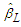 of
of 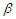 by minimizing
by minimizing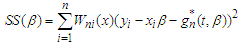 The minimizer is found to be
The minimizer is found to be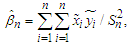 | (2.2) |
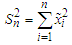 ,
,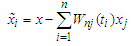 and
and 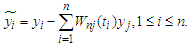 Then based on
Then based on 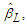 we defined the nonparametric function
we defined the nonparametric function 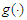 by
by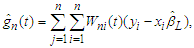 | (2.3) |
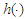 on [0,1] such that
on [0,1] such that 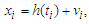 and(i)
and(i) 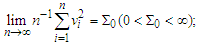 (ii)
(ii) 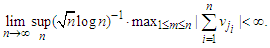 A2.
A2. 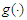 and
and 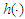 are defined on [0,1] and satisfy Lipschitz condition of order 1.A3. The probability weight function
are defined on [0,1] and satisfy Lipschitz condition of order 1.A3. The probability weight function 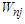 are defined on [0,1] and satisfy
are defined on [0,1] and satisfy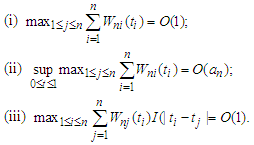 A4.
A4. 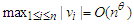 for some
for some 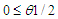 A5. There exist positive integers
A5. There exist positive integers 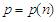 and
and 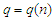 such that
such that 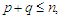
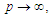
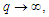
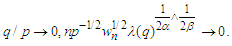 A6. The spectral density
A6. The spectral density 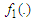 of
of 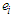 satisfies that
satisfies that 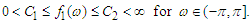 Remark 2.1 Conditions (A1)-(A3) have been used frequently by many authors. For example, Gao et al. [1996], Sun et al. [2002], You et al. [2005], Liang et al. [2006], You and Chen [2007] and so on. (A4) is adopted in Sun et al. [2002], You et al. [2005], Liang et al. [2006], Liang and Fan [2009] and so forth. Moreover, if functions
Remark 2.1 Conditions (A1)-(A3) have been used frequently by many authors. For example, Gao et al. [1996], Sun et al. [2002], You et al. [2005], Liang et al. [2006], You and Chen [2007] and so on. (A4) is adopted in Sun et al. [2002], You et al. [2005], Liang et al. [2006], Liang and Fan [2009] and so forth. Moreover, if functions 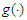 and
and 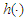 satisfy a Lipschitz condition of order 1 on [0,1], then (A3) (iii) implies that
satisfy a Lipschitz condition of order 1 on [0,1], then (A3) (iii) implies that 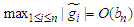 and
and 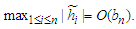
3. Main Results and Numerical Analysis
3.1. Main Results
- In this subsection, we present the Berry-Esseen type bounds for the estimators
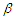 ,
, 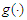 . We first introduce some notations which will be used in the theorem below.
. We first introduce some notations which will be used in the theorem below.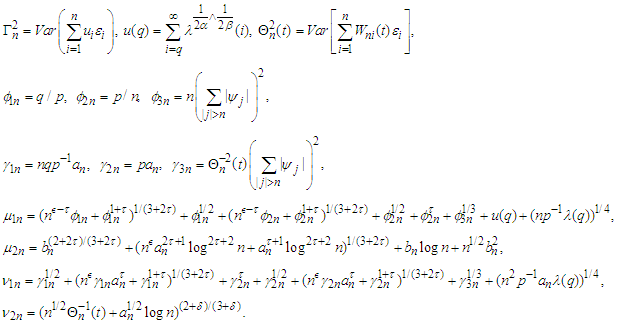 Theorem 3.1. Let
Theorem 3.1. Let 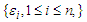 be a mean zero
be a mean zero 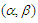 -mixing sequence, with
-mixing sequence, with 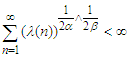 , where
, where 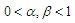 and
and 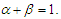 Suppose that conditions
Suppose that conditions 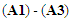 are satisfied,
are satisfied, 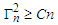 and
and 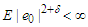 for some
for some 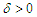 . Let
. Let 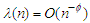 for some
for some 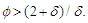 Assume that
Assume that 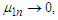
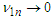 . Then, for
. Then, for 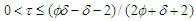 and any
and any 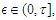 we have
we have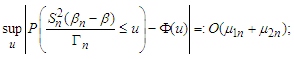 | (3.1) |
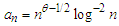 and
and 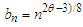 where
where 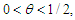 and
and 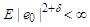 for some
for some 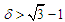 . Let
. Let 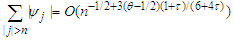 ,
, 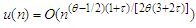 for some
for some 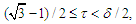 and
and 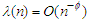 for some
for some 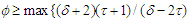 ,
, 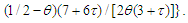 Then
Then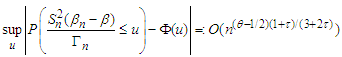 Theorem 3.2. Suppose that the conditions in theorem 3.1 hold. Let
Theorem 3.2. Suppose that the conditions in theorem 3.1 hold. Let 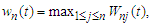
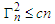 and
and 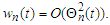 If
If 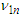 and
and 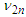 converge to zero, then
converge to zero, then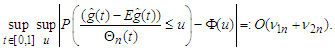 | (3.2) |
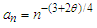 for some
for some 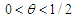 and
and 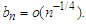 Suppose that
Suppose that 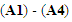 hold with
hold with 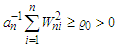 for each
for each 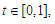 and
and 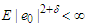 for some
for some 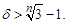 Let
Let 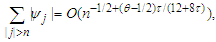
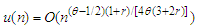 for some
for some 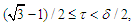 and
and 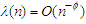 for some
for some 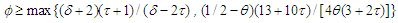 , then
, then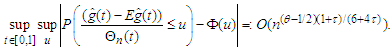
3.2. Numerical Simulation
- In this subsection, We carry out a simulation to study the asymptotic normality of the estimators
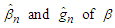 and
and 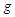 , respectively. The observations are generated for the following model:
, respectively. The observations are generated for the following model: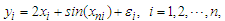 where
where 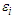 is an AR(1) type process
is an AR(1) type process 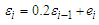 with
with 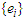 be an MA(1) process specified by
be an MA(1) process specified by 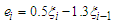 and
and 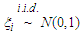 , for
, for 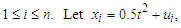 where
where 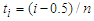 and
and 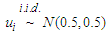 for
for 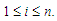 Here, we choose the nearest neighbor weights to be the weight functions
Here, we choose the nearest neighbor weights to be the weight functions 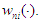 For any
For any 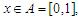 we rewrite
we rewrite 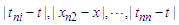 as follows
as follows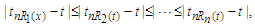 if
if 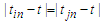 , then
, then 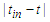 is permutated before
is permutated before 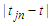 when
when 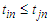 . Take
. Take 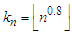 and defined the nearest neighbor weight function as follows:
and defined the nearest neighbor weight function as follows: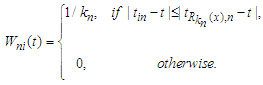 We generate the observed data with sample size
We generate the observed data with sample size 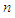 as
as 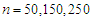 and
and 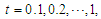 respectively. We used R software to compute
respectively. We used R software to compute 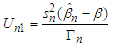 and
and 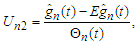 and obtained the Q-Q plots of
and obtained the Q-Q plots of 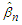 and
and 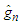 respectively, based on 500 replications.
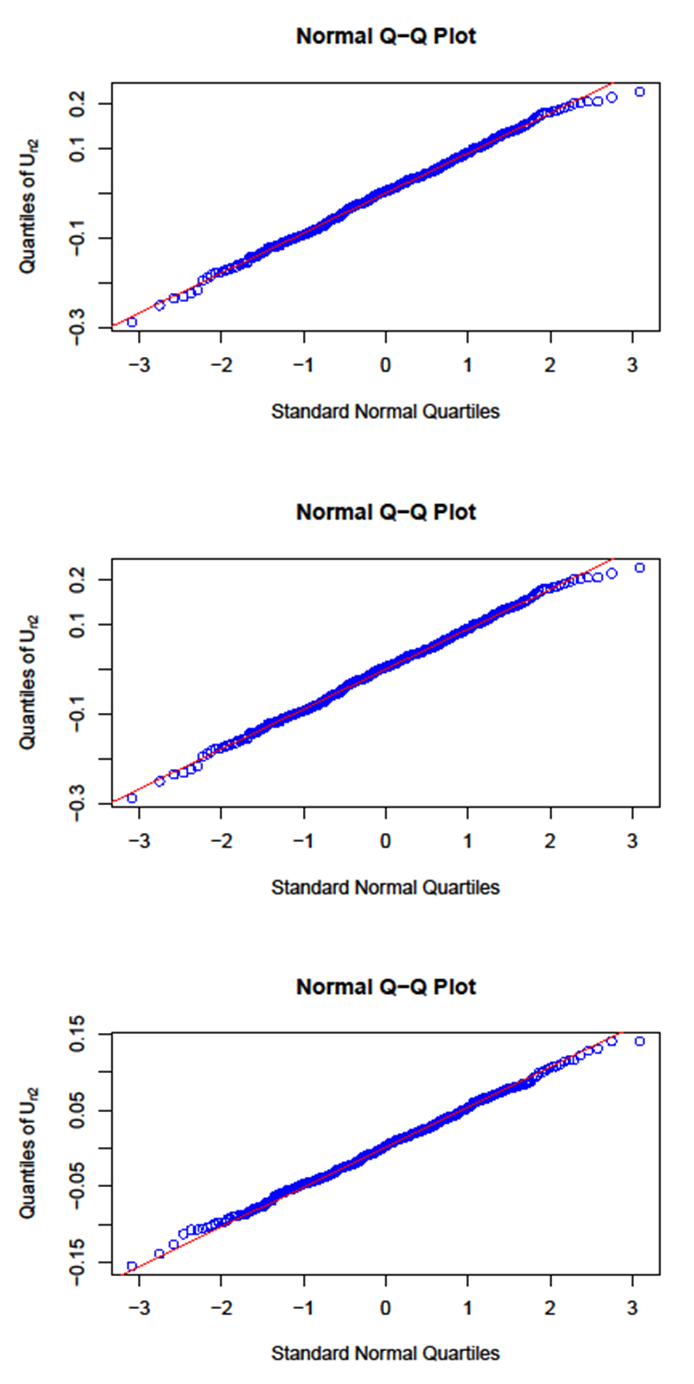
respectively, based on 500 replications.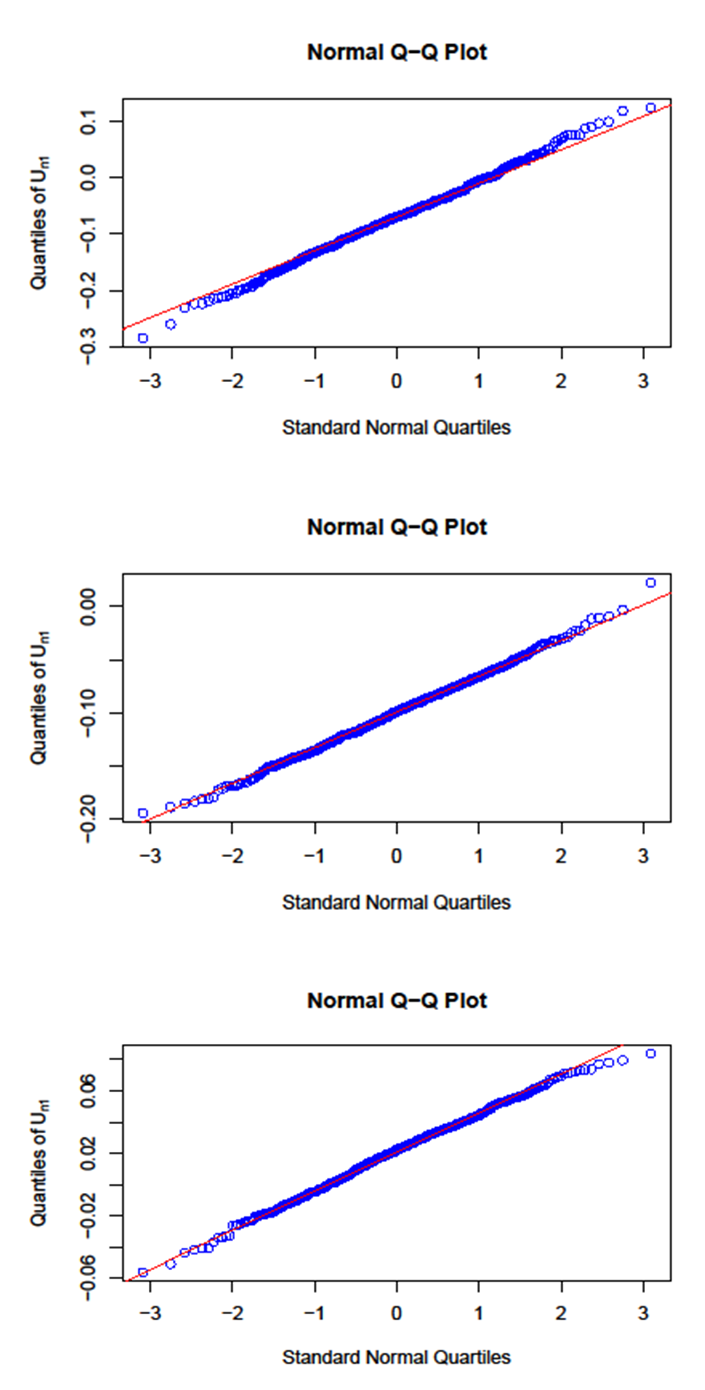 | Figure 1. Q-Q plot of  with with  =50, 100 and 150, respectively =50, 100 and 150, respectively |
 | Figure 2. Q-Q plot of  with with 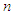 =50, 100 and 150, respectively =50, 100 and 150, respectively |
4. Proofs of the Main Results
- We first introduce several lemmas which will be used to prove the main results of the paper.Lemma 3.1. (cf. Yu, 2016) Let
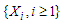 be a sequence of
be a sequence of 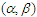 -mixing random variables with
-mixing random variables with 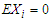 ,
, 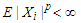 for some
for some 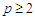 and
and 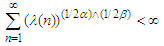 , where
, where 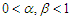 and
and 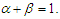 Assume that
Assume that 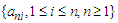 is an array of real numbers. Then there exists a positive constant
is an array of real numbers. Then there exists a positive constant 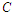 depending only on
depending only on 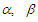 and
and 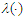 such that
such that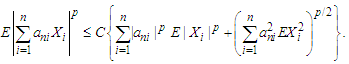 Lemma 3.2. (Liang and Fan, 2009) Let
Lemma 3.2. (Liang and Fan, 2009) Let 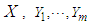 be random variables. For positive numbers
be random variables. For positive numbers 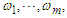 we have that
we have that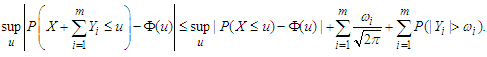 Lemma 3.3. (Lu and Lin (1997)) Let
Lemma 3.3. (Lu and Lin (1997)) Let 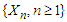 be a sequence of
be a sequence of 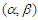 -mixing random variables. Suppose that
-mixing random variables. Suppose that 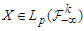 and
and 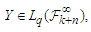 where
where 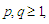 and
and 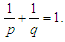 Then
Then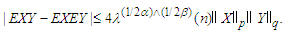 Lemma 3.4. Let
Lemma 3.4. Let 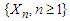 be a sequence of
be a sequence of 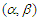 -mixing random variables. Suppose that p and q are two positive integers. Let
-mixing random variables. Suppose that p and q are two positive integers. Let 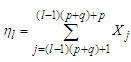 for
for 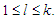 Then for any
Then for any 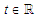
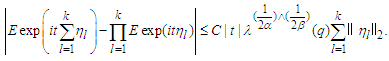 Proof. It is easily checked that
Proof. It is easily checked that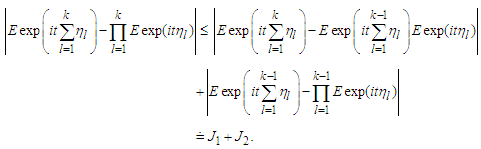 | (4.1) |
 we have
we have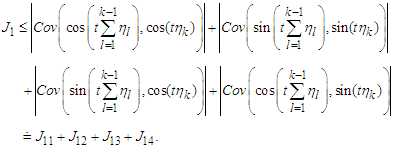 | (4.2) |
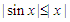 that
that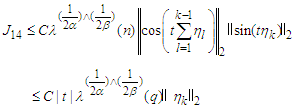 | (4.3) |
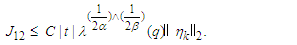 | (4.4) |
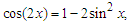 and hence applying Lemma 3.3 and invoking again the inequality
and hence applying Lemma 3.3 and invoking again the inequality 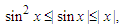 we find that
we find that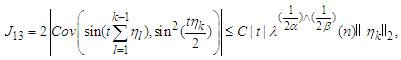 | (4.5) |
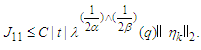 | (4.6) |
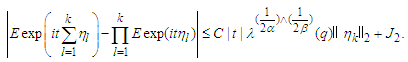 Proceeding in this manner, we obtain
Proceeding in this manner, we obtain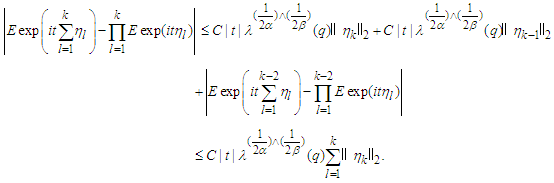 This completes the proof of the lemma.Lemma 3.5. Let
This completes the proof of the lemma.Lemma 3.5. Let 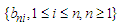 be an array of real numbers such that
be an array of real numbers such that 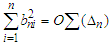 and
and 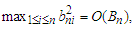 where
where 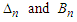 are some positive numbers. Suppose that
are some positive numbers. Suppose that 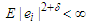 for some
for some 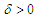 and
and 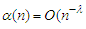 for some
for some 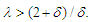 Then for any
Then for any 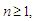
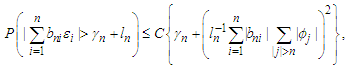 and
and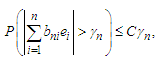 where
where 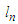 are positive numbers and
are positive numbers and 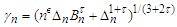 for some
for some 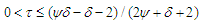 and any
and any 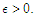 Proof. We only prove the first inequality, and the second one is completely analogous. According to the definition of
Proof. We only prove the first inequality, and the second one is completely analogous. According to the definition of 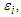 we have that
we have that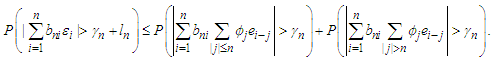 By
By 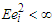 and Markov's inequality, we have
and Markov's inequality, we have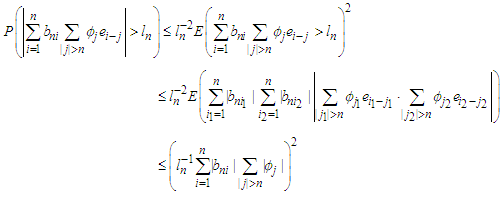 Note that
Note that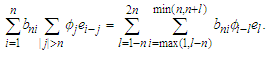 Applying Lemma 3.1 with
Applying Lemma 3.1 with 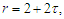
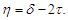 Noting that
Noting that 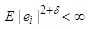 and
and 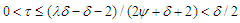 implies
implies 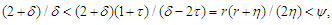 we have
we have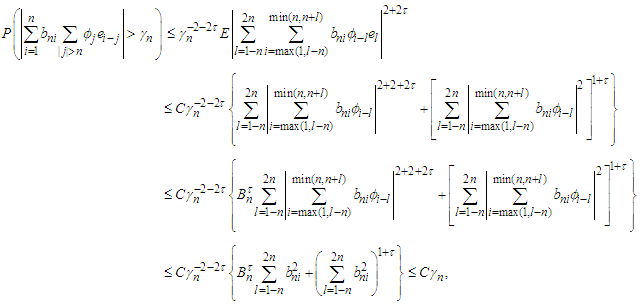 Where the inequality in the last line above follows from
Where the inequality in the last line above follows from  and changing the order of simulation. The proof is completed.Lemma 3.6. Under the assumptions of Theorem 2.1, the following statements hold.
and changing the order of simulation. The proof is completed.Lemma 3.6. Under the assumptions of Theorem 2.1, the following statements hold.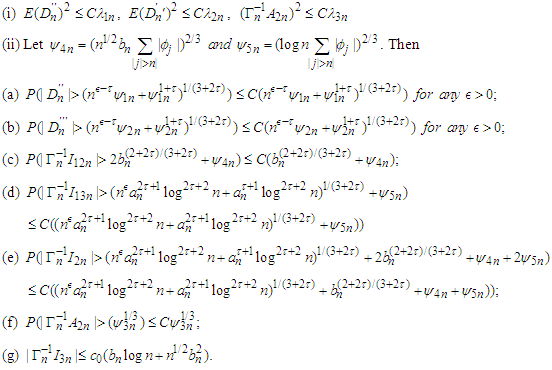 Proof. (i) Applying Lemma 3.2 with
Proof. (i) Applying Lemma 3.2 with  and
and  inequality, we have by
inequality, we have by 
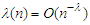 for
for 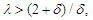 (A1) (iii) and (1.2) that
(A1) (iii) and (1.2) that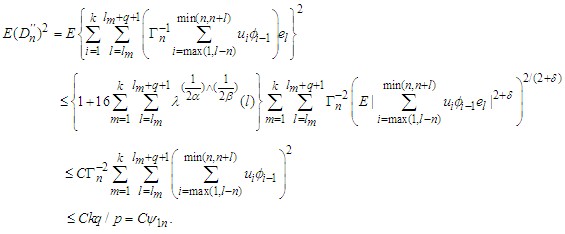 | (4.7) |
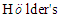 inequality again that
inequality again that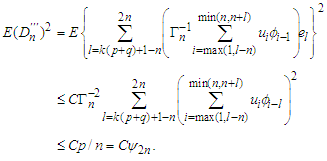 Moreover, we have by
Moreover, we have by 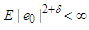 and (A1) (iii) again and
and (A1) (iii) again and 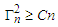 that
that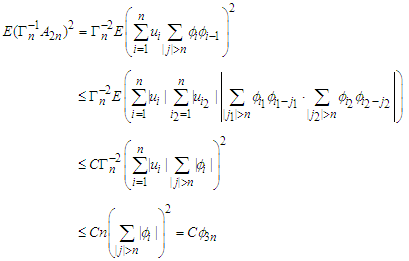 Hence (i) has been proved.(ii) The inequalities (a)-(e) can be proved by applying Lemma 3.5. Now we will verify them one by one.(a) Noting by (A1) (iii) that
Hence (i) has been proved.(ii) The inequalities (a)-(e) can be proved by applying Lemma 3.5. Now we will verify them one by one.(a) Noting by (A1) (iii) that 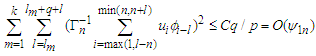 and
and 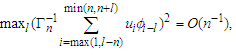 the result follows immediately form Lemma 3.5.(b) Similarly, noting additionally that
the result follows immediately form Lemma 3.5.(b) Similarly, noting additionally that 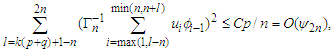 we have by Lemma 3.5 again that the result follows.(c) Note that
we have by Lemma 3.5 again that the result follows.(c) Note that 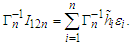 Therefore, we have
Therefore, we have 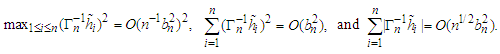 Let
Let 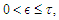 we have Lemma 3.5 again that
we have Lemma 3.5 again that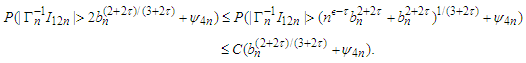 (d) Observe that
(d) Observe that 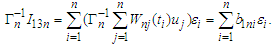 Utilizing the Abel Inequality (see Mitrinovic, 1970, Theorem 1, p.32), we have by (A1) and (A3) that
Utilizing the Abel Inequality (see Mitrinovic, 1970, Theorem 1, p.32), we have by (A1) and (A3) that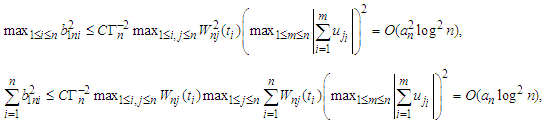 and
and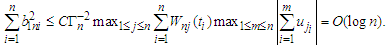 Thus the result follow from Lemma 3.5 immediately.(e) It follows
Thus the result follow from Lemma 3.5 immediately.(e) It follows 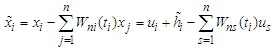 that
that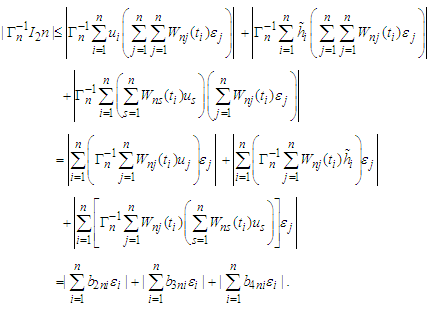 Similar to the proofs of (c) and (d), we have
Similar to the proofs of (c) and (d), we have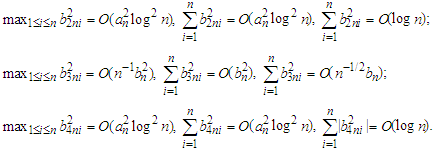 Choosing
Choosing  we have by Lemma 3.5 again that
we have by Lemma 3.5 again that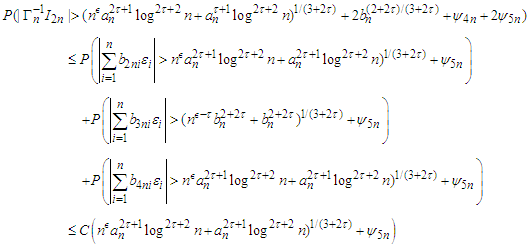 (f) The inequality (f) can be derived immediately by (i) and Markov's inequality.(g) It follows from the Abel Inequality and Remark 2.1 again that
(f) The inequality (f) can be derived immediately by (i) and Markov's inequality.(g) It follows from the Abel Inequality and Remark 2.1 again that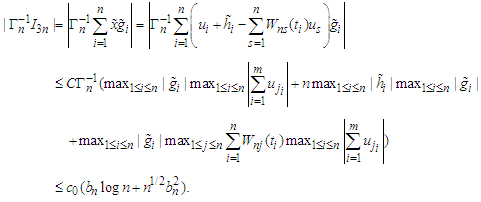 The prove is completed.Lemma 3.7 Let
The prove is completed.Lemma 3.7 Let 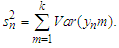 Then under the assumption of Theorem 3.1, we have
Then under the assumption of Theorem 3.1, we have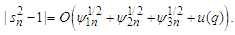 Proof. Similar to Lemma 3.6 in Liang and Fan (2009), we can complete the proof of the lemma. The details are omitted.Assume that
Proof. Similar to Lemma 3.6 in Liang and Fan (2009), we can complete the proof of the lemma. The details are omitted.Assume that 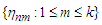 are independent random variables and
are independent random variables and 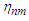 has the same distribution as that of
has the same distribution as that of 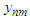 for each
for each 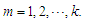 Let
Let 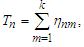 then
then 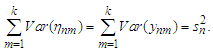 Lemma 3.7 Under the assumptions of Theorem 3.1, we have
Lemma 3.7 Under the assumptions of Theorem 3.1, we have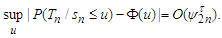 Proof. We have by Berry-Esseen inequality (Petrov, 1995, p.154, Theorem 5.7) that
Proof. We have by Berry-Esseen inequality (Petrov, 1995, p.154, Theorem 5.7) that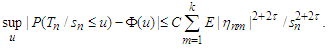 Applying Lemma 3.3 with
Applying Lemma 3.3 with 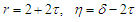 and noting that
and noting that 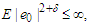 we have by choosing
we have by choosing 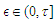 that
that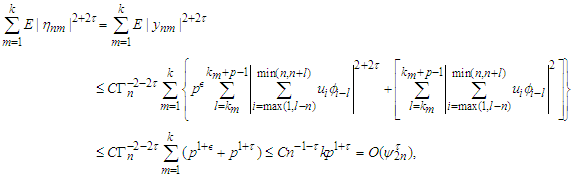 which together with
which together with 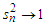 from Lemma 3.7 yields that
from Lemma 3.7 yields that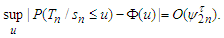 The prove is completed.Lemma 3.8 Under the assumptions of Theorem 3.1, we have
The prove is completed.Lemma 3.8 Under the assumptions of Theorem 3.1, we have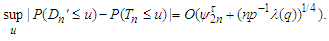 Proof. Suppose that
Proof. Suppose that 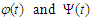 are characteristic functions of
are characteristic functions of 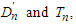 respectively.We have by Esseen inequality (Petrov, 1995, p.146, Theorem 5.3) that for any
respectively.We have by Esseen inequality (Petrov, 1995, p.146, Theorem 5.3) that for any 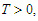
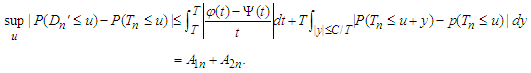 Applying Lemma 3.4 with
Applying Lemma 3.4 with  and Lemma 3.2 with
and Lemma 3.2 with  and similar to the proof of (3.2), we have by
and similar to the proof of (3.2), we have by  that
that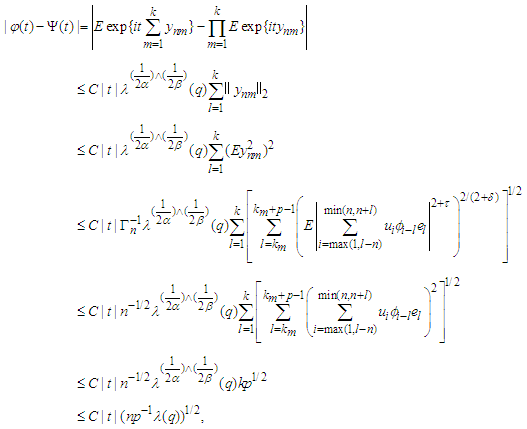 which implies that
which implies that 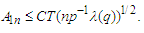 On the other hand, from Lemma 3.7 and we have
On the other hand, from Lemma 3.7 and we have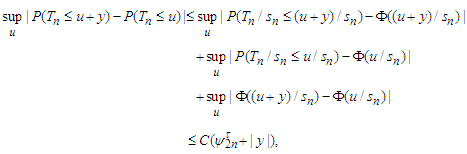 which derives that
which derives that 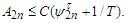 By choosing
By choosing 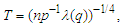 we can obtain that
we can obtain that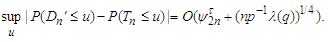 This completes the proof of the lemma.Proof of Theorem 3.1 We can observe that
This completes the proof of the lemma.Proof of Theorem 3.1 We can observe that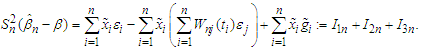 It is easy to show that
It is easy to show that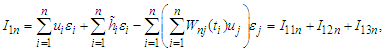 and
and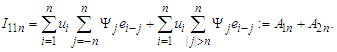 By changing the order of summation, we obtain that
By changing the order of summation, we obtain that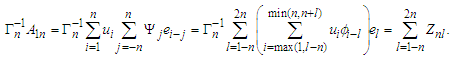 Let
Let 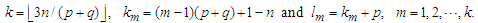 Denote
Denote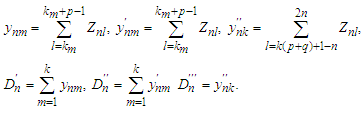 The we have that
The we have that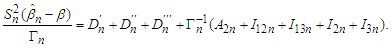 It follows from Lemma 3.7-3.9 that
It follows from Lemma 3.7-3.9 that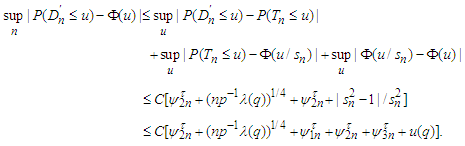 Consequently, from (3.1), Lemma 3.1 and Lemma 3.6, we have
Consequently, from (3.1), Lemma 3.1 and Lemma 3.6, we have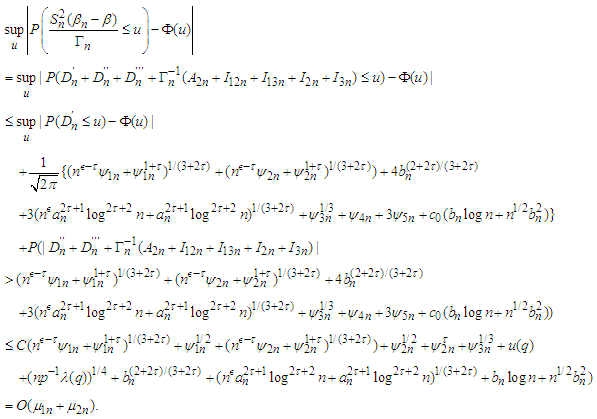 The proof of the theorem is completed.To prove Theorem 2.2, we need the following lemmas.Lemma 3.8 Under the assumption of Theorem 2.2, the following statements hold.
The proof of the theorem is completed.To prove Theorem 2.2, we need the following lemmas.Lemma 3.8 Under the assumption of Theorem 2.2, the following statements hold.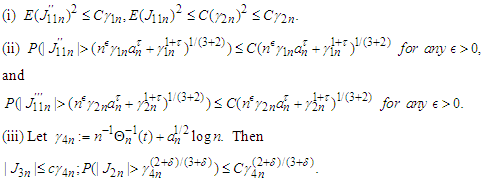 Furthermore, if
Furthermore, if 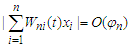 for some positive numbers
for some positive numbers 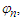 then
then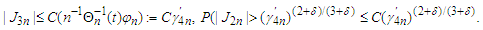 Proof. (i) Similar to the proof of (3.2), we have by
Proof. (i) Similar to the proof of (3.2), we have by 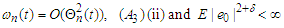 that
that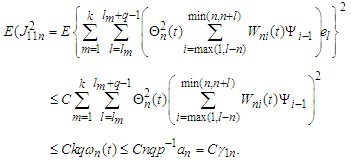 Similarly,
Similarly,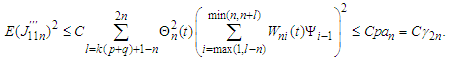 Noting that
Noting that 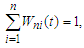 analogous to the proof of (3.3) we have
analogous to the proof of (3.3) we have 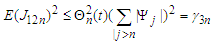 (ii) Noting that
(ii) Noting that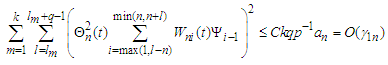 and
and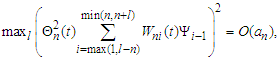 the first inequality follows immediately form Lemma 3.5.Similarly, noting that
the first inequality follows immediately form Lemma 3.5.Similarly, noting that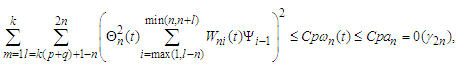 we can also get the second one from Lemma 3.5.(iii) Observe that
we can also get the second one from Lemma 3.5.(iii) Observe that 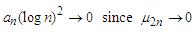 in Theorem 2.1, the proof of (iii) can be easily obtained by following the proof of Lemma 3.9 in Liang and Fan (2009). The details are omitted here.Lemma 3.11. Let
in Theorem 2.1, the proof of (iii) can be easily obtained by following the proof of Lemma 3.9 in Liang and Fan (2009). The details are omitted here.Lemma 3.11. Let 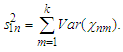 Then under the assumptions of Theorem 2.2, we have
Then under the assumptions of Theorem 2.2, we have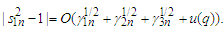 Proof. Similar to the proof of Lemma 3.10 in Liang and Fan (2009), we can prove the lemma.The details are omitted.Assume that
Proof. Similar to the proof of Lemma 3.10 in Liang and Fan (2009), we can prove the lemma.The details are omitted.Assume that 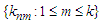 are independent random variables and
are independent random variables and 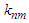 has the same distribution as that of
has the same distribution as that of 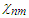 for each
for each 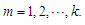 Let
Let 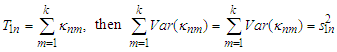 .Lemma 3.12 Under the assumptions of Theorem 2.2, we have
.Lemma 3.12 Under the assumptions of Theorem 2.2, we have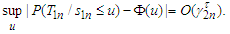 Proof. Note that
Proof. Note that 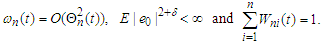 Similar to the proof of Lemma 3.8, we have by Lemma 3.3,
Similar to the proof of Lemma 3.8, we have by Lemma 3.3, 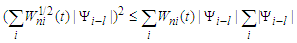 and changing the order of summation that
and changing the order of summation that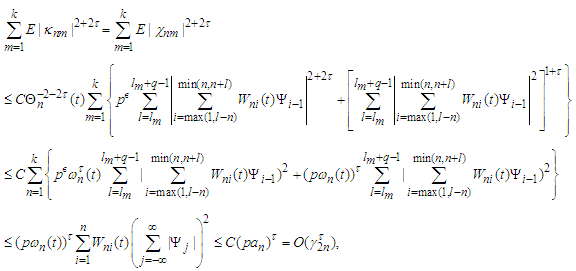 which together with
which together with 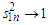 from Lemma 3.11 yields that
from Lemma 3.11 yields that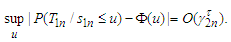 The proof is completed.Lemma 3.13 Under the assumptions of Theorem 2.2, we have
The proof is completed.Lemma 3.13 Under the assumptions of Theorem 2.2, we have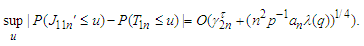 Proof. Suppose that
Proof. Suppose that 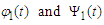 are the characteristic functions of
are the characteristic functions of 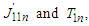 respectively. Similar to the proof of Lemma 3.9, we have
respectively. Similar to the proof of Lemma 3.9, we have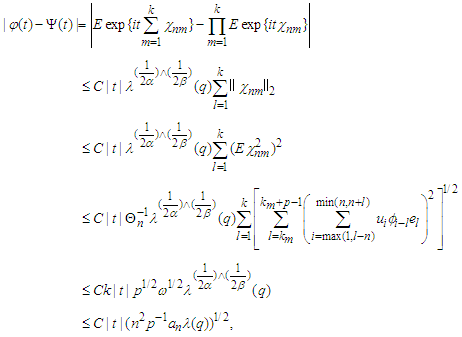 together with Lemma 3.11 and 3.12 yield that
together with Lemma 3.11 and 3.12 yield that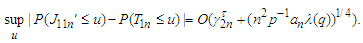 This completes the proof of the lemma.Proof of Theorem 3.1 We have that
This completes the proof of the lemma.Proof of Theorem 3.1 We have that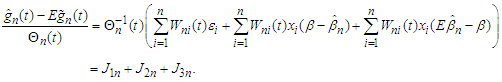 Note that
Note that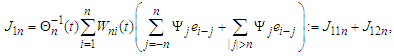 and
and Similar to the decomposition for
Similar to the decomposition for 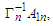 we denote
we denote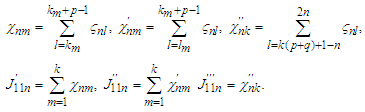 Then we have that
Then we have that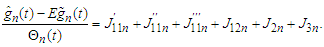 we have by Lemma 3.11-3.13 that
we have by Lemma 3.11-3.13 that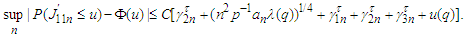 which together with (3.4), Lemma 3.1 and Lemma 3.10 yields that
which together with (3.4), Lemma 3.1 and Lemma 3.10 yields that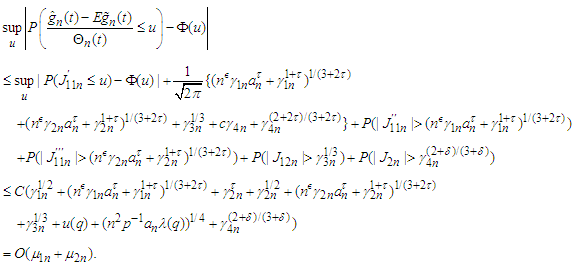 The proof is completed.
The proof is completed. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML