1. Introduction

The Burr type-XII distribution has been extensively studied in the literature as an appropriate and useful failure model for the applied statistics. Several studies were performed on Burr type-XII distribution, which includes Evans and Simon (1975) who discussed the Burr distribution as a failure model and derived the maximum likelihood estimators (MLEs) for the parametors. Evans and Ragab (1983) discussed the Bayesian estimotors for Burr distribution paramaeters based on type-II censored samples. Wu and Yu (2005) proposed some pivotal quantities to test shape parameters and established their confidence intervals based on the censored data. Soliman (2005) derived the MLE and Bayesian estimates of the parameters and some lifetime parameters. Xiuchun et al. (2007) derived the empirical Bayesian estimator for the reliability based on progressively type-II censored samples, and Liang and Yimin (2010) derived the empirical Bayesian estimators based on record values. For a comprehensive review of the Burr type-XII distribution, see Rodrignez (1977).

However, in recent years, this distribution has been used in a variety of fields such as business, see Rodringuez and Taniguchi (1980). Economics and Finance see, McDonald and Richards (1987). Hydrology, see Mielke and Johanson (1974). Quality assurance, see Burr (1976). Medicine see Wingo (1983) and Mineralogy, see Cook and Johnson (1986). Wingo (1993) derived the MLEs of the parameters under type-II censoring. Wingo (1993) derived the MLEs for fitting the Burr type-XII model based on multiply censored data. Zimmer et al. (1998) studied the reliability analysis of the Burr typ-XII distribution. Wu and Yu (2005) proposed pivotal quantities to test the shape parameter and establish confidence interval of the shape parameter for the Burr type-XII distribution under the failure-censored plan. Malinawska et al. (2006) derived the estimation paramters of the Burr type-XII model using generalized order statistics. Lio et al. (2007) derived the paramter estimates based on the progressive type-II censoring. Li et al. (2007) proposed the epmirical Bayes estimators of reliability performances for the Burr type-XII model using LINEX loss function based on progressively type-II censored samples. Wu et al. (2007) derived the MLE estimates for the Burr type-XII distribution parameters. Asgharzadeh and Valiollahi (2008) derived the parameter estimates based on progressive type-II censored data. Wing (2008) studied the statistical inference of the Burr type-XII distribution. Lee et al. (2009) obtained Bayes and empirical Bayes estimators for reliability. Asgharzadeh and Abdi (2012) derived the confidence intervals of the Burr type-XII model parameters based on records. Soliman et al. (2012) studied the Bayesian statistical inference and prediction for the Burr type-XII model based on the progressive first inference censored samples. Kumar(2017) presented some statistical properties for this distribution. Amal et al. (2018) derived the Bayesian estimate of the reliability based on a new numerical loss function. Hakim et al. (2021) presented some characteristics of this distribution and its application to heavy tailed survival time data. Thus, many aspects of the distribution have been covered by the researchers, but there is still a lack of comprehensive statistical analysis of the distribution. In this paper, the conditional inference was applied to construct confidence intervals for the Burr type-XII model parameters based on generalized order statistics. However, the conditional inference as suggested by Sir Fisher (1934) has been applied to many lifetime distributions belonging to the location-scale family, see Lawless (1973-1982) or those that can be transferred to this family, see Maswadah (2003, 2005), and Maswadah and EL-Faheem (2018). Thus, as a new application of the conditional approach, the conditional confidence intervals were generated for the Burr Type-XII model parameters based on generalized order statistics.

The Burr type-XII model was considered by Burr (1942), as a new lifetime distribution with the cumulative distribution function (cdf) and the probability density function (pdf), which are presented respectively by:

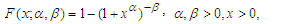(1.1)

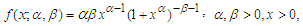(1.2)

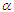and 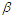are two shape parameters.

Thus, for the significance of this distribution, the confidence intervals were derived based on the conditional and the classical inferences based on generalized order statistics (GOS) that introduced by Kamps (1995) as a unified approach to ordinary OS, type-II progressive order statistics, record values and k-th record values.

Definition.

Let 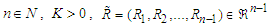be parameters such that

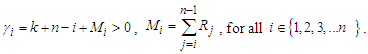The random variables 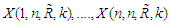are called GOS, with noting that 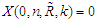, if their joint pdf can be written in the form:

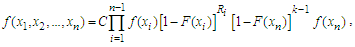(1.3)

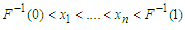On the cone of 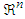, where .

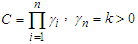2. Conditional Inference Methodology

For the first time, in this section, we will provide an outline for the conditional inference to the Burr Type-XII distribution based on the generalized order statistics.

Given a set of 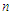GOS 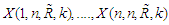with sampling density function (1.3), thus by substituting (1.1) and (1.2) in (1.3) we can derive the joint pdf as follows:

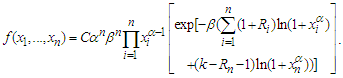(2.1)

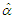For (1.1), if and 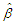be any equivariant estimators such as the MLEs for 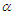and 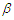, then 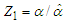and 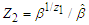are pivotal quantities and 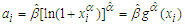, 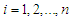form a set of ancillary statistics. With noting that .

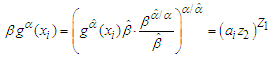Thus, based on the following theorem, we can derive the conditional densities of the pivotal quantities conditional on the ancillary statistics and the confidence intervals can be constructed and converted to 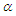and 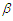fiducially.

Theorem:

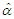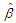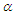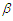Let and be any equivariant estimators of and , based on the generalized order statistics 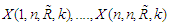. Then the conditional pdf of 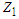and 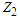given 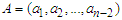can be derived in the form

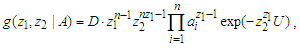(2.2)

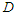is a normalizing constant depends on 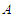only, and .

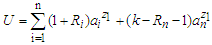Proof: see Maswadah (2003).

3. Confidence Intervals Procedures

3.1. Conditional Confidence Intervals

The marginal density of 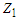and the distribution function of 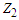can be derived from (2.2) respectively as:

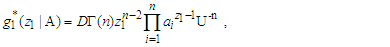(3.1)

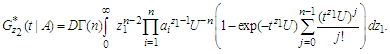(3.2)

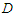is a normalizing constant does not depend on 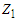and 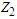, that can be derived as:

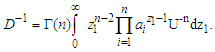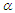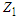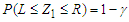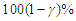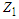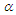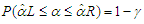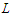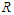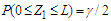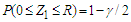To obtain confidence intervals for (say), from (3.1) the probability statement for can be obtained as , which is the confidence interval for and then transformed fiducially to as . This interval is not unique, and therefore using the tails of symmetric probability, the lower () and upper () limits of such an interval are solutions of and respectively. Similarly, the confidence interval for 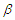can be constructed from (3.2).

3.2. Asymptotic Confidence Intervals

In this subsection, we obtained the Fisher information matrix to compute 95% asymptotic confidence intervals for the Burr type-XII distribution parameters based on maximum likelihood estimators (MLEs). The Fisher information matrix can be obtained by using loglikelihood function of (2.1). Thus, we have

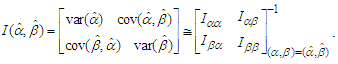Where,

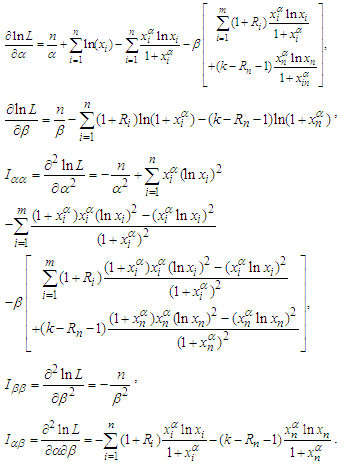Thus, the approximate 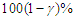two sided confidence intervals for and 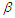can be obtained respectively by

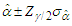and ,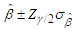

where 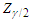is the upper 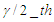percentile of a standard normal distribution, 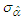and 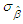are the standard deviations of the MLEs of the parameters 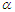and 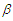respectively, where they are elements of the following AVC matrix: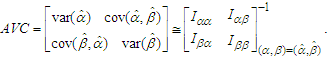

4. Simulation Studies

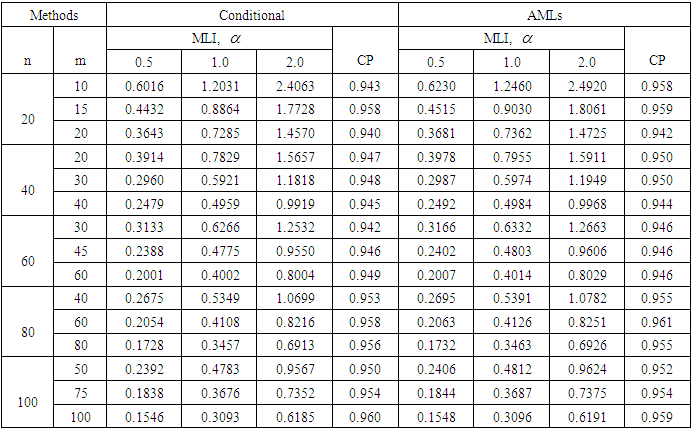
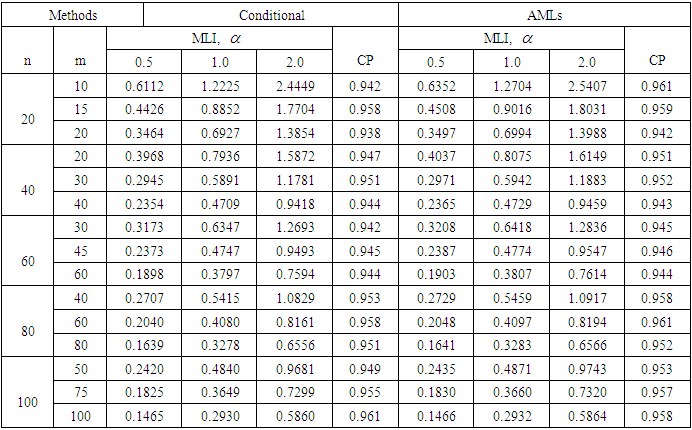
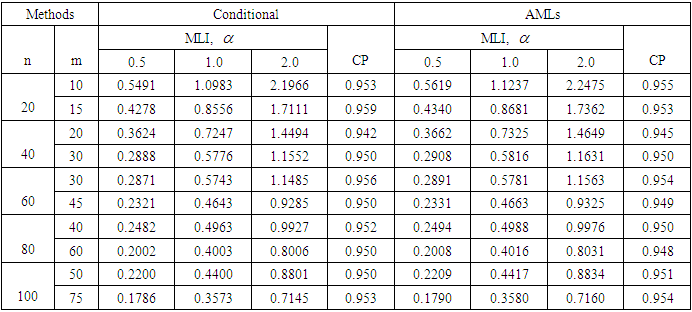
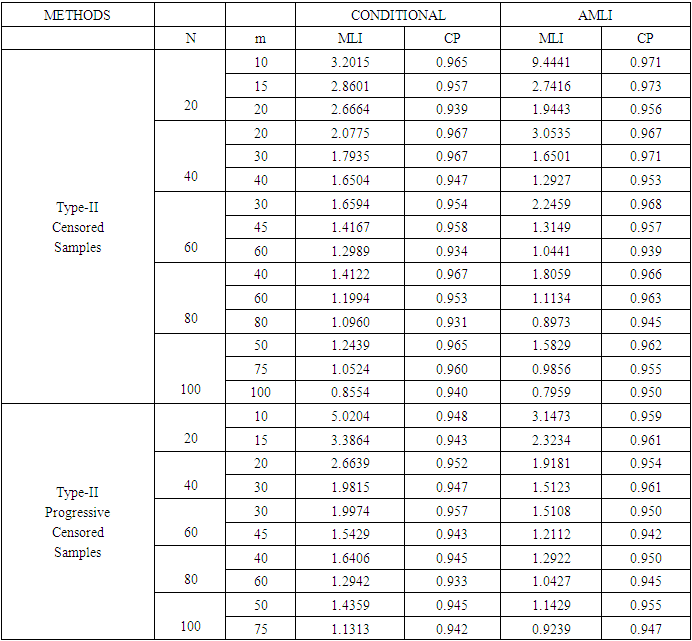
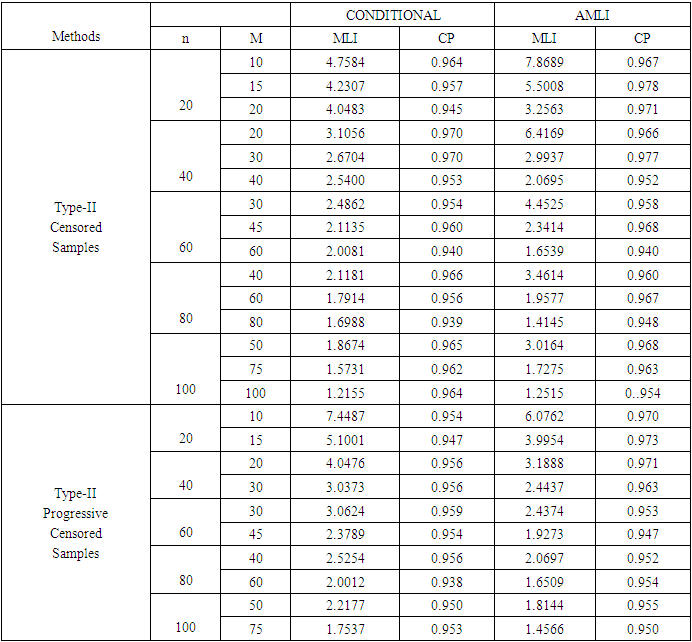
In this section we mainly present some results based on the Monte Carlo simulation, to measure the performance of the conditional confidence intervals compared to the AMLE intervals in terms of the following criteria:

1- Covering percentage

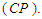2- Mean length of intervals

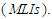Comparative results, based on 1000 Monte Carlo simulation trials are given for sample sizes n =20, 40, 60, 80 and 100 with censoring levels 0.0%, 0.25% and 0.50%, that have been generated from the Burr type-XII model for shape parameter values 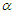= 0.5, 1, 2 and the parameter 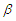= 2 and 3. For the progressive type-II censoring sampling that are carried out with binomial random removals with probablity 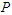= 0.5, which means the number of units removed at each failure time follows a binomial distribution with probability 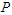, where different values of 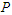do not affect the calculations.

From the simulation results that reported in Tables 2 to 7, we can summarize the following main points:

i. It is worthwhile to note that for different values of 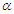, the 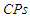are the same for the pivotal 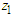as expected because its distribution is independent from the parameter 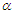. However, the values of 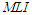for the parameter 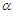increases when 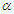increases. On the contrary the values of the 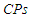and 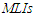for the pivotal 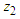are the same for all values of 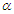as expected.

ii. Generally, the values of 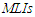decrease, the 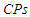almost getting increase as the sample size increases for both parameters 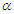and .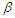

iii. For the parameter 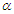, the values of 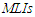and 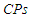decrease and the values of 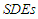getting increase for increasing the value of 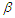, but it is not the case for highly type-II censoring, where the values of 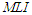getting increase. On the contrary, for the parameter 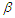, the values of 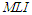and 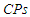increase for increasing 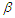as expected.

iv. The values of 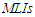for 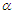based on the conditional inference are smaller than those based on the AMLEs inference, in spite of they have almost higher 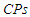based on complete and censored samples. However the values of 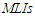for 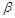based on the AMLEs inference are almost equal for two decimal places to those based on the conditinal inference, but it is not the case for highly type-II censored samples and small sample sizes.

v. Generally, the results based on the type-II progressive censored samples are better than those based on the type-II censored samples, in which they have smaller 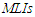and higher .

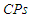Thus the simulation results indicated that the conditional confidence intervals possess good statistical properties and they can perform quite well even when the sample size is extremly small. However, the AMLE approach turns out to be impercise or even unreliable for small or highly type-II censored samples.

5. Real Data Analysis

5.1. Application Data for Joint Patients

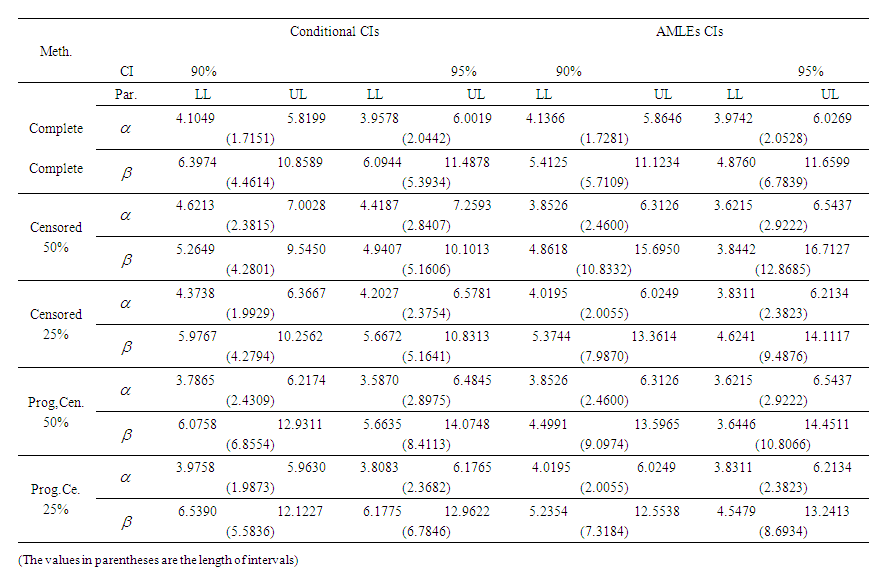
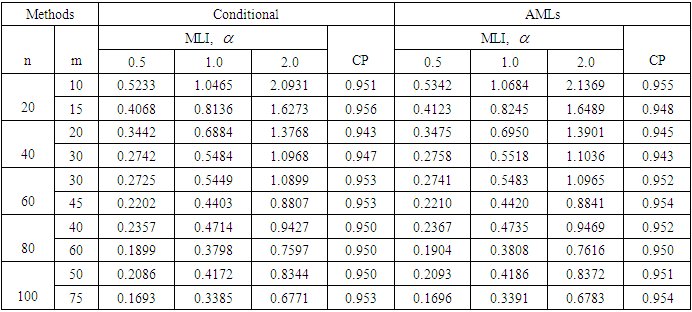
Consider data in Wingo (1983) representing the relief times in hours of 50 arthritics patients receiving a fixed dose of analgesic, which fits the Burr type-XII distribution.

0.70, 0.84, 0.58, 0.50, 0.55, 0.82, 0.59, 0.71, 0.72, 0.61, 0.62, 0.49, 0.54, 0.72, 0.36, 0.71, 0.35, 0.64, 0.85, 0.55, 0.59, 0.29, 0.75, 0.53, 0.46, 0.60, 0.60, 0.36, 0.52, 0.68, 0.80, 0.55, 0.84, 0.70, 0.34, 0.70, 0.49, 0.56, 0.71, 0.61, 0.57, 0.73, 0.75, 0.58, 0.44, 0.81, 0.80, 0.87, 0.29, 0.50

Thus, for comparison purposes, the 90% and 95% confidence intervals for the parameters 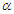and 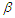are derived based on the conditional and the AMLEs approaches. The results in Table 1 indicated that the length of intervals for the parameters 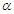and 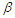based on the conditional approach are smaller than those based on the AMLEs approach that ensures the simulation results.

5.2. Application Data for Failure Components

Consider the data in Wingo (1993) representing the failure times for 30 specific electronic components included in the life test, which are censored after 20 failures using type-II censoring. These failure times (in months) are:

0.1, 0.1, 0.2, 0.3, 0.4, 0.5, 0.5, 0.6, 0.7, 0.8, 0.9, 0.9, 1.2, 1.6, 1.8, 2.3, 2.5, 2.6, 2.9, 3.1

The AMLEs for the parameters 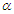and 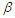are 1.29118 and 0.63779 respectively. Wingo (1993) derived the 0.90% confidence intervals for the parameters based on the pivotal quantities.

For 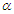, the confidence interval is (0.8528, 1.7316) with a length of 0.8788. For 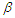the 0.90% the confidence interval is (0.44221, 0.73692) with a length of 0.29471. For the purpose of comparison, the 90% the confidence intervals of the parameters 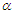and 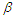are derived based on the conditional approach as follows:

For 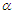, the confidence interval is (0.8455, 1.7020) with length 0.8566, which is shorter than Wingo (1993) interval. For 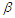the confidence interval is (0.03089, 0.7468) with a length of 0.7159 which is longer than Wingo interval. The confidence intervals based on the AMLEs approach are: For 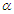the CI is (0.8525, 1.7299) with a length of 0.8774, which is longer than the conditional ones and shorter than Wingo interval.

For 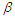the confidence interval is (0.37895, 0.89663) with a length of 0.51768, which is longer than Wingo interval. The results of this data indicate that the confidence interval based on the conditional for 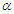is shorter than Wingo (1993) and the AMLE confidence intervals. On the contrary, for Wingo (1993) the confidence interval for 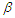is very short because the data is not good fit for the Burr type-XII distribution based on the type-II censored sample.

Table 1. The Lower (LL), the Upper limits (UL) and the interval lengths of the 90% and 95% confidence intervals (CI) for the parameters α, β based on the Conditional and the AMLEs approaches for complete, Type-II censored and Type-II progressive censored samples with binomial random removal with probability P = 0.5 for the arthritics patients data

Table 2. The mean length (MLIs ) and the coverage percentages (CPs) for the conditional and AMLEs methods with the nominal level 95% for the parameter α with β = 2 based on the complete and censored samples with censored levels (50%, 25%)

Table 3. The mean length (MLIs ) and the coverage percentages (CPs) for the conditional and AMLEs approaches with the nominal level 95% for the parameter α with β = 3 based on the complete and censored samples with censored levels (50%, 25%)

Table 4. The mean length (MLIs ) and the coverage percentages (CPs)) for the conditional and AMLEs methods when the nominal level 95% for the parameter α with β = 2 based on the progressive type-II censoring with binomal random removal with probability P = 0.5 and censored levels (50% and 25%)

Table 5. The mean length (MLIs ) and the coverage percentages (CPs) for the conditional and AMLEs methods with the nominal level 95% for the parameter α with β =3, based on the progressive type-II censoring with binomal random removal with probability P = 0.5 and censored levels (50% and 25%)

Table 6. The mean length (MLIs) and the coverage percentages (CPs) for the conditional and AMLEs methods with the nominal level 95% for the parameter β with α =2 based on the type-II censored and type-II progressively censoring with binomal random removal with probability P = 0.5 and censored levels (50%, 25%)

Table 7. The mean length (MLIs) and the coverage percentages (CPs) for the conditional and AMLEs methods with the nominal level 95% for the parameter β with α =3 based on the type-II censored and type-II progressively censoring with binomal random removal with probability P = 0.5 and censored levels (50%, 25%)

6. Conclusions

In this paper, a new application for the conditional inference has been introduced to inference on Burr type-XII distribution based on generalized order statistics. Moreover, for purpose of comparison the asymptotic maximum likelihood estimate has been applied to measure the performance of the proposed approach based on the Monte Carlo simulations that indicated the conditional approach possess good statistical properties and it can perform quite well even when the sample size is extremly small. However, the AMLEs turn out to be impercise or even unreliable for small or highly type-II censored samples.