Nelson Doe Dzivor1, Henry Otoo2, Eric Neebo Wiah2
1Department of Applied Mathematical and Statistics, Accra Technical University, Accra, Ghana
2Department of Mathematical Science, University of Mines and Technology, Tarkwa, Ghana
Copyright © 2021 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
Applications of probability distributions have spread over the years from game of chance to all facet of life and disciplines. Due to quest of precision in modeling lifetime data, existing probability distributions are been improved upon through method of parameterization. This study introduced a new distribution called Exponentiated Janardan distribution of which Janardan distribution forms the baseline. This new distribution is a three-parameter distribution. Some statistical properties such as moments, MLE, survival/hazard rate are established. The proposed distribution was run on a number of life time datasets concurrently with the baseline distribution and the output result indicates that Exponentiated Janardan distribution produces smaller AIC value than the baseline distribution in all datasets considered. This indicates that Exponentiated Janardan distribution fits lifetime data more closely than Janardan distribution. The behavior of the pdf, survival function and hazard rate function are pictorially demonstrated. The role of each parameter in the proposed distribution is also pictorially demonstrated.
Keywords:
Parameterization, Aike Information Criteria, Maximum likelihood estimation, Moment
Cite this paper: Nelson Doe Dzivor, Henry Otoo, Eric Neebo Wiah, Exponentiated Janardan Distribution: A Modification of Janardan Distribution and Application to Life Time Data, International Journal of Probability and Statistics , Vol. 10 No. 1, 2021, pp. 9-16. doi: 10.5923/j.ijps.20211001.02.
1. Introduction
Probability distribution has revolved over the years. Since 1654 “gamblers’ dispute event, many mathematicians (such Pascal, Jakob Bernoulli, Chebyshev, Kolmogorov, Poisson, Weibull, Shanker and others) have contributed immensely to the development of probabilistic theories. According to Khan (2013), probabilistic ideas have spread from the game of chance to many scientific and practical problems such as in the field engineering, medicine, actuary, finance and so on. Many more probability theory/distributions are being developed from time to time of which the classical models forming the baseline distribution through method of parameterization. The motivation of modification of existing distribution is to make them better fit data. One of the recent modifications is the Shanker’s (2013) Janardan distribution. Janardan distribution is a two-parameter distribution introduced by Shanker et al. (2013) of which one one-parameter Lindley (1958) distribution is a special case. Janardan probability distribution had been tried and tested to many lifetime datasets and proven to be more relax and better fits than Lindley distribution. However, since the introduction of Janardan, scholars (Elbatal et al., 2013; Warahena-Liyanage and Pararai, 2014; Shanker et al, 2014; Shakila and Mujahid, 2016; Amer et al., 2017; Al-khazaleh et al., 2016; Hag, 2016; Hussian, 2014; Shanker et al, 2016; Marziel et al., 2019) have one way or the other tried to modify it and enhance its usability in diverse data environment through parameterization. Diverse kinds of generators have been used by these scholars in adding parameter(s) to the Janardan distribution but none of them had used Exponential generator despite its potential in improving “scaled-parametric” models like Janardan.Shanker et al (2013) introduced Janardan distribution upon extensive review of the work of Ghitanny et al. (2008) which discussed some significant statistical properties of one one-parameter Lindley (1958) distribution. They established the Cumulative density function and probability density function of the Janardan distribution. They further went on to establish some statistical properties of this distribution. Some of statistical properties established by Shanker and the team are the mode of the distribution, the moments and its related measures, the failure rate and the mean residual life, stochastic orderings as well as estimation of parameters. They concluded their work by applying the distribution to several life data and found out that Janardan distribution provides closer fits than Lindley distribution.For a random variable that follows Janardan Distribution (JD) with parameters 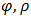 ; the probability density function is given as:
; the probability density function is given as: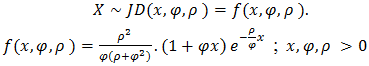 | (1.1) |
And the corresponding cumulative density function (CDF) is established as: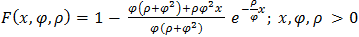 | (1.2) |
The expectation of Janardan distribution is also established as: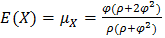 | (1.3) |
Also, the second, third and fourth moments are appropriately established.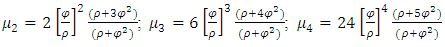 By generalization, the rth moment is given as
By generalization, the rth moment is given as 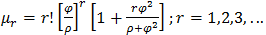 | (1.4) |
The mode of the distribution is established as:Differentiating the pdf and setting result to zero, the extrema of the Janardan distribution.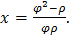 This value, the
This value, the 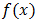 is maximum only if
is maximum only if 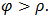 But in situation where
But in situation where 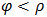 The
The 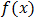 is decreasing in
is decreasing in 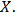 Therefore, the mode of Janardan distribution is established to be:
Therefore, the mode of Janardan distribution is established to be: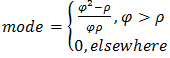 | (1.5) |
Hazard function 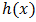 of the distribution is also established as:
of the distribution is also established as: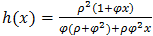 | (1.6) |
Janardan probability distribution had been tried and tested to many lifetime datasets and proven to be more relax and better fits than Lindley distribution.In this paper, a three-parameter continuous distribution for a non-negative random variable is introduced. It is named “Exponentiated Janardan”. This new distribution has Janardan distribution as baseline distribution. Visualization of the behavior of the pdf, hazard rate and survival function are presented. Also, some statistical properties are also established. Flexibility of the model is also determined in comparison with the baseline distribution.
2. Methodology
The new distribution is developed using the method of parameterization as shown in figure 2.1. According to Ramos (2018), new family of probability distribution(s) could be built using a pre-defined monotonic functions as well as a known probability distribution. One of pre-defined monotonic function is exponential generalized function whose CDF is presented in (3.1). And the known distribution (in this case) is Janardan distribution.  | Figure 2.1 |
In this case, Janardan distribution is nested into exponential generator to produce the new proposed distribution as Exponentiated Janardan and named so. The parameter estimation is done using maximum likelihood estimator by the help of R console. Decision on flexibility of the model in comparison with the baseline model was done using Aike Information Criteria (AIC).
3. Theoretical Findings of Exponentiated Janardan Distribution
This section presents a three parameter Exponentiated Janardan distribution with non-negative parameters 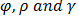 with the derived the cdf, pdf, hazard rate function, survival function as well as some statistical properties. The role of each parameter is, also, pictorially demonstrated in this section.
with the derived the cdf, pdf, hazard rate function, survival function as well as some statistical properties. The role of each parameter is, also, pictorially demonstrated in this section.
3.1. Derived functions of Exponentiated Janardan Distribution
The cumulative density function for exponential generator 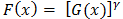 | (3.1) |
Inserting equation (1.2) into (3.1), we derived cumulative density function for Exponentiated Janardan (EJ) as: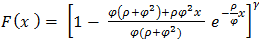 Hence, a random variable that conforms to Exponentiated Janardan distribution,
Hence, a random variable that conforms to Exponentiated Janardan distribution, 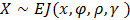 has the cdf as:
has the cdf as: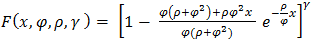 | (3.2) |
Using chain rule, we differentiate the cdf to arrive at the pdf of Exponentiated Janardan distribution as: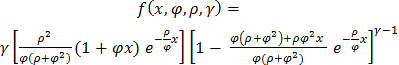 | (3.3) |
Where 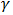 is location parameter,
is location parameter, 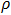 is scale parameter and
is scale parameter and 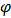 is the shape parameter (as demonstrate in fig. 3.4, 3.5 and 3.6).The shape of pdf for some arbitrary values of the parameters of Exponentiated Janardan distribution is presented in figure 3.1. Hence figure 3.1 exhibits the behavior of this proposed distribution.Another determinant of ability of distribution to model life time data is survival and hazard function of the distribution. Survival function,
is the shape parameter (as demonstrate in fig. 3.4, 3.5 and 3.6).The shape of pdf for some arbitrary values of the parameters of Exponentiated Janardan distribution is presented in figure 3.1. Hence figure 3.1 exhibits the behavior of this proposed distribution.Another determinant of ability of distribution to model life time data is survival and hazard function of the distribution. Survival function, 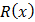 , by definition, is given as
, by definition, is given as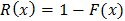 By implication, survival function for Exponentiated Janardan distribution is derived as:
By implication, survival function for Exponentiated Janardan distribution is derived as: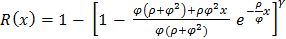 | (3.4) |
The behavior of survival function is pictorially demonstrated in fig 3.2 for some randomly selected values of the parameters of the distribution.Equation (3.5) presents hazard function of Exponentiated Janardan distribution. Hazard function, 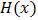 , by definition, is given as:
, by definition, is given as: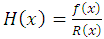 This implies that the Hazard rate function of Exponentiated Janardan distribution is derived as:
This implies that the Hazard rate function of Exponentiated Janardan distribution is derived as: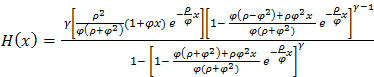 | (3.5) |
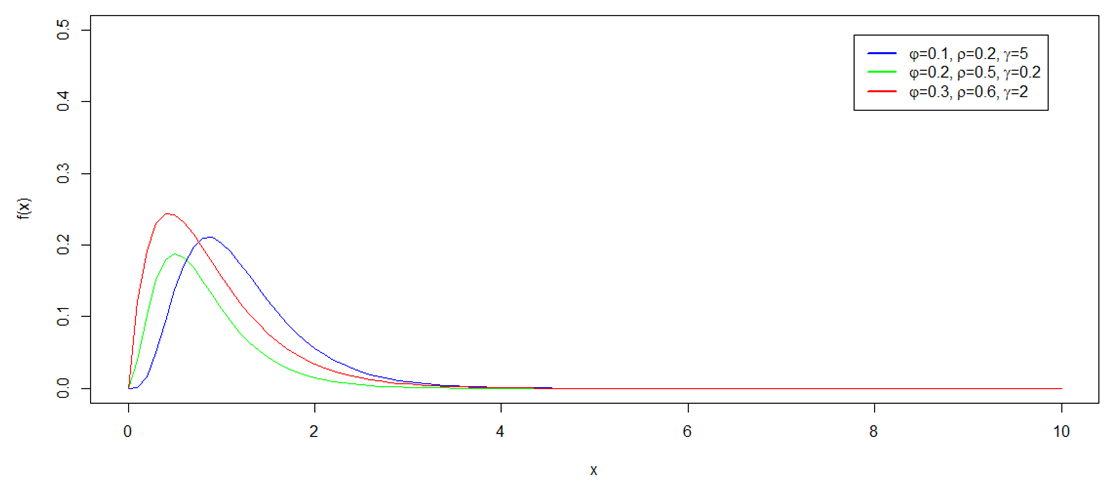 | Figure 3.1. Behaviour of PDF of EJ for some parameters |
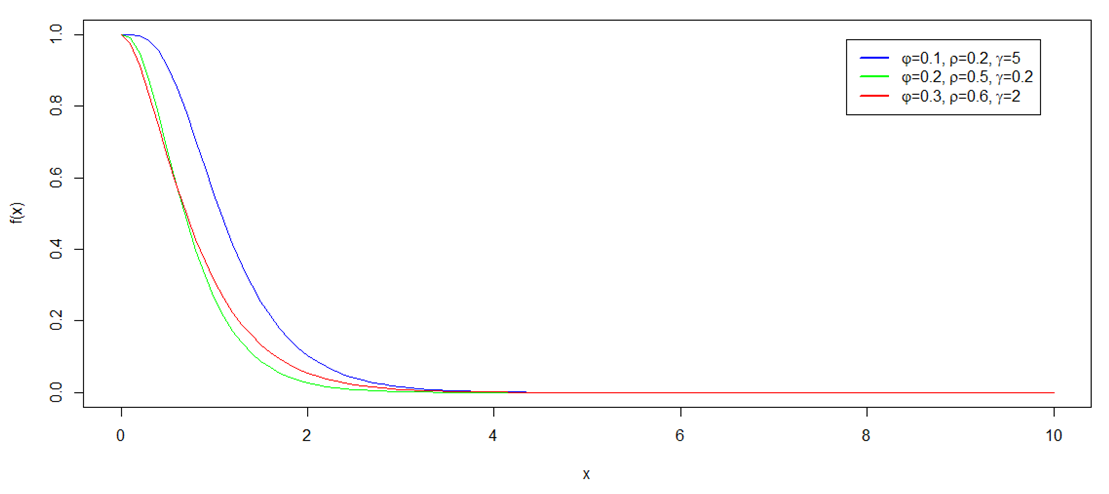 | Figure 3.2. Behaviour of Survival Function of EJ for some parameters |
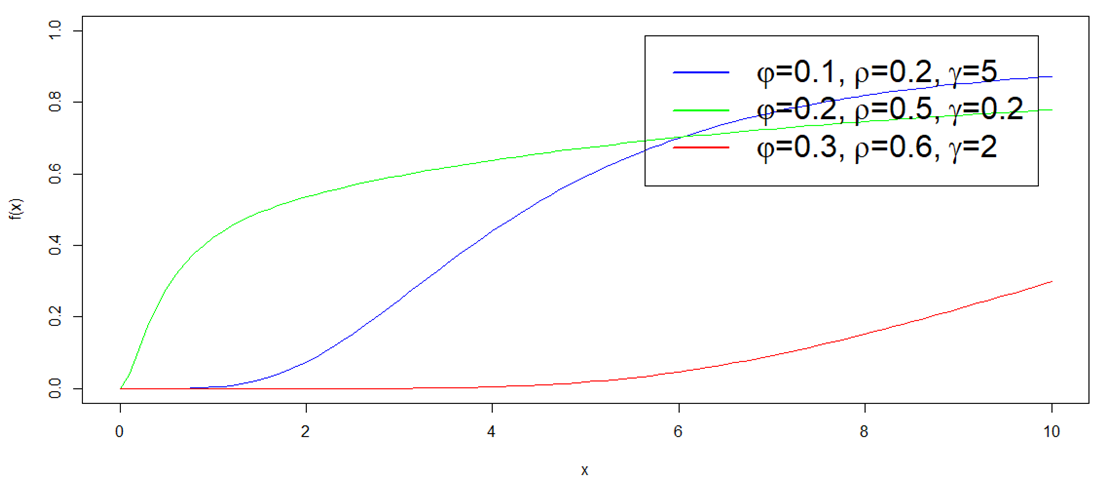 | Figure 3.3. Behaviour of Hazard Rate of EJ for some parameters |
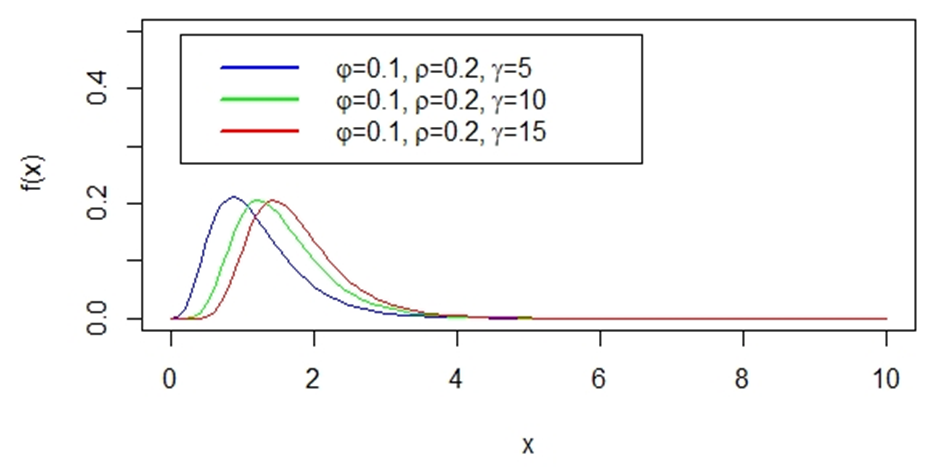 | Figure 3.4. Demostration of Effect of gamma on Behaviour of PDF of EJ |
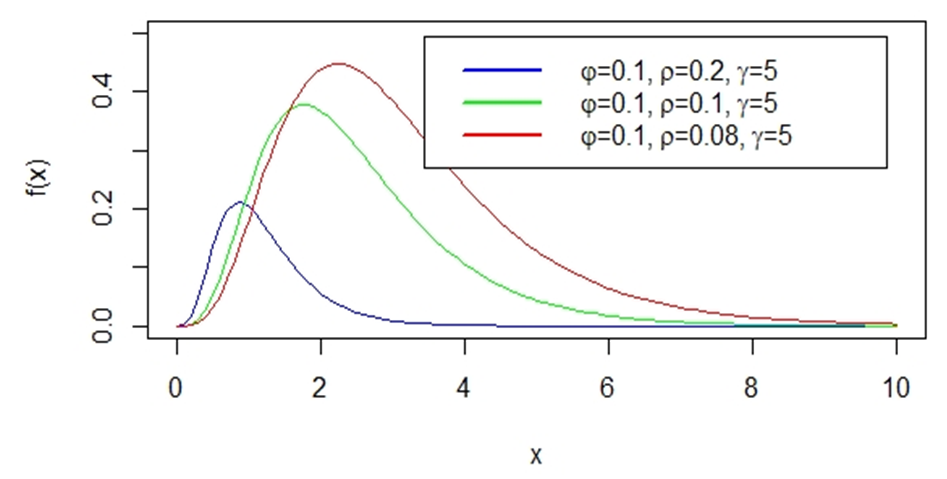 | Figure 3.5. Demostration of Effect of rho on Behaviour of PDF of EJ |
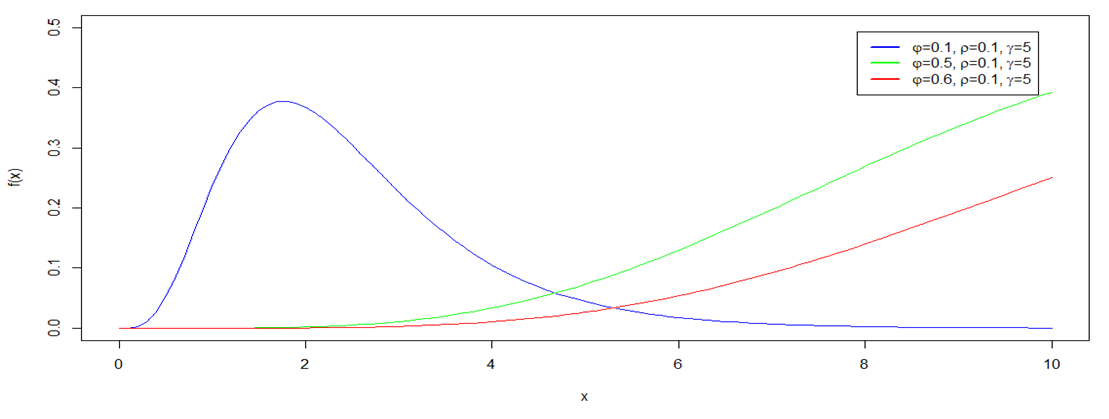 | Figure 3.6. Demostration of Effect of Varphi on Behaviour of PDF of EJ |
Furthermore, fig 3.3 demonstrates the behavior of hazard rate of Exponentiated Janardan distribution for some randomly selected values of the parameters.We, further establish the role of each of the parameters for Exponentiated Janardan distribution. This is done by varying one parameter while keeping others constant and the result is pictorially display in fig 3.4 through fig 3.6.It is conspicuously clear from fig 3.4 that parameter gamma, 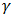 , is a location parameter. This lays credence to the proposed distribution’s ability to model lifetime data even if the data is transform or shifted. Even if the data set is shifted to the right, say,
, is a location parameter. This lays credence to the proposed distribution’s ability to model lifetime data even if the data is transform or shifted. Even if the data set is shifted to the right, say, 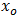 + X (Where X is random variable emanating from an unknown probability distribution), Exponentiated Janardan would be able to model without change of shape or form. More information can be gotten about impact of location parameter from Stone (1975). Fig. 3.4 indicates that the varying numeric value of
+ X (Where X is random variable emanating from an unknown probability distribution), Exponentiated Janardan would be able to model without change of shape or form. More information can be gotten about impact of location parameter from Stone (1975). Fig. 3.4 indicates that the varying numeric value of 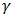 only changes the location of the curve without change of shape while maintain f(x) at same value.Furthermore, rho
only changes the location of the curve without change of shape while maintain f(x) at same value.Furthermore, rho 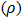 has be determined and illustrated to be scale parameter of the proposed Exponentiated Janardan distribution. Fig 3.5 reveals that, a change of numeric value of rho (holding all other parameters constant) results in change of the spread of distribution without change in the shape of the distribution. This effect is actual a behavior of scale parameter of a distribution. Scale parameter controls the variability in dataset which most lifetime data exhibit.The functional impact of varphi
has be determined and illustrated to be scale parameter of the proposed Exponentiated Janardan distribution. Fig 3.5 reveals that, a change of numeric value of rho (holding all other parameters constant) results in change of the spread of distribution without change in the shape of the distribution. This effect is actual a behavior of scale parameter of a distribution. Scale parameter controls the variability in dataset which most lifetime data exhibit.The functional impact of varphi 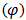 is also determined and illustrated in Fig. 3.6. This is done by keeping all other parameters constant except varphi. It is clear from the figure that, as the value of varphi changes, the shape of the distribution also change. Hence,
is also determined and illustrated in Fig. 3.6. This is done by keeping all other parameters constant except varphi. It is clear from the figure that, as the value of varphi changes, the shape of the distribution also change. Hence, 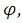 is playing the role of shape parameter in Exponentiated Janardan distribution.
is playing the role of shape parameter in Exponentiated Janardan distribution.
3.2. Statistical Properties of Exponentiated Janardan Distribution
In this subsection, we introduce some statistical properties of Exponentiated Janardan distribution. Some of the statistical properties establish are moment about the origin and maximum likelihood estimator of the parameters.
3.2.1. Moment about the Origin
Simplifying (3.3), we obtain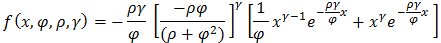 Hence, for a random variable “X” that follows Exponentiated Janardan distribution with parameters
Hence, for a random variable “X” that follows Exponentiated Janardan distribution with parameters 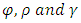 has probability density function as:
has probability density function as: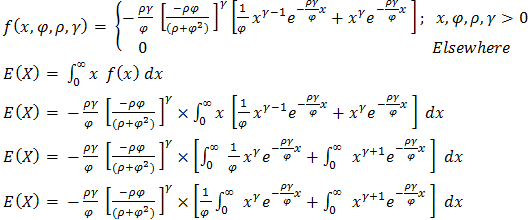 Using gamma transformation of
Using gamma transformation of 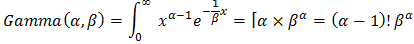 We obtain expected value of the variable
We obtain expected value of the variable 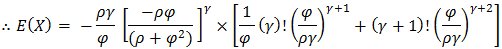 In general, the rth moment about the origin is established as follows:
In general, the rth moment about the origin is established as follows: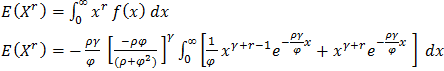 Using gamma transformation of
Using gamma transformation of 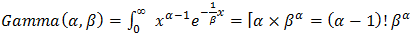 We obtain expected value of the variable
We obtain expected value of the variable 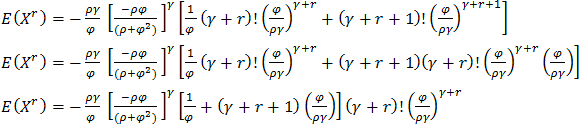 When r = 1
When r = 1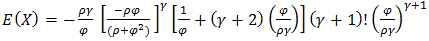 When r = 2
When r = 2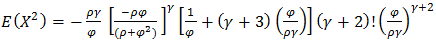 When r = 3
When r = 3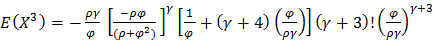
3.2.2. Maximum Likelihood Estimation
Recalling (3.3) and simplifying,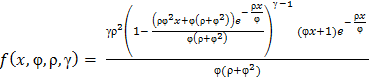 From foregoing statement, the likelihood function is obtained as:
From foregoing statement, the likelihood function is obtained as: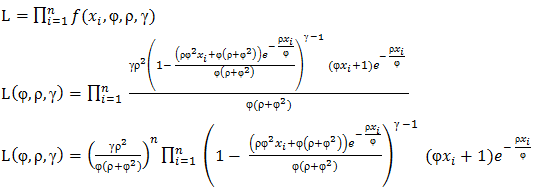 The log-likelihood function is obtained by subjecting the likelihood function to natural logarithm as:
The log-likelihood function is obtained by subjecting the likelihood function to natural logarithm as: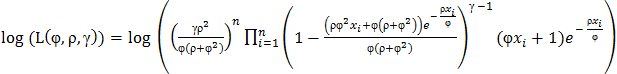 Evaluation of log-likelihood function yields:
Evaluation of log-likelihood function yields: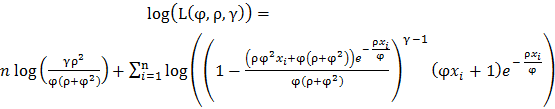 | (3.6) |
Furthermore, the maximum likelihood estimates 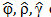 of
of 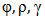 are represented as solutions to the respective optimality equations.Equation maximizer with respect to varphi is
are represented as solutions to the respective optimality equations.Equation maximizer with respect to varphi is 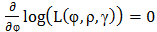 Equation maximizer with respect to rho is
Equation maximizer with respect to rho is 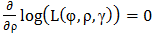 Equation maximizer with respect to gamma is
Equation maximizer with respect to gamma is 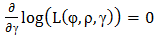
4. Application of Exponentiated Janardan to Lifetime Data
This section presents the results of applying Exponentiated Janardan distribution (EJ) as well as Janardan (J) distribution to lifetime data. Both Janardan and Exponentiated Janardan distributions have been fitted to several datasets concurrently. In all cases, Exponentiated Janardan distribution provides the smaller AIC than Janardan distribution. The datasets used in this section are dataset that had been applied to Janardan distribution.The results of the empirical optimization are given in the table below.Table 1
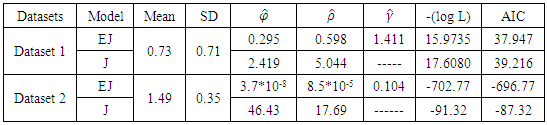 |
| |
|
5. Discussion
The lifetime dataset used in this study had been used by some scholars in determining the goodness of fit of some new distributions. Ghitany et al. (2008) introduced these datasets in analyzing Lindley distribution and its application. Shanker et al. (2016) used the same datasets and discovered that Janardan distribution provides a better fit than Lindley distribution. Marzeh et al. (2019) used the same dataset and concluded that Janardan-Poisson is remarkably better in fitting lifetime data than Lindley distribution as well as Lindley-Poisson distribution. In this current study, the same datasets are used by the researchers to compare Exponentiated Janardan distribution with Janardan distribution and conclude that Exponentiated Janardan distribution provides better fit than Janardan distribution as well as Janardan-Poisson distribution. By implication, Exponentiated Janardan distribution can model life time data better than Janardan, Janardan-Poisson, Lindley Poisson and Lindley distributions.
6. Conclusions
In this study, a new probability distribution known as Exponentiated Janardan distribution has been proposed and discussed. This probability distribution has its baseline distribution to be Janardan probability distribution. Some statistical properties of Exponentiated Janardan distribution such as the density function, cumulative density function, survival function, hazard rate function, moment and MLE are established. The behavior of the pdf, survival function and hazard rate function are pictorially demonstrated. The proposed distribution as well as the baseline distribution have been concurrently run on series of datasets and the output result indicates that Exponentiated Janardan distribution produces smaller AIC value than the baseline distribution in all datasets considered. This indicates that Exponentiated Janardan distribution fits lifetime data more closely than Janardan distribution.
References
| [1] | Al-khazaleh M., Al-Omari A.I and Al-khazaleh A.H (2016). Transmuted two-parameter Lindley distribution. Journal of Statistics Applications and Probability, 5(3), 1-11. |
| [2] | Amer I.A, Ahmed M.H.A & Loai M.A (2017). Transmuted Janardan Distribution: A Generaliztion of Jonardan Distribution. J. Stat. Appl. 5 No.2, 1-11(2017). |
| [3] | Elbatal, I., Merovci, F. and Elgarhy, M. (2013). A new generalized Lindley distribution. Mathematical Theory and Modeling, 3(13), 30-47. |
| [4] | Ghitany, M. E., Atieh, B. & Nadarajah, S. (2008). Lindley Distribution and its Application. Mathematics and computer in simulation, 78(4), 493-506. |
| [5] | Hussian M.A., (2014). Transmuted exponentiated gamma distribution: a generalization of the exponentiated gamma probability distribution. Applied Mathematical Sciences, 8(27), 1297- 1310. |
| [6] | Lindley, D. V. (1958). Fiducial Distribution and Bayes Theorm, Journal of Royal Statistical Society, Ser. B, Vol.20, 102-107. |
| [7] | Marziel, S., Hossein, Z. & Mahammad, M. S. (2019). The Compound Class of Janardan-Power Series Distributions: Properties and Applications. Journal of Data Science, 17(2), 259-278. |
| [8] | Ramos C.C, Leandro C. R, Wilson R. O (2018). Method for Generating Distributions and Classes of Probability Distributions: the Univariate Case. Hacettepe Journal of Mathematics and Statistics 48(2). |
| [9] | Shanker R., Sharma S., Shanker U. and Tekie A.L (2014). The Discrete Poison-Janardan Distribution with Application. International Journal of soft computing and engineering; Vol. 4, Issue-2. |
| [10] | Shanker, R., Sharma, S., Shanker, U. and Shanker, R. (2013). Janardan distribution and its application to waiting times data. Indian Journal of Applied Research, 3(8), 500-502. |
| [11] | Shanker, R., Fresshay, H. & Sharma, S. (2016). On Two-parameter Lindley Distribution and its Applications to Model Lifetime Data. Biometric & Biostatistics International Journal, 1(3), 1-8. |
| [12] | Stone, Charles J. (1975). Adaptive Maximum Likelihood Estimators of a Location Parameter. The Annals of Statistics. 3 (2): 267–284. |
| [13] | Tee K.F, Khan L.R, Hau-Peng C (2013). Probabilistic failure analysis of underground flexible pipes. Structural Engineering and Mechanics, Vol. 47, No. 2 (2013) 167-183. |
| [14] | Warahena-Liyanage, G. and Pararai, M. (2014). A Generalized Power Lindley Distribution with Applications. Asian Journal of Mathematics and Applications, 2014, 1-23. |


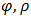 ; the probability density function is given as:
; the probability density function is given as: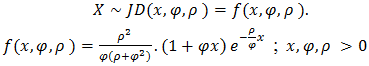
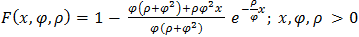
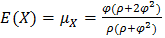
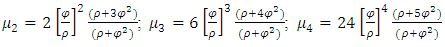 By generalization, the rth moment is given as
By generalization, the rth moment is given as 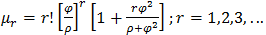
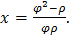 This value, the
This value, the 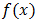 is maximum only if
is maximum only if 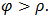 But in situation where
But in situation where 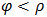 The
The 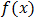 is decreasing in
is decreasing in 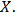 Therefore, the mode of Janardan distribution is established to be:
Therefore, the mode of Janardan distribution is established to be: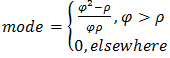
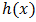 of the distribution is also established as:
of the distribution is also established as: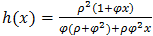

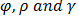 with the derived the cdf, pdf, hazard rate function, survival function as well as some statistical properties. The role of each parameter is, also, pictorially demonstrated in this section.
with the derived the cdf, pdf, hazard rate function, survival function as well as some statistical properties. The role of each parameter is, also, pictorially demonstrated in this section.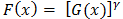
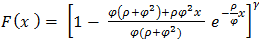 Hence, a random variable that conforms to Exponentiated Janardan distribution,
Hence, a random variable that conforms to Exponentiated Janardan distribution, 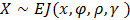 has the cdf as:
has the cdf as: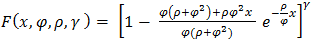
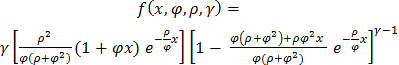
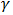 is location parameter,
is location parameter, 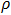 is scale parameter and
is scale parameter and 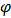 is the shape parameter (as demonstrate in fig. 3.4, 3.5 and 3.6).The shape of pdf for some arbitrary values of the parameters of Exponentiated Janardan distribution is presented in figure 3.1. Hence figure 3.1 exhibits the behavior of this proposed distribution.Another determinant of ability of distribution to model life time data is survival and hazard function of the distribution. Survival function,
is the shape parameter (as demonstrate in fig. 3.4, 3.5 and 3.6).The shape of pdf for some arbitrary values of the parameters of Exponentiated Janardan distribution is presented in figure 3.1. Hence figure 3.1 exhibits the behavior of this proposed distribution.Another determinant of ability of distribution to model life time data is survival and hazard function of the distribution. Survival function, 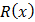 , by definition, is given as
, by definition, is given as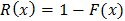 By implication, survival function for Exponentiated Janardan distribution is derived as:
By implication, survival function for Exponentiated Janardan distribution is derived as: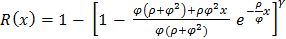
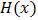 , by definition, is given as:
, by definition, is given as: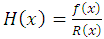 This implies that the Hazard rate function of Exponentiated Janardan distribution is derived as:
This implies that the Hazard rate function of Exponentiated Janardan distribution is derived as: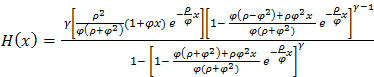






 , is a location parameter. This lays credence to the proposed distribution’s ability to model lifetime data even if the data is transform or shifted. Even if the data set is shifted to the right, say,
, is a location parameter. This lays credence to the proposed distribution’s ability to model lifetime data even if the data is transform or shifted. Even if the data set is shifted to the right, say, 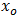 + X (Where X is random variable emanating from an unknown probability distribution), Exponentiated Janardan would be able to model without change of shape or form. More information can be gotten about impact of location parameter from Stone (1975). Fig. 3.4 indicates that the varying numeric value of
+ X (Where X is random variable emanating from an unknown probability distribution), Exponentiated Janardan would be able to model without change of shape or form. More information can be gotten about impact of location parameter from Stone (1975). Fig. 3.4 indicates that the varying numeric value of 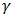 only changes the location of the curve without change of shape while maintain f(x) at same value.Furthermore, rho
only changes the location of the curve without change of shape while maintain f(x) at same value.Furthermore, rho 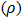 has be determined and illustrated to be scale parameter of the proposed Exponentiated Janardan distribution. Fig 3.5 reveals that, a change of numeric value of rho (holding all other parameters constant) results in change of the spread of distribution without change in the shape of the distribution. This effect is actual a behavior of scale parameter of a distribution. Scale parameter controls the variability in dataset which most lifetime data exhibit.The functional impact of varphi
has be determined and illustrated to be scale parameter of the proposed Exponentiated Janardan distribution. Fig 3.5 reveals that, a change of numeric value of rho (holding all other parameters constant) results in change of the spread of distribution without change in the shape of the distribution. This effect is actual a behavior of scale parameter of a distribution. Scale parameter controls the variability in dataset which most lifetime data exhibit.The functional impact of varphi 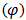 is also determined and illustrated in Fig. 3.6. This is done by keeping all other parameters constant except varphi. It is clear from the figure that, as the value of varphi changes, the shape of the distribution also change. Hence,
is also determined and illustrated in Fig. 3.6. This is done by keeping all other parameters constant except varphi. It is clear from the figure that, as the value of varphi changes, the shape of the distribution also change. Hence, 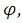 is playing the role of shape parameter in Exponentiated Janardan distribution.
is playing the role of shape parameter in Exponentiated Janardan distribution.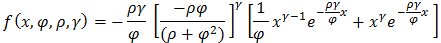 Hence, for a random variable “X” that follows Exponentiated Janardan distribution with parameters
Hence, for a random variable “X” that follows Exponentiated Janardan distribution with parameters 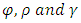 has probability density function as:
has probability density function as: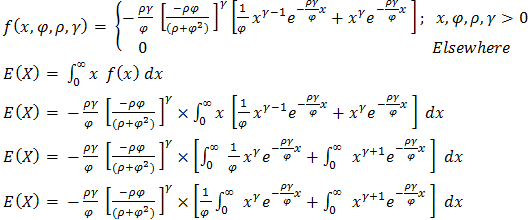 Using gamma transformation of
Using gamma transformation of 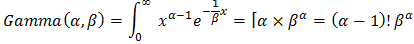 We obtain expected value of the variable
We obtain expected value of the variable 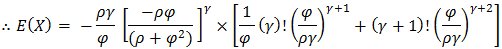 In general, the rth moment about the origin is established as follows:
In general, the rth moment about the origin is established as follows: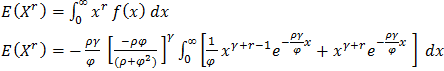 Using gamma transformation of
Using gamma transformation of 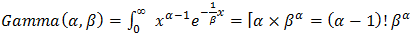 We obtain expected value of the variable
We obtain expected value of the variable 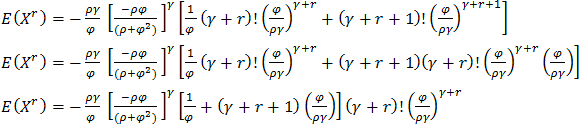 When r = 1
When r = 1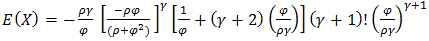 When r = 2
When r = 2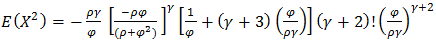 When r = 3
When r = 3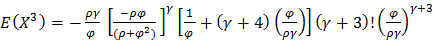
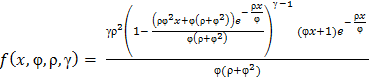 From foregoing statement, the likelihood function is obtained as:
From foregoing statement, the likelihood function is obtained as: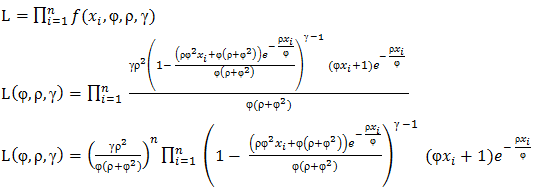 The log-likelihood function is obtained by subjecting the likelihood function to natural logarithm as:
The log-likelihood function is obtained by subjecting the likelihood function to natural logarithm as: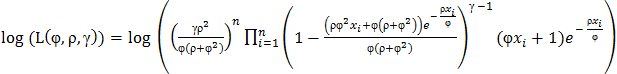 Evaluation of log-likelihood function yields:
Evaluation of log-likelihood function yields: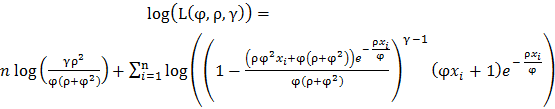
 of
of  are represented as solutions to the respective optimality equations.Equation maximizer with respect to varphi is
are represented as solutions to the respective optimality equations.Equation maximizer with respect to varphi is 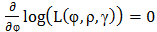 Equation maximizer with respect to rho is
Equation maximizer with respect to rho is 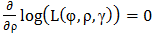 Equation maximizer with respect to gamma is
Equation maximizer with respect to gamma is 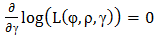
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML