Rasaki Olawale Olanrewaju1, Anthony Gichuhi Waititu2, Nafiu Lukman Abiodun3
1Pan African University, Institute for Basic Sciences, Technology and Innovation (PAUSTI), Kenya
2Department of Mathematical Sciences, Jomo Kenyatta University of Agriculture and Technology, Kenya
3Department of Mathematics and Statistics, Kabale University, Kabale, Uganda
Correspondence to: Rasaki Olawale Olanrewaju, Pan African University, Institute for Basic Sciences, Technology and Innovation (PAUSTI), Kenya.
| Email: |  |
Copyright © 2021 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
This paper describes regime-switching, full range of shape changing distributions (multimodalities), and cycles traits that were characterized by time-varying series via Weibull distributional noise for time series with fluctuations and long-memory. We developed and established a Weibull Mixture Autoregressive model of k-regimes via 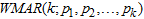 with Expectation-Maximization (EM) algorithm adopted as parameter estimation technique. The ergodic process for the
with Expectation-Maximization (EM) algorithm adopted as parameter estimation technique. The ergodic process for the 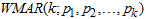 model was ascertained via the maximized derivation of the absolute value of the subtraction of its likelihood from its expected likelihood.
model was ascertained via the maximized derivation of the absolute value of the subtraction of its likelihood from its expected likelihood.
Keywords:
Expectation-Maximization, k-regimes, Mixture Autoregressive model, Regime-switching, Weibull Distribution
Cite this paper: Rasaki Olawale Olanrewaju, Anthony Gichuhi Waititu, Nafiu Lukman Abiodun, On the Estimation of k-Regimes Switching of Mixture Autoregressive Model via Weibull Distributional Random Noise, International Journal of Probability and Statistics , Vol. 10 No. 1, 2021, pp. 1-8. doi: 10.5923/j.ijps.20211001.01.
1. Introduction
Most economic and financial time series possesses traits such as regime shifting, outburst, outliers and change point like behavior that have be addressed by some non-linear time series models, such as Autoregressive Moving Average (ARMA), Self-Exciting Threshold Auto-Regressive (SETAR) and Autoregressive Conditional Heteroscedasticity (GARCH), and its variants. Problems of overall-stationarity, Conditional Heteroscedasticity, excessive skewness and kurtosis, non-linearity violation, full range of shape changing predictive distributions (multimodality) and ability to handle cycles are yet to be addressed fully in modeling fluctuating time series data [9], [2]. Financial, climate and economic time series are often driven by unimodal innovation series. This often implies a unimodal marginal and/or a unimodal conditional distribution for the time series itself. In reality, many financial, climate and economic time series exhibits multimodality either in the marginal or the conditional distribution. However, this article will be adopting a more robust marginal distributional of Weibull distributional form in the build-up of specifying the Mixture Autoregressive model denoted by 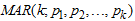 . The Weibull marginal distribution for autoregressive regimes-switching model will be adopted as a substitute for widely used Gaussian marginal distribution because of its ability to capture and model contaminated series characterized with traits such as skewness, kurtosis, k-regimes, outburst, outliers and change point like behavior [6], [5]. The
. The Weibull marginal distribution for autoregressive regimes-switching model will be adopted as a substitute for widely used Gaussian marginal distribution because of its ability to capture and model contaminated series characterized with traits such as skewness, kurtosis, k-regimes, outburst, outliers and change point like behavior [6], [5]. The 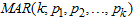 with Gaussian distributional form of the random noise lacks the ability to fully capture and represent distortion caused by contaminated series with above said traits. Therefore, this paper develops, ascertains and estimates the Mixture Autoregressive of k-regimes with Weibull marginal distributional form, denoted by
with Gaussian distributional form of the random noise lacks the ability to fully capture and represent distortion caused by contaminated series with above said traits. Therefore, this paper develops, ascertains and estimates the Mixture Autoregressive of k-regimes with Weibull marginal distributional form, denoted by 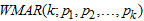 .
.
2. Literature Review
Regime-switching generalization via Mixture Autoregressive (MAR) model was propounded by [10] to relax all these mentioned stylized properties of outburst, outliers and change-point like behavior characterized linear and non-linear time series model but yet to be addressed by ARMA, ARIMAX, SETAR and GARCH. Shortly afterwards, [1], In his work “Prediction with Mixture Autoregressive models” deduced Mixture Autoregressive (MAR) models have the attractive property that the shape of the conditional distribution of a forecast depends on the recent history of the process. It was also ascertained by [1] that if the original MAR model is a mixture of normal distributions, then, the multi-step distributions are also mixtures of normal distributions. A pth ordered model and explicitly expressed dimensional stationary distribution giving a mixture of Normal distribution with constant mixing weights via a general formulation for a univariate nonlinear autoregressive model was presented by [6]. They presented an illustration via an empirical example of interest rates of ten (10) years. In advancement to [6], [5] proposed a novel nonlinear Vector Autoregressive (VAR) otherwise called Gaussian Mixture Vector autoregressive (GMVAR) model. They developed and explained its asymptotic theory of maximum likelihood whose usefulness is vital when dealing with bivariate time series settings. [3] adopted Student’s t- distribution as the error term for mixture autoregressive model via. Their intention was catering for meet inadequate ergodicity and stationary properties that had been a problem by Gaussian error term. Furthermore, [4] improved and examined Finite Mixture (FM) model accompanied with flexibility of classification of two parts of distributions based on scale mixtures of normal (TP-SMN) constitutive members. They claimed that the family make room for robust estimation of FM models development with the ability to capture and absolve asymmetric and symmetric, and heavy and fat-tailed distributions. They further maintained that TP-SMN provides an alternative family member to scale mingling of skewed normal (SMSN) family and vital traits of well-hierarchical expression of the family to obtain ML estimates of the model coefficients via an EM parameter estimation technique.From the available and reviewed literature, it was glaring that the 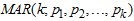 has not been subjected to any of the candidates of the Extreme Valued Distributions (EVDs). In support of the need to subject the MAR model to any of the EVDs in order to capture fluctuation caused by extreme values, this article will be adopting the Weibull as the marginal distribution (random noise) for the MAR model as well as the extreme valued distributional form. The mean and variance of the multimodal conditional distribution for the
has not been subjected to any of the candidates of the Extreme Valued Distributions (EVDs). In support of the need to subject the MAR model to any of the EVDs in order to capture fluctuation caused by extreme values, this article will be adopting the Weibull as the marginal distribution (random noise) for the MAR model as well as the extreme valued distributional form. The mean and variance of the multimodal conditional distribution for the 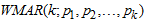 will be ascertained. The Expectation-Maximization (EM) estimation technique will be adopted via E-step and M-step leading to a system of equation and Newton-Raphson iterative technique for estimating AR coefficients, and standard errors attached to each regime. As well as the Ergodic Process for the model.
will be ascertained. The Expectation-Maximization (EM) estimation technique will be adopted via E-step and M-step leading to a system of equation and Newton-Raphson iterative technique for estimating AR coefficients, and standard errors attached to each regime. As well as the Ergodic Process for the model.
3. Detailed Description of the Gamma Mixture Autoregressive Model
Normal mixture transitional distribution (GMTD) models for conditional Normal distribution was firstly introduced by [7], it was splinted-out and viewed as a finite (countable) mixture distribution by [11] as; 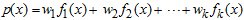 | (1) |
where 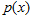 is whole mixture regime-switching probability density function of identically distributed function and
is whole mixture regime-switching probability density function of identically distributed function and 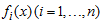 are the probability density functions which may depend on certain parameters; mixing weight or weighted probability
are the probability density functions which may depend on certain parameters; mixing weight or weighted probability 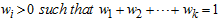 for
for 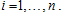 .A k-component of Mixture Autoregressive (MAR) model was defined by [9], [11] and [8] to be
.A k-component of Mixture Autoregressive (MAR) model was defined by [9], [11] and [8] to be 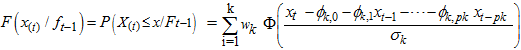 | (2) |
Extending the k-component of MAR model in (2) to Weibull Mixture Auto-Regressive 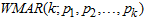 gives
gives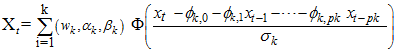 | (3) |
where; 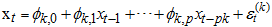
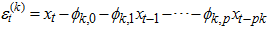
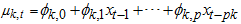 Otherwise,
Otherwise,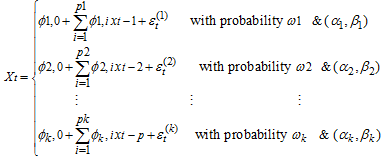 | (4) |
such that the model is denoted by 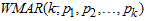 , where
, where 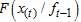 is the conditional cumulative distribution function of
is the conditional cumulative distribution function of 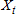 given the immediate past information, evaluated at
given the immediate past information, evaluated at 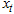 ,
, 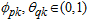 ,
, 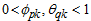 , for
, for 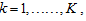 ,
, 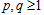 . For mixing weights (weighted probabilities)
. For mixing weights (weighted probabilities) 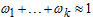 ,
, 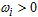 , for
, for 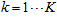 .
. 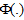 is the Cumulative Distribution Function of the standard Weibull, where
is the Cumulative Distribution Function of the standard Weibull, where 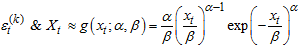 , with mean
, with mean 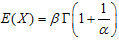 and variance
and variance 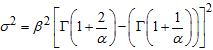 .
.
3.1. The Conditional mean and Variance for WMAR Model
The conditional mean and variance for WMA model of 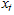 given the immediate past information is as follow:
given the immediate past information is as follow: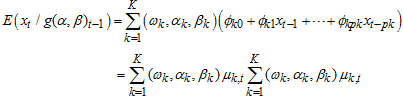 | (5) |
since, 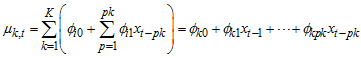 Since the mean of Weibull is
Since the mean of Weibull is 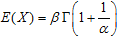 ,
,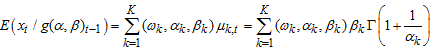 | (6) |
which depends on immediate past values of the time series and 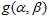 is the PDF of Weibull.
is the PDF of Weibull.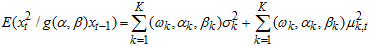 So,
So, 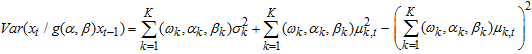 | (7) |
But, 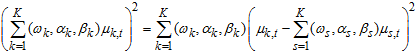 for
for 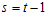 (immediate past values of the time series that depends on
(immediate past values of the time series that depends on  the present values).
the present values).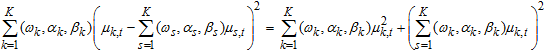 | (8) |
Therefore, 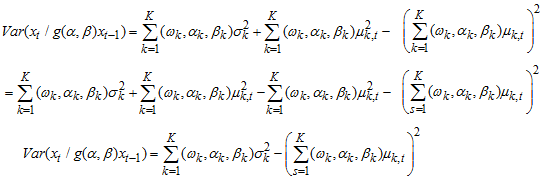 | (9) |
The expression 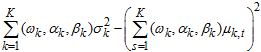 is a positive (non-negative) and would be tantamount to zero if and only if the each regime mean is equal to each other, that is,
is a positive (non-negative) and would be tantamount to zero if and only if the each regime mean is equal to each other, that is, 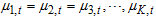 . The expression satisfies the non-negativity property of variance, so the variance for WMAR Model is non-negative.Since the mean and variance of Weibull PDF are;
. The expression satisfies the non-negativity property of variance, so the variance for WMAR Model is non-negative.Since the mean and variance of Weibull PDF are; 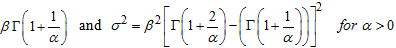 respectivelyAlternatively,
respectivelyAlternatively, 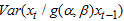 can be rewritten as
can be rewritten as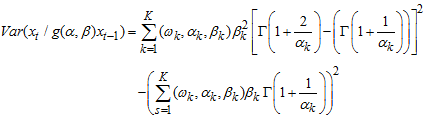 | (10) |
3.2. Parameter Estimation for WMAR via EM Algorithm
Adopting the Expectation-Maximization (EM) algorithm Let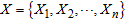 ;
; 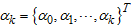 ;
; 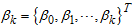 ;
; 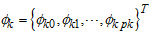 ;
; 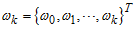 for
for 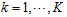 .Furthermore, let “S” be the unobserved random variable where
.Furthermore, let “S” be the unobserved random variable where 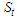 is a
is a 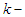 dimensional vector such that
dimensional vector such that 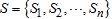
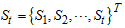 whose component is
whose component is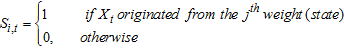 For
For 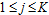 , that is,
, that is,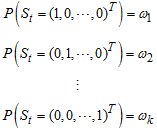 Let
Let 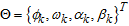 be the parameter space.Given
be the parameter space.Given 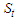 , the Weibull distribution of the complete data
, the Weibull distribution of the complete data 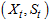 is given by
is given by 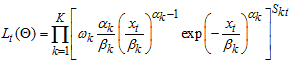 | (11) |
Allowing 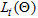 to be the conditional log-likelihood function at time
to be the conditional log-likelihood function at time 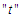 . The log-likelihood is then
. The log-likelihood is then 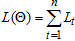 . Let
. Let 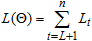 be the joint conditional log-likelihood function for large sample size (n) that makes the effect of
be the joint conditional log-likelihood function for large sample size (n) that makes the effect of 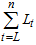 trifling. So, the maximizing the conditional log-likelihood function
trifling. So, the maximizing the conditional log-likelihood function 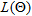 gives
gives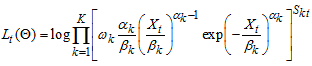 | (12) |
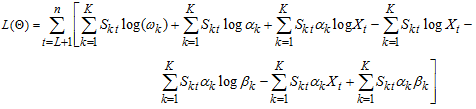 | (13) |
Where 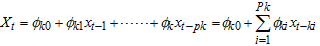 First-order derivatives of
First-order derivatives of 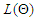 with respect to each of the parameter gives,
with respect to each of the parameter gives,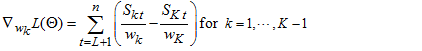 | (14) |
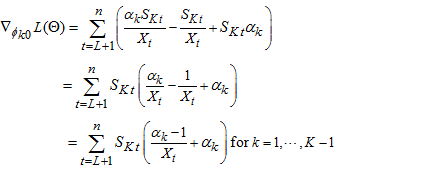 | (15) |
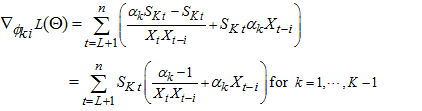 | (16) |
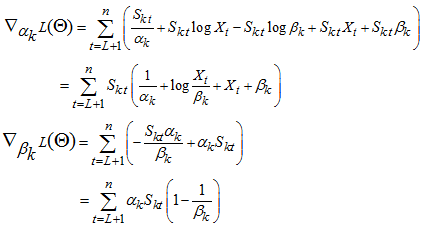 | (17) |
For 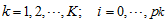 Second-order derivatives of
Second-order derivatives of 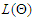 with respect to each of the parameter gives; Let the function
with respect to each of the parameter gives; Let the function 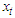 be a function of a random variable at time
be a function of a random variable at time 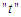 and counter
and counter 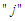
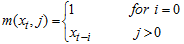 So,
So,  | (18) |
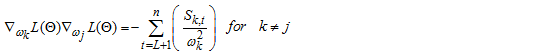 | (19) |
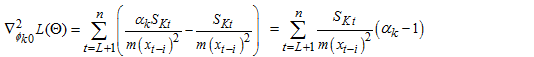 | (20) |
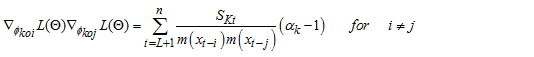 | (21) |
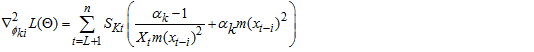 | (22) |
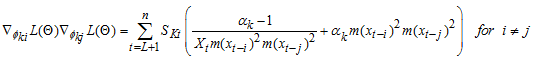 | (23) |
 | (24) |
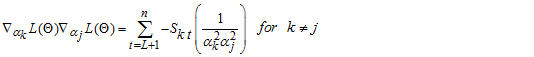 | (25) |
 | (26) |
 | (27) |
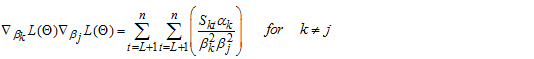 | (28) |
Employing the EM algorithm procedure for estimating 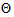 , the parameter space via the
, the parameter space via the 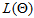 in equation (13).The first step from the acronym EM algorithm, that is the E-step, suppose the parameter space
in equation (13).The first step from the acronym EM algorithm, that is the E-step, suppose the parameter space 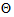 is available, then the missing values for the unobserved data
is available, then the missing values for the unobserved data 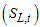 is then replaced by impose means imposed on each parameter on the observed data X. Allowing
is then replaced by impose means imposed on each parameter on the observed data X. Allowing 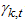 to be the imposed mean of
to be the imposed mean of 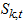 , then
, then 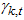 is individual transition probability of the imposed mean all over the totality of the transition probability imposed expectation (that is, Bayes’ theorem)
is individual transition probability of the imposed mean all over the totality of the transition probability imposed expectation (that is, Bayes’ theorem)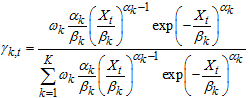 | (29) |
For 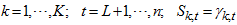 The second case (M-step) where the missing data S is assumed to be guessed and to be replaced by their imposed means on the parameters. The estimates of the parameters of the parameter space,
The second case (M-step) where the missing data S is assumed to be guessed and to be replaced by their imposed means on the parameters. The estimates of the parameters of the parameter space,  . The estimates of the parameters
. The estimates of the parameters  can be obtained via
can be obtained via 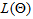 by subtracting
by subtracting 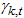 from
from 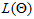 to give,
to give, 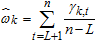 | (30) |
Such that 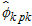
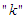 for that runs from
for that runs from 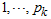 that could also be estimated via a system of equations (that is, the estimates of the parameters are then obtained by iterating these two steps until convergence) or alternatively via Newton-Raphson iterative procedure of all the parameter space at once.
that could also be estimated via a system of equations (that is, the estimates of the parameters are then obtained by iterating these two steps until convergence) or alternatively via Newton-Raphson iterative procedure of all the parameter space at once. 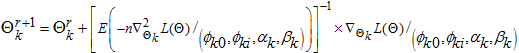 | (31) |
3.3. Ergodic Process for WMAR Model
Strictly stationary and ergodic process WMAR model would be ascertained via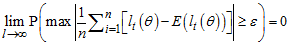 | (32) |
Where, 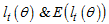 are likelihoods and expectations of likelihoods respectively.
are likelihoods and expectations of likelihoods respectively.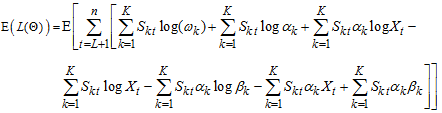 | (33) |
From Jensen’s inequality, 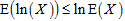 for every positively integrable X.
for every positively integrable X.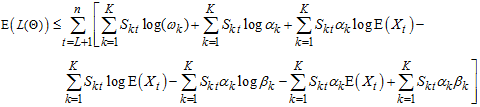 | (34) |
But, 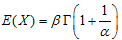
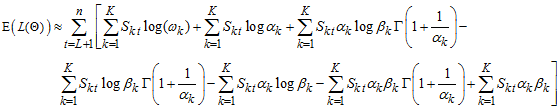 | (35) |
So, 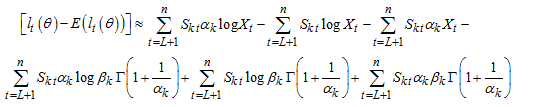 | (36) |
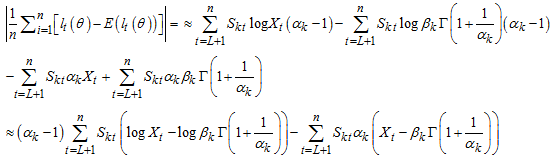 | (37) |
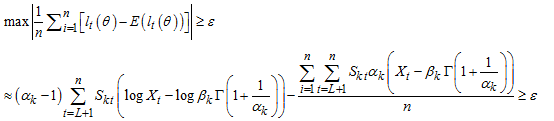 | (38) |
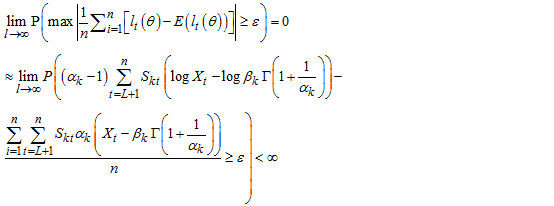 | (39) |
4. Conclusions
The proposed and formulated model of 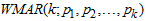 being one of the candidates models for extreme valued mixture autoregressive was designed in order to capture, and correct stylized properties; entire outrange of switching-patterns with Weibull marginal distribution(multimodalities), change points like behavior, regime-switching (capable of handling recurring periodical sequence), and time-varying volatilities (conditional means-variances). The model was also formulated to absolve heavy-tailed, long-memory and non-Gaussian MAR model characterized by positive and strictly count (discrete) valued random noises (error terms) series.
being one of the candidates models for extreme valued mixture autoregressive was designed in order to capture, and correct stylized properties; entire outrange of switching-patterns with Weibull marginal distribution(multimodalities), change points like behavior, regime-switching (capable of handling recurring periodical sequence), and time-varying volatilities (conditional means-variances). The model was also formulated to absolve heavy-tailed, long-memory and non-Gaussian MAR model characterized by positive and strictly count (discrete) valued random noises (error terms) series.
ACKNOWLEDGEMENTS
We wish to thank the reviewers.
References
| [1] | G.N. Boshankov, “Prediction with Mixture Autoregressive Models” Research Report No.6, 2006, Probability and Statistics Group School of Mathematics. The University of Manchester, 2006. |
| [2] | G. Behrooz, S.M.N. Abu Hassan, and S. Tamat, “Application of the Threshold Model for Modelling and Forecasting of Ex change Rate in Selected ASEAN Countries” Sains Malaysiana, Vol.43(10), pp. 1609-1622, 2014. |
| [3] | M. Meitz, D. Preve, and P. Saikkonen, “A mixture autoregres sive model based on Student’s t- distribution”, 2018. |
| [4] | M. Maleki, and A. R. Nematollahi, “Autoregressive Models with Mixture of Scale Mixtures of Gaussian Innovations” Iran Journal of Science and Technology: Transactions A Science. Vol. 41(4), pp. 1099–1107, 2017. https://doi.org/10.1007/s40995-017-0237-6. |
| [5] | L. Kalliovirta, M. Meitz, and P. Saikkonen,” A Guassian Mix ture Vector Autoregressive”. Journal of econometrics, Vol. 192, pp. 485-498, 2016. |
| [6] | L. Kalliovirta, M. Meitz, and P. Saikkonen, “A Guassian Mix ture autoregresive model for univariate series” Journal of Time Series Analysis, Vol. 36, pp. 247-266, 2012. |
| [7] | M. Li and M. Raftery, “Modeling flat stretches, burst and outli ers in time series using Mixture Transition Distribution Mod els” J.Am Statist. Ass., Vol. 91, pp. 1504-1514, 1966. |
| [8] | N. Nguyen, “Hidden Markov Model for Stock Trading” Inter national Journal Financial Studies, Vol 6 (36), 2018. Doi:10.3390/ijfs6020036. |
| [9] | C. S. Wong, and W. K. Li, “On a Mixture Autoregressive Mod el” Journal of Royal Statistics Society. B 62, pp. 95–115, 2000. |
| [10] | C. S. Wong, W. S. Chan, and P. L. Kam,” A Student t-mixture autoregressive Model with applications to heavy-tailed financial data” Singapore Economic Review Conference, pp. 1–10, 2009. |
| [11] | C. S. Wong, Statistical inference for some nonlinear time series models, Ph.D thesis, University of Hong Kong, Hong Kong, 1998. |


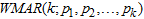 with Expectation-Maximization (EM) algorithm adopted as parameter estimation technique. The ergodic process for the
with Expectation-Maximization (EM) algorithm adopted as parameter estimation technique. The ergodic process for the 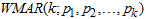 model was ascertained via the maximized derivation of the absolute value of the subtraction of its likelihood from its expected likelihood.
model was ascertained via the maximized derivation of the absolute value of the subtraction of its likelihood from its expected likelihood.
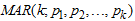 . The Weibull marginal distribution for autoregressive regimes-switching model will be adopted as a substitute for widely used Gaussian marginal distribution because of its ability to capture and model contaminated series characterized with traits such as skewness, kurtosis, k-regimes, outburst, outliers and change point like behavior [6], [5]. The
. The Weibull marginal distribution for autoregressive regimes-switching model will be adopted as a substitute for widely used Gaussian marginal distribution because of its ability to capture and model contaminated series characterized with traits such as skewness, kurtosis, k-regimes, outburst, outliers and change point like behavior [6], [5]. The 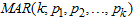 with Gaussian distributional form of the random noise lacks the ability to fully capture and represent distortion caused by contaminated series with above said traits. Therefore, this paper develops, ascertains and estimates the Mixture Autoregressive of k-regimes with Weibull marginal distributional form, denoted by
with Gaussian distributional form of the random noise lacks the ability to fully capture and represent distortion caused by contaminated series with above said traits. Therefore, this paper develops, ascertains and estimates the Mixture Autoregressive of k-regimes with Weibull marginal distributional form, denoted by 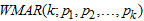 .
. 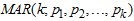 has not been subjected to any of the candidates of the Extreme Valued Distributions (EVDs). In support of the need to subject the MAR model to any of the EVDs in order to capture fluctuation caused by extreme values, this article will be adopting the Weibull as the marginal distribution (random noise) for the MAR model as well as the extreme valued distributional form. The mean and variance of the multimodal conditional distribution for the
has not been subjected to any of the candidates of the Extreme Valued Distributions (EVDs). In support of the need to subject the MAR model to any of the EVDs in order to capture fluctuation caused by extreme values, this article will be adopting the Weibull as the marginal distribution (random noise) for the MAR model as well as the extreme valued distributional form. The mean and variance of the multimodal conditional distribution for the 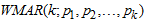 will be ascertained. The Expectation-Maximization (EM) estimation technique will be adopted via E-step and M-step leading to a system of equation and Newton-Raphson iterative technique for estimating AR coefficients, and standard errors attached to each regime. As well as the Ergodic Process for the model.
will be ascertained. The Expectation-Maximization (EM) estimation technique will be adopted via E-step and M-step leading to a system of equation and Newton-Raphson iterative technique for estimating AR coefficients, and standard errors attached to each regime. As well as the Ergodic Process for the model.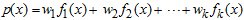
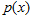 is whole mixture regime-switching probability density function of identically distributed function and
is whole mixture regime-switching probability density function of identically distributed function and 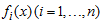 are the probability density functions which may depend on certain parameters; mixing weight or weighted probability
are the probability density functions which may depend on certain parameters; mixing weight or weighted probability 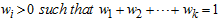 for
for 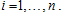 .A k-component of Mixture Autoregressive (MAR) model was defined by [9], [11] and [8] to be
.A k-component of Mixture Autoregressive (MAR) model was defined by [9], [11] and [8] to be 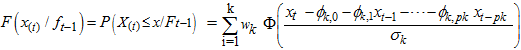
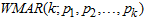 gives
gives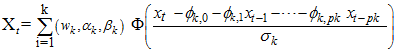
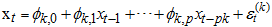
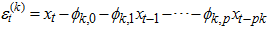
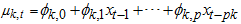 Otherwise,
Otherwise,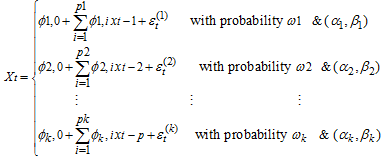
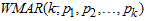 , where
, where 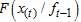 is the conditional cumulative distribution function of
is the conditional cumulative distribution function of 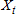 given the immediate past information, evaluated at
given the immediate past information, evaluated at 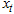 ,
, 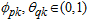 ,
, 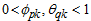 , for
, for 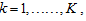 ,
, 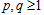 . For mixing weights (weighted probabilities)
. For mixing weights (weighted probabilities) 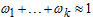 ,
, 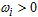 , for
, for 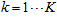 .
. 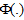 is the Cumulative Distribution Function of the standard Weibull, where
is the Cumulative Distribution Function of the standard Weibull, where 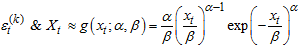 , with mean
, with mean 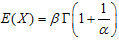 and variance
and variance 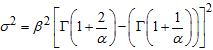 .
.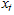 given the immediate past information is as follow:
given the immediate past information is as follow: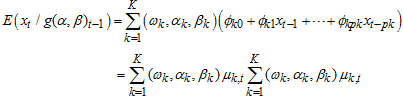
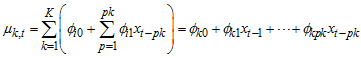 Since the mean of Weibull is
Since the mean of Weibull is 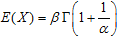 ,
,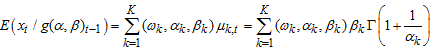
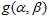 is the PDF of Weibull.
is the PDF of Weibull.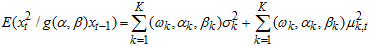 So,
So, 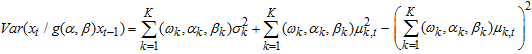
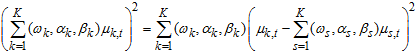 for
for 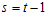 (immediate past values of the time series that depends on
(immediate past values of the time series that depends on 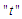 the present values).
the present values).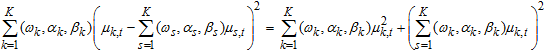
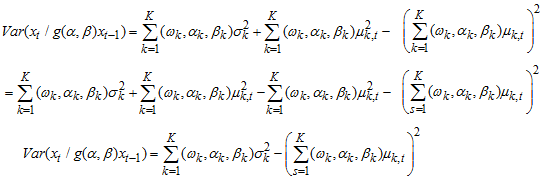
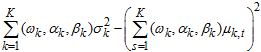 is a positive (non-negative) and would be tantamount to zero if and only if the each regime mean is equal to each other, that is,
is a positive (non-negative) and would be tantamount to zero if and only if the each regime mean is equal to each other, that is, 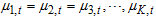 . The expression satisfies the non-negativity property of variance, so the variance for WMAR Model is non-negative.Since the mean and variance of Weibull PDF are;
. The expression satisfies the non-negativity property of variance, so the variance for WMAR Model is non-negative.Since the mean and variance of Weibull PDF are; 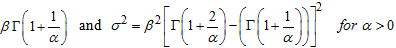 respectivelyAlternatively,
respectivelyAlternatively, 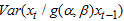 can be rewritten as
can be rewritten as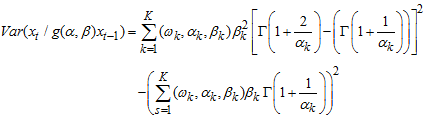
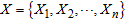 ;
; 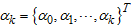 ;
; 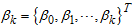 ;
; 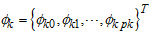 ;
; 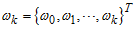 for
for 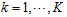 .Furthermore, let “S” be the unobserved random variable where
.Furthermore, let “S” be the unobserved random variable where 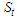 is a
is a 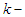 dimensional vector such that
dimensional vector such that 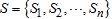
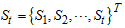 whose component is
whose component is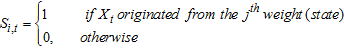 For
For 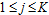 , that is,
, that is,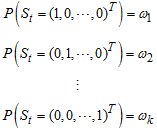 Let
Let 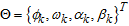 be the parameter space.Given
be the parameter space.Given 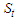 , the Weibull distribution of the complete data
, the Weibull distribution of the complete data 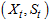 is given by
is given by 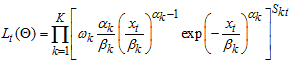
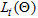 to be the conditional log-likelihood function at time
to be the conditional log-likelihood function at time 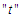 . The log-likelihood is then
. The log-likelihood is then 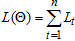 . Let
. Let 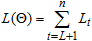 be the joint conditional log-likelihood function for large sample size (n) that makes the effect of
be the joint conditional log-likelihood function for large sample size (n) that makes the effect of 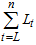 trifling. So, the maximizing the conditional log-likelihood function
trifling. So, the maximizing the conditional log-likelihood function 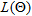 gives
gives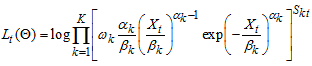
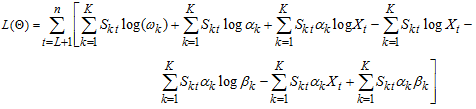
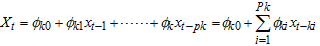 First-order derivatives of
First-order derivatives of 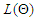 with respect to each of the parameter gives,
with respect to each of the parameter gives,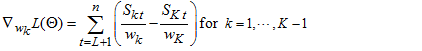
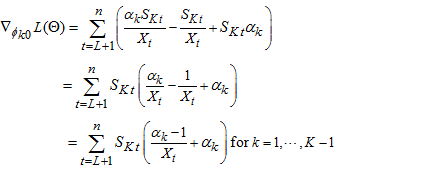
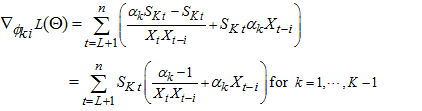
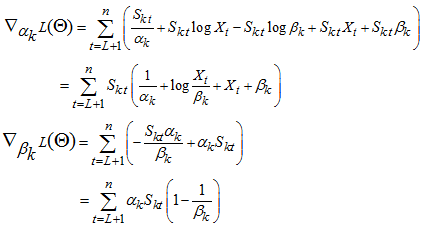
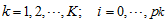 Second-order derivatives of
Second-order derivatives of 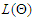 with respect to each of the parameter gives; Let the function
with respect to each of the parameter gives; Let the function 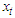 be a function of a random variable at time
be a function of a random variable at time 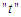 and counter
and counter 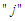
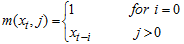 So,
So, 
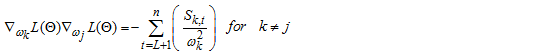
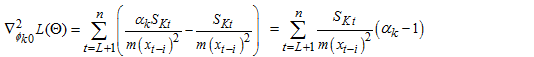
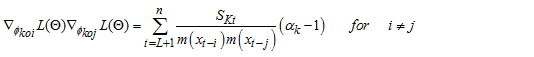
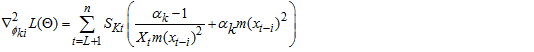
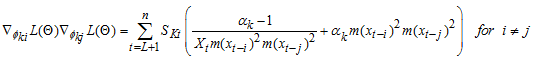

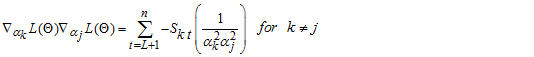


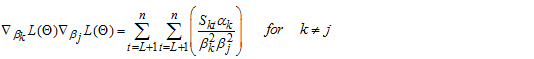
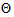 , the parameter space via the
, the parameter space via the 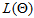 in equation (13).The first step from the acronym EM algorithm, that is the E-step, suppose the parameter space
in equation (13).The first step from the acronym EM algorithm, that is the E-step, suppose the parameter space 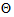 is available, then the missing values for the unobserved data
is available, then the missing values for the unobserved data 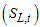 is then replaced by impose means imposed on each parameter on the observed data X. Allowing
is then replaced by impose means imposed on each parameter on the observed data X. Allowing 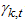 to be the imposed mean of
to be the imposed mean of 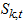 , then
, then 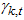 is individual transition probability of the imposed mean all over the totality of the transition probability imposed expectation (that is, Bayes’ theorem)
is individual transition probability of the imposed mean all over the totality of the transition probability imposed expectation (that is, Bayes’ theorem)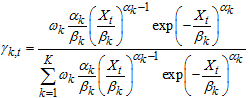
 The second case (M-step) where the missing data S is assumed to be guessed and to be replaced by their imposed means on the parameters. The estimates of the parameters of the parameter space,
The second case (M-step) where the missing data S is assumed to be guessed and to be replaced by their imposed means on the parameters. The estimates of the parameters of the parameter space,  . The estimates of the parameters
. The estimates of the parameters  can be obtained via
can be obtained via 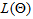 by subtracting
by subtracting 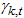 from
from 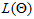 to give,
to give, 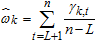
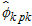
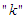 for that runs from
for that runs from 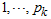 that could also be estimated via a system of equations (that is, the estimates of the parameters are then obtained by iterating these two steps until convergence) or alternatively via Newton-Raphson iterative procedure of all the parameter space at once.
that could also be estimated via a system of equations (that is, the estimates of the parameters are then obtained by iterating these two steps until convergence) or alternatively via Newton-Raphson iterative procedure of all the parameter space at once. 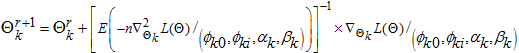
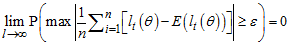
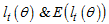 are likelihoods and expectations of likelihoods respectively.
are likelihoods and expectations of likelihoods respectively.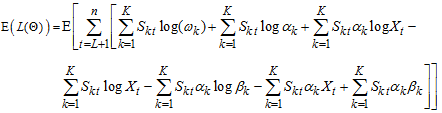
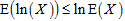 for every positively integrable X.
for every positively integrable X.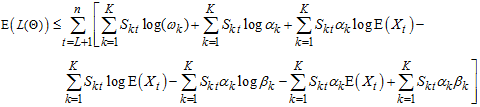
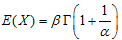
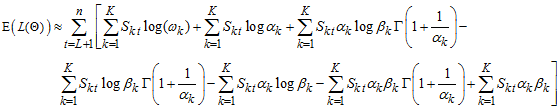
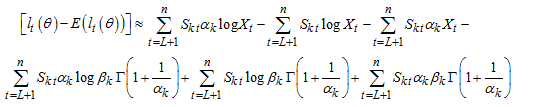
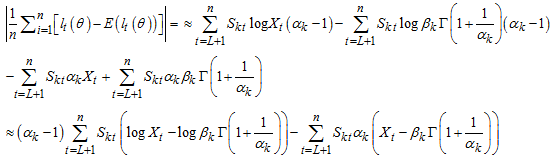
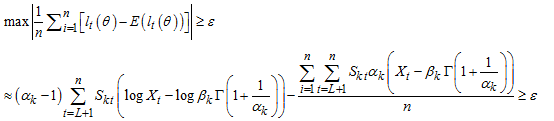
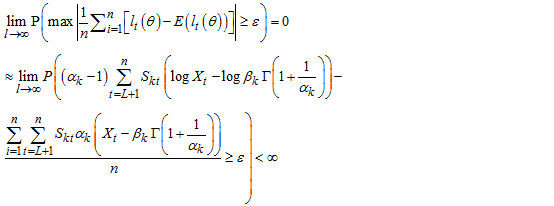
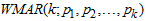 being one of the candidates models for extreme valued mixture autoregressive was designed in order to capture, and correct stylized properties; entire outrange of switching-patterns with Weibull marginal distribution(multimodalities), change points like behavior, regime-switching (capable of handling recurring periodical sequence), and time-varying volatilities (conditional means-variances). The model was also formulated to absolve heavy-tailed, long-memory and non-Gaussian MAR model characterized by positive and strictly count (discrete) valued random noises (error terms) series.
being one of the candidates models for extreme valued mixture autoregressive was designed in order to capture, and correct stylized properties; entire outrange of switching-patterns with Weibull marginal distribution(multimodalities), change points like behavior, regime-switching (capable of handling recurring periodical sequence), and time-varying volatilities (conditional means-variances). The model was also formulated to absolve heavy-tailed, long-memory and non-Gaussian MAR model characterized by positive and strictly count (discrete) valued random noises (error terms) series.  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML