International Journal of Probability and Statistics

p-ISSN: 2168-4871    e-ISSN: 2168-4863

2020;  9(2): 42-44

doi:10.5923/j.ijps.20200902.03

Received: Aug. 21, 2020; Accepted: Sep. 9, 2020; Published: Sep. 17, 2020

 

Characterizations of the New Two-Parameter Poisson-Sujatha Distribution

G. G. Hamedani

Department of Mathematical and Statistical Sciences, Marquette University, Milwaukee, WI, USA

Correspondence to: G. G. Hamedani, Department of Mathematical and Statistical Sciences, Marquette University, Milwaukee, WI, USA.

Email:

Copyright © 2020 The Author(s). Published by Scientific & Academic Publishing.

This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract

The problem of characterizing a distribution is an important problem in applied sciences, where an investigator is vitally interested to know if their model follows the right distribution. To this end the investigator relies on conditions under which their model would follow specifically the chosen distribution. In this work, we present certain characterizations of the new two-parameter Poisson-Sujatha distribution introduced by Shanker et al. (2020) with the intention of completing, in some way, their work. These characterizations are based on the conditional expectation of certain function of the random variable and in terms of the inverse hazard function.

Keywords: Poisson, Sujatha

Cite this paper: G. G. Hamedani, Characterizations of the New Two-Parameter Poisson-Sujatha Distribution, International Journal of Probability and Statistics , Vol. 9 No. 2, 2020, pp. 42-44. doi: 10.5923/j.ijps.20200902.03.

Article Outline

1. Introduction
2. Characterization Results

1. Introduction

Characterizations of distributions is an important part of the distribution theory which has attracted the attention of a good number of researchers in applied sciences, where an investigator is interested to know if their data follows the appropriate distribution. To this end, the investigator relies on the conditions under which their data would follow specifically the chosen distribution.
Shanker et al. (2020) introduced a new discrete probability model called New Two-Parameter Poisson-Sujatha (NTPPS) distribution which includes Poisson-Sujatha and Poisson Akash distributions. They argued that such a distribution is needed in the case of over-dispersed count data sets. In this very short note, we present certain characterizations of the NTPPS distribution, for simplicity, with parameters 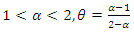, based on: (i) the conditional expectation of certain function of the random variable and (ii) in terms of the reverse hazard function. The main goal here is to complete, in some way, the work of Shanker et al. (2020).
The cumulative distribution function (cdf), the corresponding probability mass function (pmf), and the reversed hazard function, of the NTPPS distribution are given, respectively, by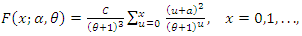
(1)
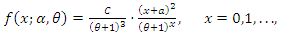(2)
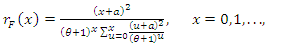(3)
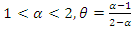where are parameters, 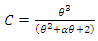is the normalizing constant and, for simplicity,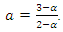

2. Characterization Results

Proposition 1. Let 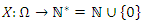be a random variable. The pmf of 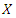is (2) if and only if
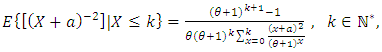(4)
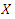Proof. If has pmf (2), then the left-hand side of (4), using the formula for the finite geometric series, will be
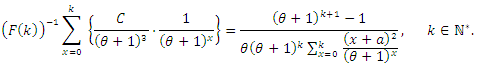Conversely, if (4) holds, then
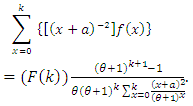(5)
From (5), we also have
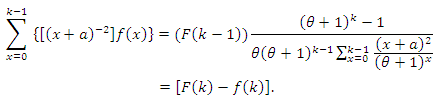(6)
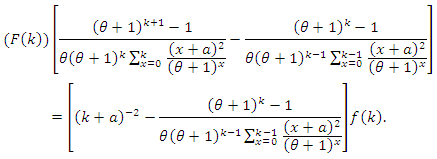Now, subtracting (6) from (5), we arrive at
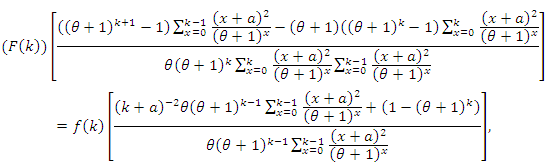or
or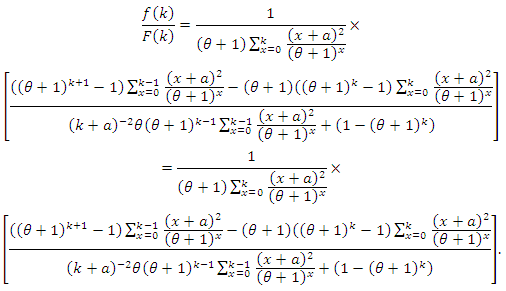
After some rearranging the terms and simplifying, we arrive at
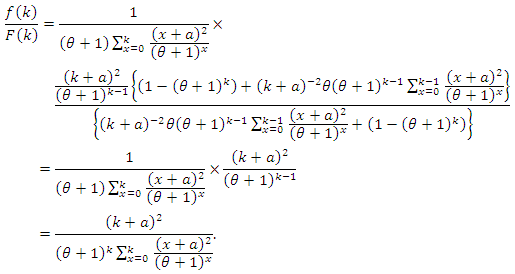From the last equality, we have
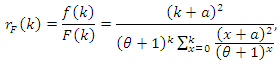which, in view of (3), implies that 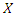has pmf (2).
Proposition 2. Let be a random variable. The pmf of 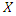is (2) if and only if its reverse hazard function, 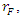satisfies the following difference equation
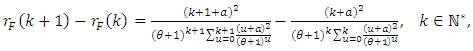(7)
with the initial condition
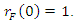Proof. Clearly, if 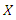has pmf (2), then (7) holds. Now, if (7) holds, then
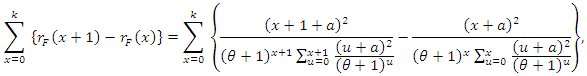or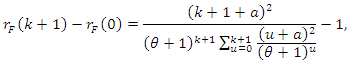
or, in view of the initial condition 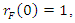we have
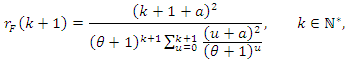which is the reverse hazard function corresponding to the pmf (2).

References

[1]  Shanker, R. (2016). The discrete Poisson-Sujatha distribution. International J. of Probability and Statistics, 5(1), 1-9.
[2]  Shanker, R. (2017). The discrete Poisson-Akash distribution. International J. of Probability and Statistics, 6(1), 1-10.
[3]  Shanker, R., Shukla, K.K. and Leonida, T.A. (2020). A new two-parameter Poisson-Sujatha distribution. International J. of Probability and Statistics, 9(2), 21-32.