Rama Shanker 1, Kamlesh Kumar Shukla 2, Tekie Asehun Leonida 3
1Department of Statistics, Assam University, Silchar, India
2Department of Statistics, Mainefhi College of Science, Asmara, Eritrea
3Department of Applied Mathematics, University of Twente, The Netherlands
Correspondence to: Rama Shanker , Department of Statistics, Assam University, Silchar, India.
| Email: |  |
Copyright © 2020 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
A new two-parameter Poisson-Sujatha distribution, a Poisson mixture of a new two-parameter Sujatha distribution, which includes Poisson-Sujatha distribution and Poisson-Akash distribution as particular cases, has been introduced. Its moments based statistical measures including coefficient of variation, skewness, kurtosis and index of dispersion have been obtained. Maximum likelihood estimation has been explained for estimating its parameters. Goodness of fit of the proposed distribution has been explained with six over-dispersed count datasets and fit has been compared with Poisson-Sujatha distribution and other generalizations of Poisson-Sujatha distributions.
Keywords:
Sujatha distribution, Poisson-Sujatha distribution, A New two-parameter Sujatha distribution, Moments based measures, Maximum likelihood estimation, Applications
Cite this paper: Rama Shanker , Kamlesh Kumar Shukla , Tekie Asehun Leonida , A New Two-Parameter Poisson-Sujatha Distribution, International Journal of Probability and Statistics , Vol. 9 No. 2, 2020, pp. 21-32. doi: 10.5923/j.ijps.20200902.01.
1. Introduction
Poisson distribution is the common distribution for modeling count data when the mean and the variance of the data are the same (equi-dispersed). However, the unique feature of equality of equi-dispersion of Poisson distribution makes it unsuitable for modeling count data which are under-dispersed (mean greater than variance) or over-dispersed (mean less than variance). In recent years, several researchers have proposed Poisson mixture of lifetime distributions which are useful for over-dispersed or under-dispersed. Some over-dispersed Poisson mixed distributions are Poisson-Lindley distribution (PLD), a Poisson mixture of Lindley distribution of Lindley (1958) proposed by Sankaran (1970), Poisson-Sujatha distribution (PSD), a Poisson mixture of Sujatha distribution of Shanker (2016 a) introduced by Shanker (2016 b), Poisson-Akash distribution of Shanker (2017), some among others.The probability density function (pdf) of Sujatha distribution having scale parameter 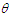 and introduced by Shanker (2016a) is
and introduced by Shanker (2016a) is 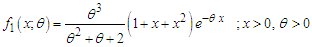 | (1.1) |
Statistical properties including shapes of the density, moments and moments based measures, skewness, kurtosis, index of dispersion, hazard rate function, mean residual life function, stochastic ordering, mean deviation, stress-strength reliability, along with the estimation of parameter and applications for modeling lifetime data from biomedical science and engineering of Sujatha distribution are available in Shanker (2016 a). Kaliraja and Perarasan (2019) studied a stochastic model on the generalization of Sujatha distribution for the effects of two types of exercise on plasma growth hormone. Shanker (2016 b) obtained Poisson-Sujatha distribution (PSD) by compounding Poisson distribution with Sujatha distribution. The PSD is defined by its probability mass function (pmf)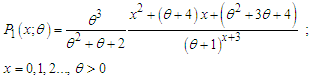 | (1.2) |
Statistical properties including shapes of pmf, moments and moments based measures, over-dispersion, unimodality and increasing hazard rate, estimation of parameters and applications o model over-dispersed data have been discussed by Shanker (2016 b). Wesley et al (2018) proposed a zero-modified Poisson-Sujatha distribution to model over-dispersed count data and discussed its several important properties and applications. Shanker et al (2017) have introduced a generalization of Sujatha distribution (AGSD) having pdf and cdf given by 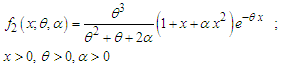 | (1.3) |
Shanker et al (2017) have discussed important statistical properties including shapes of the density, moments and moments based measures, hazard rate function, mean residual life function, stochastic ordering, mean deviations, Bonferroni and Lorenz curves, stress-strength reliability, along with estimation of parameters using maximum likelihood estimation and applications of AGSD for modeling lifetime data from engineering and medical sciences. It can be easily verified that at 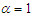 , the pdf of AGSD reduces to the corresponding pdf of Sujatha distribution. Also, at
, the pdf of AGSD reduces to the corresponding pdf of Sujatha distribution. Also, at 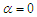 , the pdf of AGSD reduces to Lindley distribution introduced by Lindley (1958).Shanker and Shukla (2019) introduced a generalization of Poisson-Sujatha distribution (AGPSD) by compounding Poisson distribution with AGSD (1.3) and obtained the pmf in the form
, the pdf of AGSD reduces to Lindley distribution introduced by Lindley (1958).Shanker and Shukla (2019) introduced a generalization of Poisson-Sujatha distribution (AGPSD) by compounding Poisson distribution with AGSD (1.3) and obtained the pmf in the form 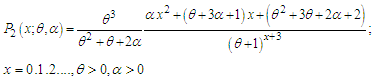 | (1.4) |
Various properties, estimation of parameters, and applications of AGPSD have been discussed by Shanker and Shukla (2019). Further, Poisson-Lindley distribution (PLD) of Sankaran (1970) and Poisson-Sujatha distribution of Shanker (2016 b) are particular cases of AGPSD.Shanker and Shukla (2020 a) proposed a two-parameter Poisson-Sujatha distribution (TPPSD) defined by its pmf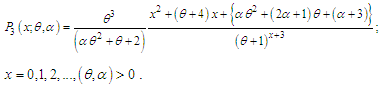 | (1.5) |
Important statistical properties, estimation of parameters using maximum likelihood estimation, applications and the superiority of TPPSD over other one parameter and two- parameter discrete distributions have been discussed by Shanker and Shukla (2020 a). It should be noted that TPPSD is a Poisson mixture of a two-parameter Sujatha distribution (TPSD) introduced by Mussie and Shanker (2018) and defined by its pdf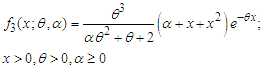 | (1.6) |
It can be easily verified that one parameter Sujatha distribution is a particular case of NTPSD for 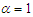 . Its moments and moments based measures including skewness, kurtosis, index of dispersion; hazard rate function, mean residual life function, stochastic ordering, mean deviations, Bonferroni and Lorenz curves, stress-strength reliability the estimation of the parameters using methods of moments and method of maximum likelihood and superiority over exponential, Lindley, Akash and Sujatha distributions have been explained in Mussie and Shanker (2018).Recently, Mussie and Shanker (2019) proposed another two-parameter Sujatha distribution (ATPSD) defined by its pdf
. Its moments and moments based measures including skewness, kurtosis, index of dispersion; hazard rate function, mean residual life function, stochastic ordering, mean deviations, Bonferroni and Lorenz curves, stress-strength reliability the estimation of the parameters using methods of moments and method of maximum likelihood and superiority over exponential, Lindley, Akash and Sujatha distributions have been explained in Mussie and Shanker (2018).Recently, Mussie and Shanker (2019) proposed another two-parameter Sujatha distribution (ATPSD) defined by its pdf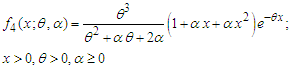 | (1.6) |
where 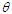 is a scale parameter and is
is a scale parameter and is 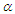 is a shape parameter. It can be easily verified that (1.3) reduces to exponential distribution and Sujatha distribution for
is a shape parameter. It can be easily verified that (1.3) reduces to exponential distribution and Sujatha distribution for 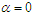 and
and 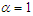 respectively. Its moments and moments based measures including skewness, kurtosis, index of dispersion; hazard rate function, mean residual life function, stochastic ordering, mean deviations, Bonferroni and Lorenz curves, stress-strength reliability the estimation of the parameters using methods of moments and method of maximum likelihood and superiority over exponential, Lindley and Sujatha distributions have been explained in Mussie and Shanker (2019). Shanker and Shukla (2020 b) suggested another two-parameter Poisson-Sujatha distribution (ATPPSD) by compounding Poisson distribution with another two-parameter Poisson-Sujatha distribution
respectively. Its moments and moments based measures including skewness, kurtosis, index of dispersion; hazard rate function, mean residual life function, stochastic ordering, mean deviations, Bonferroni and Lorenz curves, stress-strength reliability the estimation of the parameters using methods of moments and method of maximum likelihood and superiority over exponential, Lindley and Sujatha distributions have been explained in Mussie and Shanker (2019). Shanker and Shukla (2020 b) suggested another two-parameter Poisson-Sujatha distribution (ATPPSD) by compounding Poisson distribution with another two-parameter Poisson-Sujatha distribution 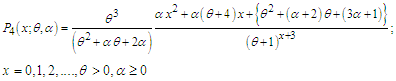 | (1.7) |
Important statistical properties, estimation of parameters using maximum likelihood estimation ,applications and the superiority of ATPPSD over other one parameter and two- parameter discrete distributions have been discussed by Shanker and Shukla (2020 b). Mussie and Shanker (2018) proposed a new two-parameter Sujatha distribution (NTPSD) defined by its pdf 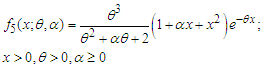 | (1.8) |
It can be easily verified that one parameter Akash distribution of Shanker (2015) and Sujatha distribution are particular cases of NTPSD for 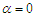 and
and 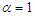 , respectively. Its moments and moments based measures including skewness, kurtosis, index of dispersion; hazard rate function, mean residual life function, stochastic ordering, mean deviations, Bonferroni and Lorenz curves, stress-strength reliability the estimation of the parameters using methods of moments and method of maximum likelihood and superiority over exponential, Lindley, Akash and Sujatha distributions have been explained in Mussie and Shanker (2018).The main motivation for proposing ATPPSD are (i) Sujatha distribution is a better model than both exponential and Lindley distribution for modeling lifetime data, and PSD being a Poisson mixture of Sujatha distribution gives better fit than both Poisson and Poisson-Lindley distribution (PLD), (ii) NTPSD gives much better fit than exponential, Lindley and Sujatha distribution, NTPPSD being a Poisson mixture of NTPSD provides better fit over PSD and other discrete distributions, and (iii) have a comparative study of NTPPSD with other two-parameter generalizations of Poisson-Sujatha distributions including AGPSD, TPPSD, and ATPPSD. Keeping these points in mind, a new two-parameter Poisson-Sujatha distribution (NTPPSD), a Poisson mixture of NTPSD has been proposed and its moments and moments based measures have been obtained and their behaviors have been studied. Maximum likelihood estimation of NTPPSD has been discussed for the estimation its parameters and its applications have been discussed with six examples of observed count datasets from various fields of knowledge.
, respectively. Its moments and moments based measures including skewness, kurtosis, index of dispersion; hazard rate function, mean residual life function, stochastic ordering, mean deviations, Bonferroni and Lorenz curves, stress-strength reliability the estimation of the parameters using methods of moments and method of maximum likelihood and superiority over exponential, Lindley, Akash and Sujatha distributions have been explained in Mussie and Shanker (2018).The main motivation for proposing ATPPSD are (i) Sujatha distribution is a better model than both exponential and Lindley distribution for modeling lifetime data, and PSD being a Poisson mixture of Sujatha distribution gives better fit than both Poisson and Poisson-Lindley distribution (PLD), (ii) NTPSD gives much better fit than exponential, Lindley and Sujatha distribution, NTPPSD being a Poisson mixture of NTPSD provides better fit over PSD and other discrete distributions, and (iii) have a comparative study of NTPPSD with other two-parameter generalizations of Poisson-Sujatha distributions including AGPSD, TPPSD, and ATPPSD. Keeping these points in mind, a new two-parameter Poisson-Sujatha distribution (NTPPSD), a Poisson mixture of NTPSD has been proposed and its moments and moments based measures have been obtained and their behaviors have been studied. Maximum likelihood estimation of NTPPSD has been discussed for the estimation its parameters and its applications have been discussed with six examples of observed count datasets from various fields of knowledge.
2. A New Two-Parameter Poisson-Sujatha Distribution
A random variable 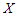 is said to follows a new two-parameter Poisson-Sujatha distribution (NTPPSD) if
is said to follows a new two-parameter Poisson-Sujatha distribution (NTPPSD) if 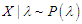 and
and 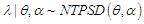 .That is,
.That is,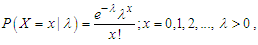 and
and 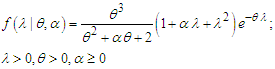 The pmf of unconditional random variable
The pmf of unconditional random variable 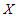 can be obtained as
can be obtained as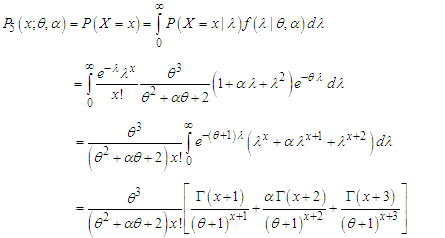 | (2.1) |
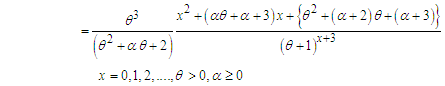 | (2.2) |
We would call this a new two-parameter Poisson-Sujatha distribution (NTPPSD) because for 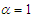 , it reduces to one parameter PSD given in (1.2). Also at
, it reduces to one parameter PSD given in (1.2). Also at 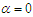 , it reduces to Poisson-Akash distribution.It can be easily shown that NTPPSD is unimodal and has increasing hazard rate. Since
, it reduces to Poisson-Akash distribution.It can be easily shown that NTPPSD is unimodal and has increasing hazard rate. Since 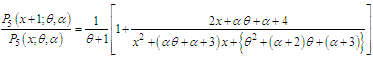 is decreasing function in
is decreasing function in  is log-concave. Now using the results of relationship between log-concavity, unimodality and increasing hazard rate (IHR) of discrete distributions available in Grandell (1997), it can concluded that NTPPSD has an increasing hazard rate and unimodal. The behavior of the pmf of NTPPSD for varying values of parameters
is log-concave. Now using the results of relationship between log-concavity, unimodality and increasing hazard rate (IHR) of discrete distributions available in Grandell (1997), it can concluded that NTPPSD has an increasing hazard rate and unimodal. The behavior of the pmf of NTPPSD for varying values of parameters 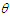 and
and 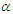 are shown in figure 1.
are shown in figure 1. 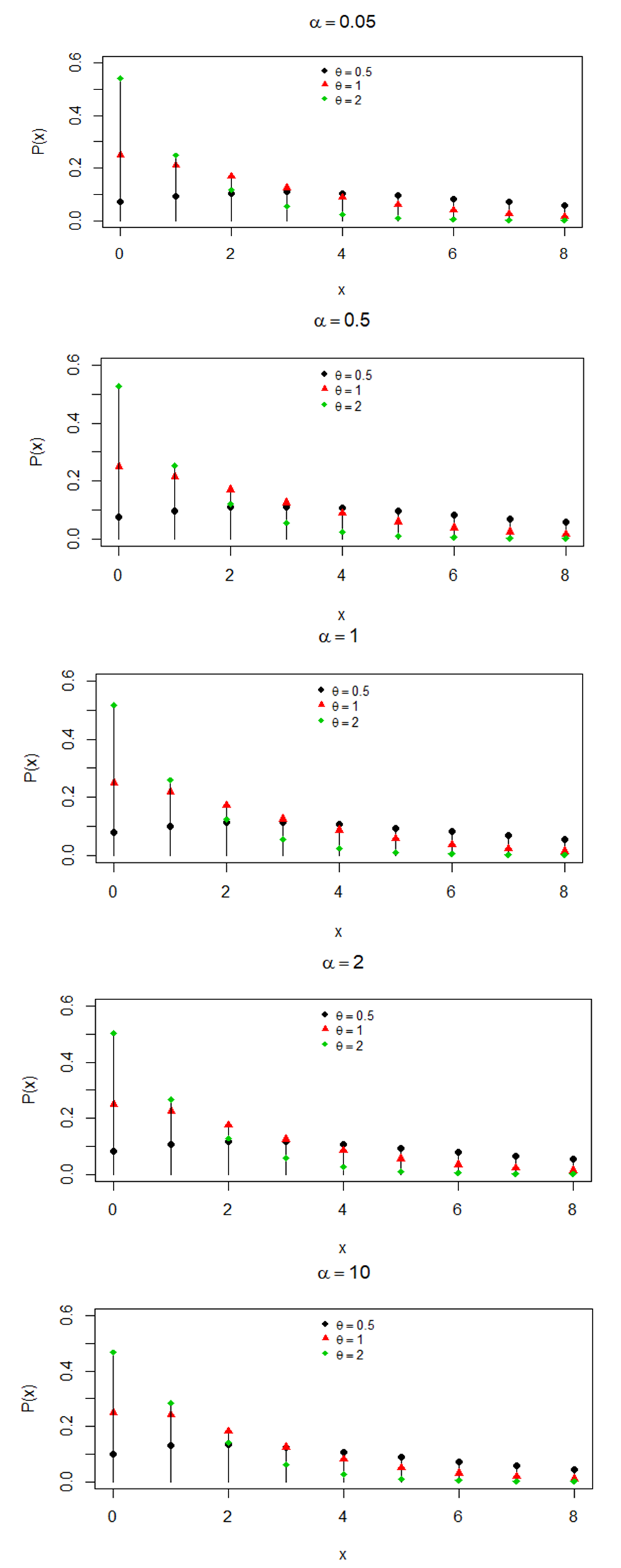 | Figure 1. Behaviour of pmf of NTPPSD for varying values of parameters 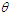 and and 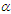 |
3. Moments Based Measures
The 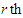 factorial moment about origin
factorial moment about origin 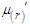 of NTPPSD can be obtained as
of NTPPSD can be obtained as 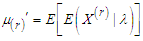 , where
, where 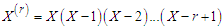 . Using (2.1), the
. Using (2.1), the 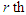 factorial moment about origin
factorial moment about origin 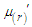 of NTPPSD can be obtained as
of NTPPSD can be obtained as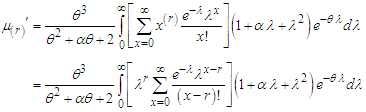 Taking
Taking  within the bracket, we get
within the bracket, we get 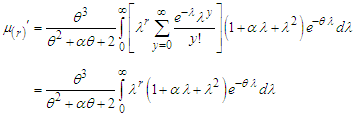 After some tedious algebraic simplification, a general expression for the
After some tedious algebraic simplification, a general expression for the 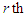 factorial moment about origin
factorial moment about origin  of NTPPSD can be expressed as
of NTPPSD can be expressed as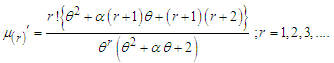 | (3.1) |
It can be easily verified that at 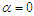 and
and 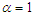 , the expression (3.1) reduces to the corresponding expression of PAD and PSD. Substituting
, the expression (3.1) reduces to the corresponding expression of PAD and PSD. Substituting 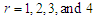 in (3.1), the first four factorial moments about origin of NTPPSD can be obtained as
in (3.1), the first four factorial moments about origin of NTPPSD can be obtained as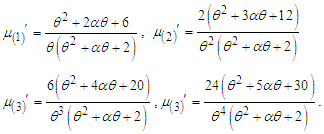 Now using the relationship between factorial moments about origin and moments about origin, the first four moment about origin of the NTPPSD are obtained as
Now using the relationship between factorial moments about origin and moments about origin, the first four moment about origin of the NTPPSD are obtained as 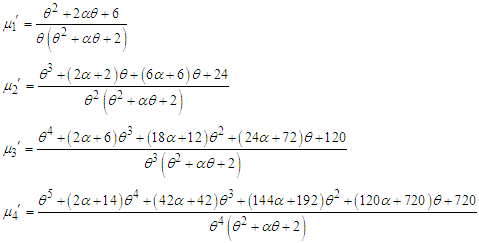 Using the relationship between moments about mean and the moments about origin, the moments about mean of NTPPSD are obtained as
Using the relationship between moments about mean and the moments about origin, the moments about mean of NTPPSD are obtained as The coefficient of variation
The coefficient of variation  , coefficient of Skewness
, coefficient of Skewness  , coefficient of Kurtosis
, coefficient of Kurtosis  , and index of dispersion
, and index of dispersion 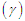 of NTPPSD are thus given by
of NTPPSD are thus given by  It can be easily verified that at
It can be easily verified that at 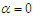 and
and 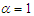 expressions of these statistical constants of NTPPSD reduce to the corresponding expressions for PAD and PSD. The behaviors of coefficient of variation (C.V), coefficient of skewness (C.S), coefficient of kurtosis (C.K) and index of dispersion (I.D) of NTPPSD for varying values of parameters
expressions of these statistical constants of NTPPSD reduce to the corresponding expressions for PAD and PSD. The behaviors of coefficient of variation (C.V), coefficient of skewness (C.S), coefficient of kurtosis (C.K) and index of dispersion (I.D) of NTPPSD for varying values of parameters 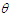 and
and 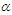 have been explained through graphs and presented in figure 2.
have been explained through graphs and presented in figure 2.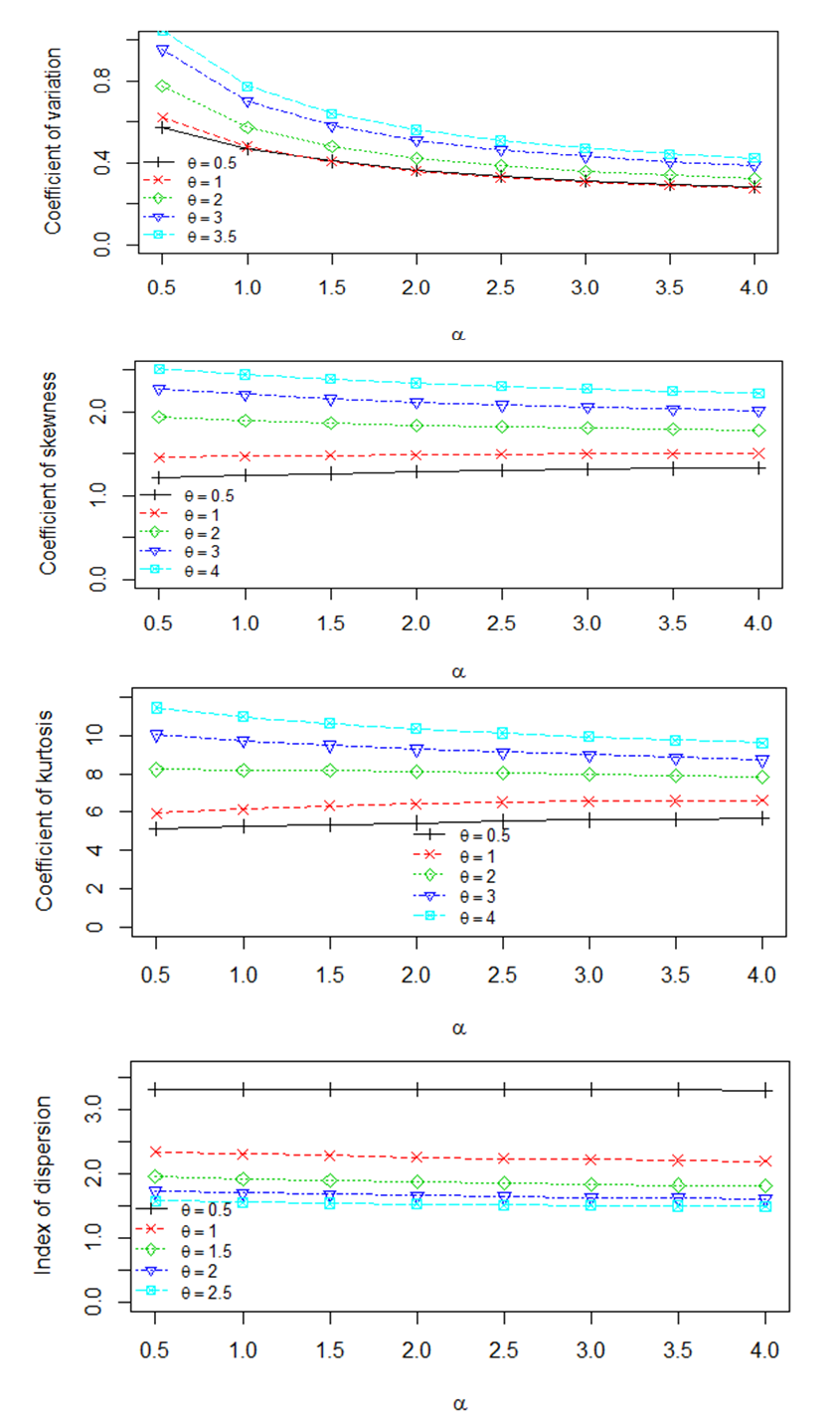 | Figure 2. Behaviors of coefficient of variation (C.V), coefficient of skewness (C.S), coefficient of kurtosis (C.K) and index of dispersion (I.D) of NTPPSD for varying values of parameters 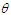 and and 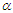 |
4. Maximum Likelihood Estimation of Parameters
Suppose 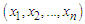 be a random sample of size
be a random sample of size 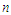 from NTPPSD and
from NTPPSD and 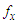 be the observed frequency in the sample corresponding to
be the observed frequency in the sample corresponding to 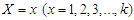 such that
such that 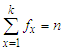 , where
, where  is the largest observed value having non-zero frequency. The likelihood function
is the largest observed value having non-zero frequency. The likelihood function 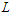 of NTPPSD is given by
of NTPPSD is given by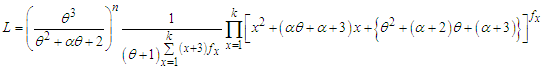 The log likelihood function is thus obtained as
The log likelihood function is thus obtained as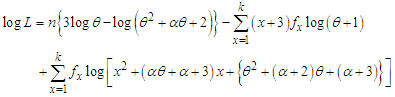 The maximum likelihood estimates
The maximum likelihood estimates 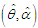 of
of 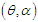 of NTPPSD is the solutions of the following log likelihood equations
of NTPPSD is the solutions of the following log likelihood equations 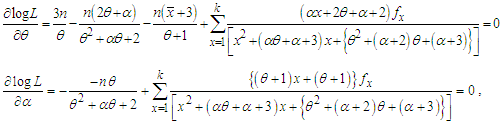 where
where 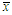 is the sample mean. These two log likelihood equations do not seem to be solved directly because they do not have closed forms. Therefore, to find the maximum likelihood estimates of parameters an iterative method such as Fisher Scoring method, Bisection method, Regula Falsi method or Newton-Raphson method can be used. In this paper Newton-Raphson method has been used using R-software.
is the sample mean. These two log likelihood equations do not seem to be solved directly because they do not have closed forms. Therefore, to find the maximum likelihood estimates of parameters an iterative method such as Fisher Scoring method, Bisection method, Regula Falsi method or Newton-Raphson method can be used. In this paper Newton-Raphson method has been used using R-software.
5. Applications
To examine the goodness of fit of NTPPSD over PSD, AGPSD, TPPSD and ATPPSD, six count datasets which are over-dispersed have been considered The goodness of fit of all these distributions are based on maximum likelihood estimation. The first dataset is regarding the number of European corn-borer available in Gosset (1908), the second dataset is regarding the number of European corn-borer available in Mc Guire et al (1957), the third dataset is regarding the accidents to 647 women working on high explosive shells in 5 weeks, available in Sankaran (1970), the fourth dataset is regarding the number of European red mites on Apple leaves, available in Bliss (1953) , the fifth dataset is regarding the distribution of epileptic seizure counts available in Chakraborty (2010) and the six dataset is regarding the observed number of households according to the number of male migrants aged 15 years and above, available in Shukla and Yadav (2006). The maximum likelihood estimates, chi-squares, value of 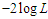 and Akaike information criterion (AIC) for the considered distributions for the given datasets have been computed and presented in the respective table. The AIC has been calculated using the formula
and Akaike information criterion (AIC) for the considered distributions for the given datasets have been computed and presented in the respective table. The AIC has been calculated using the formula 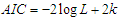 , where
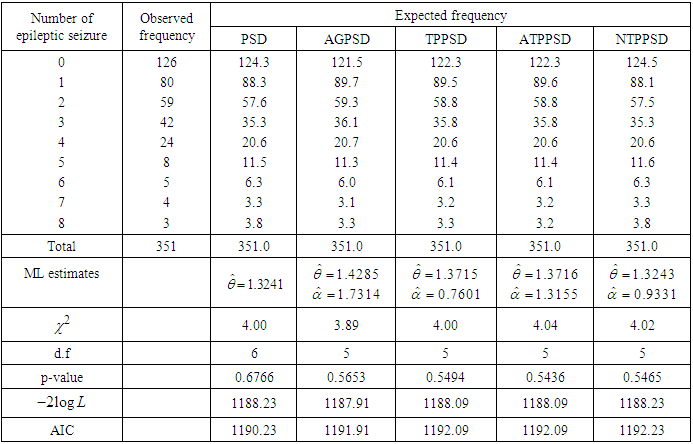
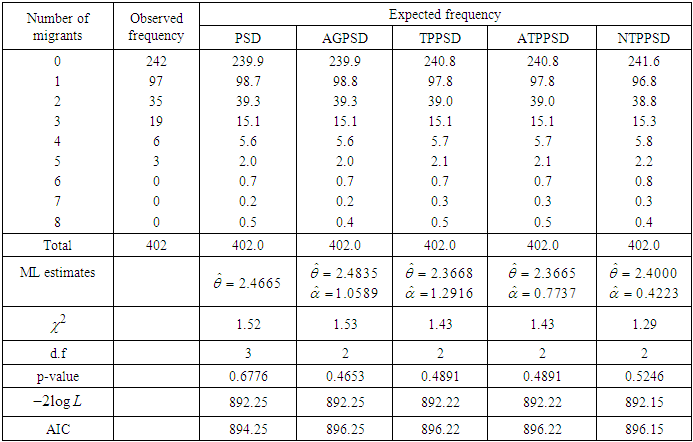
, where 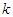 is the number of parameters involved in the distribution. In table 1, AGPSD and ATPPSD give almost the same fit. In table 2, AGPSD gives the best fit, whereas TPPSD and ATPPSD gives the second best fit. In table 3, PSD and AGPSD give almost identical and best fit whereas TPPSD and ATPPSD gives the second best fit. TPPSD and ATPPSD gives the same fit in table 4, whereas in table 5 AGPSD gives the best fit. Finally in table 6, NTPPSD gives the best fit. Therefore, we can say that NTPPSD is competing well with AGPSD, TPPSD and ATPPSD for count datasets. Therefore, it is obvious from these goodness of fit of distributions that each distribution has some advantages and disadvantages for modeling count data due to its theoretical or applied point of view. It is also true that the nature of the count data regarding degree of over-dispersion is different and hence we can not say with confidence that a particular distribution will give best fit in every datasets.
is the number of parameters involved in the distribution. In table 1, AGPSD and ATPPSD give almost the same fit. In table 2, AGPSD gives the best fit, whereas TPPSD and ATPPSD gives the second best fit. In table 3, PSD and AGPSD give almost identical and best fit whereas TPPSD and ATPPSD gives the second best fit. TPPSD and ATPPSD gives the same fit in table 4, whereas in table 5 AGPSD gives the best fit. Finally in table 6, NTPPSD gives the best fit. Therefore, we can say that NTPPSD is competing well with AGPSD, TPPSD and ATPPSD for count datasets. Therefore, it is obvious from these goodness of fit of distributions that each distribution has some advantages and disadvantages for modeling count data due to its theoretical or applied point of view. It is also true that the nature of the count data regarding degree of over-dispersion is different and hence we can not say with confidence that a particular distribution will give best fit in every datasets. Table 1. Observed and expected number of European corn-borer available in Gosset (1908)
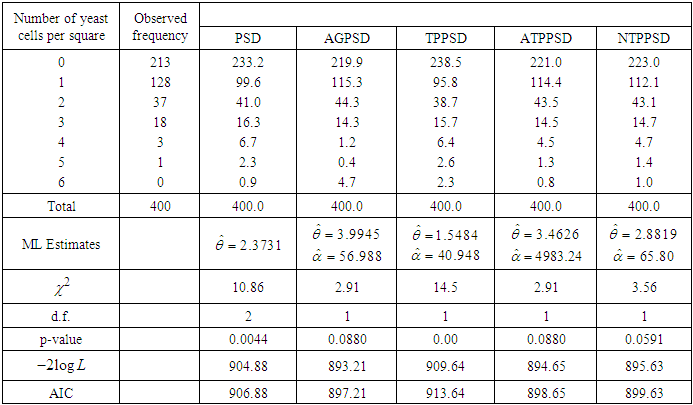 |
| |
|
Table 2. Observed and expected number of European corn-borer available in Mc Guire et al (1957)
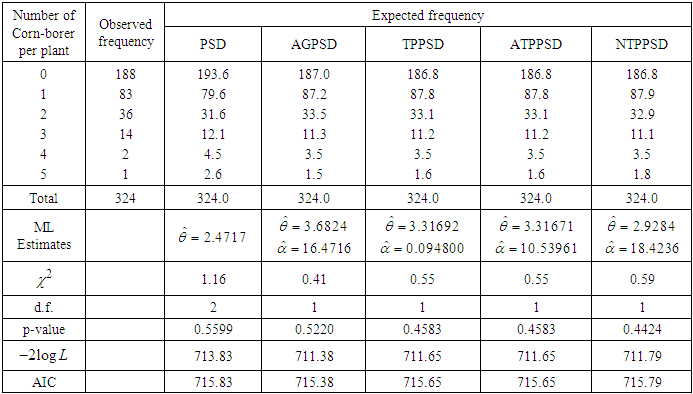 |
| |
|
Table 3. Accidents to 647 women working on high explosive shells in 5 weeks, available in Sankaran (1970)
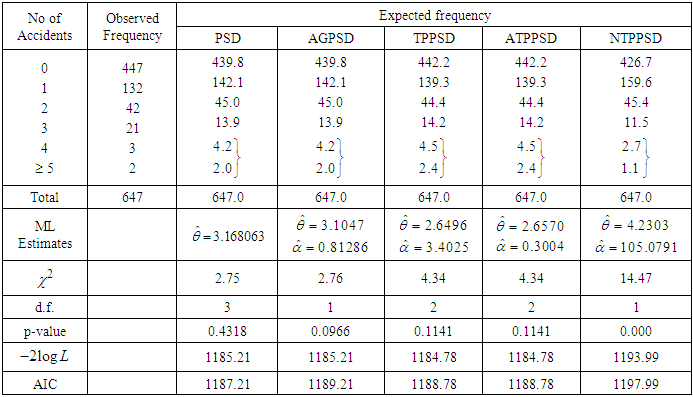 |
| |
|
Table 4. Observed and Expected number of European red mites on Apple leaves, available in Bliss (1953)
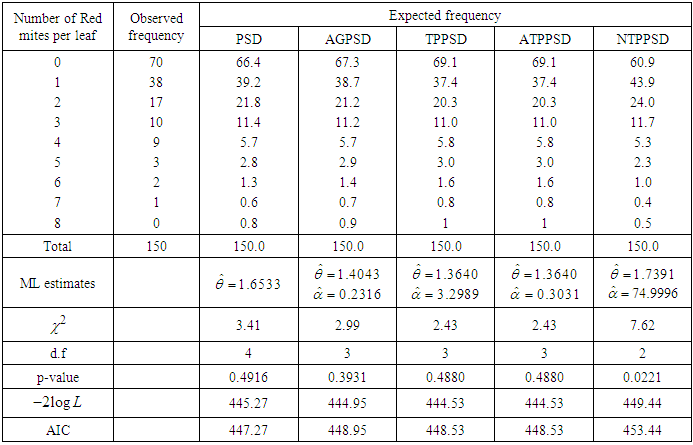 |
| |
|
Table 5. Distribution of epileptic seizure counts due to Chakraborty (2010)
 |
| |
|
Table 6. Observed and Expected number of households according to the number of male migrants aged 15 years and above, available in Shukla and Yadav (2006)
 |
| |
|
6. Concluding Remarks
In this paper, a new two-parameter Poisson Sujatha distribution (NTPPSD) which includes Poisson-Akash distribution (PAD) introduced by Shanker (2017) and Poisson-Sujatha distribution (PSD) proposed by Shanker (2016 b) as a special case has been proposed.. Its unimodality, increasing hazard rate, moments and moments based measures including coefficients of variation, skewness, kurtosis and index of dispersion has been obtained and their behaviors have been explained graphically for varying values of parameters. The method of maximum likelihood estimation has been discussed. The applications of the proposed distribution has been explained through two examples of count data from ecology and the goodness of fit of the distribution has been found quite satisfactory over PSD, AGPSD, TPPSD and ATPPSD.
ACKNOWLEDGEMENTS
Authors are grateful to the editor in chief of the journal and the anonymous reviewer for constructive comments which were helpful.
References
| [1] | Bliss, C.I. (1953): Fitting negative binomial distribution to biological data, Biometrics, 9, 177 – 200. |
| [2] | Chakraborty, S. (2010): On some distributional Properties of the family of Weighted Generalized Poisson distribution, Communication in Statistics-Theory and Methods, 39 (15), 2767 – 2788. |
| [3] | Gosset, W.S. (1908): The probable error of a mean, Biometrika, 6, 1 – 25. |
| [4] | Grandell, J. (1997): Mixed Poisson Processes, Chapman& Hall, London |
| [5] | Kaliraja, M. and Perarasan, K. (2019): A new stochastic model on the generalization of Sujatha distribution for the effects of two types of exercise on plasma growth hormone, The International Journal of Analytical and Experimental Model Analysis, 11(9), 1164 – 1170. |
| [6] | Lindley, D.V. (1958): Fiducial distributions and Bayes’ theorem, Journal of the Royal Statistical Society, Series B, 20, 102- 107. |
| [7] | Mc. Guire, JU., Brindley, TA. and Bancroft, TA. (1957): The distribution of European corn-borer larvae pyrausta in field corn, Biometrics, 13: 65-78. |
| [8] | Mussie, T. and Shanker, R. (2018): A Two-Parameter Sujatha distribution, Biometrics & Biostatistics International Journal, 7(3), 188 – 197. |
| [9] | Mussie, T. and Shanker, R. (2018): A New Two-Parameter Sujatha distribution with Properties and Applications, Turkiye Klinikleri Journal of Biostatistics, 10 (2), 96 – 113. |
| [10] | Mussie, T. and Shanker, R. (2019): Another Two-Parameter Sujatha distribution with Properties and Applications, Journal of Mathematical Sciences and Modeling, 2(1), 1 – 13. |
| [11] | Sankaran, M. (1970): The discrete Poisson-Lindley distribution, Biometrics, 1970; 26: 145-149. |
| [12] | Shanker, R. (2015): Akash Distribution and Its Applications, International Journal of Probability and Statistics, 4 (3), 65 – 75. |
| [13] | Shanker, R. (2017): The Discrete Poisson-Akash Distribution, International Journal of Probability and Statistics, 6(1), 1 -10. |
| [14] | Shanker, R. (2016 a): Sujatha distribution and Its Applications, Statistics in Transition new Series, 17 (3), 1 – 20. |
| [15] | Shanker, R. (2016 b): The discrete Poisson-Sujatha distribution, International Journal of Probability and Statistics, 5(1), 1- 9. |
| [16] | Shanker, R., Shukla, K K., and Hagos, F. (2017): A Generalization of Sujatha distribution and its Applications to Real lifetime data, Journal of Institute of Science and Technology, 22(1), 77 - 94. |
| [17] | Shanker, R. and Shukla, K.K. (2019): A generalization of Poisson-Sujatha Distribution and Its Applications to Ecology, International Journal of Biomathematics, 12 (2), 1- 11. |
| [18] | Shanker, R. and Shukla, K.K. (2020 a): A two-parameter Poisson-Sujatha distribution, to appear in American Journal of Mathematics and Statistics. |
| [19] | Shanker, R. and Shukla, K.K. (2020 b): Another two-parameter Poisson-Sujatha distribution, to appear in International Journal of Statistics and Applications. |
| [20] | Shukla, K.K. and Yadav, K.N.S. (2006): The distribution of number of migrants at household level, Journal of Population and Social Studies, 14(2), 153 – 166. |
| [21] | Wesley, B., Agelica, M.T.R., Katiane, S.C., Marinaho, G.A., and Francisco, L.N. (2018): On Zero-modified Poisson-Sujatha distribution to model over-dispersed data, Austrian Journal of Statistics, 47(3), 1 – 19. |


 and introduced by Shanker (2016a) is
and introduced by Shanker (2016a) is 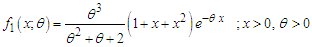
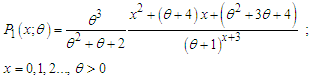
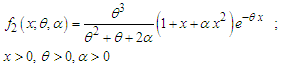
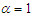 , the pdf of AGSD reduces to the corresponding pdf of Sujatha distribution. Also, at
, the pdf of AGSD reduces to the corresponding pdf of Sujatha distribution. Also, at 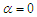 , the pdf of AGSD reduces to Lindley distribution introduced by Lindley (1958).Shanker and Shukla (2019) introduced a generalization of Poisson-Sujatha distribution (AGPSD) by compounding Poisson distribution with AGSD (1.3) and obtained the pmf in the form
, the pdf of AGSD reduces to Lindley distribution introduced by Lindley (1958).Shanker and Shukla (2019) introduced a generalization of Poisson-Sujatha distribution (AGPSD) by compounding Poisson distribution with AGSD (1.3) and obtained the pmf in the form 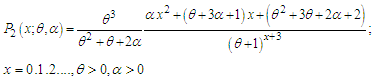
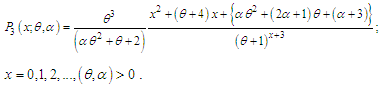
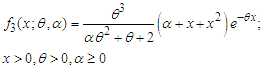
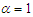 . Its moments and moments based measures including skewness, kurtosis, index of dispersion; hazard rate function, mean residual life function, stochastic ordering, mean deviations, Bonferroni and Lorenz curves, stress-strength reliability the estimation of the parameters using methods of moments and method of maximum likelihood and superiority over exponential, Lindley, Akash and Sujatha distributions have been explained in Mussie and Shanker (2018).Recently, Mussie and Shanker (2019) proposed another two-parameter Sujatha distribution (ATPSD) defined by its pdf
. Its moments and moments based measures including skewness, kurtosis, index of dispersion; hazard rate function, mean residual life function, stochastic ordering, mean deviations, Bonferroni and Lorenz curves, stress-strength reliability the estimation of the parameters using methods of moments and method of maximum likelihood and superiority over exponential, Lindley, Akash and Sujatha distributions have been explained in Mussie and Shanker (2018).Recently, Mussie and Shanker (2019) proposed another two-parameter Sujatha distribution (ATPSD) defined by its pdf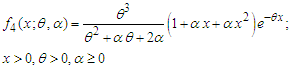
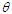 is a scale parameter and is
is a scale parameter and is 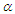 is a shape parameter. It can be easily verified that (1.3) reduces to exponential distribution and Sujatha distribution for
is a shape parameter. It can be easily verified that (1.3) reduces to exponential distribution and Sujatha distribution for 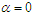 and
and 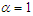 respectively. Its moments and moments based measures including skewness, kurtosis, index of dispersion; hazard rate function, mean residual life function, stochastic ordering, mean deviations, Bonferroni and Lorenz curves, stress-strength reliability the estimation of the parameters using methods of moments and method of maximum likelihood and superiority over exponential, Lindley and Sujatha distributions have been explained in Mussie and Shanker (2019). Shanker and Shukla (2020 b) suggested another two-parameter Poisson-Sujatha distribution (ATPPSD) by compounding Poisson distribution with another two-parameter Poisson-Sujatha distribution
respectively. Its moments and moments based measures including skewness, kurtosis, index of dispersion; hazard rate function, mean residual life function, stochastic ordering, mean deviations, Bonferroni and Lorenz curves, stress-strength reliability the estimation of the parameters using methods of moments and method of maximum likelihood and superiority over exponential, Lindley and Sujatha distributions have been explained in Mussie and Shanker (2019). Shanker and Shukla (2020 b) suggested another two-parameter Poisson-Sujatha distribution (ATPPSD) by compounding Poisson distribution with another two-parameter Poisson-Sujatha distribution 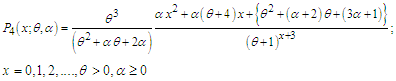
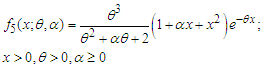
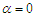 and
and 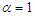 , respectively. Its moments and moments based measures including skewness, kurtosis, index of dispersion; hazard rate function, mean residual life function, stochastic ordering, mean deviations, Bonferroni and Lorenz curves, stress-strength reliability the estimation of the parameters using methods of moments and method of maximum likelihood and superiority over exponential, Lindley, Akash and Sujatha distributions have been explained in Mussie and Shanker (2018).The main motivation for proposing ATPPSD are (i) Sujatha distribution is a better model than both exponential and Lindley distribution for modeling lifetime data, and PSD being a Poisson mixture of Sujatha distribution gives better fit than both Poisson and Poisson-Lindley distribution (PLD), (ii) NTPSD gives much better fit than exponential, Lindley and Sujatha distribution, NTPPSD being a Poisson mixture of NTPSD provides better fit over PSD and other discrete distributions, and (iii) have a comparative study of NTPPSD with other two-parameter generalizations of Poisson-Sujatha distributions including AGPSD, TPPSD, and ATPPSD. Keeping these points in mind, a new two-parameter Poisson-Sujatha distribution (NTPPSD), a Poisson mixture of NTPSD has been proposed and its moments and moments based measures have been obtained and their behaviors have been studied. Maximum likelihood estimation of NTPPSD has been discussed for the estimation its parameters and its applications have been discussed with six examples of observed count datasets from various fields of knowledge.
, respectively. Its moments and moments based measures including skewness, kurtosis, index of dispersion; hazard rate function, mean residual life function, stochastic ordering, mean deviations, Bonferroni and Lorenz curves, stress-strength reliability the estimation of the parameters using methods of moments and method of maximum likelihood and superiority over exponential, Lindley, Akash and Sujatha distributions have been explained in Mussie and Shanker (2018).The main motivation for proposing ATPPSD are (i) Sujatha distribution is a better model than both exponential and Lindley distribution for modeling lifetime data, and PSD being a Poisson mixture of Sujatha distribution gives better fit than both Poisson and Poisson-Lindley distribution (PLD), (ii) NTPSD gives much better fit than exponential, Lindley and Sujatha distribution, NTPPSD being a Poisson mixture of NTPSD provides better fit over PSD and other discrete distributions, and (iii) have a comparative study of NTPPSD with other two-parameter generalizations of Poisson-Sujatha distributions including AGPSD, TPPSD, and ATPPSD. Keeping these points in mind, a new two-parameter Poisson-Sujatha distribution (NTPPSD), a Poisson mixture of NTPSD has been proposed and its moments and moments based measures have been obtained and their behaviors have been studied. Maximum likelihood estimation of NTPPSD has been discussed for the estimation its parameters and its applications have been discussed with six examples of observed count datasets from various fields of knowledge.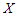 is said to follows a new two-parameter Poisson-Sujatha distribution (NTPPSD) if
is said to follows a new two-parameter Poisson-Sujatha distribution (NTPPSD) if 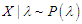 and
and 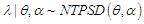 .That is,
.That is,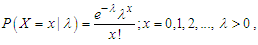 and
and 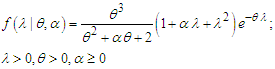 The pmf of unconditional random variable
The pmf of unconditional random variable 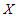 can be obtained as
can be obtained as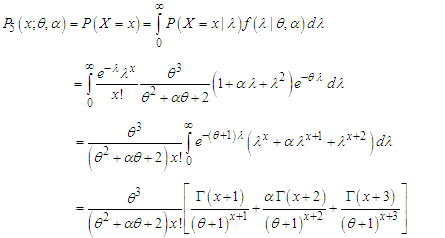
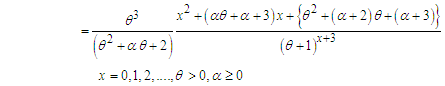
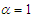 , it reduces to one parameter PSD given in (1.2). Also at
, it reduces to one parameter PSD given in (1.2). Also at 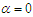 , it reduces to Poisson-Akash distribution.It can be easily shown that NTPPSD is unimodal and has increasing hazard rate. Since
, it reduces to Poisson-Akash distribution.It can be easily shown that NTPPSD is unimodal and has increasing hazard rate. Since 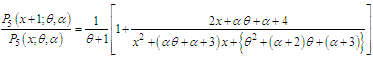 is decreasing function in
is decreasing function in 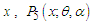 is log-concave. Now using the results of relationship between log-concavity, unimodality and increasing hazard rate (IHR) of discrete distributions available in Grandell (1997), it can concluded that NTPPSD has an increasing hazard rate and unimodal. The behavior of the pmf of NTPPSD for varying values of parameters
is log-concave. Now using the results of relationship between log-concavity, unimodality and increasing hazard rate (IHR) of discrete distributions available in Grandell (1997), it can concluded that NTPPSD has an increasing hazard rate and unimodal. The behavior of the pmf of NTPPSD for varying values of parameters 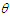 and
and 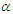 are shown in figure 1.
are shown in figure 1. 
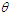 and
and 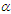
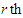 factorial moment about origin
factorial moment about origin 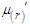 of NTPPSD can be obtained as
of NTPPSD can be obtained as 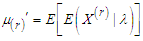 , where
, where 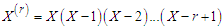 . Using (2.1), the
. Using (2.1), the 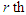 factorial moment about origin
factorial moment about origin 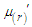 of NTPPSD can be obtained as
of NTPPSD can be obtained as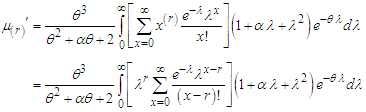 Taking
Taking 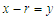 within the bracket, we get
within the bracket, we get 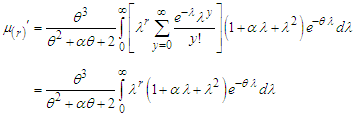 After some tedious algebraic simplification, a general expression for the
After some tedious algebraic simplification, a general expression for the 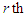 factorial moment about origin
factorial moment about origin 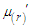 of NTPPSD can be expressed as
of NTPPSD can be expressed as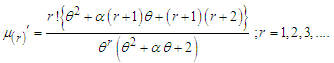
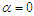 and
and 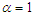 , the expression (3.1) reduces to the corresponding expression of PAD and PSD. Substituting
, the expression (3.1) reduces to the corresponding expression of PAD and PSD. Substituting 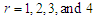 in (3.1), the first four factorial moments about origin of NTPPSD can be obtained as
in (3.1), the first four factorial moments about origin of NTPPSD can be obtained as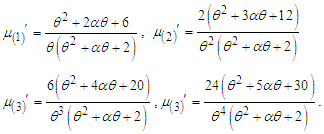 Now using the relationship between factorial moments about origin and moments about origin, the first four moment about origin of the NTPPSD are obtained as
Now using the relationship between factorial moments about origin and moments about origin, the first four moment about origin of the NTPPSD are obtained as 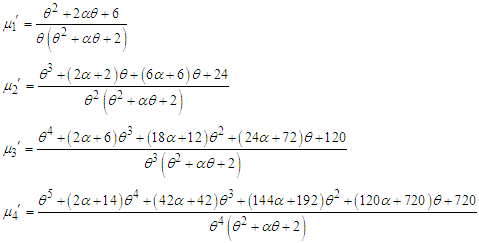 Using the relationship between moments about mean and the moments about origin, the moments about mean of NTPPSD are obtained as
Using the relationship between moments about mean and the moments about origin, the moments about mean of NTPPSD are obtained as The coefficient of variation
The coefficient of variation 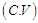 , coefficient of Skewness
, coefficient of Skewness 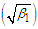 , coefficient of Kurtosis
, coefficient of Kurtosis  , and index of dispersion
, and index of dispersion 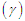 of NTPPSD are thus given by
of NTPPSD are thus given by  It can be easily verified that at
It can be easily verified that at 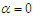 and
and 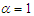 expressions of these statistical constants of NTPPSD reduce to the corresponding expressions for PAD and PSD. The behaviors of coefficient of variation (C.V), coefficient of skewness (C.S), coefficient of kurtosis (C.K) and index of dispersion (I.D) of NTPPSD for varying values of parameters
expressions of these statistical constants of NTPPSD reduce to the corresponding expressions for PAD and PSD. The behaviors of coefficient of variation (C.V), coefficient of skewness (C.S), coefficient of kurtosis (C.K) and index of dispersion (I.D) of NTPPSD for varying values of parameters 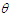 and
and 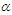 have been explained through graphs and presented in figure 2.
have been explained through graphs and presented in figure 2.
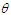 and
and 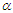
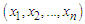 be a random sample of size
be a random sample of size 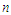 from NTPPSD and
from NTPPSD and 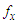 be the observed frequency in the sample corresponding to
be the observed frequency in the sample corresponding to 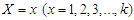 such that
such that 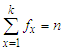 , where
, where 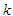 is the largest observed value having non-zero frequency. The likelihood function
is the largest observed value having non-zero frequency. The likelihood function 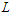 of NTPPSD is given by
of NTPPSD is given by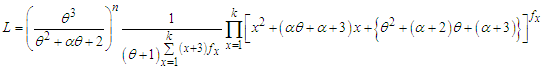 The log likelihood function is thus obtained as
The log likelihood function is thus obtained as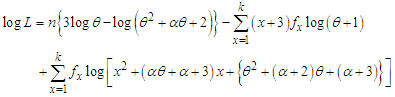 The maximum likelihood estimates
The maximum likelihood estimates 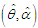 of
of 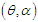 of NTPPSD is the solutions of the following log likelihood equations
of NTPPSD is the solutions of the following log likelihood equations 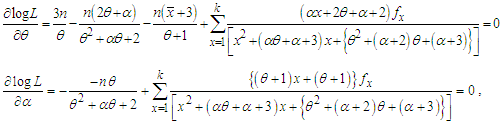 where
where 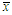 is the sample mean. These two log likelihood equations do not seem to be solved directly because they do not have closed forms. Therefore, to find the maximum likelihood estimates of parameters an iterative method such as Fisher Scoring method, Bisection method, Regula Falsi method or Newton-Raphson method can be used. In this paper Newton-Raphson method has been used using R-software.
is the sample mean. These two log likelihood equations do not seem to be solved directly because they do not have closed forms. Therefore, to find the maximum likelihood estimates of parameters an iterative method such as Fisher Scoring method, Bisection method, Regula Falsi method or Newton-Raphson method can be used. In this paper Newton-Raphson method has been used using R-software. 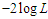 and Akaike information criterion (AIC) for the considered distributions for the given datasets have been computed and presented in the respective table. The AIC has been calculated using the formula
and Akaike information criterion (AIC) for the considered distributions for the given datasets have been computed and presented in the respective table. The AIC has been calculated using the formula 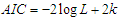 , where
, where 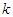 is the number of parameters involved in the distribution. In table 1, AGPSD and ATPPSD give almost the same fit. In table 2, AGPSD gives the best fit, whereas TPPSD and ATPPSD gives the second best fit. In table 3, PSD and AGPSD give almost identical and best fit whereas TPPSD and ATPPSD gives the second best fit. TPPSD and ATPPSD gives the same fit in table 4, whereas in table 5 AGPSD gives the best fit. Finally in table 6, NTPPSD gives the best fit. Therefore, we can say that NTPPSD is competing well with AGPSD, TPPSD and ATPPSD for count datasets. Therefore, it is obvious from these goodness of fit of distributions that each distribution has some advantages and disadvantages for modeling count data due to its theoretical or applied point of view. It is also true that the nature of the count data regarding degree of over-dispersion is different and hence we can not say with confidence that a particular distribution will give best fit in every datasets.
is the number of parameters involved in the distribution. In table 1, AGPSD and ATPPSD give almost the same fit. In table 2, AGPSD gives the best fit, whereas TPPSD and ATPPSD gives the second best fit. In table 3, PSD and AGPSD give almost identical and best fit whereas TPPSD and ATPPSD gives the second best fit. TPPSD and ATPPSD gives the same fit in table 4, whereas in table 5 AGPSD gives the best fit. Finally in table 6, NTPPSD gives the best fit. Therefore, we can say that NTPPSD is competing well with AGPSD, TPPSD and ATPPSD for count datasets. Therefore, it is obvious from these goodness of fit of distributions that each distribution has some advantages and disadvantages for modeling count data due to its theoretical or applied point of view. It is also true that the nature of the count data regarding degree of over-dispersion is different and hence we can not say with confidence that a particular distribution will give best fit in every datasets.  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML




