Yeqian Liu , Yingxiao Huang
Department of Mathematical Sciences, Middle Tennessee State University, Murfreesboro, USA
Correspondence to: Yeqian Liu , Department of Mathematical Sciences, Middle Tennessee State University, Murfreesboro, USA.
| Email: |  |
Copyright © 2020 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
In randomized clinical trials involving survival time, patients may initiate secondary salvage treatments during the follow-up in order to prolong survival. As a result, the effect of primary treatment is usually confounded by these secondary treatments. In addition, such secondary salvage treatments are usually time-dependent due to being initiated upon adverse reaction, disease progression, etc. In this paper, we adopt two types of structural models: structural nested models and marginal structural Cox models, and propose an inferential procedure that improves the efficiency of the usual IPTW method. We examine the finite-sample performance of the proposed method by simulation studies and by application to data from a cancer clinical trial.
Keywords:
Marginal structural model, Inverse probability weighting, Causal inference, Bivariate log-rank test, Artificial Censoring
Cite this paper: Yeqian Liu , Yingxiao Huang , Structural Models for Analyzing Survival Data with Multiple Time-dependent Treatments, International Journal of Probability and Statistics , Vol. 9 No. 1, 2020, pp. 14-19. doi: 10.5923/j.ijps.20200901.03.
1. Introduction
In randomized clinical trials, an improvement in patients’ survival time is considered the most convincing measure of drug efficacy and clinical benefit. This article is motivated by a randomized phase III clinical trial comparing Cisplatin (control) and Vinorelbine/Cisplatin combination (experimental) in patients with non-small tumor lung cancer in terms of the time to all-cause death. It was found that many patients initiated a secondary salvage chemotherapy during the follow-up after discontinuing from the study treatment. More patients in the experimental treatment arm received a secondary treatment, and the time from discontinuation of the study treatment to initiation of a secondary treatment was considerably shorter. The main goal of applying secondary treatments is to prolong patients’ survival time. However, the imbalance of secondary treatment between control and experimental arms might biased the estimation of primary treatment effect. Therefore, it is important to estimate the effect of the primary treatment under the condition of balanced secondary treatment between the two groups, namely, the direct effect [1].The initiation time of a secondary treatment is not stated in the protocol of the clinical trial but rather depend on the choices of the patients or physicians. Such decisions usually depend on patients’ baseline or post-randomization disease condition, which could potentially confound the effect of the primary treatment. Common analysis tools such as landmark analysis, time-dependent Cox models, and censoring subjects at the beginning of secondary treatment do not perform well on estimating primary treatment effect. Two types of structural models: the marginal structural Cox model [2,3] and the structural nested accelerated failure time model with the inferential method of g-estimation [5] have been developed for estimating effect of time-dependent treatments in observational studies. Both causal modes are built upon the counterfactual framework. In this paper, we adopt these two models for making causal inference, and propose an efficient inferential method in the setting of a randomized trial with a secondary treatment. The remainder of the article is organized as follows. Section 2 set ups the notation and describes the proposed method and related background. Simulation studies and analysis of the motivating study are reported in Sections 3 and 4, respectively. The article concludes with a discussion on the choice of models under different scenarios in Section 5.
2. Models and Inference Procedure
2.1. Structural Nested Failure Time Models
2.1.1. Log-rank Test
Log-rank test is one of the most commonly used method for comparing survival functions between two treatment groups. Let 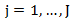 be the distinct observed failure times. For each time
be the distinct observed failure times. For each time 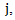 let
let 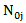 and
and 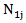 be the number of subjects at risk at the start of period
be the number of subjects at risk at the start of period 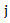 in the treatment and control arm, respectively. Let
in the treatment and control arm, respectively. Let 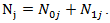 Let
Let 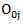 and
and 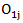 be the observed number of events in the arms respectively, and define
be the observed number of events in the arms respectively, and define 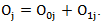 Conditional on
Conditional on 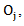 the quantity
the quantity 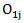 has a hypergeometric distribution with parameters
has a hypergeometric distribution with parameters 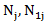 and
and 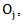 whose expectation
whose expectation 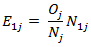 and the variance
and the variance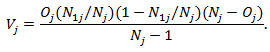 The regular log rank test statistic is given by
The regular log rank test statistic is given by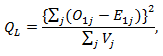 which follows a
which follows a 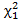 distribution under null hypothesis. Extensions of the regular log rank test have been developed to increase power under specific circumstances. The extension is done via weighing each period
distribution under null hypothesis. Extensions of the regular log rank test have been developed to increase power under specific circumstances. The extension is done via weighing each period 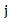 by a factor
by a factor 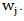 Specifically, the weighted log rank test statistic is given by
Specifically, the weighted log rank test statistic is given by in which the weight function
in which the weight function 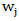 is assumed to be non-increasing. Below is a table that lists some commonly used weight functions.
is assumed to be non-increasing. Below is a table that lists some commonly used weight functions.Table 1. Commonly Used Weighted Log-rank Tests
 |
| |
|
Under null hypothesis, 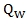 also follows a
also follows a 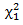 distribution. The log-rank test can be considered as a special case of the weighted log rank test by setting
distribution. The log-rank test can be considered as a special case of the weighted log rank test by setting 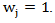
2.1.2. Rank-preserving Structural Nested Failure Time (RPSFT) Models
The RPSFT model relates 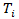 to a potential outcome
to a potential outcome 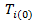 that would have been observed without treatment through a treatment effect [6]. Consider a simple rank-preserving structural nested failure time (RPSFT) model [6,8], which links potentially counterfactual
that would have been observed without treatment through a treatment effect [6]. Consider a simple rank-preserving structural nested failure time (RPSFT) model [6,8], which links potentially counterfactual 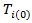 with observable
with observable 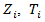 and
and 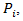
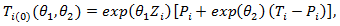 Where
Where 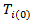 : is the counterfactual survival time of patient
: is the counterfactual survival time of patient 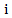 in control arm and never received secondary treatment,
in control arm and never received secondary treatment, 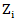 is the randomized primary treatment which equals 1 if in treatment arm and
is the randomized primary treatment which equals 1 if in treatment arm and 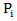 is the moment when secondary treatment is initiated if ever given, time of death otherwise. The distribution of counterfactual survival time should be independent of
is the moment when secondary treatment is initiated if ever given, time of death otherwise. The distribution of counterfactual survival time should be independent of 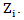 As a result, there should be no significant difference across the two primary treatment arms based on log-rank test. Following model described in [6,8], the log-rank test statistic would be bivariate
As a result, there should be no significant difference across the two primary treatment arms based on log-rank test. Following model described in [6,8], the log-rank test statistic would be bivariate
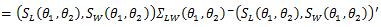 where
where 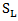 denotes log-rank score,
denotes log-rank score, 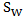 is the Prentice-Wilcoxon log-rank score, and
is the Prentice-Wilcoxon log-rank score, and 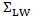 is the joint estimated covariance matrix applied to the data
is the joint estimated covariance matrix applied to the data 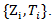 Under the null hypothesis,
Under the null hypothesis, 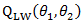 follows a
follows a 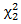 distribution. Unlike the case in treatment crossover [4] in which a regular log rank test statistic
distribution. Unlike the case in treatment crossover [4] in which a regular log rank test statistic 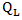 was used, it is important to employ two distinct log rank tests. Using only one log rank test can introduce identifiability issue since there are two parameters
was used, it is important to employ two distinct log rank tests. Using only one log rank test can introduce identifiability issue since there are two parameters 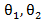 to be estimated. The estimated coefficients
to be estimated. The estimated coefficients 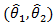 can be obtained by solving for
can be obtained by solving for 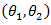 that minimizes bivariate log rank test statistic
that minimizes bivariate log rank test statistic 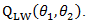 In term of finding the minimizer, the naïve grid search root finding method is usually inefficient and computational intensive. In order to increase computational efficiency, here we employ the Frank-Wolfe non-linear optimization method to find estimates. Note that the bivariate log-rank statistics is a complex function, which does not have closed form gradient, and the Frank-Wolfe optimization method does not require gradient.
In term of finding the minimizer, the naïve grid search root finding method is usually inefficient and computational intensive. In order to increase computational efficiency, here we employ the Frank-Wolfe non-linear optimization method to find estimates. Note that the bivariate log-rank statistics is a complex function, which does not have closed form gradient, and the Frank-Wolfe optimization method does not require gradient.
2.2. Marginal Structure Cox Models
Marginal structural Cox models [2] was first proposed to draw valid causal inference from observational studies, in which the assignment of treatment and control/placebo is nonrandom and time-dependent treatment in the presence of confounders. The idea of marginal structure model is to inversely weigh each observation by the probability of receiving the treatment. Through the inverse probability of treatment weighting (IPTW), we create a pseudo-population in which the distributions of covariates are similar between two treatment groups and we can draw causal inference from the pseudo-population. We consider the marginal structural Cox model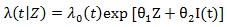 where
where  represents the treatment and
represents the treatment and 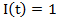 if secondary treatment is initiated at time
if secondary treatment is initiated at time 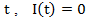 otherwise. In the model, each observation is weighted by
otherwise. In the model, each observation is weighted by 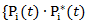 , where
, where 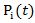 corresponds to probability of receiving secondary treatment at time t, and
corresponds to probability of receiving secondary treatment at time t, and 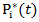 corresponds to uncensored probability at time t. Patients who have a extremely small probability of receiving secondary treatment will contribute a huge number of copies in the pseudo-population when taking the inverse of the weight. Therefore, parameter estimates may become highly unstable and have large variability. To overcome this issue, we use stabilized weights
corresponds to uncensored probability at time t. Patients who have a extremely small probability of receiving secondary treatment will contribute a huge number of copies in the pseudo-population when taking the inverse of the weight. Therefore, parameter estimates may become highly unstable and have large variability. To overcome this issue, we use stabilized weights 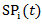 and
and 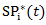 , respectively.In practice, the weights
, respectively.In practice, the weights 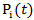 can be estimated by fitting a Cox model that models the initiation of secondary treatment as an outcome. In the Cox model, we include both baseline and time-dependent covariates that potentially affects the initiation of secondary treatment. For example, when we estimate
can be estimated by fitting a Cox model that models the initiation of secondary treatment as an outcome. In the Cox model, we include both baseline and time-dependent covariates that potentially affects the initiation of secondary treatment. For example, when we estimate 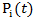 in the treatment group where
in the treatment group where 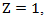 we fit the model
we fit the model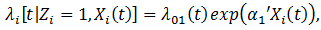 where
where  is a set of baseline and time-dependent covariates that are related to the initiation of secondary treatment and
is a set of baseline and time-dependent covariates that are related to the initiation of secondary treatment and 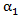 is the coefficient vector for
is the coefficient vector for 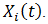 If patient
If patient 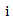 did not start secondary treatment at time t, then the estimated probability
did not start secondary treatment at time t, then the estimated probability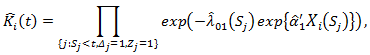 where
where 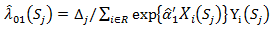 is the Breslow estimator of the baseline hazard in treatment arm and
is the Breslow estimator of the baseline hazard in treatment arm and  is the at-risk indicator. On the other hand, if the patient started secondary treatment, then the estimated probability at time
is the at-risk indicator. On the other hand, if the patient started secondary treatment, then the estimated probability at time 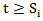 is
is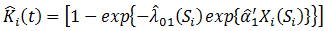
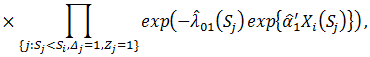 and we have estimated weight
and we have estimated weight 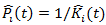 . The stabilized weights can be obtained by repeating the above procedure with the covariates
. The stabilized weights can be obtained by repeating the above procedure with the covariates 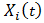 removed from the Cox model and get estimated probabilities
removed from the Cox model and get estimated probabilities 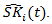 Then the stabilized weight
Then the stabilized weight 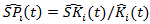 . We can also estimate the weights corresponding to censoring,
. We can also estimate the weights corresponding to censoring, 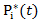 and
and 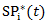 by the similar procedure. One important assumption for marginal structural model is all possible confounders must be included when estimating the weights. Obviously, there is no way to test this assumption. Therefore, it is recommended to include as many covariates in
by the similar procedure. One important assumption for marginal structural model is all possible confounders must be included when estimating the weights. Obviously, there is no way to test this assumption. Therefore, it is recommended to include as many covariates in 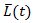 as possible in practice.
as possible in practice.
3. A Simulation Study
3.1. Data Generation
Now we present some results obtained from an extensive simulation study conducted to assess the performance of the estimation procedures proposed in the previous sections. For simplicity, we assume that the survival time and the initiation time of the secondary treatment follow exponential distributions. In specific, denote 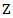 as the randomized primary treatment indicator, we generate the initiation time of the secondary treatment from the exponential distribution
as the randomized primary treatment indicator, we generate the initiation time of the secondary treatment from the exponential distribution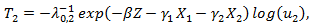 where
where 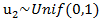 and
and 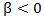 so that primary treatment is beneficial on PFS.
so that primary treatment is beneficial on PFS. 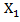 followed a Bernoulli distribution with probability 0.5, and
followed a Bernoulli distribution with probability 0.5, and  was a standard normal random variable. We then generated the counterfactual survival time if the subject never received secondary treatment
was a standard normal random variable. We then generated the counterfactual survival time if the subject never received secondary treatment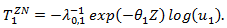 We then generate
We then generate 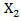 from a normal distribution that is related to both
from a normal distribution that is related to both  and
and 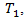 and hence
and hence 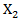 is a confounder. A time-dependent variable
is a confounder. A time-dependent variable 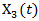 was also generated based on a Gaussian process.Suppose that the secondary treatment was initiated at time V, we generated the observable survival time in the presence of secondary treatment via
was also generated based on a Gaussian process.Suppose that the secondary treatment was initiated at time V, we generated the observable survival time in the presence of secondary treatment via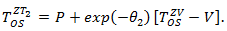 Note that
Note that 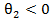 which indicated a beneficial secondary treatment. It can be seen that secondary treatment prolonged the remaining life from
which indicated a beneficial secondary treatment. It can be seen that secondary treatment prolonged the remaining life from 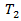 by a factor of
by a factor of  . Note the expression for
. Note the expression for 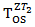 holds only when
holds only when 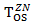 has an exponential distribution. We assume the censoring time for survival time and secondary treatment initiation time follow two independent uniform distributions. The patients entered the study at the rate of 34 per month, for 24 month. The total sample size was 816. The final analysis is conducted when we observed 451 deaths.
has an exponential distribution. We assume the censoring time for survival time and secondary treatment initiation time follow two independent uniform distributions. The patients entered the study at the rate of 34 per month, for 24 month. The total sample size was 816. The final analysis is conducted when we observed 451 deaths.
3.2. Models and Results
We compared the estimation of the treatment effects from the following four different models in our simulation study: (1) Cox proportional hazards model with only primary treatment, which ignores secondary treatment.(2) Cox proportional hazards model with both primary treatment and time-dependent secondary treatment, but ignores a confounder 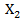 which affects both initiation of secondary treatment and survival time. In specific,
which affects both initiation of secondary treatment and survival time. In specific, 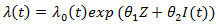 where
where 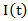 equals 1 if subject is on secondary treatment at time , 0 otherwise. (3) RPSFT model. We set the starting value for the Frank-Wolfe optimization process to be
equals 1 if subject is on secondary treatment at time , 0 otherwise. (3) RPSFT model. We set the starting value for the Frank-Wolfe optimization process to be 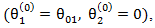 where
where 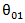 is the estimated by the Cox model with time-dependent secondary treatment. (4) Marginal structural model whose form is the same with time-dependent Cox model (2). Using inverse probability of treatment weighting (IPTW), each observation is weighted by the inverse probability estimated by fitting Cox models with covariates
is the estimated by the Cox model with time-dependent secondary treatment. (4) Marginal structural model whose form is the same with time-dependent Cox model (2). Using inverse probability of treatment weighting (IPTW), each observation is weighted by the inverse probability estimated by fitting Cox models with covariates 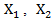 and
and 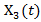 . We also computed stabilized weights to control for extreme weights. Note that in the data generating step,
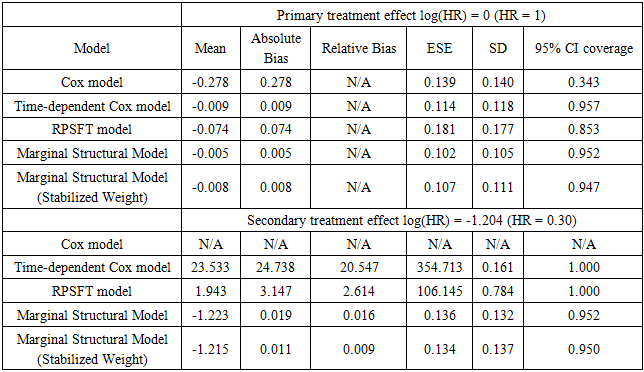
. We also computed stabilized weights to control for extreme weights. Note that in the data generating step, 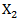 is a confounder that relates to both survival time and initiation time of the secondary treatment. Therefore, the model was misspecified and by doing so we are also able to assess the robustness of the marginal structural model towards model misspecification.Tables 2 and 3 gives the summarized simulation results. Table 3 considered the situation when primary treatment was efficacious, table 2 studied the situation when there was no primary treatment effect. One can see from the table that when secondary treatment was highly effective compared to the primary treatment (table 2), ignoring the secondary treatment can introduce large amount of bias. In addition, Cox model with time-dependent secondary treatment showed accurate estimate of primary treatment, but the estimate of secondary treatment was very inaccurate. The RPSFT model also yielded accurate primary treatment estimate, and failed to estimate secondary treatment correctly. Furthermore, marginal structural model yielded was able to estimate both primary and secondary treatment quite accurately; and it was robust to model misspecification.
is a confounder that relates to both survival time and initiation time of the secondary treatment. Therefore, the model was misspecified and by doing so we are also able to assess the robustness of the marginal structural model towards model misspecification.Tables 2 and 3 gives the summarized simulation results. Table 3 considered the situation when primary treatment was efficacious, table 2 studied the situation when there was no primary treatment effect. One can see from the table that when secondary treatment was highly effective compared to the primary treatment (table 2), ignoring the secondary treatment can introduce large amount of bias. In addition, Cox model with time-dependent secondary treatment showed accurate estimate of primary treatment, but the estimate of secondary treatment was very inaccurate. The RPSFT model also yielded accurate primary treatment estimate, and failed to estimate secondary treatment correctly. Furthermore, marginal structural model yielded was able to estimate both primary and secondary treatment quite accurately; and it was robust to model misspecification. Table 2. Effective Primary Treatment
 |
| |
|
Table 3. Ineffective Primary Treatment
 |
| |
|
4. An Application
Now we apply the methods proposed in the previous sections to clinical trial for non-small tumor lung cancer. It was a randomized, double-blinded, multicenter phase III study in patients with lung cancer receiving Cisplatin (control) vs Vinorelbine/Cisplatin combination (experimental). The median survival time and initiation time of the secondary treatment in months are summarized in table 4. Table 4. Median Survival and Secondary Treatment Initiation Time
 |
| |
|
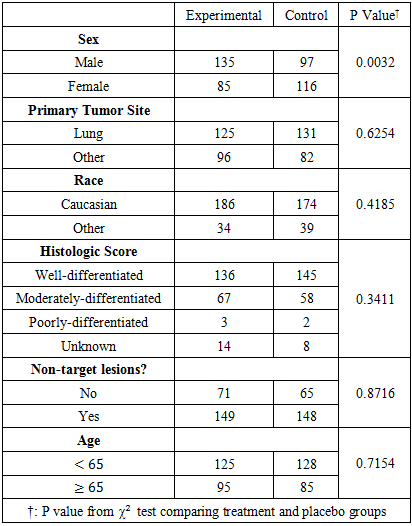
In the marginal structural Cox model, we included six baseline covariates that are potentially linked to the initiation time of the secondary treatment. Further, we examined the distributions of those covariates (table 5). We can see that randomization is doing a good job in balancing the covariate distributions in treatment and placebo groups. The distribution of covariates were balanced in both control and experimental groups except for sex, where there were more males in the experimental group. Table 5. Distribution of Patients’ Baseline Covariates
 |
| |
|
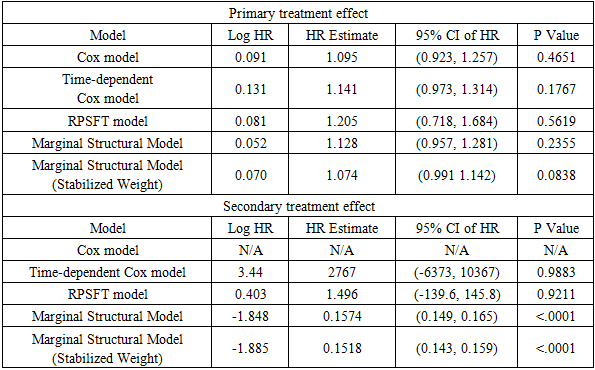
The survival data was analyzed by five models: (1) Cox model ignoring secondary treatment; (2) time-dependent Cox model; (3) RPSFT model with Frank-Wolfe optimization root-finding; (4) Marginal structural model with non-stabilized weight; (5) Marginal structural model with stabilized weight. Results are summarized in table 5. In addition, we computed descriptive statistics of stabilized and non-stabilized weights in MSM (table 6). We can see that non-stabilized weights have a much larger maximum (613.581) compared with the maximum (1.684) of stabilized weights. Therefore, the stabilizing process was able to eliminate extreme large weights. Table 6. Weights in Marginal Structural Model
 |
| |
|
Table 7. Estimates and Confidence Intervals
 |
| |
|
The primary treatment was shown to be ineffective on prolonging survival time by all five models. Only marginal structural model with stabilized weights detected a significant primary treatment effect. As for the secondary treatment effect, time-dependent Cox model and RPSFT models gave unreliable estimates, and the confidence intervals were too wide. A similar phenomenon was also observed by other studies [7]. One possible explanation of RPSFT models’ unreliability to estimate secondary treatment effect can be seen via the surface plot (figure 1): there seemed to be a flat valley of 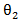 values along the section
values along the section 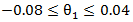 where the bivariate log-rank test statistic had uniformly small values. Therefore, the global minimum of the log-rank test statistic is hard to locate. On the other hand, the two marginal structural models yielded more reasonable estimate, indicating that the secondary treatment was highly effective.
where the bivariate log-rank test statistic had uniformly small values. Therefore, the global minimum of the log-rank test statistic is hard to locate. On the other hand, the two marginal structural models yielded more reasonable estimate, indicating that the secondary treatment was highly effective.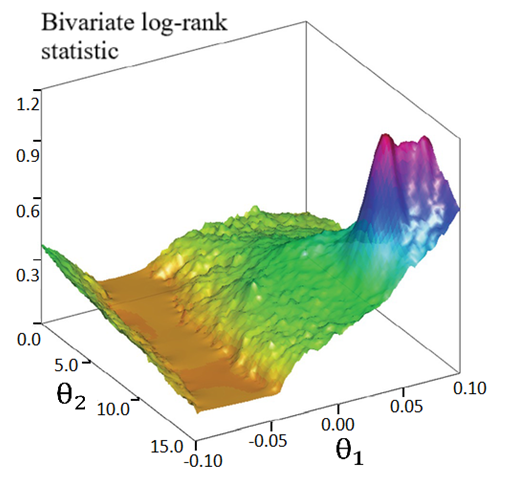 | Figure 1. Surface plot of bivariate log-rank statistic on a grid of  |
5. Conclusions
In this paper, we considered two types of structural models, structural nested failure time (RPSFT) models and marginal structural models, to draw valid causal inference with the presence of secondary salvage treatment. Comparing the results with time-dependent Cox model and marginal structural model, we notice that they both yielded accurate primary treatment effect estimates. However, the implementation of marginal structural model is much more sophisticated than that of time-dependent Cox model. The choice between time-dependent Cox model and marginal structural model depends upon whether the secondary treatment effect is of interest. On the other hand, we should chose marginal structural model when we are interested in the secondary treatment effect. Furthermore, when an Accelerated Failure Time (AFT) model is preferred, we should chose RPSFT model to obtain valid estimates of primary treatment effect. However, since RPSFT models ignore the confounders that relate to both initiation of secondary treatment and survival time, it usually fails to give accurate secondary treatment effect estimate. An extension of this model [9] was proposed to take care of this issue. Unfortunately, it did not seem to work with another study [10] since the confidence interval for  was still too wide to be reliable. In summary, time-dependent Cox model, marginal structural or RPSFT model yield correct primary treatment effect estimate. However, only marginal structural model is able to estimate secondary treatment effect accurately. More work is needed to develop an extension of RPSFT model to provide more reliable estimate of secondary treatment effect.
was still too wide to be reliable. In summary, time-dependent Cox model, marginal structural or RPSFT model yield correct primary treatment effect estimate. However, only marginal structural model is able to estimate secondary treatment effect accurately. More work is needed to develop an extension of RPSFT model to provide more reliable estimate of secondary treatment effect.
ACKNOWLEDGEMENTS
The authors are grateful to the anonymous referee for their beneficial and accurate comments that improved this paper.
References
| [1] | M. Rosenblum, N. P. Jewell, M. van der Laan, S. Shiboski, A. van der Straten, N. Padian. (2009) Analysing direct effects in randomized trials with secondary interventions: an application to human immunodeficiency virus prevention trials. Journal of the Royal Statistical Society. Series A, (Statistics in Society), 172, 443-465. |
| [2] | M. A. Hernan, B. Brumback and J. M. Robins. (2000) Marginal structural models to estimate the causal effect of zidovudine on the survival of HIV-positive men. Epidemiology, 11(5), 561-570. |
| [3] | M. A. Hernan, B. Brumback and J. M. Robins. (2001) Marginal structural models to estimate the joint causal effect of nonrandomized treatments. Journal of the American Statistical Association, 96 (454), 440-448. |
| [4] | M. A. Hernan, S. Cole, J. Margolick, M. Cohen and J. M. Robins. (2005) Structural accelerated failure time models for survival analysis in studies with time-varying treatments. Pharmacoepidemiology and Drug Safety, 14, 477-491. |
| [5] | M. M. Joffe, W. P. Yang and H. Feldman. (2012) G-estimation and artificial censoring: Problems, challenges, and applications. Biometrics 68 (1): 275-286. |
| [6] | J. M. Robins, A. A. Tsiatis. (1991) Correcting for non-compliance in randomized trials using rank preserving structural failure time models. Communications in Statistics - Theory and Methods 20(8): 2609–2631. |
| [7] | J. M. Robins and S. Greenland. (1994) Adjusting for differential rates of prophylaxis therapy for PCP in high-versus low-dose AZT treatment arms in an AIDS randomized trial. Journal of the American Statistical Association, 89 (427), 737-749. |
| [8] | L. J. WEI, Z. YING and D. Y. LIN. (1990) Linear regression analysis of censored survival data based on rank tests. Biometrika, 77(4), 845-851. |
| [9] | T. Yamaguchi and Y. Ohashi. (2004) Adjusting for differential proportions of second-line treatment in cancer clinical trials. Statistics in Medicine, 23(13), 1991-2003. |
| [10] | T. Yamaguchi and Y. Ohashi. (2004) Adjusting for differential proportions of second-line treatment in cancer clinical trials. part II: An application in a clinical trial of unresectable non-small-cell lung cancer. Statistics in Medicine, 23 (13): 2005-2022. |



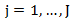 be the distinct observed failure times. For each time
be the distinct observed failure times. For each time 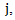 let
let 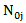 and
and 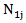 be the number of subjects at risk at the start of period
be the number of subjects at risk at the start of period 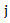 in the treatment and control arm, respectively. Let
in the treatment and control arm, respectively. Let 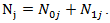 Let
Let 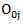 and
and 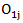 be the observed number of events in the arms respectively, and define
be the observed number of events in the arms respectively, and define 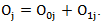 Conditional on
Conditional on 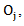 the quantity
the quantity 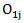 has a hypergeometric distribution with parameters
has a hypergeometric distribution with parameters 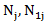 and
and 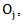 whose expectation
whose expectation 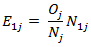 and the variance
and the variance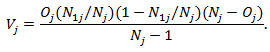 The regular log rank test statistic is given by
The regular log rank test statistic is given by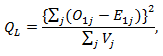 which follows a
which follows a 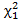 distribution under null hypothesis. Extensions of the regular log rank test have been developed to increase power under specific circumstances. The extension is done via weighing each period
distribution under null hypothesis. Extensions of the regular log rank test have been developed to increase power under specific circumstances. The extension is done via weighing each period 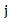 by a factor
by a factor 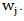 Specifically, the weighted log rank test statistic is given by
Specifically, the weighted log rank test statistic is given by in which the weight function
in which the weight function 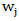 is assumed to be non-increasing. Below is a table that lists some commonly used weight functions.
is assumed to be non-increasing. Below is a table that lists some commonly used weight functions.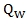 also follows a
also follows a 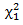 distribution. The log-rank test can be considered as a special case of the weighted log rank test by setting
distribution. The log-rank test can be considered as a special case of the weighted log rank test by setting 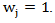
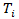 to a potential outcome
to a potential outcome 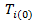 that would have been observed without treatment through a treatment effect [6]. Consider a simple rank-preserving structural nested failure time (RPSFT) model [6,8], which links potentially counterfactual
that would have been observed without treatment through a treatment effect [6]. Consider a simple rank-preserving structural nested failure time (RPSFT) model [6,8], which links potentially counterfactual 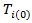 with observable
with observable 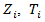 and
and 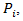
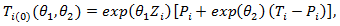 Where
Where 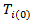 : is the counterfactual survival time of patient
: is the counterfactual survival time of patient 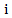 in control arm and never received secondary treatment,
in control arm and never received secondary treatment, 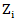 is the randomized primary treatment which equals 1 if in treatment arm and
is the randomized primary treatment which equals 1 if in treatment arm and 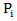 is the moment when secondary treatment is initiated if ever given, time of death otherwise. The distribution of counterfactual survival time should be independent of
is the moment when secondary treatment is initiated if ever given, time of death otherwise. The distribution of counterfactual survival time should be independent of 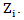 As a result, there should be no significant difference across the two primary treatment arms based on log-rank test. Following model described in [6,8], the log-rank test statistic would be bivariate
As a result, there should be no significant difference across the two primary treatment arms based on log-rank test. Following model described in [6,8], the log-rank test statistic would be bivariate
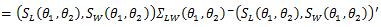 where
where 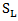 denotes log-rank score,
denotes log-rank score, 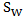 is the Prentice-Wilcoxon log-rank score, and
is the Prentice-Wilcoxon log-rank score, and 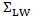 is the joint estimated covariance matrix applied to the data
is the joint estimated covariance matrix applied to the data 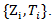 Under the null hypothesis,
Under the null hypothesis, 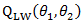 follows a
follows a 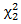 distribution. Unlike the case in treatment crossover [4] in which a regular log rank test statistic
distribution. Unlike the case in treatment crossover [4] in which a regular log rank test statistic 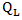 was used, it is important to employ two distinct log rank tests. Using only one log rank test can introduce identifiability issue since there are two parameters
was used, it is important to employ two distinct log rank tests. Using only one log rank test can introduce identifiability issue since there are two parameters 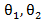 to be estimated. The estimated coefficients
to be estimated. The estimated coefficients 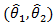 can be obtained by solving for
can be obtained by solving for 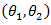 that minimizes bivariate log rank test statistic
that minimizes bivariate log rank test statistic 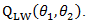 In term of finding the minimizer, the naïve grid search root finding method is usually inefficient and computational intensive. In order to increase computational efficiency, here we employ the Frank-Wolfe non-linear optimization method to find estimates. Note that the bivariate log-rank statistics is a complex function, which does not have closed form gradient, and the Frank-Wolfe optimization method does not require gradient.
In term of finding the minimizer, the naïve grid search root finding method is usually inefficient and computational intensive. In order to increase computational efficiency, here we employ the Frank-Wolfe non-linear optimization method to find estimates. Note that the bivariate log-rank statistics is a complex function, which does not have closed form gradient, and the Frank-Wolfe optimization method does not require gradient.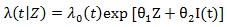 where
where  represents the treatment and
represents the treatment and 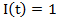 if secondary treatment is initiated at time
if secondary treatment is initiated at time 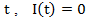 otherwise. In the model, each observation is weighted by
otherwise. In the model, each observation is weighted by 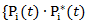 , where
, where 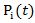 corresponds to probability of receiving secondary treatment at time t, and
corresponds to probability of receiving secondary treatment at time t, and 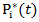 corresponds to uncensored probability at time t. Patients who have a extremely small probability of receiving secondary treatment will contribute a huge number of copies in the pseudo-population when taking the inverse of the weight. Therefore, parameter estimates may become highly unstable and have large variability. To overcome this issue, we use stabilized weights
corresponds to uncensored probability at time t. Patients who have a extremely small probability of receiving secondary treatment will contribute a huge number of copies in the pseudo-population when taking the inverse of the weight. Therefore, parameter estimates may become highly unstable and have large variability. To overcome this issue, we use stabilized weights 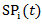 and
and 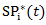 , respectively.In practice, the weights
, respectively.In practice, the weights 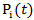 can be estimated by fitting a Cox model that models the initiation of secondary treatment as an outcome. In the Cox model, we include both baseline and time-dependent covariates that potentially affects the initiation of secondary treatment. For example, when we estimate
can be estimated by fitting a Cox model that models the initiation of secondary treatment as an outcome. In the Cox model, we include both baseline and time-dependent covariates that potentially affects the initiation of secondary treatment. For example, when we estimate 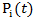 in the treatment group where
in the treatment group where 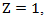 we fit the model
we fit the model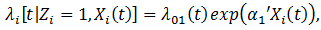 where
where  is a set of baseline and time-dependent covariates that are related to the initiation of secondary treatment and
is a set of baseline and time-dependent covariates that are related to the initiation of secondary treatment and 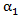 is the coefficient vector for
is the coefficient vector for 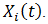 If patient
If patient 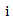 did not start secondary treatment at time t, then the estimated probability
did not start secondary treatment at time t, then the estimated probability where
where  is the Breslow estimator of the baseline hazard in treatment arm and
is the Breslow estimator of the baseline hazard in treatment arm and  is the at-risk indicator. On the other hand, if the patient started secondary treatment, then the estimated probability at time
is the at-risk indicator. On the other hand, if the patient started secondary treatment, then the estimated probability at time  is
is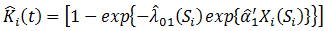
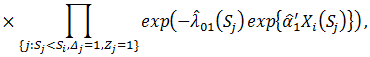 and we have estimated weight
and we have estimated weight 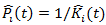 . The stabilized weights can be obtained by repeating the above procedure with the covariates
. The stabilized weights can be obtained by repeating the above procedure with the covariates 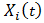 removed from the Cox model and get estimated probabilities
removed from the Cox model and get estimated probabilities 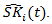 Then the stabilized weight
Then the stabilized weight 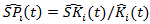 . We can also estimate the weights corresponding to censoring,
. We can also estimate the weights corresponding to censoring, 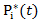 and
and 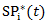 by the similar procedure. One important assumption for marginal structural model is all possible confounders must be included when estimating the weights. Obviously, there is no way to test this assumption. Therefore, it is recommended to include as many covariates in
by the similar procedure. One important assumption for marginal structural model is all possible confounders must be included when estimating the weights. Obviously, there is no way to test this assumption. Therefore, it is recommended to include as many covariates in 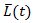 as possible in practice.
as possible in practice. 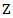 as the randomized primary treatment indicator, we generate the initiation time of the secondary treatment from the exponential distribution
as the randomized primary treatment indicator, we generate the initiation time of the secondary treatment from the exponential distribution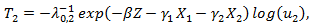 where
where 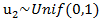 and
and 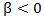 so that primary treatment is beneficial on PFS.
so that primary treatment is beneficial on PFS.  followed a Bernoulli distribution with probability 0.5, and
followed a Bernoulli distribution with probability 0.5, and  was a standard normal random variable. We then generated the counterfactual survival time if the subject never received secondary treatment
was a standard normal random variable. We then generated the counterfactual survival time if the subject never received secondary treatment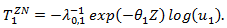 We then generate
We then generate  from a normal distribution that is related to both
from a normal distribution that is related to both  and
and 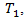 and hence
and hence 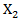 is a confounder. A time-dependent variable
is a confounder. A time-dependent variable 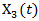 was also generated based on a Gaussian process.Suppose that the secondary treatment was initiated at time V, we generated the observable survival time in the presence of secondary treatment via
was also generated based on a Gaussian process.Suppose that the secondary treatment was initiated at time V, we generated the observable survival time in the presence of secondary treatment via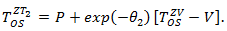 Note that
Note that 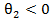 which indicated a beneficial secondary treatment. It can be seen that secondary treatment prolonged the remaining life from
which indicated a beneficial secondary treatment. It can be seen that secondary treatment prolonged the remaining life from 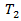 by a factor of
by a factor of  . Note the expression for
. Note the expression for 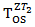 holds only when
holds only when 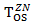 has an exponential distribution. We assume the censoring time for survival time and secondary treatment initiation time follow two independent uniform distributions. The patients entered the study at the rate of 34 per month, for 24 month. The total sample size was 816. The final analysis is conducted when we observed 451 deaths.
has an exponential distribution. We assume the censoring time for survival time and secondary treatment initiation time follow two independent uniform distributions. The patients entered the study at the rate of 34 per month, for 24 month. The total sample size was 816. The final analysis is conducted when we observed 451 deaths. 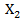 which affects both initiation of secondary treatment and survival time. In specific,
which affects both initiation of secondary treatment and survival time. In specific, 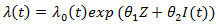 where
where 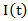 equals 1 if subject is on secondary treatment at time , 0 otherwise. (3) RPSFT model. We set the starting value for the Frank-Wolfe optimization process to be
equals 1 if subject is on secondary treatment at time , 0 otherwise. (3) RPSFT model. We set the starting value for the Frank-Wolfe optimization process to be 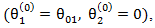 where
where 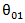 is the estimated by the Cox model with time-dependent secondary treatment. (4) Marginal structural model whose form is the same with time-dependent Cox model (2). Using inverse probability of treatment weighting (IPTW), each observation is weighted by the inverse probability estimated by fitting Cox models with covariates
is the estimated by the Cox model with time-dependent secondary treatment. (4) Marginal structural model whose form is the same with time-dependent Cox model (2). Using inverse probability of treatment weighting (IPTW), each observation is weighted by the inverse probability estimated by fitting Cox models with covariates 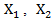 and
and 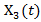 . We also computed stabilized weights to control for extreme weights. Note that in the data generating step,
. We also computed stabilized weights to control for extreme weights. Note that in the data generating step, 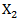 is a confounder that relates to both survival time and initiation time of the secondary treatment. Therefore, the model was misspecified and by doing so we are also able to assess the robustness of the marginal structural model towards model misspecification.Tables 2 and 3 gives the summarized simulation results. Table 3 considered the situation when primary treatment was efficacious, table 2 studied the situation when there was no primary treatment effect. One can see from the table that when secondary treatment was highly effective compared to the primary treatment (table 2), ignoring the secondary treatment can introduce large amount of bias. In addition, Cox model with time-dependent secondary treatment showed accurate estimate of primary treatment, but the estimate of secondary treatment was very inaccurate. The RPSFT model also yielded accurate primary treatment estimate, and failed to estimate secondary treatment correctly. Furthermore, marginal structural model yielded was able to estimate both primary and secondary treatment quite accurately; and it was robust to model misspecification.
is a confounder that relates to both survival time and initiation time of the secondary treatment. Therefore, the model was misspecified and by doing so we are also able to assess the robustness of the marginal structural model towards model misspecification.Tables 2 and 3 gives the summarized simulation results. Table 3 considered the situation when primary treatment was efficacious, table 2 studied the situation when there was no primary treatment effect. One can see from the table that when secondary treatment was highly effective compared to the primary treatment (table 2), ignoring the secondary treatment can introduce large amount of bias. In addition, Cox model with time-dependent secondary treatment showed accurate estimate of primary treatment, but the estimate of secondary treatment was very inaccurate. The RPSFT model also yielded accurate primary treatment estimate, and failed to estimate secondary treatment correctly. Furthermore, marginal structural model yielded was able to estimate both primary and secondary treatment quite accurately; and it was robust to model misspecification. 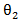 values along the section
values along the section 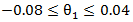 where the bivariate log-rank test statistic had uniformly small values. Therefore, the global minimum of the log-rank test statistic is hard to locate. On the other hand, the two marginal structural models yielded more reasonable estimate, indicating that the secondary treatment was highly effective.
where the bivariate log-rank test statistic had uniformly small values. Therefore, the global minimum of the log-rank test statistic is hard to locate. On the other hand, the two marginal structural models yielded more reasonable estimate, indicating that the secondary treatment was highly effective.
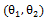
 was still too wide to be reliable. In summary, time-dependent Cox model, marginal structural or RPSFT model yield correct primary treatment effect estimate. However, only marginal structural model is able to estimate secondary treatment effect accurately. More work is needed to develop an extension of RPSFT model to provide more reliable estimate of secondary treatment effect.
was still too wide to be reliable. In summary, time-dependent Cox model, marginal structural or RPSFT model yield correct primary treatment effect estimate. However, only marginal structural model is able to estimate secondary treatment effect accurately. More work is needed to develop an extension of RPSFT model to provide more reliable estimate of secondary treatment effect. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML





