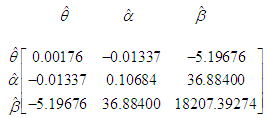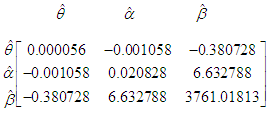Rama Shanker1, Kamlesh Kumar Shukla1, Tekie Asehun Leonida2
1Department of Statistics, Eritrea Institute of Technology, Asmara, Eritrea
2Department of Applied Mathematics, University of Twente, The Netherlands
Correspondence to: Rama Shanker, Department of Statistics, Eritrea Institute of Technology, Asmara, Eritrea.
| Email: |  |
Copyright © 2019 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
In this paper, a generalization of two-parameter Lindley distribution (GTPLD), which includes one parameter exponential and Lindley distributions, two-parameter Lindley distribution (TPLD) of Shanker and Mishra (2013), Weibull distribution, gamma distribution, generalized gamma distribution of Stacy (1962) and power Lindley distribution of Ghitany et al (2013) as particular cases, has been proposed. Its moments, hazard rate function, mean residual life function, order statistic, Renyi entropy measure has been studied. Method of maximum likelihood estimation has been discussed for estimating its parameters. Applications of the distribution have been explained with two examples of observed real lifetime datasets.
Keywords:
Two-parameter Lindley distribution, Moments, Hazard rate function, Mean residual life function, Order statistic, Renyi entropy measure, Maximum likelihood estimation, Applications
Cite this paper: Rama Shanker, Kamlesh Kumar Shukla, Tekie Asehun Leonida, A Generalization of Two-Parameter Lindley Distribution with Properties and Applications, International Journal of Probability and Statistics , Vol. 8 No. 1, 2019, pp. 1-13. doi: 10.5923/j.ijps.20190801.01.
1. Introduction
Shanker and Mishra (2013) introduced a two-parameter Lindley distribution (TPLD) defined by its probability density function (pdf) and cumulative distribution function (cdf)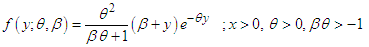 | (1.1) |
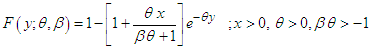 | (1.2) |
The pdf (1.1) can be expressed as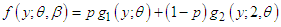 where
where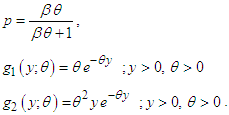 Clearly the density (1.1) is a two-component mixture of an exponential distribution with scale parameter
Clearly the density (1.1) is a two-component mixture of an exponential distribution with scale parameter 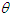 and a gamma distribution with shape parameter 2 and scale parameter
and a gamma distribution with shape parameter 2 and scale parameter 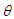 , with mixing proportion
, with mixing proportion 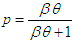 . Shanker and Mishra (2013) studied its various properties including coefficients of variation, skewness, kurtosis; hazard rate function, mean residual life function and stochastic ordering. The estimation of its parameters using both the maximum likelihood estimation and the method of moments along with applications of TPLD to model lifetime data has also been discussed by Shanker and Mishra (2013). It can be easily shown that Lindley distribution, introduced by Lindley (1958), having pdf
. Shanker and Mishra (2013) studied its various properties including coefficients of variation, skewness, kurtosis; hazard rate function, mean residual life function and stochastic ordering. The estimation of its parameters using both the maximum likelihood estimation and the method of moments along with applications of TPLD to model lifetime data has also been discussed by Shanker and Mishra (2013). It can be easily shown that Lindley distribution, introduced by Lindley (1958), having pdf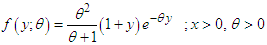 | (1.3) |
is a particular case of TPLD (1.1) at 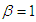 . Lindley distribution has been studied in detail by Ghitany et al (2008). Shanker et al (2015) have detailed and critical study on applications of exponential and Lindley distribution for modeling real lifetime data from biomedical sciences and engineering and observed that both exponential and Lindley are competing each other. Shanker et al (2016) have discussion on applications of gamma distribution and Weibull distribution for real lifetime data from engineering and biological sciences. Shanker (2016) has discussed various important statistical properties including coefficient of variation, skewness, kurtosis and index of dispersion along with various applications of generalized Lindley distribution (GLD) introduced by Zakerzadeh and Dolati (2009). Shanker and Shukla (2016) have detailed comparative study on applications of three-parameter generalized gamma distribution (GGD) and generalized Lindley distribution (GLD) and observed that these two distributions are competing each other for modeling lifetime data.In this paper, an attempt has been made to derive a generalization of two-parameter Lindley distribution (GTPLD), which includes one parameter exponential and Lindley distributions, two-parameter Lindley distribution (TPLD) of Shanker and Mishra (2013), Weibull distribution, gamma distribution, generalized gamma distribution of Stacy (1962) and power Lindley distribution of Ghitany et al (2013) as particular cases. The moments, hazard rate function, mean residual life function, order statistic and Renyi entropy measure of the distribution have been studied. Method of maximum likelihood estimation has been discussed for estimating its parameters. Applications of the distribution have been explained with two examples of observed real lifetime datasets and its goodness of fit has been compared with other lifetime distributions.
. Lindley distribution has been studied in detail by Ghitany et al (2008). Shanker et al (2015) have detailed and critical study on applications of exponential and Lindley distribution for modeling real lifetime data from biomedical sciences and engineering and observed that both exponential and Lindley are competing each other. Shanker et al (2016) have discussion on applications of gamma distribution and Weibull distribution for real lifetime data from engineering and biological sciences. Shanker (2016) has discussed various important statistical properties including coefficient of variation, skewness, kurtosis and index of dispersion along with various applications of generalized Lindley distribution (GLD) introduced by Zakerzadeh and Dolati (2009). Shanker and Shukla (2016) have detailed comparative study on applications of three-parameter generalized gamma distribution (GGD) and generalized Lindley distribution (GLD) and observed that these two distributions are competing each other for modeling lifetime data.In this paper, an attempt has been made to derive a generalization of two-parameter Lindley distribution (GTPLD), which includes one parameter exponential and Lindley distributions, two-parameter Lindley distribution (TPLD) of Shanker and Mishra (2013), Weibull distribution, gamma distribution, generalized gamma distribution of Stacy (1962) and power Lindley distribution of Ghitany et al (2013) as particular cases. The moments, hazard rate function, mean residual life function, order statistic and Renyi entropy measure of the distribution have been studied. Method of maximum likelihood estimation has been discussed for estimating its parameters. Applications of the distribution have been explained with two examples of observed real lifetime datasets and its goodness of fit has been compared with other lifetime distributions.
2. A Generalization of Two-Parameter Lindley Distribution
Assuming the power transformation 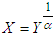 in (1.1), the pdf of
in (1.1), the pdf of  can be obtained as
can be obtained as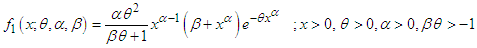 | (2.1) |
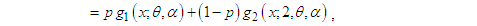 | (2.2) |
where, 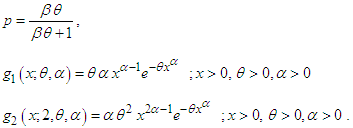 Since at
Since at 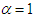 , (2.1) reduces to TPLD (1.1), we would call (2.1) a generalization of two-parameter Lindley distribution (GTPLD). Further, (2.1) is also a two-component mixture of Weibull distribution with shape parameter
, (2.1) reduces to TPLD (1.1), we would call (2.1) a generalization of two-parameter Lindley distribution (GTPLD). Further, (2.1) is also a two-component mixture of Weibull distribution with shape parameter 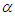 and scale parameter
and scale parameter 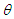 and a generalized gamma distribution with shape parameters
and a generalized gamma distribution with shape parameters 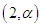 and scale parameter
and scale parameter 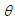 , with mixing proportion
, with mixing proportion 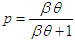 . At
. At 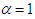 and
and 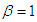 , (2.1) reduces to the Lindley distribution (1.3). At
, (2.1) reduces to the Lindley distribution (1.3). At 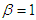 , (2.1) reduces to the Power Lindley distribution introduced by Ghitany et al (2013) having pdf
, (2.1) reduces to the Power Lindley distribution introduced by Ghitany et al (2013) having pdf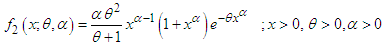 | (2.3) |
The gamma 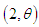 distribution and a generalized gamma
distribution and a generalized gamma 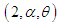 distribution are also particular cases of (2.1) for
distribution are also particular cases of (2.1) for 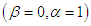 and
and 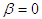 respectively. It can be easily shown that (2.1) reduces to Weibull distribution for
respectively. It can be easily shown that (2.1) reduces to Weibull distribution for 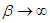 . Further, for
. Further, for 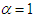 and
and 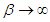 , (2.1) reduces to exponential distribution.The corresponding cdf of (2.1) can be obtained as
, (2.1) reduces to exponential distribution.The corresponding cdf of (2.1) can be obtained as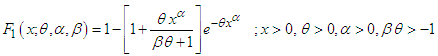 | (2.4) |
We use 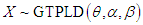 to denote a random variable having GTPLD (2.1) with parameters
to denote a random variable having GTPLD (2.1) with parameters 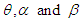 having pdf (2.1) and cdf (2.4).The behavior of the pdf and the cdf of GTPLD have been shown graphically for varying values of parameters
having pdf (2.1) and cdf (2.4).The behavior of the pdf and the cdf of GTPLD have been shown graphically for varying values of parameters 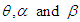 in figures 1 and 2 respectively.
in figures 1 and 2 respectively. 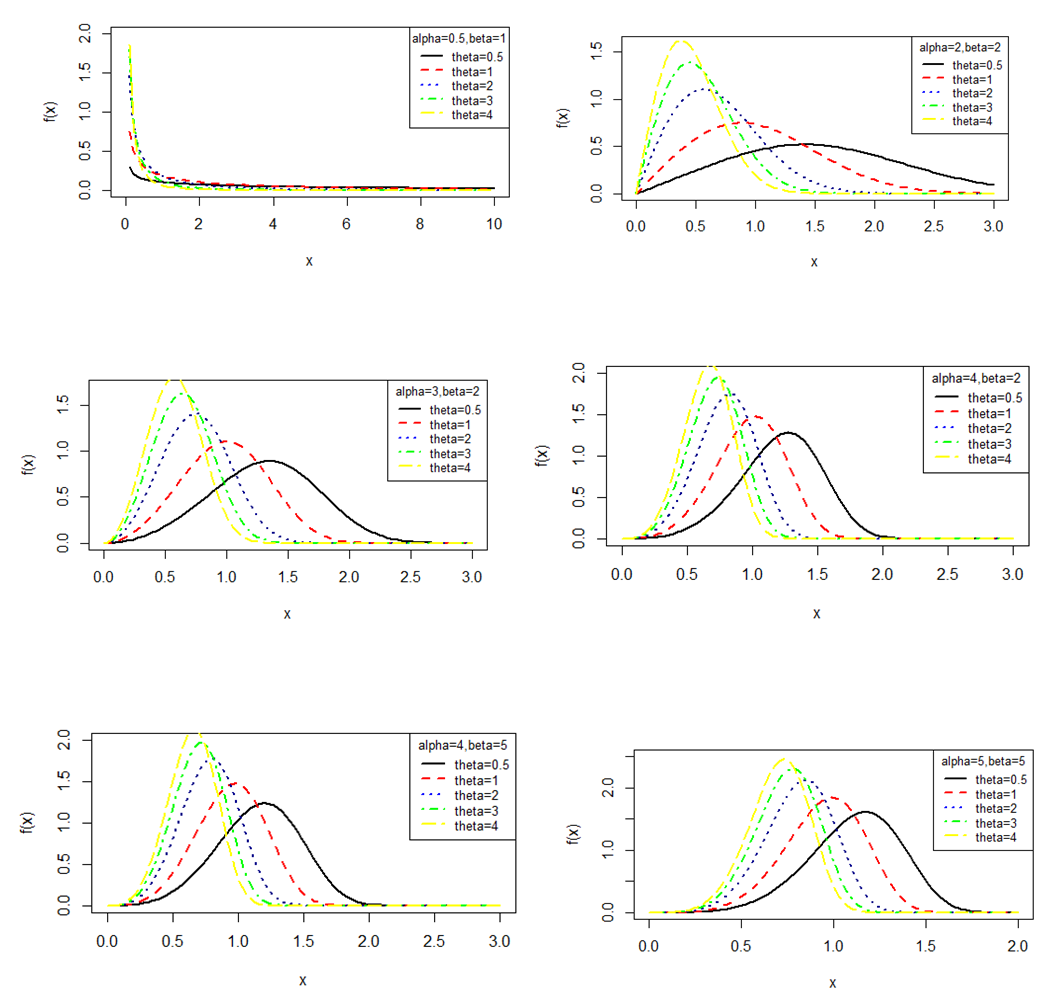 | Figure 1. Behavior of the pdf of GTPLD for varying values of parameters 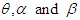 |
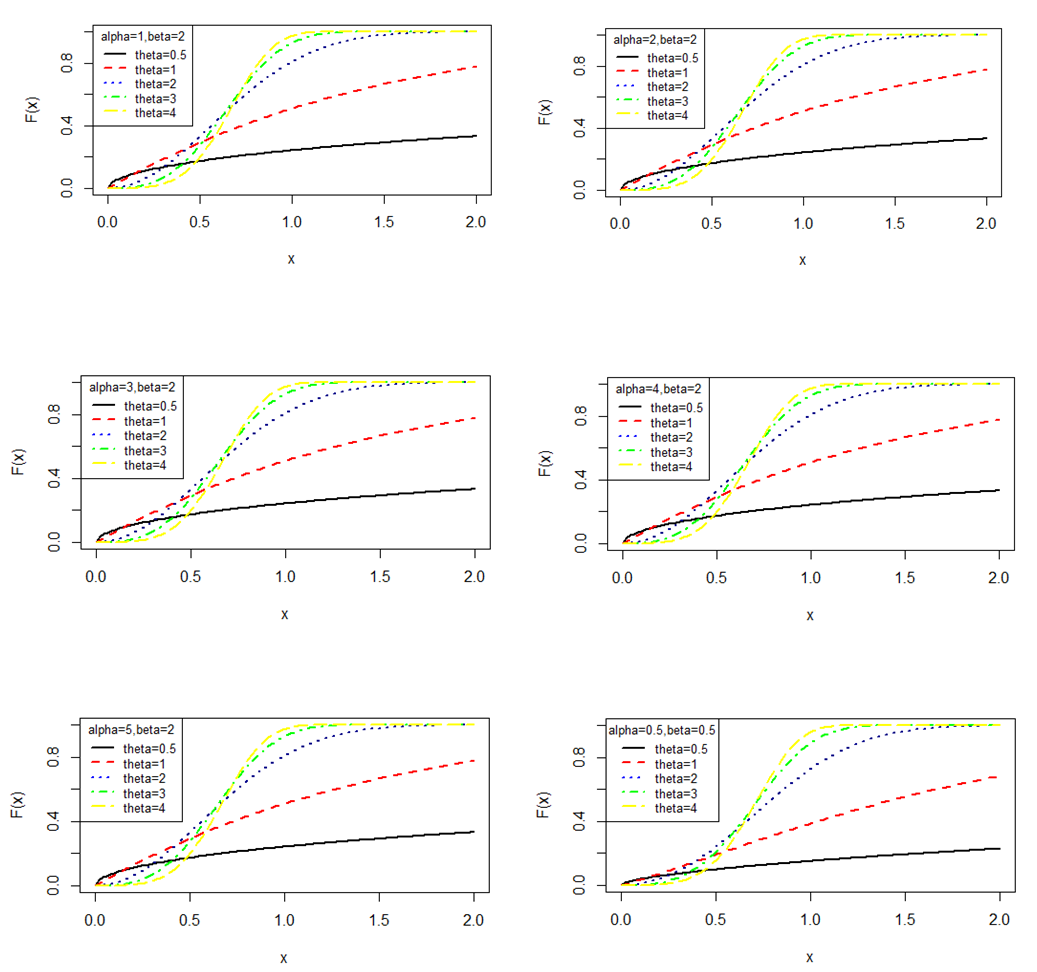 | Figure 2. Behavior of the cdf of GTPLD for varying values of parameters 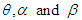 |
3. Reliability Properties
3.1. Survival Function and Hazard Rate Function
The survival function of GTPLD can be expressed as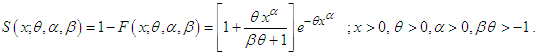 Thus the hazard rate function of GTPLD can be obtained as
Thus the hazard rate function of GTPLD can be obtained as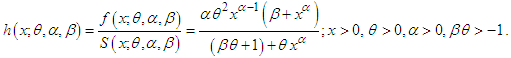 The behavior of hazard rate function of GTPLD for varying values of parameters
The behavior of hazard rate function of GTPLD for varying values of parameters 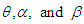 are shown in figure 3
are shown in figure 3 | Figure 3. Behavior of the hazard rate function of GTPLD for varying values of parameters 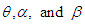 |
3.2. Mean Residual Life Function
The mean residual life function, 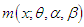 of GTPLD (2.1) can be obtained as
of GTPLD (2.1) can be obtained as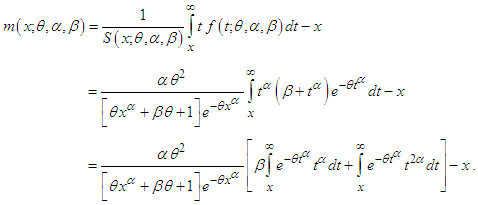 Taking
Taking 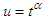 , which gives
, which gives 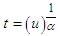 and
and 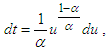 we get
we get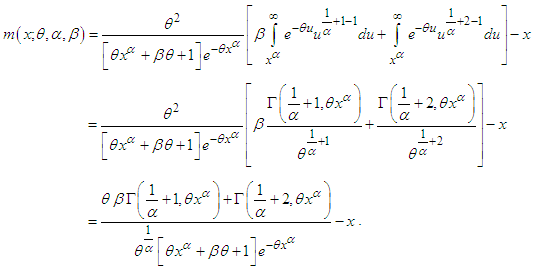 It can be easily verified that
It can be easily verified that  The behavior of
The behavior of  of GTPLD for varying values of parameters
of GTPLD for varying values of parameters  are shown in figure 4
are shown in figure 4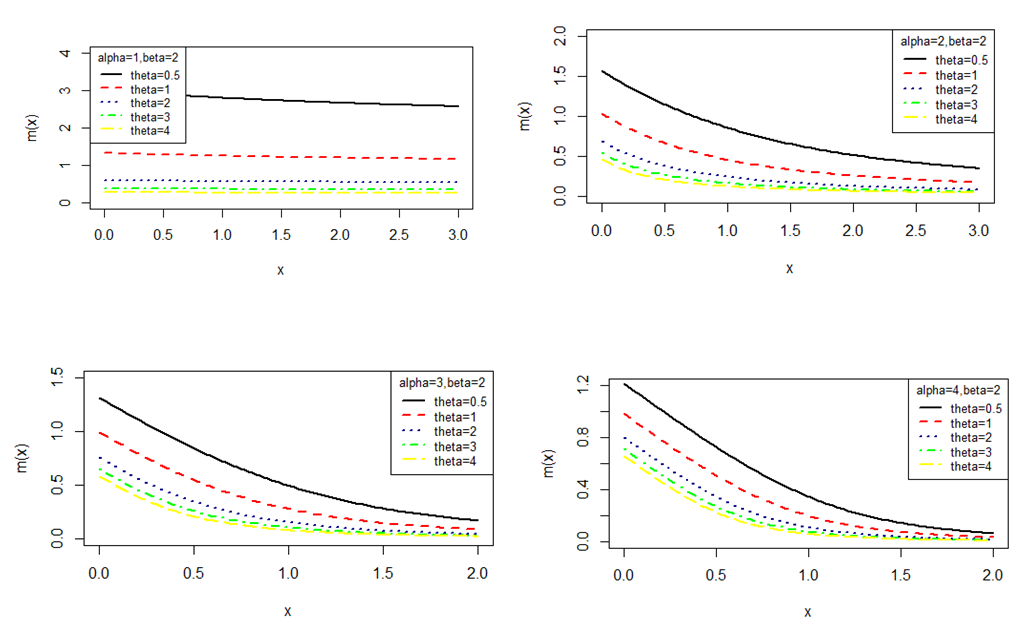 | Figure 4. Behavior of the mean residual life function of GTPLD for varying values of parameters 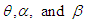 |
4. Statistical Properties
4.1. Moments
The 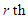 moment about origin,
moment about origin, 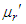 of GTPLD (2.1) can be obtained as
of GTPLD (2.1) can be obtained as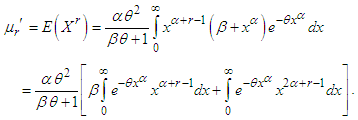 Taking
Taking 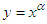 , which gives
, which gives 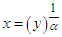 and
and 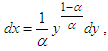 we get
we get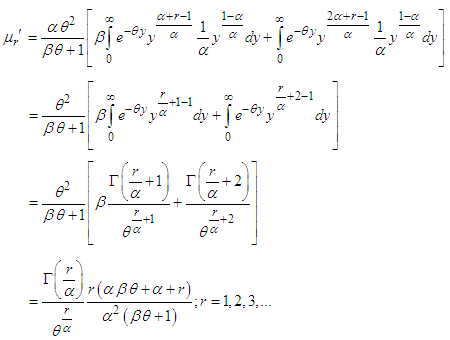 | (4.1.1) |
Taking 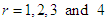 in (4.1.1), the first four moments about origin of GTPLD can be obtained as
in (4.1.1), the first four moments about origin of GTPLD can be obtained as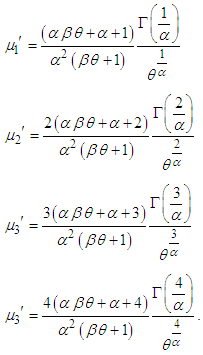 The variance of GTPLD can thus be obtained as
The variance of GTPLD can thus be obtained as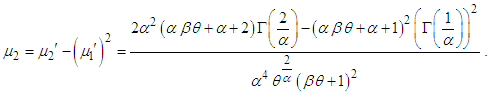 The higher central moments, if required, can be obtained using the relationship between central moments and raw moments. The skewness and kurtosis measures, upon substituting for the raw moments, can be obtained using the expressionsSkewness
The higher central moments, if required, can be obtained using the relationship between central moments and raw moments. The skewness and kurtosis measures, upon substituting for the raw moments, can be obtained using the expressionsSkewness 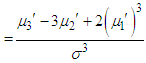 and Kurtosis
and Kurtosis 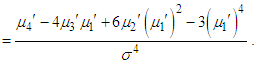
4.2. Distribution of Order Statistics
Let 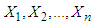 be a random sample of size
be a random sample of size 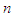 from GTPLD (2.1). Let
from GTPLD (2.1). Let 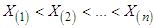 denote the corresponding order statistics. The pdf and the cdf of the
denote the corresponding order statistics. The pdf and the cdf of the 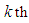 order statistic, say
order statistic, say 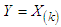 are given by
are given by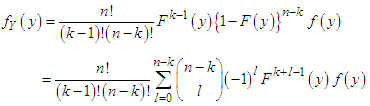 and
and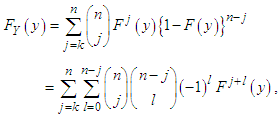 respectively, for
respectively, for 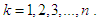 Thus, the pdf and the cdf of
Thus, the pdf and the cdf of 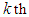 order statistics of GTPLD are given by
order statistics of GTPLD are given by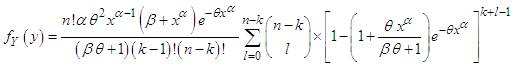 and
and 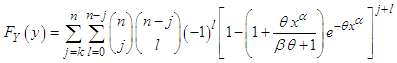
4.3. Renyi Entropy Measure
An entropy of a random variable 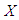 is a measure of variation of uncertainty. A popular entropy measure is Renyi entropy introduced by Renyi (1961). If
is a measure of variation of uncertainty. A popular entropy measure is Renyi entropy introduced by Renyi (1961). If 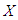 is a continuous random variable having probability density function
is a continuous random variable having probability density function 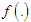 , then Renyi entropy is defined as
, then Renyi entropy is defined as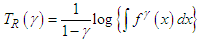 where
where 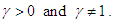 Thus, the Renyi entropy for GTPLD (2.1) can obtained as
Thus, the Renyi entropy for GTPLD (2.1) can obtained as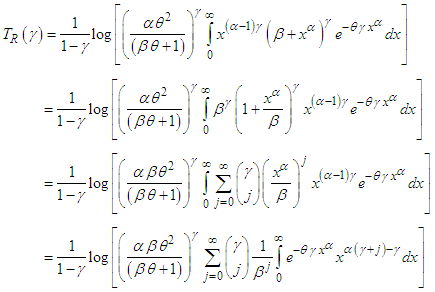 Taking
Taking  , which gives
, which gives  and
and 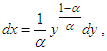 we get
we get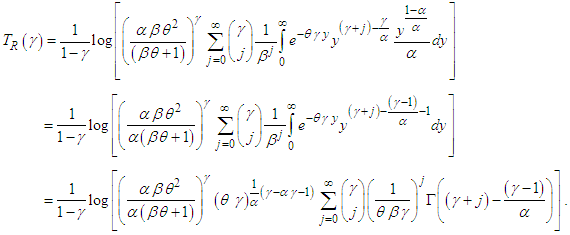
5. Maximum Likelihood Estimation of Parameters
In this section the estimation of parameters of GTPLD using maximum likelihood estimation has been discussed. Assuming 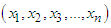 a random sample from GTPLD
a random sample from GTPLD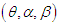 , the natural log-likelihood function,
, the natural log-likelihood function, 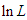 of GTPLD can be expressed as
of GTPLD can be expressed as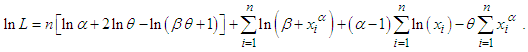 The maximum likelihood estimates
The maximum likelihood estimates 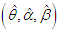 of parameters
of parameters 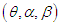 of GTPLD (2.1) is the solutions of the following natural log- likelihood equations
of GTPLD (2.1) is the solutions of the following natural log- likelihood equations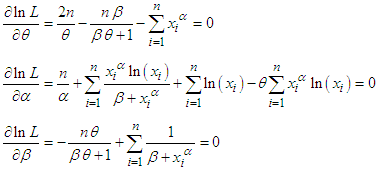 These three natural log- likelihood equations do not seem to be solved directly because they cannot be expressed in closed forms. However, the MLE’s
These three natural log- likelihood equations do not seem to be solved directly because they cannot be expressed in closed forms. However, the MLE’s 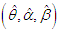 of parameters
of parameters 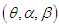 can be obtained directly by solving the log likelihood equation using Newton-Raphson iteration method available in R –Software till sufficiently close estimates of
can be obtained directly by solving the log likelihood equation using Newton-Raphson iteration method available in R –Software till sufficiently close estimates of 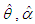 and
and 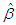 are obtained.
are obtained.
6. Numerical Examples
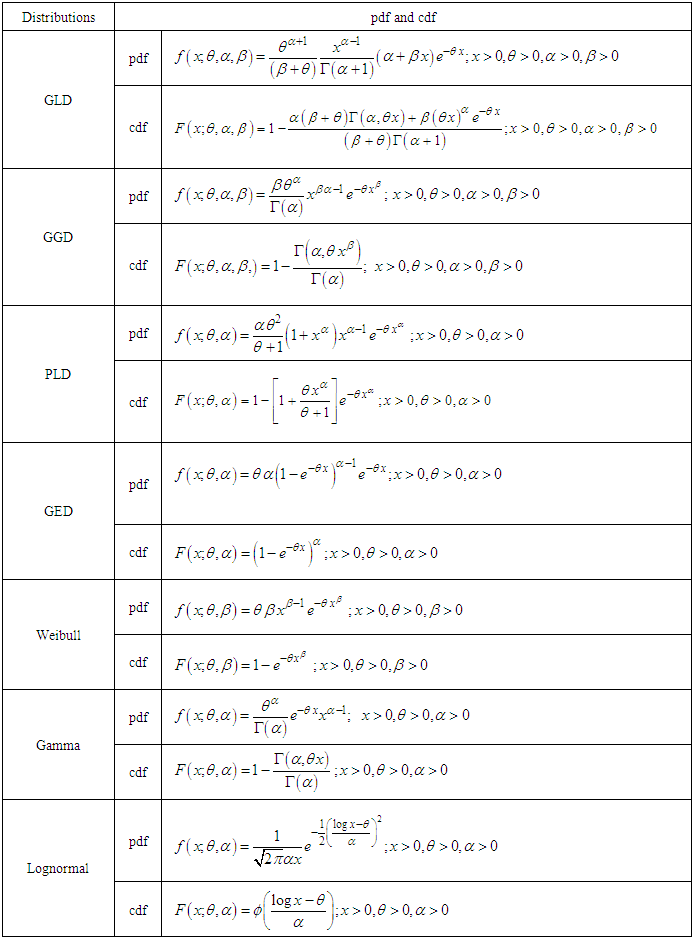
The applications of GTPLD have been explained with two real lifetime datasets regarding failure times (in minutes) from Lawless (2003) pp. 204 and 263. The goodness of fit of GTPLD has been discussed along with the goodness of fit given by generalized Lindley distribution (GLD) introduced by Zakerzadeh and Dolati (2009), generalized gamma distribution introduced by Stacy (1962), two-parameter Lindley distribution of Shanker and Mishra (2013), generalized exponential distribution proposed by Gupta and Kundu (1999), power Lindley distribution introduced by Ghitany et al (2013), gamma distribution, Weibull distribution suggested by Weibull (1951), Lognormal distribution, Lindley distribution and exponential distribution. In table 1, the pdf and the cdf of fitted distributions has been presented. The goodness of fit of the fitted distribution has been presented in tables 2 and 3, respectively.Dataset 1: The first set of data represents the failure times (in minutes) for a sample of 15 electronic components in an accelerated life test and the data are1.4, 5.1, 6.3, 10.8, 12.1, 18.5, 19.7, 22.2, 23.0, 30.6, 37.3, 46.3, 53.9, 59.8, and 66.2.Dataset 2: The following data set represents the number of cycles to failure for 25 100-cm specimens of yarn, tested at a particular strain level, Lawless (2003) pp. 204 and 263.15 20 38 42 61 76 86 98 121 146 149 157 175 176 180 180 198 220 224 251 264 282 321 325 653Table 1. The pdf and the cdf of the fitted distributions
 |
| |
|
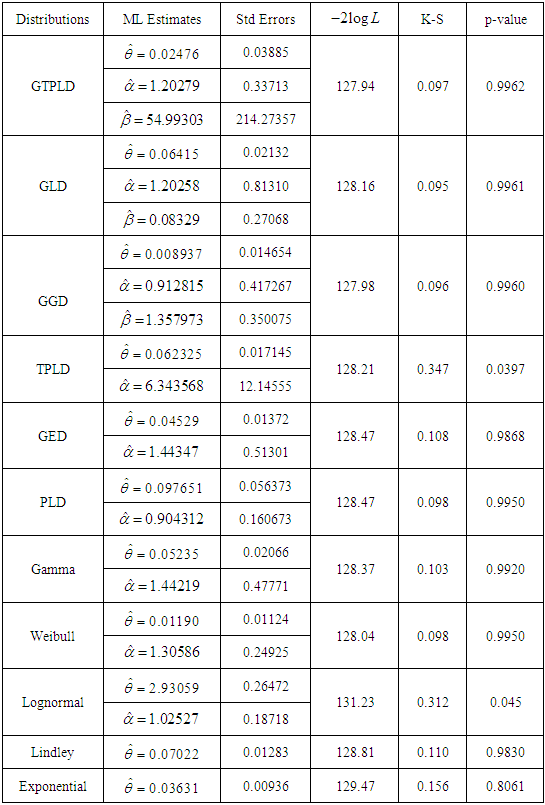
Table 2. ML estimates and summary of goodness of fit for dataset 1
 |
| |
|
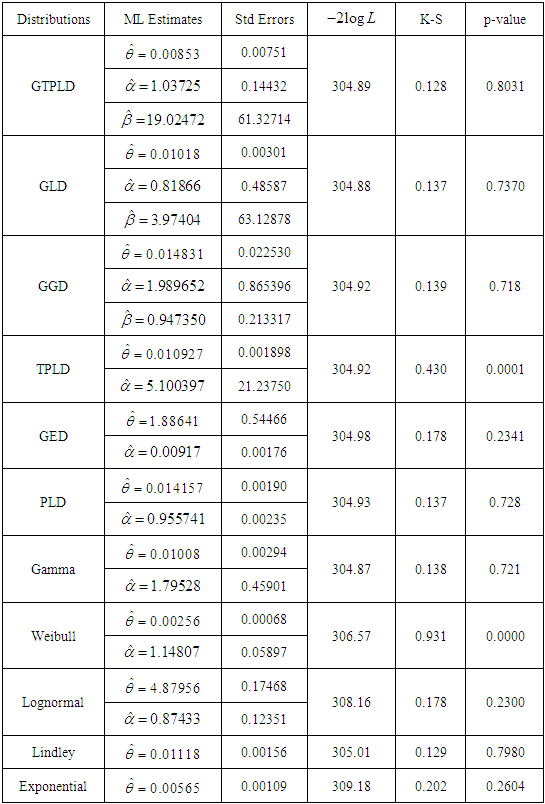
Table 3. ML estimates and summary of goodness of fit for dataset 2
 |
| |
|
It is obvious from the goodness of fit of GTPLD that GTPLD is competing well with other lifetime distributions and hence can be considered an important lifetime distribution in statistics literature. The variance-covariance matrix of the estimated parameters of the GTPLD for datasets 1 and 2 has been given in tables 4 and 5, respectively.Table 4. Variance-covariance matrix of GTPLD for dataset 1
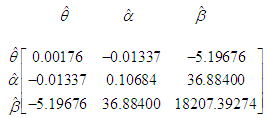 |
| |
|
Table 5. Variance-covariance matrix of GTPLD for dataset 2
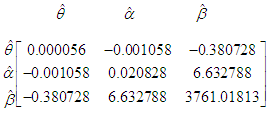 |
| |
|
7. Concluding Remarks
A generalization of two-parameter Lindley distribution (GTPLD), which includes one parameter exponential and Lindley distributions, two-parameter Lindley distribution (TPLD) of Shanker and Mishra (2013), Weibull distribution, gamma distribution, generalized gamma distribution of Stacy (1962) and power Lindley distribution of Ghitany et al (2013) as particular cases, has been proposed. Its raw moments, hazard rate function, mean residual life function, order statistic, Renyi entropy measure has been studied. Maximum likelihood estimation has been discussed for estimating its parameters. Applications of the distribution have been explained with two examples of observed real lifetime datasets from engineering and the goodness of fit is quite satisfactory over other one parameter, two-parameter and three-parameter lifetime distributions.
ACKNOWLEDGEMENTS
Authors are grateful to the editor-in-chief and the anonymous reviewer whose comments improved the quality and the presentation of the paper.
References
| [1] | Ghitany, M.E., Atieh, B. and Nadarajah, S. (2008): Lindley distribution and its Application, Mathematics Computing and Simulation, 78, 493 – 506. |
| [2] | Ghitany, M.E., Al-Mutairi, D.K., Balakrishnan, N., and Al-Enezi, L.J. (2013): Power Lindley distribution and Associated Inference, Computational Statistics and Data Analysis, 64, 20 – 33. |
| [3] | Gupta, R.D. and Kundu, D. (1999): Generalized Exponential Distribution, Austalian & New Zealand Journal of Statistics, 41(2), 173 – 188. |
| [4] | Lawless, J.F. (2003): Statistical Models and Methods for Lifetime Data, Wiley, New York. |
| [5] | Lindley, D.V. (1958): Fiducial distributions and Bayes’ Theorem, Journal of the Royal Statistical Society, Series B, 20, 102 – 107. |
| [6] | Renyi, A. (1961): On measures of entropy and information, in proceedings of the 4th berkeley symposium on Mathematical Statistics and Probability, 1, 547 – 561, Berkeley, university of California press. |
| [7] | Shanker, R. and Mishra, A. (2013): A Two-Parameter Lindley Distribution, Statistics in Transition new Series, 14(1), 45-56. |
| [8] | Shanker, R., Hagos, F, and Sujatha, S. (2015): On modeling of Lifetimes data using exponential and Lindley distributions, Biometrics & Biostatistics International Journal, 2(5), 1-9. |
| [9] | Shanker, R. (2016): On generalized Lindley distribution and its applications to model lifetime data from biomedical science and engineering, Insights in Biomedicine, 1(2), 1 – 6. |
| [10] | Shanker, R. and Shukla, K.K. (2016): On modeling of lifetime data using three-parameter Generalized Lindley and Generalized Gamma distributions, Biometrics & Biostatistics International Journal, 4(7), 1 – 7. |
| [11] | Shanker, R., Shukla, K.K., Shanker, R. and Tekie, A.L. (2016): On modeling of Lifetime data using two-parameter Gamma and Weibull distributions, Biometrics & Biostatistics International journal, 4(5), 1 – 6. |
| [12] | Stacy, E.W. (1962): A generalization of the gamma distribution, Annals of Mathematical Statistical, 33, 1187 – 1192. |
| [13] | Weibull, W. (1951): A statistical distribution of wide applicability, Journal of Applied Mathematics, 18, 293 – 297. |
| [14] | Zakerzadeh, H. and Dolati, A. (2009): Generalized Lindley distribution, Journal of Mathematical extension, 3 (2), 13 – 25. |


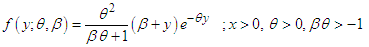
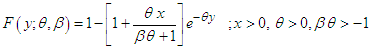
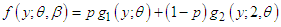 where
where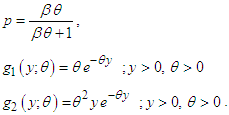 Clearly the density (1.1) is a two-component mixture of an exponential distribution with scale parameter
Clearly the density (1.1) is a two-component mixture of an exponential distribution with scale parameter 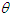 and a gamma distribution with shape parameter 2 and scale parameter
and a gamma distribution with shape parameter 2 and scale parameter 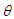 , with mixing proportion
, with mixing proportion 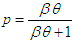 . Shanker and Mishra (2013) studied its various properties including coefficients of variation, skewness, kurtosis; hazard rate function, mean residual life function and stochastic ordering. The estimation of its parameters using both the maximum likelihood estimation and the method of moments along with applications of TPLD to model lifetime data has also been discussed by Shanker and Mishra (2013). It can be easily shown that Lindley distribution, introduced by Lindley (1958), having pdf
. Shanker and Mishra (2013) studied its various properties including coefficients of variation, skewness, kurtosis; hazard rate function, mean residual life function and stochastic ordering. The estimation of its parameters using both the maximum likelihood estimation and the method of moments along with applications of TPLD to model lifetime data has also been discussed by Shanker and Mishra (2013). It can be easily shown that Lindley distribution, introduced by Lindley (1958), having pdf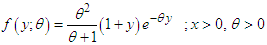
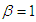 . Lindley distribution has been studied in detail by Ghitany et al (2008). Shanker et al (2015) have detailed and critical study on applications of exponential and Lindley distribution for modeling real lifetime data from biomedical sciences and engineering and observed that both exponential and Lindley are competing each other. Shanker et al (2016) have discussion on applications of gamma distribution and Weibull distribution for real lifetime data from engineering and biological sciences. Shanker (2016) has discussed various important statistical properties including coefficient of variation, skewness, kurtosis and index of dispersion along with various applications of generalized Lindley distribution (GLD) introduced by Zakerzadeh and Dolati (2009). Shanker and Shukla (2016) have detailed comparative study on applications of three-parameter generalized gamma distribution (GGD) and generalized Lindley distribution (GLD) and observed that these two distributions are competing each other for modeling lifetime data.In this paper, an attempt has been made to derive a generalization of two-parameter Lindley distribution (GTPLD), which includes one parameter exponential and Lindley distributions, two-parameter Lindley distribution (TPLD) of Shanker and Mishra (2013), Weibull distribution, gamma distribution, generalized gamma distribution of Stacy (1962) and power Lindley distribution of Ghitany et al (2013) as particular cases. The moments, hazard rate function, mean residual life function, order statistic and Renyi entropy measure of the distribution have been studied. Method of maximum likelihood estimation has been discussed for estimating its parameters. Applications of the distribution have been explained with two examples of observed real lifetime datasets and its goodness of fit has been compared with other lifetime distributions.
. Lindley distribution has been studied in detail by Ghitany et al (2008). Shanker et al (2015) have detailed and critical study on applications of exponential and Lindley distribution for modeling real lifetime data from biomedical sciences and engineering and observed that both exponential and Lindley are competing each other. Shanker et al (2016) have discussion on applications of gamma distribution and Weibull distribution for real lifetime data from engineering and biological sciences. Shanker (2016) has discussed various important statistical properties including coefficient of variation, skewness, kurtosis and index of dispersion along with various applications of generalized Lindley distribution (GLD) introduced by Zakerzadeh and Dolati (2009). Shanker and Shukla (2016) have detailed comparative study on applications of three-parameter generalized gamma distribution (GGD) and generalized Lindley distribution (GLD) and observed that these two distributions are competing each other for modeling lifetime data.In this paper, an attempt has been made to derive a generalization of two-parameter Lindley distribution (GTPLD), which includes one parameter exponential and Lindley distributions, two-parameter Lindley distribution (TPLD) of Shanker and Mishra (2013), Weibull distribution, gamma distribution, generalized gamma distribution of Stacy (1962) and power Lindley distribution of Ghitany et al (2013) as particular cases. The moments, hazard rate function, mean residual life function, order statistic and Renyi entropy measure of the distribution have been studied. Method of maximum likelihood estimation has been discussed for estimating its parameters. Applications of the distribution have been explained with two examples of observed real lifetime datasets and its goodness of fit has been compared with other lifetime distributions.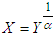 in (1.1), the pdf of
in (1.1), the pdf of 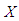 can be obtained as
can be obtained as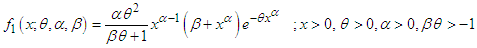
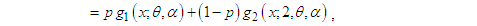
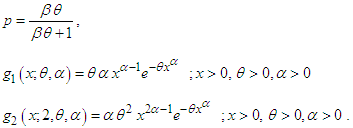 Since at
Since at 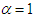 , (2.1) reduces to TPLD (1.1), we would call (2.1) a generalization of two-parameter Lindley distribution (GTPLD). Further, (2.1) is also a two-component mixture of Weibull distribution with shape parameter
, (2.1) reduces to TPLD (1.1), we would call (2.1) a generalization of two-parameter Lindley distribution (GTPLD). Further, (2.1) is also a two-component mixture of Weibull distribution with shape parameter 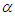 and scale parameter
and scale parameter  and a generalized gamma distribution with shape parameters
and a generalized gamma distribution with shape parameters 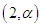 and scale parameter
and scale parameter 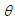 , with mixing proportion
, with mixing proportion 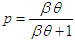 . At
. At 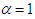 and
and 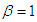 , (2.1) reduces to the Lindley distribution (1.3). At
, (2.1) reduces to the Lindley distribution (1.3). At 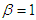 , (2.1) reduces to the Power Lindley distribution introduced by Ghitany et al (2013) having pdf
, (2.1) reduces to the Power Lindley distribution introduced by Ghitany et al (2013) having pdf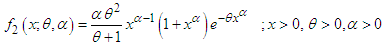
 distribution and a generalized gamma
distribution and a generalized gamma 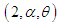 distribution are also particular cases of (2.1) for
distribution are also particular cases of (2.1) for 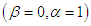 and
and 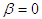 respectively. It can be easily shown that (2.1) reduces to Weibull distribution for
respectively. It can be easily shown that (2.1) reduces to Weibull distribution for 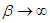 . Further, for
. Further, for 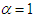 and
and 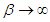 , (2.1) reduces to exponential distribution.The corresponding cdf of (2.1) can be obtained as
, (2.1) reduces to exponential distribution.The corresponding cdf of (2.1) can be obtained as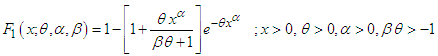
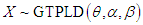 to denote a random variable having GTPLD (2.1) with parameters
to denote a random variable having GTPLD (2.1) with parameters 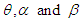 having pdf (2.1) and cdf (2.4).The behavior of the pdf and the cdf of GTPLD have been shown graphically for varying values of parameters
having pdf (2.1) and cdf (2.4).The behavior of the pdf and the cdf of GTPLD have been shown graphically for varying values of parameters 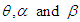 in figures 1 and 2 respectively.
in figures 1 and 2 respectively. 
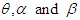

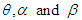
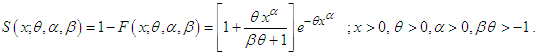 Thus the hazard rate function of GTPLD can be obtained as
Thus the hazard rate function of GTPLD can be obtained as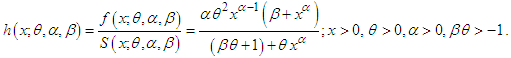 The behavior of hazard rate function of GTPLD for varying values of parameters
The behavior of hazard rate function of GTPLD for varying values of parameters 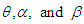 are shown in figure 3
are shown in figure 3
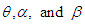
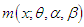 of GTPLD (2.1) can be obtained as
of GTPLD (2.1) can be obtained as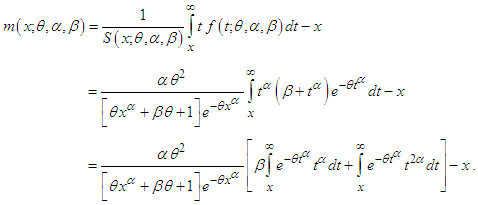 Taking
Taking 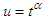 , which gives
, which gives 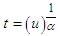 and
and 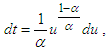 we get
we get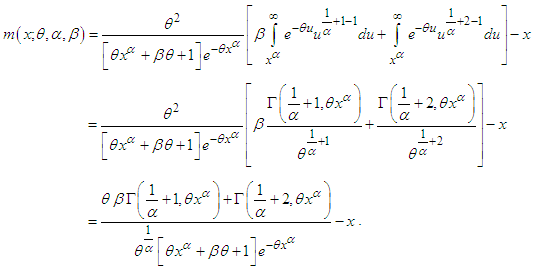 It can be easily verified that
It can be easily verified that  The behavior of
The behavior of  of GTPLD for varying values of parameters
of GTPLD for varying values of parameters  are shown in figure 4
are shown in figure 4
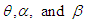
 moment about origin,
moment about origin, 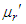 of GTPLD (2.1) can be obtained as
of GTPLD (2.1) can be obtained as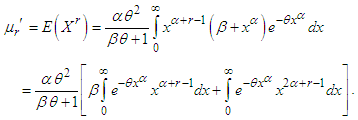 Taking
Taking 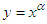 , which gives
, which gives 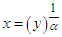 and
and 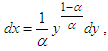 we get
we get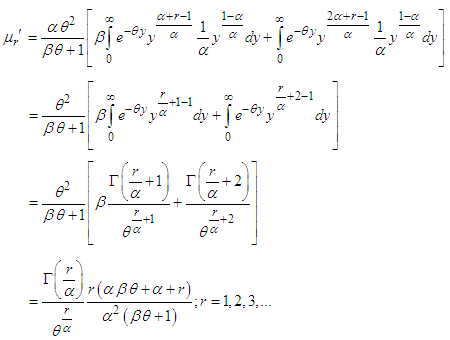
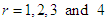 in (4.1.1), the first four moments about origin of GTPLD can be obtained as
in (4.1.1), the first four moments about origin of GTPLD can be obtained as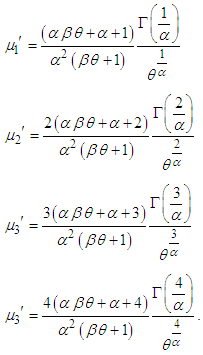 The variance of GTPLD can thus be obtained as
The variance of GTPLD can thus be obtained as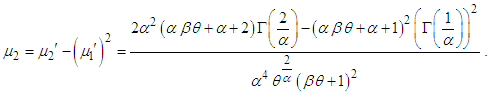 The higher central moments, if required, can be obtained using the relationship between central moments and raw moments. The skewness and kurtosis measures, upon substituting for the raw moments, can be obtained using the expressionsSkewness
The higher central moments, if required, can be obtained using the relationship between central moments and raw moments. The skewness and kurtosis measures, upon substituting for the raw moments, can be obtained using the expressionsSkewness 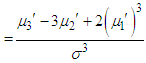 and Kurtosis
and Kurtosis 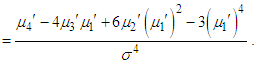
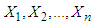 be a random sample of size
be a random sample of size 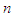 from GTPLD (2.1). Let
from GTPLD (2.1). Let 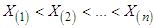 denote the corresponding order statistics. The pdf and the cdf of the
denote the corresponding order statistics. The pdf and the cdf of the 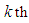 order statistic, say
order statistic, say 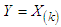 are given by
are given by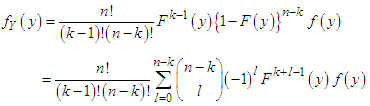 and
and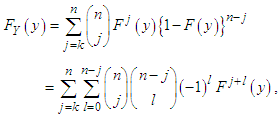 respectively, for
respectively, for 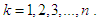 Thus, the pdf and the cdf of
Thus, the pdf and the cdf of 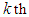 order statistics of GTPLD are given by
order statistics of GTPLD are given by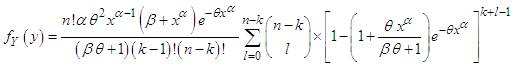 and
and 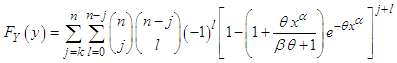
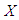 is a measure of variation of uncertainty. A popular entropy measure is Renyi entropy introduced by Renyi (1961). If
is a measure of variation of uncertainty. A popular entropy measure is Renyi entropy introduced by Renyi (1961). If 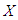 is a continuous random variable having probability density function
is a continuous random variable having probability density function 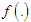 , then Renyi entropy is defined as
, then Renyi entropy is defined as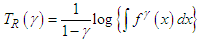 where
where 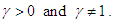 Thus, the Renyi entropy for GTPLD (2.1) can obtained as
Thus, the Renyi entropy for GTPLD (2.1) can obtained as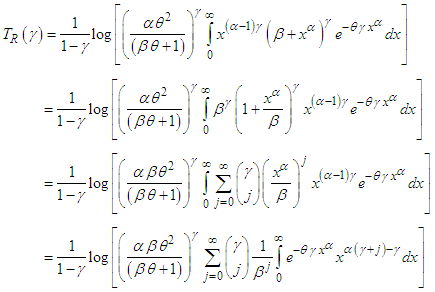 Taking
Taking  , which gives
, which gives  and
and 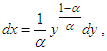 we get
we get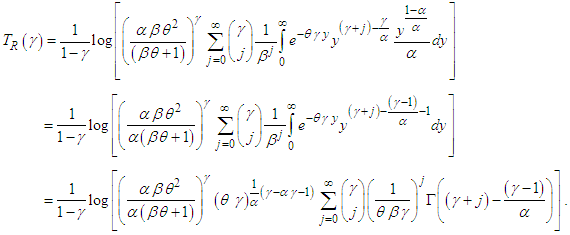
 a random sample from GTPLD
a random sample from GTPLD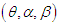 , the natural log-likelihood function,
, the natural log-likelihood function, 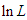 of GTPLD can be expressed as
of GTPLD can be expressed as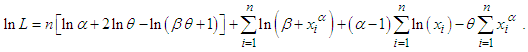 The maximum likelihood estimates
The maximum likelihood estimates 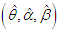 of parameters
of parameters 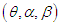 of GTPLD (2.1) is the solutions of the following natural log- likelihood equations
of GTPLD (2.1) is the solutions of the following natural log- likelihood equations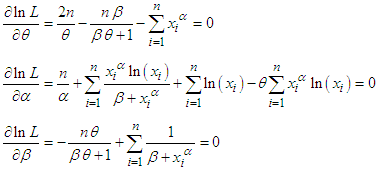 These three natural log- likelihood equations do not seem to be solved directly because they cannot be expressed in closed forms. However, the MLE’s
These three natural log- likelihood equations do not seem to be solved directly because they cannot be expressed in closed forms. However, the MLE’s 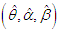 of parameters
of parameters 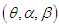 can be obtained directly by solving the log likelihood equation using Newton-Raphson iteration method available in R –Software till sufficiently close estimates of
can be obtained directly by solving the log likelihood equation using Newton-Raphson iteration method available in R –Software till sufficiently close estimates of 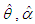 and
and 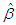 are obtained.
are obtained. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML