Winnie Mokeira Onsongo1, Romanus Odhiambo Otieno2, George Otieno Orwa3
1Department of Mathematics, Pan African University Institute of Basic Sciences, Technology and Innovation, Nairobi, Kenya
2Department of Mathematics, Meru University of Science and Technology, Meru, Kenya
3Department of Statistics and Actuarial Science, Jomo Kenyatta University of Agriculture and Technology, Nairobi, Kenya
Correspondence to: Winnie Mokeira Onsongo, Department of Mathematics, Pan African University Institute of Basic Sciences, Technology and Innovation, Nairobi, Kenya.
| Email: |  |
Copyright © 2018 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
Nonparametric estimation of population parameters for finite populations has been used with great success for data that fit the independent and identically distributed framework. However, most of these approaches do not extend to data from multistage samples. In this work, we present a method for developing a nonparametric distribution function for a finite population that has been stratified. Proportional allocation of sampling weights has been utilized alongside kernel weights. Asymptotic properties of the estimator are derived and are compared with those of existing model based estimators using the simulated sets of data. The results show that applying the bias reduction technique to a stratified population greatly improves precision of the estimator.
Keywords:
Stratified Sampling, Proportional Allocation, 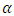 -Quantile, Multiplicative Bias Correction
-Quantile, Multiplicative Bias Correction
Cite this paper: Winnie Mokeira Onsongo, Romanus Odhiambo Otieno, George Otieno Orwa, Nonparametric Estimation of Distribution Function for Stratified Populations, International Journal of Probability and Statistics , Vol. 7 No. 5, 2018, pp. 125-129. doi: 10.5923/j.ijps.20180705.01.
1. Introduction
Estimation of population parameters is a fundamental issue in statistics because such quantities are necessary components in most theoretical studies and practical applications. The main idea of nonparametric statistics is to make inferences about unknown quantities without resorting to parametric reduction of the problem. Example, suppose that a random variable X has a distribution function F. The approach taken by parametric statistics is to assume that F belongs to a family of distributions that can be explained by a smaller number of parameters. These parameters are then estimated and inference is made about the quantities of interest.Clearly, the parametric approach relies on a tremendous reduction of the original problem. It assumes that all uncertainty regarding the distribution function can be reduced to just one or two unknown numbers. If these assumptions are true, then there is nothing wrong in making the assumptions. However if they are false, the resulting inference will be questionable and we might miss the interesting patterns in the data. On the contrary, nonparametric statistics tries to make as few assumptions as possible about the data. For instance, it allows F to be any function provided it satisfies the definition of a distribution function. This requires the development of a whole new set of tools and instead of estimating parameters, the nonparametric approach estimates the function.A number of estimation procedures have been developed to estimate the distribution of a random variable in the past (Zhao et al., 2013). For more insight on this see (Chambers and Dunstan, 1986), (Kuk, 1993), (Rao et al 1990) and (Dorfman & Hall, 1993). (Breunig, 2008) also considered a weighted, nonparametric density estimator for stratified samples. He derived the optimal bandwidth and provided a plug-in bandwidth when all strata are normally distributed. (Chambers and Clark, 2012) gave a general nonparametric methodology for estimating a distribution function for a stratified population using a linear regression model. Despite the success of using the nonparametric approach in the estimation of population parameters, there exists some tendency of the estimators being biased. Moreover, kernel smoothers tend to have boundary problems such as the bias and variance trade-off. There are many approaches to reducing the bias, but most of them do so at the cost of an increase in the variance of the estimator. Under smoothing will reduce the bias but will have a tendency of generating spurious peaks. Higher order smoothers can also be used but while this will lead to a smaller bias, the smoother will have a larger variance (Hengartner et al., 2009).(Linton and Nielsen, 1994) developed a multiplicative technique for bias reduction and (Burr et al., 2010) have since used the approach in the smoothing of low resolution gamma spectra. The results obtained showed that the technique helped in the reduction of bias with no or negligible increase in variance. (Onsongo et al., 2018) also developed a nonparametric estimator for a finite population distribution function via simple random sampling without replacement with the aid this technique.This paper considers estimation of a nonparametric estimator for finite population total and derivation of its asymptotic properties of a nonparametric distribution function estimator for a stratified population by utilizing the bias correction technique proposed by (Linton and Nielsen, 1994). The results obtained by (Linton and Nielsen, 1994) showed that the estimator of the regression function had desirable properties compared to existing estimators including solving the boundary problems hence the motivation to use it.Outline of the paperIn section 2, we propose an estimator for finite population distribution function for a stratified population using a bias correction technique. In section 3, asymptotic properties of the estimator are derived. Empirical simulation of the results is given in section 4 and the conclusion of the findings is given in section 5.
2. Proposed Estimator
In this section, we develop a nonparametric estimator for a distribution function in the event of stratification of a finite population.Consider a finite population of N units that can be classified into H strata each of size 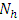 where
where 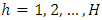 such that
such that 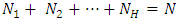 .Let
.Let 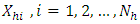 be the auxiliary variable for the
be the auxiliary variable for the 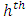 stratum with corresponding survey measurement
stratum with corresponding survey measurement 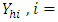
 from a common univariate distribution function.Suppose that a simple random sample of size
from a common univariate distribution function.Suppose that a simple random sample of size 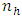 is drawn without replacement from the
is drawn without replacement from the 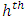 stratum such that the sample proportion
stratum such that the sample proportion 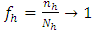 as
as 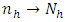 and
and 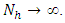 Then, the empirical distribution function for a finite population is defined as
Then, the empirical distribution function for a finite population is defined as 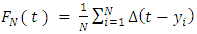 | (1) |
The corresponding estimator of a distribution function for a stratified population is defined as 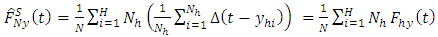 | (2) |
Where  denotes the step function of a given set, t is the
denotes the step function of a given set, t is the 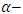 quantile and i denotes the observation made from the
quantile and i denotes the observation made from the 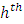 stratum.
stratum. 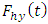 is the
is the 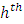 stratum distribution function for the random variable Y.Let s be a sample of
stratum distribution function for the random variable Y.Let s be a sample of 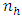 units drawn from the
units drawn from the 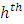 stratum via simple random sampling without replacement and
stratum via simple random sampling without replacement and 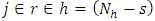 be the non-sampled units in the
be the non-sampled units in the 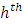 stratum.Suppose the auxiliary information is known for all elements in the population while the survey variable is only observed for the sample elements.Further, suppose that the survey variables are generated using a super population model defined by
stratum.Suppose the auxiliary information is known for all elements in the population while the survey variable is only observed for the sample elements.Further, suppose that the survey variables are generated using a super population model defined by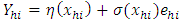 | (3) |
Where 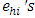 are independent and identically distributed random variables with zero mean and variance
are independent and identically distributed random variables with zero mean and variance 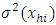 with
with 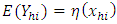 and
and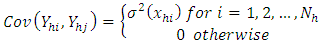 Where
Where 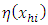 and
and 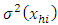 are assumed to be smooth functions of
are assumed to be smooth functions of 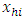 .The predictive form of the empirical distribution function for a stratified population under the model based approach therefore becomes
.The predictive form of the empirical distribution function for a stratified population under the model based approach therefore becomes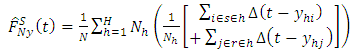 | (4) |
In this work, we propose the estimator for equation (4) as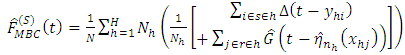 | (5) |
Where 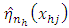 is the model-based nonparametric estimator for
is the model-based nonparametric estimator for 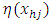 and
and 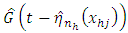 is the estimated distribution function of the residuals defined by
is the estimated distribution function of the residuals defined by 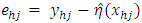 using elements drawn from the
using elements drawn from the 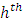 stratum.Since
stratum.Since 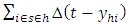 is known from the sample drawn, the task reduces to that of estimating
is known from the sample drawn, the task reduces to that of estimating 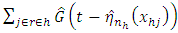 .To do this, the multiplicative bias correction technique is employed.Suppose that
.To do this, the multiplicative bias correction technique is employed.Suppose that 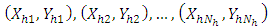 are N independent pairs of random variables with the pair
are N independent pairs of random variables with the pair 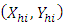 being real valued.Define a pilot smoother of the regression function as
being real valued.Define a pilot smoother of the regression function as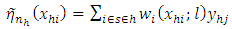 | (6) |
Where 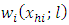 are the Nadaraya-Watson kernel weights defined by
are the Nadaraya-Watson kernel weights defined by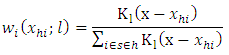 and l is the bandwidth.
and l is the bandwidth. 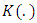 is a function that is continuous, symmetric and bounded with real values.Let the ratio
is a function that is continuous, symmetric and bounded with real values.Let the ratio 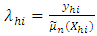 be a noisy estimate of the inverse relative estimation error of the smoother
be a noisy estimate of the inverse relative estimation error of the smoother 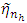 given by
given by 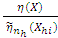 .Smoothing
.Smoothing 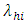 yields
yields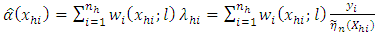 | (7) |
Equation (7) can then be used as a multiplicative correction of the pilot smoother in equation (6) which can now be defined by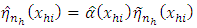 | (8) |
AssumptionsThe following assumptions are made in the estimation of 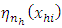 1. The regression function is twice continuously differentiable everywhere.2. The bandwidth l is such that
1. The regression function is twice continuously differentiable everywhere.2. The bandwidth l is such that 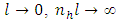 , as
, as 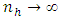 .Using equation (7) in equation (8) yields
.Using equation (7) in equation (8) yields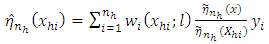 | (9) |
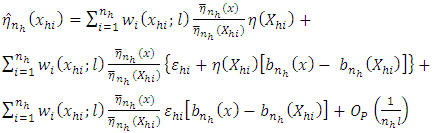 | (10) |
For a detailed review on the derivation of 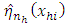 see (Onsongo et al., 2018).The estimator for the distribution function for a stratified population therefore becomes
see (Onsongo et al., 2018).The estimator for the distribution function for a stratified population therefore becomes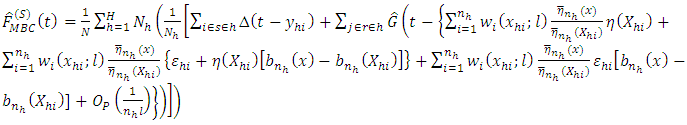
3. Asymptotic Properties of the Estimator under Stratified Sampling
3.1. Asymptotic Unbiasedness
Consider the asymptotic bias of the nonparametric estimator is defined as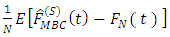 | (10) |
Where 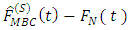 is the estimated bias under stratified sampling.Let
is the estimated bias under stratified sampling.Let 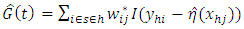 where
where 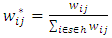 where t is the
where t is the 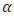 -quantile and
-quantile and 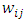 are the weights that only take non-zero values for sample units
are the weights that only take non-zero values for sample units 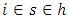 with
with 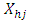 close to
close to 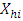 .Equation (5) can then be written as
.Equation (5) can then be written as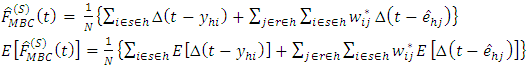 However
However 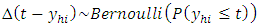 and
and 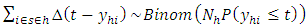 implying that
implying that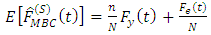 | (12) |
Next,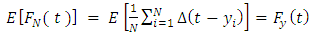 | (13) |
Substituting the results in equation (12) and equation (13) back to equation (10) yields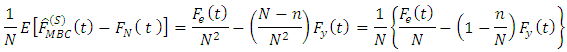
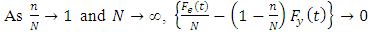
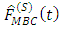 is therefore asymptotically unbiased.
is therefore asymptotically unbiased.
3.2. Asymptotic Variance
Consider the estimated bias is given by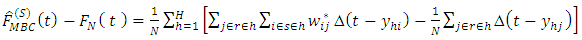 The variance of the estimated bias can therefore be written as
The variance of the estimated bias can therefore be written as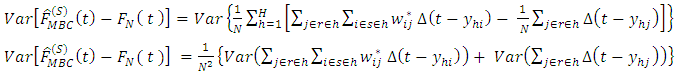 | (14) |
The errors are assumed to be independent and identically distributed and therefore have zero covariance.Consider 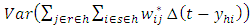 and let
and let 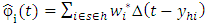 Then
Then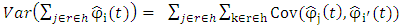 | (15) |
With 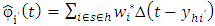 Define
Define 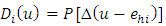
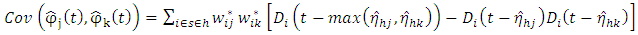 | (16) |
Suppose that 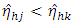 whenever
whenever 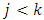 and suppose that the non-sampled units are labelled from 1 to
and suppose that the non-sampled units are labelled from 1 to 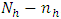 .Then
.Then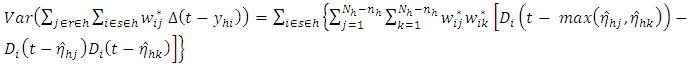 | (17) |
Next,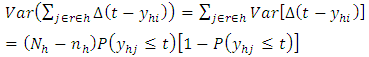 | (18) |
Substituting equations (17) and (18) into equation (14) yields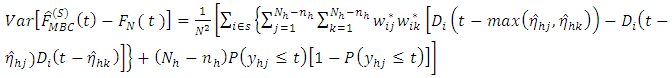 | (19) |
It is clear from this result that 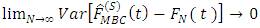 .
.
4. Results
In this section, simulation experiments were done to study the performance of the multiplicative bias corrected estimator for a stratified population.Four populations of size 500 each are generated as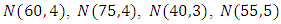 such that there is a total of 2, 000 auxiliary variables.The corresponding survey values
such that there is a total of 2, 000 auxiliary variables.The corresponding survey values 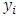 are generated using the super-population model
are generated using the super-population model 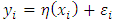 after which they are stratified according to form four strata. Proportional allocation was used to draw samples of size 100 from each stratum.The estimators
after which they are stratified according to form four strata. Proportional allocation was used to draw samples of size 100 from each stratum.The estimators 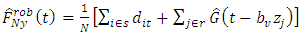 suggested by (Chambers and Clark, 2012) and
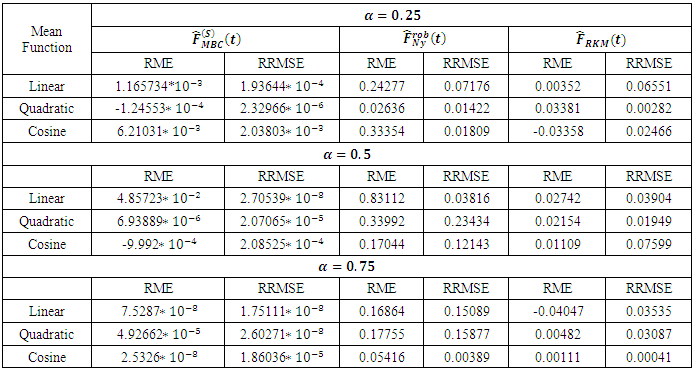
suggested by (Chambers and Clark, 2012) and 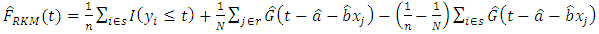 suggested by (Rao et al 1990) were then used in the comparison of results.Table 1 shows the unconditional Relative Mean Error (RME) and Relative Root Mean Error (RRME) for the estimators at various values of the quantile
suggested by (Rao et al 1990) were then used in the comparison of results.Table 1 shows the unconditional Relative Mean Error (RME) and Relative Root Mean Error (RRME) for the estimators at various values of the quantile 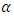 (i.e. 0.25, 0.5 and 0.75). Linear, quadratic and cosine mean functions were used to obtain the tabulated results. Similar results and conclusions can be obtained using other mean functions such as sine, cycle and bump.The conditional Relative Mean Error and Relative Root Mean Error for an estimator
(i.e. 0.25, 0.5 and 0.75). Linear, quadratic and cosine mean functions were used to obtain the tabulated results. Similar results and conclusions can be obtained using other mean functions such as sine, cycle and bump.The conditional Relative Mean Error and Relative Root Mean Error for an estimator 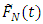 are calculated as:
are calculated as: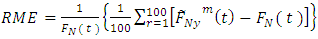 and
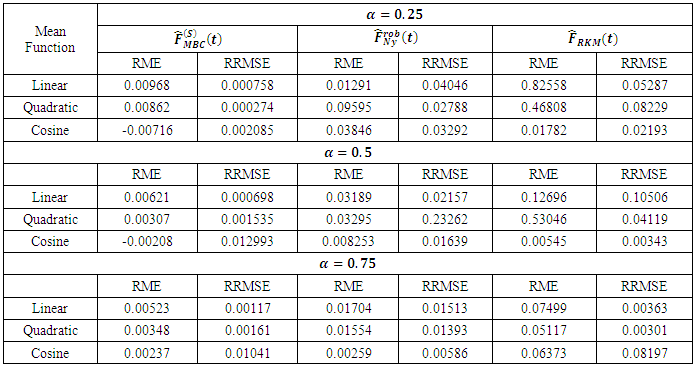
and 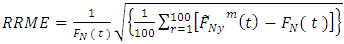 respectively where m represents the level of iteration. Table 2 shows the conditional Relative Mean Error (RME) and Relative Root Mean Error (RRME) for the estimators at various values of the quantile
respectively where m represents the level of iteration. Table 2 shows the conditional Relative Mean Error (RME) and Relative Root Mean Error (RRME) for the estimators at various values of the quantile 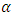 (i.e. 0.25, 0.5 and 0.75). Comparing the results in Table 1 and Table 2, it can be seen that
(i.e. 0.25, 0.5 and 0.75). Comparing the results in Table 1 and Table 2, it can be seen that 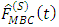 has minimum Relative Mean Error and Relative Root Mean Error followed by
has minimum Relative Mean Error and Relative Root Mean Error followed by 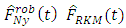 and at all levels of the
and at all levels of the 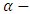 quantile.
quantile.Table 1. Unconditional Relative Mean Errors and Relative Root Mean Errors
 |
| |
|
Table 2. Conditional Relative Mean Errors and Relative Root Mean Errors
 |
| |
|
5. Conclusions
Use of 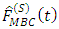 has proved to yield results with great precision.
has proved to yield results with great precision. 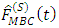 can therefore be used in estimating distribution functions for stratified populations in various sectors.
can therefore be used in estimating distribution functions for stratified populations in various sectors.
References
| [1] | Breunig, R. (2008). Nonparametric density estimation for stratified samples. Statistics and Probability Letters, 78(14): 2194-2200. |
| [2] | Burr, T., Hengartner, N., Matzner-Lober, E., Myers, S., and Rouviere, L. (2010). Smoothing low resolution gamma spectra. IEEE Transactions on Nuclear Science, 57(5): 2831–2840. |
| [3] | Chambers, R. and Clark, R. (2012). An introduction to model-based survey sampling with applications, volume 37. OUP Oxford. |
| [4] | Chambers, R. L., Dorfman, A. H., and Wehrly, T. E. (1993). Bias robust estimation in finite populations using nonparametric calibration. Journal of the American Statistical Association, 88(421): 268–277. |
| [5] | Chambers, R. L. and Dunstan, R. (1986). Estimating distribution functions from survey data. Biometrika, 73(3): 597–604. |
| [6] | Dorfman, A. H. and Hall, P. (1993). Estimators of the finite population distribution function using nonparametric regression. The Annals of Statistics, pages 1452–1475. |
| [7] | Hengartner, N., Matzner-Løber, E., Rouviere, L., and Burr, T. (2009). Multiplicative bias corrected nonparametric smoothers. arXiv preprint arXiv:0908.0128. |
| [8] | Kuk, A. Y. (1993). A kernel method for estimating finite population distribution functions using auxiliary information. Biometrika, 80(2): 385–392. |
| [9] | Linton, O. and Nielsen, J. P. (1994). A multiplicative bias reduction method for nonparametric regression. Statistics & Probability Letters, 19(3): 181–187. |
| [10] | Modarres, R. (2002). Efficient nonparametric estimation of a distribution function. Computational Statistics and Data Analysis, 39(1): 75-95. |
| [11] | Onsongo, W. M., Otieno, R. O. and Orwa, G. O. (2018). Bias reduction technique for estimating finite population distribution function under simple random sampling without replacement. International Journal of Statistics and Applications, 8(5): 259-266. |
| [12] | Rao, J. N. K., Kovar, J. G., and Mantel H. J. (1990). On Estimating Distribution Functions and Quantiles from Survey data Using Auxiliary Information. Biometrika, pages 365-375. |
| [13] | Zhao, P.-Y., Tang, M.L., and Tang, N.S. (2013). Robust estimation of distribution functions and quantiles with non-ignorable missing data. Canadian Journal of Statistics, 41(4): 575–595. |


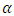 -Quantile, Multiplicative Bias Correction
-Quantile, Multiplicative Bias Correction
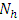 where
where 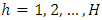 such that
such that 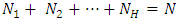 .Let
.Let 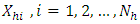 be the auxiliary variable for the
be the auxiliary variable for the 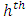 stratum with corresponding survey measurement
stratum with corresponding survey measurement 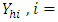
 from a common univariate distribution function.Suppose that a simple random sample of size
from a common univariate distribution function.Suppose that a simple random sample of size 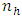 is drawn without replacement from the
is drawn without replacement from the 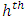 stratum such that the sample proportion
stratum such that the sample proportion 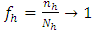 as
as 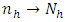 and
and 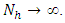 Then, the empirical distribution function for a finite population is defined as
Then, the empirical distribution function for a finite population is defined as 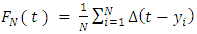
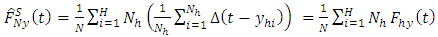
 denotes the step function of a given set, t is the
denotes the step function of a given set, t is the 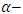 quantile and i denotes the observation made from the
quantile and i denotes the observation made from the 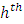 stratum.
stratum. 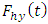 is the
is the 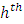 stratum distribution function for the random variable Y.Let s be a sample of
stratum distribution function for the random variable Y.Let s be a sample of 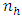 units drawn from the
units drawn from the 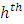 stratum via simple random sampling without replacement and
stratum via simple random sampling without replacement and 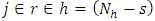 be the non-sampled units in the
be the non-sampled units in the 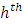 stratum.Suppose the auxiliary information is known for all elements in the population while the survey variable is only observed for the sample elements.Further, suppose that the survey variables are generated using a super population model defined by
stratum.Suppose the auxiliary information is known for all elements in the population while the survey variable is only observed for the sample elements.Further, suppose that the survey variables are generated using a super population model defined by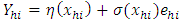
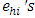 are independent and identically distributed random variables with zero mean and variance
are independent and identically distributed random variables with zero mean and variance 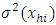 with
with 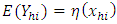 and
and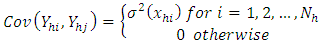 Where
Where 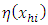 and
and 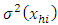 are assumed to be smooth functions of
are assumed to be smooth functions of 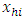 .The predictive form of the empirical distribution function for a stratified population under the model based approach therefore becomes
.The predictive form of the empirical distribution function for a stratified population under the model based approach therefore becomes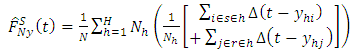
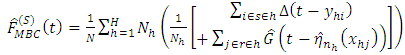
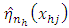 is the model-based nonparametric estimator for
is the model-based nonparametric estimator for 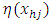 and
and 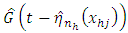 is the estimated distribution function of the residuals defined by
is the estimated distribution function of the residuals defined by 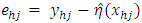 using elements drawn from the
using elements drawn from the 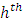 stratum.Since
stratum.Since 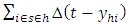 is known from the sample drawn, the task reduces to that of estimating
is known from the sample drawn, the task reduces to that of estimating 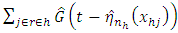 .To do this, the multiplicative bias correction technique is employed.Suppose that
.To do this, the multiplicative bias correction technique is employed.Suppose that 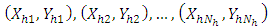 are N independent pairs of random variables with the pair
are N independent pairs of random variables with the pair 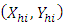 being real valued.Define a pilot smoother of the regression function as
being real valued.Define a pilot smoother of the regression function as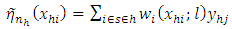
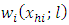 are the Nadaraya-Watson kernel weights defined by
are the Nadaraya-Watson kernel weights defined by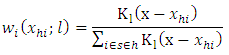 and l is the bandwidth.
and l is the bandwidth. 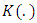 is a function that is continuous, symmetric and bounded with real values.Let the ratio
is a function that is continuous, symmetric and bounded with real values.Let the ratio 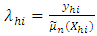 be a noisy estimate of the inverse relative estimation error of the smoother
be a noisy estimate of the inverse relative estimation error of the smoother 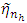 given by
given by 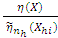 .Smoothing
.Smoothing 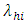 yields
yields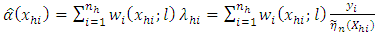
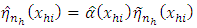
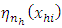 1. The regression function is twice continuously differentiable everywhere.2. The bandwidth l is such that
1. The regression function is twice continuously differentiable everywhere.2. The bandwidth l is such that 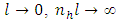 , as
, as 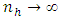 .Using equation (7) in equation (8) yields
.Using equation (7) in equation (8) yields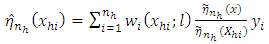
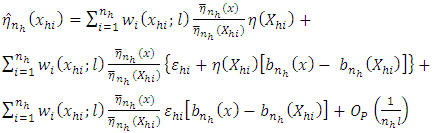
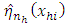 see (Onsongo et al., 2018).The estimator for the distribution function for a stratified population therefore becomes
see (Onsongo et al., 2018).The estimator for the distribution function for a stratified population therefore becomes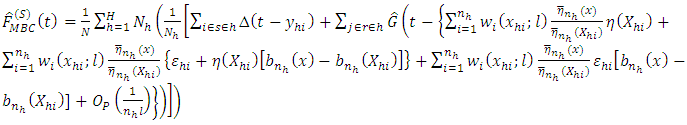
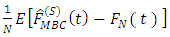
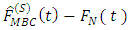 is the estimated bias under stratified sampling.Let
is the estimated bias under stratified sampling.Let 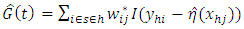 where
where 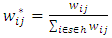 where t is the
where t is the  -quantile and
-quantile and 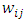 are the weights that only take non-zero values for sample units
are the weights that only take non-zero values for sample units 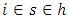 with
with 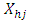 close to
close to 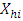 .Equation (5) can then be written as
.Equation (5) can then be written as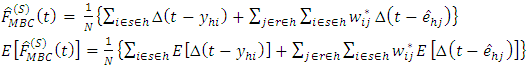 However
However 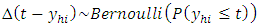 and
and 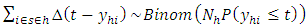 implying that
implying that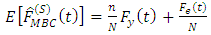
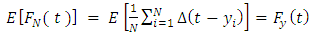
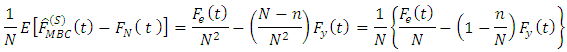
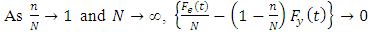
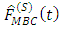 is therefore asymptotically unbiased.
is therefore asymptotically unbiased.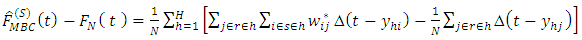 The variance of the estimated bias can therefore be written as
The variance of the estimated bias can therefore be written as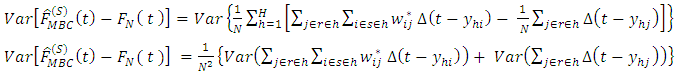
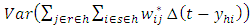 and let
and let 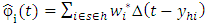 Then
Then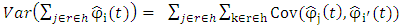
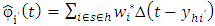 Define
Define 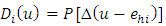
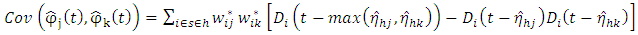
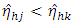 whenever
whenever 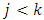 and suppose that the non-sampled units are labelled from 1 to
and suppose that the non-sampled units are labelled from 1 to 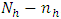 .Then
.Then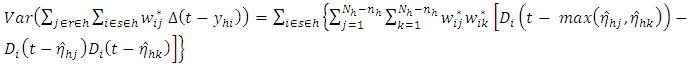
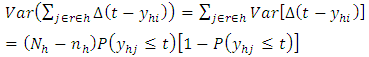
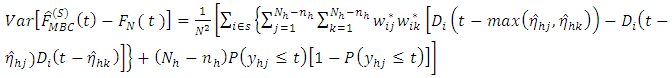
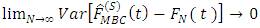 .
.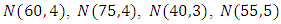 such that there is a total of 2, 000 auxiliary variables.The corresponding survey values
such that there is a total of 2, 000 auxiliary variables.The corresponding survey values 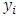 are generated using the super-population model
are generated using the super-population model 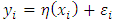 after which they are stratified according to form four strata. Proportional allocation was used to draw samples of size 100 from each stratum.The estimators
after which they are stratified according to form four strata. Proportional allocation was used to draw samples of size 100 from each stratum.The estimators 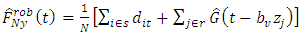 suggested by (Chambers and Clark, 2012) and
suggested by (Chambers and Clark, 2012) and 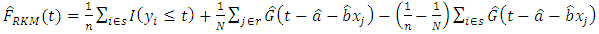 suggested by (Rao et al 1990) were then used in the comparison of results.Table 1 shows the unconditional Relative Mean Error (RME) and Relative Root Mean Error (RRME) for the estimators at various values of the quantile
suggested by (Rao et al 1990) were then used in the comparison of results.Table 1 shows the unconditional Relative Mean Error (RME) and Relative Root Mean Error (RRME) for the estimators at various values of the quantile 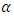 (i.e. 0.25, 0.5 and 0.75). Linear, quadratic and cosine mean functions were used to obtain the tabulated results. Similar results and conclusions can be obtained using other mean functions such as sine, cycle and bump.The conditional Relative Mean Error and Relative Root Mean Error for an estimator
(i.e. 0.25, 0.5 and 0.75). Linear, quadratic and cosine mean functions were used to obtain the tabulated results. Similar results and conclusions can be obtained using other mean functions such as sine, cycle and bump.The conditional Relative Mean Error and Relative Root Mean Error for an estimator 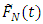 are calculated as:
are calculated as: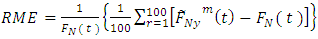 and
and 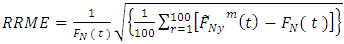 respectively where m represents the level of iteration. Table 2 shows the conditional Relative Mean Error (RME) and Relative Root Mean Error (RRME) for the estimators at various values of the quantile
respectively where m represents the level of iteration. Table 2 shows the conditional Relative Mean Error (RME) and Relative Root Mean Error (RRME) for the estimators at various values of the quantile 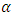 (i.e. 0.25, 0.5 and 0.75). Comparing the results in Table 1 and Table 2, it can be seen that
(i.e. 0.25, 0.5 and 0.75). Comparing the results in Table 1 and Table 2, it can be seen that 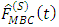 has minimum Relative Mean Error and Relative Root Mean Error followed by
has minimum Relative Mean Error and Relative Root Mean Error followed by 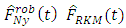 and at all levels of the
and at all levels of the 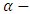 quantile.
quantile.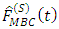 has proved to yield results with great precision.
has proved to yield results with great precision. 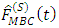 can therefore be used in estimating distribution functions for stratified populations in various sectors.
can therefore be used in estimating distribution functions for stratified populations in various sectors. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
