1. Introduction

The modeling and statistical analysis of count data are crucial in almost every fields of knowledge including biological science, insurance, medical science, and finance, some amongst others. Count data are generated by various phenomena such as the number of insurance claimants in insurance industry, number of yeast cells in biological science, number of chromosomes in genetics, etc. It has been observed that, in general, count data follows under-dispersion (variance < mean), equi-dispersion (variance = mean) or over-dispersion (variance > mean). The over-dispersion of count data have been addressed using mixed Poisson distributions by different researchers including Raghavachari et al (1997), Karlis and Xekalaki (2005), Panjeer (2006), are some among others. Mixed Poisson distributions arise when the parameter of the Poisson distribution is a random variable having some specified distributions. The distribution of the parameter of the Poisson distribution is known as mixing distribution. It has been observed that the general characteristics of the mixed Poisson distribution follow some characteristics of its mixing distributions. In distribution theory, various mixed Poisson distributions have been derived by selecting a proper mixing distribution.

The classical negative binomial distribution (NBD) derived by Greenwood and Yule (1920) is the mixed Poisson distribution where the mean of the Poisson random variable is distributed as a gamma random variable. The NBD has been used to model over-dispersed count data. However, the NBD may not be appropriate for some over-dispersed count data due to its theoretical or applied point of view. Other mixed Poisson distributions arise from the choice of alternative mixing distributions. For example, the Poisson-Lindley distribution, introduced by Sankaran (1970), is a Poisson mixture of Lindley (1958) distribution. The Poisson-Akash distribution, introduced by Shanker (2017), is a Poisson mixture of Akash distribution suggested by Shanker (2015). It has been observed by Karlis and Xekalaki (2005) that there are naturally situations where a good fit is not obtainable with a particular mixed Poisson distribution in case of over-dispersed count data. This shows that there is a need for new mixed Poisson distribution which gives a better fit as compared with the existing mixed Poisson distributions.

Shanker (2017) proposed the discrete Poisson- Akash distribution (PAD) to model count data defined by its probability mass function (pmf)

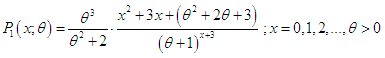(1.1)

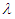Moments and moments based measures, statistical properties; estimation of parameter using both the method of moments and the method of maximum likelihood and applications of PAD has been discussed by Shanker (2017). The distribution arises from the Poisson distribution when its parameter follows Akash distribution introduced by Shanker (2015) and defined by its probability density function (pdf)

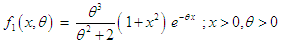(1.2)

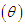The pdf (1.2) is a convex combination of exponential and gamma 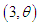distributions. Shanker (2015) discussed statistical properties including moments based coefficients, hazard rate function, mean residual life function, mean deviations, stochastic ordering, Renyi entropy measure, order statistics, Bonferroni and Lorenz curves, stress- strength reliability, along with estimation of parameter and applications to model lifetime data from biomedical science and engineering.

The first four moments about origin and the variance of PAD (1.1) obtained by Shanker (2017) are given by

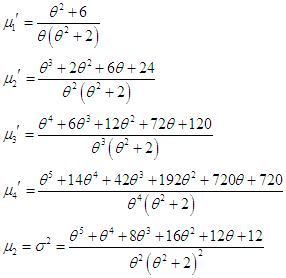Shanker and Shukla (2017) proposed a two-parameter Akash distribution (TPAD) having parameters 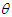and and defined by its pdf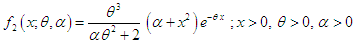

(1.3)

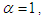Its structural properties including moments, hazard rate function, mean residual life function, mean deviations, stochastic ordering, Renyi entropy measure, order statistics, Bonferroni and Lorenz curves, stress- strength reliability , estimation of parameters and applications for modeling survival time data has been discussed in Shanker and Shukla (2017). It can be easily shown that at TPAD (1.3) reduces to Akash distribution (1.2).

The main purpose of this paper is to propose a two-parameter Poisson- Akash distribution, a Poisson mixture of two-parameter Akash distribution suggested by Shanker and Shukla (2017). Its moments based measures including coefficients of variation, skewness, kurtosis and index of dispersion have been derived and their behaviors have been discussed graphically. Its statistical properties including hazard rate function, unimodality and generating functions have been studied. The estimation of parameters has been discussed using method of moments and the method maximum likelihood. Applications and goodness of fit of the distribution has also been discussed through two examples of observed real count datasets from biological sciences and the fit has been compared with other discrete distributions.

2. A Two-Parameter Poisson-Akash Distribution

Assuming that the parameter 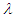of the Poisson distribution follows TPAD (1.3), the Poisson mixture of TPAD can be obtained as

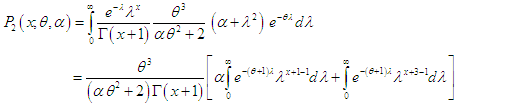(2.1)

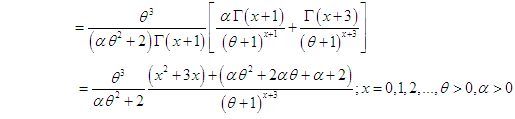(2.2)

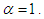We would call this pmf a two-parameter Poisson - Akash distribution (TPPAD). It can be easily verified that PAD (1.1) is a particular case of TPPAD for The nature and behavior of TPPAD for varying values of the parameters and have been explained graphically in figure 1.

Figure 1. Probability mass function plot of TPPAD for varying values of parameters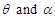

3. Statistical Constants

In this section factorial moments, raw moments, central moments and moments based statistical measures including coefficient of variation, skewness, kurtosis and index of dispersion of TPPLD has been obtained.

3.1. Factorial Moments

Using (2.1), the th factorial moment about origin of the TPPAD (2.2) can be obtained as

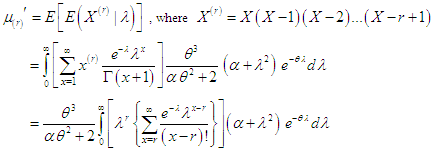Assuming 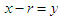, we get

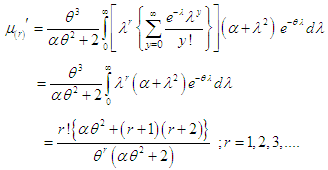(3.1.1)

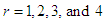Taking in (3.1.1), the first four factorial moments about origin of TPPAD (2.2) can be obtained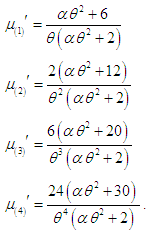

3.2. Raw Moments (Moments about Origin)

Using the relationship between factorial moments about origin and the raw moments, the first four raw moments of TPPAD (2.2) can be obtained as

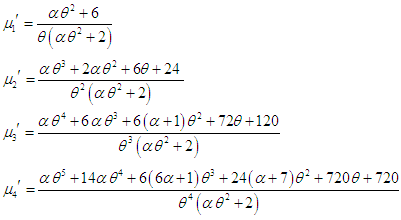
3.3. Central Moments (Moments about Mean)

Using the relationship 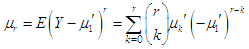between central moments and the raw moments, the central moments of the TPPAD (2.2) can be obtained as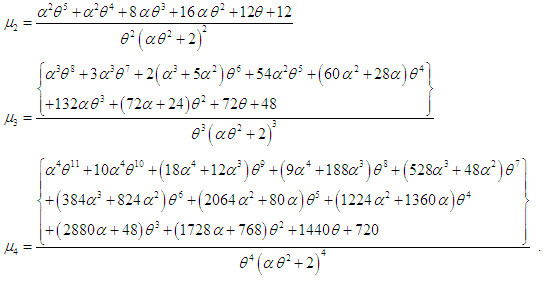

3.4. Coefficients of Variation, Skewness, Kurtosis and Index of Dispersion

The coefficient of variation 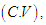coefficient of Skewness 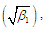coefficient of Kurtosis 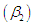and index of dispersion 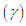of the TPPAD (2.2) are thus obtained as

Now from the index of dispersion it is obvious that if and then 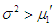(over dispersion); if 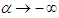and 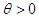, then 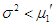(under dispersion) and if 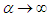and 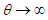, then 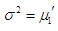(equi dispersion). Nature and behavior of coefficient of variation, coefficient of skewness, coefficient of kurtosis and index of dispersion of TPPAD for varying values of parameters 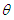and 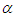have been shown graphically in figure 2.

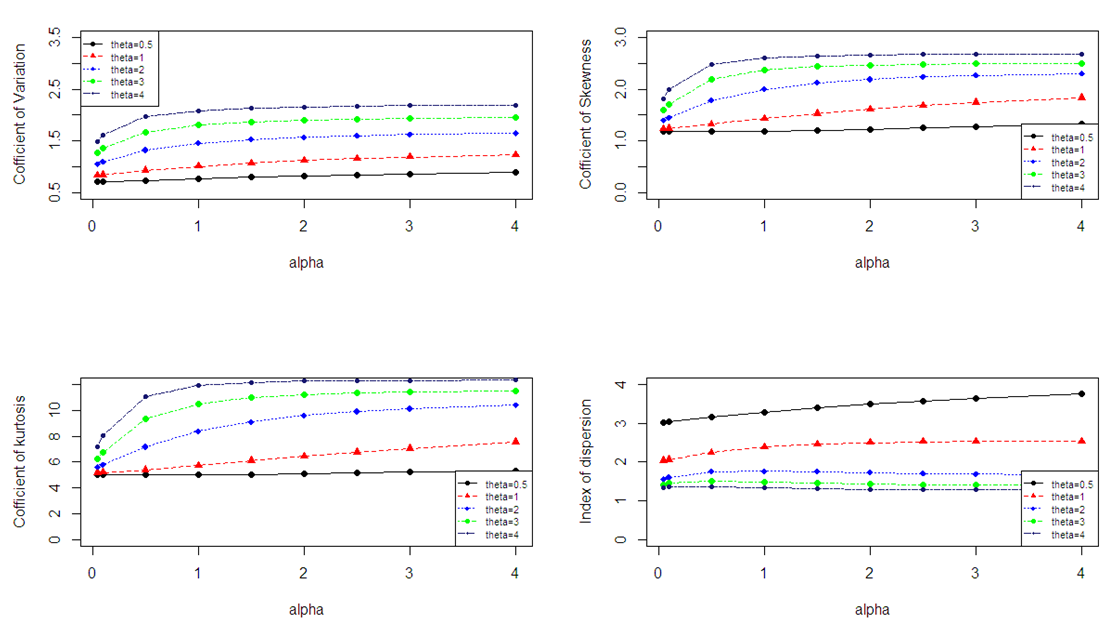Figure 2. Nature and behavior of coefficient of variation, coefficient of skewness, coefficient of kurtosis and index of dispersion of TPPAD for varying values of parameters

4. Statistical Properties

In this section the unimodality, increasing hazard rate, probability generating function and the moment generating function of TPPLD has been discussed.

4.1. Increasing Hazard Rate and Unimodality

We have

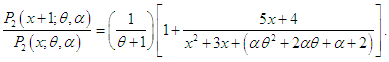It can be easily verified that this is a decreasing function in 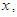and hence 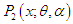is log-concave. Now using the results of relationship between log-concavity, unimodality and increasing hazard rate (IHR) of discrete distributions given in Grandell (1997), it can concluded that TPPAD (2.2) has an increasing hazard rate and is unimodal.

4.2. Generating Functions

The probability generating function of TPPAD can be obtained as

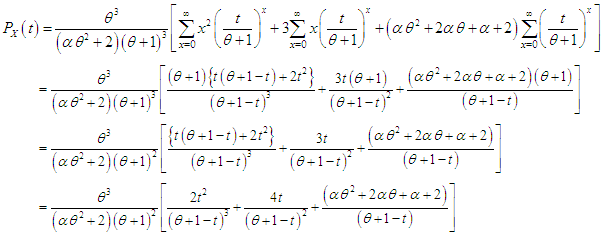The moment generating function of TPPAD is thus given by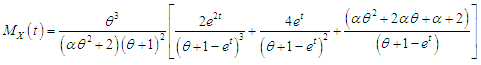

5. Estimation of Parameters

In this section the estimation of parameters of TPPLD using the method of moments and the method of maximum likelihood has been discussed.

5.1. Method of Moments Estimation of Parameters

Since TPPAD has two parameters to be estimated, taking the first two moments about origin, we have

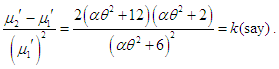Assuming 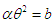, we get

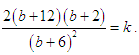This gives a quadratic equation in 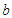as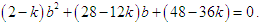

Replacing the first population moment about origin and the second population moment about origin with their respective sample moments, an estimate of 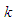can be obtained and substituting the value of in the above equation, an estimate of 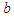can be obtained. Again, replacing the population mean with the corresponding sample mean and taking 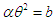in 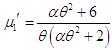, we get

This gives the method of moments estimate (MOME) 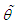of parameter 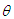as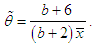

Thus the MOME 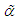of parameter 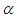is given by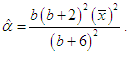

5.2. Maximum Likelihood Estimation of Parameters

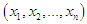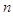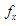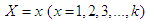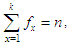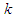Suppose be a random sample of size from the TPPAD (2.2) and let be the observed frequency in the sample corresponding to such that where is the largest observed value having non-zero frequency. The log- likelihood function of TPPAD (2.2) can be given by

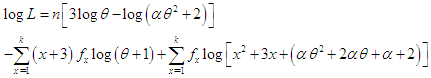The maximum likelihood estimates 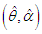of parameters 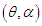of TPPAD (2.2) is the solutions of the following log- likelihood equations

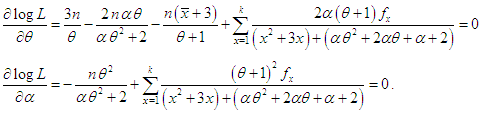where 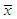is the sample mean. These two log likelihood equations do not seem to be solved directly because they are not in closed forms. These two log-likelihood equations can be solved iteratively using R-software till sufficiently close estimates of 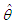and 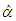are obtained.

6. Applications

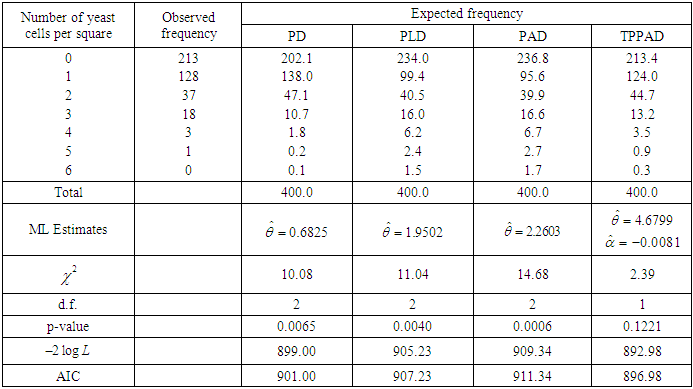
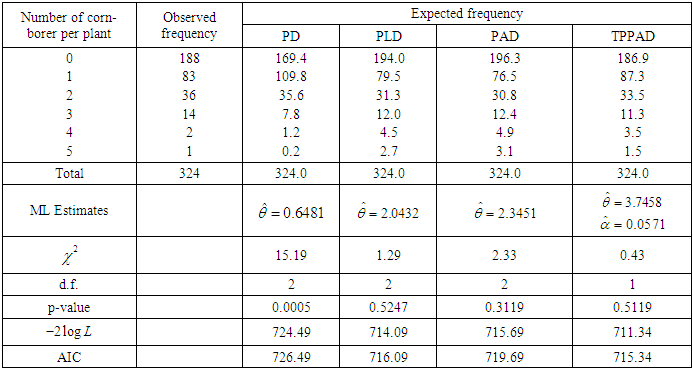
The TPPAD has been fitted to two count datasets from biological sciences to test its goodness of fit over Poisson distribution (PD), Poisson-Lindley distribution (PLD) and Poisson-Akash distribution (PAD) using maximum likelihood estimates (MLE’s) of parameters. The first dataset is the number of Student’s historic data on Haemocytometer counts of yeast cells available in Gosset (1908) and the second data set is the number of European corn- borer of Mc. Guire et al (1957). The fitted plots of distributions for datasets in tables 1 and 2 are presented in figure 3. Since the expected frequencies given by TPPAD are more closure to the original frequencies than the expected frequencies given by PD, PLD, and PAD, it is clear from the goodness of fit of TPPAD and from the fitted plots of distributions that TPPAD gives much closer fit than PD, PLD, and PAD and hence it can be considered as an important distribution in ecology.

Table 1. Observed and expected number of Haemocytometer yeast cell counts per square observed by Gosset (1908)

Table 2. Observed and expected number of European corn- borer of Mc. Guire et al (1957)

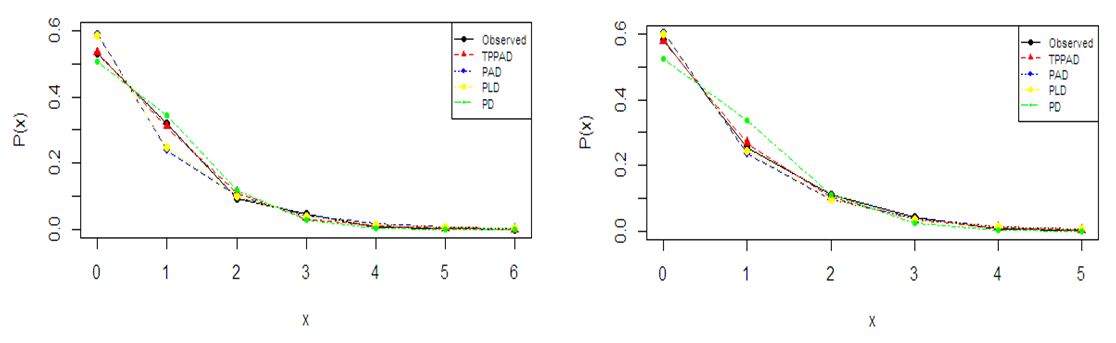Figure 3. Fitted plots of distributions for datasets 1 and 2

7. Conclusions

A two-parameter Poisson-Akash distribution (TPPAD) which includes one parameter Poisson-Akash distribution has been proposed. Its moments and moments based statistical constants have been derived and studied. Some statistical properties have been discussed. Method of moments and the method of maximum likelihood have been discussed for estimating parameters of the distribution. Finally, applications of the proposed distribution have been explained with two count datasets from biological sciences and fit has been found quite satisfactory over other discrete distributions including PD, PLD and PAD.

ACKNOWLEDGEMENTS

Authors are grateful to the editor in chief of the journal and the anonymous reviewer for their fruitful comments.