N. M. Kilany1, W. A. Hassanein2
1Faculty of Science, Menoufia University, Al Minufya, Egypt
2Faculty of Science, Tanta University, Tanta, Gharbia, Egypt
Correspondence to: N. M. Kilany, Faculty of Science, Menoufia University, Al Minufya, Egypt.
| Email: |  |
Copyright © 2018 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
Characterization of a specific probability distribution is an essential procedure to give the investigator familiarity about their model if it fits the requirements of the underlying probability distribution. A characterization results is uniquely specified the probability distribution. One of the important type of distributions, which used extensively in economic and actuarial science, is the size distributions. This paper is concerned with characterization of one of these distributions, which is Benktander type II distribution. The characterization procedure is studied via right, left truncated moments and truncated moments of order statistics. Finally, to give a validation practice that the obtained characterization results could precisely identify Benktander distribution, a simulation study for this procedure is presented.
Keywords:
Benktander type II distribution, Characterization of distributions, Truncated moments, Order statistics
Cite this paper: N. M. Kilany, W. A. Hassanein, Characterization of Benktander Type II Distribution via Truncated Moments and Order Statistics, International Journal of Probability and Statistics , Vol. 7 No. 4, 2018, pp. 106-113. doi: 10.5923/j.ijps.20180704.02.
1. Introduction
Before a specific distribution model is applied to fit the real data, it is crucial to check whether the given distribution satisfies the requirements by its characterization. Recently, a developing concentration has been focused on characterization of probability distributions. Practically, the characterization results are applied widely in insurance, economic, quality control and queuing theory. It has attracted the attention of many researchers in many fields by different methods. For example, Nanda [10] studied the characterization of exponential distribution and Rayleigh distribution through failure rate and mean residual life functions. Afify, et al. [1] used the s th conditional expectation of order statistics in terms of their failure rate to characterize the exponential and power function distributions. Kilany [8] introduced a new theorem for characterization of the continuous distribution based on truncated moments of order statistics and employ it to characterize Lindley distribution. Moreover, a characterization of Lindley distribution using the truncated moments of order statistics is presented. Ahsanullah & Hamedani [3] characterized beta of the first kind and power function distribution using order statistics. Many other papers in the literature dealing with characterization, see for instance, Huang & Su [7], Su & Huang [11] and Ahsanullah et al. ([2], [4], [5]). This paper introduces the characterization of Benktander distribution type II by truncated moments and truncated moments of order statistics. The organization of the paper is; In Section 2, Benktander type II distribution and its main statistical properties are summarized. Section 3 includes the characterization of Benktander type II by left and right truncated moments. Moreover, in Section 4, the characterization through truncated moments of order statistics of Benktander type II is derived. Finally, a simulation study is given to enable the practitioner to identify the present distribution in Section 5.
2. Benktander Type II Distribution
One of the vital size distributions is called Benktander distribution. Starting from the observation that empirical mean excess functions point to distributions that are intermediate between Pareto and exponential distributions. In 1970, Gunnar Benktander discussed two types of distributions called Benktander Type I & Type II distributions (see Kleiber & Kotz [9]). These distributions used to model heavy tailed losses commonly found in non-life and causality actuarial science using various forms of mean excess functions. The first type of Benktander is close to lognormal distribution and Benktander of the second type asymptotically resembles the mean excess function of Weibull distribution. Benktander type II (second type) is sometimes called Benktander Weibull distribution.The main statistical functions concerning Benktander Type II distribution are defined as followsŸ The probability density function (p.d.f) of Benktander Type II distribution is defined by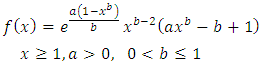 | (1) |
Ÿ The cumulative distribution function (c.d.f)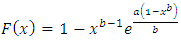 | (2) |
Ÿ The failure rate function 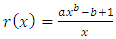 | (3) |
Ÿ The reversed failure rate function 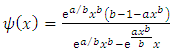 | (4) |
3. Characterization of Benktander Type II Distribution by Truncated Moments
Henceforward, let X be an absolutely continuous random variable with c.d.f.  and p.d.f
and p.d.f  . Assume
. Assume  and
and 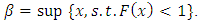 Define the failure rate function
Define the failure rate function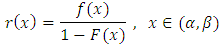 and the reversed failure rate function
and the reversed failure rate function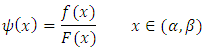
3.1. Characterization of Benktander Type II by Left Truncated Moments
The following Lemma is needed to perform the characterization procedure by left truncated moments. See, Ahsanullah et al. [5].Lemma 1.Let  be a continuous function and
be a continuous function and 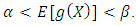 If
If 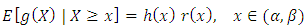 where
where 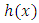 is a differentiable function in
is a differentiable function in 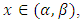 then
then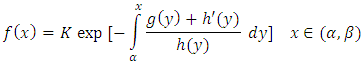 where
where 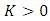 is a normalization constant.Theorem 1. A random variable, X, has Benktander Type II distribution with parameters
is a normalization constant.Theorem 1. A random variable, X, has Benktander Type II distribution with parameters 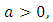
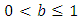 if and only if
if and only if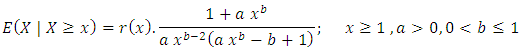 where,
where, 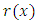 is the hazard function of Benktander Type II distribution.Proof.Necessity: Suppose X has Benktander Type II distribution with parameters
is the hazard function of Benktander Type II distribution.Proof.Necessity: Suppose X has Benktander Type II distribution with parameters 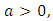
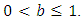 Using Equations (1) and (3)
Using Equations (1) and (3)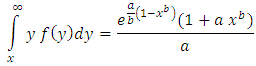 Hence,
Hence, 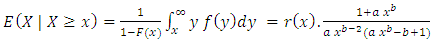 Sufficiency: Let
Sufficiency: Let  and
and 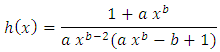 is a differentiable function in
is a differentiable function in 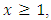
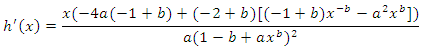 After some simplifications,
After some simplifications, 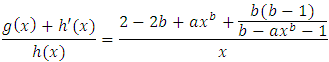 Now for all
Now for all 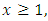
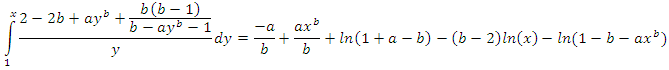 By using Lemma 1, for all
By using Lemma 1, for all 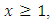 we get
we get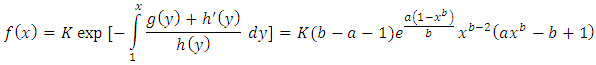 where
where 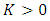 is the normalizing constant,
is the normalizing constant, 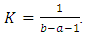 Then, the proof is completed.
Then, the proof is completed.
3.2. Characterization of Benktander Type II by Right Truncated Moments
The following Lemma is needed to obtain the characterization of Benktander Type II by right truncated moments. See, Ahsanullah et al. [5].Lemma 2.Let 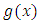 be a continuous function in
be a continuous function in 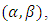 and
and 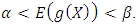 If
If 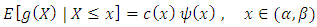 where,
where, 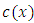 is a differentiable function in
is a differentiable function in 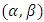 then
then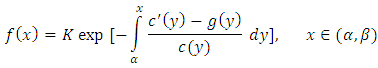 where,
where, 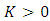 is a normalization constant.Theorem 2.A random variable, X, has Benktander Type II distribution with parameters
is a normalization constant.Theorem 2.A random variable, X, has Benktander Type II distribution with parameters 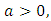
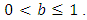 if and only if
if and only if 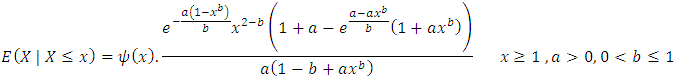 where
where 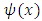 is the Benktander Type II reversed hazard function.Proof.Necessity. Suppose X has a Benktander Type II distribution with parameters
is the Benktander Type II reversed hazard function.Proof.Necessity. Suppose X has a Benktander Type II distribution with parameters 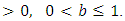 Then by using Equation (1) and (4)
Then by using Equation (1) and (4)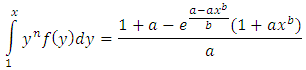
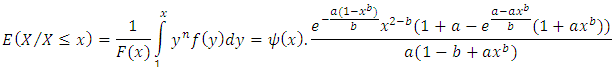 Sufficiency. Let
Sufficiency. Let 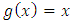 and
and 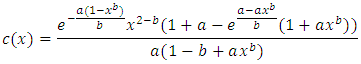 is a differentiable function in
is a differentiable function in 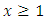 and
and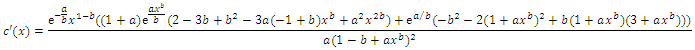 After some simplifications,
After some simplifications, 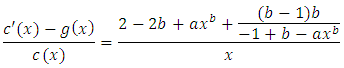 For all
For all 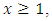
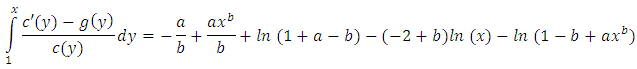 Then by using Lemma 2, the following result can be obtained
Then by using Lemma 2, the following result can be obtained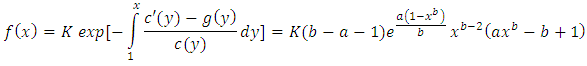 where
where 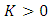 is a normalization constant,
is a normalization constant, 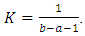 This complete the proof.
This complete the proof.
4. Characterization of Benktander Type II Distribution by Truncated Moments of Order Statistics
Suppose 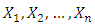 be a random sample of size n from a continuous distribution with c.d.f.
be a random sample of size n from a continuous distribution with c.d.f. 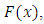 p.d.f.
p.d.f. 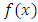 and survival function
and survival function 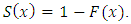 Let
Let 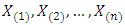 be the corresponding order statistics. Then the p.d.f. of
be the corresponding order statistics. Then the p.d.f. of 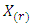 and the joint p.d.f. of
and the joint p.d.f. of 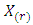 and
and 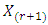 are given, respectively, as follows (Arnold et al. [6])
are given, respectively, as follows (Arnold et al. [6])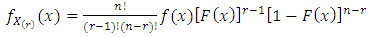 | (5) |
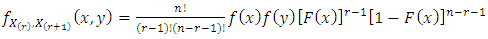 | (6) |
From Equations (5) and (6) the conditional p.d.f. of 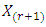 given
given 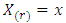 is given by
is given by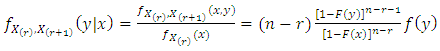 | (7) |
In this Section, Benktander type II distribution is to be characterized through truncated moments of order statistics given by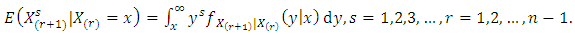 | (8) |
4.1. Characterization Results
The following theorem is presented for characterization of Benktander type II distribution based on the rth-truncated moments of the order statistics.Theorem 3.Suppose 𝑋 be a continuous random variable with distribution function 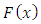 and survival function
and survival function 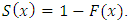 Let
Let 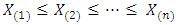 denote the order statistics of a random sample of size n from
denote the order statistics of a random sample of size n from 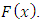 Then X has the Benktander type II distribution with parameters
Then X has the Benktander type II distribution with parameters 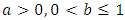 if and only if
if and only if 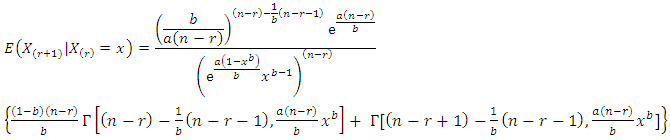 | (9) |
Proof.Necessity. Suppose X has Benktander Type II distribution with parameters 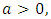
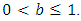 Using Equations (2), (7) and (8), the following results are abtianed
Using Equations (2), (7) and (8), the following results are abtianed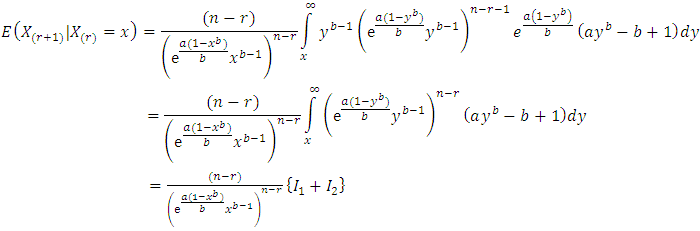 | (10) |
where,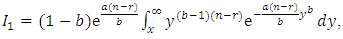
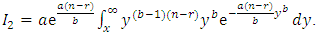 Substituting in integrations
Substituting in integrations 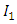 and
and 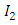 by
by 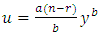 and using the definition of incomplete gamma function,
and using the definition of incomplete gamma function, 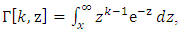
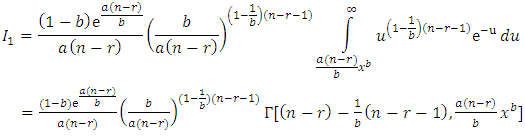 | (11) |
and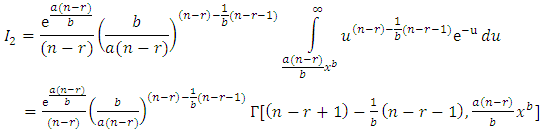 | (12) |
Substituting from Equations (11) and (12) into Equation (10), the result is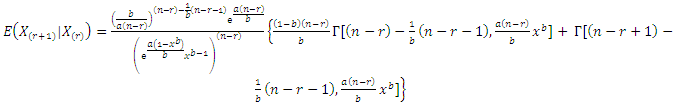 Sufficiency: Let
Sufficiency: Let 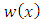 be the right hand side of Equation (9), i.e.
be the right hand side of Equation (9), i.e.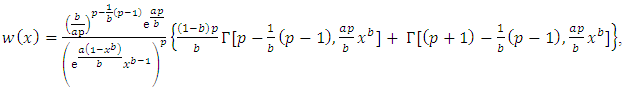 where
where 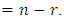 Then, Equation (9) can be rewritten as follows
Then, Equation (9) can be rewritten as follows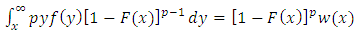 | (13) |
Differentiating both sides of Equation (13) with respect to x, then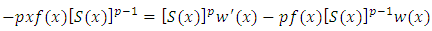 | (14) |
where 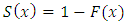 is the survival function.Dividing both sides of Equation (14) by
is the survival function.Dividing both sides of Equation (14) by 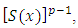 then
then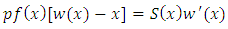 Or equivalently,
Or equivalently,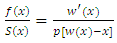 | (15) |
From the fact that 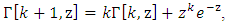 then
then 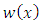 and
and 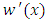 will be
will be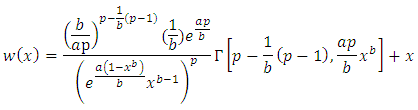 and
and 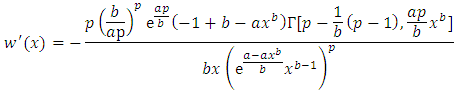 Hence, Equation (15) becomes
Hence, Equation (15) becomes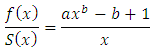 Now, for
Now, for 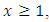 integration both sides of the above Equation with respect to x gives
integration both sides of the above Equation with respect to x gives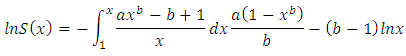 Hence,
Hence,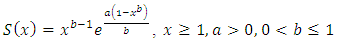 which is the survival function of the Benktander type II distribution. This completes proof of the theorem.
which is the survival function of the Benktander type II distribution. This completes proof of the theorem.
4.2. Simulation Study
The purpose of the simulation study is to give a validation procedure for simple and easily checks using the simulated data. This enables the experimenter to test whether the available data follows a specified distribution or not, instead of going to sophisticated analysis of hypothesis test.To validate the correctness of the mathematical results obtained for characterization of Benktander type II, a simulation study is showed by generating samples 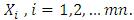 They are randomly classified into m samples, each of containing n observations. To satisfy more accurate consequence with less variability and more stability in characterization results, the study is conducted with large sample size, for example;
They are randomly classified into m samples, each of containing n observations. To satisfy more accurate consequence with less variability and more stability in characterization results, the study is conducted with large sample size, for example; 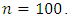 Choosing the number of samples are
Choosing the number of samples are 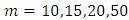 and different values of the order r with various choices of the parameter estimates a and b. Table (1) shows the L.H.S and R.H.S of Equation (9) and the absolute relative difference between them. The results indicate the closeness of both sides of Equation (9) which supporting the precision of the characterization results of Benktander distribution.
and different values of the order r with various choices of the parameter estimates a and b. Table (1) shows the L.H.S and R.H.S of Equation (9) and the absolute relative difference between them. The results indicate the closeness of both sides of Equation (9) which supporting the precision of the characterization results of Benktander distribution.Table 1. Verification of the characterization results through truncated order statistics
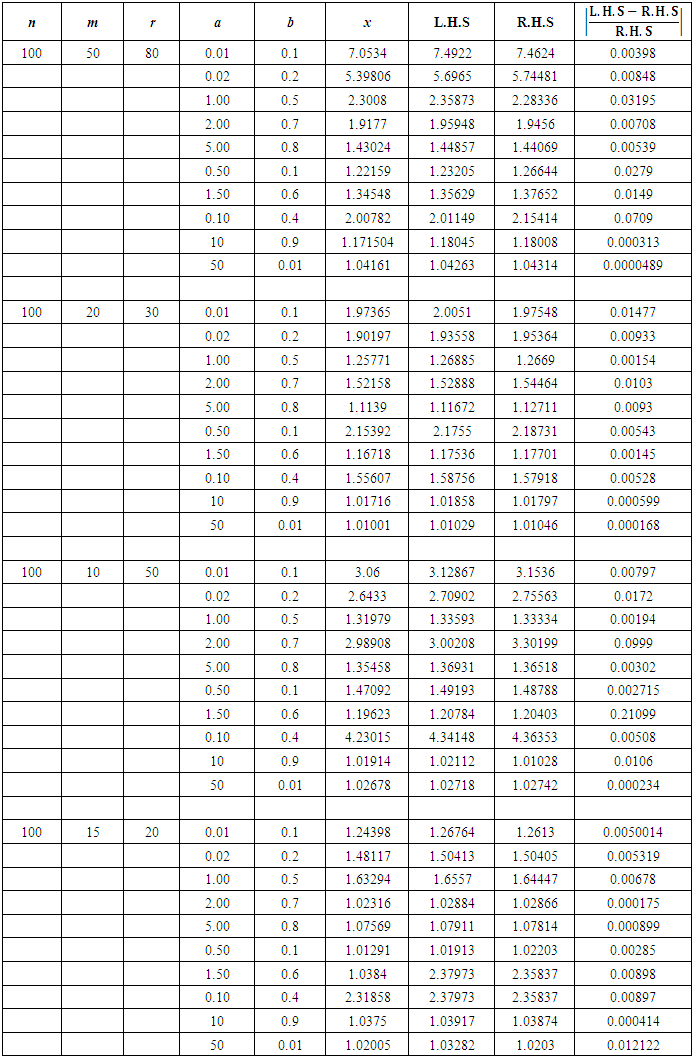 |
| |
|
References
| [1] | Afify, A., Nofal, Z. and Ahmed, A. (2013). “Characterization of Exponential and Power Function Distributions Using S th Truncated Moments of Order Statistics”. Journal of Advances in Mathematics, 4(3), 486-494. |
| [2] | Ahsanullah, M. and Aliev, F. (2008). “Some Characterizations of Exponential Distribution by Record Values”. Journal of Statistical Research, 42(2), 41-46. |
| [3] | Ahsanullah, M. and Hamedani, G.G. (2007). “Certain Characterizations of Power Function and Beta Distributions Based on Order Statistics”, Journal of Statistical Theory and Applications, 6, 220-226. |
| [4] | Ahsanullah, M. and Shakil, M. (2013). “Characterizations of Rayleigh Distribution Based on Order Statistics and Record Values”. Bulletin of the Malaysian Mathematical Sciences Society, 36(3), 625-635. |
| [5] | Ahsanullah, M. Shakil, M. and Kibra, B.M. (2016) “Characterizations of Continuous Distributions by Truncated Moments”. Journal of Modern Applied Statistical Methods, 15(1), 316-331. |
| [6] | Arnold, B.C., Balakrishnan, N. and Nagaraja, H. N. (1992). “A First Course in Order Statistics”. John Wiley & Sons, New York. |
| [7] | Huang, W.J. and Su, N.C. (2012). “Characterizations of Distributions Based on Moments of Residual Life”. Communications in Statistics -Theory and Methods, 41(15), 2750-2761. |
| [8] | Kilany, N. M. (2017). “Characterization of Lindley Distribution Based on Truncated Moments of Order Statistics. Journal of Statistics Applications and Probability, 6 (2), 1-6. |
| [9] | Kleiber, C. and Kotz, S. (2003), “Statistical Size Distributions in Economics and Actuarial Sciences". Wiely & Sons, Inc., Canada. |
| [10] | Nanda, A.K. (2010). “Characterization of Distributions through Failure Rate and Mean Residual Life Functions”. Statistics & Probability Letters, 80(9-10), 752-755. |
| [11] | Su, N.C. and Huang, W.J. (2000). “Characterizations Based on Conditional Expectations”. Statist. Papers, 41(4), 423-435. |


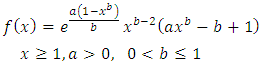
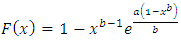
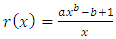
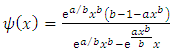
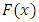 and p.d.f
and p.d.f 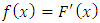 . Assume
. Assume 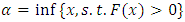 and
and 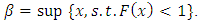 Define the failure rate function
Define the failure rate function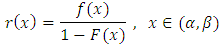 and the reversed failure rate function
and the reversed failure rate function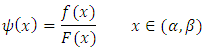
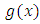 be a continuous function and
be a continuous function and 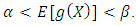 If
If 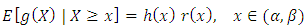 where
where 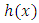 is a differentiable function in
is a differentiable function in 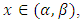 then
then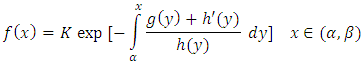 where
where 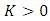 is a normalization constant.Theorem 1. A random variable, X, has Benktander Type II distribution with parameters
is a normalization constant.Theorem 1. A random variable, X, has Benktander Type II distribution with parameters 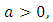
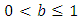 if and only if
if and only if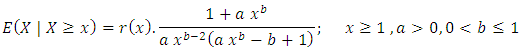 where,
where, 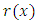 is the hazard function of Benktander Type II distribution.Proof.Necessity: Suppose X has Benktander Type II distribution with parameters
is the hazard function of Benktander Type II distribution.Proof.Necessity: Suppose X has Benktander Type II distribution with parameters 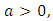
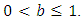 Using Equations (1) and (3)
Using Equations (1) and (3)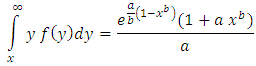 Hence,
Hence, 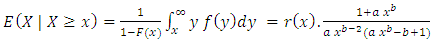 Sufficiency: Let
Sufficiency: Let  and
and  is a differentiable function in
is a differentiable function in 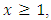
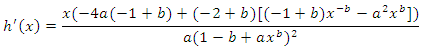 After some simplifications,
After some simplifications, 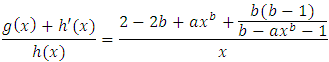 Now for all
Now for all 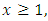
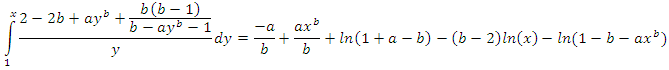 By using Lemma 1, for all
By using Lemma 1, for all 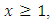 we get
we get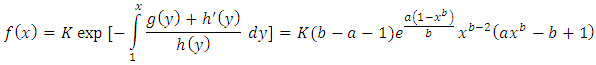 where
where 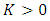 is the normalizing constant,
is the normalizing constant, 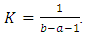 Then, the proof is completed.
Then, the proof is completed. be a continuous function in
be a continuous function in 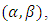 and
and 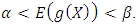 If
If 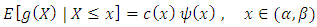 where,
where, 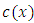 is a differentiable function in
is a differentiable function in 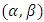 then
then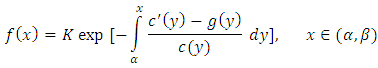 where,
where, 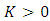 is a normalization constant.Theorem 2.A random variable, X, has Benktander Type II distribution with parameters
is a normalization constant.Theorem 2.A random variable, X, has Benktander Type II distribution with parameters 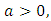
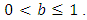 if and only if
if and only if 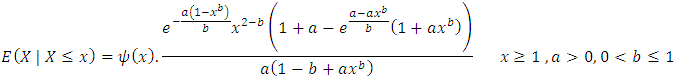 where
where 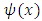 is the Benktander Type II reversed hazard function.Proof.Necessity. Suppose X has a Benktander Type II distribution with parameters
is the Benktander Type II reversed hazard function.Proof.Necessity. Suppose X has a Benktander Type II distribution with parameters 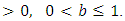 Then by using Equation (1) and (4)
Then by using Equation (1) and (4)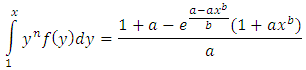
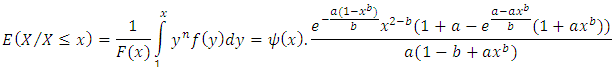 Sufficiency. Let
Sufficiency. Let 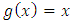 and
and 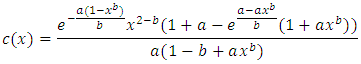 is a differentiable function in
is a differentiable function in 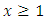 and
and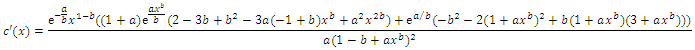 After some simplifications,
After some simplifications, 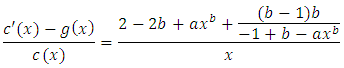 For all
For all 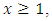
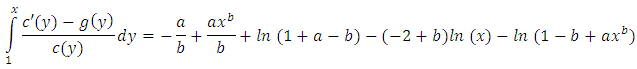 Then by using Lemma 2, the following result can be obtained
Then by using Lemma 2, the following result can be obtained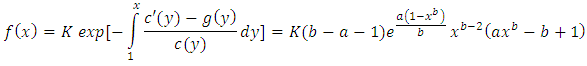 where
where 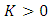 is a normalization constant,
is a normalization constant, 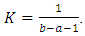 This complete the proof.
This complete the proof. be a random sample of size n from a continuous distribution with c.d.f.
be a random sample of size n from a continuous distribution with c.d.f. 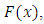 p.d.f.
p.d.f. 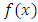 and survival function
and survival function 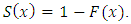 Let
Let 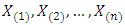 be the corresponding order statistics. Then the p.d.f. of
be the corresponding order statistics. Then the p.d.f. of 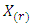 and the joint p.d.f. of
and the joint p.d.f. of 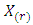 and
and 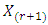 are given, respectively, as follows (Arnold et al. [6])
are given, respectively, as follows (Arnold et al. [6])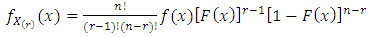
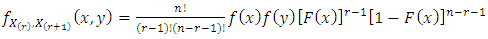
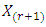 given
given 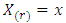 is given by
is given by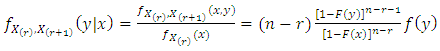
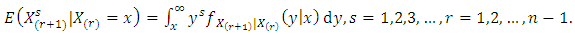
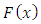 and survival function
and survival function 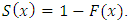 Let
Let 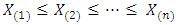 denote the order statistics of a random sample of size n from
denote the order statistics of a random sample of size n from 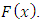 Then X has the Benktander type II distribution with parameters
Then X has the Benktander type II distribution with parameters 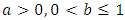 if and only if
if and only if 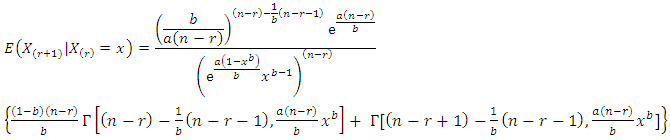
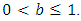 Using Equations (2), (7) and (8), the following results are abtianed
Using Equations (2), (7) and (8), the following results are abtianed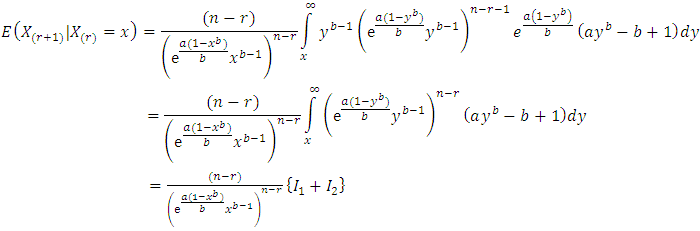
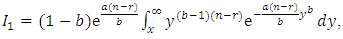
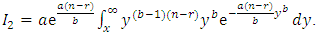 Substituting in integrations
Substituting in integrations 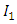 and
and 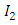 by
by 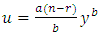 and using the definition of incomplete gamma function,
and using the definition of incomplete gamma function, 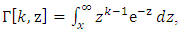
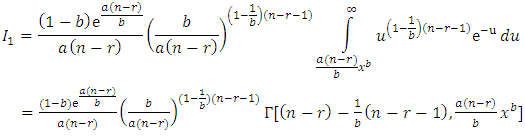
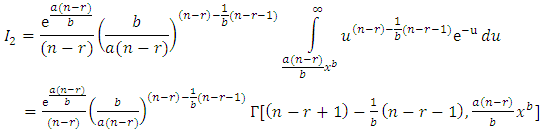
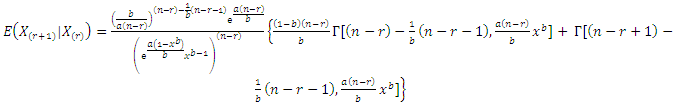 Sufficiency: Let
Sufficiency: Let 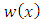 be the right hand side of Equation (9), i.e.
be the right hand side of Equation (9), i.e.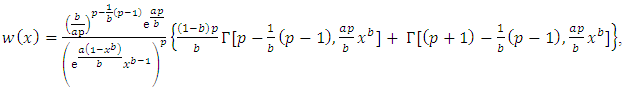 where
where 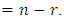 Then, Equation (9) can be rewritten as follows
Then, Equation (9) can be rewritten as follows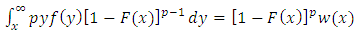
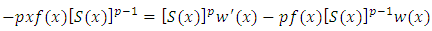
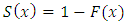 is the survival function.Dividing both sides of Equation (14) by
is the survival function.Dividing both sides of Equation (14) by 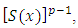 then
then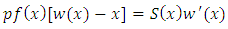 Or equivalently,
Or equivalently,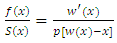
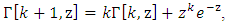 then
then 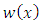 and
and 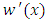 will be
will be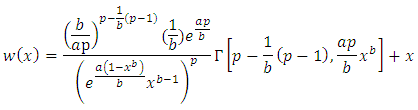 and
and 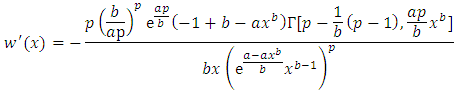 Hence, Equation (15) becomes
Hence, Equation (15) becomes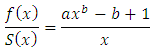 Now, for
Now, for 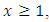 integration both sides of the above Equation with respect to x gives
integration both sides of the above Equation with respect to x gives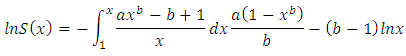 Hence,
Hence,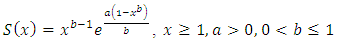 which is the survival function of the Benktander type II distribution. This completes proof of the theorem.
which is the survival function of the Benktander type II distribution. This completes proof of the theorem.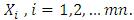 They are randomly classified into m samples, each of containing n observations. To satisfy more accurate consequence with less variability and more stability in characterization results, the study is conducted with large sample size, for example;
They are randomly classified into m samples, each of containing n observations. To satisfy more accurate consequence with less variability and more stability in characterization results, the study is conducted with large sample size, for example; 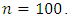 Choosing the number of samples are
Choosing the number of samples are 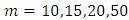 and different values of the order r with various choices of the parameter estimates a and b. Table (1) shows the L.H.S and R.H.S of Equation (9) and the absolute relative difference between them. The results indicate the closeness of both sides of Equation (9) which supporting the precision of the characterization results of Benktander distribution.
and different values of the order r with various choices of the parameter estimates a and b. Table (1) shows the L.H.S and R.H.S of Equation (9) and the absolute relative difference between them. The results indicate the closeness of both sides of Equation (9) which supporting the precision of the characterization results of Benktander distribution. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML