-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Probability and Statistics
p-ISSN: 2168-4871 e-ISSN: 2168-4863
2018; 7(4): 97-105
doi:10.5923/j.ijps.20180704.01

Fitting Multivariate Linear Mixed Model for Multiple Outcomes Longitudinal Data with Non-ignorable Dropout
Ahmed M. Gad, Niveen I. EL-Zayat
Statistics Department, Faculty of Economics and Political Science, Cairo University, Egypt
Correspondence to: Ahmed M. Gad, Statistics Department, Faculty of Economics and Political Science, Cairo University, Egypt.
| Email: |  |
Copyright © 2018 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Measurements made on several outcomes for the same unit, implying multivariate longitudinal data, are very likely to be correlated. Therefore, fitting such a data structure can be quite challenging due to the high dimensioned correlations exist within and between outcomes over time. Moreover, an additional challenge is encountered in longitudinal studies due to premature withdrawal of the subjects from the study resulting in incomplete (missing) data. Incomplete data is more problematic when missing data mechanism is related to the unobserved outcomes implying what so-called non-ignorable missing data or missing not at random (MNAR). Obtaining valid estimation under non-ignorable assumption requires that the missing-data mechanism be modeled as a part of the estimation process. The multiple continuous outcome-based data model is introduced via the Gaussian multivariate linear mixed models while the missing-data mechanism is linked to the data model via the selection model such that the missing-data mechanism parameters are fitted using the multivariate logistic regression. This article proposes and develops the stochastic expectation-maximization (SEM) algorithm to fit MLMM in the presence of non-ignorable dropout. In the M-step maximizing likelihood function is implemented via a new proposed Quasi-Newton (QN) algorithm that is of EM type, while maximizing the multivariate logistic regression is implemented via Newton-Raphson (NR) algorithm. A simulation study is conducted to assess the performance of the proposed techniques.
Keywords: Non-ignorable missing, Selection models, Multivariate linear mixed models, Stochastic EM algorithm, Newton-Raphson, Fisher-Scoring, Quasi-Newton
Cite this paper: Ahmed M. Gad, Niveen I. EL-Zayat, Fitting Multivariate Linear Mixed Model for Multiple Outcomes Longitudinal Data with Non-ignorable Dropout, International Journal of Probability and Statistics , Vol. 7 No. 4, 2018, pp. 97-105. doi: 10.5923/j.ijps.20180704.01.
Article Outline
1. Introduction
- Longitudinal studies are very common in many fields such as medicine, public health, psychology, biology and more. In the simplest design of univariate longitudinal data a single response is collected repeatedly over time, or possibly under changing experimental conditions, on each subject. A fundamental feature of longitudinal data is that the repeated measurements of the same subject tend to be highly correlated, and even more, such correlations often change over time resulting a complicated covariance structure (Diggle et al, 2002). In many applications it is common to measure a set of several responses, m, at each occasion for subjects which result in multivariate longitudinal data. The relationship among those outcomes is crucial. It requires addressing special methods of statistical analysis that can properly account for the intra-subject correlation as well as the cross-correlation between outcomes since ignoring such association structure will lead to invalid inferences. Modeling repeated measures on multivariate continuous responses is often implemented via multivariate linear mixed models. The multivariate linear mixed models are more applicable in this area due their flexibility in allowing (i) unbalanced data where a number of repeated measures might differ within subjects per outcome, (ii) using different design matrix across responses, and (iii) modeling distinct and more complex covariance structures. For a comprehensive monograph of multivariate linear mixed models see for example, Demidenko(2004) and Kim and Tim (2007).Missing data are very common in longitudinal data studies. Dealing with missing data depends on the process that generates the missing values; the missing data mechanism (MDM). A general taxonomy of MDMs, originally, introduced by Rubin (1976) and later explained by Little and Rubin (2002), differ in terms of assumptions about whether missingness is related to observed and/or unobserved responses. When dropout mechanism does not affected by the neither observed nor unobserved response values, it is called missing completely at random (MCAR). Missing data is said to be missing at random (MAR) when the missingness depends on the observed responses. Finally, missing data is missing not at random (MNAR) when missingness depends on the unobserved response. Nevertheless, it might be necessary to accommodate such type of missingness in the modeling process to reduce estimation biases (Little and Rubin, 2002). Likelihood-Based approach has been established in literature to be one of the most widely-used modern approaches of handling missing data. Parameter estimation has received a serious attention in the missing data literature. However, with non-ignorable assumption, such estimates cannot be obtained unless approaches are developed to model the missing data mechanism (Endres, 2010; Graham, 2012). Therefore, a number of selection model have been proposed to model longitudinal data in the presence of missing values aiming to characterize the joint distribution of data and the probability of missingness (Stubbendick, 2003; Little and Rubin, 2002). Direct maximization of the likelihood function, in this case, is not feasible (Jasson, and Xihong, 2002). So, numerical and iterative computations are exceedingly desired. Three generic iterative approaches such as Newton-Raphson (NR), Fisher Scoring (FS), Quasi-Newton (QN) and Expectation-Maximization (EM). EM algorithm can be used to maximiza the likelihood function. The EM algorithm is a generic iterative approach to find the maximum likelihood estimates (MLEs) for the model parameters when there is missing data or when the model contains unobserved latent variables (Demidenko, 2004).The multivariate linear mixed models (MLMM) have received more attention in literature particularly under non-ignorable MD. Reinsel (1982, 1984) considered fitting the MLMM by a closed form with complete and balanced data. While Shah et al. (1997) extended the work of Laird and Ware (1982) to the bivariate setting (m=2) using the EM algorithm to obtain the estimates of the model parameters under unbalanced and ignorable missing data. Schafer and Yucel (2002) and later Yucel (2015) proposed a variant technique of EM algorithm again for estimating the MLMM with ignorable missing data. Their EM algorithm considers the fisher scoring procedure in the M-step which fastens the convergence. Under non-ignorable assumption Roy and Lin (2002) consider fitting the MLMM under non-ignorable assumption covering the missingness in covariates as well as the multiple responses. They assumed that the dropout process depends on the latent variable and applied the selection model in order to account for non-ignorable missing data. Luwanda and Mwambi (2016) considered fitting nonlinear mixed-effects models to fit the multivariate longitudinal data in the presence of non-ignorable dropout. They proposed the stochastic approximation EM (SAEM) algorithm and apply the proposed technique to estimate parameters characterising human immunodeficiency virus (HIV) disease dynamics.The aim of this article is to address statistical modeling of the multivariate longitudinal data with continuous responses via the Gaussian multivariate linear mixed models (MLMM) under non-ignorable incomplete data. The missing-data mechanism is linked to the data model via the selection model such that the missing-data mechanism parameters are fitted using the multivariate logistic regression. The article proposes a stochastic EM algorithm to estimate the parameters of the model.The paper is organized as follow. The Multivariate linear mixed model for multivariate longitudinal data is presented in Section 2. This section also presents the dropout model for multivariate longitudinal data and formulates the joint distribution of the dropout mechanism and multivariate longitudinal response in the form of the full likelihood function. Section 3 introduces the proposed method for estimating the multivariate linear mixed model parameters in the presence of non-ignorable dropout. The estimation process involves estimating the dropout parameters and the response model parameters. An SEM algorithm combined with Newton-Raphson approach is proposed to estimate the dropout parameters. Also, a new proposed Quasi-Newton algorithm that is of EM type to estimate the response model parameters. The requied equations for the estimation are derived. In section 4, simulation studies are conducted to evaluate the performance of the proposed technique. Finally, concluding remarks are provided in Section 5.
2. Models and Likelihood Function
- In this section we introduce the used models; the multivariate linear mixed model and the dropout model. Also, the needed likelihood functions are defined. Multivariate linear mixed model (MLMM)Assume that the number of subjects are
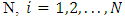 and there are
and there are 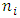 repeated measures on each subject. Also, assume that there are m outcomes on each subject,
repeated measures on each subject. Also, assume that there are m outcomes on each subject, 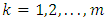 . The reponses for the subject i are collected in the response matrix
. The reponses for the subject i are collected in the response matrix 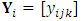 . The
. The 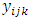 denotes the measurement of the
denotes the measurement of the 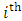 subject of the
subject of the 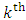 outcome at the
outcome at the 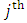 occasion. Assume that
occasion. Assume that 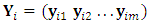 is the
is the 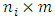 response matrix of the
response matrix of the 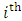 subject where each of
subject where each of 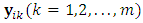 is the
is the 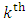 response
response 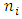 -vector measuremnets of subject i. It is very common that some subjects may withdraw from the study prematuraly which results in droput. The multivariate longitudinal data can be modeled using the multivariate linear mixed model (MLMM), where for the
-vector measuremnets of subject i. It is very common that some subjects may withdraw from the study prematuraly which results in droput. The multivariate longitudinal data can be modeled using the multivariate linear mixed model (MLMM), where for the 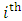 subject the response is modeled as:
subject the response is modeled as: 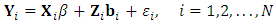 | (1) |
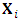 is the
is the 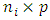 fixed between-subject design matrix,
fixed between-subject design matrix, 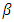 is the
is the 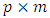 matrix of fixed effects assumed to be common for all subjects,
matrix of fixed effects assumed to be common for all subjects, 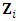 is the
is the 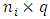 random within-subject design matrix,
random within-subject design matrix, 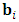 is the
is the 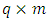 matrix of random effects, and
matrix of random effects, and 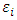 is the
is the 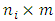 matrix of the measurements errors associated with the response matrix
matrix of the measurements errors associated with the response matrix 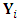 . The distributional assumptions that are often related to the MLMM are: Ÿ The
. The distributional assumptions that are often related to the MLMM are: Ÿ The 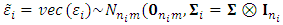 ; the rows of
; the rows of 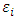 are normally distributed with mean 0 and
are normally distributed with mean 0 and 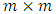 unstructured covariance matrix
unstructured covariance matrix 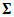 . The
. The 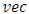 is the vectorized operator that stacks all columns of the matrix
is the vectorized operator that stacks all columns of the matrix 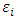 vertically. Ÿ The random effects
vertically. Ÿ The random effects 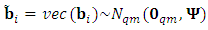 , where
, where 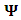 is
is 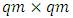 unstructured matrix. Moreover,
unstructured matrix. Moreover, 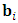 and
and 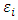 are assumed to be independent. Ÿ The marginal distribution of
are assumed to be independent. Ÿ The marginal distribution of 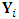 has normal distribution with expectation
has normal distribution with expectation 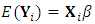 and dispersion matrix
and dispersion matrix 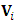 of dimension
of dimension 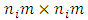 ;
; 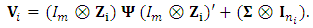 | (2) |
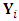 can be expressed as
can be expressed as 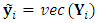 where
where 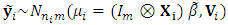 , and can be modelled as:
, and can be modelled as: 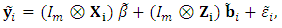 | (3) |
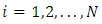 , and
, and 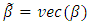 . The p.d.f. of
. The p.d.f. of 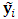 is given by
is given by 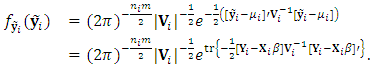 | (4) |
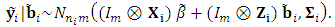 | (5) |
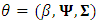 , can be obtained as
, can be obtained as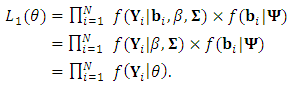 | (6) |
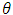 can be obtained by maximizing the likelihood function in Eq. (6). Note that this function is based on the marginal distribution function of the response
can be obtained by maximizing the likelihood function in Eq. (6). Note that this function is based on the marginal distribution function of the response 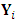 in the absence of the random effects. The random effects can be considered as nuisance parameters as long as the major interest is on the variance structure introduced by
in the absence of the random effects. The random effects can be considered as nuisance parameters as long as the major interest is on the variance structure introduced by 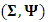 . Hence the log-likelihood function, based on Eq. (4) for the whole sample is
. Hence the log-likelihood function, based on Eq. (4) for the whole sample is 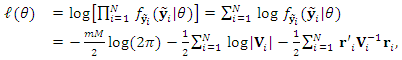 | (7) |
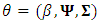 , is considered the parameter matrix of interest,
, is considered the parameter matrix of interest, 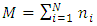 , while
, while 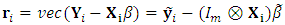 . A simpler form of the log-likelihood function is given by (Schafer and Yucel, 2002)
. A simpler form of the log-likelihood function is given by (Schafer and Yucel, 2002)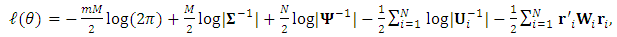 | (8) |
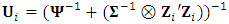 , and
, and 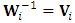 .We assume that the variance-covariance matrices,
.We assume that the variance-covariance matrices, 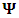 and
and 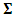 , are unstructured. Moreover, we represent these matrices in terms of their precision form,
, are unstructured. Moreover, we represent these matrices in terms of their precision form, 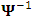 and
and 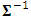 . These forms are obtained as linear functions as.
. These forms are obtained as linear functions as.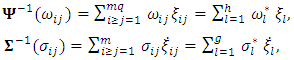 | (9) |
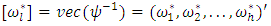 and
and 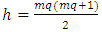 is the number of diagnol and off-diagonal elements of
is the number of diagnol and off-diagonal elements of 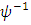 . Thus
. Thus  , such that
, such that 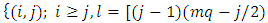
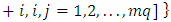 . Similarly,
. Similarly, 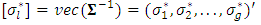 ,
, 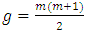 , and
, and 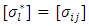 , such that
, such that 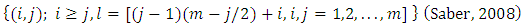 Further, each of
Further, each of 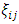 and
and 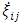 are square matrices of order
are square matrices of order 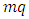 and m, respectively, with one on the
and m, respectively, with one on the 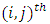 position and zero elsewhere. Hence, the response model parameter vector
position and zero elsewhere. Hence, the response model parameter vector 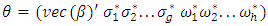 and the total number of parameters is
and the total number of parameters is 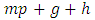 .Missing data model and likelihood functionAssume that, for subject i,
.Missing data model and likelihood functionAssume that, for subject i, 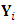 is subject to non-random dropout at a certain occasion
is subject to non-random dropout at a certain occasion 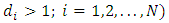 . The responses
. The responses 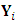 can be partitioned into two components; the observed part
can be partitioned into two components; the observed part 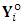 of dimension
of dimension 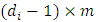 and missing part
and missing part 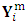 of dimension
of dimension 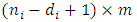 . Also, the response matrix using the
. Also, the response matrix using the 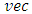 operator can be partitioned into two parts;
operator can be partitioned into two parts; 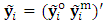 , where
, where 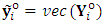 , and
, and 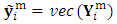 . Assume that the missing data indicator
. Assume that the missing data indicator 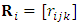 of dimension
of dimension 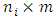 where
where 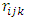 is defined as
is defined as 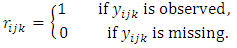 For monotone missing data we can define
For monotone missing data we can define 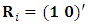 , where 1 is the matrix of ones of dimension
, where 1 is the matrix of ones of dimension 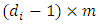 and 0 is the matrix of zeros of dimension
and 0 is the matrix of zeros of dimension 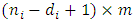 . The Diggle and Kenward (1994) model has been proposed for univariate longitudinal data setting. We extend this model to the multivariate longitudinal data of m outcomes. Assume that the dropout of subject i occurs at time
. The Diggle and Kenward (1994) model has been proposed for univariate longitudinal data setting. We extend this model to the multivariate longitudinal data of m outcomes. Assume that the dropout of subject i occurs at time 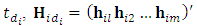 denotes the
denotes the 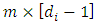 matrix of observed responses history of the m outcomes up to the time
matrix of observed responses history of the m outcomes up to the time 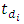 , where each of
, where each of 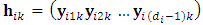 corresponds the row vector of length
corresponds the row vector of length 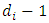 of observed responses of
of observed responses of 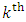 outcome. Diggle and Kenward (1994) modeled the probability of dropout in terms of the history
outcome. Diggle and Kenward (1994) modeled the probability of dropout in terms of the history 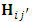 up to occasion
up to occasion 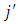 and the possibly missing current response,
and the possibly missing current response, 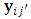 as
as 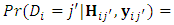
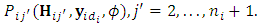 This probability is computed for each subject across all occasions as follows:
This probability is computed for each subject across all occasions as follows: 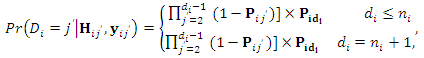 | (10) |
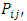 can be obtained by
can be obtained by 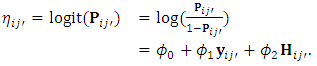 | (11) |
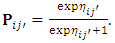 | (12) |
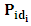 can be computed as
can be computed as 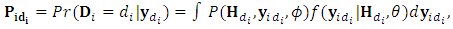 | (13) |
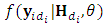 is the conditional probability of the missing given the observed responses. Hence the integral in Eq. (13) can be approximated using Monte Carol expectation (Gad and Ahmed, 2006). The complete-data log-likelihood for the N subjects can be given by
is the conditional probability of the missing given the observed responses. Hence the integral in Eq. (13) can be approximated using Monte Carol expectation (Gad and Ahmed, 2006). The complete-data log-likelihood for the N subjects can be given by 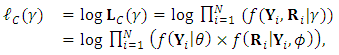 | (14) |
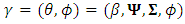 . Also, it can be re-expressed as
. Also, it can be re-expressed as 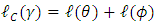 | (15) |
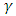 can be obtained maximizing each of the two components in Eq. (15) separately. Direct maximization is not feasible because it requires multidimensional integration and maximization (Jason and Xihong, 2002). Numerical and iterative computations are exceedingly required.
can be obtained maximizing each of the two components in Eq. (15) separately. Direct maximization is not feasible because it requires multidimensional integration and maximization (Jason and Xihong, 2002). Numerical and iterative computations are exceedingly required.3. The Proposed SEM Approach
- Maximizion of the log-likelihood function can be carried using iterative approaches to obtain the maximum-likelihood estimates (MLEs) such as Newton-Raphson (NR), Fisher Scoring algorithm(FS), Quasi-Newton (QN) and Expectation-Maximization (EM). Expectation-Maximization algorithm proposed by Dempster et al. (1977). It overcomes the difficulties involved with obtaining MLEs in the presence of missing values. The EM algorithm generally contains of two main steps; an Expectation step (E-step) and a Maximization step (M-step). For more details see McLachlan and Krishnan (2008). The E-step is often difficult to be evaluated. Celuex (1985) proposes the SEM algorithm as an alternative to the EM by replacing the E-step by a simulation step (S-step). Gad and Ahmed (2006) proposed SEM algorithm to fit the univariate longitudinal data in the presence of non-ignorable dropout. In this article we propose an SEM algorithm to fit the multivariate linear mixed model for multivariate longitudinal data with non-ignorable dropout. The M-step is implemented via two sub-steps. In the first sub-step the Newton-Raphson algorithm is developed to obtain the MLEs of the dropout parameters
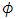 . In the second sub-step a new type of Quasi-Newton algorithm is proposed to obtain the MLEs of the response parameter
. In the second sub-step a new type of Quasi-Newton algorithm is proposed to obtain the MLEs of the response parameter 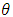 .The S-Step (Simulation step)Let
.The S-Step (Simulation step)Let 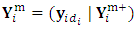 denotes the missing components of the response matrix
denotes the missing components of the response matrix 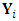 over the m outcomes such that
over the m outcomes such that 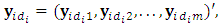 indicates the first
indicates the first 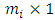 missing vector, while the second matrix of order
missing vector, while the second matrix of order 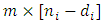 is introduced by
is introduced by 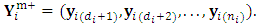 In this step (the S-step), we simulate m-vector from
In this step (the S-step), we simulate m-vector from 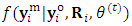 to represent the responses of the m outcomes at the time of dropout
to represent the responses of the m outcomes at the time of dropout 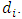 This conditional disribution can be factorized, up to a constant of proportionality, as
This conditional disribution can be factorized, up to a constant of proportionality, as 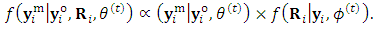 | (16) |
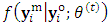 , then it is passed through the following accept-reject procedure;1. Simulate a candidate m-vector
, then it is passed through the following accept-reject procedure;1. Simulate a candidate m-vector 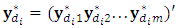 , from the conditional distribution
, from the conditional distribution 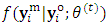 which is m-multivariate normal distribution with parameters
which is m-multivariate normal distribution with parameters 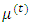 and
and 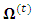 ; the
; the 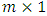 location vector and the
location vector and the 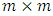 dispersion matrix respectively, are given by
dispersion matrix respectively, are given by 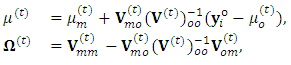 | (17) |
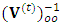 is the variance matrix corresponds of the observed response matrix
is the variance matrix corresponds of the observed response matrix 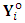 ;
; 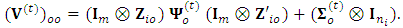 2. Compute the m-vector probability of dropout for the candidate vector
2. Compute the m-vector probability of dropout for the candidate vector 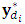 based on the dropout model
based on the dropout model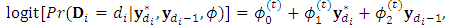 | (18) |
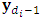 comprises the m-vector of responses at
comprises the m-vector of responses at 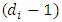 ; the occasion precedes the dropout occasion. The dropout probability vector,
; the occasion precedes the dropout occasion. The dropout probability vector, 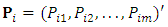 , is evaluated using the inverse transformation in Eq. (12). Then define
, is evaluated using the inverse transformation in Eq. (12). Then define 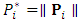 . 3. Simulate a random m-vector U from uniform distribution over the interval
. 3. Simulate a random m-vector U from uniform distribution over the interval 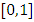 , then take
, then take 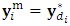 if
if 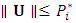 , otherwise repeat step 1. We argue that the remaining missing values, following the first missing value, can be considered as missing at random.The M-Step (Maximization step)The joint probability function of the pseudo-observed data is
, otherwise repeat step 1. We argue that the remaining missing values, following the first missing value, can be considered as missing at random.The M-Step (Maximization step)The joint probability function of the pseudo-observed data is 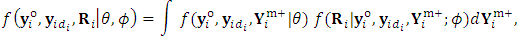 | (19) |
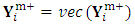 . Since
. Since 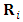 does not depend on
does not depend on 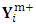 by construction, the above equation can be simplified to
by construction, the above equation can be simplified to 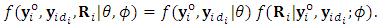 | (20) |
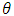 and
and 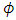 will be any function of
will be any function of 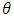 and
and 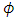 proportional to
proportional to 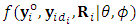 . Moreover, based on the selection model,
. Moreover, based on the selection model, 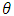 and
and 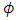 are assumed to be distinct by definition. Hence,
are assumed to be distinct by definition. Hence, 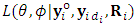 is the same as likelihood
is the same as likelihood 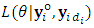 .The M-step of the algorithm comprises two substeps; the logistic step (M1-Step), and the normal step (M2-Step):The M1-Step (the logistic step):In this substep the MLEs of the dropout parameter,
.The M-step of the algorithm comprises two substeps; the logistic step (M1-Step), and the normal step (M2-Step):The M1-Step (the logistic step):In this substep the MLEs of the dropout parameter, 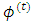 , is estimated numerically using Newton-Raphson approach. A step halfing algorithm is adopted to guarantee that the log-likelihood function increasing toward the maxima over the iterations. Moreover, in case when the Hessian matrix of
, is estimated numerically using Newton-Raphson approach. A step halfing algorithm is adopted to guarantee that the log-likelihood function increasing toward the maxima over the iterations. Moreover, in case when the Hessian matrix of 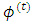 is not negative definite, the Newton direction
is not negative definite, the Newton direction 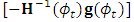 may not point in an ascent direction. Therefore, a modification is adopted using the Levenberg-Marquardt technique, to ensure that the search direction is an ascent direction, hence the algorithm guides the process to the maximum point (Chong and Zak, 2013).The basic Newton-Raphson algorithm is used to obtain the MLEs for the dropout parameters of the multivariate logistic regression model. The algorithm seeks for optimizing, the log-likelihood function
may not point in an ascent direction. Therefore, a modification is adopted using the Levenberg-Marquardt technique, to ensure that the search direction is an ascent direction, hence the algorithm guides the process to the maximum point (Chong and Zak, 2013).The basic Newton-Raphson algorithm is used to obtain the MLEs for the dropout parameters of the multivariate logistic regression model. The algorithm seeks for optimizing, the log-likelihood function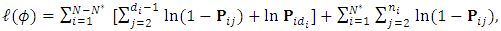 | (21) |
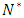 refers to the subjects who complete the study (the completers), hence,
refers to the subjects who complete the study (the completers), hence, 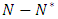 refers to dropout subjects. The probabilities vector
refers to dropout subjects. The probabilities vector 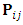 is computed using Eq. (11) for any occasion
is computed using Eq. (11) for any occasion 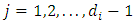 , and form Eq. (18) at the occasion of dropout
, and form Eq. (18) at the occasion of dropout 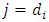 . Implementing the algorithm needs computing the gradient
. Implementing the algorithm needs computing the gradient 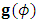 vector and the Hessian matrix
vector and the Hessian matrix 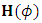 . First, the elements of the gradient vector
. First, the elements of the gradient vector 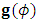 are obtained as follow:
are obtained as follow: 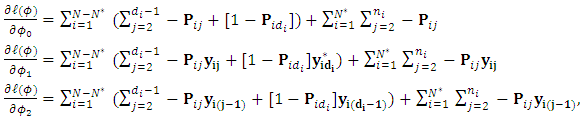 where
where 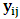 is the m-vector of the responses at occasion j. The elements of the Hessian matrix are obtained as follow:
is the m-vector of the responses at occasion j. The elements of the Hessian matrix are obtained as follow: 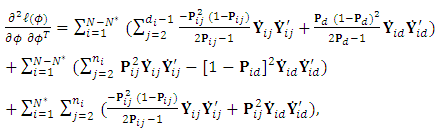 where
where 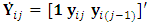 is the response matrix of order
is the response matrix of order 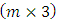 . It is worth noting that at an initial value
. It is worth noting that at an initial value 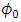 that might be chosen at which the Hessian matrix
that might be chosen at which the Hessian matrix 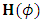 is not negative definite, the Levenberg-Marquardt modification of Newton’s algorithm will be adopted. That approach approximates
is not negative definite, the Levenberg-Marquardt modification of Newton’s algorithm will be adopted. That approach approximates 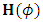 with another matrix
with another matrix 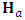 , such that
, such that 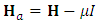 , where the scalar
, where the scalar 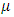 is chosen large enough such that
is chosen large enough such that 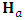 is negative definite (Chong and Zak, 2013).The M2-Step (the normal step):In this substep the MLEs of the parameters,
is negative definite (Chong and Zak, 2013).The M2-Step (the normal step):In this substep the MLEs of the parameters, 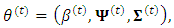 for the multivariate normal is estimated numerically using a new proposed approach of Quazi-Newton type. The proposed Quazi-Newton algorithm begins with initial values of
for the multivariate normal is estimated numerically using a new proposed approach of Quazi-Newton type. The proposed Quazi-Newton algorithm begins with initial values of 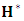 with
with 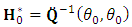 , where
, where 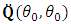 is computed as
is computed as 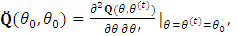 | (22) |
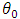 is the initial values vector of the parameter
is the initial values vector of the parameter 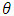 and the function
and the function 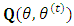 as in the EM algorithm. Generally, the algorithm proceeds as follows:1. Initiate the algorithm with
as in the EM algorithm. Generally, the algorithm proceeds as follows:1. Initiate the algorithm with 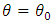 , then compute the corresponding
, then compute the corresponding 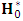 and
and 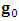 , where
, where 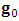 is the gradient of the observed log-likelihood function.2. Compute the step direction vector
is the gradient of the observed log-likelihood function.2. Compute the step direction vector 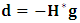 , then use the line search algorithm to specify
, then use the line search algorithm to specify 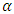 that maximizes
that maximizes 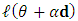 . The Golden-Section algorithm is adopted here to specify the single parameter
. The Golden-Section algorithm is adopted here to specify the single parameter 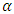 that maximize
that maximize 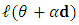 along the search direction d from the point
along the search direction d from the point 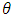 . 3. Set
. 3. Set 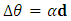 , and compute
, and compute 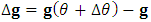 . 4. Based on
. 4. Based on 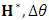 , and
, and 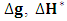 can be evaluated as
can be evaluated as 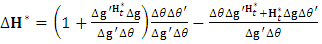 . 5. Replace
. 5. Replace 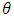 by
by 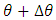 ,
, 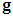 by
by 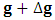 , and
, and 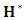 by
by 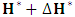 and return to step (2) or stop based on a stopping criterion.To implement the above algorithm, the quantities
and return to step (2) or stop based on a stopping criterion.To implement the above algorithm, the quantities 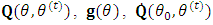 , and
, and 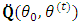 are needed. Deviations of such quantities are obtained as follows. First, the EM-quantity,
are needed. Deviations of such quantities are obtained as follows. First, the EM-quantity, 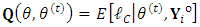 , can be easily deduced by taking the expectation of the log-likelihood of the complete-data given the observed responses
, can be easily deduced by taking the expectation of the log-likelihood of the complete-data given the observed responses 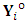 and the current values of the parameter vector
and the current values of the parameter vector 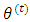 . This function is given by
. This function is given by 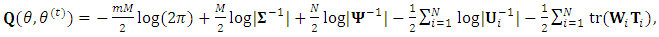 | (23) |
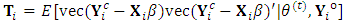 and
and 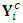 indicates the complete-data response matrix. To compute this expectation, set
indicates the complete-data response matrix. To compute this expectation, set 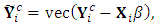 where
where 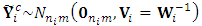 . Further the complete-data matrix,
. Further the complete-data matrix, 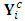 , is partitioned into
, is partitioned into 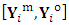 , similarly,
, similarly, 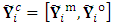 . Based on axioms of conditional normal distribution, it can be easily shown that
. Based on axioms of conditional normal distribution, it can be easily shown that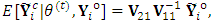 where
where 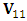 is the square submatrix of
is the square submatrix of 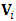 corresponding to the observed elements, and
corresponding to the observed elements, and 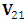 is the rectangle sub-matrix of covariances between the missing and the observed elements. On the other hand, it also can be shown that
is the rectangle sub-matrix of covariances between the missing and the observed elements. On the other hand, it also can be shown that 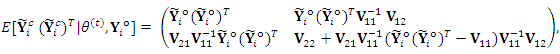 where
where 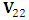 is the square submatrix of covariances between the missing elements.The gradient of the observed log-likelihood,
is the square submatrix of covariances between the missing elements.The gradient of the observed log-likelihood, 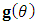 , is derived as
, is derived as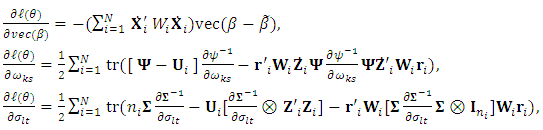 where,
where, 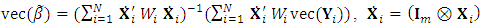 , and
, and 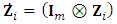 . Further,
. Further, 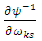 and
and 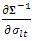 are replaced with
are replaced with 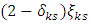 and
and 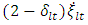 , respectively, such that, the scalar
, respectively, such that, the scalar 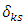 which is intensively known as Kronecker delta, equals 1 when
which is intensively known as Kronecker delta, equals 1 when 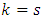 and 0 otherwise, where
and 0 otherwise, where 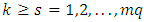 , while
, while 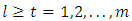 .The second derivatives of the EM-Q function are needed. The computation of the first and the second derivative of the EM-Q function are
.The second derivatives of the EM-Q function are needed. The computation of the first and the second derivative of the EM-Q function are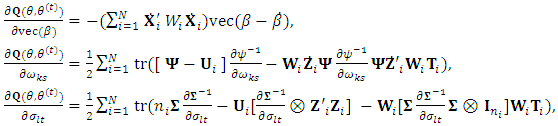 where
where 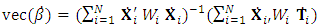 and
and 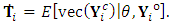
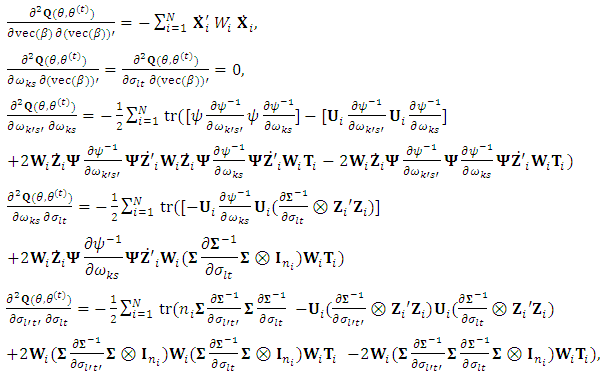 For a parameter
For a parameter 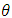 , the SEM estimates is taken as the mean of the sequence
, the SEM estimates is taken as the mean of the sequence 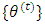 as
as 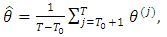 | (24) |
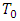 is the length of burn-in period.In the above derivations of the gradient vector and the derivatives of the EM-Q function, the quantities;
is the length of burn-in period.In the above derivations of the gradient vector and the derivatives of the EM-Q function, the quantities; 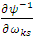 and
and 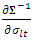 are replaced with
are replaced with 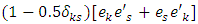 and
and 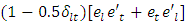 , respectively. The scalar
, respectively. The scalar 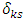 is Kronecker delta which equals 1 when
is Kronecker delta which equals 1 when 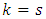 and 0 otherwise, where
and 0 otherwise, where 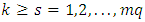 . Similarly the scalar
. Similarly the scalar 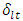 is defined for
is defined for 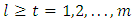 . The vector
. The vector 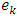 is the basis vector of length mq with
is the basis vector of length mq with 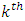 element equals 1 and all other elements are zeros.
element equals 1 and all other elements are zeros. 4. Simulation Study
- The aim of this simulation is to evaluate the performance of the proposed approach. The evaluation criteria is the relative bias. Simulation Setting and data generation Two sample sizes were assumed;
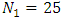 , and
, and 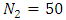 to generate data. The number of outcomes for each subject is assumed to be three outcomes;
to generate data. The number of outcomes for each subject is assumed to be three outcomes; 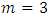 . The number of time points is fixed at 10;
. The number of time points is fixed at 10; 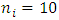 . The number of replications is chosen as 200. It is assumed that subjects are allocated to one of three treatments A, B, and C. Hence, there are a matrix of dimension
. The number of replications is chosen as 200. It is assumed that subjects are allocated to one of three treatments A, B, and C. Hence, there are a matrix of dimension 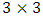 of fixed-effects
of fixed-effects 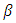 of the three covariates across the three outcomes. The subject-specific design matrix is assumed to have two columns
of the three covariates across the three outcomes. The subject-specific design matrix is assumed to have two columns 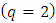 ; the random intercept and slope. Such that, the two subject-specific covariates
; the random intercept and slope. Such that, the two subject-specific covariates 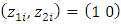 , for odd subject, and
, for odd subject, and 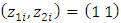 , for even subjects. Also the random design matrix
, for even subjects. Also the random design matrix 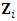 is assumed to be time-invariant. Consequently, the individual level matrix of random-effect parameters is
is assumed to be time-invariant. Consequently, the individual level matrix of random-effect parameters is 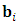 is of order
is of order 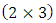 . It represents the parameters of random-effects across outcomes. This matrix is generated for each subject as
. It represents the parameters of random-effects across outcomes. This matrix is generated for each subject as 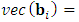
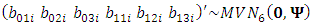 , where
, where 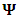 is of dimension
is of dimension 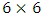 assumed to be unstructured matrix. The measurement errors associated with the three outcomes are assumed to be independent over the repeated measure having a common unstructured variance-covariance matrix
assumed to be unstructured matrix. The measurement errors associated with the three outcomes are assumed to be independent over the repeated measure having a common unstructured variance-covariance matrix 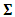 of dimension
of dimension 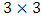 . Hence, for each subject the matrix
. Hence, for each subject the matrix 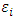 is generated from a matrix normal distribution of parameters
is generated from a matrix normal distribution of parameters 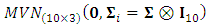 . The true value of the elements of the parameter matrices;
. The true value of the elements of the parameter matrices; 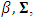 and
and 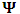 are assumed as
are assumed as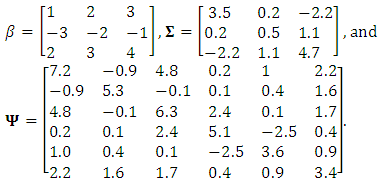 The response matrix
The response matrix 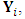 for each subject, is generated from the model
for each subject, is generated from the model 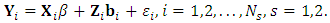 | (25) |
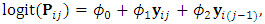 | (26) |
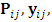 and
and 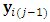 is a 3-column vector, indicates the probabilities of dropout at the occasion j associated to the vector of responses, the vector of responses that were planned to be measured at occasion j, and the vector of responses at the previous occasion
is a 3-column vector, indicates the probabilities of dropout at the occasion j associated to the vector of responses, the vector of responses that were planned to be measured at occasion j, and the vector of responses at the previous occasion 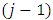 , respectively. However, if the dropout occasion, for a subject i, is specified as
, respectively. However, if the dropout occasion, for a subject i, is specified as 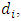 then the dropout probability is computed as a probability of the dropout time
then the dropout probability is computed as a probability of the dropout time 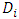 at all possible occasion as follow
at all possible occasion as follow 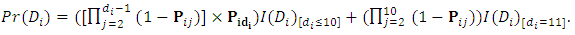 For each subject, the response matrix generated in the previous step is exposed to a non-random dropping process on the occasion level. Precisely, at occasion j, after the baseline
For each subject, the response matrix generated in the previous step is exposed to a non-random dropping process on the occasion level. Precisely, at occasion j, after the baseline 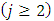 , the response vector
, the response vector 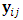 has been checked to be whether retained or dropped as follow: 1. The initial values for the parameter vector of logistic dropout model is assumed to be
has been checked to be whether retained or dropped as follow: 1. The initial values for the parameter vector of logistic dropout model is assumed to be 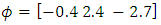 . 2. The probability vector
. 2. The probability vector 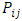 is computed based on Eq. (26). 3. A random variable U is generated from uniform (0,1). 4. The response vector
is computed based on Eq. (26). 3. A random variable U is generated from uniform (0,1). 4. The response vector 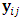 is dropped if
is dropped if 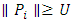 , otherwise it is retained. Simulation Results The proposed approach introduced has been applied to data. For each of the two maximization steps the stopping criterion that is suggested in Demidenko (2004) is used. Precisely, the iteration will be terminated if the norm value of the absolute difference of two successive values of the gradient vector at fixed parameter values is less that 0.0001. To accelerate the algorithm the study adopted the Levenberg-Marquardt technique to modify each of the Hessian matrix of the dropout parameters and the second derivative matrix of the Q function of the model precision parameters, to be negative definite. The SEM algorithm is iterated for 500 iterations with a burn-in period of 250 iterations. The MLEs for the parameters were taken as the averages of the last 250 iterations. The performance of the proposed approach is evaluated via the relative bias (RB) of its obtained MLEs, which was computed as follow:
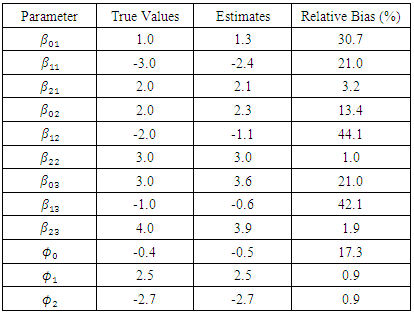
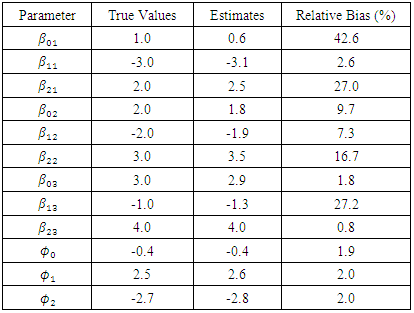
, otherwise it is retained. Simulation Results The proposed approach introduced has been applied to data. For each of the two maximization steps the stopping criterion that is suggested in Demidenko (2004) is used. Precisely, the iteration will be terminated if the norm value of the absolute difference of two successive values of the gradient vector at fixed parameter values is less that 0.0001. To accelerate the algorithm the study adopted the Levenberg-Marquardt technique to modify each of the Hessian matrix of the dropout parameters and the second derivative matrix of the Q function of the model precision parameters, to be negative definite. The SEM algorithm is iterated for 500 iterations with a burn-in period of 250 iterations. The MLEs for the parameters were taken as the averages of the last 250 iterations. The performance of the proposed approach is evaluated via the relative bias (RB) of its obtained MLEs, which was computed as follow: 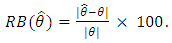 The parameter estimates are displayed in Table (1) for N = 25 and Table (2) for N = 50.
The parameter estimates are displayed in Table (1) for N = 25 and Table (2) for N = 50.
|
|
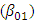 of the first outcome show maximum bias in both tables (30.7%, and 42.6%). For sample size N = 25, the estimate of the effect of the first treatment on the second and third outcomes show somewhat large bias (44.1%, and 42.1% receptively). Generally, the second table show less bias for most parameters (except for the estimate of the first intercept). It almost does not exceed 27.0% approximately. Thus, the proposed approach show higher performance with large sample sizes.
of the first outcome show maximum bias in both tables (30.7%, and 42.6%). For sample size N = 25, the estimate of the effect of the first treatment on the second and third outcomes show somewhat large bias (44.1%, and 42.1% receptively). Generally, the second table show less bias for most parameters (except for the estimate of the first intercept). It almost does not exceed 27.0% approximately. Thus, the proposed approach show higher performance with large sample sizes.5. Conclusions and Future Research
- The study introduces a new estimating approach for modeling multiple outcomes longitudinal data under the multivariate linear mixed model (MLMM) in the presence of non-ignorable missingness. The missing pattern was assumed to be monotone, such that the m outcomes have the same pattern of dropout, while the covariates were assumed to be fully observed. To obtain valid estimates of the model parameters, the study incorporates the model of missing data into the estimation process via the logit selection model. The SEM algorithm is used as estimation approach. The S-Step of the algorithm was implemented via accept-reject principle for simulating the m-vector of outcomes at the dropout occasion from the specified distribution. The algorithm suggested two maximization steps; M1-Step to maximize the likelihood function of the dropout parameters of the multivariate logistic model, and M2-Step to maximize the likelihood function of the response model parameters. The study proposed a novel algorithm to implement the second maximization which is a new form of Quasi-Newton algorithm that incorporates EM-related quantity which is the Q function. The resulted proposed approach is a QN of EM-type. The proposed approach in efficient in at least major two respects. It suggested using a new version of Quasi-Newton algorithm that embedded with some EM quantities. It takes the advantage of the EM algorithm in handling incomplete data by augmenting the missing and the observed observation to produce better estimates. However, it avoids complicated computation of the EM algorithm due to its iterating on the E-step which is infeasible with models with multi-parameters. So, it suggested computing the matrix of the second derivatives of the Q function with respect to the current guess of the precision parameters only once to initiate the basic Quasi-Newton algorithm. Some possible extensions to the current study are recommended for further investigation. The current study could be extended assuming the intermittent pattern. Consequently, different likelihood function for the missing data mechanism parameters should be derived to fit such pattern. Moreover, it is very practically to violate the assumption that all outcomes have the same pattern of missingness. Violating such assumption will cause a considerable modification in the computation of the Q function. One further extension is to admit possible missing covariates. This will motivate incorporating missing data mechanism of the covariates into the estimation process. It is very common to assume that the measurement errors within subjects are autocorrelated. It is possible to extend the variance structure of the errors from
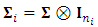 to be
to be 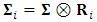 , where the matrix
, where the matrix 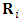 can take a simple autoregressive pattern. However, this will imply estimating more parameters. The performance of the proposed approach is evaluated by a simulation study assuming three outcomes. The study is needed to be extended to check its applicability for a higher number of outcomes.
can take a simple autoregressive pattern. However, this will imply estimating more parameters. The performance of the proposed approach is evaluated by a simulation study assuming three outcomes. The study is needed to be extended to check its applicability for a higher number of outcomes.  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML