Deapon Biswas
Transport Officer, Private Concern, Chittagong, Bangladesh
Correspondence to: Deapon Biswas, Transport Officer, Private Concern, Chittagong, Bangladesh.
| Email: |  |
Copyright © 2018 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
In this chapter we can find various numbers of EB members of the experiment “M sided N dice taken V at a time”. Beside this we can find various numbers of IB members of different IB experiment i.e., of the experiments M sided N dice taken V at a time in which first v dice are identified in the first way or second way or both way. Again various numbers of B events can be calculated from different CB experiments i.e., of the experiments M sided N dice taken V at a time in which first v dice are identified in the first way or second way or both way. Moreover we can find varies numbers of GB members of different GB experiment i.e., of the experiments M sided N dice taken V at a time in which X is observed in the first way or Y is observed in the second way or X, Y are observed in the both way at a time. X and Y are variables. Beside this we can get combination theorems, permutation theorems, formation theorems and homogenation theorems from these theorems.
Keywords:
Biswas theorem, EB theorem, IB theorem, CB theorem, GB theorem
Cite this paper: Deapon Biswas, Biswas Theorem, International Journal of Probability and Statistics , Vol. 7 No. 3, 2018, pp. 82-96. doi: 10.5923/j.ijps.20180703.03.
1. Introduction
First of all I discussed Biswas theorem and then elementary B theorems. They are divided into four parts; both way selected B (SB) theorem, both way arranged B (AB) theorem, first way selected and second way arranged B (SAB) theorem and first way arranged and second way selected B (ASB) theorem.Then identified B theorems are divided into four parts i.e.,(i) both way selected B (SB) theorem(ii) both way arranged B (AB) theorem(iii) first way selected and second way arranged B (SAB) theorem(iv) first way arranged and second way selected B (ASB) theorem. Similarly characterizing B theorems and general B theorems are divided into the same.
2. Findings
2.1. Biswas Theorem
Theorem 2.1 Biswas theorem: The number of GB members of the GB space 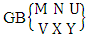 denoted by
denoted by 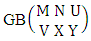 is
is 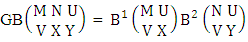 | (2.1) |
where, min(M, U) − M + 1 ≤ X ≤ min(M, U, V)min(N, U) − N + V ≤ Y ≤ min(N, U, V)M ≥ U and N ≥ U for first way and second way respectively. And 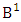 is the B first number to be hold the number of homogenations or formations and
is the B first number to be hold the number of homogenations or formations and 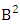 is the B second number to be hold the number of permutations or combinations.Proof: We know the B number is to be product of B first number and B second number. As the theorem is from a GB experiment so we get the B first number from general homogenation theorem or general formations theorem and it is to be
is the B second number to be hold the number of permutations or combinations.Proof: We know the B number is to be product of B first number and B second number. As the theorem is from a GB experiment so we get the B first number from general homogenation theorem or general formations theorem and it is to be 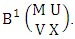 Again B second number get from general permutation theorem or general combination theorem and it is to be
Again B second number get from general permutation theorem or general combination theorem and it is to be 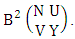 Performing the two cases we get the number of GB members as
Performing the two cases we get the number of GB members as 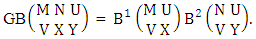
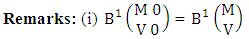 | (2.2) |
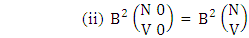 | (2.3) |
Proofs: Let B first number is for number of homogenations then 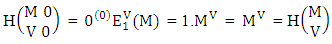 Again let B first number is for number of formations then
Again let B first number is for number of formations then 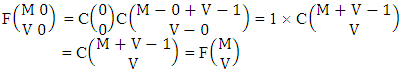 Now for the B second number let it is represent for number of permutations then
Now for the B second number let it is represent for number of permutations then 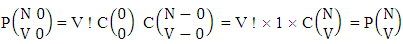 Again let B second number is represent for number of combinations then
Again let B second number is represent for number of combinations then 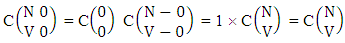 Example 2.1: Find the number of GB members of the GB space
Example 2.1: Find the number of GB members of the GB space 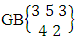 chosen first way arranged and second way selected and 2 is observed in the first way.Solution: From the theorem 2.1 we get
chosen first way arranged and second way selected and 2 is observed in the first way.Solution: From the theorem 2.1 we get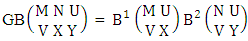 As X is observed in the first way so we get
As X is observed in the first way so we get 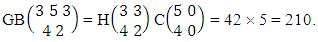
2.2. EB Theorem
Theorem 2.2 EB theorem: The number of B members of the experiment M sided N dice taken V at a time, denoted by 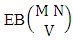 is
is 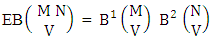 | (2.4) |
where 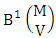 called B first number is the number of homogenations or formations of M sided V dice experiment and
called B first number is the number of homogenations or formations of M sided V dice experiment and 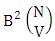 called B second number is the number of permutations or combinations of N dice (things) taken V at a time.Proof: Let M sided 1 dice is tossed, then we get the number of B members is
called B second number is the number of permutations or combinations of N dice (things) taken V at a time.Proof: Let M sided 1 dice is tossed, then we get the number of B members is 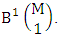 In the same why M sided 2 dice is tossed then we get the number of B members is
In the same why M sided 2 dice is tossed then we get the number of B members is 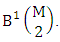 In the same why M sided 3 dice is tossed then we get the number of B members is
In the same why M sided 3 dice is tossed then we get the number of B members is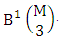 Similarly for M sided V dice experiment we get the number of B members is
Similarly for M sided V dice experiment we get the number of B members is 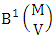 . In the other hand, N dice (or things) taken 1at a time then we get the number of B members is
. In the other hand, N dice (or things) taken 1at a time then we get the number of B members is 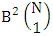 . Again N dice (or things) taken 2 at a time then we get the number of B members is
. Again N dice (or things) taken 2 at a time then we get the number of B members is 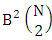 . In the same way N dice (or things) taken 3 at a time then we get the number of B members is
. In the same way N dice (or things) taken 3 at a time then we get the number of B members is 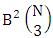 . Similarly for N dice (or things) taken V at a time then we get the number of B members is
. Similarly for N dice (or things) taken V at a time then we get the number of B members is 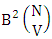 . When the two case performed in the same time then we get the number of B members of M sided N dice taken V at a time is
. When the two case performed in the same time then we get the number of B members of M sided N dice taken V at a time is 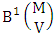
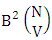 i.e.,
i.e., 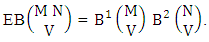 Hence the proof.Example 2.2: Find the number of B members of the experiment 6 sided 10 dice taken 5 at a time where B first number is the number of homogenations and B second number is the number of combinations.Solution: The numbers of B members is
Hence the proof.Example 2.2: Find the number of B members of the experiment 6 sided 10 dice taken 5 at a time where B first number is the number of homogenations and B second number is the number of combinations.Solution: The numbers of B members is 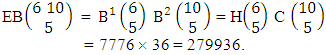 Theorem 2.3 ESB theorem: The number of ESB members of the experiment M sided N dice taken V at a time, denoted by
Theorem 2.3 ESB theorem: The number of ESB members of the experiment M sided N dice taken V at a time, denoted by 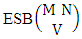 is
is 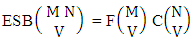 | (2.5) |
where 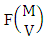 is the number of formations of M sided V dice experiment and
is the number of formations of M sided V dice experiment and 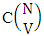 is the number of combinations of N dice (things) taken V at a time.Proof: The experiment gives the outcomes selected i.e., ESB members. Firstly M sided 1 die is tossed, then the B first number gives the number of formations is
is the number of combinations of N dice (things) taken V at a time.Proof: The experiment gives the outcomes selected i.e., ESB members. Firstly M sided 1 die is tossed, then the B first number gives the number of formations is 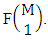 Secondly M sided 2 dice is tossed then the B first number i.e., the number of formations is
Secondly M sided 2 dice is tossed then the B first number i.e., the number of formations is 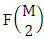 . Thirdly M sided 3 dice is tossed then the B first number i.e., the number of formations is
. Thirdly M sided 3 dice is tossed then the B first number i.e., the number of formations is 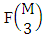 . Similarly for M sided V dice experiment we get the number of formations is
. Similarly for M sided V dice experiment we get the number of formations is 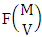 . Again for N dice (things) taken 1 at a time then the B second number gives the number of combinations is
. Again for N dice (things) taken 1 at a time then the B second number gives the number of combinations is 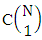 . Secondly N dice (things) taken 2 at a time then the B second number i.e., number of combinations is
. Secondly N dice (things) taken 2 at a time then the B second number i.e., number of combinations is 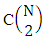 . Thirdly for the same reason when N dice (things) taken 3 at a time then the B second number i.e., the number of combinations is
. Thirdly for the same reason when N dice (things) taken 3 at a time then the B second number i.e., the number of combinations is 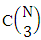 . Similarly we get for N dice (things) taken V at a time the number is
. Similarly we get for N dice (things) taken V at a time the number is 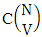 . Now for the two case performed in the same time the number of ESB members of M sided N dice taken V at a time is
. Now for the two case performed in the same time the number of ESB members of M sided N dice taken V at a time is 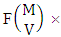
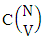 i.e.,
i.e., 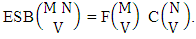 Example 2.3: Find the number of ESB members of the experiment 3 sided 5 dice taken 4 at a time.Solution: The number of ESB members is
Example 2.3: Find the number of ESB members of the experiment 3 sided 5 dice taken 4 at a time.Solution: The number of ESB members is 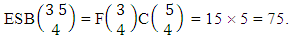 Corollary 2.1: The number of ESB members of the experiment 1 sided N dice taken V at a time is the same as the numbers of combinations of N things taken V at a time i.e.,
Corollary 2.1: The number of ESB members of the experiment 1 sided N dice taken V at a time is the same as the numbers of combinations of N things taken V at a time i.e.,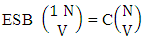 | (2.6) |
Corollary 2.2: The number of ESB members of the experiment M sided V dice taken all at a time is the same as the number of formations of M sided V dice experiment i.e.,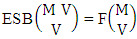 | (2.7) |
Theorem 2.4 EAB theorem: The number of EAB members of the experiment M sided N dice taken V at a time, denoted by 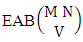 is
is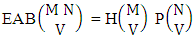 | (2.8) |
where 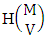 is the number of homogenations of M sided V dice experiment and
is the number of homogenations of M sided V dice experiment and 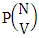 is the number of permutations of N dice (things) taken V at a time.Proof: Here the experiment results all the B members arranged i.e., EAB members. Now M sided 1 die is tossed then the B first number gives the number of homogenations is
is the number of permutations of N dice (things) taken V at a time.Proof: Here the experiment results all the B members arranged i.e., EAB members. Now M sided 1 die is tossed then the B first number gives the number of homogenations is 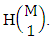 Again M sided 2 dice is tossed then the B first number i.e., number of homogenations is
Again M sided 2 dice is tossed then the B first number i.e., number of homogenations is 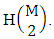 For the same reason when M sided 3 dice is tossed then the B first number i.e., the number of homogenations is
For the same reason when M sided 3 dice is tossed then the B first number i.e., the number of homogenations is 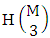 . Similarly for M sided V dice experiment we get the number of homogenations is
. Similarly for M sided V dice experiment we get the number of homogenations is 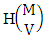 . On the other hand when N dice (things) taken 1 at a time then the B second number gives the number of permutations is
. On the other hand when N dice (things) taken 1 at a time then the B second number gives the number of permutations is 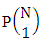 . Again N dice (things) taken 2 at a time then the B second number i.e., the number of permutations is
. Again N dice (things) taken 2 at a time then the B second number i.e., the number of permutations is 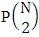 . For the same reason when N dice (things) taken 3 at a time then the B second number i.e., the number of permutations is
. For the same reason when N dice (things) taken 3 at a time then the B second number i.e., the number of permutations is 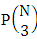 . Similarly for N dice (things) taken V at a time we get the number of permutations is
. Similarly for N dice (things) taken V at a time we get the number of permutations is 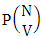 . When the two cases performed in the same time then we get the number of EAB members of M sided N dice taken V at a time is
. When the two cases performed in the same time then we get the number of EAB members of M sided N dice taken V at a time is 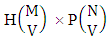 i.e.,
i.e.,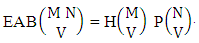 Example 2.4: Find the number of EAB members of the experiment 3 sided 8 dice taken 4 at a time.Solution: The number of AB members is
Example 2.4: Find the number of EAB members of the experiment 3 sided 8 dice taken 4 at a time.Solution: The number of AB members is 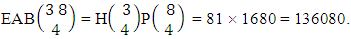 Corollary 2.3: The number of EAB members of the experiment 1 sided N dice taken V at a time is the same as the number of permutations of N taken things V at a time i.e.,
Corollary 2.3: The number of EAB members of the experiment 1 sided N dice taken V at a time is the same as the number of permutations of N taken things V at a time i.e.,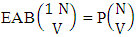 | (2.9) |
Theorem 2.5 ESAB theorem: The number of ESAB members of the experiment M sided N dice taken V at a time, denoted by 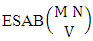 is
is 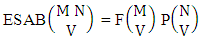 | (2.10) |
where 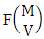 is the number of formations of M sided V dice experiment and
is the number of formations of M sided V dice experiment and 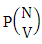 is the number of permutations of N dice (things) taken V at a time.Proof: The above experiment gives the B members first way selected and second way arranged. We now firstly M sided 1 die is tossed, then the B first number gives the number of formations is
is the number of permutations of N dice (things) taken V at a time.Proof: The above experiment gives the B members first way selected and second way arranged. We now firstly M sided 1 die is tossed, then the B first number gives the number of formations is 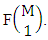 Secondly M sided 2 dice is tossed then the B first number i.e., the number of formations is
Secondly M sided 2 dice is tossed then the B first number i.e., the number of formations is 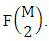 Thirdly M sided 3 dice is tossed then the B first number i.e., the number of formations is
Thirdly M sided 3 dice is tossed then the B first number i.e., the number of formations is 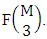 In the same way when M sided V dice tossed then we get the number of formations is
In the same way when M sided V dice tossed then we get the number of formations is 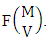 In the other hand N dice (things) taken 1 at a time then the B second number gives the number of permutations is
In the other hand N dice (things) taken 1 at a time then the B second number gives the number of permutations is 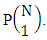 Secondly when N dice (things) taken 2 at a time the B second number i.e., the number of permutations is
Secondly when N dice (things) taken 2 at a time the B second number i.e., the number of permutations is 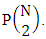 Thirdly when N dice (things) taken 3 at a time then the B second number i.e., the number of permutations is
Thirdly when N dice (things) taken 3 at a time then the B second number i.e., the number of permutations is 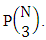 In the same way we get for N dice (things) taken V at a time the number of permutations is
In the same way we get for N dice (things) taken V at a time the number of permutations is 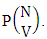 Performing the two cases at a time we get the number of ESAB members of N sided N dice taken V at a time is
Performing the two cases at a time we get the number of ESAB members of N sided N dice taken V at a time is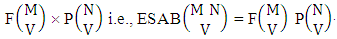 Example 2.5: Find the number of ESAB members of the experiment 6 sided 4 dice taken 2 at a time.Solution: The number of ESAB members is
Example 2.5: Find the number of ESAB members of the experiment 6 sided 4 dice taken 2 at a time.Solution: The number of ESAB members is 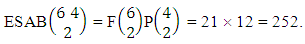 Corollary 2.4: The number of ESAB members of the experiment 1 sided N dice taken V at a time is the same as the number of permutations of N things taken V at a time i.e.,
Corollary 2.4: The number of ESAB members of the experiment 1 sided N dice taken V at a time is the same as the number of permutations of N things taken V at a time i.e.,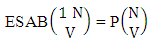 | (2.11) |
Theorem 2.6 EASB theorem: The number of EASB members of the experiment M sided N dice taken V at a time, denoted by 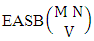 is
is 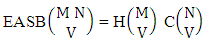 | (2.12) |
where 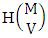 is the number of homogenations of M sided V dice experiment and
is the number of homogenations of M sided V dice experiment and 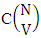 is the number of combinations of N dice (things) taken V at a time.Proof: The experiment gives the outcomes first way arranged and second way selected. Now in first M sided 1 die is tossed then the B first number gives the number of homogenations is
is the number of combinations of N dice (things) taken V at a time.Proof: The experiment gives the outcomes first way arranged and second way selected. Now in first M sided 1 die is tossed then the B first number gives the number of homogenations is 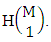 In second M sided 2 dice is tossed, then the B first number i.e., the number of homogenations is
In second M sided 2 dice is tossed, then the B first number i.e., the number of homogenations is 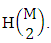 In third M sided 3 dice is tossed, then the B first number i.e., the number of homogenations is
In third M sided 3 dice is tossed, then the B first number i.e., the number of homogenations is 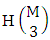 . Similarly when M sided V dice tossed then we get the number of homogenations is
. Similarly when M sided V dice tossed then we get the number of homogenations is 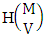 . On the other hand N dice (things) taken 1 at a time then the B second number i.e., the number of combinations is
. On the other hand N dice (things) taken 1 at a time then the B second number i.e., the number of combinations is 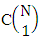 . In second when N dice (things) taken 2 at a time then the B second number i.e., the number of combinations is
. In second when N dice (things) taken 2 at a time then the B second number i.e., the number of combinations is 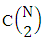 . In third when N dice (things) taken 3 at a time then the B second number i.e., the number of combinations is
. In third when N dice (things) taken 3 at a time then the B second number i.e., the number of combinations is 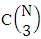 . Similarly we get for N dice (things) taken V at a time the number of combinations is
. Similarly we get for N dice (things) taken V at a time the number of combinations is 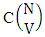 . Now performing the two cases altogether we get the number of EASB members of M sided N dice taken V at a time is
. Now performing the two cases altogether we get the number of EASB members of M sided N dice taken V at a time is 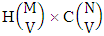 i.e.,
i.e., 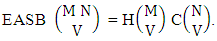 Example 2.6: Find the number of EASB members of the experiment 3 sided 10 dice taken 6 at a time.Solution: The number of EASB members is
Example 2.6: Find the number of EASB members of the experiment 3 sided 10 dice taken 6 at a time.Solution: The number of EASB members is 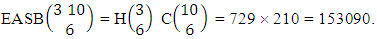 Corollary 2.5: The number EASB members of the experiment 1 sided N dice taken V at a time is the same as the number of combinations of N things taken V at a time i.e.,
Corollary 2.5: The number EASB members of the experiment 1 sided N dice taken V at a time is the same as the number of combinations of N things taken V at a time i.e.,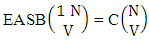 | (2.13) |
Corollary 2.6: The number of EASB members of the experiment M sided V dice taken all at a time is the same as the number of homojenations of M sided V dice experiment i.e.,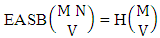 | (2.14) |
2.3. IB Theorem
Theorem 2.7 IB theorem: The number of IB members of the B event 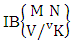 denoted by
denoted by 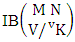 is
is 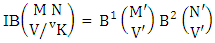 | (2.15) |
where M′, N′ and V′ are to be called affected M, N and V respectively and 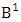 is the B first number is to be holds the number of homogenations or formations and
is the B first number is to be holds the number of homogenations or formations and 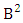 is the B second number is to be holds the number of permutations or combinations.Proof: As the IB members are identified so the parameters M, N, V are to be affected as possible. Let M sided V dice are tossed then as there are v dice identified in the first way or second way or both way so the parameters M and V may be affected as M′ and V′ respectively. Hence the first number is to be
is the B second number is to be holds the number of permutations or combinations.Proof: As the IB members are identified so the parameters M, N, V are to be affected as possible. Let M sided V dice are tossed then as there are v dice identified in the first way or second way or both way so the parameters M and V may be affected as M′ and V′ respectively. Hence the first number is to be 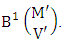 Again when N dice (objects) taken V at time then for the same reason the parameters may be affected as N′ and V′ respectively. So the B second number is to be
Again when N dice (objects) taken V at time then for the same reason the parameters may be affected as N′ and V′ respectively. So the B second number is to be 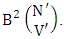 Performing the two cases at a time we get the number of IB members is
Performing the two cases at a time we get the number of IB members is 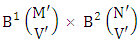 i.e.,
i.e., 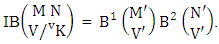 Example 2.7: Find the number of IB members of the B event
Example 2.7: Find the number of IB members of the B event 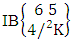 where B first number is the number of formations and B second number is the number of combinations.Solution: From the theorem 2.7 we get
where B first number is the number of formations and B second number is the number of combinations.Solution: From the theorem 2.7 we get 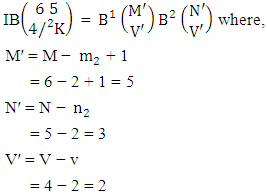 Thus,
Thus, 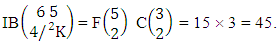 Corollary 2.7: The number of IB members of the B events
Corollary 2.7: The number of IB members of the B events 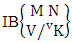 is the same as the number of B members of the B space
is the same as the number of B members of the B space 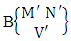 i.e.,
i.e.,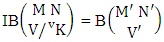 | (2.16) |
Theorem 2.8 ISB theorem: The number of ISB members of the SB event 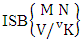 denoted by
denoted by 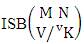 is
is 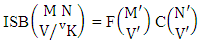 | (2.17) |
where M′, N′ and V′ are to be called affected M, N and V respectively.Proof: As the ISB members are identified so the parameters M, N and V are to be affected as possible. Now M sided V dice are tossed in which first v dice are identified in the first way or second way or both way, the parameters M and V may be affected as M′ and V′ respectively. So the number of formations is to be 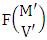 . Again when N dice (objects) taken V at a time then for the same reason the parameters may be affected as N′ and V′ respectively. So the number of combinations is to be
. Again when N dice (objects) taken V at a time then for the same reason the parameters may be affected as N′ and V′ respectively. So the number of combinations is to be 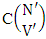 . Performing the two cases at the same time we get the number of ISB members is
. Performing the two cases at the same time we get the number of ISB members is 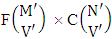 i.e.,
i.e., 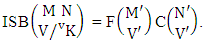 Example 2.8: Find the number of ISB members of the SB event
Example 2.8: Find the number of ISB members of the SB event 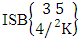 where
where 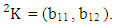 Solution: From the theorem 2.8 we get
Solution: From the theorem 2.8 we get 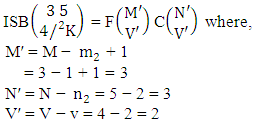 Thus,
Thus, 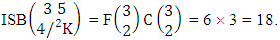 Corollary 2.8: The number of ISB members of the SB event
Corollary 2.8: The number of ISB members of the SB event 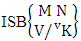 is the same as the number of SB members of the SB space
is the same as the number of SB members of the SB space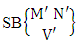 i.e.,
i.e., 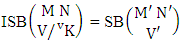 | (2.18) |
Theorem 2.9 IAB theorem: The number of IAB members of the AB event 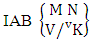 denoted by
denoted by 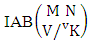 is
is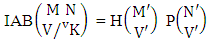 | (2.19) |
where M′, N′ and V′ are to be called affected M, N and V respectively.Proof: As the IAB members are identified so the parameters M, N, V are to be affected as possible. Here the B first number is to be number of homogenations and the B second number is to be number of permutations. Now M sided V dice are tossed in which first v dice identified in the first way or second way or both way, then the parameters M and V may be affected as M′ and V′ respectively. So the number of homogenations is to be 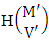 . Again when N dice (object) taken V at a time then for the same reason the parameters may be affected as N′ and V′ respectively. So the number of permutations is to be
. Again when N dice (object) taken V at a time then for the same reason the parameters may be affected as N′ and V′ respectively. So the number of permutations is to be 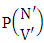 . Performing the two cases at a time the number of IAB members becomes
. Performing the two cases at a time the number of IAB members becomes 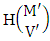
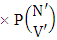 i.e.,
i.e., 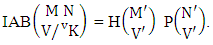 Example 2.9: Find the number of IAB members of the AB event
Example 2.9: Find the number of IAB members of the AB event 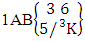 where
where 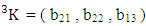 .Solution: From the theorem 2.9 we get
.Solution: From the theorem 2.9 we get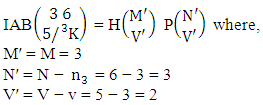 Thus,
Thus, 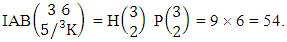 Corollary 2.9: The number of IAB members of the AB event
Corollary 2.9: The number of IAB members of the AB event 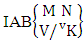 is the same as the number of AB members of the AB space
is the same as the number of AB members of the AB space 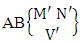 i.e.,
i.e.,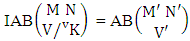 | (2.20) |
Theorem 2.10 ISAB theorem: The number of ISAB members of the SAB event 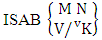 denoted by
denoted by 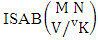 is
is 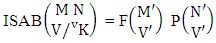 | (2.21) |
where M′, N′ and V′ are to be called affected M, N and V respectively.Proof: As the ISAB members are identified so the parameters M, N and V are to be affected as possible. Let M sided V dice are tossed in which first v dice identified in the first way or second way or both way then the parameters M and V may be affected as M′ and V′ respectively. Thus the number of formations is to be 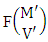 . Again when N dice (objects) taken V at a time then for the same reason the parameters possibly affected as N′ and V′ respectively. Hence the number of permutations is to be
. Again when N dice (objects) taken V at a time then for the same reason the parameters possibly affected as N′ and V′ respectively. Hence the number of permutations is to be 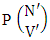 . Performing the two cases at the same time we get the number of ISAB members is
. Performing the two cases at the same time we get the number of ISAB members is 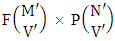 i.e.,
i.e., 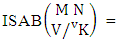
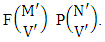 Example 2.10 : Find the number of ISAB members of the SAB event
Example 2.10 : Find the number of ISAB members of the SAB event 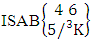 where
where 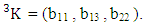 Solution: From the theorem 2.10 we get
Solution: From the theorem 2.10 we get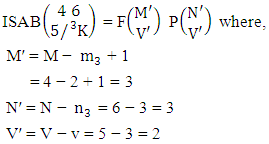 Thus
Thus 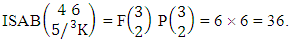 Corollary 2.10: The number of ISAB members of the SAB event
Corollary 2.10: The number of ISAB members of the SAB event 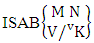 is the same as the number of SAB members of the SAB space
is the same as the number of SAB members of the SAB space 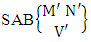 i.e.,
i.e., 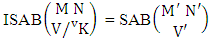 | (2.22) |
Theorem 2.11 IASB theorem: The number of IASB members of the ASB event 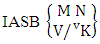 denoted by
denoted by 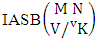 is
is 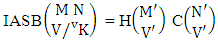 | (2.23) |
where M′, N′ and V′ are to be called affected M, N and V respectively.Proof: As the IASB members are identified so the parameters M, N and V are to be affected as possible. Let M sided V dice are tossed in which first v dice are identified in the first way or second way or both way, the parameters M and V may be affected as M′ and V′ respectively. So the number of homogenations is to be 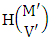 . Again when N dice (objects) taken V at a time then for the same reason the parameters may be effected as N′ and V′ respectively. Thus the number of combinations is to be
. Again when N dice (objects) taken V at a time then for the same reason the parameters may be effected as N′ and V′ respectively. Thus the number of combinations is to be 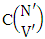 . Performing the two cases at the same time we get the number of IASB members is
. Performing the two cases at the same time we get the number of IASB members is 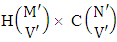 i.e.,
i.e., 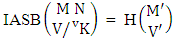
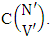 Example 2.11: Find the number of IASB members of the ASB event
Example 2.11: Find the number of IASB members of the ASB event 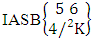 where
where 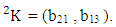 Solution: From the theorem 2.11 we get
Solution: From the theorem 2.11 we get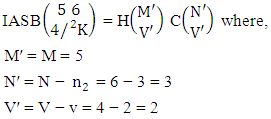 Thus
Thus 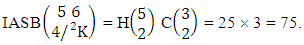 Corollary 2.11: The number of IASB members of the ASB event
Corollary 2.11: The number of IASB members of the ASB event 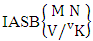 is the same as the number of ASB members of the ASB space
is the same as the number of ASB members of the ASB space 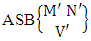 i.e.,
i.e.,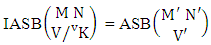 | (2.24) |
Now we describe three kinds of IB theorems i.e., first way IB theorem, second way IB theorem and both way IB theorem and their different forms.Theorem 2.12 First way IB theorem: The number of IB members of the first way B event 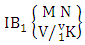 denoted by
denoted by 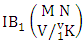 is
is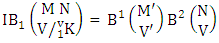 | (2.25) |
where M′ and V′ are to be called affected M and V respectively and 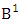 is called to be B first number to be holds the number homogenations or formations and
is called to be B first number to be holds the number homogenations or formations and 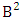 is called to be B second number to be holds the number of permutations or combinations.Proof: Here the IB members are identified in the first way so the parameters hold to the B first number possibly affected and the parameters hold to the B second number do not be affected. Now let M sided V dice tossed in which first v dice identified in the first way so the parameters M and V be affected as M′ and V′ respectively. So the B first number is to be
is called to be B second number to be holds the number of permutations or combinations.Proof: Here the IB members are identified in the first way so the parameters hold to the B first number possibly affected and the parameters hold to the B second number do not be affected. Now let M sided V dice tossed in which first v dice identified in the first way so the parameters M and V be affected as M′ and V′ respectively. So the B first number is to be 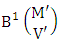 . Again let N dice (objects) taken V at a time in which first v dice are not identified so the parameters N and V not be affected. Hence the B second number is to be
. Again let N dice (objects) taken V at a time in which first v dice are not identified so the parameters N and V not be affected. Hence the B second number is to be 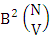 . Performing the two cases at a time we get the number of IB members is
. Performing the two cases at a time we get the number of IB members is 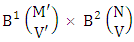 i.e.,
i.e.,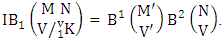 Example 2.12: Find the number of IB members of the B event
Example 2.12: Find the number of IB members of the B event 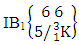 where B first number is the number of formations and B second number is the number of combinations and first 3 identified m’s are 2, 3 and 4. Solution: From the theorem 2.12 we get
where B first number is the number of formations and B second number is the number of combinations and first 3 identified m’s are 2, 3 and 4. Solution: From the theorem 2.12 we get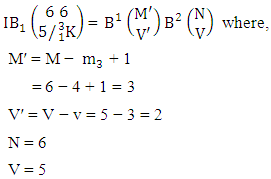 Thus
Thus 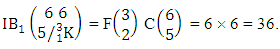 Theorem 2.13 Second way IB theorem: The number of IB members of the second way B event
Theorem 2.13 Second way IB theorem: The number of IB members of the second way B event 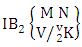 denoted by
denoted by 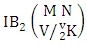 is
is 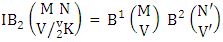 | (2.26) |
where N′ and V′ are to be called affected N and V respectively and 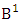 is called to be B first number holds the number of homogenations or formations and
is called to be B first number holds the number of homogenations or formations and 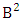 is called to be B second number holds the number of permutations or combinations.Proof: Here the IB members are identified in the second way so the parameters hold to the B first number do not affected and the parameters hold to the B second number possibly affected. Let M sided V dice tossed in which first v dice not identified so the parameters M and V are not be affected. Thus the B first number is to be
is called to be B second number holds the number of permutations or combinations.Proof: Here the IB members are identified in the second way so the parameters hold to the B first number do not affected and the parameters hold to the B second number possibly affected. Let M sided V dice tossed in which first v dice not identified so the parameters M and V are not be affected. Thus the B first number is to be 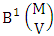 . Again let N dice (objects) taken V at a time in which first v dice identified in the second way so the parameters N and V be affected as N′ and V′ respectively. So the B second number is to be
. Again let N dice (objects) taken V at a time in which first v dice identified in the second way so the parameters N and V be affected as N′ and V′ respectively. So the B second number is to be 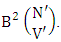 Performing the two cases at the same time we get the number of IB members is
Performing the two cases at the same time we get the number of IB members is 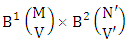 i.e.,
i.e.,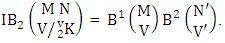 Example 2.13: Find the number of IB members of the B event
Example 2.13: Find the number of IB members of the B event 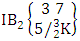 where B first number is the number of formations and B second number is the number of combinations and first 3 identified n’s are 1, 3 and 5.Solution: From the theorem 2.13 we get
where B first number is the number of formations and B second number is the number of combinations and first 3 identified n’s are 1, 3 and 5.Solution: From the theorem 2.13 we get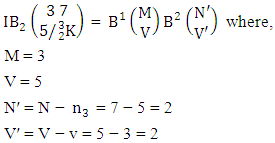 Thus
Thus 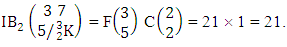 Theorem 2.14 Both way IB theorem: The number of IB members of the both way B event
Theorem 2.14 Both way IB theorem: The number of IB members of the both way B event 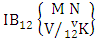 denoted by
denoted by 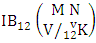 is
is 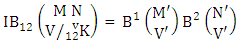 | (2.27) |
where M′, N′ and V′ are to be called affected M, N and V respectively and 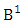 is the B first number to be holds the number of homogenations or formations and
is the B first number to be holds the number of homogenations or formations and 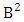 is the B second number to be holds the number of permutations or combinations.Proof: Here the IB members are identified in the both way so the parameters hold to the both B first number and B second number possibly affected. Now let M sided V dice tossed in which first v dice identified in the first way so the parameters M and V be affected as M′ and V′ respectively. Thus the B first number is to be
is the B second number to be holds the number of permutations or combinations.Proof: Here the IB members are identified in the both way so the parameters hold to the both B first number and B second number possibly affected. Now let M sided V dice tossed in which first v dice identified in the first way so the parameters M and V be affected as M′ and V′ respectively. Thus the B first number is to be 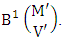 Again let N dice (objects) taken V at a time in which first v dice identified in the second way so the parameters N and V be affected as N′ and V′ respectively. Thus the B second number is to be
Again let N dice (objects) taken V at a time in which first v dice identified in the second way so the parameters N and V be affected as N′ and V′ respectively. Thus the B second number is to be 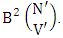 Performing the two cases at the same time we get the number of IB members is
Performing the two cases at the same time we get the number of IB members is 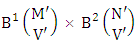 i.e.,
i.e.,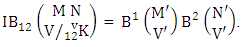 Example 2.14: Find the number of IB members of the B event
Example 2.14: Find the number of IB members of the B event 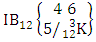 where B first number is the number of formations and B second number is the number of permutations and first 3 identified m’s are 1, 2, 2 and n’s are 2, 3, 4.Solution: From the theorem 2.14 we get
where B first number is the number of formations and B second number is the number of permutations and first 3 identified m’s are 1, 2, 2 and n’s are 2, 3, 4.Solution: From the theorem 2.14 we get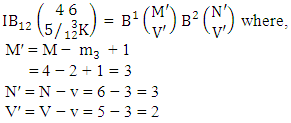 Thus
Thus 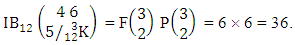 Theorem 2.15 First way ISB theorem: The number of ISB members of the first way SB event
Theorem 2.15 First way ISB theorem: The number of ISB members of the first way SB event 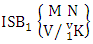 denoted by
denoted by 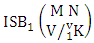 is
is 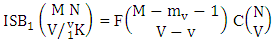 | (2.28) |
Theorem 2.16 Second way ISB theorem: The number of ISB members of the second way SB event 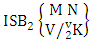 denoted by
denoted by 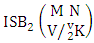 is
is 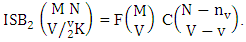 | (2.29) |
Theorem 2.17 Both way ISB theorem: The number of ISB members of the both way SB event 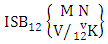 denoted by
denoted by 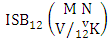 is
is 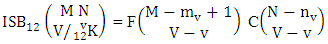 | (2.30) |
Example 2.15: Find the number of ISB members of the SB event 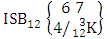 where first 3 m’s are 1, 2, 4 and n’s are 1, 2, 4.Solution: From the theorem 2.17 we get
where first 3 m’s are 1, 2, 4 and n’s are 1, 2, 4.Solution: From the theorem 2.17 we get 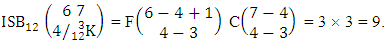 Corollary 2.12: The number of ISB members of the SB event
Corollary 2.12: The number of ISB members of the SB event 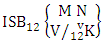 is the same as the number of SB members of the SB space
is the same as the number of SB members of the SB space 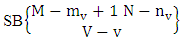 i.e.,
i.e.,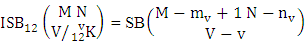 | (2.31) |
Theorem 2.18 First way IAB theorem: The number of IAB members of the first way AB event 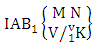 denoted by
denoted by 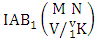 is
is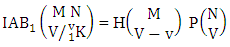 | (2.32) |
Theorem 2.19 Second way IAB theorem: The number of IAB members of the second way AB event 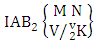 denoted by
denoted by 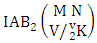 is
is 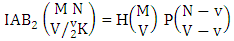 | (2.33) |
Theorem 2.20 Both way IAB theorem: The number of IAB members of the both way AB event 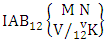 denoted by
denoted by 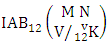 is
is 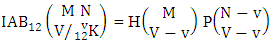 | (2.34) |
Example 2.16: Find the number of IAB members of the AB event 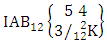 where first m’s are 4, 3 and n’s are 2, 4.Solution: From the theorem 23.20 we get
where first m’s are 4, 3 and n’s are 2, 4.Solution: From the theorem 23.20 we get 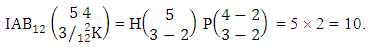 Corollary 2.13: The number of IAB members of the AB event
Corollary 2.13: The number of IAB members of the AB event 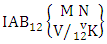 is the same as the number of AB members of the AB space
is the same as the number of AB members of the AB space 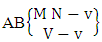 i.e.,
i.e., 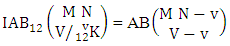 | (2.35) |
Theorem 2.21 First way ISAB theorem: The number of ISAB members of the first way SAB event 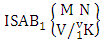 denoted by
denoted by 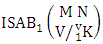 is
is 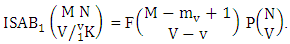 | (2.36) |
Theorem 23.22 Second way ISAB theorem: The number of ISAB members of the second way SAB event 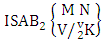 denoted by
denoted by 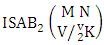 is
is 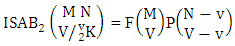 | (2.37) |
Theorem 2.23 Both way ISAB theorem: The number of ISAB members of the both way SAB event 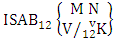 denoted by
denoted by 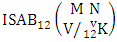 is
is 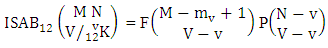 | (2.38) |
Example 2.17: Find the number of ISAB members of the SAB event 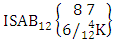 where first 4 identified m’s are 1, 3, 4, 6 and n’s are 2, 3, 4, 6.Solution: From the theorem 2.23 we get
where first 4 identified m’s are 1, 3, 4, 6 and n’s are 2, 3, 4, 6.Solution: From the theorem 2.23 we get 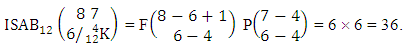 Corollary 2.14: The number of ISAB members of the SAB event
Corollary 2.14: The number of ISAB members of the SAB event 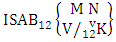 is the same as the number of SAB members of the SAB space
is the same as the number of SAB members of the SAB space 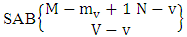 i.e.,
i.e.,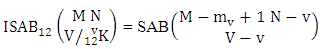 | (2.39) |
Theorem 2.24 First way IASB theorem: The number of IASB members of the first way ASB event 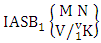 denoted by
denoted by 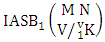 is
is 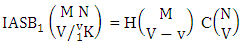 | (2.40) |
Theorem 2.25 Second way IASB theorem: The number of IASB members of the second way ASB event 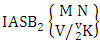 denoted by
denoted by 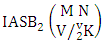 is
is 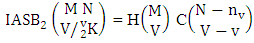 | (2.41) |
Theorem 2.26 Both way IASB theorem: The number of IASB members of the both way ASB event 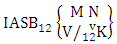 denoted by
denoted by 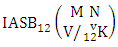 is
is 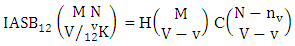 | (2.42) |
Example 2.18: Find the number of IASB members of the ASB event 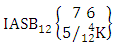 where first 4 identified m’s are 6, 7, 3, 4 and n’s are 2, 3, 4, 5.Solution: From the theorem 2.26 we get
where first 4 identified m’s are 6, 7, 3, 4 and n’s are 2, 3, 4, 5.Solution: From the theorem 2.26 we get 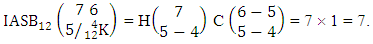 Corollary 2.15: The number of IASB members of the ASB event
Corollary 2.15: The number of IASB members of the ASB event 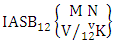 is the same as the number of ASB members of the ASB space
is the same as the number of ASB members of the ASB space 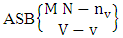 i.e.,
i.e.,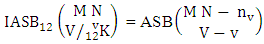 | (2.43) |
2.4. CB Theorem
Theorem 2.27 CB theorem: The number of B events of the CB space 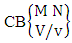 denoted by
denoted by 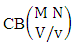 is
is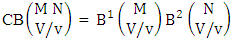 | (2.44) |
where 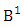 is the B first number to be holds the number of homogenations or formations and
is the B first number to be holds the number of homogenations or formations and 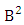 is the B second number to be holds the number of permutations or combinations.Proof: From the theorem 2.2 we get the B number is equal to the product of B first number and B second number. We get more the B first number is the number of events of homoganations or formations and the B second number is the number of events of permutations and combination. Now the B members are characterized at the vth die, so the B first number is to be
is the B second number to be holds the number of permutations or combinations.Proof: From the theorem 2.2 we get the B number is equal to the product of B first number and B second number. We get more the B first number is the number of events of homoganations or formations and the B second number is the number of events of permutations and combination. Now the B members are characterized at the vth die, so the B first number is to be 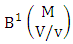 and B second number is to be
and B second number is to be 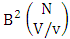 . Hence the theorem.
. Hence the theorem. 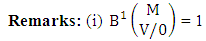 | (2.45) |
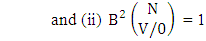 | (2.46) |
Explanations: The number of B members of M sided V dice experiment in which no dice characterized is the B space itself of M sided V dice experiment. Again for the second remark the number of B members of N objects taken V at a time in which no objects characterized is the B space itself of N objects taken V at a time.Example 2.19: Find the number of B events of the CB space 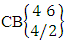 where B first number is the number of events of formations and second die characterized in the first way.Solution: From the theorem 2.27 we get
where B first number is the number of events of formations and second die characterized in the first way.Solution: From the theorem 2.27 we get 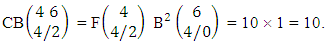 Theorem 2.28 CSB theorem: The number of SB events of the CSB space
Theorem 2.28 CSB theorem: The number of SB events of the CSB space 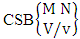 denoted by
denoted by 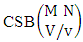 is
is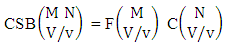 | (2.47) |
Proof: From the theorem 2.3 we get the SB number is equal to the product of number of formations and number of combinations. Now the SB members are characterized at the vth die, so the number of events of formations is 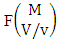 and the number of events of combinations is
and the number of events of combinations is 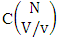 . Hence the number of events of SB members is to be
. Hence the number of events of SB members is to be 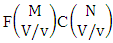 .Example 2.20: Find the number of SB events of the CSB space
.Example 2.20: Find the number of SB events of the CSB space 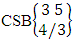 where third die characterized in the second way.Solution: From the theorem 2.28 we get
where third die characterized in the second way.Solution: From the theorem 2.28 we get 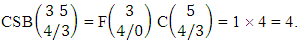 Theorem 2.29 CAB theorem: The number of AB events of the CAB space
Theorem 2.29 CAB theorem: The number of AB events of the CAB space 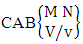 denoted by
denoted by 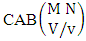 is
is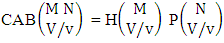 | (2.48) |
Proof: From the theorem 2.4 we get the AB number is equal to the product of number of homoganations and number of permutation. Now the AB members are characterized at the vth die, so the number of events of homoganations is 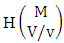 and the number of event of permutations is
and the number of event of permutations is 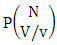 . Hence the number of events of AB members is
. Hence the number of events of AB members is 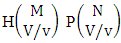 .Example 2.21: Find the number of AB events of the CAB space
.Example 2.21: Find the number of AB events of the CAB space 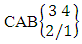 where first die characterized in the first way.Solution: From the theorem 2.29 we get
where first die characterized in the first way.Solution: From the theorem 2.29 we get 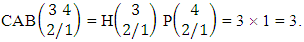 Theorem 2.30 CSAB theorem: The number of SAB events of the CSAB space
Theorem 2.30 CSAB theorem: The number of SAB events of the CSAB space 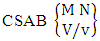 denoted by
denoted by 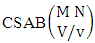 is
is 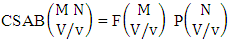 | (2.49) |
Proof: From the theorem 2.5 we get the SAB number is equal to the product of number of formations and number of permutations. Now the SAB members are characterized at the vth die, so the number of events of formations is 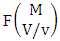 and the number of events of permutations is
and the number of events of permutations is 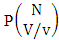 . Hence the number of events of SAB members is to be
. Hence the number of events of SAB members is to be 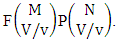 Example 2.22: Find the numbers of SAB events of the CSAB space
Example 2.22: Find the numbers of SAB events of the CSAB space 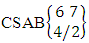 where second die characterized in the first way.Solution: From the theorem 2.30 we get
where second die characterized in the first way.Solution: From the theorem 2.30 we get 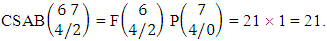 Theorem 2.31 CASB theorem: The number of ASB events of the CASB space
Theorem 2.31 CASB theorem: The number of ASB events of the CASB space 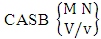 denoted by
denoted by 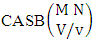 is
is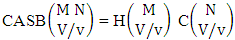 | (2.50) |
Proof: From the theorem 2.6 we get the ASB number is equal to the product of number of homogenations and number of combinations. Now the ASB members are characterized at the vth die, so the number of event of homogenations is 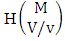 and the number of events of combinations is
and the number of events of combinations is 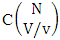 . Hence the number of events of ASB members is
. Hence the number of events of ASB members is 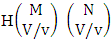 .Example 2.23: Find the number of ASB events of the CASB space
.Example 2.23: Find the number of ASB events of the CASB space 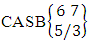 where third die characterized in the second way.Solution: From the theorem 2.31 we get
where third die characterized in the second way.Solution: From the theorem 2.31 we get 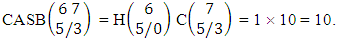 Here we describe three kinds of CB theorems i.e., first way CB theorem, second way CB theorem and both way CB theorem and their different forms. Theorem 2.32 First way CB theorem: The number of B events of the first way CB space
Here we describe three kinds of CB theorems i.e., first way CB theorem, second way CB theorem and both way CB theorem and their different forms. Theorem 2.32 First way CB theorem: The number of B events of the first way CB space 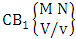 denoted by
denoted by 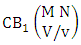 is
is 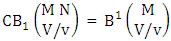 | (2.51) |
where 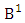 is the B first number to be holds the number of homogenations or formations.Proof: From the theorem 2.2 we get the B number is equal to the product of B first number and B second number. As the vth die characterized in the first way so from equation (2.46) the B second number is equal to one and the B first number as the number of B members characterized at the vth die is
is the B first number to be holds the number of homogenations or formations.Proof: From the theorem 2.2 we get the B number is equal to the product of B first number and B second number. As the vth die characterized in the first way so from equation (2.46) the B second number is equal to one and the B first number as the number of B members characterized at the vth die is 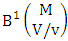 . Hence the theorem.Example 2.24: Find the number of B events of the first way CB space
. Hence the theorem.Example 2.24: Find the number of B events of the first way CB space 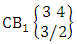 where B first number is the number of events of homogenations.Solution: From the theorem 2.32 we get
where B first number is the number of events of homogenations.Solution: From the theorem 2.32 we get 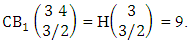 Theorem 2.33 Second way CB theorem: The number of B events of the second way CB space
Theorem 2.33 Second way CB theorem: The number of B events of the second way CB space 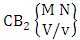 denoted by
denoted by 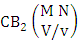 is
is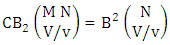 | (2.52) |
where 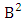 is the B second number to be holds the number of permutations or combinations.Proof: From the theorem 2.2 we get the B number is equal to the product of B first number and B second number. As the vth die characterized in the second way so from equation (2.45) the B first number is equal to one and the B second number as the number of B members characterized at the vth die is
is the B second number to be holds the number of permutations or combinations.Proof: From the theorem 2.2 we get the B number is equal to the product of B first number and B second number. As the vth die characterized in the second way so from equation (2.45) the B first number is equal to one and the B second number as the number of B members characterized at the vth die is 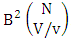 . Hence the theorem.Example 2.25: Find the number of B events of the second way CB space
. Hence the theorem.Example 2.25: Find the number of B events of the second way CB space 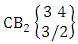 where B second number is the number of events of permutations.Solution: From the theorem 2.33 we get
where B second number is the number of events of permutations.Solution: From the theorem 2.33 we get 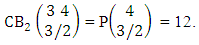 Theorem 2.34 Both way CB theorem: The number of B events of the both way CB space
Theorem 2.34 Both way CB theorem: The number of B events of the both way CB space 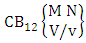 denoted by
denoted by 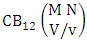 is
is 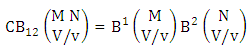 | (2.53) |
Where 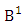 is the B first number to be holds the number of events of homogenations or formations and
is the B first number to be holds the number of events of homogenations or formations and 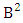 is the B second number to be holds number of events of permutations or combinations.Proof: From the theorem 2.2 we get the B number is equal to the product of B first number and B second number. As the vth die characterized in the both way so the B first number is
is the B second number to be holds number of events of permutations or combinations.Proof: From the theorem 2.2 we get the B number is equal to the product of B first number and B second number. As the vth die characterized in the both way so the B first number is 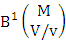 and the B second number is
and the B second number is 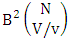 . Hence the number of B events is
. Hence the number of B events is 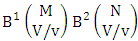 .Example 2.26: Find the number of B events of the both way CB space
.Example 2.26: Find the number of B events of the both way CB space 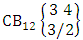 where B first number is the number of events of homogenations and B second number is the number of events of permutations.Solution: From the theorem 2.34 we get
where B first number is the number of events of homogenations and B second number is the number of events of permutations.Solution: From the theorem 2.34 we get 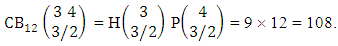 Theorem 2.35 First way CSB theorem: The number of SB events of the first way CSB space
Theorem 2.35 First way CSB theorem: The number of SB events of the first way CSB space 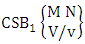 denoted by
denoted by 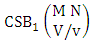 is
is 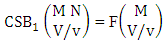 | (2.54) |
Theorem 2.36 Second way CSB theorem: The number of SB events of the second way CSB space 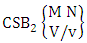 denoted by
denoted by 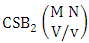 is
is 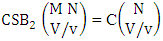 | (2.55) |
Theorem 2.37 Both way CSB theorem: The number of SB events of the both way CSB space 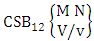 denoted by
denoted by 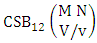 is
is 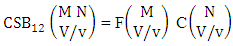 | (2.56) |
Example 2.27: Find the number of SB events of the both way CSB space 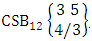 Solution: From the theorem 2.37 we get
Solution: From the theorem 2.37 we get 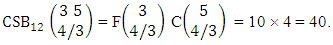 Theorem 2.38 First way CAB theorem: The number of AB events of the first way CAB space
Theorem 2.38 First way CAB theorem: The number of AB events of the first way CAB space 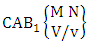 denoted by
denoted by 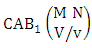 is
is 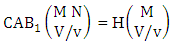 | (2.57) |
Theorem 2.39 Second way CAB theorem: The number of AB events of the second way CAB space 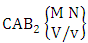 denoted by
denoted by 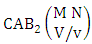 is
is 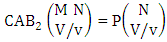 | (2.58) |
Theorem 2.40 Both way CAB theorem: The number of AB events of the both way CAB space 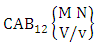 denoted by
denoted by 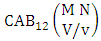 is
is 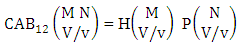 | (2.59) |
Example 2.28: Find the number of AB events of the both way CAB space 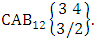 Solution: The solution is the same as the solution of example 2.26 i.e.,
Solution: The solution is the same as the solution of example 2.26 i.e., 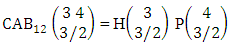 = 9 12 = 108.Theorem 2.41 First way CSAB theorem: The number of SAB events of the first way CSAB space
= 9 12 = 108.Theorem 2.41 First way CSAB theorem: The number of SAB events of the first way CSAB space 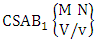 denoted by
denoted by 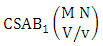 is
is 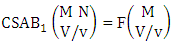 | (2.60) |
Theorem 2.42 Second way CSAB theorem: The number of SAB events of the second way CSAB space 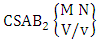 denoted by
denoted by 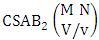 is
is 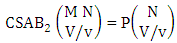 | (2.61) |
Theorem 2.43 Both way CSAB theorem: The number of SAB events of the second way CSAB space 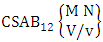 denoted by
denoted by 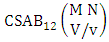 is
is 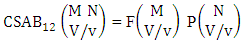 | (2.62) |
Example 2.29: Find the number of SAB events of the both way CSAB space 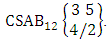 Solution: From the theorem 2.43 we get
Solution: From the theorem 2.43 we get 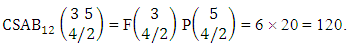 Theorem 2.44 First way CASB theorem: The number of ASB events of the first way CASB space
Theorem 2.44 First way CASB theorem: The number of ASB events of the first way CASB space 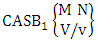 denoted by
denoted by 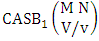 is
is 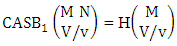 | (2.63) |
Theorem 2.45 Second way CASB theorem: The number of ASB events of the second way CASB space 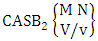 denoted by
denoted by 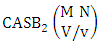 is
is 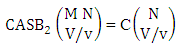 | (2.64) |
Theorem 2.46 Both way CASB theorem: The number of ASB events of the both way CASB space 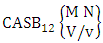 denoted by
denoted by 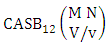 is
is 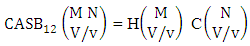 | (2.65) |
Example 2.30: Find the number of ASB events of the both way CASB space 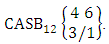 Solution: From the theorem 2.46 we get
Solution: From the theorem 2.46 we get 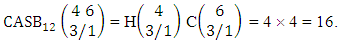
2.5. GB Theorem
Theorem 2.47 GB theorem: The number of GB members of the GB space 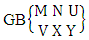 denoted by
denoted by 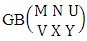 is
is 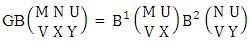 | (2.66) |
where, min(M, U) − M + 1 ≤ X ≤ min(M, U, V)min(N, U) − N + V ≤ Y ≤ min(N, U, V)M ≥ U and N ≥ U for first way and second way respectively. And 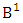 is the B first number to be hold the number of homogenations or formations and
is the B first number to be hold the number of homogenations or formations and 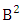 is the B second number to be hold the number of permutations or combinations.Proof: This theorem is the Biswas theorem itself. So the proof is the same as the theorem of Biswas theorem.Theorem 2.48 GSB theorem: The number of GSB members of the GSB space
is the B second number to be hold the number of permutations or combinations.Proof: This theorem is the Biswas theorem itself. So the proof is the same as the theorem of Biswas theorem.Theorem 2.48 GSB theorem: The number of GSB members of the GSB space 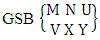 denoted by
denoted by 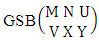 is
is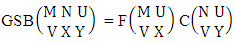 | (2.67) |
where, min(M, U) − M + 1 ≤ X ≤ min(M, U, V)min(N, U) − N + V ≤ Y ≤ min(N, U, V)M ≥ U and N ≥ U for first way and second way respectively. Proof: We know the B number is to be product of B first number and B second number. As the space is a GSB space so B first number get from general formations theorem and B second number get from generation combination theorem. Thus the two numbers are 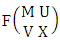 and
and 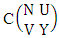 respectively. Now multiflying the two numbers we get the desired GSB number.Example 2.31: Find the number of GSB members of the GSB space
respectively. Now multiflying the two numbers we get the desired GSB number.Example 2.31: Find the number of GSB members of the GSB space 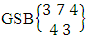 where 3 is observed in the second way.Solution: From the theorem 2.48 we get
where 3 is observed in the second way.Solution: From the theorem 2.48 we get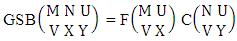 As Y is observed in the second way so we get
As Y is observed in the second way so we get 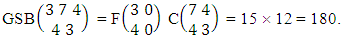 Theorem 2.49 GAB theorem: The number of GAB members of the GAB space
Theorem 2.49 GAB theorem: The number of GAB members of the GAB space 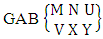 denoted by
denoted by 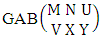 is
is 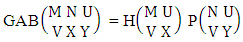 | (2.68) |
where, min(M, U) − M + 1 ≤ X ≤ min(M, U, V)min(N, U) − N + V ≤ Y ≤ min(N, U, V)M ≥ U and N ≥ U for first way and second way respectively.Proof: We know the B number is to be product of B first number and B second number. As the space is a GAB space so B first number get from general homogenation theorem and B second number get from general permutation theorem. Thus the two numbers are 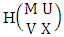 and
and 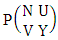 respectively. Multiplying the two numbers we get the desired GAB number.Example 2.32: Find the number of GAB members of the GAB space
respectively. Multiplying the two numbers we get the desired GAB number.Example 2.32: Find the number of GAB members of the GAB space  where 2 is observed in the second way.Solution: From the theorem 2.49 we get
where 2 is observed in the second way.Solution: From the theorem 2.49 we get 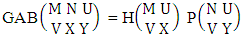 As Y is observed in the second way so we get
As Y is observed in the second way so we get 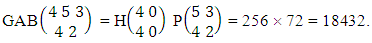 Theorem 2.50 GSAB theorem: The number of GSAB members of the GSAB space
Theorem 2.50 GSAB theorem: The number of GSAB members of the GSAB space 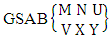 denoted by
denoted by 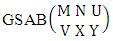 is
is 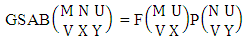 | (2.69) |
where, min(M, U) − M + 1 ≤ X ≤ min(M, U, V)min(N, U) − N + V ≤ Y ≤ min(N, U, V)M ≥ U and N ≥ U for first way and second way respectively.Proof: We know the B number is to be product of B first number and B second number. As the space is a GSAB space so B first number get from general formation theorem and B second number get from general permutation theorem. Thus the two numbers are 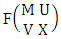 and
and 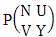 respectively. Now multiplying the two numbers we get the desired GSAB number.Example 2.33: Find the number of GSAB members of the GSAB space
respectively. Now multiplying the two numbers we get the desired GSAB number.Example 2.33: Find the number of GSAB members of the GSAB space 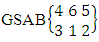 where 1 is observed in the first way and 2 in the second way. Solution: From the theorem 2.50 we get
where 1 is observed in the first way and 2 in the second way. Solution: From the theorem 2.50 we get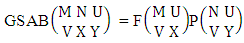 As 1 is observed in the first way and 2 in the second way and M ≥ U for first way we take U = 4, Then
As 1 is observed in the first way and 2 in the second way and M ≥ U for first way we take U = 4, Then 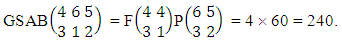 Theorem 2.51 GASB theorem: The number of GASB members of the GASB space
Theorem 2.51 GASB theorem: The number of GASB members of the GASB space 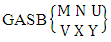 denoted by
denoted by 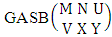 is
is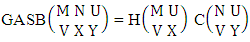 | (2.70) |
where, min(M, U) − M + 1 ≤ X ≤ min(M, U, V)min(N, U) − N + V ≤ Y ≤ min(N, U, V)M ≥ U and N ≥ U for first way and second way respectively. Proof: We know the B number is to be product of B first number and B second number. As the space is a GASB space so B first number get from general homogenation theorem and B second number get from general combination theorem. Thus the two numbers are 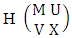 and
and 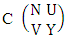 respectively. Now multiplying the two numbers we get the desired GASB number.Example 2.34: Find the number of GASB members of the GASB space
respectively. Now multiplying the two numbers we get the desired GASB number.Example 2.34: Find the number of GASB members of the GASB space 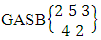 where 2 is observed in the both way. Solution: From the theorem 2.51 we get
where 2 is observed in the both way. Solution: From the theorem 2.51 we get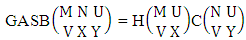 As X, Y are observed in the both way and for M ≥ U we take U = 2 for the first way
As X, Y are observed in the both way and for M ≥ U we take U = 2 for the first way 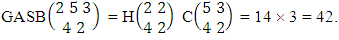 Here we describe three kinds of GB numbers i.e., first way GB theorem, second way GB theorem and both way GB theorem and their different forms.Theorem 2.52 First way GB theorem: The number of GB members of the first way GB space
Here we describe three kinds of GB numbers i.e., first way GB theorem, second way GB theorem and both way GB theorem and their different forms.Theorem 2.52 First way GB theorem: The number of GB members of the first way GB space 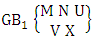 denoted by
denoted by 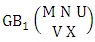 is
is 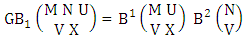 | (2.71) |
where, min(M, U) − M + 1 ≤ X ≤ min(M, U, V)and M ≥ U And 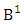 is the B first number to be hold the number of homogenations or formations and
is the B first number to be hold the number of homogenations or formations and 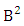 is the B second number to be hold the number of permutations or combinations.Proof: We know the B number is to be product of B first number and B second number. As we consider a first way GB experiment so we get the B first number from general homogenation theorem or general formation theorem and the number is
is the B second number to be hold the number of permutations or combinations.Proof: We know the B number is to be product of B first number and B second number. As we consider a first way GB experiment so we get the B first number from general homogenation theorem or general formation theorem and the number is 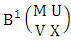 . Again B second number get from elementary permutation theorem or elementary combination theorem and the number is
. Again B second number get from elementary permutation theorem or elementary combination theorem and the number is 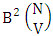 . Now multiplying the two numbers we get the desired first way GB number. Example 2.35: Find the number of GB members of the first way GB space
. Now multiplying the two numbers we get the desired first way GB number. Example 2.35: Find the number of GB members of the first way GB space 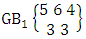 chosen first way selected and second way arranged.Solution: From the theorem 2.52 we get
chosen first way selected and second way arranged.Solution: From the theorem 2.52 we get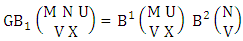
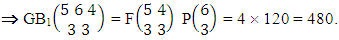 Theorem 2.53 Second way GB theorem: The number of GB members of the second way GB space
Theorem 2.53 Second way GB theorem: The number of GB members of the second way GB space 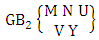 denoted by
denoted by 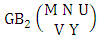 is
is 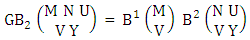 | (2.72) |
where, min(N, U) − N + V ≤ Y ≤ min(N, U, V)and N ≥ U and 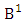 is the B first number to be hold the number of homogenations or formations and
is the B first number to be hold the number of homogenations or formations and 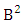 is the B second number to be hold the number of permutations or combinations.Proof: We know the B number is to be product of B first number and B second number. As we consider a second way GB experiment so we get the B first number from elementary homogenation theorem or elementary formation theorem and the number is
is the B second number to be hold the number of permutations or combinations.Proof: We know the B number is to be product of B first number and B second number. As we consider a second way GB experiment so we get the B first number from elementary homogenation theorem or elementary formation theorem and the number is 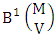 . Again B second number get from general permutation theorem or general combination theorem and the number is
. Again B second number get from general permutation theorem or general combination theorem and the number is 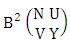 . Now multiplying the two numbers we get the desired second way GB number. Example 2.36: Find the number of GB members of the second way GB space
. Now multiplying the two numbers we get the desired second way GB number. Example 2.36: Find the number of GB members of the second way GB space 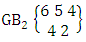 chosen both way selected.Solution: From the theorem 2.53 we get
chosen both way selected.Solution: From the theorem 2.53 we get 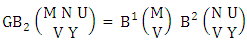
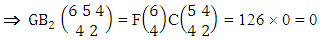 Here we get
Here we get 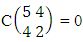 as X ranges from 3 to 4 So,
as X ranges from 3 to 4 So, 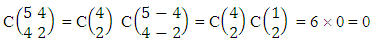 Theorem 2.54 Both way GB theorem: The number of GB members of the both way GB space
Theorem 2.54 Both way GB theorem: The number of GB members of the both way GB space 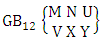 denoted by
denoted by 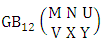 is
is 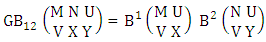 | (2.73) |
where, min(M, U) − M + 1 ≤ X ≤ min(M, U, V)min(N, U) − N + V ≤ Y ≤ min(N, U, V)M ≥ U and N ≥ U for first way and second way respectively.And 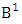 is the B first number to be hold the number of homogenations or formations and
is the B first number to be hold the number of homogenations or formations and 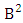 is the B second number to be hold the number of permutations or combinations. Proof: We know the B number is to be product of B first number and B second number. As we consider a both way GB experiment so we get the B first number from general homogenation theorem or general formation theorem and the number is
is the B second number to be hold the number of permutations or combinations. Proof: We know the B number is to be product of B first number and B second number. As we consider a both way GB experiment so we get the B first number from general homogenation theorem or general formation theorem and the number is 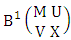 . Again B second number get from generation permutation theorem or general combination theorem and the number is
. Again B second number get from generation permutation theorem or general combination theorem and the number is 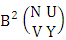 . Now multiplying the two numbers we get the desired both way GB number. Example 2.37: Find the number of GB members of the both way GB space
. Now multiplying the two numbers we get the desired both way GB number. Example 2.37: Find the number of GB members of the both way GB space 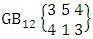 chosen both way arranged.Solution: From the theorem 2.54 we get
chosen both way arranged.Solution: From the theorem 2.54 we get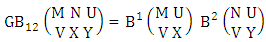 As 1 is observed in the first way and 3 is observed in the second way and M ≥ U for first way we take U = 3. Then
As 1 is observed in the first way and 3 is observed in the second way and M ≥ U for first way we take U = 3. Then 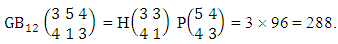 Theorem 2.55 First way GSB theorem: The number of GSB members of the first way GSB space
Theorem 2.55 First way GSB theorem: The number of GSB members of the first way GSB space 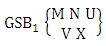 denoted by
denoted by 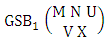 is
is 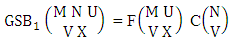 | (2.74) |
where, min(M, U) − M + 1 ≤ X ≤ min(M, U, V)and M ≥ UTheorem 2.56 Second way GSB theorem: The number of GSB members of the second way GSB space 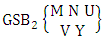 denoted by
denoted by 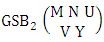 is
is 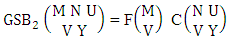 | (2.75) |
where, min(N, U) − N + V ≤ Y ≤ min(N, U, V)and N ≥ UTheorem 2.57 Both way GSB theorem: The number of GSB members of the both way GSB space 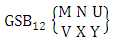 denoted by
denoted by 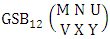 is
is 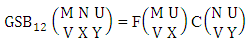 | (2.76) |
where, min(M, U) − M + 1 ≤ X ≤ min(M, U, V)min(N, U) − N + V ≤ Y ≤ min(N, U, V)M ≥ U and N ≥ U for first way and second way respectively.Example 2.38: Find the number of GSB members of the both way GSB space 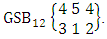 Solution: From the theorem 2.57 we get
Solution: From the theorem 2.57 we get 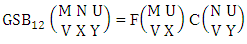
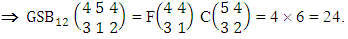 Theorem 2.58 First way GAB theorem: The number of GAB members of the first way GAB space
Theorem 2.58 First way GAB theorem: The number of GAB members of the first way GAB space 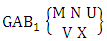 denoted by
denoted by 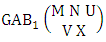 is
is 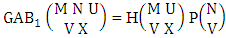 | (2.77) |
where, min(M, U) − M + 1 ≤ X ≤ min(M, U, V)and M ≥ U Theorem 2.59 Second way GAB theorem: The number of GAB members of the second way GAB space 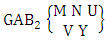 denoted by
denoted by 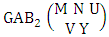 is
is 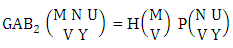 | (2.78) |
where, min(N, U) − N + V ≤ Y ≤ min(N, U, V)and N ≥ UTheorem 2.60 Both way GAB theorem: The number of GAB members of the both way GAB space 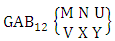 denoted by
denoted by 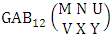 is
is 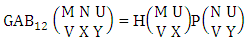 | (2.79) |
where, min(M, U) − M + 1 ≤ X ≤ min(M, U, V)min(N, U) − N + V ≤ Y ≤ min(N, U, V)M ≥ U and N ≥ U for first way and second way respectively.Example 2.39: Find the number of GAB members of the both way GAB space 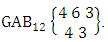 Solution: From the theorem 2.60 we get
Solution: From the theorem 2.60 we get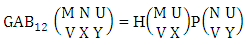
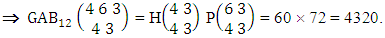 Theorem 2.61 First way GSAB theorem: The number of GSAB members of the first way GSAB space
Theorem 2.61 First way GSAB theorem: The number of GSAB members of the first way GSAB space 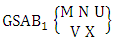 denoted by
denoted by 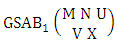 is
is 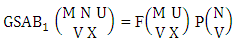 | (2.80) |
where, min(M, U) − M + 1 ≤ X ≤ min(M, U, V)and M ≥ UTheorem 2.62 Second way GSAB theorem: The number of GSAB members of the second way GSAB space 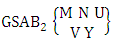 denoted by
denoted by 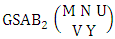 is
is 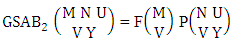 | (2.81) |
where, min(N, U) − N + V ≤ Y ≤ min(N, U, V)and N ≥ UTheorem 2.63 Both way GSAB theorem: The number of GSAB members of the both way GSAB space 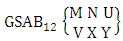 denoted by
denoted by 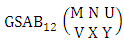 is
is 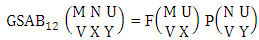 | (2.82) |
where, min(M, U) − M + 1 ≤ X ≤ min(M, U, V)min(N, U) − N + V ≤ Y ≤ min(N, U, V)M ≥ U and N ≥ U for first way and second way respectively.Example 2.40: Find the number of GSAB members of the both way GSAB space 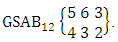 Solution: From the theorem 2.63 we get
Solution: From the theorem 2.63 we get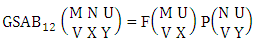 As 3 is observed in the first way and 2 is observed in the second way so we get
As 3 is observed in the first way and 2 is observed in the second way so we get 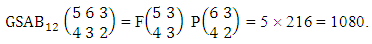 Theorem 2.64 First way GASB theorem: The number of GASB members of the first way GASB space
Theorem 2.64 First way GASB theorem: The number of GASB members of the first way GASB space 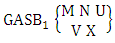 denoted by
denoted by 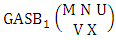 is
is 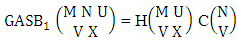 | (2.83) |
where, min(M, U) − M + 1 ≤ X ≤ min(M, U, V)and M ≥ UTheorem 2.65 Second way GASB theorem: The number of GASB members of the second way GASB space 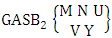 denoted by
denoted by 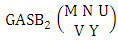 is
is 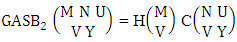 | (2.84) |
where, min(N, U) − N + V ≤ Y ≤ min(N, U, V)and N ≥ UTheorem 2.66 Both way GASB theorem: The number of GASB members of the both way GASB space 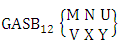 denoted by
denoted by 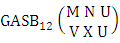 is
is 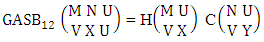 | (2.85) |
where, min(M, U) − M + 1 ≤ X ≤ min(M, U, V)min(N, U) − N + V ≤ Y ≤ min(N, U, V)M ≥ U and N ≥ U for first way and second way respectively.Example 2.41: Find the number of GASB members of the both way GASB space 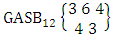 .Solution: From the theorem 2.66 we get
.Solution: From the theorem 2.66 we get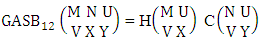 Using M ≥ U for first way we take U = 3, thus
Using M ≥ U for first way we take U = 3, thus 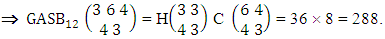
3. Conclusions
First of all we get from this paper an interesting Biswas theorem and its related theorems. The related theorems are EB theorems, IB theorems, CB related theorems and GB theorems. We get combination theorem, permutation theorem, formation theorem and homogenation theorem from these related theorems.
References
| [1] | Deapon Biswas, Paper 4, B space, Bystematics My Classic, 2010 Self published, Chittagong, 2016 Monon Prokashon, Chittagong, Bystematics Vol. I and II, My Classic, 2018 Scholar’s Press EU, ISBN: 987- 620-2-30664-5 and 987- 620-2-30960-8. |
| [2] | Deapon Biswas, Paper 13, On the combinations, Bystematics My Classic, 2010 Self published, Chittagong, 2016 Monon Prokashon, Chittagong, Bystematics Vol. I and II, My Classic, 2018 Scholar’s Press EU, ISBN: 987- 620-2-30664-5 and 987- 620-2-30960-8. |
| [3] | Deapon Biswas, Paper 16, On the permutations, Bystematics My Classic, 2010 Self published, Chittagong, 2016 Monon Prokashon, Chittagong, Bystematics Vol. I and II, My Classic, 2018 Scholar’s Press EU, ISBN: 987- 620-2-30664-5 and 987- 620-2-30960-8. |
| [4] | Deapon Biswas, Paper 18, Fomrations, Bystematics My Classic, 2010 Self published, Chittagong, 2016 Monon Prokashon, Chittagong, Bystematics Vol. I and II, My Classic, 2018 Scholar’s Press EU, ISBN: 987- 620-2-30664-5 and 987- 620-2-30960-8. |
| [5] | Deapon Biswas, Paper 20, Homogenations, Bystematics My Classic, 2010 Self published, Chittagong, 2016 Monon Prokashon, Chittagong, Bystematics Vol. I and II, My Classic, 2018 Scholar’s Press EU, ISBN: 987- 620-2-30664-5 and 987- 620-2-30960-8. |
| [6] | Deapon Biswas, Paper 23, EB members, Bystematics My Classic, 2010 Self published, Chittagong, 2016 Monon Prokashon, Chittagong, Bystematics Vol. I and II, My Classic, 2018 Scholar’s Press EU, ISBN: 987- 620-2-30664-5 and 987- 620-2-30960-8. |
| [7] | Deapon Biswas, Paper 24, IB members, Bystematics My Classic, 2010 Self published, Chittagong, 2016 Monon Prokashon, Chittagong, Bystematics Vol. I and II, My Classic, 2018 Scholar’s Press EU, ISBN: 987- 620-2-30664-5 and 987- 620-2-30960-8. |
| [8] | Deapon Biswas, Paper 25, CB members, Bystematics My Classic, 2010 Self published, Chittagong, 2016 Monon Prokashon, Chittagong, Bystematics Vol. I and II, My Classic, 2018 Scholar’s Press EU, ISBN: 987- 620-2-30664-5 and 987- 620-2-30960-8. |
| [9] | Deapon Biswas, Paper 26, GB members, Bystematics My Classic, 2010 Self published, Chittagong, 2016 Monon Prokashon, Chittagong, Bystematics Vol. I and II, My Classic, 2018 Scholar’s Press EU, ISBN: 987- 620-2-30664-5 and 987- 620-2-30960-8. |
| [10] | Deapon Biswas, Biswas theorem and related theorems. International Journal of Probability and Statistics. |



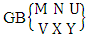 denoted by
denoted by 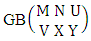 is
is 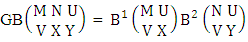
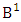 is the B first number to be hold the number of homogenations or formations and
is the B first number to be hold the number of homogenations or formations and 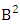 is the B second number to be hold the number of permutations or combinations.Proof: We know the B number is to be product of B first number and B second number. As the theorem is from a GB experiment so we get the B first number from general homogenation theorem or general formations theorem and it is to be
is the B second number to be hold the number of permutations or combinations.Proof: We know the B number is to be product of B first number and B second number. As the theorem is from a GB experiment so we get the B first number from general homogenation theorem or general formations theorem and it is to be 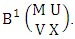 Again B second number get from general permutation theorem or general combination theorem and it is to be
Again B second number get from general permutation theorem or general combination theorem and it is to be 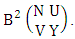 Performing the two cases we get the number of GB members as
Performing the two cases we get the number of GB members as 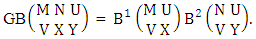
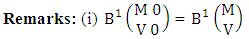
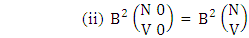
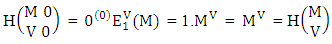 Again let B first number is for number of formations then
Again let B first number is for number of formations then 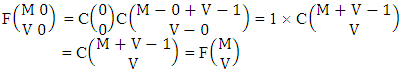 Now for the B second number let it is represent for number of permutations then
Now for the B second number let it is represent for number of permutations then 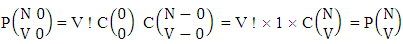 Again let B second number is represent for number of combinations then
Again let B second number is represent for number of combinations then 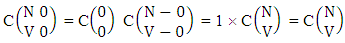 Example 2.1: Find the number of GB members of the GB space
Example 2.1: Find the number of GB members of the GB space 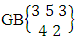 chosen first way arranged and second way selected and 2 is observed in the first way.Solution: From the theorem 2.1 we get
chosen first way arranged and second way selected and 2 is observed in the first way.Solution: From the theorem 2.1 we get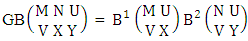 As X is observed in the first way so we get
As X is observed in the first way so we get 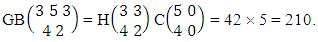
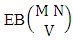 is
is 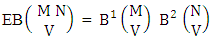
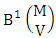 called B first number is the number of homogenations or formations of M sided V dice experiment and
called B first number is the number of homogenations or formations of M sided V dice experiment and 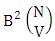 called B second number is the number of permutations or combinations of N dice (things) taken V at a time.Proof: Let M sided 1 dice is tossed, then we get the number of B members is
called B second number is the number of permutations or combinations of N dice (things) taken V at a time.Proof: Let M sided 1 dice is tossed, then we get the number of B members is 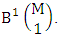 In the same why M sided 2 dice is tossed then we get the number of B members is
In the same why M sided 2 dice is tossed then we get the number of B members is 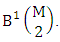 In the same why M sided 3 dice is tossed then we get the number of B members is
In the same why M sided 3 dice is tossed then we get the number of B members is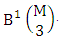 Similarly for M sided V dice experiment we get the number of B members is
Similarly for M sided V dice experiment we get the number of B members is 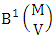 . In the other hand, N dice (or things) taken 1at a time then we get the number of B members is
. In the other hand, N dice (or things) taken 1at a time then we get the number of B members is 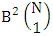 . Again N dice (or things) taken 2 at a time then we get the number of B members is
. Again N dice (or things) taken 2 at a time then we get the number of B members is 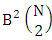 . In the same way N dice (or things) taken 3 at a time then we get the number of B members is
. In the same way N dice (or things) taken 3 at a time then we get the number of B members is 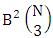 . Similarly for N dice (or things) taken V at a time then we get the number of B members is
. Similarly for N dice (or things) taken V at a time then we get the number of B members is 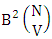 . When the two case performed in the same time then we get the number of B members of M sided N dice taken V at a time is
. When the two case performed in the same time then we get the number of B members of M sided N dice taken V at a time is 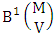
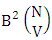 i.e.,
i.e., 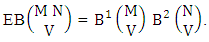 Hence the proof.Example 2.2: Find the number of B members of the experiment 6 sided 10 dice taken 5 at a time where B first number is the number of homogenations and B second number is the number of combinations.Solution: The numbers of B members is
Hence the proof.Example 2.2: Find the number of B members of the experiment 6 sided 10 dice taken 5 at a time where B first number is the number of homogenations and B second number is the number of combinations.Solution: The numbers of B members is 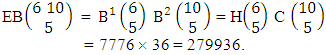 Theorem 2.3 ESB theorem: The number of ESB members of the experiment M sided N dice taken V at a time, denoted by
Theorem 2.3 ESB theorem: The number of ESB members of the experiment M sided N dice taken V at a time, denoted by 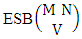 is
is 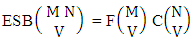
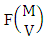 is the number of formations of M sided V dice experiment and
is the number of formations of M sided V dice experiment and 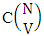 is the number of combinations of N dice (things) taken V at a time.Proof: The experiment gives the outcomes selected i.e., ESB members. Firstly M sided 1 die is tossed, then the B first number gives the number of formations is
is the number of combinations of N dice (things) taken V at a time.Proof: The experiment gives the outcomes selected i.e., ESB members. Firstly M sided 1 die is tossed, then the B first number gives the number of formations is 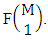 Secondly M sided 2 dice is tossed then the B first number i.e., the number of formations is
Secondly M sided 2 dice is tossed then the B first number i.e., the number of formations is 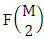 . Thirdly M sided 3 dice is tossed then the B first number i.e., the number of formations is
. Thirdly M sided 3 dice is tossed then the B first number i.e., the number of formations is 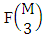 . Similarly for M sided V dice experiment we get the number of formations is
. Similarly for M sided V dice experiment we get the number of formations is 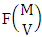 . Again for N dice (things) taken 1 at a time then the B second number gives the number of combinations is
. Again for N dice (things) taken 1 at a time then the B second number gives the number of combinations is 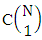 . Secondly N dice (things) taken 2 at a time then the B second number i.e., number of combinations is
. Secondly N dice (things) taken 2 at a time then the B second number i.e., number of combinations is 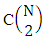 . Thirdly for the same reason when N dice (things) taken 3 at a time then the B second number i.e., the number of combinations is
. Thirdly for the same reason when N dice (things) taken 3 at a time then the B second number i.e., the number of combinations is 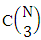 . Similarly we get for N dice (things) taken V at a time the number is
. Similarly we get for N dice (things) taken V at a time the number is 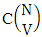 . Now for the two case performed in the same time the number of ESB members of M sided N dice taken V at a time is
. Now for the two case performed in the same time the number of ESB members of M sided N dice taken V at a time is 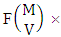
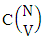 i.e.,
i.e., 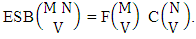 Example 2.3: Find the number of ESB members of the experiment 3 sided 5 dice taken 4 at a time.Solution: The number of ESB members is
Example 2.3: Find the number of ESB members of the experiment 3 sided 5 dice taken 4 at a time.Solution: The number of ESB members is 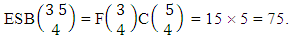 Corollary 2.1: The number of ESB members of the experiment 1 sided N dice taken V at a time is the same as the numbers of combinations of N things taken V at a time i.e.,
Corollary 2.1: The number of ESB members of the experiment 1 sided N dice taken V at a time is the same as the numbers of combinations of N things taken V at a time i.e.,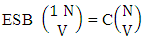
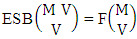
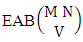 is
is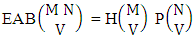
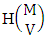 is the number of homogenations of M sided V dice experiment and
is the number of homogenations of M sided V dice experiment and 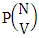 is the number of permutations of N dice (things) taken V at a time.Proof: Here the experiment results all the B members arranged i.e., EAB members. Now M sided 1 die is tossed then the B first number gives the number of homogenations is
is the number of permutations of N dice (things) taken V at a time.Proof: Here the experiment results all the B members arranged i.e., EAB members. Now M sided 1 die is tossed then the B first number gives the number of homogenations is 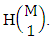 Again M sided 2 dice is tossed then the B first number i.e., number of homogenations is
Again M sided 2 dice is tossed then the B first number i.e., number of homogenations is 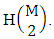 For the same reason when M sided 3 dice is tossed then the B first number i.e., the number of homogenations is
For the same reason when M sided 3 dice is tossed then the B first number i.e., the number of homogenations is 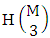 . Similarly for M sided V dice experiment we get the number of homogenations is
. Similarly for M sided V dice experiment we get the number of homogenations is 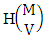 . On the other hand when N dice (things) taken 1 at a time then the B second number gives the number of permutations is
. On the other hand when N dice (things) taken 1 at a time then the B second number gives the number of permutations is 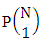 . Again N dice (things) taken 2 at a time then the B second number i.e., the number of permutations is
. Again N dice (things) taken 2 at a time then the B second number i.e., the number of permutations is 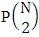 . For the same reason when N dice (things) taken 3 at a time then the B second number i.e., the number of permutations is
. For the same reason when N dice (things) taken 3 at a time then the B second number i.e., the number of permutations is 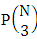 . Similarly for N dice (things) taken V at a time we get the number of permutations is
. Similarly for N dice (things) taken V at a time we get the number of permutations is 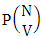 . When the two cases performed in the same time then we get the number of EAB members of M sided N dice taken V at a time is
. When the two cases performed in the same time then we get the number of EAB members of M sided N dice taken V at a time is 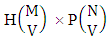 i.e.,
i.e.,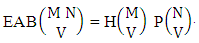 Example 2.4: Find the number of EAB members of the experiment 3 sided 8 dice taken 4 at a time.Solution: The number of AB members is
Example 2.4: Find the number of EAB members of the experiment 3 sided 8 dice taken 4 at a time.Solution: The number of AB members is 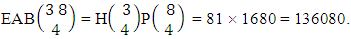 Corollary 2.3: The number of EAB members of the experiment 1 sided N dice taken V at a time is the same as the number of permutations of N taken things V at a time i.e.,
Corollary 2.3: The number of EAB members of the experiment 1 sided N dice taken V at a time is the same as the number of permutations of N taken things V at a time i.e.,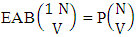
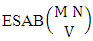 is
is 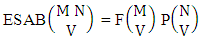
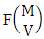 is the number of formations of M sided V dice experiment and
is the number of formations of M sided V dice experiment and 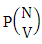 is the number of permutations of N dice (things) taken V at a time.Proof: The above experiment gives the B members first way selected and second way arranged. We now firstly M sided 1 die is tossed, then the B first number gives the number of formations is
is the number of permutations of N dice (things) taken V at a time.Proof: The above experiment gives the B members first way selected and second way arranged. We now firstly M sided 1 die is tossed, then the B first number gives the number of formations is 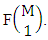 Secondly M sided 2 dice is tossed then the B first number i.e., the number of formations is
Secondly M sided 2 dice is tossed then the B first number i.e., the number of formations is 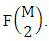 Thirdly M sided 3 dice is tossed then the B first number i.e., the number of formations is
Thirdly M sided 3 dice is tossed then the B first number i.e., the number of formations is 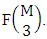 In the same way when M sided V dice tossed then we get the number of formations is
In the same way when M sided V dice tossed then we get the number of formations is 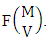 In the other hand N dice (things) taken 1 at a time then the B second number gives the number of permutations is
In the other hand N dice (things) taken 1 at a time then the B second number gives the number of permutations is 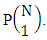 Secondly when N dice (things) taken 2 at a time the B second number i.e., the number of permutations is
Secondly when N dice (things) taken 2 at a time the B second number i.e., the number of permutations is 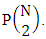 Thirdly when N dice (things) taken 3 at a time then the B second number i.e., the number of permutations is
Thirdly when N dice (things) taken 3 at a time then the B second number i.e., the number of permutations is 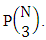 In the same way we get for N dice (things) taken V at a time the number of permutations is
In the same way we get for N dice (things) taken V at a time the number of permutations is 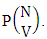 Performing the two cases at a time we get the number of ESAB members of N sided N dice taken V at a time is
Performing the two cases at a time we get the number of ESAB members of N sided N dice taken V at a time is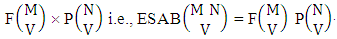 Example 2.5: Find the number of ESAB members of the experiment 6 sided 4 dice taken 2 at a time.Solution: The number of ESAB members is
Example 2.5: Find the number of ESAB members of the experiment 6 sided 4 dice taken 2 at a time.Solution: The number of ESAB members is 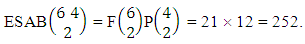 Corollary 2.4: The number of ESAB members of the experiment 1 sided N dice taken V at a time is the same as the number of permutations of N things taken V at a time i.e.,
Corollary 2.4: The number of ESAB members of the experiment 1 sided N dice taken V at a time is the same as the number of permutations of N things taken V at a time i.e.,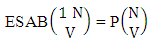
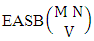 is
is 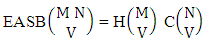
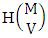 is the number of homogenations of M sided V dice experiment and
is the number of homogenations of M sided V dice experiment and 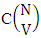 is the number of combinations of N dice (things) taken V at a time.Proof: The experiment gives the outcomes first way arranged and second way selected. Now in first M sided 1 die is tossed then the B first number gives the number of homogenations is
is the number of combinations of N dice (things) taken V at a time.Proof: The experiment gives the outcomes first way arranged and second way selected. Now in first M sided 1 die is tossed then the B first number gives the number of homogenations is 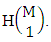 In second M sided 2 dice is tossed, then the B first number i.e., the number of homogenations is
In second M sided 2 dice is tossed, then the B first number i.e., the number of homogenations is 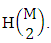 In third M sided 3 dice is tossed, then the B first number i.e., the number of homogenations is
In third M sided 3 dice is tossed, then the B first number i.e., the number of homogenations is 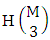 . Similarly when M sided V dice tossed then we get the number of homogenations is
. Similarly when M sided V dice tossed then we get the number of homogenations is 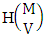 . On the other hand N dice (things) taken 1 at a time then the B second number i.e., the number of combinations is
. On the other hand N dice (things) taken 1 at a time then the B second number i.e., the number of combinations is 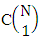 . In second when N dice (things) taken 2 at a time then the B second number i.e., the number of combinations is
. In second when N dice (things) taken 2 at a time then the B second number i.e., the number of combinations is 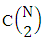 . In third when N dice (things) taken 3 at a time then the B second number i.e., the number of combinations is
. In third when N dice (things) taken 3 at a time then the B second number i.e., the number of combinations is 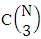 . Similarly we get for N dice (things) taken V at a time the number of combinations is
. Similarly we get for N dice (things) taken V at a time the number of combinations is 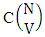 . Now performing the two cases altogether we get the number of EASB members of M sided N dice taken V at a time is
. Now performing the two cases altogether we get the number of EASB members of M sided N dice taken V at a time is 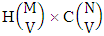 i.e.,
i.e., 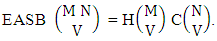 Example 2.6: Find the number of EASB members of the experiment 3 sided 10 dice taken 6 at a time.Solution: The number of EASB members is
Example 2.6: Find the number of EASB members of the experiment 3 sided 10 dice taken 6 at a time.Solution: The number of EASB members is 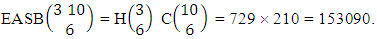 Corollary 2.5: The number EASB members of the experiment 1 sided N dice taken V at a time is the same as the number of combinations of N things taken V at a time i.e.,
Corollary 2.5: The number EASB members of the experiment 1 sided N dice taken V at a time is the same as the number of combinations of N things taken V at a time i.e.,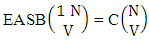
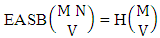
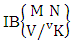 denoted by
denoted by 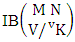 is
is 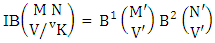
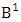 is the B first number is to be holds the number of homogenations or formations and
is the B first number is to be holds the number of homogenations or formations and 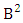 is the B second number is to be holds the number of permutations or combinations.Proof: As the IB members are identified so the parameters M, N, V are to be affected as possible. Let M sided V dice are tossed then as there are v dice identified in the first way or second way or both way so the parameters M and V may be affected as M′ and V′ respectively. Hence the first number is to be
is the B second number is to be holds the number of permutations or combinations.Proof: As the IB members are identified so the parameters M, N, V are to be affected as possible. Let M sided V dice are tossed then as there are v dice identified in the first way or second way or both way so the parameters M and V may be affected as M′ and V′ respectively. Hence the first number is to be 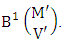 Again when N dice (objects) taken V at time then for the same reason the parameters may be affected as N′ and V′ respectively. So the B second number is to be
Again when N dice (objects) taken V at time then for the same reason the parameters may be affected as N′ and V′ respectively. So the B second number is to be 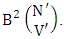 Performing the two cases at a time we get the number of IB members is
Performing the two cases at a time we get the number of IB members is 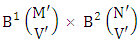 i.e.,
i.e., 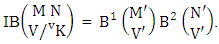 Example 2.7: Find the number of IB members of the B event
Example 2.7: Find the number of IB members of the B event 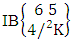 where B first number is the number of formations and B second number is the number of combinations.Solution: From the theorem 2.7 we get
where B first number is the number of formations and B second number is the number of combinations.Solution: From the theorem 2.7 we get 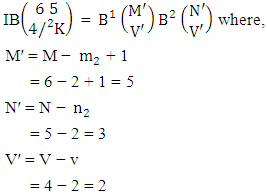 Thus,
Thus, 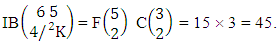 Corollary 2.7: The number of IB members of the B events
Corollary 2.7: The number of IB members of the B events 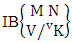 is the same as the number of B members of the B space
is the same as the number of B members of the B space 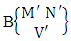 i.e.,
i.e.,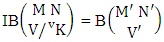
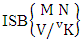 denoted by
denoted by 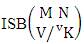 is
is 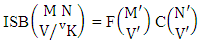
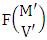 . Again when N dice (objects) taken V at a time then for the same reason the parameters may be affected as N′ and V′ respectively. So the number of combinations is to be
. Again when N dice (objects) taken V at a time then for the same reason the parameters may be affected as N′ and V′ respectively. So the number of combinations is to be 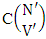 . Performing the two cases at the same time we get the number of ISB members is
. Performing the two cases at the same time we get the number of ISB members is 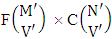 i.e.,
i.e., 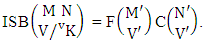 Example 2.8: Find the number of ISB members of the SB event
Example 2.8: Find the number of ISB members of the SB event 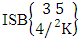 where
where  Solution: From the theorem 2.8 we get
Solution: From the theorem 2.8 we get 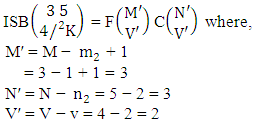 Thus,
Thus, 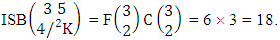 Corollary 2.8: The number of ISB members of the SB event
Corollary 2.8: The number of ISB members of the SB event 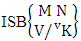 is the same as the number of SB members of the SB space
is the same as the number of SB members of the SB space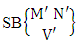 i.e.,
i.e., 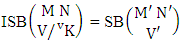
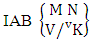 denoted by
denoted by 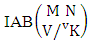 is
is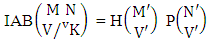
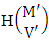 . Again when N dice (object) taken V at a time then for the same reason the parameters may be affected as N′ and V′ respectively. So the number of permutations is to be
. Again when N dice (object) taken V at a time then for the same reason the parameters may be affected as N′ and V′ respectively. So the number of permutations is to be 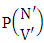 . Performing the two cases at a time the number of IAB members becomes
. Performing the two cases at a time the number of IAB members becomes 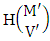
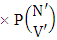 i.e.,
i.e., 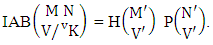 Example 2.9: Find the number of IAB members of the AB event
Example 2.9: Find the number of IAB members of the AB event 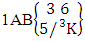 where
where 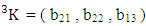 .Solution: From the theorem 2.9 we get
.Solution: From the theorem 2.9 we get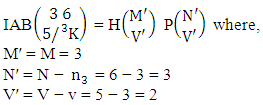 Thus,
Thus, 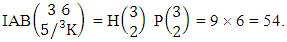 Corollary 2.9: The number of IAB members of the AB event
Corollary 2.9: The number of IAB members of the AB event 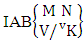 is the same as the number of AB members of the AB space
is the same as the number of AB members of the AB space 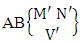 i.e.,
i.e.,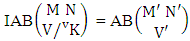
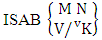 denoted by
denoted by 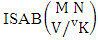 is
is 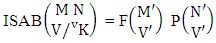
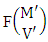 . Again when N dice (objects) taken V at a time then for the same reason the parameters possibly affected as N′ and V′ respectively. Hence the number of permutations is to be
. Again when N dice (objects) taken V at a time then for the same reason the parameters possibly affected as N′ and V′ respectively. Hence the number of permutations is to be 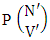 . Performing the two cases at the same time we get the number of ISAB members is
. Performing the two cases at the same time we get the number of ISAB members is 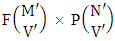 i.e.,
i.e., 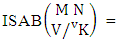
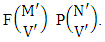 Example 2.10 : Find the number of ISAB members of the SAB event
Example 2.10 : Find the number of ISAB members of the SAB event 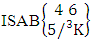 where
where 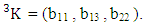 Solution: From the theorem 2.10 we get
Solution: From the theorem 2.10 we get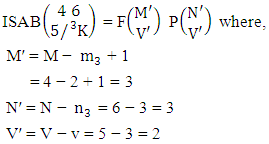 Thus
Thus 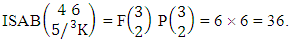 Corollary 2.10: The number of ISAB members of the SAB event
Corollary 2.10: The number of ISAB members of the SAB event 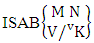 is the same as the number of SAB members of the SAB space
is the same as the number of SAB members of the SAB space 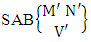 i.e.,
i.e., 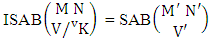
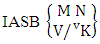 denoted by
denoted by 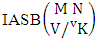 is
is 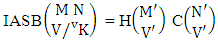
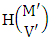 . Again when N dice (objects) taken V at a time then for the same reason the parameters may be effected as N′ and V′ respectively. Thus the number of combinations is to be
. Again when N dice (objects) taken V at a time then for the same reason the parameters may be effected as N′ and V′ respectively. Thus the number of combinations is to be 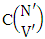 . Performing the two cases at the same time we get the number of IASB members is
. Performing the two cases at the same time we get the number of IASB members is 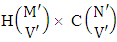 i.e.,
i.e., 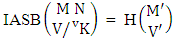
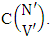 Example 2.11: Find the number of IASB members of the ASB event
Example 2.11: Find the number of IASB members of the ASB event 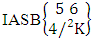 where
where 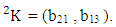 Solution: From the theorem 2.11 we get
Solution: From the theorem 2.11 we get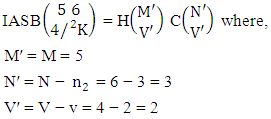 Thus
Thus 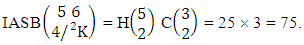 Corollary 2.11: The number of IASB members of the ASB event
Corollary 2.11: The number of IASB members of the ASB event 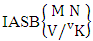 is the same as the number of ASB members of the ASB space
is the same as the number of ASB members of the ASB space 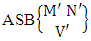 i.e.,
i.e.,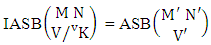
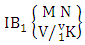 denoted by
denoted by 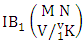 is
is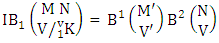
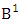 is called to be B first number to be holds the number homogenations or formations and
is called to be B first number to be holds the number homogenations or formations and 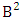 is called to be B second number to be holds the number of permutations or combinations.Proof: Here the IB members are identified in the first way so the parameters hold to the B first number possibly affected and the parameters hold to the B second number do not be affected. Now let M sided V dice tossed in which first v dice identified in the first way so the parameters M and V be affected as M′ and V′ respectively. So the B first number is to be
is called to be B second number to be holds the number of permutations or combinations.Proof: Here the IB members are identified in the first way so the parameters hold to the B first number possibly affected and the parameters hold to the B second number do not be affected. Now let M sided V dice tossed in which first v dice identified in the first way so the parameters M and V be affected as M′ and V′ respectively. So the B first number is to be 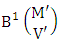 . Again let N dice (objects) taken V at a time in which first v dice are not identified so the parameters N and V not be affected. Hence the B second number is to be
. Again let N dice (objects) taken V at a time in which first v dice are not identified so the parameters N and V not be affected. Hence the B second number is to be 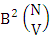 . Performing the two cases at a time we get the number of IB members is
. Performing the two cases at a time we get the number of IB members is 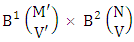 i.e.,
i.e.,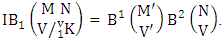 Example 2.12: Find the number of IB members of the B event
Example 2.12: Find the number of IB members of the B event 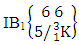 where B first number is the number of formations and B second number is the number of combinations and first 3 identified m’s are 2, 3 and 4. Solution: From the theorem 2.12 we get
where B first number is the number of formations and B second number is the number of combinations and first 3 identified m’s are 2, 3 and 4. Solution: From the theorem 2.12 we get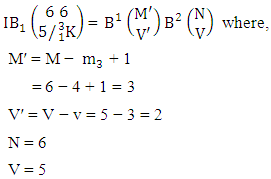 Thus
Thus 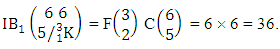 Theorem 2.13 Second way IB theorem: The number of IB members of the second way B event
Theorem 2.13 Second way IB theorem: The number of IB members of the second way B event 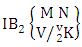 denoted by
denoted by 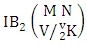 is
is 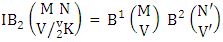
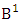 is called to be B first number holds the number of homogenations or formations and
is called to be B first number holds the number of homogenations or formations and 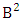 is called to be B second number holds the number of permutations or combinations.Proof: Here the IB members are identified in the second way so the parameters hold to the B first number do not affected and the parameters hold to the B second number possibly affected. Let M sided V dice tossed in which first v dice not identified so the parameters M and V are not be affected. Thus the B first number is to be
is called to be B second number holds the number of permutations or combinations.Proof: Here the IB members are identified in the second way so the parameters hold to the B first number do not affected and the parameters hold to the B second number possibly affected. Let M sided V dice tossed in which first v dice not identified so the parameters M and V are not be affected. Thus the B first number is to be 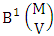 . Again let N dice (objects) taken V at a time in which first v dice identified in the second way so the parameters N and V be affected as N′ and V′ respectively. So the B second number is to be
. Again let N dice (objects) taken V at a time in which first v dice identified in the second way so the parameters N and V be affected as N′ and V′ respectively. So the B second number is to be 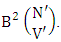 Performing the two cases at the same time we get the number of IB members is
Performing the two cases at the same time we get the number of IB members is 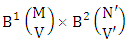 i.e.,
i.e.,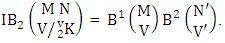 Example 2.13: Find the number of IB members of the B event
Example 2.13: Find the number of IB members of the B event 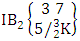 where B first number is the number of formations and B second number is the number of combinations and first 3 identified n’s are 1, 3 and 5.Solution: From the theorem 2.13 we get
where B first number is the number of formations and B second number is the number of combinations and first 3 identified n’s are 1, 3 and 5.Solution: From the theorem 2.13 we get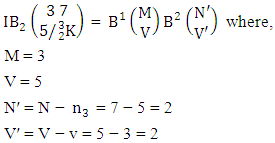 Thus
Thus 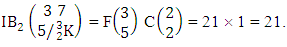 Theorem 2.14 Both way IB theorem: The number of IB members of the both way B event
Theorem 2.14 Both way IB theorem: The number of IB members of the both way B event 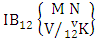 denoted by
denoted by 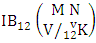 is
is 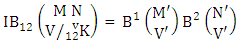
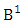 is the B first number to be holds the number of homogenations or formations and
is the B first number to be holds the number of homogenations or formations and 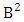 is the B second number to be holds the number of permutations or combinations.Proof: Here the IB members are identified in the both way so the parameters hold to the both B first number and B second number possibly affected. Now let M sided V dice tossed in which first v dice identified in the first way so the parameters M and V be affected as M′ and V′ respectively. Thus the B first number is to be
is the B second number to be holds the number of permutations or combinations.Proof: Here the IB members are identified in the both way so the parameters hold to the both B first number and B second number possibly affected. Now let M sided V dice tossed in which first v dice identified in the first way so the parameters M and V be affected as M′ and V′ respectively. Thus the B first number is to be 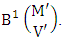 Again let N dice (objects) taken V at a time in which first v dice identified in the second way so the parameters N and V be affected as N′ and V′ respectively. Thus the B second number is to be
Again let N dice (objects) taken V at a time in which first v dice identified in the second way so the parameters N and V be affected as N′ and V′ respectively. Thus the B second number is to be 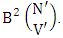 Performing the two cases at the same time we get the number of IB members is
Performing the two cases at the same time we get the number of IB members is 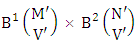 i.e.,
i.e.,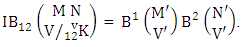 Example 2.14: Find the number of IB members of the B event
Example 2.14: Find the number of IB members of the B event 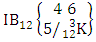 where B first number is the number of formations and B second number is the number of permutations and first 3 identified m’s are 1, 2, 2 and n’s are 2, 3, 4.Solution: From the theorem 2.14 we get
where B first number is the number of formations and B second number is the number of permutations and first 3 identified m’s are 1, 2, 2 and n’s are 2, 3, 4.Solution: From the theorem 2.14 we get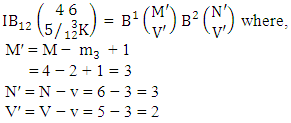 Thus
Thus 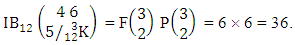 Theorem 2.15 First way ISB theorem: The number of ISB members of the first way SB event
Theorem 2.15 First way ISB theorem: The number of ISB members of the first way SB event 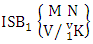 denoted by
denoted by 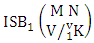 is
is 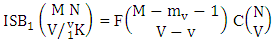
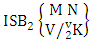 denoted by
denoted by 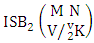 is
is 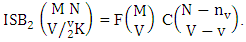
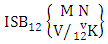 denoted by
denoted by 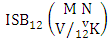 is
is 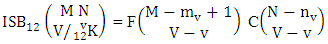
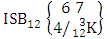 where first 3 m’s are 1, 2, 4 and n’s are 1, 2, 4.Solution: From the theorem 2.17 we get
where first 3 m’s are 1, 2, 4 and n’s are 1, 2, 4.Solution: From the theorem 2.17 we get 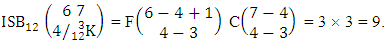 Corollary 2.12: The number of ISB members of the SB event
Corollary 2.12: The number of ISB members of the SB event 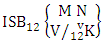 is the same as the number of SB members of the SB space
is the same as the number of SB members of the SB space 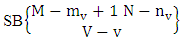 i.e.,
i.e.,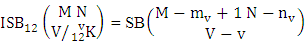
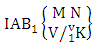 denoted by
denoted by 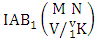 is
is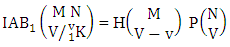
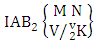 denoted by
denoted by 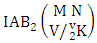 is
is 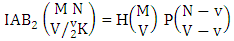
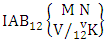 denoted by
denoted by 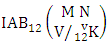 is
is 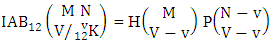
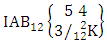 where first m’s are 4, 3 and n’s are 2, 4.Solution: From the theorem 23.20 we get
where first m’s are 4, 3 and n’s are 2, 4.Solution: From the theorem 23.20 we get 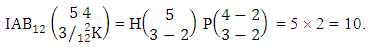 Corollary 2.13: The number of IAB members of the AB event
Corollary 2.13: The number of IAB members of the AB event 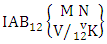 is the same as the number of AB members of the AB space
is the same as the number of AB members of the AB space 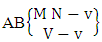 i.e.,
i.e., 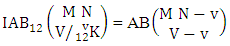
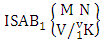 denoted by
denoted by 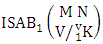 is
is 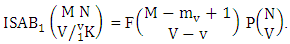
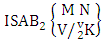 denoted by
denoted by 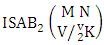 is
is 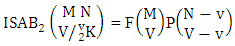
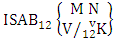 denoted by
denoted by 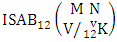 is
is 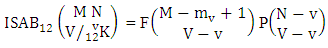
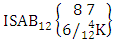 where first 4 identified m’s are 1, 3, 4, 6 and n’s are 2, 3, 4, 6.Solution: From the theorem 2.23 we get
where first 4 identified m’s are 1, 3, 4, 6 and n’s are 2, 3, 4, 6.Solution: From the theorem 2.23 we get 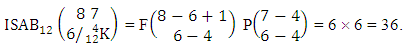 Corollary 2.14: The number of ISAB members of the SAB event
Corollary 2.14: The number of ISAB members of the SAB event 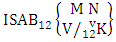 is the same as the number of SAB members of the SAB space
is the same as the number of SAB members of the SAB space 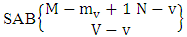 i.e.,
i.e.,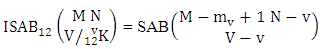
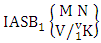 denoted by
denoted by 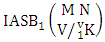 is
is 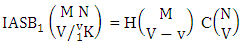
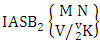 denoted by
denoted by 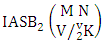 is
is 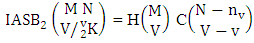
 denoted by
denoted by  is
is 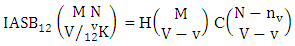
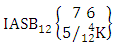 where first 4 identified m’s are 6, 7, 3, 4 and n’s are 2, 3, 4, 5.Solution: From the theorem 2.26 we get
where first 4 identified m’s are 6, 7, 3, 4 and n’s are 2, 3, 4, 5.Solution: From the theorem 2.26 we get 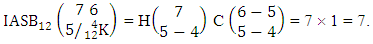 Corollary 2.15: The number of IASB members of the ASB event
Corollary 2.15: The number of IASB members of the ASB event 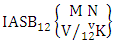 is the same as the number of ASB members of the ASB space
is the same as the number of ASB members of the ASB space 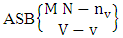 i.e.,
i.e.,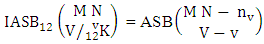
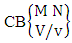 denoted by
denoted by 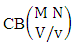 is
is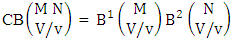
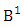 is the B first number to be holds the number of homogenations or formations and
is the B first number to be holds the number of homogenations or formations and 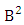 is the B second number to be holds the number of permutations or combinations.Proof: From the theorem 2.2 we get the B number is equal to the product of B first number and B second number. We get more the B first number is the number of events of homoganations or formations and the B second number is the number of events of permutations and combination. Now the B members are characterized at the vth die, so the B first number is to be
is the B second number to be holds the number of permutations or combinations.Proof: From the theorem 2.2 we get the B number is equal to the product of B first number and B second number. We get more the B first number is the number of events of homoganations or formations and the B second number is the number of events of permutations and combination. Now the B members are characterized at the vth die, so the B first number is to be 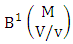 and B second number is to be
and B second number is to be 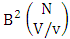 . Hence the theorem.
. Hence the theorem. 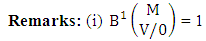
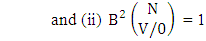
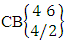 where B first number is the number of events of formations and second die characterized in the first way.Solution: From the theorem 2.27 we get
where B first number is the number of events of formations and second die characterized in the first way.Solution: From the theorem 2.27 we get 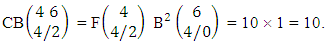 Theorem 2.28 CSB theorem: The number of SB events of the CSB space
Theorem 2.28 CSB theorem: The number of SB events of the CSB space 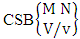 denoted by
denoted by 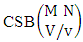 is
is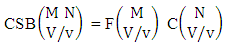
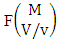 and the number of events of combinations is
and the number of events of combinations is 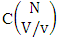 . Hence the number of events of SB members is to be
. Hence the number of events of SB members is to be 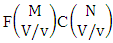 .Example 2.20: Find the number of SB events of the CSB space
.Example 2.20: Find the number of SB events of the CSB space 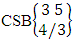 where third die characterized in the second way.Solution: From the theorem 2.28 we get
where third die characterized in the second way.Solution: From the theorem 2.28 we get 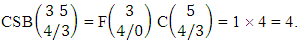 Theorem 2.29 CAB theorem: The number of AB events of the CAB space
Theorem 2.29 CAB theorem: The number of AB events of the CAB space 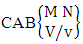 denoted by
denoted by 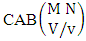 is
is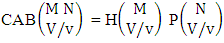
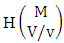 and the number of event of permutations is
and the number of event of permutations is 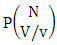 . Hence the number of events of AB members is
. Hence the number of events of AB members is 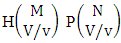 .Example 2.21: Find the number of AB events of the CAB space
.Example 2.21: Find the number of AB events of the CAB space 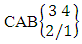 where first die characterized in the first way.Solution: From the theorem 2.29 we get
where first die characterized in the first way.Solution: From the theorem 2.29 we get 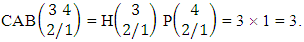 Theorem 2.30 CSAB theorem: The number of SAB events of the CSAB space
Theorem 2.30 CSAB theorem: The number of SAB events of the CSAB space 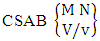 denoted by
denoted by 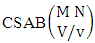 is
is 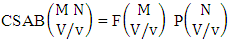
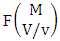 and the number of events of permutations is
and the number of events of permutations is 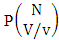 . Hence the number of events of SAB members is to be
. Hence the number of events of SAB members is to be 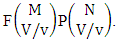 Example 2.22: Find the numbers of SAB events of the CSAB space
Example 2.22: Find the numbers of SAB events of the CSAB space 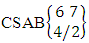 where second die characterized in the first way.Solution: From the theorem 2.30 we get
where second die characterized in the first way.Solution: From the theorem 2.30 we get 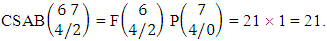 Theorem 2.31 CASB theorem: The number of ASB events of the CASB space
Theorem 2.31 CASB theorem: The number of ASB events of the CASB space 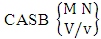 denoted by
denoted by 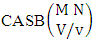 is
is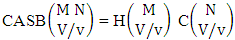
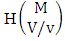 and the number of events of combinations is
and the number of events of combinations is 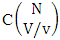 . Hence the number of events of ASB members is
. Hence the number of events of ASB members is 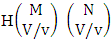 .Example 2.23: Find the number of ASB events of the CASB space
.Example 2.23: Find the number of ASB events of the CASB space 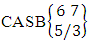 where third die characterized in the second way.Solution: From the theorem 2.31 we get
where third die characterized in the second way.Solution: From the theorem 2.31 we get 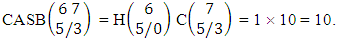 Here we describe three kinds of CB theorems i.e., first way CB theorem, second way CB theorem and both way CB theorem and their different forms. Theorem 2.32 First way CB theorem: The number of B events of the first way CB space
Here we describe three kinds of CB theorems i.e., first way CB theorem, second way CB theorem and both way CB theorem and their different forms. Theorem 2.32 First way CB theorem: The number of B events of the first way CB space 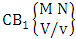 denoted by
denoted by 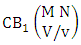 is
is 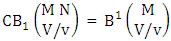
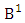 is the B first number to be holds the number of homogenations or formations.Proof: From the theorem 2.2 we get the B number is equal to the product of B first number and B second number. As the vth die characterized in the first way so from equation (2.46) the B second number is equal to one and the B first number as the number of B members characterized at the vth die is
is the B first number to be holds the number of homogenations or formations.Proof: From the theorem 2.2 we get the B number is equal to the product of B first number and B second number. As the vth die characterized in the first way so from equation (2.46) the B second number is equal to one and the B first number as the number of B members characterized at the vth die is 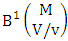 . Hence the theorem.Example 2.24: Find the number of B events of the first way CB space
. Hence the theorem.Example 2.24: Find the number of B events of the first way CB space 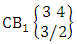 where B first number is the number of events of homogenations.Solution: From the theorem 2.32 we get
where B first number is the number of events of homogenations.Solution: From the theorem 2.32 we get 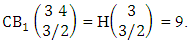 Theorem 2.33 Second way CB theorem: The number of B events of the second way CB space
Theorem 2.33 Second way CB theorem: The number of B events of the second way CB space 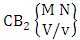 denoted by
denoted by 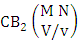 is
is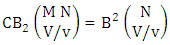
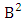 is the B second number to be holds the number of permutations or combinations.Proof: From the theorem 2.2 we get the B number is equal to the product of B first number and B second number. As the vth die characterized in the second way so from equation (2.45) the B first number is equal to one and the B second number as the number of B members characterized at the vth die is
is the B second number to be holds the number of permutations or combinations.Proof: From the theorem 2.2 we get the B number is equal to the product of B first number and B second number. As the vth die characterized in the second way so from equation (2.45) the B first number is equal to one and the B second number as the number of B members characterized at the vth die is 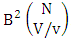 . Hence the theorem.Example 2.25: Find the number of B events of the second way CB space
. Hence the theorem.Example 2.25: Find the number of B events of the second way CB space 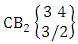 where B second number is the number of events of permutations.Solution: From the theorem 2.33 we get
where B second number is the number of events of permutations.Solution: From the theorem 2.33 we get 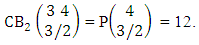 Theorem 2.34 Both way CB theorem: The number of B events of the both way CB space
Theorem 2.34 Both way CB theorem: The number of B events of the both way CB space 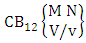 denoted by
denoted by 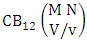 is
is 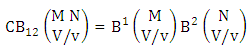
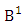 is the B first number to be holds the number of events of homogenations or formations and
is the B first number to be holds the number of events of homogenations or formations and 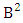 is the B second number to be holds number of events of permutations or combinations.Proof: From the theorem 2.2 we get the B number is equal to the product of B first number and B second number. As the vth die characterized in the both way so the B first number is
is the B second number to be holds number of events of permutations or combinations.Proof: From the theorem 2.2 we get the B number is equal to the product of B first number and B second number. As the vth die characterized in the both way so the B first number is 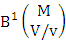 and the B second number is
and the B second number is 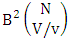 . Hence the number of B events is
. Hence the number of B events is 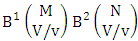 .Example 2.26: Find the number of B events of the both way CB space
.Example 2.26: Find the number of B events of the both way CB space 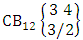 where B first number is the number of events of homogenations and B second number is the number of events of permutations.Solution: From the theorem 2.34 we get
where B first number is the number of events of homogenations and B second number is the number of events of permutations.Solution: From the theorem 2.34 we get 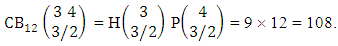 Theorem 2.35 First way CSB theorem: The number of SB events of the first way CSB space
Theorem 2.35 First way CSB theorem: The number of SB events of the first way CSB space 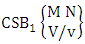 denoted by
denoted by 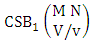 is
is 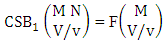
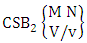 denoted by
denoted by 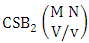 is
is 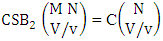
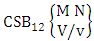 denoted by
denoted by 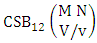 is
is 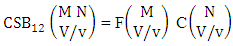
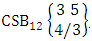 Solution: From the theorem 2.37 we get
Solution: From the theorem 2.37 we get 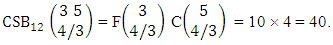 Theorem 2.38 First way CAB theorem: The number of AB events of the first way CAB space
Theorem 2.38 First way CAB theorem: The number of AB events of the first way CAB space 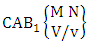 denoted by
denoted by 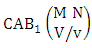 is
is 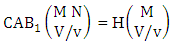
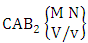 denoted by
denoted by 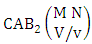 is
is 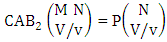
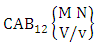 denoted by
denoted by 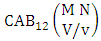 is
is 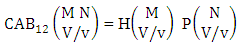
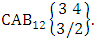 Solution: The solution is the same as the solution of example 2.26 i.e.,
Solution: The solution is the same as the solution of example 2.26 i.e., 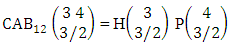 = 9 12 = 108.Theorem 2.41 First way CSAB theorem: The number of SAB events of the first way CSAB space
= 9 12 = 108.Theorem 2.41 First way CSAB theorem: The number of SAB events of the first way CSAB space 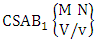 denoted by
denoted by 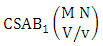 is
is 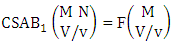
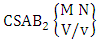 denoted by
denoted by 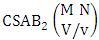 is
is 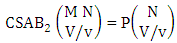
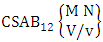 denoted by
denoted by 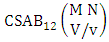 is
is 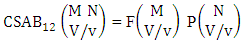
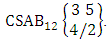 Solution: From the theorem 2.43 we get
Solution: From the theorem 2.43 we get 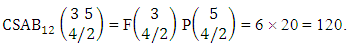 Theorem 2.44 First way CASB theorem: The number of ASB events of the first way CASB space
Theorem 2.44 First way CASB theorem: The number of ASB events of the first way CASB space 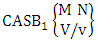 denoted by
denoted by 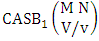 is
is 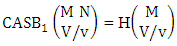
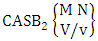 denoted by
denoted by 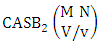 is
is 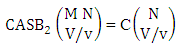
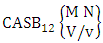 denoted by
denoted by 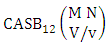 is
is 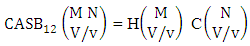
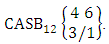 Solution: From the theorem 2.46 we get
Solution: From the theorem 2.46 we get 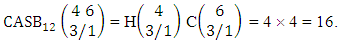
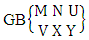 denoted by
denoted by 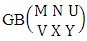 is
is 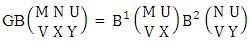
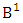 is the B first number to be hold the number of homogenations or formations and
is the B first number to be hold the number of homogenations or formations and 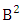 is the B second number to be hold the number of permutations or combinations.Proof: This theorem is the Biswas theorem itself. So the proof is the same as the theorem of Biswas theorem.Theorem 2.48 GSB theorem: The number of GSB members of the GSB space
is the B second number to be hold the number of permutations or combinations.Proof: This theorem is the Biswas theorem itself. So the proof is the same as the theorem of Biswas theorem.Theorem 2.48 GSB theorem: The number of GSB members of the GSB space 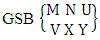 denoted by
denoted by 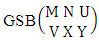 is
is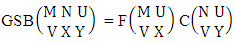
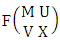 and
and 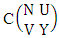 respectively. Now multiflying the two numbers we get the desired GSB number.Example 2.31: Find the number of GSB members of the GSB space
respectively. Now multiflying the two numbers we get the desired GSB number.Example 2.31: Find the number of GSB members of the GSB space 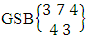 where 3 is observed in the second way.Solution: From the theorem 2.48 we get
where 3 is observed in the second way.Solution: From the theorem 2.48 we get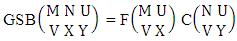 As Y is observed in the second way so we get
As Y is observed in the second way so we get 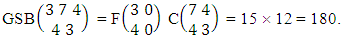 Theorem 2.49 GAB theorem: The number of GAB members of the GAB space
Theorem 2.49 GAB theorem: The number of GAB members of the GAB space 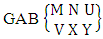 denoted by
denoted by 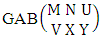 is
is 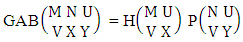
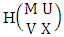 and
and 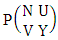 respectively. Multiplying the two numbers we get the desired GAB number.Example 2.32: Find the number of GAB members of the GAB space
respectively. Multiplying the two numbers we get the desired GAB number.Example 2.32: Find the number of GAB members of the GAB space  where 2 is observed in the second way.Solution: From the theorem 2.49 we get
where 2 is observed in the second way.Solution: From the theorem 2.49 we get 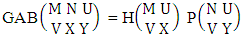 As Y is observed in the second way so we get
As Y is observed in the second way so we get 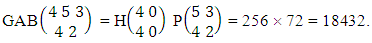 Theorem 2.50 GSAB theorem: The number of GSAB members of the GSAB space
Theorem 2.50 GSAB theorem: The number of GSAB members of the GSAB space 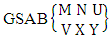 denoted by
denoted by 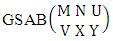 is
is 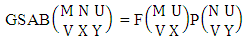
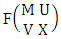 and
and 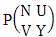 respectively. Now multiplying the two numbers we get the desired GSAB number.Example 2.33: Find the number of GSAB members of the GSAB space
respectively. Now multiplying the two numbers we get the desired GSAB number.Example 2.33: Find the number of GSAB members of the GSAB space 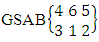 where 1 is observed in the first way and 2 in the second way. Solution: From the theorem 2.50 we get
where 1 is observed in the first way and 2 in the second way. Solution: From the theorem 2.50 we get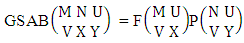 As 1 is observed in the first way and 2 in the second way and M ≥ U for first way we take U = 4, Then
As 1 is observed in the first way and 2 in the second way and M ≥ U for first way we take U = 4, Then 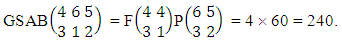 Theorem 2.51 GASB theorem: The number of GASB members of the GASB space
Theorem 2.51 GASB theorem: The number of GASB members of the GASB space 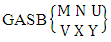 denoted by
denoted by 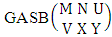 is
is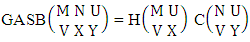
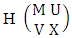 and
and 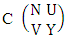 respectively. Now multiplying the two numbers we get the desired GASB number.Example 2.34: Find the number of GASB members of the GASB space
respectively. Now multiplying the two numbers we get the desired GASB number.Example 2.34: Find the number of GASB members of the GASB space 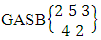 where 2 is observed in the both way. Solution: From the theorem 2.51 we get
where 2 is observed in the both way. Solution: From the theorem 2.51 we get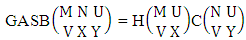 As X, Y are observed in the both way and for M ≥ U we take U = 2 for the first way
As X, Y are observed in the both way and for M ≥ U we take U = 2 for the first way 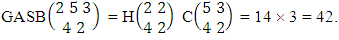 Here we describe three kinds of GB numbers i.e., first way GB theorem, second way GB theorem and both way GB theorem and their different forms.Theorem 2.52 First way GB theorem: The number of GB members of the first way GB space
Here we describe three kinds of GB numbers i.e., first way GB theorem, second way GB theorem and both way GB theorem and their different forms.Theorem 2.52 First way GB theorem: The number of GB members of the first way GB space 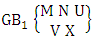 denoted by
denoted by 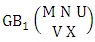 is
is 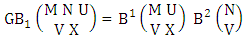
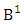 is the B first number to be hold the number of homogenations or formations and
is the B first number to be hold the number of homogenations or formations and 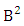 is the B second number to be hold the number of permutations or combinations.Proof: We know the B number is to be product of B first number and B second number. As we consider a first way GB experiment so we get the B first number from general homogenation theorem or general formation theorem and the number is
is the B second number to be hold the number of permutations or combinations.Proof: We know the B number is to be product of B first number and B second number. As we consider a first way GB experiment so we get the B first number from general homogenation theorem or general formation theorem and the number is 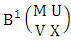 . Again B second number get from elementary permutation theorem or elementary combination theorem and the number is
. Again B second number get from elementary permutation theorem or elementary combination theorem and the number is 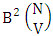 . Now multiplying the two numbers we get the desired first way GB number. Example 2.35: Find the number of GB members of the first way GB space
. Now multiplying the two numbers we get the desired first way GB number. Example 2.35: Find the number of GB members of the first way GB space 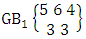 chosen first way selected and second way arranged.Solution: From the theorem 2.52 we get
chosen first way selected and second way arranged.Solution: From the theorem 2.52 we get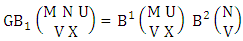
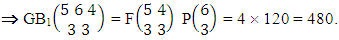 Theorem 2.53 Second way GB theorem: The number of GB members of the second way GB space
Theorem 2.53 Second way GB theorem: The number of GB members of the second way GB space 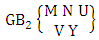 denoted by
denoted by 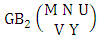 is
is 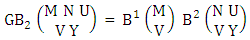
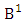 is the B first number to be hold the number of homogenations or formations and
is the B first number to be hold the number of homogenations or formations and 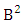 is the B second number to be hold the number of permutations or combinations.Proof: We know the B number is to be product of B first number and B second number. As we consider a second way GB experiment so we get the B first number from elementary homogenation theorem or elementary formation theorem and the number is
is the B second number to be hold the number of permutations or combinations.Proof: We know the B number is to be product of B first number and B second number. As we consider a second way GB experiment so we get the B first number from elementary homogenation theorem or elementary formation theorem and the number is 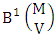 . Again B second number get from general permutation theorem or general combination theorem and the number is
. Again B second number get from general permutation theorem or general combination theorem and the number is 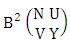 . Now multiplying the two numbers we get the desired second way GB number. Example 2.36: Find the number of GB members of the second way GB space
. Now multiplying the two numbers we get the desired second way GB number. Example 2.36: Find the number of GB members of the second way GB space 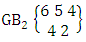 chosen both way selected.Solution: From the theorem 2.53 we get
chosen both way selected.Solution: From the theorem 2.53 we get 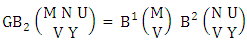
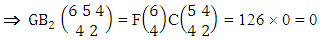 Here we get
Here we get 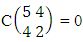 as X ranges from 3 to 4 So,
as X ranges from 3 to 4 So, 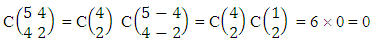 Theorem 2.54 Both way GB theorem: The number of GB members of the both way GB space
Theorem 2.54 Both way GB theorem: The number of GB members of the both way GB space  denoted by
denoted by  is
is 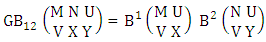
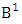 is the B first number to be hold the number of homogenations or formations and
is the B first number to be hold the number of homogenations or formations and 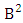 is the B second number to be hold the number of permutations or combinations. Proof: We know the B number is to be product of B first number and B second number. As we consider a both way GB experiment so we get the B first number from general homogenation theorem or general formation theorem and the number is
is the B second number to be hold the number of permutations or combinations. Proof: We know the B number is to be product of B first number and B second number. As we consider a both way GB experiment so we get the B first number from general homogenation theorem or general formation theorem and the number is 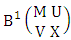 . Again B second number get from generation permutation theorem or general combination theorem and the number is
. Again B second number get from generation permutation theorem or general combination theorem and the number is 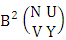 . Now multiplying the two numbers we get the desired both way GB number. Example 2.37: Find the number of GB members of the both way GB space
. Now multiplying the two numbers we get the desired both way GB number. Example 2.37: Find the number of GB members of the both way GB space 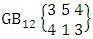 chosen both way arranged.Solution: From the theorem 2.54 we get
chosen both way arranged.Solution: From the theorem 2.54 we get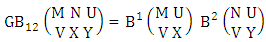 As 1 is observed in the first way and 3 is observed in the second way and M ≥ U for first way we take U = 3. Then
As 1 is observed in the first way and 3 is observed in the second way and M ≥ U for first way we take U = 3. Then 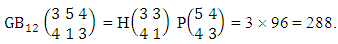 Theorem 2.55 First way GSB theorem: The number of GSB members of the first way GSB space
Theorem 2.55 First way GSB theorem: The number of GSB members of the first way GSB space 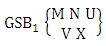 denoted by
denoted by 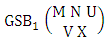 is
is 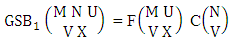
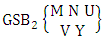 denoted by
denoted by 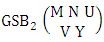 is
is 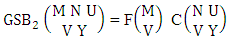
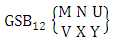 denoted by
denoted by 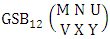 is
is 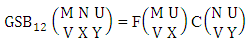
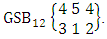 Solution: From the theorem 2.57 we get
Solution: From the theorem 2.57 we get 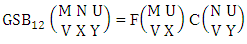
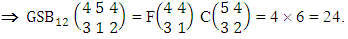 Theorem 2.58 First way GAB theorem: The number of GAB members of the first way GAB space
Theorem 2.58 First way GAB theorem: The number of GAB members of the first way GAB space 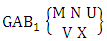 denoted by
denoted by 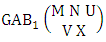 is
is 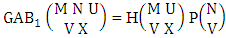
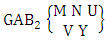 denoted by
denoted by 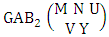 is
is 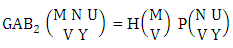
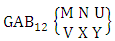 denoted by
denoted by 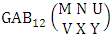 is
is 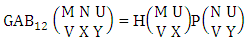
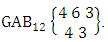 Solution: From the theorem 2.60 we get
Solution: From the theorem 2.60 we get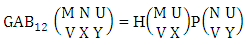
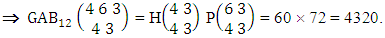 Theorem 2.61 First way GSAB theorem: The number of GSAB members of the first way GSAB space
Theorem 2.61 First way GSAB theorem: The number of GSAB members of the first way GSAB space 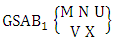 denoted by
denoted by 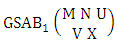 is
is 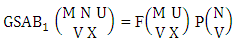
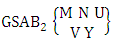 denoted by
denoted by 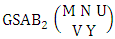 is
is 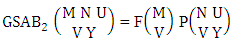
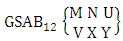 denoted by
denoted by 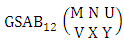 is
is 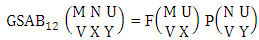
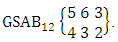 Solution: From the theorem 2.63 we get
Solution: From the theorem 2.63 we get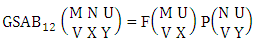 As 3 is observed in the first way and 2 is observed in the second way so we get
As 3 is observed in the first way and 2 is observed in the second way so we get 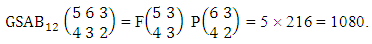 Theorem 2.64 First way GASB theorem: The number of GASB members of the first way GASB space
Theorem 2.64 First way GASB theorem: The number of GASB members of the first way GASB space 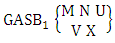 denoted by
denoted by 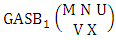 is
is 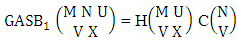
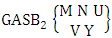 denoted by
denoted by 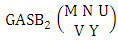 is
is 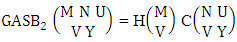
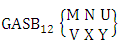 denoted by
denoted by 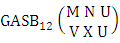 is
is 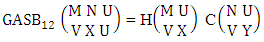
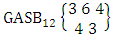 .Solution: From the theorem 2.66 we get
.Solution: From the theorem 2.66 we get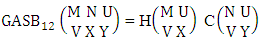 Using M ≥ U for first way we take U = 3, thus
Using M ≥ U for first way we take U = 3, thus 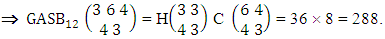
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML