Ehab Mohamed Almetwaly1, Hisham Mohamed Almongy2
1Demonstrator of Statistics, Higher Institute of Computer and Management Information Systems, Cairo
2Lecturer of Applied Statistics, Faculty of Commerce -Mansoura University, Al-Mansoura
Correspondence to: Ehab Mohamed Almetwaly, Demonstrator of Statistics, Higher Institute of Computer and Management Information Systems, Cairo.
| Email: |  |
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
In this paper, we compared between the maximum likelihood estimator (MLE) and Bayesian estimation for the shape parameters 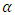 and
and 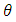 of the generalized power Weibull (GPW) distribution based on complete censoring data, type-II censoring scheme and type-II progressive censoring scheme. The Bayesian estimates for the GPW parameters are obtained based on binary loss function and squared error loss function. The optimal censoring scheme has been suggested using two different optimality criteria (mean squared of error (MSE) and Bias). This comparison was done by using simulation study and application on real life of data. We discussed the method of obtaining the optimal type-II progressive censoring schemes.
of the generalized power Weibull (GPW) distribution based on complete censoring data, type-II censoring scheme and type-II progressive censoring scheme. The Bayesian estimates for the GPW parameters are obtained based on binary loss function and squared error loss function. The optimal censoring scheme has been suggested using two different optimality criteria (mean squared of error (MSE) and Bias). This comparison was done by using simulation study and application on real life of data. We discussed the method of obtaining the optimal type-II progressive censoring schemes.
Keywords:
Generalized power Weibull, Type-II progressive censoring, Maximum likelihood estimation, Bayesian estimation
Cite this paper: Ehab Mohamed Almetwaly, Hisham Mohamed Almongy, Estimation of the Generalized Power Weibull Distribution Parameters Using Progressive Censoring Schemes, International Journal of Probability and Statistics , Vol. 7 No. 2, 2018, pp. 51-61. doi: 10.5923/j.ijps.20180702.03.
1. Introduction
The Weibull distribution is one of the most popular distributions in analyzing lifetime data. This weibull family, which was presented at first by Bagdonavicius and Nikulin (2001), contains four shapes of the hazard function and it is mostly used in the reliability and survival analysis domains. This Weibull family is often used for constructing accelerated failures times (AFT) models which describe dependence of the lifetime distribution on explanatory variables. Pham, and Lai, (2007) introduced, the generalized power Weibull (GPW) distribution as a another extension of the Weibull family. Nikulin and Haghighi (2007), introduced the cumulative distribution function of the generalized power Weibull (GPW) family is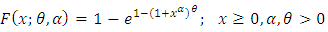 | (1) |
and its the corresponding probability density function is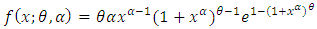 | (2) |
The quantile function of the generalized power Weibull family is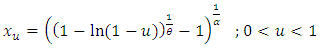 | (3) |
The survival function is 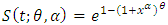 | (4) |
Particular cases of the generalized power Weibull distribution are: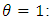 the family of Weibull distributions;
the family of Weibull distributions; and
and 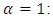 the family of exponential distributions.A sample is said to be censored if while it is drawn from a complete population, the item values of some of its members are unknown. Such sample members are themselves called censored. Kundu and Pradhan (2009) discussed the two most common censoring schemes are termed as type-I and type-II censoring schemes. Briefly, they can be described as follows; consider n items under observation in a particular experiment. In the conventional type-I censoring scheme, the experiment continues up to a pre-specified time T. On the other hand the conventional type-II censoring scheme requires the experiment to continue until a pre-specified number of failures
the family of exponential distributions.A sample is said to be censored if while it is drawn from a complete population, the item values of some of its members are unknown. Such sample members are themselves called censored. Kundu and Pradhan (2009) discussed the two most common censoring schemes are termed as type-I and type-II censoring schemes. Briefly, they can be described as follows; consider n items under observation in a particular experiment. In the conventional type-I censoring scheme, the experiment continues up to a pre-specified time T. On the other hand the conventional type-II censoring scheme requires the experiment to continue until a pre-specified number of failures 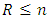 occur. Kim and Han (2009) discussed, progressively type II censored sampling is an important method of obtaining data in lifetime studies. Live units removed early can be readily used in other tests, thereby saving costs to the experimenter, and a compromise can be achieved between time consumption and the observation of some extreme values. Balakrishnan and Chen (2004) introduced, a progressively type II censored sample as follows. Suppose that n experimental units are placed on a life test, and suppose that the experimenter decides to have only m of these n units fail. At the time of the first failure, it is decided that
occur. Kim and Han (2009) discussed, progressively type II censored sampling is an important method of obtaining data in lifetime studies. Live units removed early can be readily used in other tests, thereby saving costs to the experimenter, and a compromise can be achieved between time consumption and the observation of some extreme values. Balakrishnan and Chen (2004) introduced, a progressively type II censored sample as follows. Suppose that n experimental units are placed on a life test, and suppose that the experimenter decides to have only m of these n units fail. At the time of the first failure, it is decided that 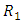 of the
of the 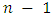 surviving units are randomly removed from the life testing experiment. Continuing on, at the time of the second failure,
surviving units are randomly removed from the life testing experiment. Continuing on, at the time of the second failure, 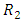 of the
of the 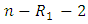 surviving units are randomly removed. Finally, at the time of the
surviving units are randomly removed. Finally, at the time of the 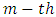 failure, all of the remaining
failure, all of the remaining 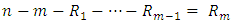 surviving units are withdrawn from the experiment. For more examples, see Dey et al (2014), Dey et al (2016), see for instance the book by Balakrishnan and Aggrawalla (2000), and an excellent review article by Balakrishnan et al (2007).
surviving units are withdrawn from the experiment. For more examples, see Dey et al (2014), Dey et al (2016), see for instance the book by Balakrishnan and Aggrawalla (2000), and an excellent review article by Balakrishnan et al (2007).
2. Maximum Likelihood Estimation for the Parameter of the GPW Distribution
The estimation problem of the unknown parameters of the GPW distribution has been discussed by many authors using complete samples, Type II censored sample and Progressive Type-II Censoring Scheme.
2.1. Complete Sample
Balakrishnan et al (2007), introduced the maximum likelihood estimators (MLE) of the parameters assuming a cumulative exposure model with lifetimes being exponentially distributed. Consider a random sample from the Generalized Power Weibull distribution (2). The likelihood function is given by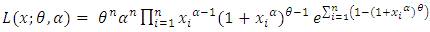 | (5) |
The natural logarithm of the likelihood function equation can be obtained as follows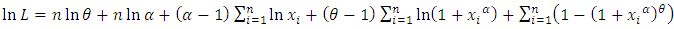 | (6) |
The estimates of all parameters are obtained by differentiating the log-likelihood function in (6) with respect to 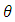 and
and 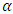 and equating them to zero. Basing on this, differentiating the log-likelihood function with respect to
and equating them to zero. Basing on this, differentiating the log-likelihood function with respect to 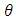 is given as
is given as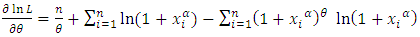 | (7) |
Differentiating the log-likelihood function in (6) with respect to 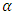 is given as
is given as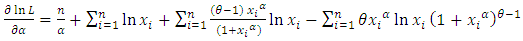 | (8) |
But the three equation has to be performed numerically using a nonlinear optimization algorithm.
2.2. Type II Censored Sample
A life test is terminated after a specified number of failures have been occurred is known as ''failure censoring'' or ''type II censoring''. The likelihood function can be written as: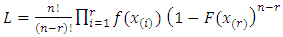 | (9) |
Considering the Equation (9), the log likelihood function of a generalized power Weibull distribution used type II censored is defined as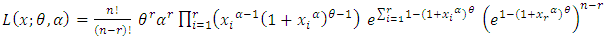 | (10) |
the natural logarithm of the likelihood function is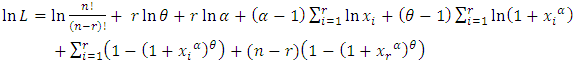 | (11) |
to obtain the normal equations for the unknown parameters, we differentiate (11) partially with respect to the parameters 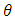 and
and 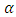 and equate them to zero. The estimators for
and equate them to zero. The estimators for 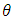 and
and 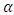 can be obtained as the solution of the following equations.Differentiating the log-likelihood function in (11) with respect to
can be obtained as the solution of the following equations.Differentiating the log-likelihood function in (11) with respect to 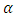 is given as
is given as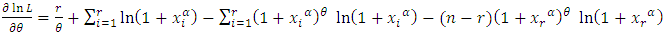 | (12) |
and 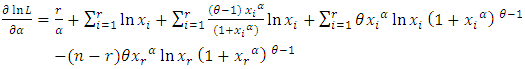 | (13) |
But the three equation has to be performed numerically using a nonlinear optimization algorithm.Dey et al (2014) introduced among the different censoring schemes, Type-II are the most popular censoring schemes. Unfortunately, in any of these censoring schemes, it is not possible to withdraw live items during the experiment. In this paper, we consider a generalization of the classical Type-II censoring scheme, where it is possible to withdraw live items during the experiment, and it is known as progressive Type-II censoring scheme.
2.3. Progressive Type-II Censoring Scheme
Dey et al (2016) discussed Progressive Type-II censoring scheme can be described as follows: Suppose n units are placed on a life test and the experimenter decides beforehand the quantity m, the number of failures to be observed. Now at the time of the first failure,  of the remaining
of the remaining  surviving units are randomly removed from the experiment. At the time of the second failure,
surviving units are randomly removed from the experiment. At the time of the second failure, 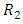 of the remaining
of the remaining 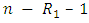 units are randomly removed from the experiment. Finally, at the time of the m-th failure, all the remaining surviving units
units are randomly removed from the experiment. Finally, at the time of the m-th failure, all the remaining surviving units 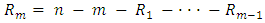 are removed from the experiment. Therefore, a progressive Type-II censoring scheme consists of m, and
are removed from the experiment. Therefore, a progressive Type-II censoring scheme consists of m, and 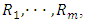 such that
such that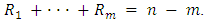 The
The 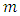 failure times obtained from a progressive Type-II censoring scheme will be denoted by
failure times obtained from a progressive Type-II censoring scheme will be denoted by 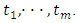 We observed the data
We observed the data 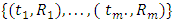 in a progressive censoring scheme. Although we have included
in a progressive censoring scheme. Although we have included 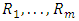 as part of the data, these are known in advance.
as part of the data, these are known in advance. 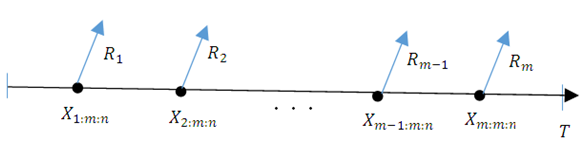 | Figure 1. Plot the progressive type-II censoring scheme |
Based on the observed sample 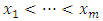 from a progressive Type-II censoring scheme,
from a progressive Type-II censoring scheme,  the likelihood function can be written as
the likelihood function can be written as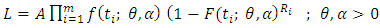 | (14) |
where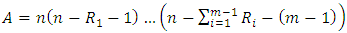 The likelihood function can be written as
The likelihood function can be written as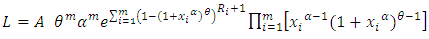 | (15) |
the natural logarithm of the likelihood function is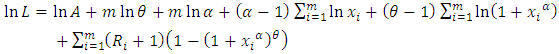 | (16) |
To obtain the normal equations for the unknown parameters, we differentiate (16) partially with respect to the parameters 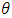 and
and 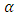 and equate them to zero. The estimators for
and equate them to zero. The estimators for 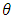 and
and 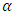 can be obtained as the solution of the following equations.
can be obtained as the solution of the following equations.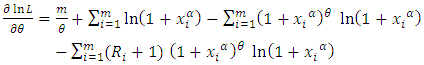 | (17) |
Differentiating the log-likelihood function in (16) with respect to 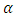 is given as
is given as | (18) |
The MLE 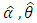 can be obtained by solving simultaneously the likelihood equations
can be obtained by solving simultaneously the likelihood equations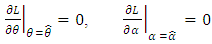 But the equation (17), (18) has to be performed numerically using a nonlinear optimization algorithm.
But the equation (17), (18) has to be performed numerically using a nonlinear optimization algorithm.
3. Bayesian Estimation of the GPW Distribution
In this section we consider the Bayesian estimation for the parameters of the GPW distribution under the assumption that the random variables 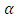 and
and 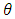 have an independent gamma distribution is a conjugate prior to the GPW distributions. Assumed that
have an independent gamma distribution is a conjugate prior to the GPW distributions. Assumed that 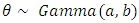 and
and 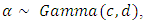 then, the joint prior density of
then, the joint prior density of 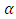 and
and 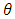 can be written as
can be written as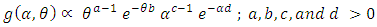 | (19) |
here all the hyper parameters 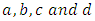 are known and non-negative.
are known and non-negative.
3.1. Bayesian Estimation in Complete Data
Based on the likelihood function (5) and the joint prior density (19), the joint posterior of complete (c) data (GPW) density of 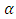 and
and 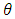 is
is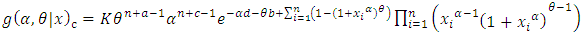 | (20) |
here the normalizing constant K is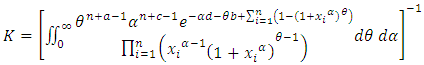 | (21) |
under binary loss function it should be the estimation of all parameters are obtained by differentiating the posterior function in (20) with respect to 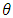 and
and 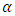 and equating them to zero.
and equating them to zero.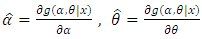 | (22) |
under square error loss function it should be the estimation of all parameters are obtained by 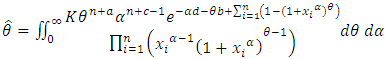 | (23) |
and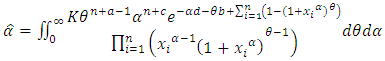 | (24) |
but the equations (22, 23 and 24) has to be performed numerically using a nonlinear optimization algorithm.
3.2. Bayesian Estimation in Type II Censored
Based on the likelihood function (10) and the joint prior density (19), the joint posterior of Type II censored of 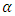 and
and 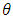 is
is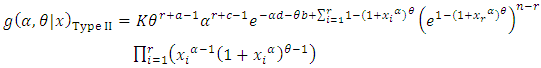 | (25) |
here the normalizing constant K is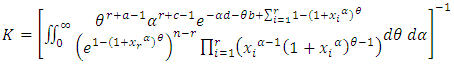 | (26) |
under binary loss function it should be the estimation of all parameters are obtained by differentiating the posterior function in (25) with respect to 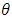 and
and 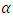 and equating them to zero.
and equating them to zero.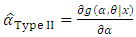 | (27) |
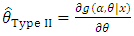 | (28) |
under square error loss function it should be the estimation of all parameters are obtained by 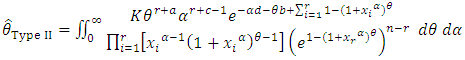 | (29) |
and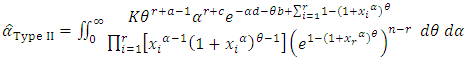 | (30) |
but the equation (28), (29) and (30) has to be performed numerically using a nonlinear optimization algorithm.
3.3. Bayesian Estimation in Progressive Type-II Censoring Scheme
Based on the likelihood function (15) and the joint prior density (19), the joint posterior of Progressive (P) Type-II censored of 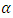 and
and 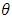 is
is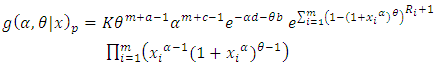 | (31) |
here the normalizing constant K is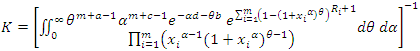 | (32) |
under binary loss function it should be the estimation of all parameters are obtained by differentiating the posterior function in (31) with respect to 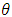 and
and 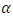 and equating them to zero.
and equating them to zero.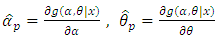 | (33) |
under square error loss function it should be the estimation of all parameters are obtained by 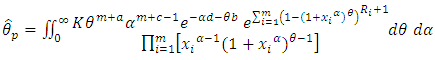 | (34) |
and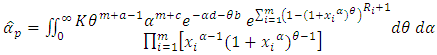 | (35) |
and equating them to zero. But the equation (33, 34 and 35) has to be performed numerically using a nonlinear optimization algorithm.
4. Simulation Study
In this section; Monte Carlo simulation is done for comparison between estimation methods based on censoring in complete data, Type-II Censoring Scheme and Progressive Type-II Censoring Scheme. For estimating GPW Distribution in life time by R language.
4.1. Simulation Algorithm Scheme
Monte Carlo experiments were carried out based on the following data- generated form Generalized Power Weibull Distribution, where x are distributed as GPW, shape parameter 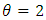 and shape parameter
and shape parameter 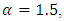 for different sample size
for different sample size 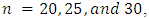 different effective sample sizes (m), and set of different samples schemes. The parameters of prior distribution are
different effective sample sizes (m), and set of different samples schemes. The parameters of prior distribution are 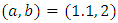 and
and 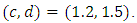 All computations are obtained based on the R language. The Balakrishnan and Aggarwala (2000) introduced optimal censoring schemes: we could define the best scheme as the scheme which minimizes the mean squared error (MSE) of the estimator. That is, the objective function (to be minimized in this case) would be
All computations are obtained based on the R language. The Balakrishnan and Aggarwala (2000) introduced optimal censoring schemes: we could define the best scheme as the scheme which minimizes the mean squared error (MSE) of the estimator. That is, the objective function (to be minimized in this case) would be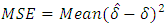 | (36) |
where 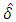 is the estimated value of
is the estimated value of 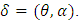
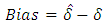 | (37) |
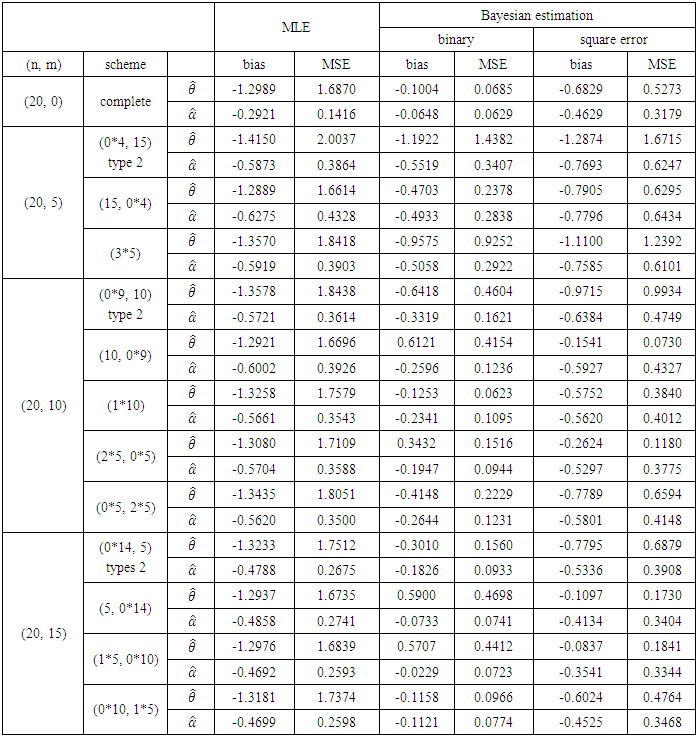
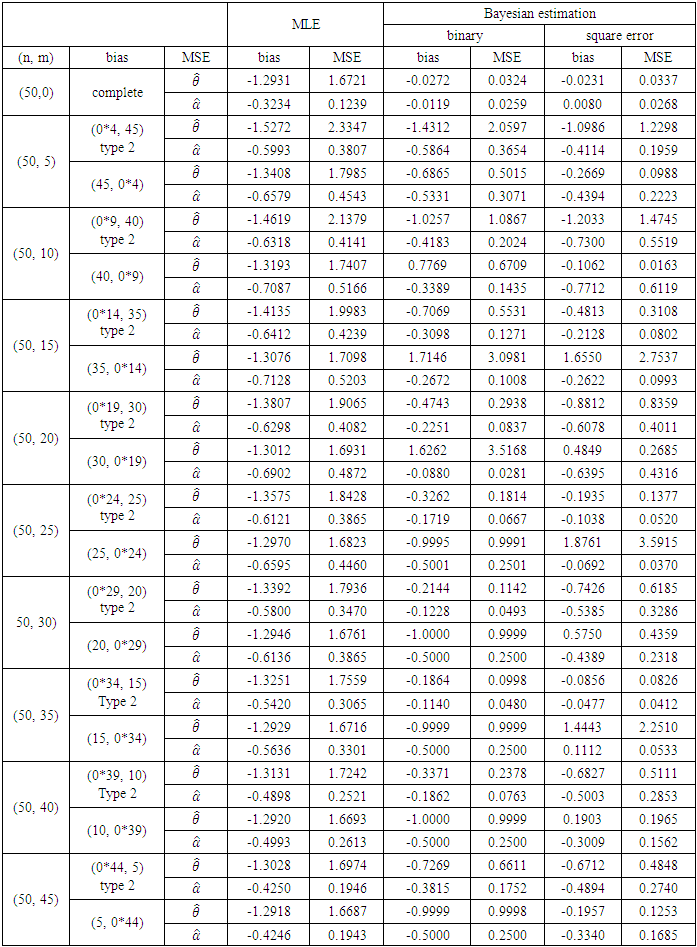
The simulation methods are compared using MSE and Bias for the parameters using GPW distribution, and this assess their performance through a Monte Carlo simulation study, we restricted the number of repeated-samples to 1000.In table 1, (n, m)=(20,0), the scheme (0) is special case of progressive type II censoring (complete sample), and (n, m) = (20, 5), the scheme (0*4, 15) is special case of progressive type II censoring (type II censoring), in other schemes they are could progressive type II censoring, we note that the Bias and the MSE in progressive type II censoring is lower than the type II censoring. In general the progressive type II to censoring scheme is more efficient than type II censoring. We note the best method is Bayesian estimation based on binary loss function, since the MSE of binary loss function is less than MSE of square errors. We note the estimation of the complete sample has the least MSE, where it consist of full observation. In general the Bayesian estimation based on binary loss function is the best method in small sample (20, 25, and 30), but in the large sample the Bayesian estimation based on square error is the best method.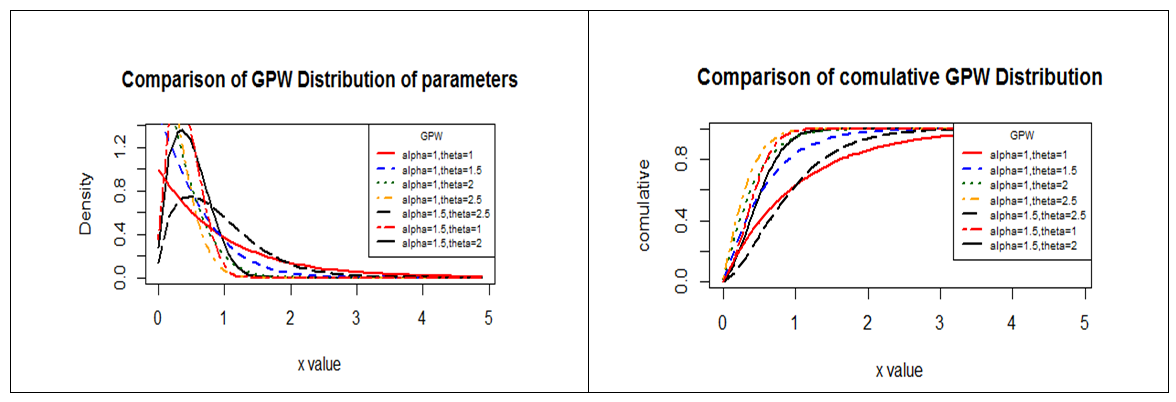 | Figure 2. Plot of GPW distribution |
Table 1. Estimation to Progressive Type-II Censoring Scheme when n=20
 |
| |
|
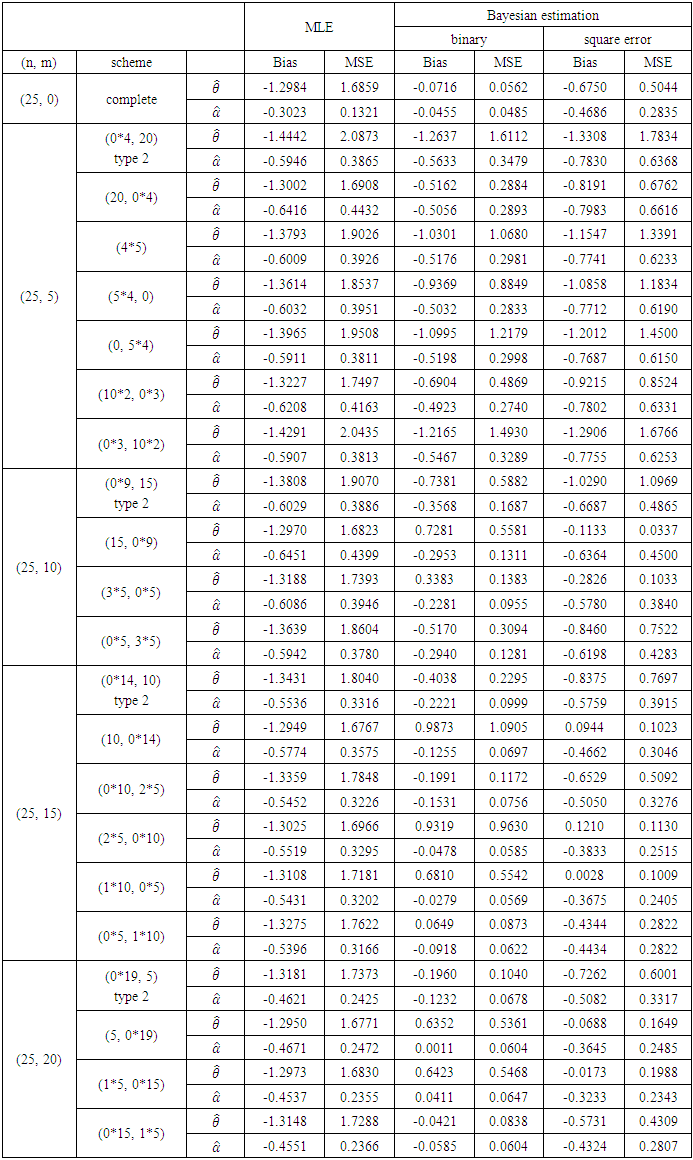
Table 2. Estimation to Progressive Type-II Censoring Scheme when n=25
 |
| |
|
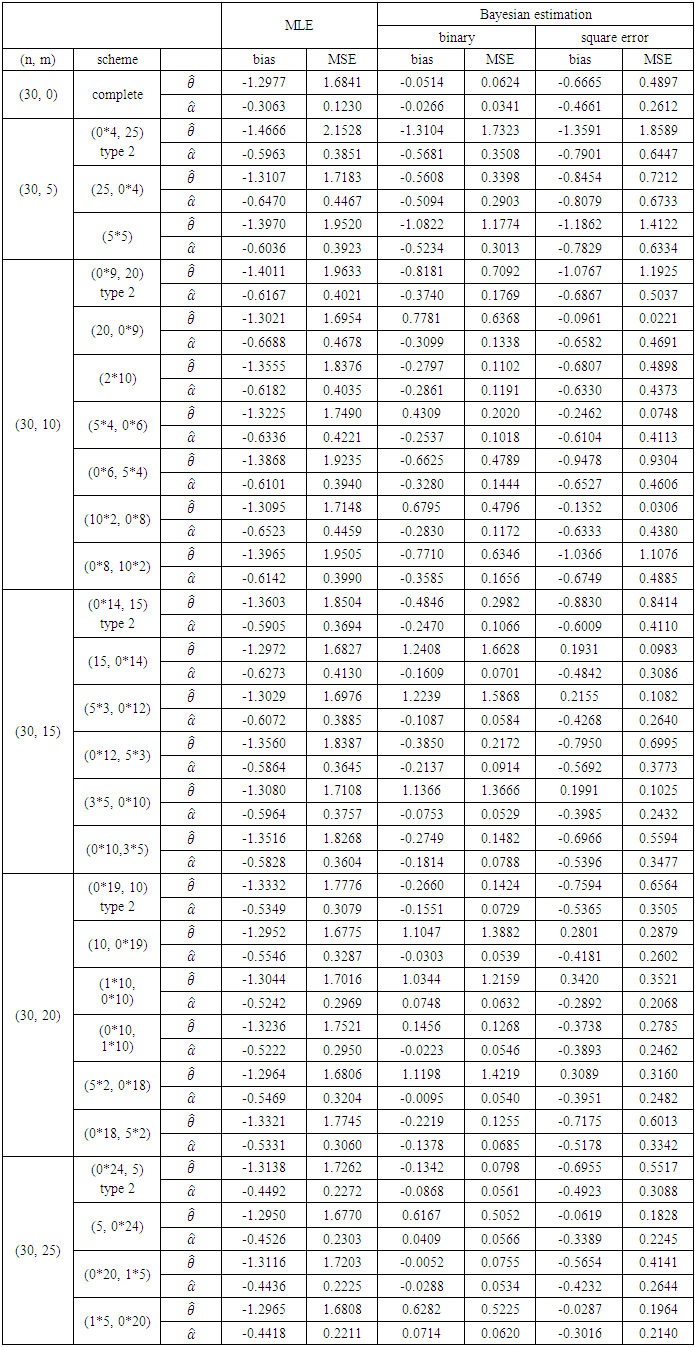
Table 3. Estimation to Progressive Type-II Censoring Scheme when n=30
 |
| |
|
Table 4. Estimation to Progressive Type-II Censoring Scheme when n=50
 |
| |
|
5. Application of Real Data
The data set from Chhikara, and Folks, (1989). This data represents the repair-times correspond to maintenance data on active repair times in hours for an airborne communications transceiver. A vector containing 46 observations and also several data sets related to life test are available in the “reliaR” package, which have been taken from the literature.The empirical distribution function is defined as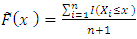 | (38) |
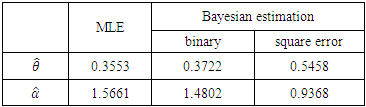
Table 5. Estimation for Complete data
 |
| |
|
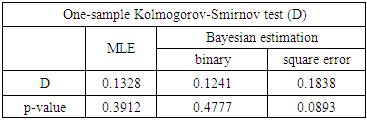
Table 6. Goodness of Fit data
 |
| |
|
Table 7. Estimation for Progressive Type-II Censoring Scheme of real data
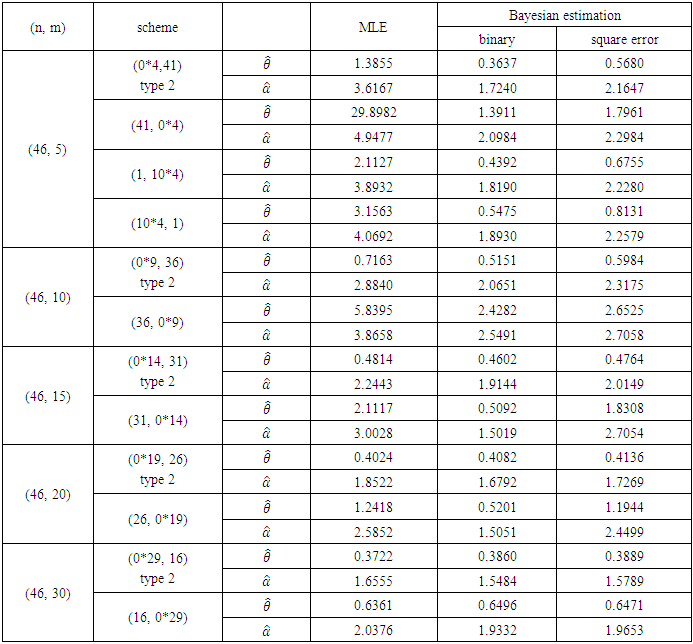 |
| |
|
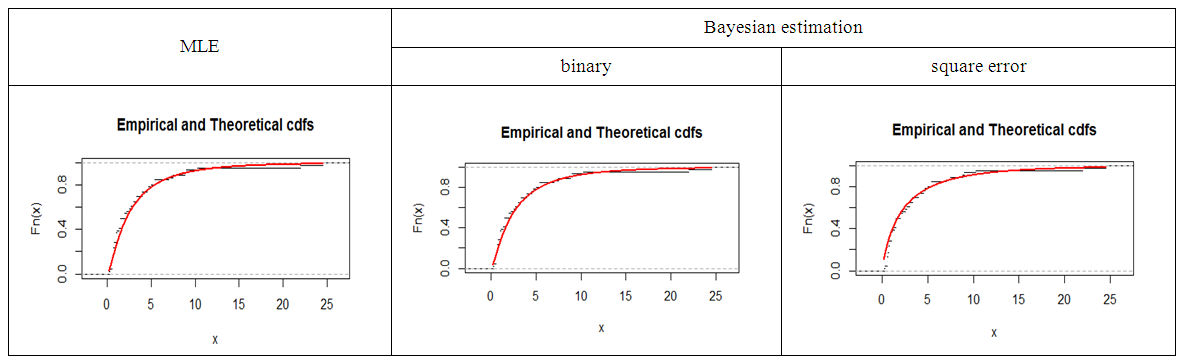 | Figure 3. Plot the maximum distance between the empirical and theoretical CDF |
6. Conclusions
In this paper, we discussed the estimation problem of the unknown parameters of the GPW distribution based on progressive type-II censoring scheme, type-II censoring data and complete censoring data. We used MLE and Bayesian estimation methods to estimate the unknown parameters. The performances of the maximum likelihood estimators are also quite satisfactory. We obtained the Bayes estimates based on binary loss function and square error loss function under the assumption of independent gamma priors. A real data set is used to show how the scheme works in practice. The performance of the different estimator’s optimal censoring schemes is compared based on simulation study to determine the optimal censoring schemes by using MSE and Bias. It is observed that Bayesian estimates with respect to the gamma priors behave quite similarly with the corresponding MLE in terms of mean squared errors. We note that the complete censoring is a special case of the progressive type II censoring scheme that can be obtained simply by taking 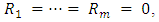 and note that the usual type II censoring scheme is a special case of the progressive type II censoring scheme that can be obtained simply by taking
and note that the usual type II censoring scheme is a special case of the progressive type II censoring scheme that can be obtained simply by taking 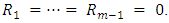 We note that, the Bayesian estimation is better method, where Bias and MSE decreases in Bayesian estimation than the maximum likelihood estimation method. In small sample, we note that the binary loss function is the best method, but in large sample the square error loss function is the best method under the assumption of independent gamma priors.
We note that, the Bayesian estimation is better method, where Bias and MSE decreases in Bayesian estimation than the maximum likelihood estimation method. In small sample, we note that the binary loss function is the best method, but in large sample the square error loss function is the best method under the assumption of independent gamma priors.
ACKNOWLEDGMENTS
The authors wish to thank the editor, an associate editor, and reviewers for their helpful comments on an earlier version of this paper. We also thank anonymous for their encouragement and support.
References
| [1] | Bagdonavicius, V., & Nikulin, M. (2001). Accelerated life models: modeling and statistical analysis. CRC press. |
| [2] | Balakrishnan, N., & Aggarwala, R. (2000). Progressive censoring: theory, methods, and applications. Springer Science & Business Media. |
| [3] | Balakrishnan, N. (2007). Progressive censoring methodology: an appraisal. Test. |
| [4] | Balakrishnan, N., Kundu, D., Ng, K. T., & Kannan, N. (2007). Point and interval estimation for a simple step-stress model with Type-II censoring. Journal of Quality Technology, 39(1), 35-47. ISO 690. |
| [5] | Chhikara, R. S. and Folks, J. L. (1989). The Inverse Gaussian Distribution. Marcel Dekker, New York. |
| [6] | Dey, S., Dey, T., & Kundu, D. (2014). Two-parameter Rayleigh distribution: different methods of estimation. American Journal of Mathematical and Management Sciences, 33(1), 55-74. |
| [7] | Dey, T., Dey, S., & Kundu, D. (2016). On Progressively Type-II Censored Two-parameter Rayleigh Distribution. Communications in Statistics-Simulation and Computation, 45(2), 438-455. |
| [8] | Kim, C., & Han, K. (2009). Estimation of the scale parameter of the Rayleigh distribution under general progressive censoring. Journal of the Korean Statistical Society, 38(3), 239-246. |
| [9] | Kundu, D. (2008). Bayesian inference and life testing plan for the Weibull distribution in presence of progressive censoring. Technometrics, 50(2), 144-154. |
| [10] | Kundu, D., & Pradhan, B. (2009). Estimating the parameters of the generalized exponential distribution in presence of hybrid censoring. Communications in Statistics—Theory and Methods, 38(12), 2030-2041. |
| [11] | Ng, H. K. T., Chan, P. S., & Balakrishnan, N. (2004). Optimal progressive censoring plans for the Weibull distribution. Technometrics, 46(4), 470-481. |
| [12] | Nikulin, M., & Haghighi, F. (2007). A chi-squared test for the genralized power Weibull family for the head-and-neck cancer censored data. Journal of Mathematical Sciences, 142(3), 2204-2204. |
| [13] | Pham, H. and Lai, C.D. (2007). On recent generalizations of the Weibull distribution, IEEE Trans. on Reliability, Vol. 56(3), 454-458. |



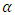 and
and 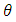 of the generalized power Weibull (GPW) distribution based on complete censoring data, type-II censoring scheme and type-II progressive censoring scheme. The Bayesian estimates for the GPW parameters are obtained based on binary loss function and squared error loss function. The optimal censoring scheme has been suggested using two different optimality criteria (mean squared of error (MSE) and Bias). This comparison was done by using simulation study and application on real life of data. We discussed the method of obtaining the optimal type-II progressive censoring schemes.
of the generalized power Weibull (GPW) distribution based on complete censoring data, type-II censoring scheme and type-II progressive censoring scheme. The Bayesian estimates for the GPW parameters are obtained based on binary loss function and squared error loss function. The optimal censoring scheme has been suggested using two different optimality criteria (mean squared of error (MSE) and Bias). This comparison was done by using simulation study and application on real life of data. We discussed the method of obtaining the optimal type-II progressive censoring schemes.
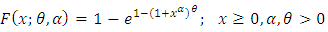
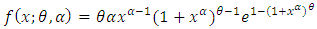
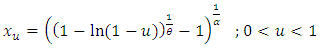
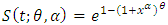
 the family of Weibull distributions;
the family of Weibull distributions; and
and 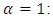 the family of exponential distributions.A sample is said to be censored if while it is drawn from a complete population, the item values of some of its members are unknown. Such sample members are themselves called censored. Kundu and Pradhan (2009) discussed the two most common censoring schemes are termed as type-I and type-II censoring schemes. Briefly, they can be described as follows; consider n items under observation in a particular experiment. In the conventional type-I censoring scheme, the experiment continues up to a pre-specified time T. On the other hand the conventional type-II censoring scheme requires the experiment to continue until a pre-specified number of failures
the family of exponential distributions.A sample is said to be censored if while it is drawn from a complete population, the item values of some of its members are unknown. Such sample members are themselves called censored. Kundu and Pradhan (2009) discussed the two most common censoring schemes are termed as type-I and type-II censoring schemes. Briefly, they can be described as follows; consider n items under observation in a particular experiment. In the conventional type-I censoring scheme, the experiment continues up to a pre-specified time T. On the other hand the conventional type-II censoring scheme requires the experiment to continue until a pre-specified number of failures 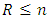 occur. Kim and Han (2009) discussed, progressively type II censored sampling is an important method of obtaining data in lifetime studies. Live units removed early can be readily used in other tests, thereby saving costs to the experimenter, and a compromise can be achieved between time consumption and the observation of some extreme values. Balakrishnan and Chen (2004) introduced, a progressively type II censored sample as follows. Suppose that n experimental units are placed on a life test, and suppose that the experimenter decides to have only m of these n units fail. At the time of the first failure, it is decided that
occur. Kim and Han (2009) discussed, progressively type II censored sampling is an important method of obtaining data in lifetime studies. Live units removed early can be readily used in other tests, thereby saving costs to the experimenter, and a compromise can be achieved between time consumption and the observation of some extreme values. Balakrishnan and Chen (2004) introduced, a progressively type II censored sample as follows. Suppose that n experimental units are placed on a life test, and suppose that the experimenter decides to have only m of these n units fail. At the time of the first failure, it is decided that 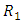 of the
of the 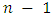 surviving units are randomly removed from the life testing experiment. Continuing on, at the time of the second failure,
surviving units are randomly removed from the life testing experiment. Continuing on, at the time of the second failure, 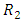 of the
of the 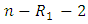 surviving units are randomly removed. Finally, at the time of the
surviving units are randomly removed. Finally, at the time of the 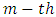 failure, all of the remaining
failure, all of the remaining 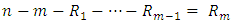 surviving units are withdrawn from the experiment. For more examples, see Dey et al (2014), Dey et al (2016), see for instance the book by Balakrishnan and Aggrawalla (2000), and an excellent review article by Balakrishnan et al (2007).
surviving units are withdrawn from the experiment. For more examples, see Dey et al (2014), Dey et al (2016), see for instance the book by Balakrishnan and Aggrawalla (2000), and an excellent review article by Balakrishnan et al (2007).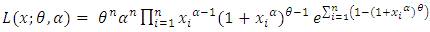
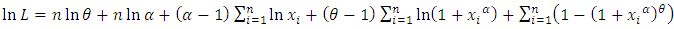
 and
and  and equating them to zero. Basing on this, differentiating the log-likelihood function with respect to
and equating them to zero. Basing on this, differentiating the log-likelihood function with respect to 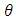 is given as
is given as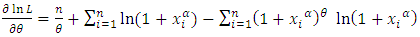
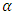 is given as
is given as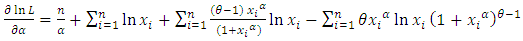
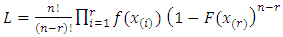
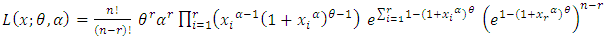
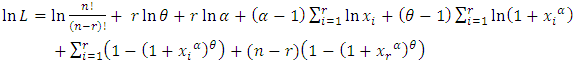
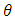 and
and 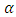 and equate them to zero. The estimators for
and equate them to zero. The estimators for 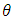 and
and 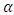 can be obtained as the solution of the following equations.Differentiating the log-likelihood function in (11) with respect to
can be obtained as the solution of the following equations.Differentiating the log-likelihood function in (11) with respect to 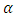 is given as
is given as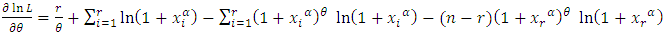
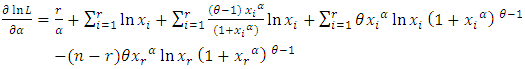
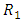 of the remaining
of the remaining 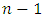 surviving units are randomly removed from the experiment. At the time of the second failure,
surviving units are randomly removed from the experiment. At the time of the second failure, 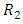 of the remaining
of the remaining 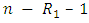 units are randomly removed from the experiment. Finally, at the time of the m-th failure, all the remaining surviving units
units are randomly removed from the experiment. Finally, at the time of the m-th failure, all the remaining surviving units 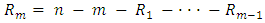 are removed from the experiment. Therefore, a progressive Type-II censoring scheme consists of m, and
are removed from the experiment. Therefore, a progressive Type-II censoring scheme consists of m, and 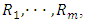 such that
such that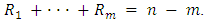 The
The 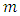 failure times obtained from a progressive Type-II censoring scheme will be denoted by
failure times obtained from a progressive Type-II censoring scheme will be denoted by 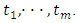 We observed the data
We observed the data 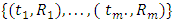 in a progressive censoring scheme. Although we have included
in a progressive censoring scheme. Although we have included 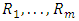 as part of the data, these are known in advance.
as part of the data, these are known in advance. 
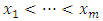 from a progressive Type-II censoring scheme,
from a progressive Type-II censoring scheme,  the likelihood function can be written as
the likelihood function can be written as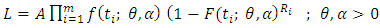
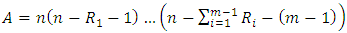 The likelihood function can be written as
The likelihood function can be written as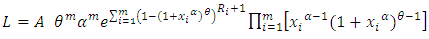
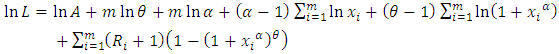
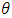 and
and 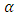 and equate them to zero. The estimators for
and equate them to zero. The estimators for 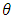 and
and 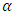 can be obtained as the solution of the following equations.
can be obtained as the solution of the following equations.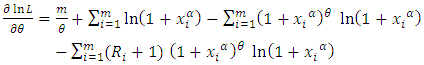
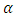 is given as
is given as
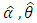 can be obtained by solving simultaneously the likelihood equations
can be obtained by solving simultaneously the likelihood equations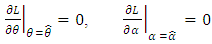 But the equation (17), (18) has to be performed numerically using a nonlinear optimization algorithm.
But the equation (17), (18) has to be performed numerically using a nonlinear optimization algorithm.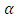 and
and 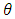 have an independent gamma distribution is a conjugate prior to the GPW distributions. Assumed that
have an independent gamma distribution is a conjugate prior to the GPW distributions. Assumed that 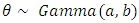 and
and 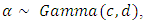 then, the joint prior density of
then, the joint prior density of 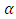 and
and 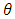 can be written as
can be written as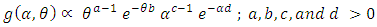
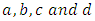 are known and non-negative.
are known and non-negative.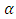 and
and 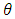 is
is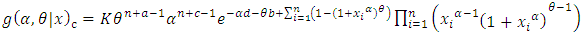
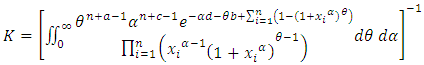
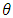 and
and 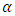 and equating them to zero.
and equating them to zero.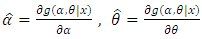
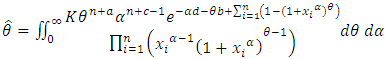
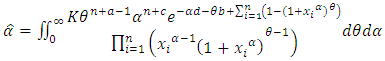
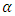 and
and 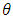 is
is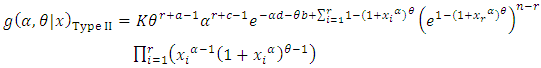
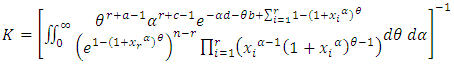
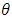 and
and 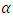 and equating them to zero.
and equating them to zero.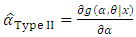
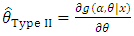
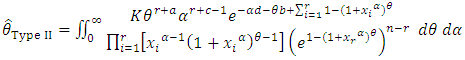
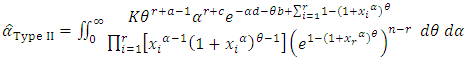
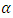 and
and 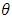 is
is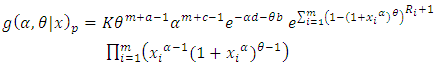
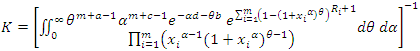
 and
and  and equating them to zero.
and equating them to zero.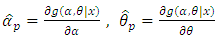
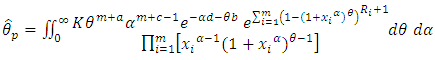
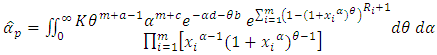
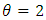 and shape parameter
and shape parameter 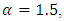 for different sample size
for different sample size 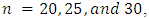 different effective sample sizes (m), and set of different samples schemes. The parameters of prior distribution are
different effective sample sizes (m), and set of different samples schemes. The parameters of prior distribution are 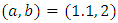 and
and 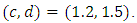 All computations are obtained based on the R language. The Balakrishnan and Aggarwala (2000) introduced optimal censoring schemes: we could define the best scheme as the scheme which minimizes the mean squared error (MSE) of the estimator. That is, the objective function (to be minimized in this case) would be
All computations are obtained based on the R language. The Balakrishnan and Aggarwala (2000) introduced optimal censoring schemes: we could define the best scheme as the scheme which minimizes the mean squared error (MSE) of the estimator. That is, the objective function (to be minimized in this case) would be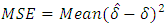
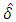 is the estimated value of
is the estimated value of 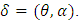
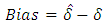

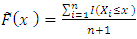

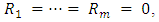 and note that the usual type II censoring scheme is a special case of the progressive type II censoring scheme that can be obtained simply by taking
and note that the usual type II censoring scheme is a special case of the progressive type II censoring scheme that can be obtained simply by taking 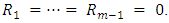 We note that, the Bayesian estimation is better method, where Bias and MSE decreases in Bayesian estimation than the maximum likelihood estimation method. In small sample, we note that the binary loss function is the best method, but in large sample the square error loss function is the best method under the assumption of independent gamma priors.
We note that, the Bayesian estimation is better method, where Bias and MSE decreases in Bayesian estimation than the maximum likelihood estimation method. In small sample, we note that the binary loss function is the best method, but in large sample the square error loss function is the best method under the assumption of independent gamma priors. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML





