Summaira Manzoor1, 2, Ahmed Zogo Memon2, Maryam Firdos1, Tahira Kanwal1, Rabia Manzoor3
1Department of Statistics, University of Azad Jammu and Kashmir, Muzaffarabad, Pakistan
2Department of Statistics, College of Statistical and Actuarial Sciences, University of the Punjab, Lahore, Pakistan
3Department of Soil Science and SWC, PAMS Aried Agriculture University, Rawalpindi, Pakistan
Correspondence to: Summaira Manzoor, Department of Statistics, University of Azad Jammu and Kashmir, Muzaffarabad, Pakistan.
| Email: |  |
Copyright © 2018 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
In this paper Lloyd’s method is applied for the estimation of scale and location parameters of Inverse Rayleigh distribution for Type II singly and doubly censored data based on a sample size up to 15. Some further analysis is done to determine the variance range for the censored estimators of the scale parameter when the same number of observations is included in a censored sample. Lloyd’s estimators are compared for the scale parameter in situations where one or both Inverse Rayleigh distribution parameters are unknown.
Keywords:
Type II censoring, Efficiency, Best linear unbiased estimator
Cite this paper: Summaira Manzoor, Ahmed Zogo Memon, Maryam Firdos, Tahira Kanwal, Rabia Manzoor, Estimation of Inverse Rayleigh Distribution Parameters for Type II Singly and Doubly Censored Data Based on Lower Record Values, International Journal of Probability and Statistics , Vol. 7 No. 1, 2018, pp. 1-13. doi: 10.5923/j.ijps.20180701.01.
1. Introduction
Ordered random variables such as record values have gained a lot of importance during the past years. Record values are widely used in many situations of daily life as well as in statistical modelling and inference; to describe random variables arranged in order of magnitude.Inverse Rayleigh distribution (IRD) is used in the area of acceptance sampling plan in which life time of a product follows the IRD. The software developed by Wood [1] is used for fitting data to this distribution. The IRD is considered as a model for a life time random variable, and has been assumed by Rosiah and Kantam [2]. The probability density function of two parameter IRD with location parameter 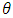 and scale parameter λ is
and scale parameter λ is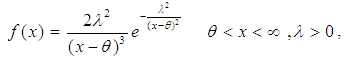 | (1) |
Hirai [3] estimated the location and scale parameters of Rayleigh distribution by quadratic coefficients method. Dyer and Whisenand [4] derived the best linear unbiased estimator (BLUE) of the parameter of the Rayleigh distribution using order statistics in a Type II censored sample. The concept of record values from normal distribution was discussed by Balakrishnan and Chan [5]. They computed mean, variance and covariance’s for the record values from normal distribution and gave the BLUEs of location and scale parameter for the first n record values. Aleem [6] found concomitants of order statistics for bivariate IRD and their moments. Hirai and Akhter [7] discussed cubic coefficients estimates and asymptotic properties of the estimates from the two parameters Rayleigh distribution. Shawky and Bakoban [8] considered order statistics from an exponentiated Gamma distribution. Estimates of the scale parameter of exponentiated Gamma distribution under Type II censoring were obtained. Akhter and Hirai [9] estimates the scale parameter based on order statistics from Rayleigh distribution using type II singly and doubly censored samples by BLUE and Bloom’s method for sample size up to 8. Azaz and Akhter [10] discussed the estimation of location and scale parameters using upper record values of Rayleigh distribution by BLUE and alternative best linear unbiased estimates (ABLUE) from Type II singly and doubly censored samples. Tables of coefficients for BLUE and ABLUE of location and scale parameters were presented for various choices of censoring for 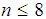 . Feroze and Aslam [11] discussed the Bayesian analysis of IRD under singly and doubly Type II censored data. The Bayes estimators and corresponding risks have been derived under the assumption of non-informative priors and using symmetric and asymmetric loss functions. Jabeen et al. [12] discussed the estimation of location and scale parameters of Weibull distribution using concept of generalized order statistics by the BLUE and ABLUE from Type II singly and doubly censored samples. This paper is designed for estimation of parameters of IRD for Type II singly and doubly censored data based on lower record values for a sample size up to 15. Moments of Record values are discussed in section 2. The estimation of location and scale parameters of IRD using Type II singly and doubly censored data under lower record values is described in section 3. Estimation of location and scale parameters of IRD under censoring with 10 missing observations are presented in section 4. Finally, conclusions are reported in Section 5.
. Feroze and Aslam [11] discussed the Bayesian analysis of IRD under singly and doubly Type II censored data. The Bayes estimators and corresponding risks have been derived under the assumption of non-informative priors and using symmetric and asymmetric loss functions. Jabeen et al. [12] discussed the estimation of location and scale parameters of Weibull distribution using concept of generalized order statistics by the BLUE and ABLUE from Type II singly and doubly censored samples. This paper is designed for estimation of parameters of IRD for Type II singly and doubly censored data based on lower record values for a sample size up to 15. Moments of Record values are discussed in section 2. The estimation of location and scale parameters of IRD using Type II singly and doubly censored data under lower record values is described in section 3. Estimation of location and scale parameters of IRD under censoring with 10 missing observations are presented in section 4. Finally, conclusions are reported in Section 5.
2. Moments of Record Values Relating IRD
The ith moment of 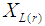 is given by
is given by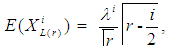 | (2) |
For i =1 and 2.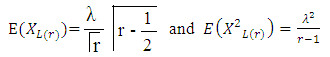 The product moment of
The product moment of 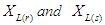 is (r < s)
is (r < s)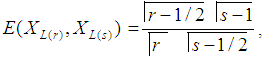 | (3) |
Variance of the rth lower record value is given as: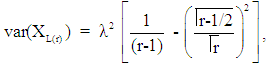 | (4) |
and covariance is: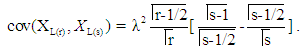 | (5) |
Tables 1 and 2 provides the means and the variance-covariance of the rth lower record values for the IRD with λ=1 for r up to 15. | Table 1. Means of lower record values for the Inverse Rayleigh distribution for 2 ≤ r ≤ 15 |
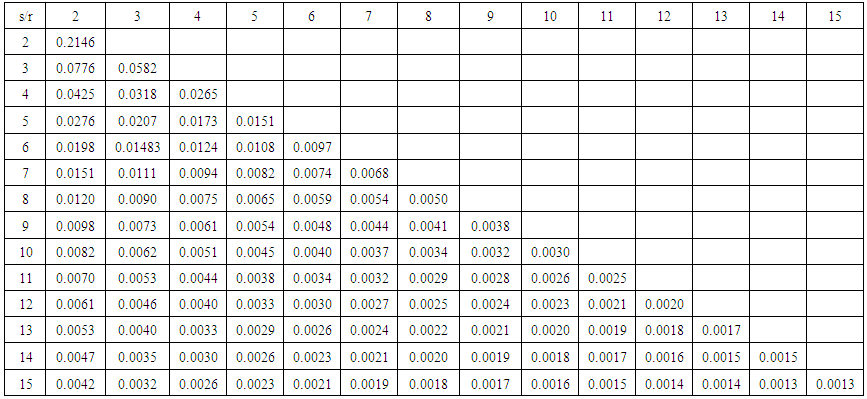 | Table 2. Variance-Covariance of Lower Record values from the Inverse Rayleigh distribution 2 ≤ r ≤ s ≤ 15 |
3. Type II Singly and Doubly Censored Data under Lower Record Values
Lloyd’s method using lower record values is used to the censored samples. The BLUE’s of θ and λ are given by 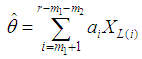 | (6) |
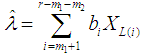 | (7) |
where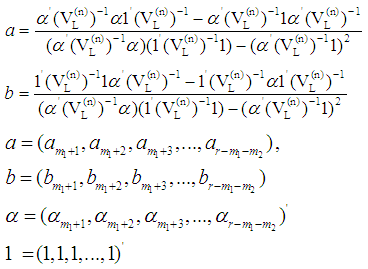 and
and 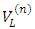 is the variance covariance matrix of r-m1-m2 record values. Where m1 and m2 indicate the number of missing observations from left and right side respectively. Furthermore, the variance and covariance of these BLUE’s are given by
is the variance covariance matrix of r-m1-m2 record values. Where m1 and m2 indicate the number of missing observations from left and right side respectively. Furthermore, the variance and covariance of these BLUE’s are given by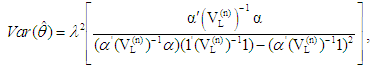 | (8) |
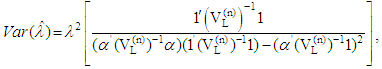 | (9) |
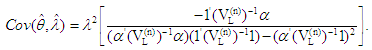 | (10) |
The values of coefficients ai and bi of Lloyd’s estimators of θ and λ are obtained when record numbers are 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, and 15 for all possible choice of censoring. Variances and covariance’s of the these estimators are provided in Appendix-I.
4. Estimation of Location and Scale Parameters of IRD under Censoring with 10 Missing Observations
We consider the estimation of scale and location parameters of IRD when a total of 10 observations are missing on left or on right side for the case r =15. The purpose is to investigate the impact of different combinations of m1 and m2 on variances of 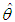 and
and 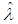 such that m1+ m2=10.
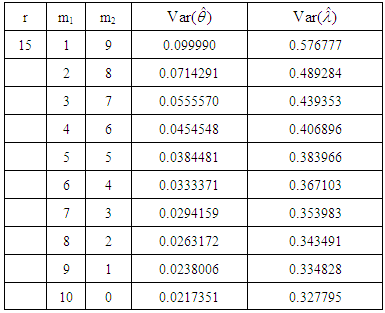
such that m1+ m2=10.Table 3. Variances of scale and location parameters for censored data with 10 missing observations
 |
| |
|
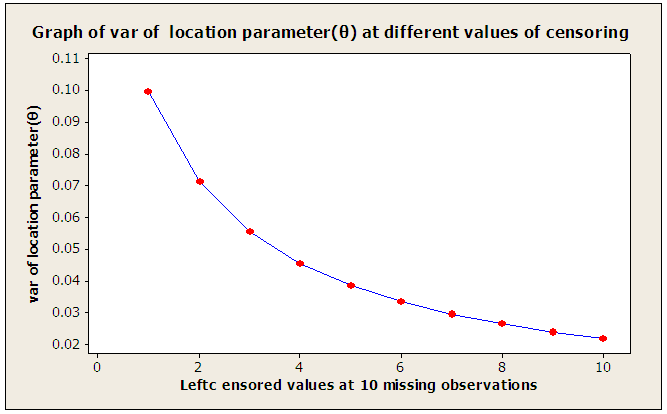 | Figure 1. Variance of θ (10 missing observations) |
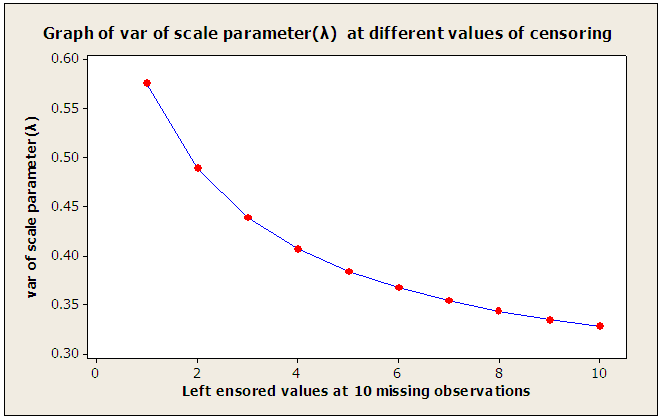 | Figure 2. Variance of λ (10 missing observations) |
From figures 1 and 2 when Type II singly and doubly censoring done by Lloyd’s method we may conclude: • Left censoring provides much more precise estimators of λ and θ than the right censoring when the same number of observations is not available in the sample.• For the same sample size r when m1 increases the estimator of λ and θ gradually loses their efficiency.• Also, for the same r when m2 increases the estimator of λ and θ again loses their efficiency.• When m1 and m2 both increase within the same sample size r efficiency of these estimators decreases.So the variance of the estimators of the scale and location parameters under censoring depends on whether the censoring is left, or right, or double censoring. Also, it depends on the number of observations censored. For example, if only 5 observations are to be included in a sample of size 7 we can have two ways of doing it when m1=1, m2=1 and m1=2, m2=0. The corresponding censored estimators have the variances 0.576777 and 0.489284 respectively.For different combinations of m1 and m2 with m1+m2 remaining fixed within sample size r the variances of the estimators change e.g. with m1=1, m2=1 and m1=2, m2=0 the range of variances of scale parameter is 0.087493. We have developed below a table that provides such information based on different sample sizes.Thus a censored sample including the same number of observations may yield a large range. The range decreases when the number of available observations increases for the same sample size. But it increases when the sample size increases including the same number of available observations. The above information is useful for planning a sampling scheme for the estimation of location and scale parameters.Table 4. Variance range for censored estimators of the scale parameter
 |
| |
|
5. Conclusions
It is interesting to discover that left censoring provides much more precise estimators of λ and θ than the right censoring when the same number of observations is missing in the sample. Furthermore, as the sample size increases but the number of censored observations remains constant, the precision of these estimates increases exponentially. Covariance’s of the above estimators also display a noteworthy behaviour. Firstly, these covariance’s are negative. Secondly, right censoring provides larger covariance’s of Lloyd’s estimators of λ and θ than the left censoring. Also as the sample size increases but the number of censored observations remains constant, these covariance’s approach zero rapidly. A censored sample including the same number of observations may yield a large range. The range decreases when the number of available observations increases for the same sample size. But it increases when the sample size increases including the same number of available observations. This aspect therefore must not be ignore when planning a censored sampling scheme for the estimation of location and scale parameters.
Appendix-I
 | Appendix-I. Variances and covariance’s of BLUEs for location and scale based on singly and doubly censored samples |
References
| [1] | A. Wood, “Predicting software reliability”, IEEE Transactions on Software Engineering, vol. 22, pp. 69-77, 1996. |
| [2] | K. Rosaiah, and R. R. L. Kantam, “Acceptance Sampling Based on the Inverse Rayleigh Distribution”, Economic Quality Control, vol. 20, no. 2, pp. 277-286, 2005. |
| [3] | A. S. Hirai, “Estimation of scale and location parameters using Quadratic Coefficients”, Australian Journal of statistics, vol. 14, no. 3, pp. 222-226, 1972. |
| [4] | D. D. Dyer, and C. W. Whisenand, “Best Linear Unbiased Estimator of the Parameter of the Rayleigh Distribution Part I: Small sample Theory for Censored Order Statistics”, IEEE Transactions on Reliability, vol. R-22, pp. 27-34, 1973. |
| [5] | N. Balakrishan, and P. S. Chan, “On the normal Record values and associated Inference”, Statistics and Probability Letters, vol. 39, pp. 73-80, 1998. |
| [6] | M. Aleem, “Concomitants of Order statistics from Bivariate Inverse Rayleigh Distribution”, Pak. J. Stat. Oper. Research, vol. 2, no. 1, pp. 45-48, 2006. |
| [7] | A. S. Hirai, and A. S. Akhtar, “Bivariate Rayleigh distribution and its Properties”, Pak. J. Stat. Oper. Research, vol. 3, pp. 1, pp. 35-38, 2007. |
| [8] | A. I. Shawky, and R. A. Bakoban, “Order Statistics from Exponentiated Gamma Distribution and Associated Inference”, Int. J. Contemp. Math. Sciences, vol. 4, no. 2, pp. 71-91, 2009. |
| [9] | A. S. Akhter, and A. S. Hirai, “Estimation of the scale parameter from the Rayleigh distribution from Type II singly and doubly censored data, Pakistan Journal of Statistics and Operation Research, vol. 5, no. 1, pp. 31-45, 2009. |
| [10] | A. Azaz, and A. S. Akhter, “Estimation of the scale and location parameters based upon the upper record values of Rayleigh distribution from Type II singly and doubly censored data”, Proceedings third international conference on statistical sciences. University of the Punjab, 2010. |
| [11] | N. Feroze, and M. Aslam, “On posterior analysis of inverse Rayleigh distribution under singly and doubly Type II censored data”, International Journal of Probability and Statistics, vol. 1, no. 5, pp. 145-152, 2012. |
| [12] | R. Jabeen, A. Ahmad, N. Feroze, and G. Masood, “Estimation of location and scale parameters of Weibull distribution using generalized order statistics under Type II singly and doubly censored data”, Int. J. Adv. Science and Technology, vol. 55, pp. 67-80, 2013. |


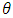 and scale parameter λ is
and scale parameter λ is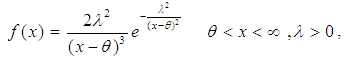
 . Feroze and Aslam [11] discussed the Bayesian analysis of IRD under singly and doubly Type II censored data. The Bayes estimators and corresponding risks have been derived under the assumption of non-informative priors and using symmetric and asymmetric loss functions. Jabeen et al. [12] discussed the estimation of location and scale parameters of Weibull distribution using concept of generalized order statistics by the BLUE and ABLUE from Type II singly and doubly censored samples. This paper is designed for estimation of parameters of IRD for Type II singly and doubly censored data based on lower record values for a sample size up to 15. Moments of Record values are discussed in section 2. The estimation of location and scale parameters of IRD using Type II singly and doubly censored data under lower record values is described in section 3. Estimation of location and scale parameters of IRD under censoring with 10 missing observations are presented in section 4. Finally, conclusions are reported in Section 5.
. Feroze and Aslam [11] discussed the Bayesian analysis of IRD under singly and doubly Type II censored data. The Bayes estimators and corresponding risks have been derived under the assumption of non-informative priors and using symmetric and asymmetric loss functions. Jabeen et al. [12] discussed the estimation of location and scale parameters of Weibull distribution using concept of generalized order statistics by the BLUE and ABLUE from Type II singly and doubly censored samples. This paper is designed for estimation of parameters of IRD for Type II singly and doubly censored data based on lower record values for a sample size up to 15. Moments of Record values are discussed in section 2. The estimation of location and scale parameters of IRD using Type II singly and doubly censored data under lower record values is described in section 3. Estimation of location and scale parameters of IRD under censoring with 10 missing observations are presented in section 4. Finally, conclusions are reported in Section 5.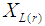 is given by
is given by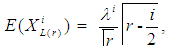
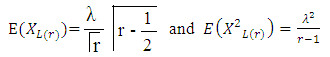 The product moment of
The product moment of  is (r < s)
is (r < s)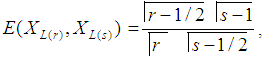
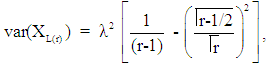
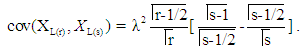


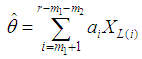
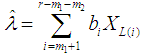
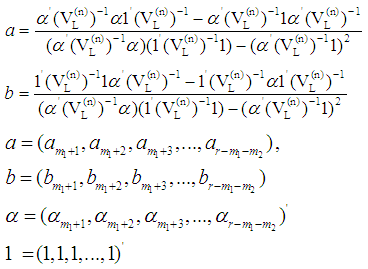 and
and 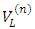 is the variance covariance matrix of r-m1-m2 record values. Where m1 and m2 indicate the number of missing observations from left and right side respectively. Furthermore, the variance and covariance of these BLUE’s are given by
is the variance covariance matrix of r-m1-m2 record values. Where m1 and m2 indicate the number of missing observations from left and right side respectively. Furthermore, the variance and covariance of these BLUE’s are given by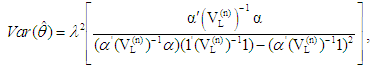
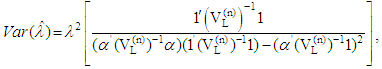
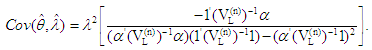
 and
and  such that m1+ m2=10.
such that m1+ m2=10.

 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML

