1. Introduction

Sampling theory develops sampling methods. The basic method of drawing a sample from a population is the Simple Random Sampling (SRS) method and it is a source of inspiration to other methods ([1], [5], [21]). In the SRS method, there are many new estimators proposed in the literature on classical, ratio, product and regression estimators. The “exponential” estimators, which form the basis of our study, increasingly become the focus of interest.

In the sampling theory, the use of auxiliary information has a primary precaution. In sampling studies, the use of auxiliary information is quite common to obtain improved designs for the population parameters such as population sum, population mean and population ratio and to achieve higher efficiencies. Ratio type estimators are used when the correlation between the auxiliary information and the study variable is positive. If it is negative, the use of product type estimators is more convenient. It is known that these estimators have, under some conditions, smaller variances when compared to the classical mean-per unit estimator in SRS. In order to initiate statistical studies successfully, sampling method and estimators to be used must be correctly determined.

In this study, many exponential-ratio type estimators and exponential-product type estimators, which are proposed for the population mean in the SRS scheme, are examined, chronologically. Bias and MSE equations of the estimators are derived, theoretically. In order to show the efficiencies of the estimators in practice, in the application part of the study, the oil olive production data for 2014 is used in the province of Muğla in Turkey. The best and the worst estimates of the average oil olive production are determined by taking into consideration the data structure.

2. Literature Review

The estimator in which the auxiliary information is first used is the ratio estimator proposed by [4].

[3] proposed new ratio and product type exponential estimators in SRS for the estimation of the mean of the study variable Y, depending on an X auxiliary variable whose population mean is known.

Following [3], [16] proposed new ratio and product type exponential estimators and family of estimators for proportion estimation in SRS inspired by ratio and product estimators proposed in SRS.

Since the ratio and product estimators proposed by [3] are biased; [17] proposed a new almost unbiased estimator following the study of [20].

Following [14], [15] proposed a new family of exponential estimators as a combination of [3]’s ratio and product- exponential estimators dependent on auxiliary variable whose population mean is known.

[19] proposed new ratio and product type exponential estimators using known parameters of auxiliary variable.

Inspired by [9], [10] and [11], [18] proposed new ratio-exponential estimator for the estimation of the population mean using the values of known population parameters.

Following [13] and [3], [7] proposed a new exponential estimator for the estimation of population mean.

Following [7], [8] proposed a new ratio-exponential estimator when the population ratio is known.

Inspired by the ratio and product type exponential estimators proposed by [3], [22] proposed new ratio and product type exponential estimators under the large sample approach.

[23] proposed efficient exponential estimators for the population mean using some known parameters of auxiliary information.

[2] proposed new ratio and product type estimators in the estimation of the population mean using two auxiliary variables.

[6] proposed new ratio-exponential type estimators which are more efficient than linear regression estimators and other estimators in this form.

[12] proposed new ratio and product type mean estimators based on the known population proportion.

3. Exponential Type Mean Estimators in Simple Random Sampling Scheme

The list of the exponential type mean estimators in SRS in current literature, Mean Square Error (MSE) and Bias equations are presented in Table 1.

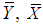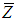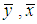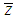Definitions of some statements in Table 1 are given below. and denote the population mean and and denote the sample mean of Y, X and Z, respectively.

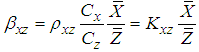represents regression coefficient and 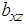is the estimation of 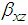between auxiliary variables X and Z.

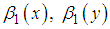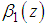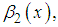
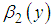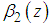and represent the curtosis and and denote the skewness of X, Y and Z, respectively.

Here, correction multiplier is defined as,

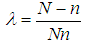(3.1)

and correlation coefficients of population between Y and X; Y and Z; and X and Z are expressed as follows.

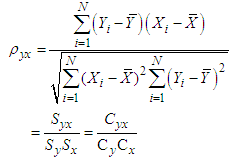(3.2)

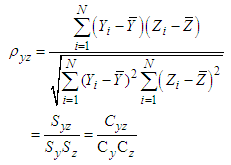(3.3)

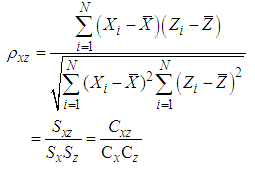(3.4)

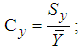The coefficient of variation of Y, X and Z is given in Eq. (3.5)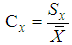, Eq. (3.6) 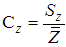and Eq. (3.7), respectively.

(3.5)

(3.6)

(3.7)

Coefficients of population variation between Y and X; Y and Z, and X and Z are given below.

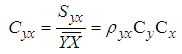(3.8)

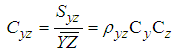(3.9)

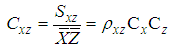(3.10)

Sample variances of Y, X and Z are given as follows.

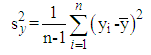(3.11)

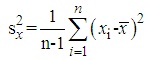(3.12)

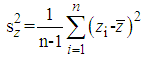(3.13)

Population variances are given below.

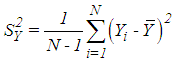(3.14)

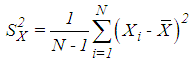(3.15)

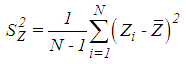(3.16)

In addition, the following definitions are used for convenience in formulations.

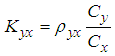(3.17)

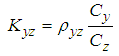(3.18)

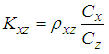(3.19)

Table 1. The Chronological Order of Exponential Type Mean Estimators in SRS Scheme

Table 1. (Continued)

Table 1. (Continued)

Table 1. (Continued)

Table 1. (Continued)

4. Application

In this part of the study, in order to investigate the effectiveness of the exponential mean estimators which are theoretically examined in the SRS plan, oil olive production data obtained from 205 regions in Muğla province of the year 2014 from Turkish Statistical Institute are used [24].

Exponential estimators that predict the best and the worst of the average oil olive production are determined in accordance with the known data structure of population information. The aim is to determine the exponential estimator that gives the best estimate of the average amount of oil olive produced Muğla in the related year in Muğla using the information of the area of bulk fruits (Z) and the number of fruit trees (X). Definitions of the variables are given below.

Y: Amount of oil olive produced (ton)

X: Number of fruit trees

Z: Area of bulk fruits (Decar)

In the estimation of sample size in SRS, following equations are used.

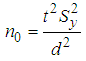(4.1)

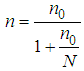(4.2)

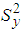Here, t is the t table value, is the population variance of the variable Y and d is the amount of tolerance value. The sample size in SRS plan is obtained as,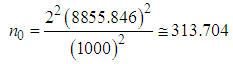

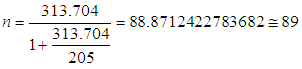where the population unit is districts.

The correlation between the study variable Y and the auxiliary variables X and Z is examined and it is observed that the same directional relationships existed. Therefore, it is expected that ratio type exponential estimators will give more effective results than product type exponential estimators in SRS plan, while the average oil olive production is estimated.

The population and sample information obtained for oil olive production is shown in Table 2 and Table 3, respectively. Some information on the proposed estimators is given in Table 4. The estimated values of the estimators, Bias, MSE and Relative Efficiency (RE) values relative to the classical mean-per unit estimator are presented in Table 5.

When we examine Table 5, it is observed that many proposed exponential type estimators are more efficient than simple classical estimator when the high correlation between the study variable Y and the auxiliary variables X and Z are taken into consideration.

In comparisons made over the MSE values of the estimators, the most efficient estimate of the average oil olive production is obtained from the generalized ratio-cum-ratio exponential estimator 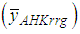and product-cum-product exponential estimator 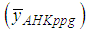of [2]. The worst estimate is obtained from the classical product estimator .

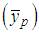In RE comparisons, it is observed that the estimators of [2] are about 6.3 times more efficient than the classical mean estimator. In addition, they appear approximately 2.45 times more efficient than the first proposed ratio type exponential estimator and approximately 14.75 times more efficient than the first proposed product type exponential estimator [3].

Since [2] used information of two auxiliary variables in the ratio-cum-ratio and product-cum-product exponential estimators, increasing efficiency in estimators is expected. It is also predictable result that the efficiency level of the product estimators will be lower than the ratio estimators when the correlation coefficient between the study variable Y and the auxiliary variables is positive.

When new modified ratio and product exponential estimators in SRS plan are examined, because these estimators belong to the same family of estimators and the MSE values are calculated over the optimal values for constants such as “a” and “b” in the formulations, they have the same MSE values.

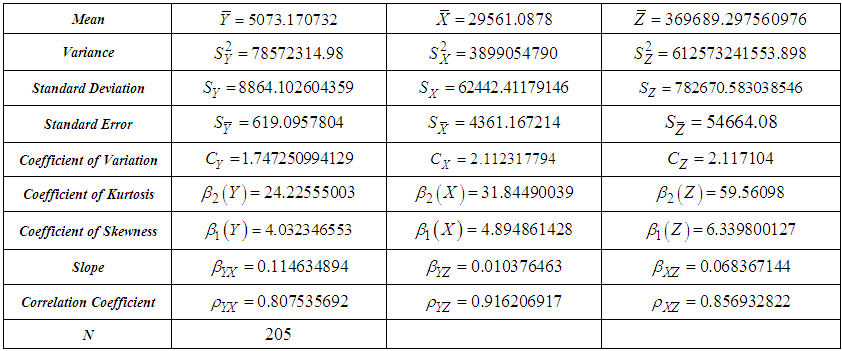Table 2. Population Information Related to the Oil Olive Production Data

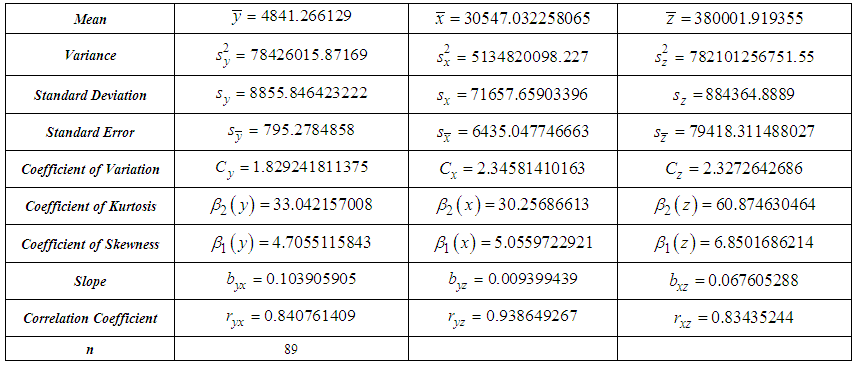Table 3. Sample Information Related to the Oil Olive Production Data

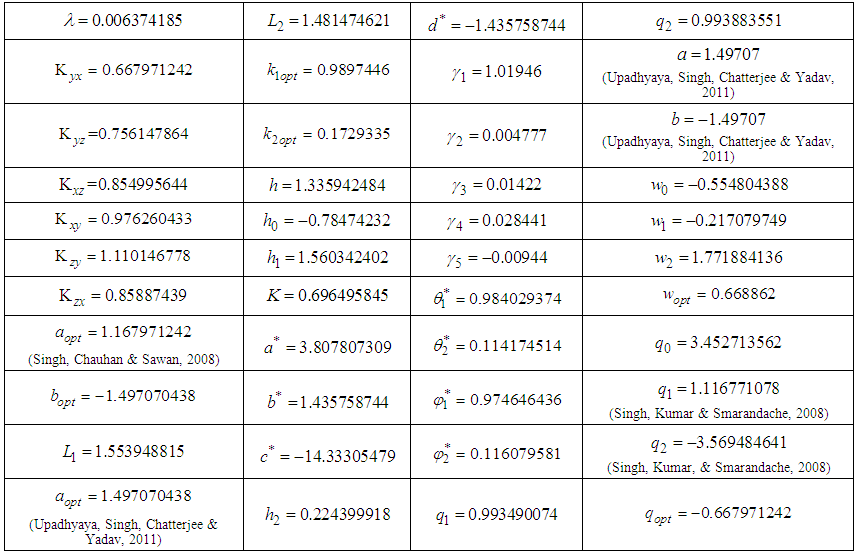Table 4. Information on Exponential Estimators Proposed in Simple Random Sampling Plan

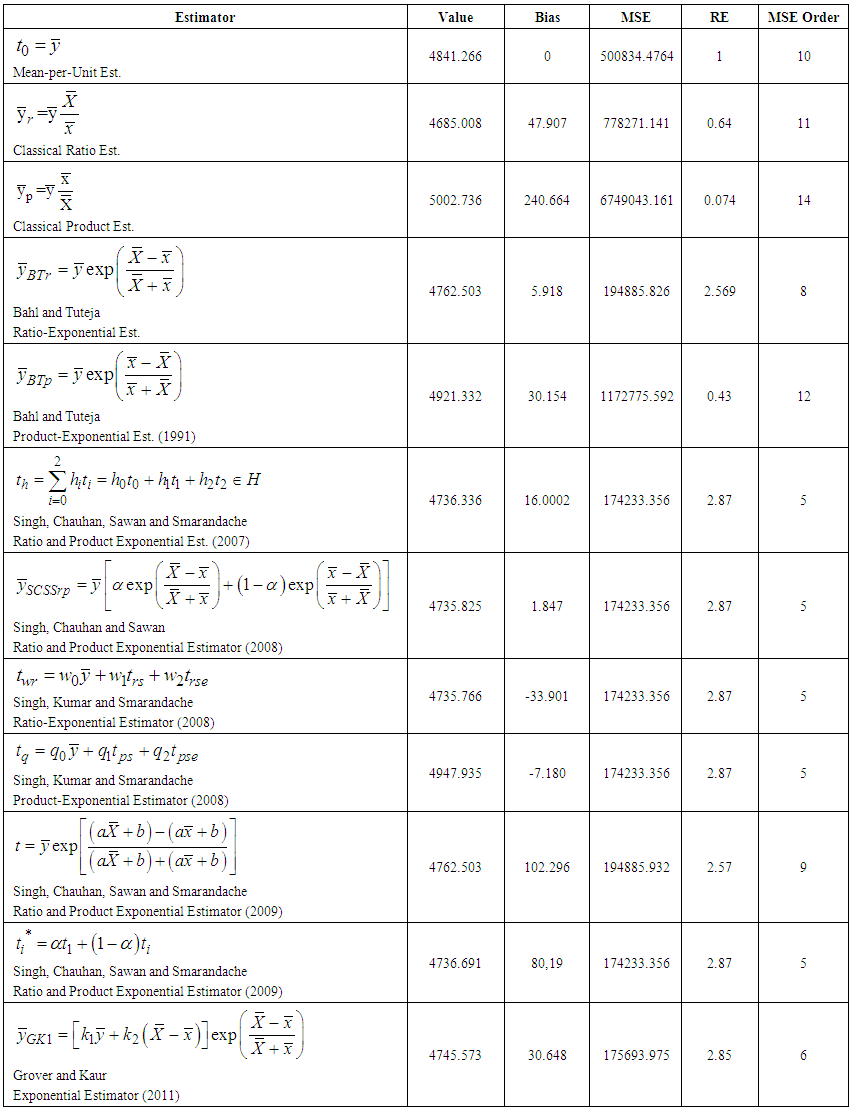Table 5. Bias, MSE and Relative Efficiency Values of the Proposed Estimators for Oil Olive Production Data

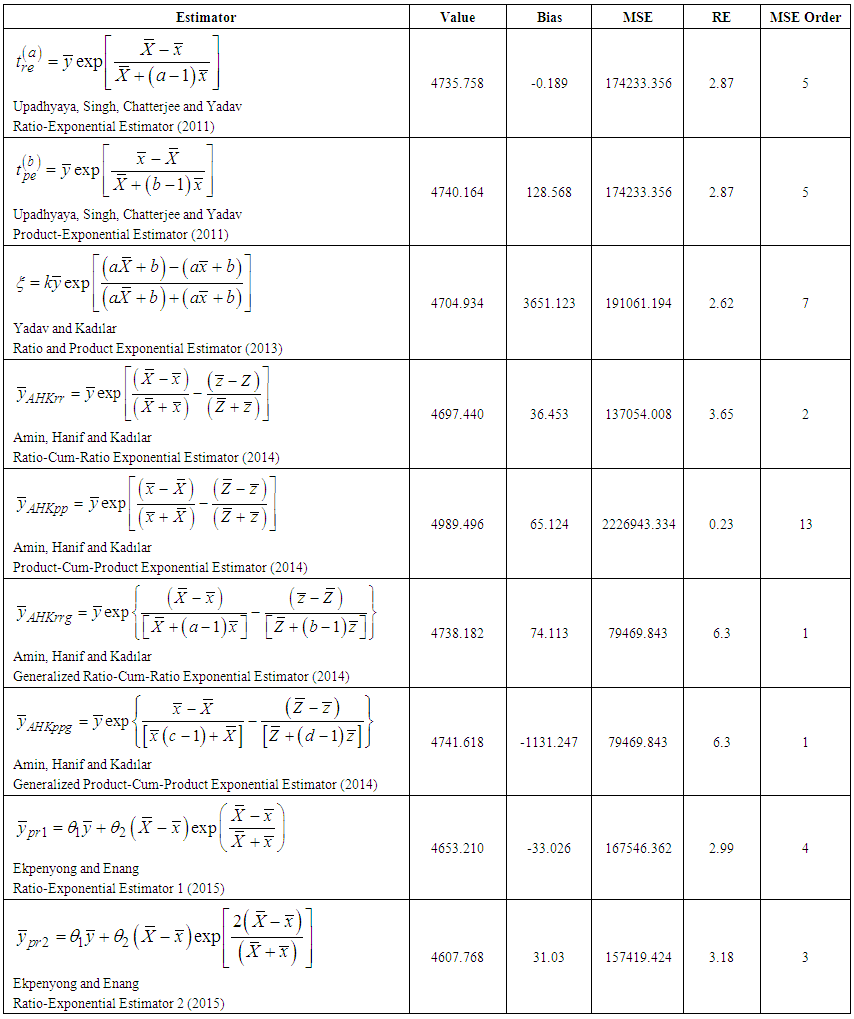Table 5. (Continued)

5. Theoretical Efficiency Comparisons

In the application section, it was concluded that the classical product estimator proposed by Cochran (1977) is less efficient when compared with the mean-per-unit estimator given the data characteristics used. The most efficient family of estimators are the generalized ratio-cum-ratio and generalized product-cum-product exponential estimators proposed by Amin, Hanif and Kadılar (2014).

It is possible to theoretically find out the validity of the findings obtained and the efficiency conditions by comparing the MSE values of the estimators. Theoretical comparisons are given below.

Cochran’s Classical Product Estimator (1977) and Mean-Per-Unit Estimator

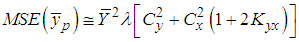(6.1)

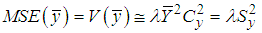(6.2)

In that case, the classical product estimator is more efficient than the mean-per unit estimator if the following condition is met.

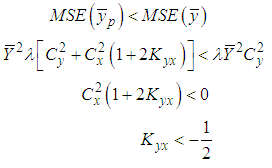(6.3)

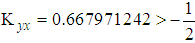Because , it is concluded that the mean-per-unit estimator is more efficient than the classical product estimator.

Amin, Hanif, Kadılar (2014) and Mean-Per-Unit Estimator

The MSE equation of the generalized ratio-cum-ratio and generalized product-cum-product exponential estimators of Amin, Hanif and Kadılar is given below.

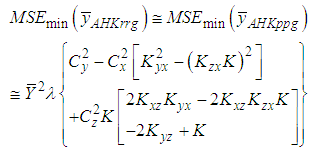(6.4)

Using Eq.(6.4) and Eq.(6.2), we can theoretically determine the efficiency conditions. Amin, Hanif and Kadirar estimators will be more efficient than the mean-per unit estimator if the following condition is met.

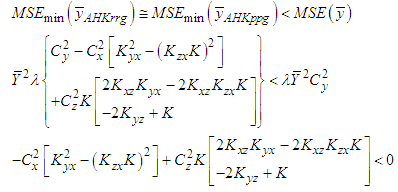When the values given in Table 2, Table 3 and Table 4 are used for the data set, the result is negative.

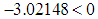Thus, it is once again proven both theoretically and practically that the Amin, Hanif and Kadılar estimators are more efficient than mean-per-unit estimator.

6. Results

It should be decided which of the estimators proposed in various sampling plans would give the most efficient estimates appropriate for the structure of the data set being examined.

In this study, many ratio and product type exponential mean estimators proposed in the SRS plan in the literature is introduced, and Bias and MSE values are derived, theoretically.

The validity of theoretical findings is investigated using data from the Turkish Statistical Institute on oil olive production from 205 regions in 2014 and the performances of the estimators are compared under the assumption that no population information of auxiliary variable is available.

When the results are examined in general, it is observed that the most efficient estimation is obtained using the generalized ratio-cum-ratio and generalized product-cum-product 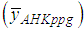exponential estimators proposed by [2]. The worst estimate is obtained from the classical product estimator .

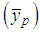It is observed that estimators proposed by [2] are about 6.3 times more efficient than the classical mean estimator; approximately 2.45 times more efficient than the ratio-exponential type estimator and approximately 14.75 times more efficient than product type exponential estimator proposed by [3].

This study provides information on exponential mean estimators proposed in the SRS plan. Researchers studying in this area will have a chance to see the estimators as a whole. Inspired by these estimators, researchers could propose new estimators, which are more efficient than these estimators, under certain conditions or in all cases. In addition, the exponential mean estimators proposed in the SRS plan can be adapted to other sampling plans.

ACKNOWLEDGEMENTS

We are thankful to Scientific Research Unit of Muğla Sıtkı Koçman University for their financial support and for providing necessary guidance concerning projects implementation.