| [1] | Alavi, S.M.R. and Chinipardaz, R. (2009): Form-invariance under weighted sampling, Statistics, 43, 81 – 90. |
| [2] | Barlow, R.E. and Proschan, F. (1981): Statistical Theory of Reliability and Life Testing, Silver Spring, MD. |
| [3] | Correa, J.A. and Wolfson, D.B. (2007): Length-bias: some Characterizations and applications, Journal of Statistical Computation and Simulation, 64, 209 – 219. |
| [4] | Cullen, M.J., Walsh, J., Nicholson, L.V., and Harris, J.B. (1990): Ultrastructural localization of dystrophin in human muscle by using gold immunolabelling, Proceedings of the Royal Society of London, 20, 197-210. |
| [5] | Ducey, M.J. (2009): Sampling trees with probability nearly proportional to biomass, For. Ecol. Manage., 258, 2110 – 2116. |
| [6] | Ducey, M.J. and Gove, J.H. (2015): Size-biased distributions in the generalized beta distribution family, with applications to forestry, Forestry- An International Journal of Forest Research. 88, 143 – 151. |
| [7] | Drummer, T.D. and MacDonald, L.L. (1987): Size biased in line transect sampling, Biometrics, 43, 13 – 21. |
| [8] | Fisher, R.A. (1934): The effects of methods of ascertainment upon the estimation of frequencies, Ann. Eugenics, 6, 13 – 25. |
| [9] | Ghitany, M.E. and Al-Mutairi, D.K. (2008): Size-biased Poisson-Lindley distribution and Its Applications, Metron - International Journal of Statistics, LXVI (3), 299 – 311. |
| [10] | Gove, J.H. (2000): Some observations on fitting assumed diameter distributions to horizontal point sampling data, Can. J. For. Res., 30, 521 – 533. |
| [11] | Gove, J.H. (2003): Estimation and applications of size-biased distributions in forestry. In Modeling Forest Systems. A Amaro, D. Reed and P. Soares (Eds), CABI Publishing, pp. 201 – 212. |
| [12] | Hogg, R.V., Mckean, J.W. and Craig, A.T. (2005): Introduction to Mathematical Statistics, 6th edition, Pearson Prentice hall, New Jersey. |
| [13] | Keith, L.B. and Meslow, E.C. (1968): Trap Response by snowshoe hares, Journal of Wildlife Management, 20, 795- 801. |
| [14] | Lappi, J. and bailey, R.L. (1987): Estimation of diameter increment function or other tree relations using angle-count samples, Forest science, 33, 725 – 739. |
| [15] | Lindley, D.V. (1958): Fiducial distributions and Bayes theorem, Journal of the Royal Statistical Society, 20 (1), 102- 107. |
| [16] | McDonald, J.B. (1984): Some generalized functions for the size distribution of income, Econometrics, 52, 647 – 664. |
| [17] | Patil, G.P. (1981): Studies in statistical ecology involving weighted distributions. In Applications and New Directions, J.K. Ghosh and J. Roy (eds). Proceeding of Indian Statistical Institute. Golden Jubliee, Statistical Publishing society, pp. 478 – 503. |
| [18] | Patil, G.P. and Ord, J.K. (1976): On size-biased sampling and related form-invariant weighted distributions, Sankhya Ser. B, 38, 48 – 61. |
| [19] | Patil, G.P. and Rao, C.R. (1977): The Weighted distributions: A survey and their applications. In applications of Statistics, Ed P.R. Krishnaiah, 383 – 405, North Holland Publications Co., Amsterdam. |
| [20] | Patil, G.P. and Rao, C.R. (1978): Weighted distributions and size-biased sampling with applications to wild-life populations and human families, Biometrics, 34, 179 – 189. |
| [21] | Rao, C.R. (1965): On discrete distributions arising out of methods of ascertainment In: Patil, G.P. (eds) Classical and Contagious Discrete Distributions. Statistical Publishing Society, Calcutta, 320 – 332. |
| [22] | Sankaran, M. (1970): The discrete Poisson-Lindley distribution, Biometrics, 26, 145- 149. |
| [23] | Scheaffer, R.L. (1972): Size-biased sampling, Technometrics, 14, 635 – 644. |
| [24] | Shanker, R. (2015): Shanker distribution and Its Applications, International Journal of Statistics and Applications, 5(6), 338 – 348. |
| [25] | Shanker, R. (2016): The discrete Poisson-Shanker distribution, Jacobs Journal of Biostatistics, 1(1), 1 – 7. |
| [26] | Shanker, R., Hagos, F. and Abrehe, Y. (2015): On Size –Biased Poisson-Lindley Distribution and Its Applications to Model Thunderstorms, American Journal of Mathematics and Statistics, 5 (6), 354 – 360. |
| [27] | Singh, S.K. and Maddala, G.S. (1976): A function for the size distribution of incomes, Econometrica, 44, 963 – 970. |
| [28] | Van Deusen, P.C. (1986): Fitting assumed distributions to horizontal point sample diameters, For. Sci., 32, 146 -148. |


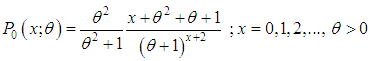
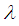 follows a lifetime distribution named Shanker distribution introduced by Shanker (2015) having probability density function (p.d.f.)
follows a lifetime distribution named Shanker distribution introduced by Shanker (2015) having probability density function (p.d.f.)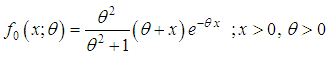
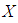 has original probability distribution
has original probability distribution 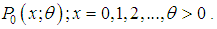 Suppose the sample units are weighted or selected with probability proportional to some measure
Suppose the sample units are weighted or selected with probability proportional to some measure 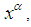 where
where 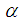 is a positive integer. Then the corresponding size-biased probability distribution of order
is a positive integer. Then the corresponding size-biased probability distribution of order 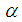 can be defined by its probability mass function
can be defined by its probability mass function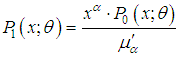 where
where 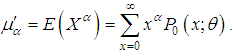 If
If 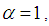 then the distribution is known as simple size-biased and is applicable for size-biased sampling in sampling theory. If
then the distribution is known as simple size-biased and is applicable for size-biased sampling in sampling theory. If 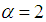 , then the distribution is known as area-biased distribution and is applicable for area-biased sampling in forestry.The p.m.f. of the size-biased Poisson-Shanker distribution (SBPSD) with parameter
, then the distribution is known as area-biased distribution and is applicable for area-biased sampling in forestry.The p.m.f. of the size-biased Poisson-Shanker distribution (SBPSD) with parameter 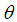 can thus be be obtained as
can thus be be obtained as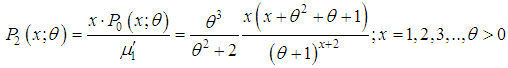
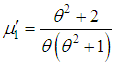 is the mean of the Poisson-Shanker distribution (PSD) with p.m.f. (1.1).Recall that the probability mass function of size-biased Poisson-Lindley distribution (SBPLD) with parameter
is the mean of the Poisson-Shanker distribution (PSD) with p.m.f. (1.1).Recall that the probability mass function of size-biased Poisson-Lindley distribution (SBPLD) with parameter 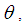 obtained by Ghitany and Mutairi (2008), is given by
obtained by Ghitany and Mutairi (2008), is given by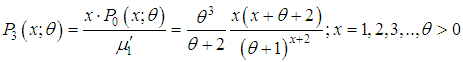

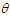
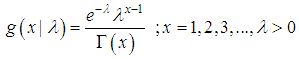
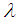 follows size-biased Shanker distribution (SBSD) with p.d.f.
follows size-biased Shanker distribution (SBSD) with p.d.f.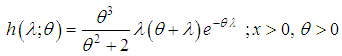
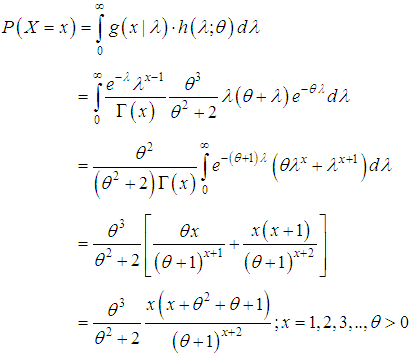
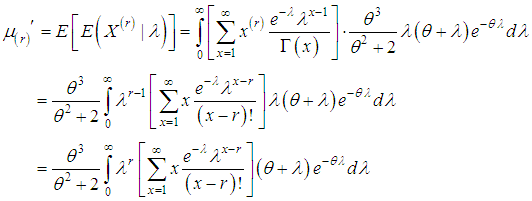 Taking
Taking 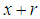 in place of
in place of 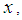 we get
we get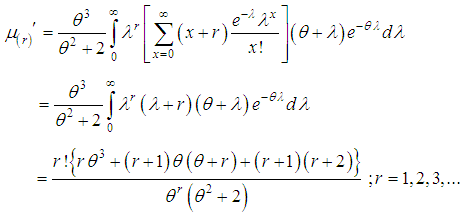
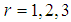 and 4 in (2.1), first four factorial moments about origin can be obtained and then using the relationship between factorial moments about origin and moments about origin, the first four moments about origin of SBPSD (1.3) can be obtained as
and 4 in (2.1), first four factorial moments about origin can be obtained and then using the relationship between factorial moments about origin and moments about origin, the first four moments about origin of SBPSD (1.3) can be obtained as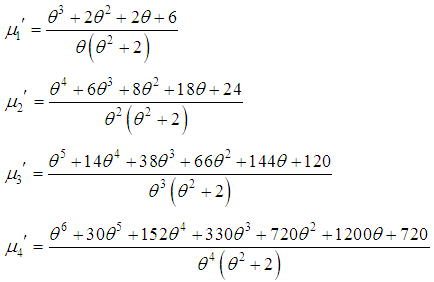 Again using the relationship between moments about mean and the moments about origin, the moments about mean of the SBPSD (1.3) are obtained as
Again using the relationship between moments about mean and the moments about origin, the moments about mean of the SBPSD (1.3) are obtained as The coefficient of variation
The coefficient of variation  coefficient of Skewness
coefficient of Skewness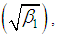 coefficient of Kurtosis
coefficient of Kurtosis 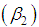 and index of dispersion
and index of dispersion 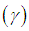 of the SBPSD (1.3) are thus obtained as
of the SBPSD (1.3) are thus obtained as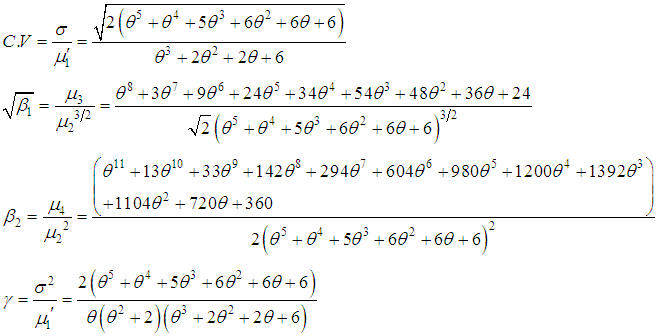 It can be easily verified that SBPSD is over-dispersed
It can be easily verified that SBPSD is over-dispersed 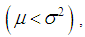 equi-dispersed
equi-dispersed 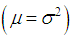 and under-dispersed
and under-dispersed 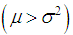 for
for 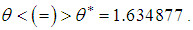 The graphs of coefficient of variation, coefficient of skewness, coefficient of kurtosis, and index of dispersion of SBPSD for varying values of parameter
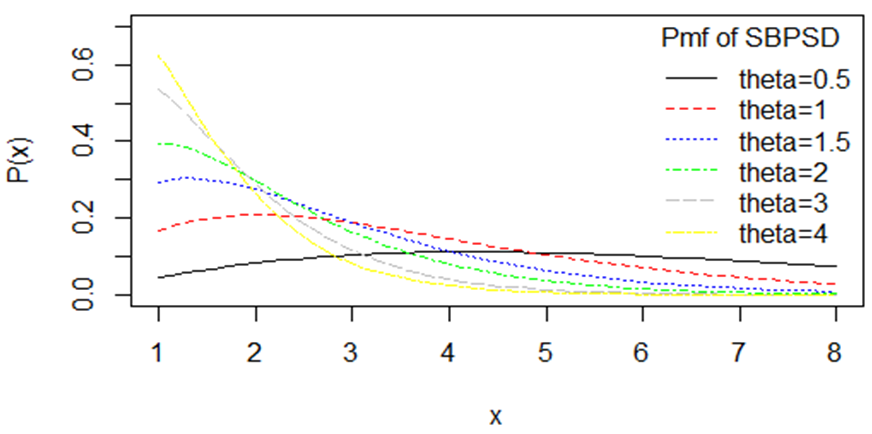
The graphs of coefficient of variation, coefficient of skewness, coefficient of kurtosis, and index of dispersion of SBPSD for varying values of parameter 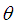 are shown in figure 3.
are shown in figure 3.
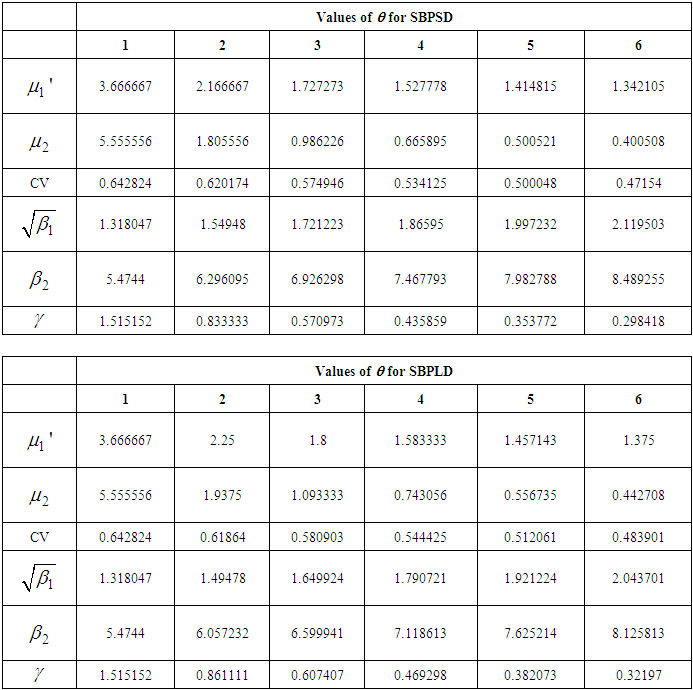
 of the SBPSD for varying values of parameter
of the SBPSD for varying values of parameter 
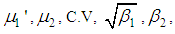 and
and 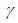 has been prepared for varying values of the parameter
has been prepared for varying values of the parameter 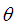 and presented in table 1.
and presented in table 1.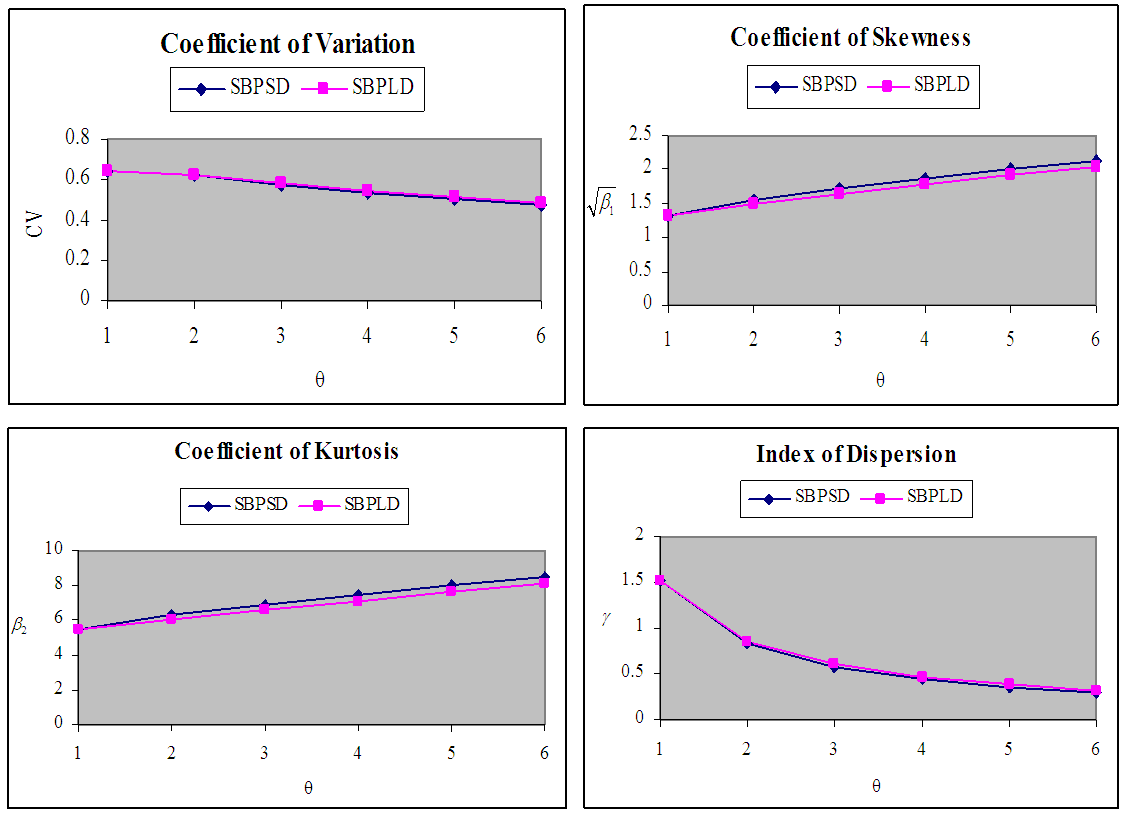
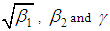 of the SBPSD and SBPLD for varying values of parameter
of the SBPSD and SBPLD for varying values of parameter 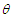
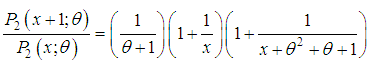 is a deceasing function of
is a deceasing function of 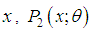 is log-concave. Therefore, SBPSD is unimodal, has an increasing failure rate (IFR), and hence increasing failure rate average (IFRA). It is new better than used in expectation (NBUE) and has decreasing mean residual life (DMRL). Detailed discussion and definitions of these aging concepts can be seen in Barlow and Proschan (1981).
is log-concave. Therefore, SBPSD is unimodal, has an increasing failure rate (IFR), and hence increasing failure rate average (IFRA). It is new better than used in expectation (NBUE) and has decreasing mean residual life (DMRL). Detailed discussion and definitions of these aging concepts can be seen in Barlow and Proschan (1981).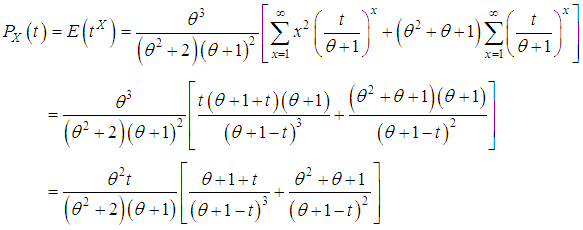 Moment Generating Function: The moment generating function of the SBPSD (1.3) is given by
Moment Generating Function: The moment generating function of the SBPSD (1.3) is given by 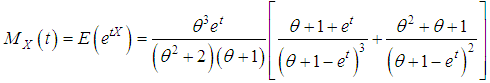
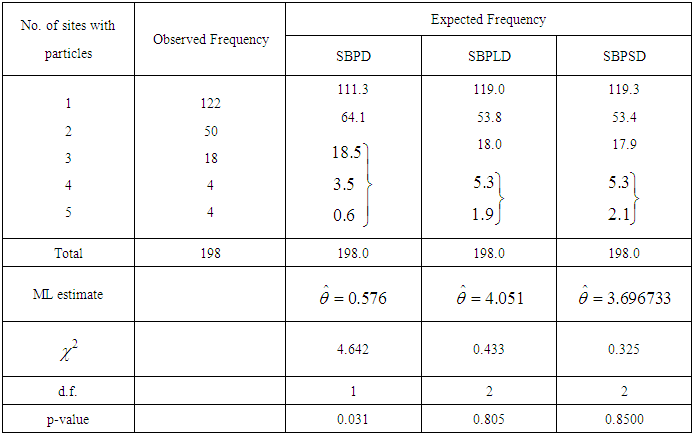
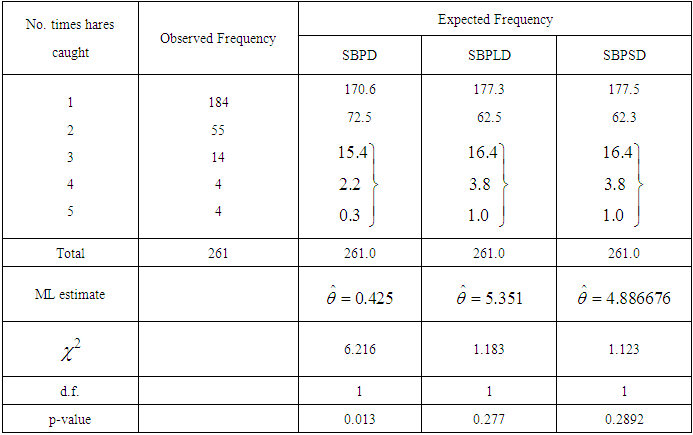
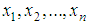 be a random sample of size n from the SBPSD (1.3) and let
be a random sample of size n from the SBPSD (1.3) and let 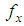 be the observed frequency in the sample corresponding to
be the observed frequency in the sample corresponding to 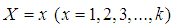 such that
such that 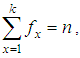 where
where 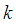 is the largest observed value having non-zero frequency. The likelihood function
is the largest observed value having non-zero frequency. The likelihood function 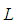 of the SBPSD (1.3) is given by
of the SBPSD (1.3) is given by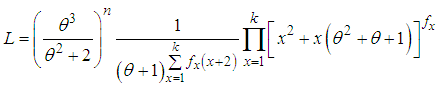 The log likelihood function is obtained as
The log likelihood function is obtained as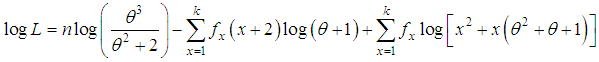 The first derivative of the log likelihood function is given by
The first derivative of the log likelihood function is given by 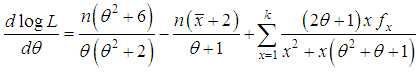 where
where 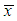 is the sample mean.The maximum likelihood estimate (MLE),
is the sample mean.The maximum likelihood estimate (MLE), 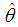 of
of 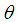 is the solution of the equation
is the solution of the equation 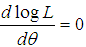 and is given by the solution of the non-linear equation
and is given by the solution of the non-linear equation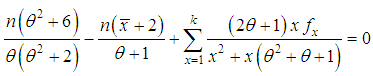
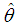 of
of 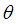 of the SBPSD is consistent and asymptotically normal. That is,
of the SBPSD is consistent and asymptotically normal. That is, 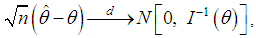 where
where 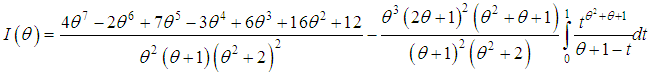 is the Fisher’s information about
is the Fisher’s information about 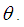 Proof: The SBPSD satisfies the regularity conditions under which the ML estimator
Proof: The SBPSD satisfies the regularity conditions under which the ML estimator 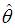 of
of 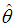 is consistent and asymptotically normal [see Hogg et al (2005), chapter 6]. Finally, we have
is consistent and asymptotically normal [see Hogg et al (2005), chapter 6]. Finally, we have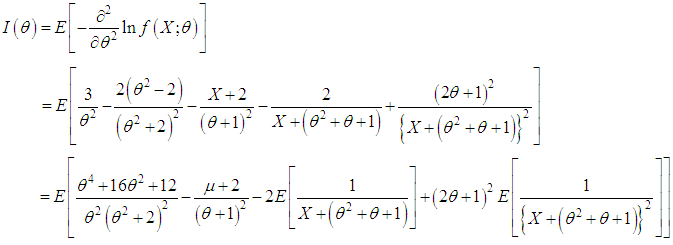
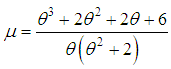
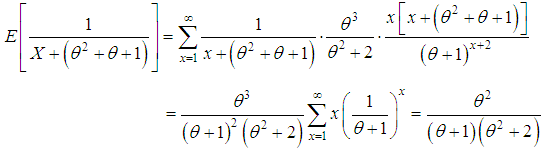
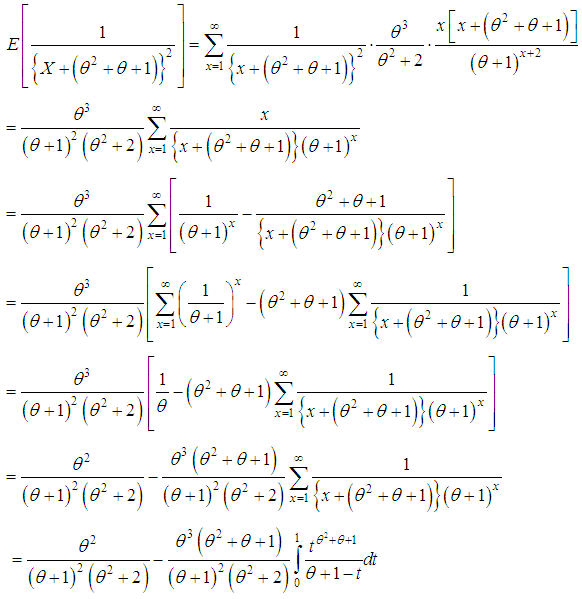
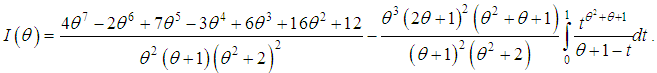 4.2. Method of Moment Estimate (MOME): Let
4.2. Method of Moment Estimate (MOME): Let 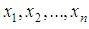 be a random sample of size n from the SBPSD (1.3). Equating population mean to the corresponding sample mean, the MOME
be a random sample of size n from the SBPSD (1.3). Equating population mean to the corresponding sample mean, the MOME 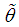 of
of 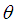 of SBPSD is the solution of the following cubic equation in
of SBPSD is the solution of the following cubic equation in 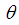
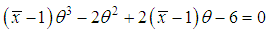
 is the sample mean.
is the sample mean. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML of SBPSD and SBPLD for varying values of the parameter θ
of SBPSD and SBPLD for varying values of the parameter θ