-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Probability and Statistics
p-ISSN: 2168-4871 e-ISSN: 2168-4863
2016; 5(3): 65-72
doi:10.5923/j.ijps.20160503.01

Regression Estimation in the Presence of Outliers: A Comparative Study
1Statistics Department, Faculty of Economics and Political Science, Cairo University, Egypt
2Department of Statistics, Mathematics & Insurance, Faculty of Commerce, Banha University, Egypt
Correspondence to: Ahmed M. Gad, Statistics Department, Faculty of Economics and Political Science, Cairo University, Egypt.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

In linear models, the ordinary least squares (OLS) estimators of parameters have always turned out to be the best linear unbiased estimators. However, if the data contain outliers, this may affect the least-squares estimates. So, an alternative approach; the so-called robust regression methods, is needed to obtain a better fit of the model or more precise estimates of parameters. In this article, various robust regression methods have been reviewed. The focus is on the presence of outliers in the y-direction (response direction). Comparison of the properties of these methods is done through a simulation study. The comparison's criteria were the efficiency and breakdown point. Also, the methods are applied to a real data set.
Keywords: Linear regression, Outliers, High breakdown estimators, Efficiency estimators, Mean square errors
Cite this paper: Ahmed M. Gad, Maha E. Qura, Regression Estimation in the Presence of Outliers: A Comparative Study, International Journal of Probability and Statistics , Vol. 5 No. 3, 2016, pp. 65-72. doi: 10.5923/j.ijps.20160503.01.
Article Outline
1. Introduction
- Regression analysis is a statistical tool that is useful in all areas of sciences. The objective of linear regression analysis is to study how a dependent variable is linearly related to a set of explanatory variables. The linear regression model is given by
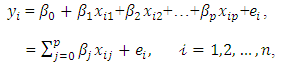 | (1) |
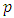 is the number of explanatory variables
is the number of explanatory variables 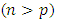 , and
, and 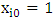 . The
. The 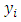 denotes the
denotes the 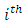 observed response, the
observed response, the 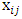 represents the
represents the 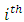 observation of the explanatory variable
observation of the explanatory variable 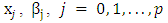 , denote the regression coefficients, and
, denote the regression coefficients, and 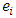 represents the random error (Birkes and Dodge, 1993). On the basis of the estimated parameters
represents the random error (Birkes and Dodge, 1993). On the basis of the estimated parameters 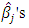 it is possible to fit the dependent variable as
it is possible to fit the dependent variable as 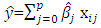 , and the estimates of the residuals
, and the estimates of the residuals 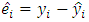 for
for 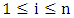 . In matrix notation the model can be written as
. In matrix notation the model can be written as 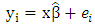 .The objective of regression analysis is to find the estimates of the unknown parameters,
.The objective of regression analysis is to find the estimates of the unknown parameters, 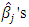 . One method of obtaining the estimates of
. One method of obtaining the estimates of 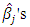 is the method of least squares, which minimizes the sum of squared distances of all the points from the actual observation to the regression surface (Fox, 1997). Therefore, the objective is to find those values of
is the method of least squares, which minimizes the sum of squared distances of all the points from the actual observation to the regression surface (Fox, 1997). Therefore, the objective is to find those values of 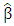 that lead to the minimum value of
that lead to the minimum value of 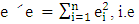 .
.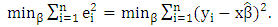 | (2) |
 are unbiased if
are unbiased if 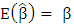 . Among the class of linear unbiased estimators for
. Among the class of linear unbiased estimators for 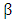 , the estimator
, the estimator 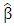 is the best in the sense that the variance of
is the best in the sense that the variance of 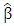 is the minimum,
is the minimum, 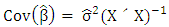 , where
, where 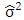 is the mean square
is the mean square 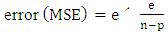 . For this reason the least squares estimates are the best linear unbiased estimators, referred to as BLUE. In order to use regression correctly, the assumptions on which it is based need to be met. The assumptions of the OLS are that the errors are normally distributed, have equal variance at all levels of the independent variables (homoscedasticity), and are uncorrelated with both the independent variables and with each other. It is also assumed that the variables are measured without error. When the assumptions are met, model inferences such as confidence intervals and hypothesis testing are very powerful. A common problem in regression analysis is the presence of outliers. As defined by Barnett and Lewis (1994), outliers are observations that appear inconsistent with the rest of data. The outliers may occur as a result of unusual but explainable events, such as faulty measurement, incorrect recording of data, failure of a measurement instrument, etc. Each different reason may require different treatment. Heavy-tailed distributions usually generate outliers, and these outliers may have a marked influence on parameter estimates (Chatterjee and Hadi, 1986). Rousseeuw and Leroy (1987) classified outliers as vertical outliers, good leverage points and bad leverage points. Vertical outliers are those observations have outlying values for the corresponding error term (on the y-direction) but are not outlying in the space of explanatory variables (the x-dimension). Good leverage points are those observations that are outlying in the space of explanatory variables but that are located close to the regression line. Bad leverage points are those observations that are both outlying in the space of explanatory variables and located far from the true regression line. There are outliers in both the directions (x, direction of the explanatory variables and y, direction of the response variable).The aim of this paper is to compare the robust methods of estimation of regression parameters. This is specific to the outliers in y-direction. The comparison is conducted via simulation study and a real application. The paper is organized as follows. Section 2 is devoted to the evaluation and comparison criteria of regression estimators. In Section 3 we review the robust regression methods that achieve high breakdown point, high efficiency or both. Section 4 is devoted for the simulation study and Section 5 for the real application. In Section 6 we conclude the paper.
. For this reason the least squares estimates are the best linear unbiased estimators, referred to as BLUE. In order to use regression correctly, the assumptions on which it is based need to be met. The assumptions of the OLS are that the errors are normally distributed, have equal variance at all levels of the independent variables (homoscedasticity), and are uncorrelated with both the independent variables and with each other. It is also assumed that the variables are measured without error. When the assumptions are met, model inferences such as confidence intervals and hypothesis testing are very powerful. A common problem in regression analysis is the presence of outliers. As defined by Barnett and Lewis (1994), outliers are observations that appear inconsistent with the rest of data. The outliers may occur as a result of unusual but explainable events, such as faulty measurement, incorrect recording of data, failure of a measurement instrument, etc. Each different reason may require different treatment. Heavy-tailed distributions usually generate outliers, and these outliers may have a marked influence on parameter estimates (Chatterjee and Hadi, 1986). Rousseeuw and Leroy (1987) classified outliers as vertical outliers, good leverage points and bad leverage points. Vertical outliers are those observations have outlying values for the corresponding error term (on the y-direction) but are not outlying in the space of explanatory variables (the x-dimension). Good leverage points are those observations that are outlying in the space of explanatory variables but that are located close to the regression line. Bad leverage points are those observations that are both outlying in the space of explanatory variables and located far from the true regression line. There are outliers in both the directions (x, direction of the explanatory variables and y, direction of the response variable).The aim of this paper is to compare the robust methods of estimation of regression parameters. This is specific to the outliers in y-direction. The comparison is conducted via simulation study and a real application. The paper is organized as follows. Section 2 is devoted to the evaluation and comparison criteria of regression estimators. In Section 3 we review the robust regression methods that achieve high breakdown point, high efficiency or both. Section 4 is devoted for the simulation study and Section 5 for the real application. In Section 6 we conclude the paper.2. Evaluating Regression Estimators
- The regression estimators can be evaluated and compared using different criteria. Although some criteria are more important than others, for a particular type of datasets, the ideal estimator would have positive characteristics of all criteria. These criteria include the following.
2.1. The Breakdown Point
- The breakdown is the degree of robustness of an estimate in the presence of outliers (Hampel, 1974). The smallest possible breakdown point is 1/n which tends to 0% when the sample size n becomes large. This is the case in the least squares estimators. If a robust estimator has a 50% breakdown point then 50% of the data could contain outliers and the coefficients would remain useable.One aim of robust estimators is a high finite sample breakdown point
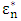 . A formal finite sample definition of breakdown is given in Rousseeuw and Leroy (1987). Using a sample of n data points such that
. A formal finite sample definition of breakdown is given in Rousseeuw and Leroy (1987). Using a sample of n data points such that 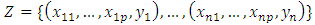 and let T be a regression estimator. Applying T to the sample Z yields the regression estimator T(Z) =
and let T be a regression estimator. Applying T to the sample Z yields the regression estimator T(Z) = 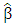 . Consider all possible corrupted samples
. Consider all possible corrupted samples 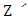 obtained by replacing the data points by the arbitrary values which allows for very bad outliers. The maximum bias that can be caused by this contamination is
obtained by replacing the data points by the arbitrary values which allows for very bad outliers. The maximum bias that can be caused by this contamination is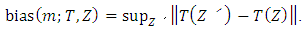 | (3) |
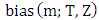 is infinite, then the m outliers can have an arbitrarily large effect on T, which may be expressed by saving that estimator breaks down. Thus, the finite sample breakdown point
is infinite, then the m outliers can have an arbitrarily large effect on T, which may be expressed by saving that estimator breaks down. Thus, the finite sample breakdown point 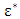 of the estimator
of the estimator 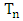 at the sample of Z is defined as:
at the sample of Z is defined as: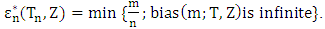 | (4) |
2.2. The Mean Square Errors (MSE)
- One of the performance criteria used to evaluate techniques (methods) of regression is the mean square errors which is given by
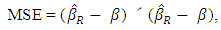 | (5) |
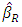 is a vector of robust parameter estimates and
is a vector of robust parameter estimates and 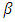 is the vector of the true model coefficients.
is the vector of the true model coefficients.2.3. The Bounded Influence
- Bounded influence in the X-space is the estimator’s resistance to being pulled towards the extreme observations in the X-space. Determining whether or not an estimator has a bounded influence is obtained by a study of the influence function. As defined by Seber (1977) influence function (IF) is a measure of the rate at which the estimator (T) responds to a small amount of contamination on x.Hampel (1968, 1974) defined the influence function
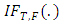 of the estimator T, at the underlying probability distribution, F, by
of the estimator T, at the underlying probability distribution, F, by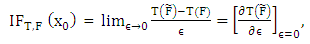 | (6) |
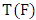 denotes the estimator of interest, expressed as a functional. The functional
denotes the estimator of interest, expressed as a functional. The functional 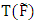 represent the estimator of interest under this altered c.d.f.. Thus, the influence function is actually a first derivative of an estimator, viewed as functional, and measures the influence of the point
represent the estimator of interest under this altered c.d.f.. Thus, the influence function is actually a first derivative of an estimator, viewed as functional, and measures the influence of the point 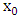 on the estimator T.
on the estimator T. 3. Robust Regression Methods
- Many robust methods have been proposed in literature to achieve high breakdown point, high efficiency or both. Therefore, robust regression methods can be divided into three broad categories: high-breakdown point estimators, high efficiency estimators and multiple property estimators (related classes of efficient high-breakdown estimators). Each category contains a class of estimators derived under similar conditions and with comparable theoretical statistical properties.
3.1. High-Breakdown Point Estimators
- High-breakdown point (HBP) regression estimators, also known as resistant estimators, can achieve up to a 50% breakdown point. They are useful for outliers detection and initial estimators. However, these estimators have low efficiency and unbounded influence. Due to this fact these estimators cannot be used as stand-alone estimators. The common estimators of this type are outlined in the following lines.The repeated median (RM) estimatorSiegel and Benson (1982) propose the repeated median (RM) estimator with a 50% breakdown point. For any p observations
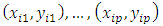 the repeated median estimator determines a unique parameter vector
the repeated median estimator determines a unique parameter vector 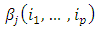 which is defined as
which is defined as 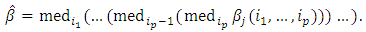 | (7) |
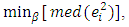 | (8) |
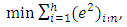 | (9) |
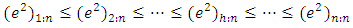 are the ordered squared residuals from the smallest to the largest. Rousseeuw and Leroy (1987) recommend using
are the ordered squared residuals from the smallest to the largest. Rousseeuw and Leroy (1987) recommend using 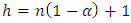 , where
, where 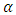 is the trimmed percentage.Rousseeuw and van Driessen (2006) propose that the LMS estimator should be replaced by the least trimmed squares (LTS) estimator for large data sets. The best robustness properties are achieved when h is approximately n/2. In this case the breakdown point attains 50% (Rousseeuw and Leroy, 1987). The breakdown point of the LMS and the LTS are equal if
is the trimmed percentage.Rousseeuw and van Driessen (2006) propose that the LMS estimator should be replaced by the least trimmed squares (LTS) estimator for large data sets. The best robustness properties are achieved when h is approximately n/2. In this case the breakdown point attains 50% (Rousseeuw and Leroy, 1987). The breakdown point of the LMS and the LTS are equal if 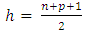 . The LTS has
. The LTS has 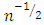 convergence rate and it converges at a rate similar to the M-estimators (Rousseeuw, 1984). Zaman et al. (2001) mention that although the LTS method is good at finding out the outliers, it may sometimes eliminate too many observations and this may not give the true regression relation about the data. The LTS estimator is regression, scale, and affine equivariant (Rousseeuw and Leroy, 1987). The LTS-estimator statistical efficiency is better than the LMS, with higher asymptotic Gaussian efficiency of 7.1% (Rousseeuw and van Driessen, 2006). The least Winsorized squares (LWS) estimatorAnother alternative method to the LS estimation procedure is the Winsorized regression which is applied by altering the data values based upon the magnitude of the residuals (Yale and Forsythe, 1976). The aim of Winsorization is to diminish the effect of contamination on the estimators by reducing the effect of outliers in the sample. The estimator is given as:
convergence rate and it converges at a rate similar to the M-estimators (Rousseeuw, 1984). Zaman et al. (2001) mention that although the LTS method is good at finding out the outliers, it may sometimes eliminate too many observations and this may not give the true regression relation about the data. The LTS estimator is regression, scale, and affine equivariant (Rousseeuw and Leroy, 1987). The LTS-estimator statistical efficiency is better than the LMS, with higher asymptotic Gaussian efficiency of 7.1% (Rousseeuw and van Driessen, 2006). The least Winsorized squares (LWS) estimatorAnother alternative method to the LS estimation procedure is the Winsorized regression which is applied by altering the data values based upon the magnitude of the residuals (Yale and Forsythe, 1976). The aim of Winsorization is to diminish the effect of contamination on the estimators by reducing the effect of outliers in the sample. The estimator is given as: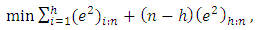 | (10) |
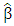 is defined by
is defined by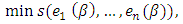 | (11) |
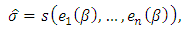 | (12) |
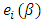 is the
is the 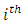 residual for candidate
residual for candidate 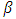 . The dispersions
. The dispersions 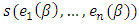 are defined as the solution of the equation:
are defined as the solution of the equation: 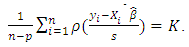 | (13) |
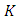 may be defined as
may be defined as 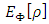 or
or 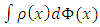 to ensure that the S-estimator of the residual scale
to ensure that the S-estimator of the residual scale 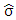 is consistent for
is consistent for 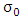 whenever it is assumed that the error distribution is normal with zero mean and
whenever it is assumed that the error distribution is normal with zero mean and 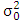 variance, where
variance, where 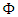 is the standard normal distribution. The function
is the standard normal distribution. The function 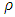 must satisfy the following conditions:1.
must satisfy the following conditions:1. 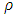 is symmetric, continuously differentiable and
is symmetric, continuously differentiable and 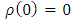 .2. There exists the constant
.2. There exists the constant 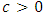 such that
such that 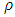 is strictly increasing on
is strictly increasing on 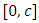 and constant on
and constant on 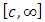 .The term S-estimator is used to describe the class of robust estimation because it is derived from a scale statistic in an implicit way. For
.The term S-estimator is used to describe the class of robust estimation because it is derived from a scale statistic in an implicit way. For 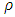 one often chooses the function
one often chooses the function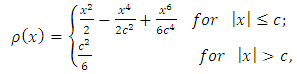 | (14) |
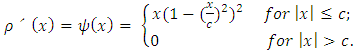 | (15) |
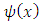 will always be zero for
will always be zero for 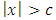 because of condition 2; such
because of condition 2; such 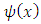 functions are usually called “re-descending” (Rousseeuw and Yohai, 1984). The breakdown point of the S-estimator can be 50%, assuming a condition is satisfied relating the constant
functions are usually called “re-descending” (Rousseeuw and Yohai, 1984). The breakdown point of the S-estimator can be 50%, assuming a condition is satisfied relating the constant 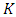 with the
with the 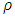 function such that
function such that 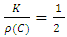 .The S-estimator is regression, scale, and affine equivariant. It is also asymptotically normal with
.The S-estimator is regression, scale, and affine equivariant. It is also asymptotically normal with 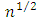 rate of convergence. Efficiency of the S-estimators can be increased at the expense of decreases in breakdown point (Rousseeuw and Leory, 1987). The S-estimator perform marginally better than the LMS and the LTS because the S-estimator can be used either as a high breakdown initial estimate with a high efficiency, or as a moderate breakdown (25%), moderate efficiency (75.9%) estimator (Rousseeuw and Leroy, 1987).
rate of convergence. Efficiency of the S-estimators can be increased at the expense of decreases in breakdown point (Rousseeuw and Leory, 1987). The S-estimator perform marginally better than the LMS and the LTS because the S-estimator can be used either as a high breakdown initial estimate with a high efficiency, or as a moderate breakdown (25%), moderate efficiency (75.9%) estimator (Rousseeuw and Leroy, 1987).3.2. Efficiency Estimators
- An efficient estimator provides parameter estimates close to those from an the OLS (the best linear unbiased estimator) which fits in an uncontaminated sample NID error terms. While the common efficient techniques are not high breakdown nor bounded-influence. The
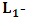 norm or Least Absolute Deviations (LAD) EstimatorBoscovich introduced the method of least absolute deviations (LAD) in 1757, almost 50 years before the method of least squares was discovered by Legendre in France around 1805 (Birkes and Dodge, 1993). The least absolute deviations (LAD), also known as least absolute errors (LAE), the least absolute value (LAV) or the
norm or Least Absolute Deviations (LAD) EstimatorBoscovich introduced the method of least absolute deviations (LAD) in 1757, almost 50 years before the method of least squares was discovered by Legendre in France around 1805 (Birkes and Dodge, 1993). The least absolute deviations (LAD), also known as least absolute errors (LAE), the least absolute value (LAV) or the 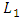 regression, is a mathematical optimization technique similar to the popular least squares technique in the attempts to find a function which closely approximates a set of data. (Cankaya, 2009).In the LAD method, the coefficients are chosen so that the sum of the absolute deviations of the residuals is minimized as:
regression, is a mathematical optimization technique similar to the popular least squares technique in the attempts to find a function which closely approximates a set of data. (Cankaya, 2009).In the LAD method, the coefficients are chosen so that the sum of the absolute deviations of the residuals is minimized as: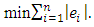 | (16) |
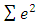 used in the LS estimation by another function of residuals,
used in the LS estimation by another function of residuals, 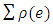 .
. 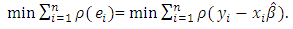 | (17) |
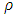 gives the contribution of each residual to the objective function. A reasonable
gives the contribution of each residual to the objective function. A reasonable 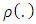 should posses the following properties:
should posses the following properties: 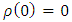 ;
; 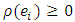 (non-negativity);
(non-negativity); 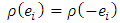 (symmetric);
(symmetric); 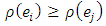 for
for 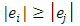 (monotonicity or non-decreasing function of
(monotonicity or non-decreasing function of 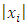 and
and 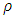 is continuous (
is continuous (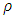 is differentiable). Because the M- estimator is not scale invariant the minimization problem is modified by dividing the
is differentiable). Because the M- estimator is not scale invariant the minimization problem is modified by dividing the 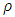 function by a robust estimate of scale s, so the formula becomes
function by a robust estimate of scale s, so the formula becomes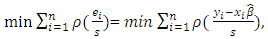 | (18) |
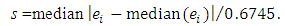 The least squares estimator is a special case of the
The least squares estimator is a special case of the 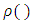 function where
function where 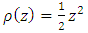 . The system of normal equations to solve this minimization problem is found by taking partial derivatives with respect to
. The system of normal equations to solve this minimization problem is found by taking partial derivatives with respect to 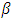 and setting them equal to 0, yielding
and setting them equal to 0, yielding 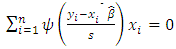 , where
, where 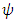 is the derivative of
is the derivative of 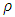 . In general, the
. In general, the 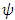 function is nonlinear and formula (18) must be solved by iterative methods. While several nonlinear optimization techniques could be employed, iteratively reweighted least squares (IRLS) is most widely used in practice and it is the only one considered for this research. The M-estimators can almost equivalently be described by a
function is nonlinear and formula (18) must be solved by iterative methods. While several nonlinear optimization techniques could be employed, iteratively reweighted least squares (IRLS) is most widely used in practice and it is the only one considered for this research. The M-estimators can almost equivalently be described by a 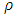 function (posing a minimization problem) or by its derivative, an
function (posing a minimization problem) or by its derivative, an 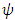 function (yielding a set of implicit equation(s)), which is proportional to the influence function. Robust regression procedures can be classified by the behavior of their
function (yielding a set of implicit equation(s)), which is proportional to the influence function. Robust regression procedures can be classified by the behavior of their 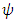 function. The key to M- estimation is finding a good
function. The key to M- estimation is finding a good 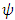 function.Although there are many specific proposals for the
function.Although there are many specific proposals for the 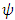 -function, they can all be grouped into one of two classes: monotone and redescending. A monotone
-function, they can all be grouped into one of two classes: monotone and redescending. A monotone 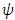 -function (e.g. Huber’s estimator) does not weight large outliers as much as least squares. The
-function (e.g. Huber’s estimator) does not weight large outliers as much as least squares. The 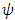 -function of Huber estimator is constant-linearly increasing-constant. A re-descending
-function of Huber estimator is constant-linearly increasing-constant. A re-descending 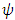 -function (e.g. Hample’s and. Ramsay’s) increases the weight assigned to an outlier until a specified distance and then decreases the weight to 0 as the outlying distance gets larger. Montgomery et al. (2012) introduce two types of a re-descending
-function (e.g. Hample’s and. Ramsay’s) increases the weight assigned to an outlier until a specified distance and then decreases the weight to 0 as the outlying distance gets larger. Montgomery et al. (2012) introduce two types of a re-descending 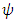 -function: soft re-descender and hard re-descender. Alamgir et al. (2013) propose a new re-descending M-estimator, called Alamgir re-descending M-estimator abbreviated as (ALARM). The
-function: soft re-descender and hard re-descender. Alamgir et al. (2013) propose a new re-descending M-estimator, called Alamgir re-descending M-estimator abbreviated as (ALARM). The 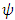 -function of ALARM estimator is defined as
-function of ALARM estimator is defined as 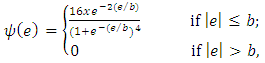 | (19) |
3.3. Multiple Property Estimators (Related classes of efficient high breakdown estimators)
- The discussion of robust estimators has clearly shown that no estimator has all the desirable properties. The multiple property estimators have been proposed to combine several properties into a single estimator.The multi-stage (MM) estimator Yohai (1987) introduces the multi-stage estimator (MM-estimator), which combines high breakdown with high efficiency. The MM-estimator is obtained using a three-stage procedure. In the first stage, an initial consistent estimate
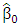 with high breakdown point but possibly low normal efficiency is obtained. Yohai (1987) suggests using the S-estimator for this stage. In the second stage, a robust M-estimator of scale parameter
with high breakdown point but possibly low normal efficiency is obtained. Yohai (1987) suggests using the S-estimator for this stage. In the second stage, a robust M-estimator of scale parameter 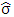 of the residuals based on the initial value is obtained. In the third stage, an M-estimator
of the residuals based on the initial value is obtained. In the third stage, an M-estimator 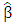 starting at
starting at 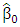 is obtained.In practice, the LMS or S-estimate with Huber or bi-square functions is typically used as the initial estimate
is obtained.In practice, the LMS or S-estimate with Huber or bi-square functions is typically used as the initial estimate 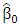 . Let
. Let 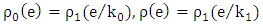 and assume that each of the
and assume that each of the 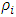 functions is bounded, i = 0 and 1. The scale estimate
functions is bounded, i = 0 and 1. The scale estimate 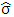 satisfies the following equation:
satisfies the following equation: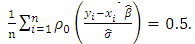 | (20) |
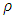 function is biweight, then
function is biweight, then 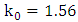 ensures that the estimator has the asymptotic BP = 0.5. Although the MM-estimators have a high breakdown and are efficient, they do not necessarily have bounded influence, meaning that they may not perform especially well in the presence of high leverage points.The
ensures that the estimator has the asymptotic BP = 0.5. Although the MM-estimators have a high breakdown and are efficient, they do not necessarily have bounded influence, meaning that they may not perform especially well in the presence of high leverage points.The 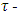 estimatorYohai and Zamar (1988) introduce a new class of robust estimators; the
estimatorYohai and Zamar (1988) introduce a new class of robust estimators; the 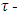 estimator. The
estimator. The 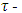 estimator has, simultaneously, the following properties: i) they are qualitatively robust, ii) their breakdown point is 0.5, and iii) they are highly efficient for regression models with normal errors. In the
estimator has, simultaneously, the following properties: i) they are qualitatively robust, ii) their breakdown point is 0.5, and iii) they are highly efficient for regression models with normal errors. In the 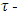 estimator, the coefficients are chosen so that a new estimator of the scale of the residuals is minimized as:
estimator, the coefficients are chosen so that a new estimator of the scale of the residuals is minimized as: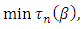 | (21) |
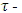 scale
scale 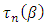 is given by
is given by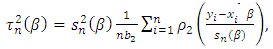 | (22) |
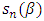 is the M-estimator of scale that satisfies the solution
is the M-estimator of scale that satisfies the solution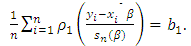 | (23) |
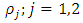 are assumed to be symmetric, continuously differentiable bounded, strictly increasing on
are assumed to be symmetric, continuously differentiable bounded, strictly increasing on 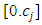 , and constant on
, and constant on 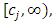 with
with 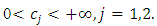 The parameters
The parameters 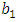 and
and 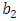 are tuned to obtain consistency for the scale at the normal error model:
are tuned to obtain consistency for the scale at the normal error model: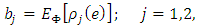 | (24) |
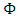 is the standard normal distribution. Like the MM-estimators, the
is the standard normal distribution. Like the MM-estimators, the 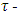 estimators have the breakdown point of an S-estimator based on the loss function
estimators have the breakdown point of an S-estimator based on the loss function 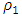 , while its efficiency is determined by the function
, while its efficiency is determined by the function 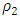 which is used in Eq. (18) (Yohai and Zamar, 1988). The
which is used in Eq. (18) (Yohai and Zamar, 1988). The 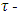 estimators possess theoretical advantages over the MM-estimators: they are associated with a robust and efficient scale estimate (Barrera et al., 2008).The robust and efficiency weighted least squares (REWLSE) estimator Gervini and Yohai (2002) introduce a new class of estimators that simultaneously attain the maximum breakdown point and full asymptotic efficiency under normal errors. They weight the least squares estimators with adaptively computed weights using the empirical distribution of the residuals of an initial robust estimator. Consider a pair of initial robust estimators of parameters and scale
estimators possess theoretical advantages over the MM-estimators: they are associated with a robust and efficient scale estimate (Barrera et al., 2008).The robust and efficiency weighted least squares (REWLSE) estimator Gervini and Yohai (2002) introduce a new class of estimators that simultaneously attain the maximum breakdown point and full asymptotic efficiency under normal errors. They weight the least squares estimators with adaptively computed weights using the empirical distribution of the residuals of an initial robust estimator. Consider a pair of initial robust estimators of parameters and scale 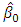 and
and 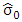 respectively. If
respectively. If 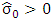 , the standardized residuals are defined as:
, the standardized residuals are defined as: 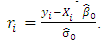 | (25) |
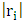 would suggest that
would suggest that 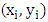 is an outlier. In order to maintain the breakdown point value of the initial estimator and to have a high efficiency, they proposed the use of an adapted cut-off value,
is an outlier. In order to maintain the breakdown point value of the initial estimator and to have a high efficiency, they proposed the use of an adapted cut-off value, 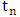 , as
, as 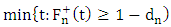 where
where 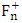 is the empirical cumulative distribution function of the standardized absolute residuals and
is the empirical cumulative distribution function of the standardized absolute residuals and 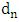 is the measure of the proportion of the outliers in the sample. The values of
is the measure of the proportion of the outliers in the sample. The values of 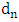 are given as
are given as 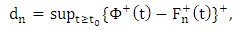 | (26) |
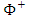 denotes the normal cumulative distribution of the random errors,
denotes the normal cumulative distribution of the random errors, 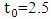 is the initial cut-off value and
is the initial cut-off value and 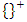 denotes the positive part between
denotes the positive part between 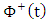 and
and 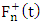 . The form of the weights, W, and the REWLS estimator,
. The form of the weights, W, and the REWLS estimator, 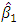 , are defined as
, are defined as 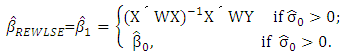 | (27) |
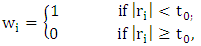 | (28) |
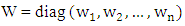 .Note that with these weights,
.Note that with these weights, 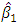 estimator maintains the same breakdown point value of the initial estimator
estimator maintains the same breakdown point value of the initial estimator 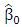 . Touati et al. (2010) modify the robust estimator of Gervini and Yohai (2002) and labeled it as the Robust and Efficient Weighted Least Squares Estimator (REWLSE), which simultaneously combines high statistical efficiency and high breakdown point by replacing the weight function by a new weight function.
. Touati et al. (2010) modify the robust estimator of Gervini and Yohai (2002) and labeled it as the Robust and Efficient Weighted Least Squares Estimator (REWLSE), which simultaneously combines high statistical efficiency and high breakdown point by replacing the weight function by a new weight function. 4. Simulation Study
- A simulation study is conducted to compare different methods of estimation. These methods are: 1. The ordinary least squares estimator (OLS); 2. The least median squares estimator (LMS); 3. The least trimmed squares estimator (LTS); 4. The S-estimator (S); 5. The least absolute value estimator (LAV); 6. The M-estimator; the Huber's M-estimator (MHuber) with b=1.345;7. The Tukey's M-estimator (MTukey) with k1 = 4.685; and 8. The Hampel's M-estimators (MHampel) with a=1.7, b=3.4, and c=8.5; 9. The MM-estimators (MM) using bi-square weights and k1 =4.685, and 10. The robust and efficiency weighted least squares estimator (RWLSE).The comparison criteria are the mean squares error (MSE), total mean squares error (TMSE), absolute bias (AB) and total absolute bias (TAB) of the estimates of the regression coefficients. The data are generated according to the multiple linear regression model:
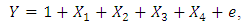 where
where 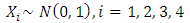 and the
and the 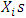 are independent. The true value of the regression parameters are all equal one;
are independent. The true value of the regression parameters are all equal one; 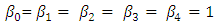 . The data simulation is repeated 5000 times to obtain 5000 independent samples of Y and X of a given size n. The used sample sizes are n = 30 and n = 100. Comparisons of the properties of some robust methods are based on outliers in the y-direction (response direction). In order to cover the effects of various situations on the regression coefficients, seven scenarios of the density function of the errors (e) have been used. These scenarios are:Scenario I: e ~ N (0, 1); the standard normal distribution.Scenario II: e ~ t-distribution with df = 1; the t-distribution with degrees of freedom 1 (Cauchy distribution).Scenario III: e ~ t-distribution with df = 5; the t-distribution with degrees of freedom 5.Scenario IV: e ~ slash (0, 1); the slash distribution denoted by N (0, 1)/U (0, 1).Scenario V: e ~ N (0, 1) with 20% outliers in y-direction generated from N (0, 10).Scenario VI: e ~ N (0, 1) with 40% outliers in y-direction generated from N (0, 10).Scenario VII: e ~ 0.80*N(0,1) + 0.20*N(0,10); contaminated mixture of normal.For each scenario the mean square error (MSE), the total mean square error (TMSE), the absolute bias (AB) and the total absolute bias (TAB) have been obtained using the OLS-estimator, the LTS-estimator, the LMS-estimator, the S-estimator, the LAV-estimator, the M-estimators, the MM-estimator and the REWLSE. The results are not displayed for the sake of parsimony, however the following conclusions can be drawn.Scenario I: the OLS estimate achieves the best performance. The decline in the performance of the other estimates compared to the performance of the OLS-estimate is the price paid by the methods due to the existence of outliers. The M-estimate, the MM-estimate, the REWLSE, and the LAV-estimate have better performance comparable to the estimates, as well as they provide a performance equal to the performance of the OLS-estimate. The performance of the high breakdown point estimates are poor compared to the OLS-estimate, the M-estimate, the LAV-estimate, the MM-estimate, or the REWLSE. As the sample size increases, the value of both the TMSE and the TAB decrease.Scenario II: The OLS estimates give the worst result with regard to the TAB and the TMSE. The MTukey -estimate, the MM-estimate, the LAV-estimate, the REWLSE and the S-estimate tend to give lower TMSE and TAB values than other robust estimators. The LMS estimate and the LTS estimate have higher TMSE and TAB values than other robust estimators.Scenario III: The OLS estimates give the highest TMSE and TAB values. The MHuber estimates and the MM-estimates tend to give smaller TMSE and TAB values than the others. The LMS-estimates, the LTS estimates and the S-estimates have higher TMSE and TAB values. If the errors follow the t-distribution, the TMSE and TAB of each estimate decreases as the degrees of freedom (df) increases.Scenario IV: The OLS estimates have the largest TMSE and TAB values. The MTukey estimate and the MM-estimates tend to give smaller TMSE and TAB than others. The LMS estimates and the LTS-estimates tend to give a higher TMSE and TAB than others.Scenario V: It is noticed that when the data contain 20% outliers from the N (0, 10) in the y-direction, the OLS-estimate has the largest TMSE and TAB. The REWLSE, the MTukey estimator and the MM-estimator, tend to give a lower TMSE and TAB than others. Scenario VI: We can see that when the data contain 40% outliers from N (0, 10) in the y-direction, the OLS estimator decline in performance, while most of the other estimators are have good performances depending on the percentage and direction of contaminations. In general, the TMSE and TAB values decrease when the sample sizes increase while the TMSE and TAB values increase as the proportion of contaminations "outliers" increases.Scenario VII: The OLS estimator has the largest TMSE and TAB values. The REWLSE, the MTukey estimator and the MM-estimator tend to give lower TMSE and TAB values than other robust estimators. The LMS-estimator and the LTS estimator achieve higher TMSE and TAB values than other robust estimators.
. The data simulation is repeated 5000 times to obtain 5000 independent samples of Y and X of a given size n. The used sample sizes are n = 30 and n = 100. Comparisons of the properties of some robust methods are based on outliers in the y-direction (response direction). In order to cover the effects of various situations on the regression coefficients, seven scenarios of the density function of the errors (e) have been used. These scenarios are:Scenario I: e ~ N (0, 1); the standard normal distribution.Scenario II: e ~ t-distribution with df = 1; the t-distribution with degrees of freedom 1 (Cauchy distribution).Scenario III: e ~ t-distribution with df = 5; the t-distribution with degrees of freedom 5.Scenario IV: e ~ slash (0, 1); the slash distribution denoted by N (0, 1)/U (0, 1).Scenario V: e ~ N (0, 1) with 20% outliers in y-direction generated from N (0, 10).Scenario VI: e ~ N (0, 1) with 40% outliers in y-direction generated from N (0, 10).Scenario VII: e ~ 0.80*N(0,1) + 0.20*N(0,10); contaminated mixture of normal.For each scenario the mean square error (MSE), the total mean square error (TMSE), the absolute bias (AB) and the total absolute bias (TAB) have been obtained using the OLS-estimator, the LTS-estimator, the LMS-estimator, the S-estimator, the LAV-estimator, the M-estimators, the MM-estimator and the REWLSE. The results are not displayed for the sake of parsimony, however the following conclusions can be drawn.Scenario I: the OLS estimate achieves the best performance. The decline in the performance of the other estimates compared to the performance of the OLS-estimate is the price paid by the methods due to the existence of outliers. The M-estimate, the MM-estimate, the REWLSE, and the LAV-estimate have better performance comparable to the estimates, as well as they provide a performance equal to the performance of the OLS-estimate. The performance of the high breakdown point estimates are poor compared to the OLS-estimate, the M-estimate, the LAV-estimate, the MM-estimate, or the REWLSE. As the sample size increases, the value of both the TMSE and the TAB decrease.Scenario II: The OLS estimates give the worst result with regard to the TAB and the TMSE. The MTukey -estimate, the MM-estimate, the LAV-estimate, the REWLSE and the S-estimate tend to give lower TMSE and TAB values than other robust estimators. The LMS estimate and the LTS estimate have higher TMSE and TAB values than other robust estimators.Scenario III: The OLS estimates give the highest TMSE and TAB values. The MHuber estimates and the MM-estimates tend to give smaller TMSE and TAB values than the others. The LMS-estimates, the LTS estimates and the S-estimates have higher TMSE and TAB values. If the errors follow the t-distribution, the TMSE and TAB of each estimate decreases as the degrees of freedom (df) increases.Scenario IV: The OLS estimates have the largest TMSE and TAB values. The MTukey estimate and the MM-estimates tend to give smaller TMSE and TAB than others. The LMS estimates and the LTS-estimates tend to give a higher TMSE and TAB than others.Scenario V: It is noticed that when the data contain 20% outliers from the N (0, 10) in the y-direction, the OLS-estimate has the largest TMSE and TAB. The REWLSE, the MTukey estimator and the MM-estimator, tend to give a lower TMSE and TAB than others. Scenario VI: We can see that when the data contain 40% outliers from N (0, 10) in the y-direction, the OLS estimator decline in performance, while most of the other estimators are have good performances depending on the percentage and direction of contaminations. In general, the TMSE and TAB values decrease when the sample sizes increase while the TMSE and TAB values increase as the proportion of contaminations "outliers" increases.Scenario VII: The OLS estimator has the largest TMSE and TAB values. The REWLSE, the MTukey estimator and the MM-estimator tend to give lower TMSE and TAB values than other robust estimators. The LMS-estimator and the LTS estimator achieve higher TMSE and TAB values than other robust estimators.5. Application
- A real data set (growth data) given by De Long and Summers (1991) is used. The aim is to evaluate the performance of various estimators. This data set measures the national growth of 61 countries from all over the world from the years 1960 to 1985. The data set contains many variables. They are the GDP growth per worker (GDP) which the response variable, the labor force growth (LFG), the relative GDP gap (GAP), the equipment investment (EQP), and non-equipment investment (NEQ). The main claim is that there is a strong and clear relationship between equipment investment and productivity growth. The regression equation they used:
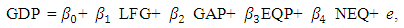 | (29) |
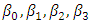 and
and 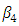 are regression parameters. Zaman et al. (2001) note that the growth study of De Long and Summers suffers from the problem of outliers in the y-direction (response direction). Zaman et al. (2001) use robust regression techniques and show that the 60th country in the data is an outlier. We compare the OLS estimator, the LMS-estimator, the LTS-estimator, the S-estimator, the LAV-estimator, the Huber's M-estimator, the Tukey's M-estimator, the Hampel's M-estimator, the MM-estimator and the REWLSE by using bias and Mean square error values.The results of the estimated regression parameters for the ten methods with all data points (complete data) are presented in Table (1). Also, results of the OLS method are displayed for the 60 data point (subset) ignoring the outlier; Zambia. The value of the bias and the MSE for the OLS estimate change from 0.1261 and 0.0302 (complete data) to 0 and 0.0139 (subset data). Thus, it is clear that the outlier strongly influences the OLS estimate. High-breakdown estimates (the LTS estimate, the LMS estimate, and the S-estimate) have low performance when the contamination is in the direction of the response variable only. The LAV estimate also has poor performance in this real data example.Depending on the bias we can conclude that the Hampel's M-estimate and the REWLSE perform better than the others. When the MSE is considered, it indicates that the Hampel's M-estimate and the Huber's M-estimate perform better than the others.
are regression parameters. Zaman et al. (2001) note that the growth study of De Long and Summers suffers from the problem of outliers in the y-direction (response direction). Zaman et al. (2001) use robust regression techniques and show that the 60th country in the data is an outlier. We compare the OLS estimator, the LMS-estimator, the LTS-estimator, the S-estimator, the LAV-estimator, the Huber's M-estimator, the Tukey's M-estimator, the Hampel's M-estimator, the MM-estimator and the REWLSE by using bias and Mean square error values.The results of the estimated regression parameters for the ten methods with all data points (complete data) are presented in Table (1). Also, results of the OLS method are displayed for the 60 data point (subset) ignoring the outlier; Zambia. The value of the bias and the MSE for the OLS estimate change from 0.1261 and 0.0302 (complete data) to 0 and 0.0139 (subset data). Thus, it is clear that the outlier strongly influences the OLS estimate. High-breakdown estimates (the LTS estimate, the LMS estimate, and the S-estimate) have low performance when the contamination is in the direction of the response variable only. The LAV estimate also has poor performance in this real data example.Depending on the bias we can conclude that the Hampel's M-estimate and the REWLSE perform better than the others. When the MSE is considered, it indicates that the Hampel's M-estimate and the Huber's M-estimate perform better than the others.
|
6. Conclusions
- The mean square errors (MSE) and the bias are of interest in regression analysis in presence of outliers. The performances of different estimates are studied using a simulation study and a real data for outliers in y-direction. The estimates of the regression coefficients using nine methods are compared with the ordinary least-squares. Depending on the simulation study the Tukey's M-estimator give a lowest TAB and TMSE values than others, for all sample sizes and when the contamination is in the y-direction. For the real data the Hampel's M-estimators gives lower bias and MSE values than others when the contamination is in the y-direction. The work can be extended in future to handle outliers in x-direction; good leverage points. Another possible future direction is to compare robust methods when outliers are in both y-direction and x-direction (bad leverage points).
ACKNOWLEDGEMENTS
- The authors would like to thank referees and editors for their help and constructive comments that improve significantly the manuscript.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML