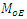Mukesh K. Sharma, Sarbjit S. Brar, Harinder Kaur
Department of Statistics, Punjabi University, Patiala, India
Correspondence to: Sarbjit S. Brar, Department of Statistics, Punjabi University, Patiala, India.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
In this paper, a new parametric relationship for population mode (Mo) has been established after involving an unknown constant ‘k’. The optimum value of ‘k’ is obtained by minimizing the MSE, upto terms of order n-1, of consistent estimator of mode 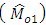 . Further, for bivariate populations, the ratio-type and product type estimators of Mo have been proposed. At optimum value of ‘k’, the expressions of biases and MSE’s of proposed estimators have been obtained and compared with each other. Also, the conditions for ratio-type and product-type estimators of Mo have been found out for which these estimators are more efficient than
. Further, for bivariate populations, the ratio-type and product type estimators of Mo have been proposed. At optimum value of ‘k’, the expressions of biases and MSE’s of proposed estimators have been obtained and compared with each other. Also, the conditions for ratio-type and product-type estimators of Mo have been found out for which these estimators are more efficient than 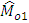 . The authenticity of new parametric relation of mode has also been verified for some theoretical univariate and bivariate distributions. Empirically, the values of minimum MSE’s of proposed estimators have been obtained for some specific populations and also the authenticity of the relationship has been verified for these populations.
. The authenticity of new parametric relation of mode has also been verified for some theoretical univariate and bivariate distributions. Empirically, the values of minimum MSE’s of proposed estimators have been obtained for some specific populations and also the authenticity of the relationship has been verified for these populations.
Keywords:
Estimation, Mode, Skewness, Coefficients of skewness, Univariate and bivariate normal distributions, Poisson distribution, Chi-square distribution, Ratio estimator, Product estimator, Bias, Mean squared error
Cite this paper: Mukesh K. Sharma, Sarbjit S. Brar, Harinder Kaur, Estimators of Population Mode Using New Parametric Relationship for Mode, International Journal of Probability and Statistics , Vol. 5 No. 1, 2016, pp. 18-24. doi: 10.5923/j.ijps.20160501.03.
1. Introduction
In sample surveys, researchers generally estimate the population mean as a measure of location. Many estimators like mean per unit estimator, usual ratio estimator, usual product estimator etc are available in literature to estimate population mean under SRS. These estimators are used because mean is generally more stable measure of location as compared to the others. But, in some situations, median and mode are also more important than the mean. Median is often used as the measure of location for skewed distribution because it is insensitive to extreme values. In this direction, Gross (1980) for the first time proposed sample median as a consistent estimator of population median. Further, Kuk and Mak (1989) suggested ratio estimator for population median. Moreover, a number of estimators for population median have been proposed by the researchers in last two decades. Mode is another measure of location which has been neglected so far in sample surveys. But in case of unimodal distribution, unique mode represents most likely value of the population. Due to this property, mode sometimes becomes more appropriate measure of location as compared to mean and median. It is especially useful in finding the most popular size in studies related to marketing, trade and industry etc. For example, in the manufacturing of shoes or ready-made garments, one is interested to know which size of shoe or garment is most popular. Also, in the medical field, a medical researcher would normally be more interested in the most probable value of the heart rate than in the total of heart rate measurements divided by the number of measurements.In literature, very few researchers paid the attention for estimation of population mode, all using different techniques. Initially, Parzan (1962) estimated the mode first estimating the probability density function of the population and then mode. Bickel (2010) estimated the mode first transforming the data to the approximate normal and then estimated the mean which is equals to the mode for the transformed data. Chen et al. (2014) defined the sequence of (k, ρ)-modes where a point is (k, ρ)-mode iff its probability density is higher than all the points within distance k under a distance metric ρ. Recently Sedory and Singh (2014), first estimated the median using technique of Kuk and Mak (1989) then using the empirical relationship for mean, median and mode, defined the estimator of mode.In this paper, we develop the new simple and efficient technique of estimating the population mode by using well known measures of skewness (Karl Pearson and based upon central moments). Here we first establish the new parametric relationship for population mode involving population parameters and an unknown constant 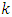 . By proposing the conventional consistent estimator
. By proposing the conventional consistent estimator 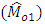 of population mode
of population mode 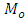 , we find the approximate value of
, we find the approximate value of 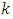 by minimizing the
by minimizing the 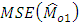 , upto terms of order
, upto terms of order 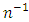 . Further, for the bivariate
. Further, for the bivariate  -population, we have also proposed ratio-type
-population, we have also proposed ratio-type 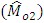 and product-type
and product-type 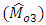 estimators of
estimators of 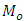 . We have checked authenticity of the new parametric relationship for
. We have checked authenticity of the new parametric relationship for 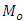 . Upto terms of order
. Upto terms of order 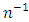 , the optimum biases and minimum MSE's of the proposed estimators are obtained and compared with each other. Empirically, we have also checked the authenticity of the parametric relationship by showing that for the given population established new parametric relation is more accurate than the empirical relationship for mean, median and mode, and obtained the values of minimum MSE's of the proposed estimators.
, the optimum biases and minimum MSE's of the proposed estimators are obtained and compared with each other. Empirically, we have also checked the authenticity of the parametric relationship by showing that for the given population established new parametric relation is more accurate than the empirical relationship for mean, median and mode, and obtained the values of minimum MSE's of the proposed estimators.
2. Notations and Expectations
Suppose a simple random sample of size 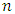 is drawn from a finite population of size
is drawn from a finite population of size  without replacement and observations on both study variables
without replacement and observations on both study variables 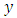 and auxiliary variable
and auxiliary variable 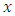 are taken. Let the values of variable
are taken. Let the values of variable 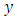 and
and 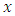 be denoted by
be denoted by  and
and 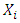 respectively on the
respectively on the  unit of the population
unit of the population 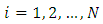 and the corresponding small letters
and the corresponding small letters 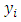 and
and  denote the values corresponding to the
denote the values corresponding to the  unit in the sample. Taking,
unit in the sample. Taking,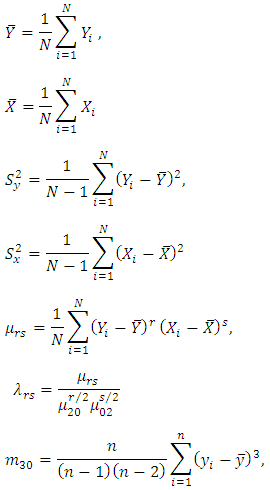 Obviously
Obviously Defining,
Defining,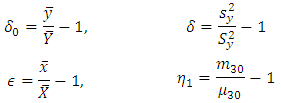 For the sake of simplicity, assume that
For the sake of simplicity, assume that 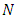 is large enough as compares to
is large enough as compares to 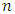 so that finite population correction (fpc) terms are ignored throughout.For the given SRSWOR, we have the following expectations,
so that finite population correction (fpc) terms are ignored throughout.For the given SRSWOR, we have the following expectations,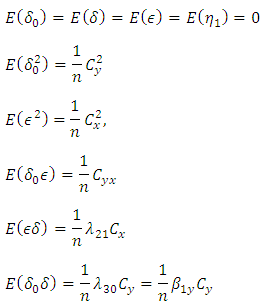 and up to terms of order
and up to terms of order 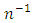
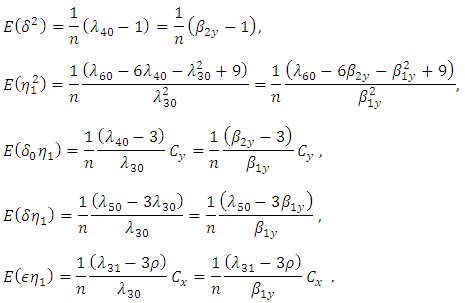
3. Proposed Estimators and Their Biases and MSE’s
Karl Pearson coefficient of skewness and coefficient of skewness based upon moments are respectively given by | (3.1) |
and 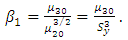 | (3.2) |
Without loss of generality, we can take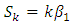 where
where 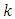 is unknown constant to be determined.Therefore,
is unknown constant to be determined.Therefore,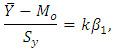 That implies
That implies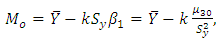 | (3.3) |
which is a new parametric functional relationship for population mode for any population.We here propose three estimators of 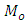 under the three different situations as
under the three different situations as 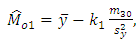 | (3.4) |
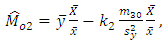 | (3.5) |
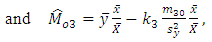 | (3.6) |
where 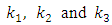 are unknown constants, whose values are determined by minimizing the MSE’s of respective estimators
are unknown constants, whose values are determined by minimizing the MSE’s of respective estimators 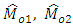 and
and 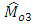 . Here the estimator
. Here the estimator 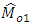 uses no information on auxiliary variable
uses no information on auxiliary variable 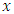 which is highly correlated with
which is highly correlated with 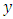 , whereas
, whereas 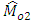 and
and 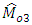 uses the known information of
uses the known information of 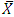 , which are of ratio and product type estimators respectively.To find the biases and MSE’s of
, which are of ratio and product type estimators respectively.To find the biases and MSE’s of 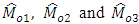 , we expand them in terms of
, we expand them in terms of 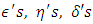 and then taking the expectations as given in section 2, upto terms of order
and then taking the expectations as given in section 2, upto terms of order 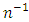 , we get,
, we get,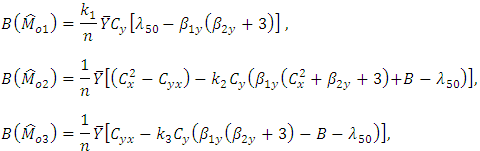 and
and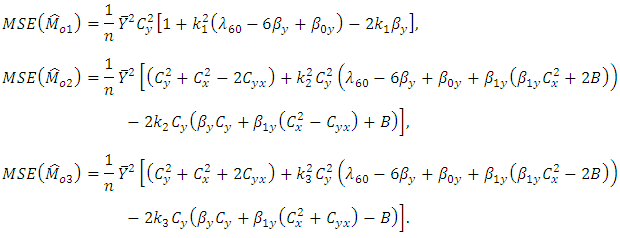 The above MSE’s of
The above MSE’s of 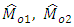 and
and 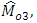 are minimised for
are minimised for 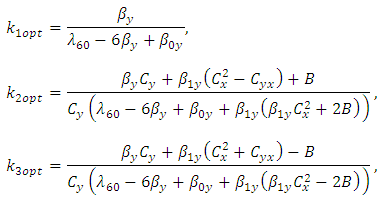 and the Biases and minimum MSE’s are given as,
and the Biases and minimum MSE’s are given as,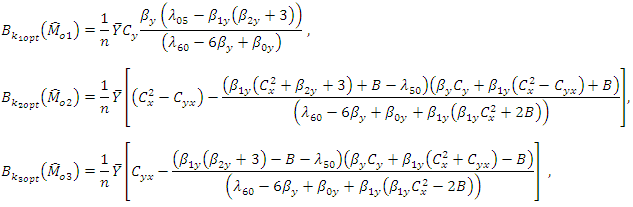 and
and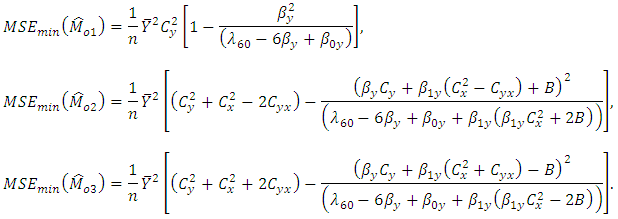 Where,
Where,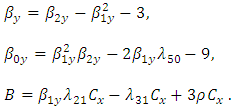 Srivastava and Jhajj (1983) have shown that if we replace the parameters involved in the optimum value of the unknown constant by their consistent estimators then upto terms of order
Srivastava and Jhajj (1983) have shown that if we replace the parameters involved in the optimum value of the unknown constant by their consistent estimators then upto terms of order 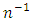 , the MSE remains the same. Using this, if we replace the parameters involved in
, the MSE remains the same. Using this, if we replace the parameters involved in  and
and  by their consistent estimators then their estimators say become
by their consistent estimators then their estimators say become  and
and 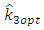 respectively. Then our estimators reduce to
respectively. Then our estimators reduce to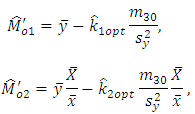 and
and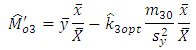 Among the three estimators, the most efficient is
Among the three estimators, the most efficient is 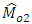 iff
iff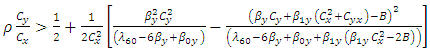 | (3.7) |
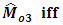
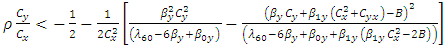 | (3.8) |
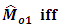
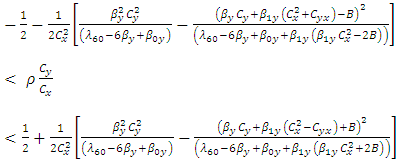 | (3.9) |
Above conditions (3.7), (3.8) and (3.9) represent the optimum situations for 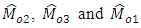 respectively.
respectively.
4. Authenticity of Parametric Functional Relationship for 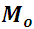
The new parametric functional relationship for 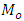 is
is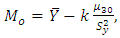 | (4.1) |
where 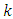 is an unknown constant whose value is to be determined for the given population. If
is an unknown constant whose value is to be determined for the given population. If  is optimised by minimising the MSE of conventional consistent estimator
is optimised by minimising the MSE of conventional consistent estimator 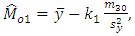 (up to the order
(up to the order 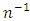 ), the above functional relationship reduced to
), the above functional relationship reduced to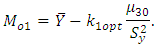 As in sampling theory, the nature of the population under study is not known. To see the authenticity of approximate parametric relation
As in sampling theory, the nature of the population under study is not known. To see the authenticity of approximate parametric relation  , we have to consider the population of particular nature. The approximation is due to the fact that we are using the optimum value
, we have to consider the population of particular nature. The approximation is due to the fact that we are using the optimum value 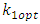 of unknown constant
of unknown constant 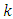 , not the exact value. When the population is univariate, one can check the relationship for
, not the exact value. When the population is univariate, one can check the relationship for 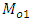 easily. But, if the population is
easily. But, if the population is 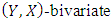 , then it is very difficult check this relationship because for this we need the bivariate moments and marginal distributions of
, then it is very difficult check this relationship because for this we need the bivariate moments and marginal distributions of  and
and 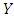 . No doubt, this relationship can be checked by researchers in inference. So this problem is open for researchers involved in statistical Inference. But in sampling theory, for the known value of
. No doubt, this relationship can be checked by researchers in inference. So this problem is open for researchers involved in statistical Inference. But in sampling theory, for the known value of 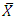 we can increase the precision of the estimators
we can increase the precision of the estimators 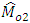 and
and 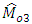 . Following particular populations are considered to check the authenticity of
. Following particular populations are considered to check the authenticity of 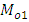 :(i) Population is Normal:(a) Let
:(i) Population is Normal:(a) Let 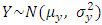 , then we know
, then we know 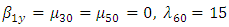 and
and 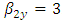 . Using these values, we get,
. Using these values, we get,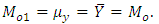 Because
Because 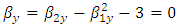 in numerator of
in numerator of 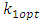 and also,
and also, 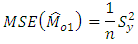 which is variance of
which is variance of 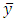 when fpc are ignored. So
when fpc are ignored. So 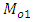 is verified for univariate normal population.(b) Let
is verified for univariate normal population.(b) Let 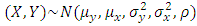 , then we know
, then we know 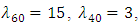
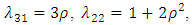
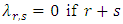 is odd. Also,
is odd. Also, 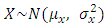 and
and 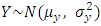 . Using these values, we get,
. Using these values, we get,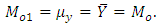 The expressions for MSE’s are
The expressions for MSE’s are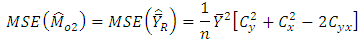 and
and 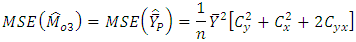 So,
So, 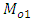 is verified for bivariate normal population and upto terms of order
is verified for bivariate normal population and upto terms of order 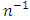 , we have
, we have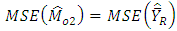 and
and 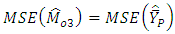 So the relation
So the relation 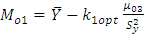 is true for univariate as well as for bivariate normal populations and in general true for all symmetrical populations.(ii) Population is Poisson: Let
is true for univariate as well as for bivariate normal populations and in general true for all symmetrical populations.(ii) Population is Poisson: Let 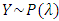 . We then have
. We then have 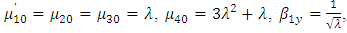 so Poisson distribution is always positively skewed,
so Poisson distribution is always positively skewed, 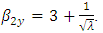 Using these values, we get
Using these values, we get 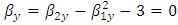 , so
, so 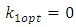 and
and 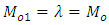 if
if 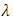 is not integer and
is not integer and 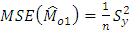 .Hence this relation is also verified for positively skewed distributions.(iii) Population is
.Hence this relation is also verified for positively skewed distributions.(iii) Population is  : Let
: Let 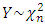 , then we have
, then we have 
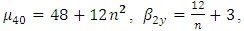
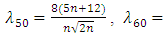
 (positively skewed).(iv) Particular cases:
(positively skewed).(iv) Particular cases: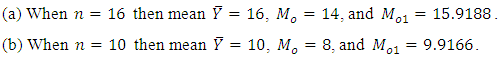 Hence we conclude that the new functional relationship for
Hence we conclude that the new functional relationship for 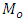 is always true for symmetric populations whether univariate or bivariate. In general, it is approximately true for all populations, whereas for the skewed distribution, it is approximately true. The approximation is due to the fact that we use the optimum value of
is always true for symmetric populations whether univariate or bivariate. In general, it is approximately true for all populations, whereas for the skewed distribution, it is approximately true. The approximation is due to the fact that we use the optimum value of 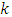 not the exact one.
not the exact one.
5. Numerical Illustrations
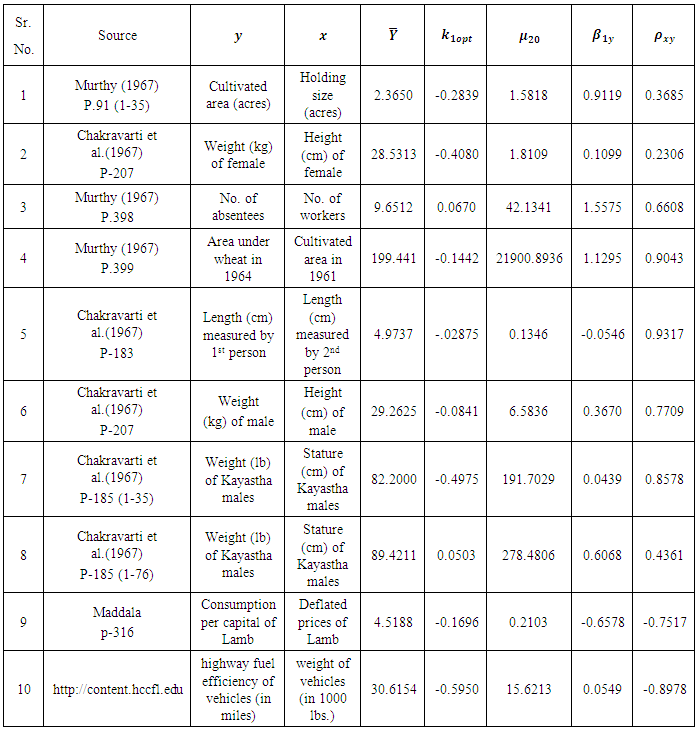
To illustrate the result numerically, we have made computations for 10 populations taken from literature by using Microsoft Excel 2010.The source of the populations, the nature of the variables, the values of 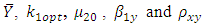 are listed in Table 1. In Table 2, we have given the true value of population Mode
are listed in Table 1. In Table 2, we have given the true value of population Mode 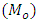 , the values of the population mode obtained by using the new parametric functional relationship of
, the values of the population mode obtained by using the new parametric functional relationship of 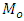 and values of population mode
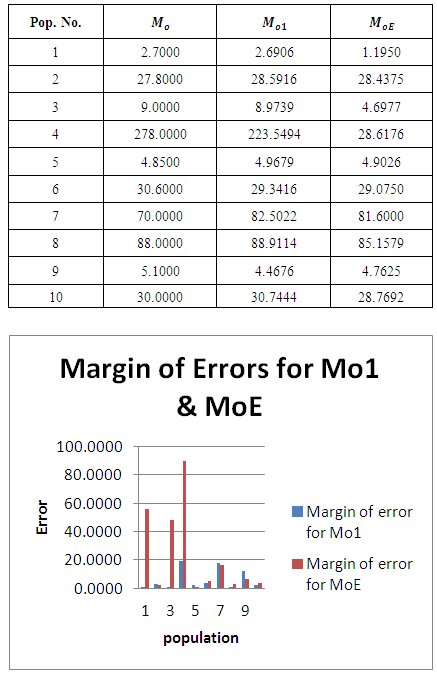
and values of population mode  obtained by using the empirical relationship ‘Mode =3 Median- 2 mean’ for different populations.The efficiencies of proposed estimators are given in Table 3.From Table 2, we observe that the values obtained from the new parametric functional relationship for mode i.e.
obtained by using the empirical relationship ‘Mode =3 Median- 2 mean’ for different populations.The efficiencies of proposed estimators are given in Table 3.From Table 2, we observe that the values obtained from the new parametric functional relationship for mode i.e. 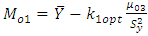 , are close to the true value of the population mode
, are close to the true value of the population mode  , as compared to the values of population mode obtained by using the empirical relationship for it. The small amount of errors
, as compared to the values of population mode obtained by using the empirical relationship for it. The small amount of errors  is due to the fact that we are using the optimum value of
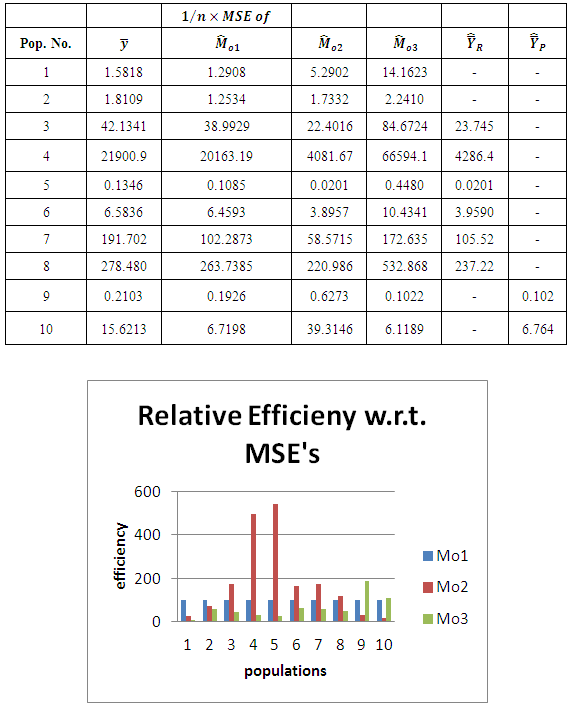
is due to the fact that we are using the optimum value of  not the exact value. So, empirically, this relation is verified.From Table 3, at the end, we observe that in the sampling theory, for the bivariate population, the known value of
not the exact value. So, empirically, this relation is verified.From Table 3, at the end, we observe that in the sampling theory, for the bivariate population, the known value of 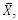 increases the accuracy of the estimators of population mode
increases the accuracy of the estimators of population mode 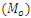 . We note that the MSE’s of all
. We note that the MSE’s of all 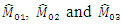 are less than
are less than 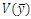 , at the same time MSE’s of
, at the same time MSE’s of 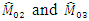 are less than
are less than 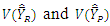 respectively. When the conditions (3.7) and (3.8) are satisfied then
respectively. When the conditions (3.7) and (3.8) are satisfied then 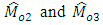 are more efficient than
are more efficient than 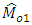 respectively, otherwise
respectively, otherwise 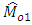 is more efficient than the others.
is more efficient than the others.Table 1. Description of populations
 |
| |
|
Table 2. Values of population mode
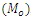 , values obtained from new parametric relationship , values obtained from new parametric relationship
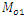 and empirical relationship and empirical relationship
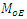
 |
| |
|
Table 3.

 |
| |
|
6. Conclusions
The empirical study shows that the new parametric relationship for population mode is more beneficial for estimating population mode than the empirical relationship between mean, median and mode. Also, the values of MSEs of the proposed estimators for mode are less than the values of MSEs of mean per unit estimator of population mean. It means that the proposed estimators of population mode are more stable than the mean per unit estimator of population mean. Further, the conditions have been found out where ratio-type and product-type estimators of population mode are more efficient than 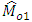 . Also, the new parametric relationship for population mode provides a new way to estimate population mode for further study.
. Also, the new parametric relationship for population mode provides a new way to estimate population mode for further study.
References
| [1] | Bickel DR (2010) Robust and Efficient Estimation of the Mode of Continuous Data: The Mode as a Viable Measure of Central Tendency, Journal of Statistical Computation and Simulation, Vol. 73 Issue 12, pp 899-912. |
| [2] | Chakravarty I, Laha R, Roy J (1967) Handbook of Methods of Applied Statistics: Techniques of Computation, Descriptive Methods, and Statistical Inference. John Wiley & Sons. |
| [3] | Chen C, Liu H, Metaxas DN, Zhao T (2014) Mode Estimation for High Dimensional Discrete Tree Graphical Models, NIPS, pp 1323-1331. |
| [4] | Gross S (1980) Median estimation in sample surveys. In: Proceedings of the Section on Survey Research Methods, American Statistical Association Alexandia, VA, pp 181-184. |
| [5] | Kuk AY, Mak T (1989) Median estimation in the presence of auxiliary information. Journal of the Royal Statistical Society Series B (Methodological) pp 261-269. |
| [6] | Maddala GS, Lahiri K (1992) Introduction to econometrics, vol 2. Macmillan New York. |
| [7] | Murthy MN (1967) Sampling theory and methods. Calcutta-35: Statistical Publishing Society. |
| [8] | Parzen E (1962) On Estimation of a Probability Density Function and Mode, Annals of Mathematical Statistics, Vol. 33, Issue 3, pp 1065-1076. |
| [9] | Sedory SA, Singh S (2014) Estimation of mode using auxiliary information. Communications in Statistics- Simulation and Computation 43(10):2390-2402. |
| [10] | Srivastava S, Jhajj H (1983) A class of estimators of the population mean using multi-auxiliary information. Cal Statist Assoc Bull 32:47-56. |


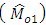 . Further, for bivariate populations, the ratio-type and product type estimators of Mo have been proposed. At optimum value of ‘k’, the expressions of biases and MSE’s of proposed estimators have been obtained and compared with each other. Also, the conditions for ratio-type and product-type estimators of Mo have been found out for which these estimators are more efficient than
. Further, for bivariate populations, the ratio-type and product type estimators of Mo have been proposed. At optimum value of ‘k’, the expressions of biases and MSE’s of proposed estimators have been obtained and compared with each other. Also, the conditions for ratio-type and product-type estimators of Mo have been found out for which these estimators are more efficient than 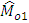 . The authenticity of new parametric relation of mode has also been verified for some theoretical univariate and bivariate distributions. Empirically, the values of minimum MSE’s of proposed estimators have been obtained for some specific populations and also the authenticity of the relationship has been verified for these populations.
. The authenticity of new parametric relation of mode has also been verified for some theoretical univariate and bivariate distributions. Empirically, the values of minimum MSE’s of proposed estimators have been obtained for some specific populations and also the authenticity of the relationship has been verified for these populations.
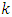 . By proposing the conventional consistent estimator
. By proposing the conventional consistent estimator 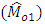 of population mode
of population mode 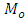 , we find the approximate value of
, we find the approximate value of 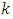 by minimizing the
by minimizing the 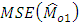 , upto terms of order
, upto terms of order 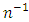 . Further, for the bivariate
. Further, for the bivariate 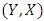 -population, we have also proposed ratio-type
-population, we have also proposed ratio-type 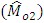 and product-type
and product-type 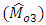 estimators of
estimators of 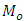 . We have checked authenticity of the new parametric relationship for
. We have checked authenticity of the new parametric relationship for 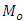 . Upto terms of order
. Upto terms of order 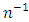 , the optimum biases and minimum MSE's of the proposed estimators are obtained and compared with each other. Empirically, we have also checked the authenticity of the parametric relationship by showing that for the given population established new parametric relation is more accurate than the empirical relationship for mean, median and mode, and obtained the values of minimum MSE's of the proposed estimators.
, the optimum biases and minimum MSE's of the proposed estimators are obtained and compared with each other. Empirically, we have also checked the authenticity of the parametric relationship by showing that for the given population established new parametric relation is more accurate than the empirical relationship for mean, median and mode, and obtained the values of minimum MSE's of the proposed estimators.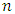 is drawn from a finite population of size
is drawn from a finite population of size  without replacement and observations on both study variables
without replacement and observations on both study variables 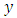 and auxiliary variable
and auxiliary variable 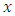 are taken. Let the values of variable
are taken. Let the values of variable 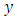 and
and 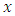 be denoted by
be denoted by  and
and 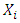 respectively on the
respectively on the  unit of the population
unit of the population 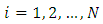 and the corresponding small letters
and the corresponding small letters 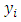 and
and  denote the values corresponding to the
denote the values corresponding to the 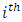 unit in the sample. Taking,
unit in the sample. Taking,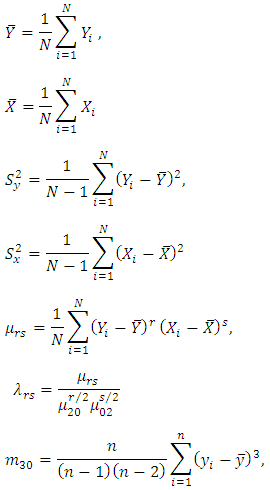 Obviously
Obviously Defining,
Defining,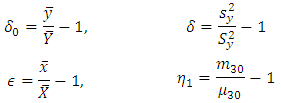 For the sake of simplicity, assume that
For the sake of simplicity, assume that 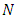 is large enough as compares to
is large enough as compares to 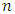 so that finite population correction (fpc) terms are ignored throughout.For the given SRSWOR, we have the following expectations,
so that finite population correction (fpc) terms are ignored throughout.For the given SRSWOR, we have the following expectations,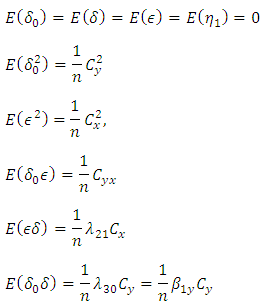 and up to terms of order
and up to terms of order 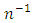
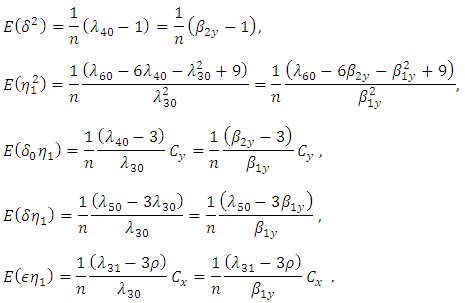

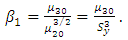
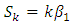 where
where 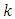 is unknown constant to be determined.Therefore,
is unknown constant to be determined.Therefore,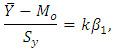 That implies
That implies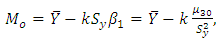
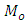 under the three different situations as
under the three different situations as 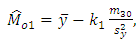
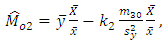
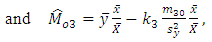
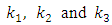 are unknown constants, whose values are determined by minimizing the MSE’s of respective estimators
are unknown constants, whose values are determined by minimizing the MSE’s of respective estimators 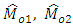 and
and 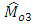 . Here the estimator
. Here the estimator 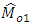 uses no information on auxiliary variable
uses no information on auxiliary variable 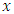 which is highly correlated with
which is highly correlated with 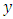 , whereas
, whereas 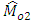 and
and 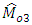 uses the known information of
uses the known information of 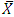 , which are of ratio and product type estimators respectively.To find the biases and MSE’s of
, which are of ratio and product type estimators respectively.To find the biases and MSE’s of 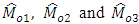 , we expand them in terms of
, we expand them in terms of 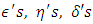 and then taking the expectations as given in section 2, upto terms of order
and then taking the expectations as given in section 2, upto terms of order 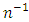 , we get,
, we get,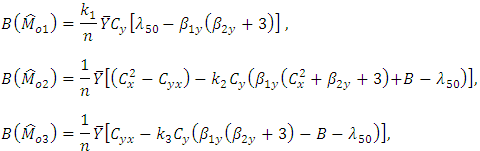 and
and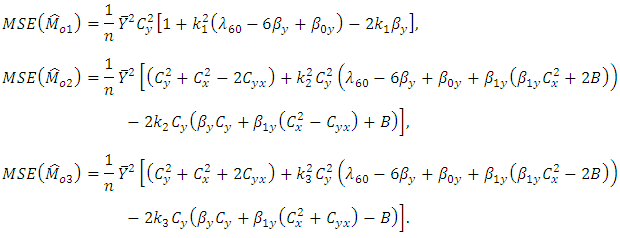 The above MSE’s of
The above MSE’s of  and
and  are minimised for
are minimised for 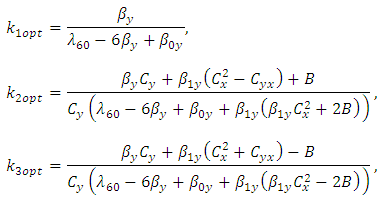 and the Biases and minimum MSE’s are given as,
and the Biases and minimum MSE’s are given as,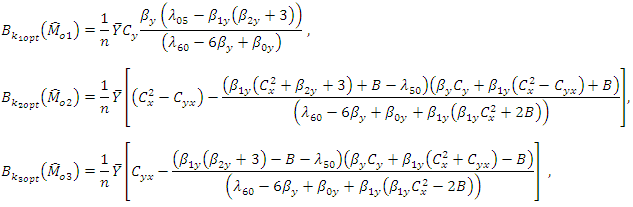 and
and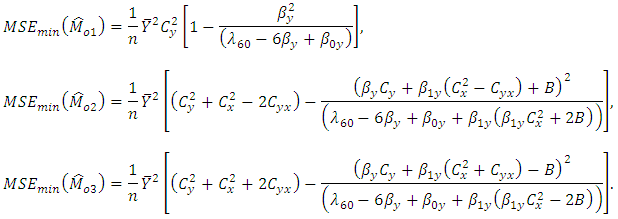 Where,
Where,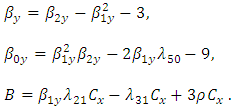 Srivastava and Jhajj (1983) have shown that if we replace the parameters involved in the optimum value of the unknown constant by their consistent estimators then upto terms of order
Srivastava and Jhajj (1983) have shown that if we replace the parameters involved in the optimum value of the unknown constant by their consistent estimators then upto terms of order 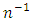 , the MSE remains the same. Using this, if we replace the parameters involved in
, the MSE remains the same. Using this, if we replace the parameters involved in  and
and  by their consistent estimators then their estimators say become
by their consistent estimators then their estimators say become  and
and 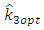 respectively. Then our estimators reduce to
respectively. Then our estimators reduce to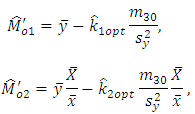 and
and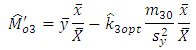 Among the three estimators, the most efficient is
Among the three estimators, the most efficient is 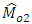 iff
iff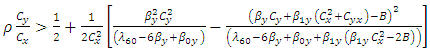
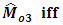
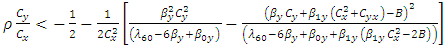
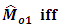
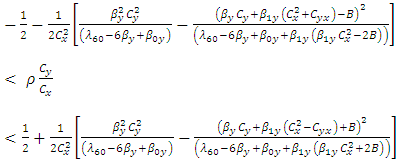
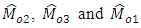 respectively.
respectively.
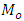 is
is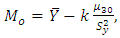
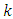 is an unknown constant whose value is to be determined for the given population. If
is an unknown constant whose value is to be determined for the given population. If  is optimised by minimising the MSE of conventional consistent estimator
is optimised by minimising the MSE of conventional consistent estimator 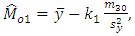 (up to the order
(up to the order 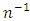 ), the above functional relationship reduced to
), the above functional relationship reduced to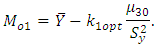 As in sampling theory, the nature of the population under study is not known. To see the authenticity of approximate parametric relation
As in sampling theory, the nature of the population under study is not known. To see the authenticity of approximate parametric relation  , we have to consider the population of particular nature. The approximation is due to the fact that we are using the optimum value
, we have to consider the population of particular nature. The approximation is due to the fact that we are using the optimum value 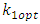 of unknown constant
of unknown constant 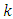 , not the exact value. When the population is univariate, one can check the relationship for
, not the exact value. When the population is univariate, one can check the relationship for 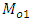 easily. But, if the population is
easily. But, if the population is 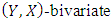 , then it is very difficult check this relationship because for this we need the bivariate moments and marginal distributions of
, then it is very difficult check this relationship because for this we need the bivariate moments and marginal distributions of  and
and 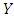 . No doubt, this relationship can be checked by researchers in inference. So this problem is open for researchers involved in statistical Inference. But in sampling theory, for the known value of
. No doubt, this relationship can be checked by researchers in inference. So this problem is open for researchers involved in statistical Inference. But in sampling theory, for the known value of 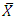 we can increase the precision of the estimators
we can increase the precision of the estimators 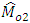 and
and 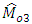 . Following particular populations are considered to check the authenticity of
. Following particular populations are considered to check the authenticity of 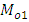 :(i) Population is Normal:(a) Let
:(i) Population is Normal:(a) Let 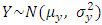 , then we know
, then we know 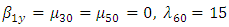 and
and 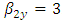 . Using these values, we get,
. Using these values, we get,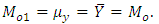 Because
Because 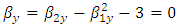 in numerator of
in numerator of 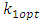 and also,
and also, 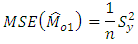 which is variance of
which is variance of 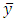 when fpc are ignored. So
when fpc are ignored. So 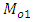 is verified for univariate normal population.(b) Let
is verified for univariate normal population.(b) Let 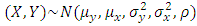 , then we know
, then we know 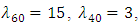
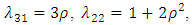
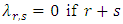 is odd. Also,
is odd. Also, 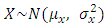 and
and 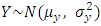 . Using these values, we get,
. Using these values, we get,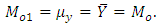 The expressions for MSE’s are
The expressions for MSE’s are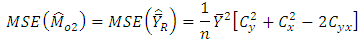 and
and 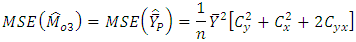 So,
So, 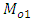 is verified for bivariate normal population and upto terms of order
is verified for bivariate normal population and upto terms of order 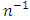 , we have
, we have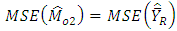 and
and 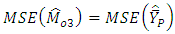 So the relation
So the relation 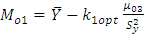 is true for univariate as well as for bivariate normal populations and in general true for all symmetrical populations.(ii) Population is Poisson: Let
is true for univariate as well as for bivariate normal populations and in general true for all symmetrical populations.(ii) Population is Poisson: Let 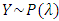 . We then have
. We then have 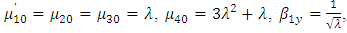 so Poisson distribution is always positively skewed,
so Poisson distribution is always positively skewed, 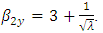 Using these values, we get
Using these values, we get 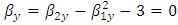 , so
, so 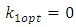 and
and 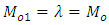 if
if 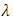 is not integer and
is not integer and 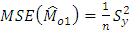 .Hence this relation is also verified for positively skewed distributions.(iii) Population is
.Hence this relation is also verified for positively skewed distributions.(iii) Population is  : Let
: Let 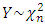 , then we have
, then we have 
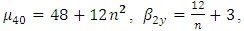
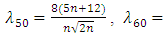
 (positively skewed).(iv) Particular cases:
(positively skewed).(iv) Particular cases: Hence we conclude that the new functional relationship for
Hence we conclude that the new functional relationship for  is always true for symmetric populations whether univariate or bivariate. In general, it is approximately true for all populations, whereas for the skewed distribution, it is approximately true. The approximation is due to the fact that we use the optimum value of
is always true for symmetric populations whether univariate or bivariate. In general, it is approximately true for all populations, whereas for the skewed distribution, it is approximately true. The approximation is due to the fact that we use the optimum value of  not the exact one.
not the exact one.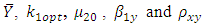 are listed in Table 1. In Table 2, we have given the true value of population Mode
are listed in Table 1. In Table 2, we have given the true value of population Mode 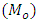 , the values of the population mode obtained by using the new parametric functional relationship of
, the values of the population mode obtained by using the new parametric functional relationship of 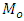 and values of population mode
and values of population mode  obtained by using the empirical relationship ‘Mode =3 Median- 2 mean’ for different populations.The efficiencies of proposed estimators are given in Table 3.From Table 2, we observe that the values obtained from the new parametric functional relationship for mode i.e.
obtained by using the empirical relationship ‘Mode =3 Median- 2 mean’ for different populations.The efficiencies of proposed estimators are given in Table 3.From Table 2, we observe that the values obtained from the new parametric functional relationship for mode i.e. 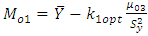 , are close to the true value of the population mode
, are close to the true value of the population mode 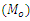 , as compared to the values of population mode obtained by using the empirical relationship for it. The small amount of errors
, as compared to the values of population mode obtained by using the empirical relationship for it. The small amount of errors 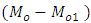 is due to the fact that we are using the optimum value of
is due to the fact that we are using the optimum value of 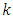 not the exact value. So, empirically, this relation is verified.From Table 3, at the end, we observe that in the sampling theory, for the bivariate population, the known value of
not the exact value. So, empirically, this relation is verified.From Table 3, at the end, we observe that in the sampling theory, for the bivariate population, the known value of 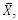 increases the accuracy of the estimators of population mode
increases the accuracy of the estimators of population mode 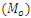 . We note that the MSE’s of all
. We note that the MSE’s of all 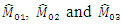 are less than
are less than 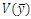 , at the same time MSE’s of
, at the same time MSE’s of 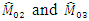 are less than
are less than 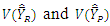 respectively. When the conditions (3.7) and (3.8) are satisfied then
respectively. When the conditions (3.7) and (3.8) are satisfied then 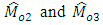 are more efficient than
are more efficient than 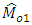 respectively, otherwise
respectively, otherwise 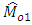 is more efficient than the others.
is more efficient than the others.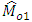 . Also, the new parametric relationship for population mode provides a new way to estimate population mode for further study.
. Also, the new parametric relationship for population mode provides a new way to estimate population mode for further study. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
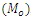 , values obtained from new parametric relationship
, values obtained from new parametric relationship 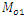 and empirical relationship
and empirical relationship