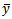F. B. Adebola1, N. A. Adegoke1, Ridwan A. Sanusi2
1Department of Statistics, Federal University of Technology Akure, Nigeria
2Department of Mathematics and Statistics, King Fahd University of Petroleum and Minerals, Saudi Arabia
Correspondence to: N. A. Adegoke, Department of Statistics, Federal University of Technology Akure, Nigeria.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
Abstract
This paper examines a class of regression estimator with cum-dual ratio estimator as intercept for estimating the mean of the study variable Y using auxiliary variable X. We obtained the bias and the mean square error of the proposed estimator, also, the asymptotically optimum estimator (AOE) was obtained along with its mean square error. Theoretical and numerical validation of the proposed estimator were done to show it’s superiority over the usual simple random sampling estimator and ratio estimator, product estimator, cum-dual ratio and product estimator. It was found that the estimator while performed better than other competing estimators, performed in almost the same way as the usual regression estimator when compared with the usual simple random estimator for estimating the average sleeping hours of undergraduate students of the department of statistics, Federal University of Technology Akure, Nigeria.
Keywords:
Difference estimator, Auxiliary variable, Cum-Dual ratio estimator, Bias, Mean square error, Efficiency
Cite this paper: F. B. Adebola, N. A. Adegoke, Ridwan A. Sanusi, A Class of Regression Estimator with Cum-Dual Ratio Estimator as Intercept, International Journal of Probability and Statistics , Vol. 4 No. 2, 2015, pp. 42-50. doi: 10.5923/j.ijps.20150402.02.
1. Introduction
Ratio estimation has gained relevance in estimation theory because of its improved precision in estimating the population parameters. It has been widely applied in agriculture to estimate the mean yield of crops in a certain area and in forestry, to estimate with high precision, the mean number of trees or crops in a forest or plantation. Other areas of relevance include economics and Population studies to estimate the ratio of income to family size. Utilizing Information from high resolution satellite data, [1] examined the possibilities of different forms of auxiliary information derived from remote sensing data in two-phase sampling design and suggested an appropriate estimator that would be of broad interest and applications by proposing a new class of regression-cum estimators in two-phase sampling. He found it to be more efficient than the usual regression and ratio estimators. A class of product-cum-dual to product estimators was proposed by [2] for estimating finite population mean of the study variate. The use of auxiliary information at the estimation stage to increase the efficiency of the study variable was proposed by [3]. He used supplementary information on an auxiliary variable X positively correlated with Y to develop the ratio estimator to estimate the population mean or total of the study variable Y. The ratio-estimator is always more efficient than the normal SRS when the relationship between the study variable Y and the auxiliary variable X is linear through the origin, and Y is proportional to X [4]. Product estimator was proposed by [5]. [6] suggested the use of ratio estimator 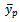 when
when 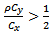 and unbiased estimator
and unbiased estimator 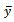 when
when 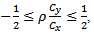 where
where 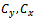 and
and 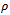 are coefficient of variation of y, coefficient of variation of x and correlation between y and x respectively. A lots of work have been done using auxiliary information. A ratio-cum-dual to ratio estimator was proposed for finite population mean. It was shown that the proposed estimator is more efficient than the simple mean estimator, usual ratio estimator and dual to ratio estimator under certain given conditions [7]. [8] proposed a modified ratio-cum-product estimator of finite population mean of the study variate Y using known correlation coefficient between two auxiliary characters X1 and X2, while [9] proposed a ratio-cum-product estimator of finite population mean using information on coefficient of variation and coefficient of kurtosis of auxiliary variate and showed that the proposed estimator is more efficient than the sample mean estimator, usual ratio and product estimators and estimators proposed by [10] under certain given conditions. Moreover, two exponential ratio estimators of population mean in simple random sampling without replacement were shown to be more efficient than the regression estimator and some existing estimators under review based on their biases, mean squared errors and also by using analytical and numerical results (at optimal conditions) for comparison [11]. Also, [12] suggested a ratio-cum product estimator of a finite population mean using information on the coefficient of variation and the coefficient of kurtosis of auxiliary variate in stratified random sampling.Suppose that simple random sampling without replacement (SRSWOR) of n units is drawn from a population of N units to estimate the population mean
are coefficient of variation of y, coefficient of variation of x and correlation between y and x respectively. A lots of work have been done using auxiliary information. A ratio-cum-dual to ratio estimator was proposed for finite population mean. It was shown that the proposed estimator is more efficient than the simple mean estimator, usual ratio estimator and dual to ratio estimator under certain given conditions [7]. [8] proposed a modified ratio-cum-product estimator of finite population mean of the study variate Y using known correlation coefficient between two auxiliary characters X1 and X2, while [9] proposed a ratio-cum-product estimator of finite population mean using information on coefficient of variation and coefficient of kurtosis of auxiliary variate and showed that the proposed estimator is more efficient than the sample mean estimator, usual ratio and product estimators and estimators proposed by [10] under certain given conditions. Moreover, two exponential ratio estimators of population mean in simple random sampling without replacement were shown to be more efficient than the regression estimator and some existing estimators under review based on their biases, mean squared errors and also by using analytical and numerical results (at optimal conditions) for comparison [11]. Also, [12] suggested a ratio-cum product estimator of a finite population mean using information on the coefficient of variation and the coefficient of kurtosis of auxiliary variate in stratified random sampling.Suppose that simple random sampling without replacement (SRSWOR) of n units is drawn from a population of N units to estimate the population mean 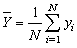 of the study variable Y. All the sample units are observed for the variables Y and X. Let
of the study variable Y. All the sample units are observed for the variables Y and X. Let 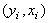 where
where 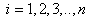 denotes the set of the observation for the study variable Y and X. Let the sample means
denotes the set of the observation for the study variable Y and X. Let the sample means 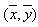 be unbiased of the population means of the auxiliary variable
be unbiased of the population means of the auxiliary variable 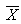 and study variable
and study variable 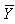 based on the n observations.The usual ratio estimator of
based on the n observations.The usual ratio estimator of 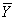 is given as
is given as 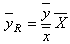 and the usual regression estimator is given as
and the usual regression estimator is given as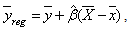 where
where 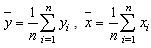 and
and 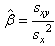 is the estimate slope of regression coefficient of Y and X. [13] obtained dual to ratio-cum estimator given as
is the estimate slope of regression coefficient of Y and X. [13] obtained dual to ratio-cum estimator given as 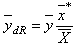 , where
, where 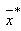 is the un-sampled auxiliary variable in X given as
is the un-sampled auxiliary variable in X given as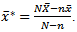 The use of auxiliary information in sample surveys was extensively discussed in well-known classical text books such as [14], [15], [16], [17] and [18] among others. Recent developments in ratio and product methods of estimation along with their variety of modified forms are lucidly described in detail by [19].In this paper, we proposed a class of difference estimator with dual to ratio cum as the slope of the estimator instead of
The use of auxiliary information in sample surveys was extensively discussed in well-known classical text books such as [14], [15], [16], [17] and [18] among others. Recent developments in ratio and product methods of estimation along with their variety of modified forms are lucidly described in detail by [19].In this paper, we proposed a class of difference estimator with dual to ratio cum as the slope of the estimator instead of 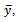 also,
also, 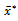 was used instead of x in the usual regression estimator. The proposed estimator is used to estimate the average sleeping hours of undergraduate students of the department of statistics, Federal University of Technology Akure, Nigeria.The organization of this article is as follows: In Section 2, we provide the conceptual framework of the proposed class of estimator. We derived its bias, Mean Squared Error (MSE) and the resulting optimum value of the MSE, with their rigorous proofs up to order one. In section 3, we compared the MSE of the proposed estimator
was used instead of x in the usual regression estimator. The proposed estimator is used to estimate the average sleeping hours of undergraduate students of the department of statistics, Federal University of Technology Akure, Nigeria.The organization of this article is as follows: In Section 2, we provide the conceptual framework of the proposed class of estimator. We derived its bias, Mean Squared Error (MSE) and the resulting optimum value of the MSE, with their rigorous proofs up to order one. In section 3, we compared the MSE of the proposed estimator 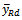 with the MSE of
with the MSE of 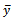 under Simple Random Sampling Scheme, in Section 4, we provide the numerical validation of the proposed estimator by using data on the ages and hours of sleeping by the undergraduate students of the Department of Statistics Federal University of Technology Akure, Ondo State, Nigeria. Finally, Section 5 provides the conclusion of our findings.
under Simple Random Sampling Scheme, in Section 4, we provide the numerical validation of the proposed estimator by using data on the ages and hours of sleeping by the undergraduate students of the Department of Statistics Federal University of Technology Akure, Ondo State, Nigeria. Finally, Section 5 provides the conclusion of our findings.
2. The Proposed Class of Estimator
For estimating population mean 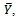 we have proposed a class of difference estimator with dual to Ratio cum as the intercept given as
we have proposed a class of difference estimator with dual to Ratio cum as the intercept given as
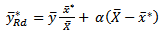 | (1) |
Where α is a suitably chosen scalar. The bias and mean square error (MSE) of 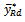 to the first order approximation is obtained by substituting
to the first order approximation is obtained by substituting 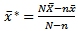 into equation (1), hence, equation (1) becomes,
into equation (1), hence, equation (1) becomes, 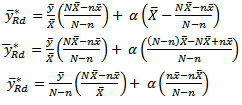 | (2) |
We write,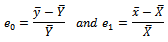 This implies that
This implies that 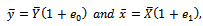 Respectively. Hence, equation (2) becomes,
Respectively. Hence, equation (2) becomes, 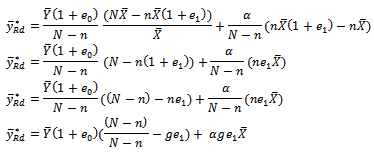 Where
Where 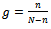
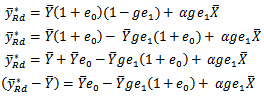 | (3) |
By taking the expectation of equation (3) we have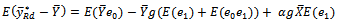 | (4) |
But, 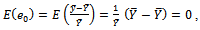
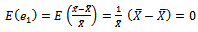 and
and 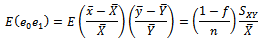 Hence, equation (4) becomes,
Hence, equation (4) becomes, 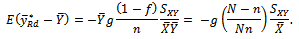 Recall,
Recall, 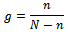
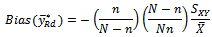
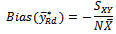 The Mean Square Error of the estimator given as
The Mean Square Error of the estimator given as 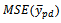 is obtained by squaring both sides of equation (3) and taking the expectation. We have
is obtained by squaring both sides of equation (3) and taking the expectation. We have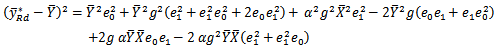 Ignoring the higher powers of error greater than or equal to 3, we have.
Ignoring the higher powers of error greater than or equal to 3, we have.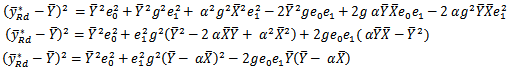 | (5) |
Take the expectation of (5) we have 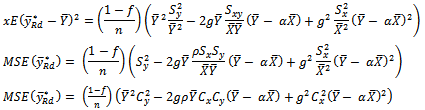 | (6) |
Where 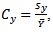 and
and 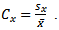 The optimum value of the
The optimum value of the 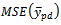 is given as
is given as 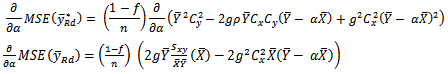 | (7) |
Set equation (7) to zero; we have 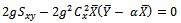
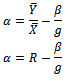 Where
Where 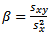 and
and 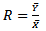 Thus, the resulting OPTIMUM MSE of
Thus, the resulting OPTIMUM MSE of 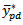 is given as
is given as 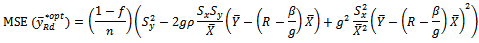 By substituting
By substituting 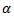 in equation (6)
in equation (6)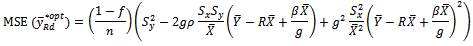 Where
Where 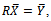
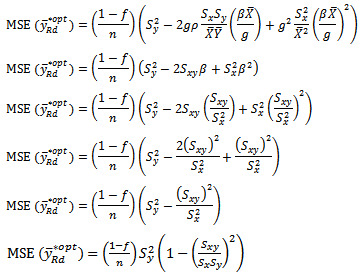 | (7) |
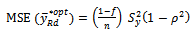 Equation (7) shows that the
Equation (7) shows that the 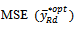 is the same as the MSE Regression estimator.Remark The Bias of
is the same as the MSE Regression estimator.Remark The Bias of 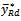 is the same as Bias of the dual ratio estimator
is the same as Bias of the dual ratio estimator 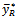 and when
and when 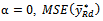 becomes
becomes 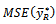 of dual to ratio estimator
of dual to ratio estimator 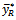 proposed by [13].The bias of
proposed by [13].The bias of 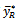 is given as
is given as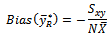 The
The 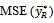 is given as
is given as 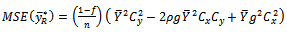 | (7a) |
3. Efficiency Comparisons
In this section, we compared the MSE of the proposed estimator 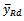 with the MSE of
with the MSE of 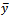 under Simple Random Sampling Scheme given as,
under Simple Random Sampling Scheme given as, 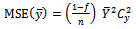 | (8) |
From equations (5) and (8), the proposed estimator is better than that the usual estimator 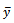 if,
if, 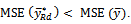 That is,
That is,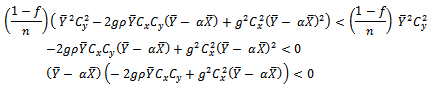 This holds if and only if,
This holds if and only if,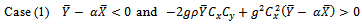 Or
Or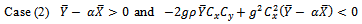 The Range of α under which the proposed estimator
The Range of α under which the proposed estimator 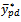 is more efficient than
is more efficient than 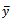 is given as,
is given as,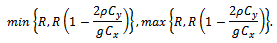 We also compared the proposed estimator
We also compared the proposed estimator 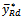 with the usual ratio estimator
with the usual ratio estimator 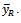 The MSE of the
The MSE of the 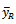 is given as
is given as 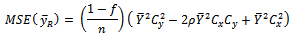 It is found that the proposed estimator
It is found that the proposed estimator 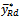 will be more efficient than the usual ratio estimator
will be more efficient than the usual ratio estimator 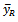 if
if 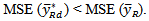 That is,
That is, This holds if the following two conditions are satisfied
This holds if the following two conditions are satisfied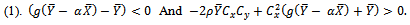 Or
Or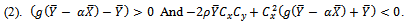 This condition holds if
This condition holds if 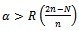 and
and 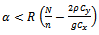 or
or 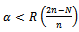 and
and 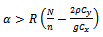
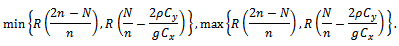 We also compared the proposed estimator
We also compared the proposed estimator  with the usual product estimator
with the usual product estimator 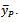 The MSE of the
The MSE of the 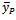 is given as
is given as 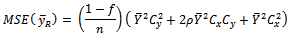 It is found that the proposed estimator
It is found that the proposed estimator 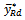 will be more efficient than the usual ratio estimator
will be more efficient than the usual ratio estimator 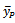 if
if 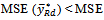
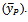 That is,
That is,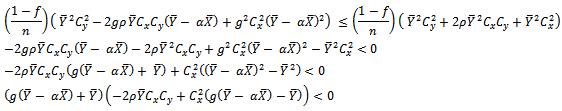 This holds if the following two conditions are satisfied
This holds if the following two conditions are satisfied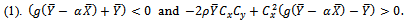 Or
Or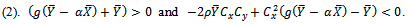 This condition holds if
This condition holds if 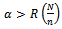 and
and 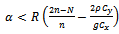 or
or 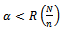 and
and 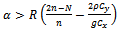
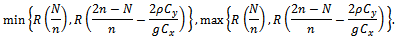 We also compared the MSE of the proposed estimator with MSE of dual product estimator
We also compared the MSE of the proposed estimator with MSE of dual product estimator 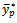 proposed by [20]. The MSE
proposed by [20]. The MSE 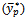 proposed by [20] (1980) is given as
proposed by [20] (1980) is given as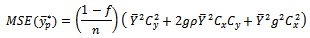 It is found that the proposed estimator
It is found that the proposed estimator 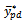 will be more efficient than that of [20] estimator
will be more efficient than that of [20] estimator 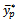 if
if 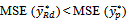 That is
That is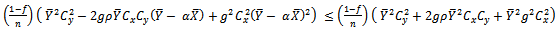 That is,
That is,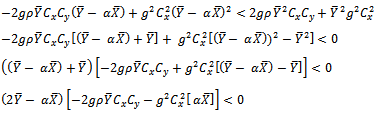 This holds if,
This holds if,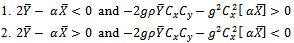 This condition holds if
This condition holds if 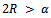 and
and 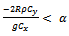 or
or 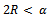 and
and 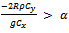 The range of α under which the proposed estimator
The range of α under which the proposed estimator 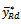 iS more efficient than
iS more efficient than 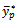 is
is 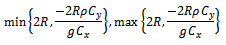 Lastly, we compared MSE of the proposed estimator
Lastly, we compared MSE of the proposed estimator 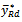 with that of dual to ratio estimator
with that of dual to ratio estimator 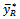 proposed [13] given in equation (7a). The proposed estimator will be more efficient than
proposed [13] given in equation (7a). The proposed estimator will be more efficient than 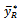 if
if 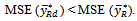 That is,
That is, 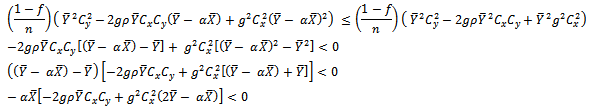 This holds if
This holds if 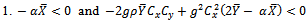 Or
Or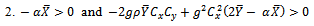 This condition holds if
This condition holds if 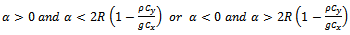 Therefore, the range of α under which the proposed estimator
Therefore, the range of α under which the proposed estimator 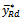 is more efficient than dual ratio estimator
is more efficient than dual ratio estimator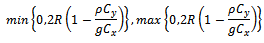 Thus it seems from the above that the proposed estimator
Thus it seems from the above that the proposed estimator 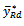 may be made better than the usual estimator, ratio estimator, product estimator, dual to product estimator
may be made better than the usual estimator, ratio estimator, product estimator, dual to product estimator 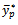 and the dual to ratio estimator
and the dual to ratio estimator 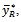 if the given conditions are satisfied.Comparison of ‘AOE’ to
if the given conditions are satisfied.Comparison of ‘AOE’ to 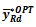
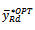 is more efficient than the other existing estimators
is more efficient than the other existing estimators 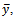 the ratio estimator
the ratio estimator 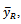 the product estimator
the product estimator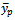 , the dual to ratio estimator
, the dual to ratio estimator 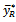 and the dual to product estimator
and the dual to product estimator 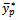 since
since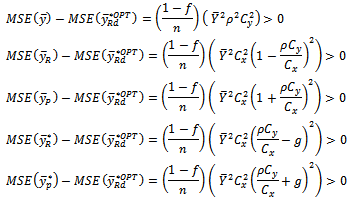 Hence, we conclude that the proposed class of estimator
Hence, we conclude that the proposed class of estimator 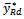 is more efficient than other estimator in case of its optimality.
is more efficient than other estimator in case of its optimality.
4. Numerical Validation
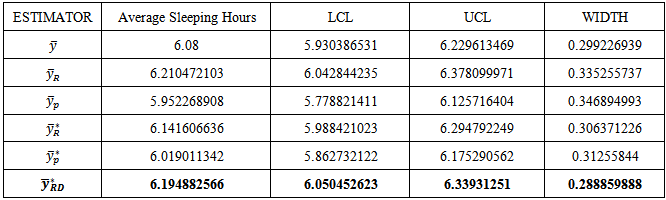
To illustrate the efficiency of the proposed estimator over the other estimators  Data on the ages and hours of sleeping by the undergraduate students of the Department of Statistics Federal University of Technology Akure, Ondo State, Nigeria. A sample of 150 out of 461 students of the department was obtained using simple random sampling without replacement. The information on the age of the students was used as auxiliary information to increase the precision of the estimate of the average sleeping hours. The estimate of the average hours of sleeping of the students were obtained and also the 95% confidence intervals of the average hours of sleeping were obtained for the proposed estimator and the other estimators. Table 1., gives the estimates of the average sleeping hours and the 95% confidence Interval. As shown in Table 1.0, the proposed estimator performed better than the other estimators, the width of the confidence interval of the proposed estimator is smallest than the other competing estimators.
Data on the ages and hours of sleeping by the undergraduate students of the Department of Statistics Federal University of Technology Akure, Ondo State, Nigeria. A sample of 150 out of 461 students of the department was obtained using simple random sampling without replacement. The information on the age of the students was used as auxiliary information to increase the precision of the estimate of the average sleeping hours. The estimate of the average hours of sleeping of the students were obtained and also the 95% confidence intervals of the average hours of sleeping were obtained for the proposed estimator and the other estimators. Table 1., gives the estimates of the average sleeping hours and the 95% confidence Interval. As shown in Table 1.0, the proposed estimator performed better than the other estimators, the width of the confidence interval of the proposed estimator is smallest than the other competing estimators.Table 1. Average Sleeping Hours and 95% confidence intervals for Different Estimators for the undergraduate Students of Department of Statistics, Federals University of Technology Akure. Nigeria
 |
| |
|
The proposed estimator performed the same way as the regression estimator when compared with the usual simple random sampling. The average Sleeping Hours and 95% confidence intervals for the proposed estimator and the regression estimator is given below, the two estimators have the same width.To examine the gain in the efficiency of the proposed estimator 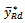 over the estimator
over the estimator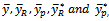 we obtained the percentage relative efficiency of different estimator of
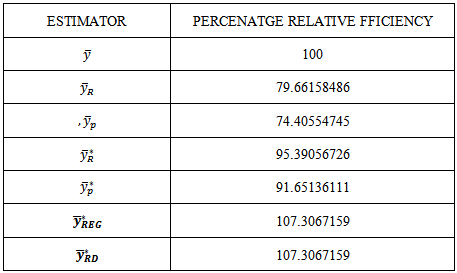
we obtained the percentage relative efficiency of different estimator of 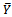 with respect to the usual unbiased estmator
with respect to the usual unbiased estmator 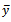 in Table 2. The proposed estimator
in Table 2. The proposed estimator 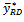 performed better than the other estimators
performed better than the other estimators 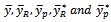 and perfoirmed exactly the same way as regression estimator.
and perfoirmed exactly the same way as regression estimator.Table 2. Average Sleeping Hours and 95% confidence intervals for the proposed estimators and regression estimators for the undergraduate Students of Department of Statistics, Federals University of Technology Akure. Nigeria
 |
| |
|
Table 3. The percentage relative efficiency of different estimator of
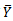 with respect to the usual unbiased estimator with respect to the usual unbiased estimator
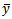
 |
| |
|
5. Conclusions
We have proposed a class of regression estimator with cum-dual ratio estimator as intercept for estimating the mean of the study variable Y using auxiliary variable X as in equation (1) and obtained ‘AOE’ for the proposed estimator. Theoretically, we have demonstrated that proposed estimator is always more efficient than other under the effective ranges of 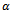 and its optimum values. Table 1. shows that the proposed estimator performed better than the other estimators as the width of the confidence interval of the proposed estimator is smallest than the other competing estimators. The percentage relative efficiency of different estimator of
and its optimum values. Table 1. shows that the proposed estimator performed better than the other estimators as the width of the confidence interval of the proposed estimator is smallest than the other competing estimators. The percentage relative efficiency of different estimator of 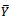 with respects to the usual unbiased estimator
with respects to the usual unbiased estimator 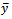 in Table 2. shows that the proposed estimator
in Table 2. shows that the proposed estimator 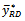 performed better than the other estimators
performed better than the other estimators 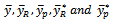 and performed exactly the same way as regression estimator. Hence, it is preferred to use the proposed class of estimator in practice.
and performed exactly the same way as regression estimator. Hence, it is preferred to use the proposed class of estimator in practice.
References
| [1] | B. K. Handique, “A Class of Regression-Cum-Ratio Estimators in Two-Phase Sampling for Utilizing Information From High Resolution Satellite Data,” ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci., vol. I–4, pp. 71–76, Jul. 2012. |
| [2] | S. Choudhury and B. K. Singh, “A Class of Product-cum-dual to Product Estimators of the Population Mean in Survey Sampling Using Auxiliary Information,” Asian J Math Stat, vol. 6, 2012. |
| [3] | W. G. Cochran, “The estimation of the yields of cereal experiments by sampling for the ratio of grain to total produce,” J. Agric. Sci., vol. 30, no. 02, pp. 262–275, 1940. |
| [4] | S. Choudhury and B. K. Singh, “An efficient class of dual to product-cum-dual to ratio estimators of finite population mean in sample surveys,” Glob. J. Sci. Front. Res., vol. 12, no. 3-F, 2012. |
| [5] | D. S. Robson, “Applications of multivariate polykays to the theory of unbiased ratio-type estimation,” J. Am. Stat. Assoc., vol. 52, no. 280, pp. 511–522, 1957. |
| [6] | M. N. Murthy, “Product method of estimation,” Sankhyā Indian J. Stat. Ser. A, pp. 69–74, 1964. |
| [7] | B. Sharma and R. Tailor, “A new ratio-cum-dual to ratio estimator of finite population mean in simple random sampling,” Glob. J. Sci. Front. Res., vol. 10, no. 1, 2010. |
| [8] | H. P. Singh, “Estimation of finite population mean using known correlation coefficient between auxiliary characters,” Statistica, vol. 65, no. 4, pp. 407–418, 2005. |
| [9] | R. Tailor and B. K. Sharma, “A modified ratio-cum-product estimator of finite population mean using known coefficient of variation and coefficient of kurtosis,” Stat. Transition-new Ser., vol. 10, p. 1, 2009. |
| [10] | L. N. Upadhyaya and H. P. Singh, “Use of transformed auxiliary variable in estimating the finite population mean,” Biometrical J., vol. 41, no. 5, pp. 627–636, 1999. |
| [11] | E. J. Ekpenyong and E. I. Enang, “Efficient Exponential Ratio Estimator for Estimating the Population Mean in Simple Random Sampling.” |
| [12] | R. Tailor, B. Sharma, and J.-M. Kim, “A generalized ratio-cum-product estimator of finite population mean in stratified random sampling,” Commun Korea Stat Soc, vol. 18, no. 1, pp. 111–118, 2011. |
| [13] | T. Srivenkataramana, “A dual to ratio estimator in sample surveys,” Biometrika, vol. 67, no. 1, pp. 199–204, 1980. |
| [14] | W. G. Cochran, “Sampling techniques.,” 1977. |
| [15] | P. V Sukhatme and B. V Sukhatme, “Sampling theory of surveys with applications,” 1970. |
| [16] | P. V Sukhatme, B. V Sukhatme, S. Sukhatme, and C. Asok, “Sampling theory of surveys with applications.,” 1984. |
| [17] | M. N. Murthy, “Sampling theory and methods.,” Sampl. theory methods., 1967. |
| [18] | F. Yates, “Sampling methods for censuses and surveys.,” Griffin Books Stat., 1960. |
| [19] | S. Singh, Advanced Sampling Theory With Applications: How Michael Selected Amy, vol. 2. Springer Science & Business Media, 2003. |
| [20] | S. Bandyopadhyay, “Improved ratio and product estimators,” Sankhya Ser. C, vol. 42, no. 2, pp. 45–49, 1980. |
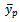 when
when 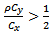 and unbiased estimator
and unbiased estimator 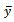 when
when 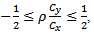 where
where 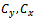 and
and 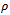 are coefficient of variation of y, coefficient of variation of x and correlation between y and x respectively. A lots of work have been done using auxiliary information. A ratio-cum-dual to ratio estimator was proposed for finite population mean. It was shown that the proposed estimator is more efficient than the simple mean estimator, usual ratio estimator and dual to ratio estimator under certain given conditions [7]. [8] proposed a modified ratio-cum-product estimator of finite population mean of the study variate Y using known correlation coefficient between two auxiliary characters X1 and X2, while [9] proposed a ratio-cum-product estimator of finite population mean using information on coefficient of variation and coefficient of kurtosis of auxiliary variate and showed that the proposed estimator is more efficient than the sample mean estimator, usual ratio and product estimators and estimators proposed by [10] under certain given conditions. Moreover, two exponential ratio estimators of population mean in simple random sampling without replacement were shown to be more efficient than the regression estimator and some existing estimators under review based on their biases, mean squared errors and also by using analytical and numerical results (at optimal conditions) for comparison [11]. Also, [12] suggested a ratio-cum product estimator of a finite population mean using information on the coefficient of variation and the coefficient of kurtosis of auxiliary variate in stratified random sampling.Suppose that simple random sampling without replacement (SRSWOR) of n units is drawn from a population of N units to estimate the population mean
are coefficient of variation of y, coefficient of variation of x and correlation between y and x respectively. A lots of work have been done using auxiliary information. A ratio-cum-dual to ratio estimator was proposed for finite population mean. It was shown that the proposed estimator is more efficient than the simple mean estimator, usual ratio estimator and dual to ratio estimator under certain given conditions [7]. [8] proposed a modified ratio-cum-product estimator of finite population mean of the study variate Y using known correlation coefficient between two auxiliary characters X1 and X2, while [9] proposed a ratio-cum-product estimator of finite population mean using information on coefficient of variation and coefficient of kurtosis of auxiliary variate and showed that the proposed estimator is more efficient than the sample mean estimator, usual ratio and product estimators and estimators proposed by [10] under certain given conditions. Moreover, two exponential ratio estimators of population mean in simple random sampling without replacement were shown to be more efficient than the regression estimator and some existing estimators under review based on their biases, mean squared errors and also by using analytical and numerical results (at optimal conditions) for comparison [11]. Also, [12] suggested a ratio-cum product estimator of a finite population mean using information on the coefficient of variation and the coefficient of kurtosis of auxiliary variate in stratified random sampling.Suppose that simple random sampling without replacement (SRSWOR) of n units is drawn from a population of N units to estimate the population mean 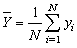 of the study variable Y. All the sample units are observed for the variables Y and X. Let
of the study variable Y. All the sample units are observed for the variables Y and X. Let 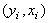 where
where 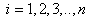 denotes the set of the observation for the study variable Y and X. Let the sample means
denotes the set of the observation for the study variable Y and X. Let the sample means 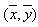 be unbiased of the population means of the auxiliary variable
be unbiased of the population means of the auxiliary variable 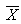 and study variable
and study variable 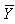 based on the n observations.The usual ratio estimator of
based on the n observations.The usual ratio estimator of 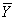 is given as
is given as 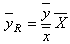 and the usual regression estimator is given as
and the usual regression estimator is given as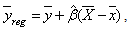 where
where 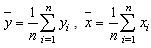 and
and 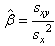 is the estimate slope of regression coefficient of Y and X. [13] obtained dual to ratio-cum estimator given as
is the estimate slope of regression coefficient of Y and X. [13] obtained dual to ratio-cum estimator given as 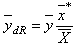 , where
, where 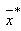 is the un-sampled auxiliary variable in X given as
is the un-sampled auxiliary variable in X given as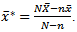 The use of auxiliary information in sample surveys was extensively discussed in well-known classical text books such as [14], [15], [16], [17] and [18] among others. Recent developments in ratio and product methods of estimation along with their variety of modified forms are lucidly described in detail by [19].In this paper, we proposed a class of difference estimator with dual to ratio cum as the slope of the estimator instead of
The use of auxiliary information in sample surveys was extensively discussed in well-known classical text books such as [14], [15], [16], [17] and [18] among others. Recent developments in ratio and product methods of estimation along with their variety of modified forms are lucidly described in detail by [19].In this paper, we proposed a class of difference estimator with dual to ratio cum as the slope of the estimator instead of 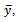 also,
also, 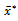 was used instead of x in the usual regression estimator. The proposed estimator is used to estimate the average sleeping hours of undergraduate students of the department of statistics, Federal University of Technology Akure, Nigeria.The organization of this article is as follows: In Section 2, we provide the conceptual framework of the proposed class of estimator. We derived its bias, Mean Squared Error (MSE) and the resulting optimum value of the MSE, with their rigorous proofs up to order one. In section 3, we compared the MSE of the proposed estimator
was used instead of x in the usual regression estimator. The proposed estimator is used to estimate the average sleeping hours of undergraduate students of the department of statistics, Federal University of Technology Akure, Nigeria.The organization of this article is as follows: In Section 2, we provide the conceptual framework of the proposed class of estimator. We derived its bias, Mean Squared Error (MSE) and the resulting optimum value of the MSE, with their rigorous proofs up to order one. In section 3, we compared the MSE of the proposed estimator 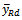 with the MSE of
with the MSE of 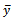 under Simple Random Sampling Scheme, in Section 4, we provide the numerical validation of the proposed estimator by using data on the ages and hours of sleeping by the undergraduate students of the Department of Statistics Federal University of Technology Akure, Ondo State, Nigeria. Finally, Section 5 provides the conclusion of our findings.
under Simple Random Sampling Scheme, in Section 4, we provide the numerical validation of the proposed estimator by using data on the ages and hours of sleeping by the undergraduate students of the Department of Statistics Federal University of Technology Akure, Ondo State, Nigeria. Finally, Section 5 provides the conclusion of our findings.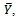 we have proposed a class of difference estimator with dual to Ratio cum as the intercept given as
we have proposed a class of difference estimator with dual to Ratio cum as the intercept given as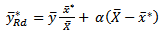
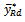 to the first order approximation is obtained by substituting
to the first order approximation is obtained by substituting 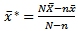 into equation (1), hence, equation (1) becomes,
into equation (1), hence, equation (1) becomes, 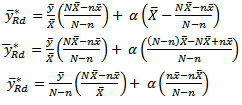
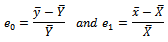 This implies that
This implies that 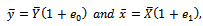 Respectively. Hence, equation (2) becomes,
Respectively. Hence, equation (2) becomes, 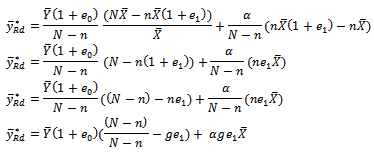 Where
Where 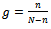
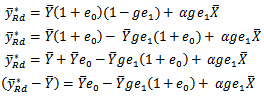
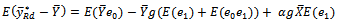
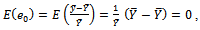
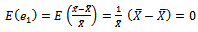 and
and 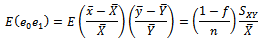 Hence, equation (4) becomes,
Hence, equation (4) becomes, 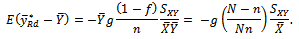 Recall,
Recall, 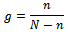
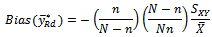
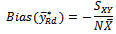 The Mean Square Error of the estimator given as
The Mean Square Error of the estimator given as 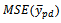 is obtained by squaring both sides of equation (3) and taking the expectation. We have
is obtained by squaring both sides of equation (3) and taking the expectation. We have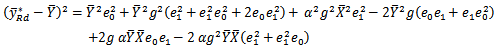 Ignoring the higher powers of error greater than or equal to 3, we have.
Ignoring the higher powers of error greater than or equal to 3, we have.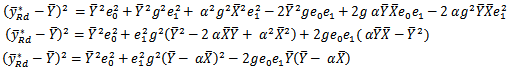
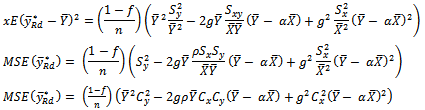
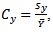 and
and 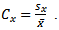 The optimum value of the
The optimum value of the 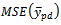 is given as
is given as 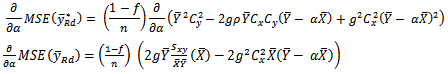
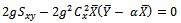
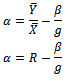 Where
Where 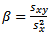 and
and 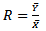 Thus, the resulting OPTIMUM MSE of
Thus, the resulting OPTIMUM MSE of 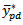 is given as
is given as 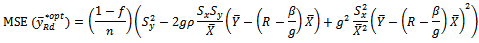 By substituting
By substituting 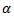 in equation (6)
in equation (6)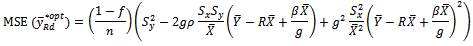 Where
Where 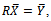
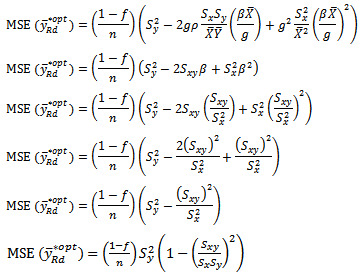
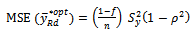 Equation (7) shows that the
Equation (7) shows that the 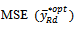 is the same as the MSE Regression estimator.Remark The Bias of
is the same as the MSE Regression estimator.Remark The Bias of 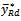 is the same as Bias of the dual ratio estimator
is the same as Bias of the dual ratio estimator 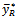 and when
and when 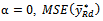 becomes
becomes 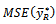 of dual to ratio estimator
of dual to ratio estimator 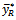 proposed by [13].The bias of
proposed by [13].The bias of 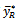 is given as
is given as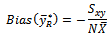 The
The 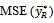 is given as
is given as 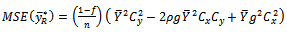
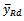 with the MSE of
with the MSE of 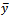 under Simple Random Sampling Scheme given as,
under Simple Random Sampling Scheme given as, 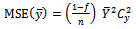
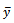 if,
if, 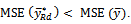 That is,
That is,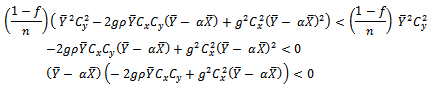 This holds if and only if,
This holds if and only if,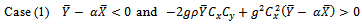 Or
Or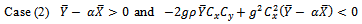 The Range of α under which the proposed estimator
The Range of α under which the proposed estimator 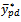 is more efficient than
is more efficient than 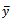 is given as,
is given as,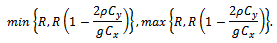 We also compared the proposed estimator
We also compared the proposed estimator  with the usual ratio estimator
with the usual ratio estimator  The MSE of the
The MSE of the 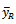 is given as
is given as 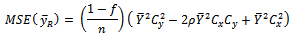 It is found that the proposed estimator
It is found that the proposed estimator 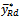 will be more efficient than the usual ratio estimator
will be more efficient than the usual ratio estimator 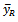 if
if 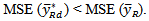 That is,
That is, This holds if the following two conditions are satisfied
This holds if the following two conditions are satisfied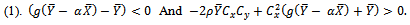 Or
Or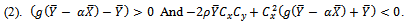 This condition holds if
This condition holds if 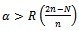 and
and 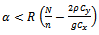 or
or 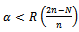 and
and 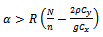
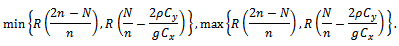 We also compared the proposed estimator
We also compared the proposed estimator  with the usual product estimator
with the usual product estimator 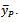 The MSE of the
The MSE of the 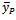 is given as
is given as 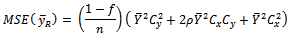 It is found that the proposed estimator
It is found that the proposed estimator 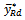 will be more efficient than the usual ratio estimator
will be more efficient than the usual ratio estimator 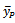 if
if 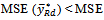
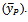 That is,
That is,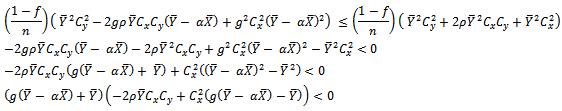 This holds if the following two conditions are satisfied
This holds if the following two conditions are satisfied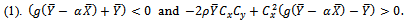 Or
Or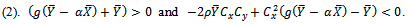 This condition holds if
This condition holds if 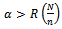 and
and 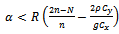 or
or 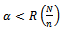 and
and 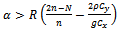
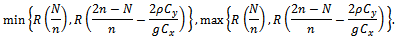 We also compared the MSE of the proposed estimator with MSE of dual product estimator
We also compared the MSE of the proposed estimator with MSE of dual product estimator 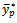 proposed by [20]. The MSE
proposed by [20]. The MSE 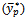 proposed by [20] (1980) is given as
proposed by [20] (1980) is given as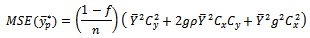 It is found that the proposed estimator
It is found that the proposed estimator 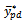 will be more efficient than that of [20] estimator
will be more efficient than that of [20] estimator 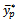 if
if 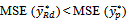 That is
That is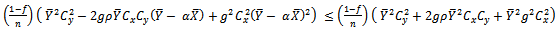 That is,
That is,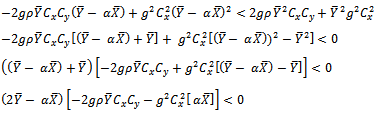 This holds if,
This holds if,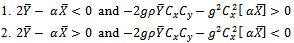 This condition holds if
This condition holds if 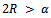 and
and 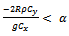 or
or 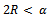 and
and 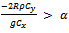 The range of α under which the proposed estimator
The range of α under which the proposed estimator 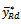 iS more efficient than
iS more efficient than 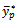 is
is 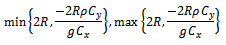 Lastly, we compared MSE of the proposed estimator
Lastly, we compared MSE of the proposed estimator 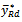 with that of dual to ratio estimator
with that of dual to ratio estimator 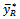 proposed [13] given in equation (7a). The proposed estimator will be more efficient than
proposed [13] given in equation (7a). The proposed estimator will be more efficient than 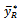 if
if 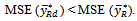 That is,
That is, 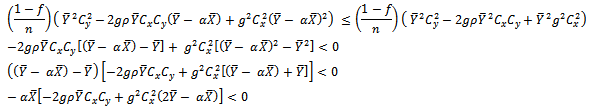 This holds if
This holds if 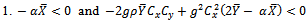 Or
Or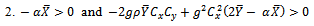 This condition holds if
This condition holds if 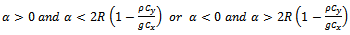 Therefore, the range of α under which the proposed estimator
Therefore, the range of α under which the proposed estimator 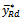 is more efficient than dual ratio estimator
is more efficient than dual ratio estimator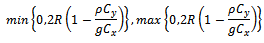 Thus it seems from the above that the proposed estimator
Thus it seems from the above that the proposed estimator 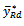 may be made better than the usual estimator, ratio estimator, product estimator, dual to product estimator
may be made better than the usual estimator, ratio estimator, product estimator, dual to product estimator 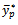 and the dual to ratio estimator
and the dual to ratio estimator 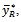 if the given conditions are satisfied.Comparison of ‘AOE’ to
if the given conditions are satisfied.Comparison of ‘AOE’ to 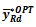
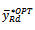 is more efficient than the other existing estimators
is more efficient than the other existing estimators 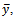 the ratio estimator
the ratio estimator 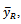 the product estimator
the product estimator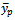 , the dual to ratio estimator
, the dual to ratio estimator 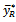 and the dual to product estimator
and the dual to product estimator 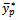 since
since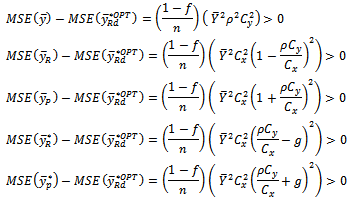 Hence, we conclude that the proposed class of estimator
Hence, we conclude that the proposed class of estimator 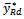 is more efficient than other estimator in case of its optimality.
is more efficient than other estimator in case of its optimality.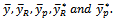 Data on the ages and hours of sleeping by the undergraduate students of the Department of Statistics Federal University of Technology Akure, Ondo State, Nigeria. A sample of 150 out of 461 students of the department was obtained using simple random sampling without replacement. The information on the age of the students was used as auxiliary information to increase the precision of the estimate of the average sleeping hours. The estimate of the average hours of sleeping of the students were obtained and also the 95% confidence intervals of the average hours of sleeping were obtained for the proposed estimator and the other estimators. Table 1., gives the estimates of the average sleeping hours and the 95% confidence Interval. As shown in Table 1.0, the proposed estimator performed better than the other estimators, the width of the confidence interval of the proposed estimator is smallest than the other competing estimators.
Data on the ages and hours of sleeping by the undergraduate students of the Department of Statistics Federal University of Technology Akure, Ondo State, Nigeria. A sample of 150 out of 461 students of the department was obtained using simple random sampling without replacement. The information on the age of the students was used as auxiliary information to increase the precision of the estimate of the average sleeping hours. The estimate of the average hours of sleeping of the students were obtained and also the 95% confidence intervals of the average hours of sleeping were obtained for the proposed estimator and the other estimators. Table 1., gives the estimates of the average sleeping hours and the 95% confidence Interval. As shown in Table 1.0, the proposed estimator performed better than the other estimators, the width of the confidence interval of the proposed estimator is smallest than the other competing estimators.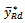 over the estimator
over the estimator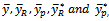 we obtained the percentage relative efficiency of different estimator of
we obtained the percentage relative efficiency of different estimator of 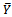 with respect to the usual unbiased estmator
with respect to the usual unbiased estmator 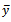 in Table 2. The proposed estimator
in Table 2. The proposed estimator 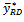 performed better than the other estimators
performed better than the other estimators 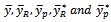 and perfoirmed exactly the same way as regression estimator.
and perfoirmed exactly the same way as regression estimator.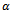 and its optimum values. Table 1. shows that the proposed estimator performed better than the other estimators as the width of the confidence interval of the proposed estimator is smallest than the other competing estimators. The percentage relative efficiency of different estimator of
and its optimum values. Table 1. shows that the proposed estimator performed better than the other estimators as the width of the confidence interval of the proposed estimator is smallest than the other competing estimators. The percentage relative efficiency of different estimator of 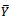 with respects to the usual unbiased estimator
with respects to the usual unbiased estimator 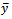 in Table 2. shows that the proposed estimator
in Table 2. shows that the proposed estimator 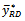 performed better than the other estimators
performed better than the other estimators 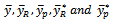 and performed exactly the same way as regression estimator. Hence, it is preferred to use the proposed class of estimator in practice.
and performed exactly the same way as regression estimator. Hence, it is preferred to use the proposed class of estimator in practice. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML

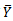 with respect to the usual unbiased estimator
with respect to the usual unbiased estimator