-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Probability and Statistics
p-ISSN: 2168-4871 e-ISSN: 2168-4863
2014; 3(3): 41-49
doi:10.5923/j.ijps.20140303.01
Simulation Based Method for Bearings-Only Tracking Application
1Department of Mathematics, University of Lagos, Nigeria
2Department of Computer Sciences, University of Lagos, Nigeria
Correspondence to: Nkemnole E. B., Department of Mathematics, University of Lagos, Nigeria.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
Target tracking is the problem of generating an inference engine on the state of a target using a sequence of observations in time, which is to recursively estimate the probability density function of the target state. Traditionally, linearized models are used, where the uncertainty in the sensor and motion models is typically modeled by Gaussian densities. In this paper, the sequential Monte Carlo (SMC) method is developed based on Student’s-t distribution, which is heavier tailed than Gaussians and hence more robust, The SMC method, or particle filter, provides an approximate solution to non-Gaussian estimation problem. To estimate the target state based on samples, an EM-type algorithm is developed and embedded in the Student’s-t particle filter. The expectation (E) step is implemented by the particle filter. Within this step, the distribution of the states given the observations, and the state vector are estimated. Consequently, in the maximization (M) step, we approximate the nonlinear observation equation as a mixture of Gaussians model and the Student’s-t model. A bearings-only tracking (BOT) problem is simulated to present the implementation of the particle filter algorithm based on both the mixture of Gaussians model and the Student’s-t. Simulations have demonstrated the effectiveness and the improved performance of the Student’s-t based particle filter over Gaussians mixture model. Additionally, the method is applied to real life data taken from the digital GSM real-time data logging tracking system. It is again shown that the Student’s-t based algorithm is successful in accommodating nonlinear model for a target tracking scenario.
Keywords: Bearing-Only Tracking, Sequential Monte Carlo, Expectation Maximization, Student’s-t Distribution, Mixture of Normal (MoN), State-space Model
Cite this paper: Nkemnole E. B., Abass O., Simulation Based Method for Bearings-Only Tracking Application, International Journal of Probability and Statistics , Vol. 3 No. 3, 2014, pp. 41-49. doi: 10.5923/j.ijps.20140303.01.
Article Outline
1. Introduction
- Target tracking is an important component of many modern applications, including: robots localization, visual tracking, radar tracking, and satellite navigation. In addition, it involves tracking of an object (typical examples include ships, planes and other moving vehicles). The key to a successful target tracking depends on an effective extraction of the useful information about the target state from available observations.From a Bayesian perspective, the tracking problem can be solved by recursively calculating some degree of belief in the target state, taking different values, given available observations. Thus, it is generally required to construct the conditional probability density function (PDF) of the target state. Since the target state uncertainty and the measurement-originated uncertainty are the two major unavoidable obstacles for target tracking, a good model of the target motion will effectively facilitate the design of the required tracking algorithm. Assume the target motion and its measurements can be reasonably represented by some known mathematical models; the commonly used models are the state space model described in the following form:
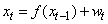 | (1) |
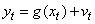 | (2) |
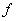 and
and 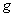 are either linear or nonlinear functions,
are either linear or nonlinear functions, 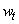 and
and 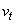 represent i.i.d process and measurement noise sequence, respectively.
represent i.i.d process and measurement noise sequence, respectively. 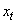 and
and 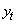 denote the target state vector and the measurement at sample time
denote the target state vector and the measurement at sample time 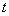 , respectively. Models represented by (1) - (2) are referred to as state space model. This includes such models as the bearings-only tracking.The aim of Bayesian tracking is to estimate recursively conditional PDF
, respectively. Models represented by (1) - (2) are referred to as state space model. This includes such models as the bearings-only tracking.The aim of Bayesian tracking is to estimate recursively conditional PDF 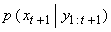 using prediction and an updating procedure as follows:Using (1) to obtain the predictive PDF of
using prediction and an updating procedure as follows:Using (1) to obtain the predictive PDF of 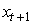 for a known PDF
for a known PDF 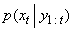 at time
at time 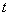 : prediction:
: prediction: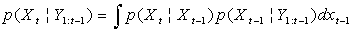 | (3) |
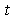 , the predictive PDF (3) is updated by the information contained in the measurement
, the predictive PDF (3) is updated by the information contained in the measurement 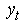 through Bayesian Formula: updating:
through Bayesian Formula: updating: 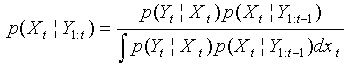 | (4) |
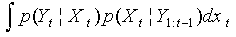 is calculated and which depends on the Likelihood function of
is calculated and which depends on the Likelihood function of 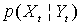 .The recurrence relationships in (3) and (4) form the basis of Bayesian tracking. In general, such recursive propagation of the density is generally difficult to analytically determine their compact mathematical expressions since they require the evaluation of complex high-dimensional integrals. When the system is linear with a Gaussian noise, the Kalman filter constitutes an optimal Bayesian solution Anderson and Moore (1979). However, for most non-linear non-Gaussian models, it is not possible to compute these distributions in closed-form and we need to employ numerical methods.The problem of target tracking using bearings-only measurements is a difficult task. The filtering algorithms involve a nonlinear measurement process, which, when linearized, can lead to time-varying parameters, biases as explained by Aidala (1979). The common estimation algorithms used for bearings-only target tracking are: Least Squares (batch and recursive forms), Maximum Likelihood Estimator, Extended Kalman Filter (EKF), and Particle Filters or Bayesian Methods.Most researchers in the field of bearings-only tracking have concentrated on tracking a nonmanoeuvring target. Due to inherent nonlinearity and observability issues, it is difficult to construct a finite-dimensional optimal filter even for this relatively simple problem. As for the bearings-only tracking of a manoeuvring target, the problem is much more difficult. Early research focuses mainly on analytical derivations for the observability criteria of the estimation process, and comparisons of the convergence properties and performance of the different types of method used for target tracking. Since bearings-only target estimation involves a non-linear measurement process, several filtering and observability complications arise. Lindgren and Gong (1978) analyze the observability associated with a least-squares estimation approach and show that, for a constant velocity target and a constant velocity vehicle moving in a 2-D plane, the target estimation is unobservable until the vehicle executes a maneuver (change in heading). Kalman Filtering techniques are used by Aidala (1979) and by Nardone, et al., (1984). Since the bearings-only estimation problem involves nonlinear measurements, an EKF approach needs to be used instead of the normal Kalman Filter. The EKF however is sensitive to initialization techniques and measurement errors which can cause early covariance collapse and other filter instabilities Aidala (1979). The moving vehicle trajectory affects the observability and convergence of the target estimation, suggesting that a good trajectory design can reduce filter instability and estimation errors. A pseudolinear filter formulation is proposed by Aidala and Nardone (1982), which attempts to linearize the dynamics and measurement models. However by linearizing the dynamics the noise becomes non-Gaussian which, when propagated through the filter, causes estimation bias. For the bearings-only tracking problem, the bias is introduced only in the position estimate, and is highly dependent on the geometry of the vehicle maneuvers, once again suggesting that the estimation performance can be improved by proper design of the vehicle trajectory. Comparisons of the properties and performance between several different filtering algorithms are explored by Nardone, et al., (1984). Aidala and Hammel (1983) proposed the modified polar coordinates filter. The filter uses an EKF algorithm with a state vector choice, based on polar coordinates, that attempts to separate the observable and unobservable components of the estimated state by using a different coordinate system. The resulting filter is stable and asymptotically unbiased. The modified polar coordinate filter shows the dependence of the target estimation on the vehicle maneuvers, once again suggesting that the estimation can be improved by designing a good trajectory. De Vlieger (1992) used a piecewise linear model of the target motion and a Maximum Likelihood Estimator approach for target tracking. He uses numerical methods to condition the measurement model to increase the observability of the estimation. Goshen-Meskin and Bar-Itzhack, (1992) derive the observability requirements for piecewise constant linear systems. Tao et al., (1996) shows that for a MLE approach it is important to consider the correlation of the noise, and that ignoring it degrades the performance of the estimation. Several modifications to the classical estimation algorithms have been explored. Some attempt to smooth the trajectory, within the constraints of a known target behavior model. Others consist of designing multiple filters for different known target scenario and using statistical properties of the innovation to switch between the algorithms. Another approach has been to support multiple Kalman filters simultaneously and develop an estimate by combining all the filters. Later research by Bar-Shalom et al. (2002) has focused on using interacting multiple models (IMM). These algorithms employ a constant velocity (CV) model along with manoeuvre models to capture the dynamic behaviour of a manoeuvring target scenario. Le Cadre and Tremois, (1998) modelled the manoeuvring target using the CV model with Gaussian noise and developed a tracking filter in the hidden Markov model framework.Particle filtering or Sequential Monte Carlo techniques have also been explored by Liu et al., (2002), Bar-Shalom et al., (2001), Ristic et al., (2004). Particle filters have the advantage of being able to deal with nonlinear systems and non-Gaussian noise models making them particularly well suited to bearings-only tracking. They can also accommodate unknown and stochastic target models making them more versatile than classical filters. However, they require increased computational resources and, for fast convergence, need a fairly accurate description of the measurement likelihood function and a good initial distribution on the estimated target location.In this paper, the particle filter is developed based on the Student’s-t distribution for nonlinear bearing-only tracking problem and compare with the Mixture of Normal (MoN) based particle filter of Kim and Stoffer (2008). The outline of the remainder of this article is organized as follows: section 2 is a general presentation of the BOT problem. Section 3 gives a succinct analysis of the basic theory of the EM procedure and the SMC methods. The details of the proposed EM–SMC (particle filter) algorithm follow. The implementation of the E-step using a particle filter, and the M-step by fitting a Student’s-t model to the estimated data, are provided as well. Simulation results and application to the real data that confirms the proposed method based on Student’s-t are presented in section 4, while section 5 concludes the work.
.The recurrence relationships in (3) and (4) form the basis of Bayesian tracking. In general, such recursive propagation of the density is generally difficult to analytically determine their compact mathematical expressions since they require the evaluation of complex high-dimensional integrals. When the system is linear with a Gaussian noise, the Kalman filter constitutes an optimal Bayesian solution Anderson and Moore (1979). However, for most non-linear non-Gaussian models, it is not possible to compute these distributions in closed-form and we need to employ numerical methods.The problem of target tracking using bearings-only measurements is a difficult task. The filtering algorithms involve a nonlinear measurement process, which, when linearized, can lead to time-varying parameters, biases as explained by Aidala (1979). The common estimation algorithms used for bearings-only target tracking are: Least Squares (batch and recursive forms), Maximum Likelihood Estimator, Extended Kalman Filter (EKF), and Particle Filters or Bayesian Methods.Most researchers in the field of bearings-only tracking have concentrated on tracking a nonmanoeuvring target. Due to inherent nonlinearity and observability issues, it is difficult to construct a finite-dimensional optimal filter even for this relatively simple problem. As for the bearings-only tracking of a manoeuvring target, the problem is much more difficult. Early research focuses mainly on analytical derivations for the observability criteria of the estimation process, and comparisons of the convergence properties and performance of the different types of method used for target tracking. Since bearings-only target estimation involves a non-linear measurement process, several filtering and observability complications arise. Lindgren and Gong (1978) analyze the observability associated with a least-squares estimation approach and show that, for a constant velocity target and a constant velocity vehicle moving in a 2-D plane, the target estimation is unobservable until the vehicle executes a maneuver (change in heading). Kalman Filtering techniques are used by Aidala (1979) and by Nardone, et al., (1984). Since the bearings-only estimation problem involves nonlinear measurements, an EKF approach needs to be used instead of the normal Kalman Filter. The EKF however is sensitive to initialization techniques and measurement errors which can cause early covariance collapse and other filter instabilities Aidala (1979). The moving vehicle trajectory affects the observability and convergence of the target estimation, suggesting that a good trajectory design can reduce filter instability and estimation errors. A pseudolinear filter formulation is proposed by Aidala and Nardone (1982), which attempts to linearize the dynamics and measurement models. However by linearizing the dynamics the noise becomes non-Gaussian which, when propagated through the filter, causes estimation bias. For the bearings-only tracking problem, the bias is introduced only in the position estimate, and is highly dependent on the geometry of the vehicle maneuvers, once again suggesting that the estimation performance can be improved by proper design of the vehicle trajectory. Comparisons of the properties and performance between several different filtering algorithms are explored by Nardone, et al., (1984). Aidala and Hammel (1983) proposed the modified polar coordinates filter. The filter uses an EKF algorithm with a state vector choice, based on polar coordinates, that attempts to separate the observable and unobservable components of the estimated state by using a different coordinate system. The resulting filter is stable and asymptotically unbiased. The modified polar coordinate filter shows the dependence of the target estimation on the vehicle maneuvers, once again suggesting that the estimation can be improved by designing a good trajectory. De Vlieger (1992) used a piecewise linear model of the target motion and a Maximum Likelihood Estimator approach for target tracking. He uses numerical methods to condition the measurement model to increase the observability of the estimation. Goshen-Meskin and Bar-Itzhack, (1992) derive the observability requirements for piecewise constant linear systems. Tao et al., (1996) shows that for a MLE approach it is important to consider the correlation of the noise, and that ignoring it degrades the performance of the estimation. Several modifications to the classical estimation algorithms have been explored. Some attempt to smooth the trajectory, within the constraints of a known target behavior model. Others consist of designing multiple filters for different known target scenario and using statistical properties of the innovation to switch between the algorithms. Another approach has been to support multiple Kalman filters simultaneously and develop an estimate by combining all the filters. Later research by Bar-Shalom et al. (2002) has focused on using interacting multiple models (IMM). These algorithms employ a constant velocity (CV) model along with manoeuvre models to capture the dynamic behaviour of a manoeuvring target scenario. Le Cadre and Tremois, (1998) modelled the manoeuvring target using the CV model with Gaussian noise and developed a tracking filter in the hidden Markov model framework.Particle filtering or Sequential Monte Carlo techniques have also been explored by Liu et al., (2002), Bar-Shalom et al., (2001), Ristic et al., (2004). Particle filters have the advantage of being able to deal with nonlinear systems and non-Gaussian noise models making them particularly well suited to bearings-only tracking. They can also accommodate unknown and stochastic target models making them more versatile than classical filters. However, they require increased computational resources and, for fast convergence, need a fairly accurate description of the measurement likelihood function and a good initial distribution on the estimated target location.In this paper, the particle filter is developed based on the Student’s-t distribution for nonlinear bearing-only tracking problem and compare with the Mixture of Normal (MoN) based particle filter of Kim and Stoffer (2008). The outline of the remainder of this article is organized as follows: section 2 is a general presentation of the BOT problem. Section 3 gives a succinct analysis of the basic theory of the EM procedure and the SMC methods. The details of the proposed EM–SMC (particle filter) algorithm follow. The implementation of the E-step using a particle filter, and the M-step by fitting a Student’s-t model to the estimated data, are provided as well. Simulation results and application to the real data that confirms the proposed method based on Student’s-t are presented in section 4, while section 5 concludes the work. 2. Bearings-Only Tracking
- Bearings-only tracking involves estimating the target states based on angle measurements at a sensor node. The target is assumed to move in the x-y plane and to follow a constant-velocity motion model Bar-Shalom and Fortmann (1988) with a state update period of 1s. The state vector
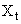 contains the positions and velocities of the object in the
contains the positions and velocities of the object in the 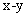 directions respectively:
directions respectively: 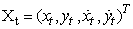 , where
, where 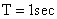 denotes the sampling period. One possible discretization of this model, is given by Gordon et al., (1993)
denotes the sampling period. One possible discretization of this model, is given by Gordon et al., (1993)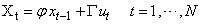 | (5) |
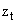 , is
, is 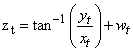 | (6) |
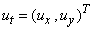 ,
,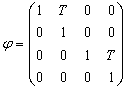 ,
, 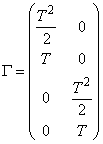 Parameter
Parameter 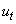 represents the system noise and is Gaussian distributed with covariance
represents the system noise and is Gaussian distributed with covariance 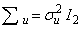 where
where 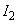 is a
is a 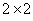 identity matrix. This vector can be thought of as representing the acceleration in the
identity matrix. This vector can be thought of as representing the acceleration in the 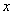 and
and 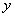 directions.
directions. 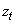 represents the observed bearing of the object measured by the sensor at time
represents the observed bearing of the object measured by the sensor at time 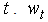 represents a Gaussian measurement noise with mean zero and variance
represents a Gaussian measurement noise with mean zero and variance 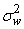 . Before measurements are taken, the particle filter recursion is started with initial state vector in the form of a 4 dimensional Gaussian variable with known mean and covariance matrix. As can be seen, this model is 4 dimensional and nonlinear due to a transcendental function in the observation equation. The particle filters handle these situations efficiently. It has been shown through intense simulations in Gordon et al., (1993), that particle filters are much more efficient for this problem than the traditional EKF. The BOT problem is illustrated in figure 1.
. Before measurements are taken, the particle filter recursion is started with initial state vector in the form of a 4 dimensional Gaussian variable with known mean and covariance matrix. As can be seen, this model is 4 dimensional and nonlinear due to a transcendental function in the observation equation. The particle filters handle these situations efficiently. It has been shown through intense simulations in Gordon et al., (1993), that particle filters are much more efficient for this problem than the traditional EKF. The BOT problem is illustrated in figure 1.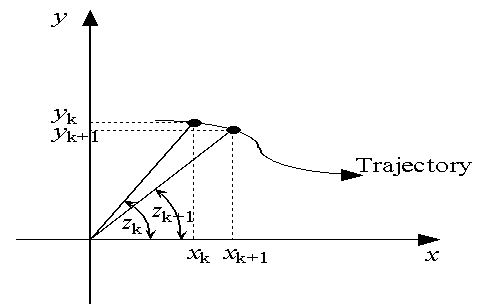 | Figure 1. The Bearings-Only Tracking (BOT) problem |
3. Nonlinear State Estimation Using Expectation-Maximization (EM)
- State estimation in a nonlinear state-space dynamical system whose evolution process is described as in equation (1) consists of estimating the state data vector using a sequence of noisy measurements given by the model in equation (2). The main idea in EM-based algorithms is to solve the state estimation problem in the presence of model uncertainty in two iterative steps Baum et al, (1970), Dempster et al. (1977). Starting from some initial parameters
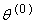 the algorithm iteratively applies:E-step: Compute the expected likelihood,
the algorithm iteratively applies:E-step: Compute the expected likelihood, 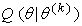
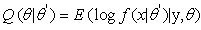 M-step: Choose
M-step: Choose 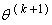 the parameter values that maximizes the function,
the parameter values that maximizes the function, 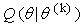 .In the E-step, it is assumed that the model is known perfectly and therefore standard estimation methods are used to estimate the states. The primary purpose of the E-step is to estimate the hidden states. This is accomplished by determining the best distribution which makes the expectation of log-likelihood maximum. The M-step involves estimating the model parameters
.In the E-step, it is assumed that the model is known perfectly and therefore standard estimation methods are used to estimate the states. The primary purpose of the E-step is to estimate the hidden states. This is accomplished by determining the best distribution which makes the expectation of log-likelihood maximum. The M-step involves estimating the model parameters 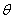 using the states estimated in the previous E-step and their corresponding measurements. Different implementations of the E and the M steps have resulted in different algorithms suitable for different applications.In the E-step of the proposed algorithm, an approximation of the desired distribution of the states given the measurements is formulated. This distribution is then used to estimate the states. In nonlinear systems this conditional density is generally non-Gaussian and can be quite complex. We use a SMC (particle filter) Doucet et. al. (2001) algorithm to estimate and recursively update this distribution in time. This greatly assists the algorithm in converging to the global optimum. In the maximization (M) step, the unknown measurement process is approximated by fitting the observations to a Student’s-t model using the current estimate of the states.
using the states estimated in the previous E-step and their corresponding measurements. Different implementations of the E and the M steps have resulted in different algorithms suitable for different applications.In the E-step of the proposed algorithm, an approximation of the desired distribution of the states given the measurements is formulated. This distribution is then used to estimate the states. In nonlinear systems this conditional density is generally non-Gaussian and can be quite complex. We use a SMC (particle filter) Doucet et. al. (2001) algorithm to estimate and recursively update this distribution in time. This greatly assists the algorithm in converging to the global optimum. In the maximization (M) step, the unknown measurement process is approximated by fitting the observations to a Student’s-t model using the current estimate of the states.3.1. Sequential Monte Carlo Methods
- After the introduction of SMC in the 1960’s, it has become an emerging methodology for the nonlinear or non-Gaussian state-space models. SMC methods or particle filters are a class of recursive simulation methods for solving filtering problems Doucet et. al., (2001), Gordon et. al., (1993). The chief initiative is to represent the interested density function
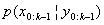 at time
at time 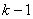 by a set of random samples with associated weights,
by a set of random samples with associated weights, 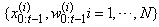 and compute estimates based on these samples and associated weights. As the number of samples becomes very large, this Monte Carlo characterization develops into an equivalent representation to the functional description of the posterior probability density function (Arulampalam, et. al., 2002). If we let
and compute estimates based on these samples and associated weights. As the number of samples becomes very large, this Monte Carlo characterization develops into an equivalent representation to the functional description of the posterior probability density function (Arulampalam, et. al., 2002). If we let 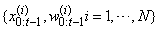 be samples and associated weights approximating the density function
be samples and associated weights approximating the density function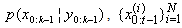 is a set of particles with associated weights
is a set of particles with associated weights 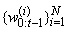 with
with 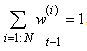 , then the density function are approximated by
, then the density function are approximated by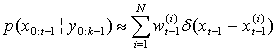
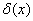 signifies the Dirac delta role. The particle approximation
signifies the Dirac delta role. The particle approximation 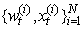 are transformed into an equally weighted random sample from
are transformed into an equally weighted random sample from 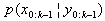 by sampling, with replacement, from the discrete distribution
by sampling, with replacement, from the discrete distribution 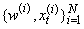 . This procedure, otherwise called resampling, produces a new sample with uniformly distributed weights so that
. This procedure, otherwise called resampling, produces a new sample with uniformly distributed weights so that 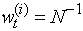 . Particle filters use a combination of importance sampling, weight update and resampling to sequentially obtain and update the distribution. Importance sampling approximates a probability distribution using a set of
. Particle filters use a combination of importance sampling, weight update and resampling to sequentially obtain and update the distribution. Importance sampling approximates a probability distribution using a set of 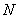 weighted particles
weighted particles 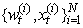 , where
, where 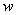 represents the state and the corresponding weight for the
represents the state and the corresponding weight for the 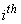 particle. The weight update stage uses measurements to update particle weights. The updated particles are used to make inferences on the state. The resampling stage avoids degeneracy by removing particles with low weights and replicating particles with high weights.
particle. The weight update stage uses measurements to update particle weights. The updated particles are used to make inferences on the state. The resampling stage avoids degeneracy by removing particles with low weights and replicating particles with high weights.3.1.1. Particle Filter Algorithm
- Suppose that we have at time
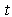 weighted particles
weighted particles 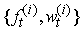 drawn from
drawn from 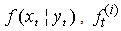 is a set of particle filter with associated weight
is a set of particle filter with associated weight 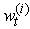 . This is considered as an empirical approximation for the density made up of point masses,
. This is considered as an empirical approximation for the density made up of point masses,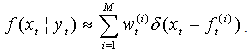 Kitagawa and Sato (2001) and Kitagawa (1996) give an algorithm for filtering in general state space model thus:Monte Carlo filtering for general state-space models1. For
Kitagawa and Sato (2001) and Kitagawa (1996) give an algorithm for filtering in general state space model thus:Monte Carlo filtering for general state-space models1. For 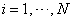 , generate a random number
, generate a random number 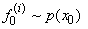 2. Repeat the following steps for
2. Repeat the following steps for 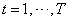 .a. For
.a. For 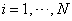 , generate a random number
, generate a random number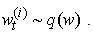 b. For
b. For 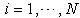 , Compute
, Compute 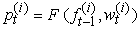 c. For
c. For 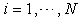 , Compute
, Compute 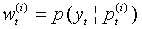 d. Generate
d. Generate 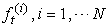 by resampling
by resampling 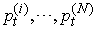 3. This Monte Carlo filter returns
3. This Monte Carlo filter returns 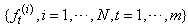 so that
so that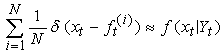
3.1.2. Particle Smoothing Algorithm
- If we let
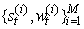 be set of particle smoothers and associated weights approximating the density function
be set of particle smoothers and associated weights approximating the density function 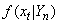 , then the density function are approximated by
, then the density function are approximated by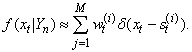 The problem with smoothed estimates is degeneracy. Godsill et al. (2004) suggested a new smoothing method (particle smoother using backwards simulation). The method assumes that the filtering has already been performed. Thus, the particles and associated weights,
The problem with smoothed estimates is degeneracy. Godsill et al. (2004) suggested a new smoothing method (particle smoother using backwards simulation). The method assumes that the filtering has already been performed. Thus, the particles and associated weights, 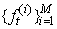 ,
, 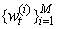 can approximate the filtering density,
can approximate the filtering density, 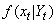 , by
, by 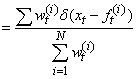 . The following is the algorithm from Godsill et al. (2004):Particle smoother using backwards simulationSuppose weighted particles
. The following is the algorithm from Godsill et al. (2004):Particle smoother using backwards simulationSuppose weighted particles 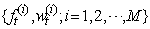 are available for
are available for 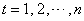 . For
. For 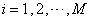 ,1. Choose
,1. Choose 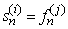 with probability
with probability 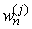 2. For
2. For 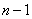 to
to 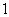 a. Calculate
a. Calculate 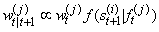 for each
for each 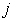 .b. Choose
.b. Choose 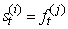 with probability
with probability 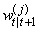 .3.
.3. 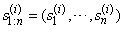 is an approximate realization from
is an approximate realization from 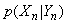 .
.3.1.3. Sequential Monte Carlo Expectation maximization (SMCEM) for Bearings-Only Tracking
- The entire procedure based on Student’s-t distribution consists of three main steps: filtering, smoothing, and estimation. With the output of filtering and smoothing step an approximate expected likelihood is calculated. Filtering Step:The below algorithm for the filtering and smoothing steps shows an extension of Godsill et al., (2004) and Kim and Stoffer (2008) results. From here,
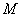 samples from
samples from 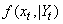 for each were obtained.1) Generate
for each were obtained.1) Generate 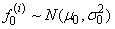 2) For
2) For 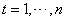 a. Generate a random number
a. Generate a random number 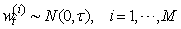 b. Compute
b. Compute 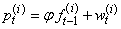 c. Compute
c. Compute 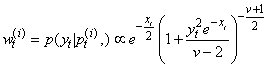 d. Generate
d. Generate 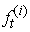 by resampling with weights,
by resampling with weights, 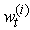 Smoothing stepIn the smoothing step, particle smoothers that are needed to get the expected likelihood in the expectation step of the EM algorithm were obtained: Suppose that equally weighted particles
Smoothing stepIn the smoothing step, particle smoothers that are needed to get the expected likelihood in the expectation step of the EM algorithm were obtained: Suppose that equally weighted particles 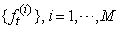 from
from 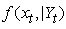 are available for
are available for 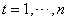 from the filtering step.1) Choose
from the filtering step.1) Choose 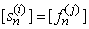 with probability
with probability 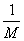 .2) For
.2) For 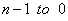 a. Calculate
a. Calculate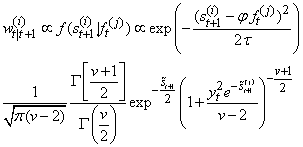 for each
for each 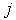 b. Choose
b. Choose 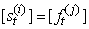 with probability
with probability 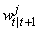 .d.
.d. 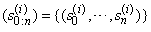 is the random sample from
is the random sample from 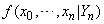 . 4) Repeat steps (1) – (3), for
. 4) Repeat steps (1) – (3), for 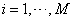 and calculate
and calculate 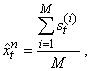
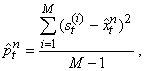
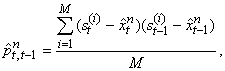
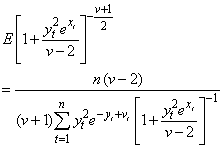 .Estimation StepWe view
.Estimation StepWe view 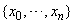 as unobserved and apply the EM algorithm. However, problems arise when the model is not Gaussian because it can be difficult to compute the expected likelihood. As such, a simulation-based particle filters and smoothers are used to obtain the values needed for calculating the expected likelihood. The procedure performed in this algorithm consists of running a filtering and smoothing step for the given parameters, and then running an estimation step to get updated parameter estimates.Using equation (5) and (6), the proposed technique for target tracking is applied. The state update is used to propose new particles. This provides a sub-optimal recursive estimate of the target position in the
as unobserved and apply the EM algorithm. However, problems arise when the model is not Gaussian because it can be difficult to compute the expected likelihood. As such, a simulation-based particle filters and smoothers are used to obtain the values needed for calculating the expected likelihood. The procedure performed in this algorithm consists of running a filtering and smoothing step for the given parameters, and then running an estimation step to get updated parameter estimates.Using equation (5) and (6), the proposed technique for target tracking is applied. The state update is used to propose new particles. This provides a sub-optimal recursive estimate of the target position in the 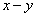 plane. Previous approaches to density estimation have mostly focused on Gaussian nonlinear measurement dynamics in practice. The SMCEM algorithm is developed based on non-Gaussian, which are heavier tailed than Gaussians and hence more robust. Simulations have demonstrated not only the effectiveness but also the improved performance of the non-Gaussian distribution over Gaussian.As we observed the target in its motion, new data
plane. Previous approaches to density estimation have mostly focused on Gaussian nonlinear measurement dynamics in practice. The SMCEM algorithm is developed based on non-Gaussian, which are heavier tailed than Gaussians and hence more robust. Simulations have demonstrated not only the effectiveness but also the improved performance of the non-Gaussian distribution over Gaussian.As we observed the target in its motion, new data 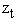 accrue, along with new parameters
accrue, along with new parameters 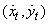 . The vector of unknown at time
. The vector of unknown at time 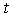 is
is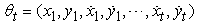 ,and the data are
,and the data are 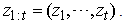 Therefore, the target distribution evolves in an expanding space,
Therefore, the target distribution evolves in an expanding space, 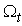 . As
. As 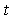 increases, the aim here is to maintain a set of sampled particles in
increases, the aim here is to maintain a set of sampled particles in 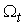 which can be used to estimate aspect of the distribution of interest. In particular, these particles can be used at any given time point
which can be used to estimate aspect of the distribution of interest. In particular, these particles can be used at any given time point 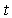 to approximate the conditional distribution for the current state of the object, given the data,
to approximate the conditional distribution for the current state of the object, given the data, 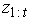 accumulated up to that point. The procedure for the BOT problem is summarized below.Given the observed data
accumulated up to that point. The procedure for the BOT problem is summarized below.Given the observed data 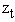 at
at 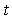 For
For 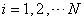 sample particles,
sample particles, 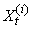 are drawn from the density
are drawn from the density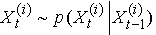 using (5).
using (5).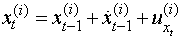
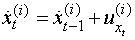
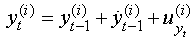
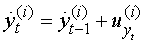 the weights are updated recursively using
the weights are updated recursively using 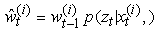 where
where 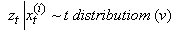 We evaluate this distribution at time
We evaluate this distribution at time 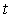 for the parameters estimation by using the EM algorithm and SMC, and then calculate the output:
for the parameters estimation by using the EM algorithm and SMC, and then calculate the output: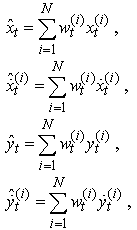 The mean estimate of the target state and the covariance matrix of the estimate error are approximated by
The mean estimate of the target state and the covariance matrix of the estimate error are approximated by 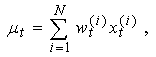
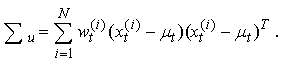
4. Experiment Results - Tracking Performance
- An in-depth analysis of the tracking performance for the BOT problem is investigated in various works including Gordon et al., (1993) and Doucet et al., (2001). A bearings-only tracking problem is simulated to present implementation of the SMCEM algorithm based on both the mixture of Gaussians model of Kim and Stoffer (2008) and the Student’s-t. A target trajectory and associated measurements is generated according to equations (5) and (6) with the parameter values
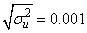 ,
, 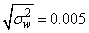 the initial state of the target
the initial state of the target 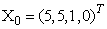 and covariance
and covariance 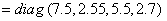 . The time between successive measurements is
. The time between successive measurements is 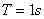 and a single bearing measurement is obtained in each time step.
and a single bearing measurement is obtained in each time step. 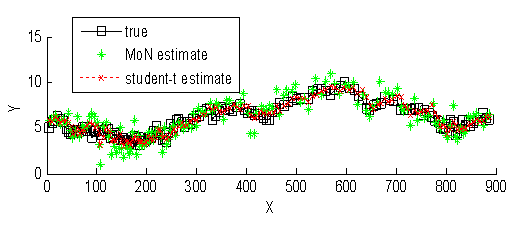 | Figure 2. Three scenarios for the BOT. Representation of the trajectories of the true target path (shown by a square), MoN (shown by an asterisk) and the Student’s-t estimate |
|
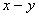 plane, with the position of the target at each time being shown by a square and the mixture of normal by an asterisk. The result of applying the SMCEM with
plane, with the position of the target at each time being shown by a square and the mixture of normal by an asterisk. The result of applying the SMCEM with 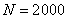 particles is shown in the figure. The number of particles was chosen such that further increase in
particles is shown in the figure. The number of particles was chosen such that further increase in 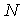 does not bring a significant improvement in the tracking performance. The cross symbol gives the Student’s-t estimate such that the estimate moves towards the true target path. The performance is evaluated using the mean square error (MSE) and chi-square criterion Gallant and Long (1997) for each time. According to Sanjeev et al., (2004)
does not bring a significant improvement in the tracking performance. The cross symbol gives the Student’s-t estimate such that the estimate moves towards the true target path. The performance is evaluated using the mean square error (MSE) and chi-square criterion Gallant and Long (1997) for each time. According to Sanjeev et al., (2004) 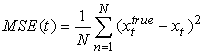 | (7) |
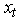 denotes the estimate at time
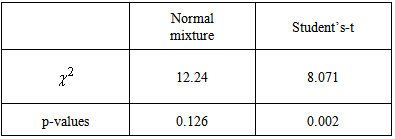
denotes the estimate at time 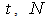 is the total number of realizations over which the MSE is averaged. Each of these realizations used observations from the same generated true state. Obviously, with increasing particles, the performance in terms of mean square error (MSE) improves. The MSE value (7.2197 and 11.0112 for mixture normal and Student’s-t) is obtained independently for each element of the state in the BOT problem. For the Student’s-t based filter, no tracks diverged. It can be seen that the accuracy of the position estimation of the Student’s-t particle filter is significantly higher than that of the normal mixture. Furthermore, our empirical implementation based on chi-square criterion, [Gallant and Long (1997), [see table] reveals that the technique based on the Student’s-t is statistically significant at 1% significance level.
is the total number of realizations over which the MSE is averaged. Each of these realizations used observations from the same generated true state. Obviously, with increasing particles, the performance in terms of mean square error (MSE) improves. The MSE value (7.2197 and 11.0112 for mixture normal and Student’s-t) is obtained independently for each element of the state in the BOT problem. For the Student’s-t based filter, no tracks diverged. It can be seen that the accuracy of the position estimation of the Student’s-t particle filter is significantly higher than that of the normal mixture. Furthermore, our empirical implementation based on chi-square criterion, [Gallant and Long (1997), [see table] reveals that the technique based on the Student’s-t is statistically significant at 1% significance level.4.1. Dynamic Modeling of a Vehicle Tracking
- The proposed estimation technique was also applied to the problem of tracking a moving vehicle. Data were taken from the digital GSM real-time data logging tracking system, (see www.trackingtheworld.com). It models the dynamic properties of the tracked vehicle and estimates it using the proposed technique. From the data collected, we estimate the vehicle’s position
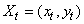 at time
at time 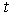 , and its velocity
, and its velocity 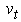 . Also at each time step we obtain a new measurement
. Also at each time step we obtain a new measurement 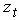 . the velocity evolves over time according to
. the velocity evolves over time according to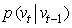 .The vehicle moves based on the evolved velocity according to a dynamics model:
.The vehicle moves based on the evolved velocity according to a dynamics model: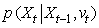 .The measurements are governed by a measurement model:
.The measurements are governed by a measurement model: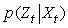 .The measurement likelihood factor is
.The measurement likelihood factor is 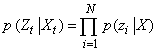 .At each time step
.At each time step 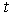 , we produce an estimate of the proposed technique about the tracked vehicle trajectory and velocity based on a set of measurements:
, we produce an estimate of the proposed technique about the tracked vehicle trajectory and velocity based on a set of measurements: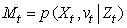 | (8) |
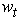 for all particles:
for all particles: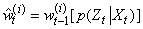 where
where 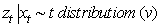 . The results for this case are presented in Figure 3. The Student’s-t based SMCEM algorithm is able to track the true path of the vehicle being tracked and remains stable and converges, showing that increasing the information provided by the measurements improves the accuracy and convergence of the estimation.
. The results for this case are presented in Figure 3. The Student’s-t based SMCEM algorithm is able to track the true path of the vehicle being tracked and remains stable and converges, showing that increasing the information provided by the measurements improves the accuracy and convergence of the estimation.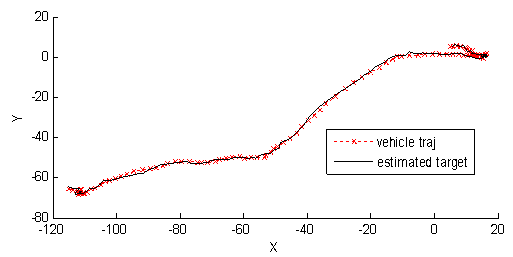 | Figure 3. Estimates of the vehicle being tracked |
5. Conclusions
- It has been shown in this paper that a Student’s-t distribution based particle filter provides a much better performance than the normal mixture based particle filter. An EM-type algorithm for solving a joint estimation-identification problem for nonlinear non-Gaussian state-space estimation when the observation model is uncertain is proposed. The expectation (E) step is implemented by the particle filter. Within this step, the distribution of states given the measurements as well as the state vectors is estimated. Consequently, in the maximization (M) step, the nonlinear measurement process parameters are approximated as a mixture of Normal model and as a Student’s-t model. The SMCEM algorithm based on both the mixture of Gaussians model of Kim and Stoffer (2008) and the Student-t is used to solve a nonlinear bearing-only tracking problem. It is shown that the accuracy of the position estimation of the Student’s-t filter is significantly higher than that of the normal mixture. Additionally, the method is applied to real life data taken from the digital GSM real-time data logging tracking system. It is again shown that the Student’s-t based algorithm is successful in accommodating nonlinear model for a target tracking scenario.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML