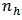E. P. Clement1, G. A. Udofia2, E. I. Enang2
1Department of Mathematics and Statistics, University of Uyo, Uyo, Nigeria
2Department of Mathematics, Statistics and Computer Science, University of Calabar, Calabar, Nigeria
Correspondence to: E. P. Clement, Department of Mathematics and Statistics, University of Uyo, Uyo, Nigeria.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The phenomenon of nonresponse in a sample survey reduces the precision of parameters estimates and increases bias in estimates resulting in larger mean square error, thus ultimately reducing their efficiency. An important technique to address these problems is by calibration. We proposed calibration estimators for totals of domain of study. Sample designs and in particular sample sizes are chosen so as to provide reliable estimates for domains of study. But budget and other constraints usually prevent the allocation of sufficiently large samples to domains to provide reliable estimates using traditional statistical techniques. We have developed an approach for finding the best sample design for the domain calibration estimators subject to a cost constraint and derived optimum stratum sample sizes that minimized the variances of the proposed domain calibration estimators and reduced the objective function. The efficacy of the proposed domain calibration estimators was tested through a real data analysis. Results of the analytical study using real data showed that our proposed domain calibration estimator is substantially superior to the traditional GREG-estimator with relatively small bias, mean square error and average length of confidence interval.
Keywords:
Design weights, Domain of study, GREG-estimator, Nonresponse, Optimum stratum sample sizes
Cite this paper: E. P. Clement, G. A. Udofia, E. I. Enang, Sample Design for Domain Calibration Estimators, International Journal of Probability and Statistics , Vol. 3 No. 1, 2014, pp. 8-14. doi: 10.5923/j.ijps.20140301.02.
1. Introduction
Nonresponse always exists when surveying human populations as people hesitate to respond in surveys. Nonresponse as an aspect in almost every type of sample survey creates problems for estimation which cannot simply be eliminated by increasing sample size.This phenomenon of nonresponse in a sample survey reduces the precision of parameters estimates and increases bias in estimates resulting in larger mean square error, thus ultimately reducing their efficiency.An important technique to address these problems is by calibration. Calibration as a tool for reweighting for nonresponse was first introduced by[4] for the estimation of finite population characteristics like means ratios and totals. Deville and Sarndal calibration estimation procedure provides a valuable class of techniques for combining data sources. The basic idea is to use estimates from one set of sources, which may be treated as sufficient accurate to act as benchmark. Estimates based on data from further sample source are then adjusted so as to agree with these benchmarks. The process of adjustment is called Calibration. The constraints that the estimates of the benchmarks based on this source should agree with the benchmarks are called Calibration Constraints.The problem of calibration of design weights is well known in the literature of survey sampling.[4] used the method of calibration of estimators using auxiliary information. Their calibration method provides a class of estimates. Some of the well known estimators such as classical ratio estimator belong to this class. Several authors including[5-6, 9-13] among others considered the[4] method and derived important calibrated estimators. But so far derivation of calibrated estimators from the class of calibrated estimators derived by[4] method in the context of domain estimation is not well known in the literature. Our objective therefore is to extend calibration estimation to domain estimation.Consider the finite population under study 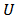 of size
of size 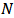 divided into
divided into 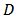 domains;
domains; 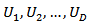 of sizes
of sizes 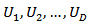 respectively. Domain membership of any population unit is unknown before sampling. It is assumed that domains are quite large[7].The technique of estimation by calibration is based on the idea to use auxiliary information to obtain a better estimate of a population statistic. Consider a finite population
respectively. Domain membership of any population unit is unknown before sampling. It is assumed that domains are quite large[7].The technique of estimation by calibration is based on the idea to use auxiliary information to obtain a better estimate of a population statistic. Consider a finite population  of size
of size  with units labels
with units labels  Let
Let 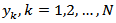 be the study variable and
be the study variable and 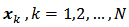 be the
be the 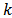 -dimensional vector of auxiliary variables associated with unit
-dimensional vector of auxiliary variables associated with unit 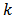 .Suppose we are interested in estimating the domain total
.Suppose we are interested in estimating the domain total 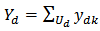 . We draw a sample
. We draw a sample  using a probability sampling design
using a probability sampling design 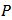 , with probability
, with probability 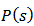 , where the first and second order inclusion probabilities are
, where the first and second order inclusion probabilities are 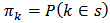 and
and 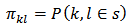 respectively.An estimate of
respectively.An estimate of 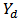 is the Horvitz-Thompson (HT) estimator
is the Horvitz-Thompson (HT) estimator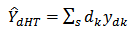 | (1) |
where 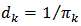 is the sampling weight defined as the inverse of the inclusion probability
is the sampling weight defined as the inverse of the inclusion probability 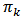 for unit
for unit 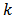 .An attractive property of the HT-estimator is that it is guaranteed to be unbiased regardless of the sampling design
.An attractive property of the HT-estimator is that it is guaranteed to be unbiased regardless of the sampling design 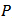 [8]. It variance under
[8]. It variance under 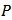 is given as:
is given as: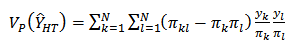 | (2) |
Suppose there are 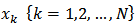 auxiliary variables at unit
auxiliary variables at unit 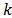 and
and 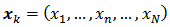 may or may not be known a priori.
may or may not be known a priori. 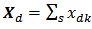 is the domain total for
is the domain total for 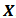 , and is known a priori. Ideally, we would like
, and is known a priori. Ideally, we would like 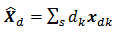 | (3) |
but often times this is not true.The idea behind calibration estimation is to find weights 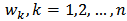 close to
close to 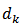 based on a distance function such that
based on a distance function such that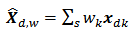 | (4) |
Equation (4) is the calibration constraint. We wish to find weights 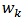 similar to
similar to 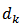 so as to preserve the unbiased property of the HT-estimator. Once
so as to preserve the unbiased property of the HT-estimator. Once 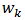 is found, then our propose calibration estimator for
is found, then our propose calibration estimator for 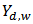 is:
is: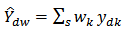 | (5) |
where 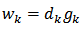 .Thus
.Thus 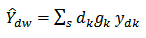 | (6) |
This can be written in regression form as in equation (13). In section 2 we discuss how to find the design weights 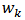 for a given sample
for a given sample 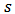 given a distance function. The expectation, variance, and variance estimation of the domain calibration estimator as well as the relationship of the domain calibration estimator to the generalized regression (GREG) estimator is also discussed. In section 3, we discuss the approach for finding the best sample design for the domain calibration estimator using appropriate design weights. Section 4 discusses the approach for the derivation of optimum stratum sample sizes that would minimize the variance of the domain calibration estimator and reduce the objective function under six different criteria. In section 5 we present data analysis and discussion. Section 6 presents the conclusions for the paper.
given a distance function. The expectation, variance, and variance estimation of the domain calibration estimator as well as the relationship of the domain calibration estimator to the generalized regression (GREG) estimator is also discussed. In section 3, we discuss the approach for finding the best sample design for the domain calibration estimator using appropriate design weights. Section 4 discusses the approach for the derivation of optimum stratum sample sizes that would minimize the variance of the domain calibration estimator and reduce the objective function under six different criteria. In section 5 we present data analysis and discussion. Section 6 presents the conclusions for the paper.
2. Derivation of Calibration Estimators for Domain
Given a sample 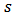 , we want to find
, we want to find 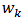 close to
close to 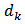 based on a distance function
based on a distance function 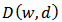 subject to the constraint in equation (4). This is an optimization problem where we wish to minimize
subject to the constraint in equation (4). This is an optimization problem where we wish to minimize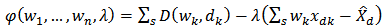 | (7) |
using the method of Lagrange Multipliers. We will derive our calibration weights using the chi-squared distance 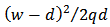 where
where 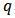 is a tuning parameter that can be manipulated to achieve the optimal minimum of equation (7).However, in practice, it should be noted that the choice of distance function
is a tuning parameter that can be manipulated to achieve the optimal minimum of equation (7).However, in practice, it should be noted that the choice of distance function 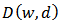 depends on the statistician and the problem considered.
depends on the statistician and the problem considered.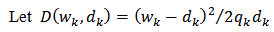 | (8) |
Thus equation (7) becomes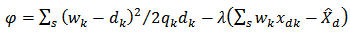 | (9) |
Differentiating equation (9) with respect to 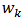 and equating to zero we have
and equating to zero we have 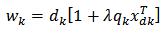 | (10) |
substituting equation (10) into (4) and solving for 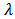 we have
we have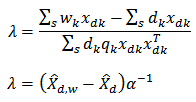 | (11) |
where 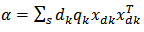 .substituting (11) into (10) we have
.substituting (11) into (10) we have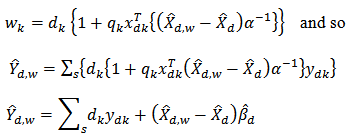 | (12) |
Where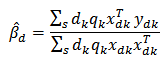 Following from equation (1): That is
Following from equation (1): That is 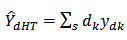 Thus
Thus 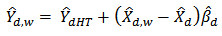 | (13) |
Equation (13) is our proposed calibration estimator. It is a version of the Generalized Regression Estimator (GREG - estimator). This implies that the GREG-estimator is a special case of the calibration estimator in equation (5). Our result in (13) conforms to the GREG-estimator proposed by[2]. In fact, the GREG-estimator is a special case of the calibration estimator when the chosen distance function is the chi-square distance (see[4]).
2.1. Variance and Variance Estimation
We will follow the procedure proposed by[4] to derive an approximate variance for our proposed calibration estimator 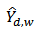 .To find the expectation and variance of
.To find the expectation and variance of 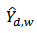 , we use the linearization technique to find an approximation of
, we use the linearization technique to find an approximation of  and
and 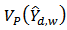 with respect to a probability design
with respect to a probability design 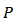 . Let
. Let 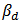 be the population level version of
be the population level version of 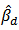 . Then a linear approximation of
. Then a linear approximation of 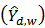 is:
is: 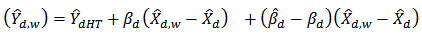 | (14) |
Where the first term is of order 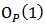 , the second term is of order
, the second term is of order 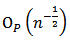 and the last term is of order
and the last term is of order 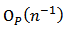 as shown by[4]. Consequently, the last term can be omitted since it is of order
as shown by[4]. Consequently, the last term can be omitted since it is of order 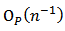 . Thus, we can rewrite (14) as:
. Thus, we can rewrite (14) as: 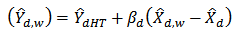 | (15) |
Using equation (15), the design-based expectation of 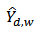 is:
is: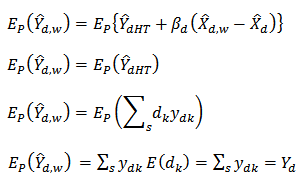 | (16) |
Thus 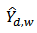 is an approximately design-unbiased estimator of the domain total
is an approximately design-unbiased estimator of the domain total 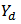 . Note that
. Note that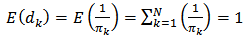 since
since 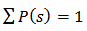 Again using equation (15), the design-based asymptotic variance of
Again using equation (15), the design-based asymptotic variance of 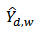 is
is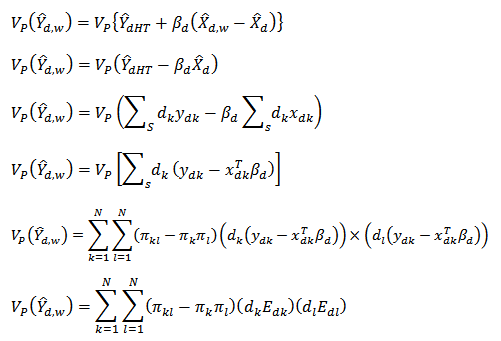 | (17) |
where 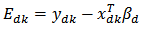 The variance estimator is;
The variance estimator is;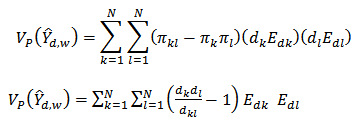 | (18) |
Note that the 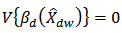 , a consistent and approximate unbiased estimator of variance (18) is:
, a consistent and approximate unbiased estimator of variance (18) is: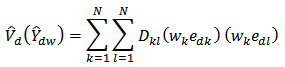 where
where 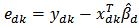 .It should be noted that, it is acceptable to use the design weights
.It should be noted that, it is acceptable to use the design weights 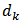 in the variance estimation as in equation (18), but[4] suggest that the calibration weights
in the variance estimation as in equation (18), but[4] suggest that the calibration weights 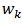 be used in equation (18) as this makes the variance estimator both design-consistent and nearly model unbiased. Moreover, since the calibration estimator is asymptotically equivalent to the GREG-estimator, it can be inferred that calibration estimators are more efficient compared to HT-estimator if there is a strong correlation between
be used in equation (18) as this makes the variance estimator both design-consistent and nearly model unbiased. Moreover, since the calibration estimator is asymptotically equivalent to the GREG-estimator, it can be inferred that calibration estimators are more efficient compared to HT-estimator if there is a strong correlation between 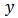 and
and 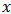 [2].
[2].
3. Sample Design for the Calibration Estimator
Consider a stratified random sampling design with 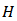 strata and such that
strata and such that 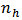 elements are considered from
elements are considered from 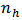 in stratum
in stratum 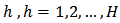 . Then, the design weights needed for the point estimation are
. Then, the design weights needed for the point estimation are 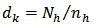 for all
for all 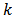 in stratum
in stratum 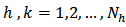 . However, the design weights
. However, the design weights 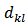 needed for the variance estimation if
needed for the variance estimation if 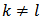 and both
and both 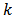 and
and 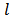 are in different strata, say stratum
are in different strata, say stratum 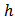 and stratum
and stratum 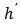 is:
is: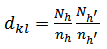 | (19) |
Using equation (18): 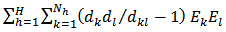 .Then, we have;
.Then, we have;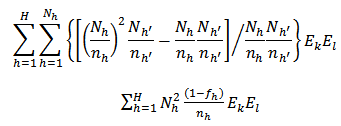 | (20) |
It should be noted that in calibration, it is assumed that elements respond independently so that 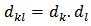 . Consequently, from the following Theorem in stratified sampling design according to[3];Theorem If the samples are drawn independently in different strata,
. Consequently, from the following Theorem in stratified sampling design according to[3];Theorem If the samples are drawn independently in different strata,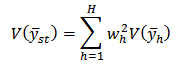 where
where 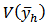 is the variance of
is the variance of 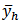 over repeated samples from stratum
over repeated samples from stratum 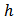 .Since
.Since 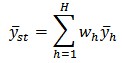
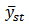 is a linear function of the
is a linear function of the 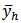 with fixed weights
with fixed weights 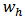 . Hence we may quote the result in statistics for the variance of a linear function
. Hence we may quote the result in statistics for the variance of a linear function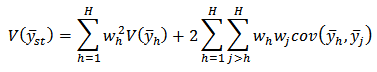 But since samples are drawn independently in different strata, all covariance terms varnish[3 p. 92].We have variance estimator of (18) as:
But since samples are drawn independently in different strata, all covariance terms varnish[3 p. 92].We have variance estimator of (18) as: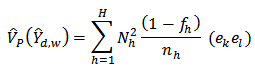
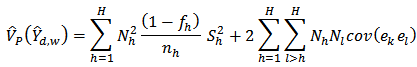
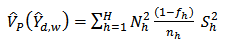 | (21) |
4. Optimal Sample Allocations
We shall now deduce the optimum 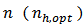 , that minimize the variances of the proposed calibration estimators for a specified cost, or that minimize the cost for a specified variance.Let us consider the simple linear sampling cost function of the form:
, that minimize the variances of the proposed calibration estimators for a specified cost, or that minimize the cost for a specified variance.Let us consider the simple linear sampling cost function of the form: 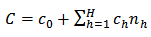 | (22) |
where 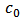 is the overhead cost and
is the overhead cost and 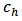 is the cost per unit of obtaining the necessary information in
is the cost per unit of obtaining the necessary information in 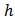 -th stratum. In this paper, we shall consider the following allocation methods: optimum allocation, Neyman allocation, optimal power allocation, Neyman power allocation, square root allocation and Neyman square root allocation.(i) Optimum allocationThe problem of optimum allocation consists in minimizing the sampling variance for a given overall sampling cost of the survey or minimizing the overall sampling cost for specified sampling variance.Let us consider the simple linear sampling cost function of equation (22), the corresponding Lagragian is:
-th stratum. In this paper, we shall consider the following allocation methods: optimum allocation, Neyman allocation, optimal power allocation, Neyman power allocation, square root allocation and Neyman square root allocation.(i) Optimum allocationThe problem of optimum allocation consists in minimizing the sampling variance for a given overall sampling cost of the survey or minimizing the overall sampling cost for specified sampling variance.Let us consider the simple linear sampling cost function of equation (22), the corresponding Lagragian is: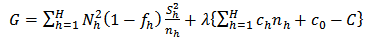 | (23) |
Differentiating (23) with respect to 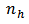 and
and 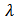 and equating to zero we have respectively
and equating to zero we have respectively 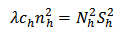 and
and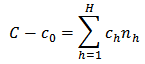 Thus
Thus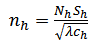 | (24) |
and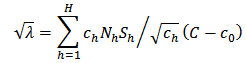 Finally to obtain a solution for
Finally to obtain a solution for 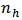 , we substitute for
, we substitute for 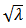 into (24) as follows:
into (24) as follows: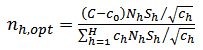 | (25) |
(ii) Neyman allocationIf the cost per unit is the same in all strata, (that is, 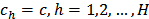 ) , then (25) reduces to
) , then (25) reduces to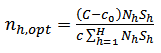 | (26) |
The type of allocation of (26) where 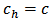 (that is, where the cost per unit is the same in all strata) is called the Neyman allocation.(iii) Optimal power allocationThe power allocation was first considered by[1]. He considered a compromise allocation between equal allocation and Neyman allocation in which the within stratum sample size is proportional to
(that is, where the cost per unit is the same in all strata) is called the Neyman allocation.(iii) Optimal power allocationThe power allocation was first considered by[1]. He considered a compromise allocation between equal allocation and Neyman allocation in which the within stratum sample size is proportional to 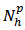 and called it power allocation. Suppose that a stratified random sampling is to be selected. Let
and called it power allocation. Suppose that a stratified random sampling is to be selected. Let 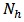 be some measure of size or importance for the
be some measure of size or importance for the 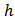 th stratum. It is desired to determine stratum sample sizes
th stratum. It is desired to determine stratum sample sizes 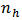 , that the loss function
, that the loss function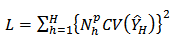 | (27) |
is minimized subject to the constraint 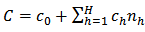 where
where 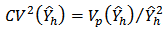 and
and 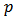 is a constant in the range
is a constant in the range 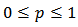 and is called the power of the allocation.Following from our sample design, the loss function is
and is called the power of the allocation.Following from our sample design, the loss function is The corresponding lagragian is
The corresponding lagragian is | (28) |
Differentiating (28) with respect to  and
and  and equating to zero we have
and equating to zero we have 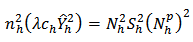 and
and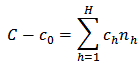 Thus,
Thus,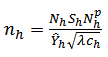 | (29) |
and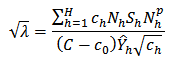 Finally to obtain a solution for
Finally to obtain a solution for 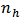 , we substitute for
, we substitute for 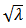 into (29) as follows:
into (29) as follows: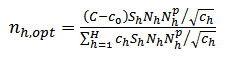 | (30) |
The exponent 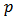 is called the power of the allocation. The choice of
is called the power of the allocation. The choice of 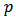 results in significantly different allocations, for example, if the cost per unit is the same across strata (that is,
results in significantly different allocations, for example, if the cost per unit is the same across strata (that is, 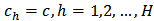 ) and setting
) and setting 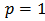 , we obtain the Neyman allocation of (26). Choosing a value of
, we obtain the Neyman allocation of (26). Choosing a value of 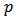 between 0 and 1 can be viewed as a compromise allocation between Neyman allocation and the equal allocation.(iv) Neyman power allocationIf the cost per unit is the same across strata, then;
between 0 and 1 can be viewed as a compromise allocation between Neyman allocation and the equal allocation.(iv) Neyman power allocationIf the cost per unit is the same across strata, then;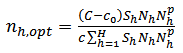 | (31) |
(v) Square root allocationThe square root allocation is a special case of the power allocation. When the power of the allocation 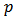 is set to one-half (that is, setting
is set to one-half (that is, setting 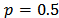 ), we obtain
), we obtain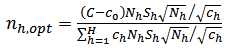 | (32) |
(vi) Neyman square root allocationAgain, if the cost per unit is the same across strata (that is, 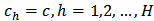 ), and the power of the allocation
), and the power of the allocation 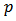 is set to one-half (that is, setting
is set to one-half (that is, setting 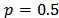 ), then, we obtain what may be called the Neyman square root allocation as:
), then, we obtain what may be called the Neyman square root allocation as: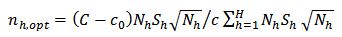 | (33) |
5. Data Analysis and Discussion
5.1. Background and Analytical Set-up
The data used is obtained from the 2005 socio-economic household survey of Akwa Ibom State conducted by the ministry of economic development, Uyo, Akwa Ibom State, Nigeria.The study variable, 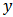 , represents the household expenditure on food and auxiliary variable,
, represents the household expenditure on food and auxiliary variable, 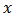 , represents the household income. The statistic of interest is the total cost of food for household and its corresponding estimator for male and female heads of household.The population of household heads was stratified into two strata that constitute the domains; as the male household heads and the female household heads respectively. For the population of individual household heads, we want a separate estimates for male and female household heads defined as two domains of the population. The number of the male household heads and female household heads in the survey are known. We used the calibration estimator for the domain total
, represents the household income. The statistic of interest is the total cost of food for household and its corresponding estimator for male and female heads of household.The population of household heads was stratified into two strata that constitute the domains; as the male household heads and the female household heads respectively. For the population of individual household heads, we want a separate estimates for male and female household heads defined as two domains of the population. The number of the male household heads and female household heads in the survey are known. We used the calibration estimator for the domain total 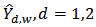 and the following formulation is specified: The number of male household heads,
and the following formulation is specified: The number of male household heads, 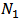 and female household heads,
and female household heads, 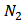 are known and the auxiliary vector has two possible values; namely,
are known and the auxiliary vector has two possible values; namely, 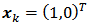 for all male household heads and
for all male household heads and 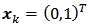 for all female household heads. The population total of the auxiliary vector
for all female household heads. The population total of the auxiliary vector 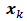 is
is 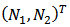 which is also known and
which is also known and 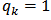 for all
for all 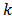 .An assisting model of the form
.An assisting model of the form 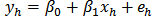 was designed for the calibration estimators, where
was designed for the calibration estimators, where 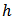 is the number of strata (domains) and
is the number of strata (domains) and 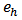 are independently generated by the standard normal distribution.
are independently generated by the standard normal distribution.
5.2. The Sampling Design Variance Estimation
To obtain an optimum value of 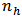 that minimizes the design variance
that minimizes the design variance 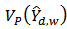 , a population was generated with the following parameters:
, a population was generated with the following parameters: 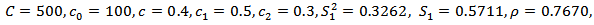
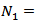
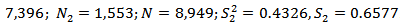 . Table 1 shows the summary of values of
. Table 1 shows the summary of values of 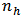 for the six allocation criteria. The variance for the domain calibration estimator using the optimum values of
for the six allocation criteria. The variance for the domain calibration estimator using the optimum values of 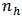 from the six different allocation criteria are presented in table 2.
from the six different allocation criteria are presented in table 2.Table 1. Optimum Value of
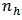
 |
| |
|
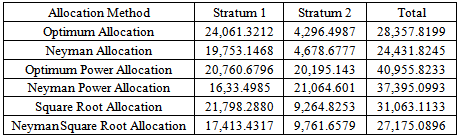
Table 2. Optimum Variance
 |
| |
|
The variance estimator from the stratified random sampling design is;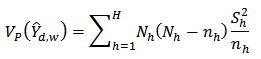 where
where 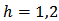 and
and 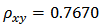 and
and 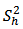 is the stratum variance of the residuals
is the stratum variance of the residuals 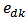 where
where 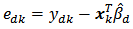 . The optimum value of
. The optimum value of 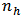 for the Neyman allocation gave the minimum variance. The results of the design variance estimation are presented in table 3.
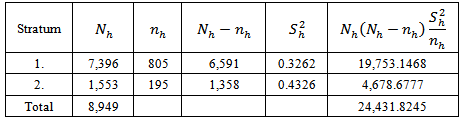
for the Neyman allocation gave the minimum variance. The results of the design variance estimation are presented in table 3.Table 3. Variance Estimation
 |
| |
|
5.3. Comparisons with Greg-estimator
To compare the performance of each estimator we use the following criteria; bias (B), relative bias (RB), mean square error (MSE), average length of confidence interval (AL) and the coverage probability (CP) of 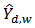 . Let
. Let 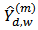 be the estimate of
be the estimate of 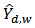 in the
in the 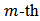 simulation run;
simulation run; 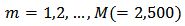 we define
we define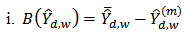 where
where 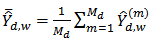
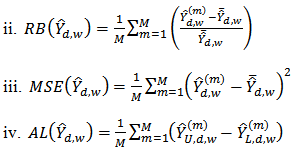 where
where 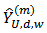 and
and 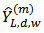 are the upper and lower confidence limit of the corresponding confidence interval.
are the upper and lower confidence limit of the corresponding confidence interval.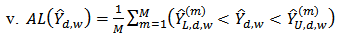 Coverage probability of 95% confidence interval is the ratio of the number of times the true domain total is included in the interval to the total number of runs or the number of replicates. For each estimator of
Coverage probability of 95% confidence interval is the ratio of the number of times the true domain total is included in the interval to the total number of runs or the number of replicates. For each estimator of 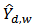 , a 95% confidence interval
, a 95% confidence interval 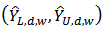 is constructed, where
is constructed, where 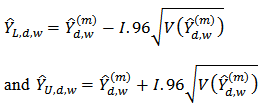 where
where 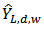 is the lower confidence limit,
is the lower confidence limit, 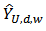 is the upper confidence limit and
is the upper confidence limit and 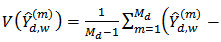
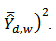 .The analytical study was conducted using the R-statistical package. There were
.The analytical study was conducted using the R-statistical package. There were 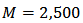 runs in total. For the
runs in total. For the 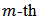 run
run 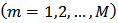 , a Bernoulli sample is drawn where each unit is selected into the sample independently, with inclusion probability
, a Bernoulli sample is drawn where each unit is selected into the sample independently, with inclusion probability 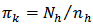 where
where 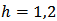 . Following the results of analysis for optimum stratum sample sizes, we fixed
. Following the results of analysis for optimum stratum sample sizes, we fixed 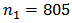 and
and 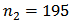 and the corresponding calibration estimators of the domain totals were computed. For simplicity, the tuning parameter
and the corresponding calibration estimators of the domain totals were computed. For simplicity, the tuning parameter 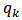 was set to unity
was set to unity 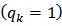 .For each estimator of
.For each estimator of 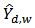 , a 95% confidence interval
, a 95% confidence interval 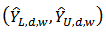 is constructed, where
is constructed, where 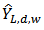 is the lower confidence limit, and
is the lower confidence limit, and 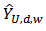 is the upper confidence limit.The results of the analysis are given in table 4.
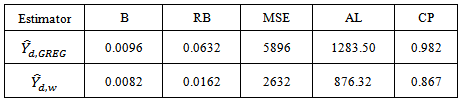
is the upper confidence limit.The results of the analysis are given in table 4.Table 4. Comparison of estimators from analytical study
 |
| |
|
5.4. Discussion
An assisting model of the form 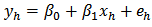 was designed where
was designed where 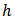 is the number of strata (domains) and
is the number of strata (domains) and 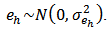 The results of the residual diagnostics showed the
The results of the residual diagnostics showed the 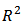 value as 0.588 indicating that the model is significant and that the calibration estimators are unbiased with respect to the sampling design. The correlation between the study variable
value as 0.588 indicating that the model is significant and that the calibration estimators are unbiased with respect to the sampling design. The correlation between the study variable 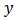 and the auxiliary variable
and the auxiliary variable 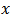 is
is 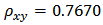 is strong and sufficient implying that the calibration estimators would provide better estimates of the domain totals. The Neyman allocation criterion provides the optimum stratum sample sizes
is strong and sufficient implying that the calibration estimators would provide better estimates of the domain totals. The Neyman allocation criterion provides the optimum stratum sample sizes 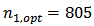 and
and 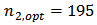 that minimized the variance of the calibration estimators as reflected in table 2. The design strata estimates are 19,753.1468 and 4,678.6777 for stratum 1 and stratum 2 respectively. Similarly, the variance estimate is 24,431.8245. Following from the above estimates, we deduced that the design strata estimates sum up to the finite population estimates. Analysis for the comparison of performance of estimators showed that the biases of 0.82 percent and 0.96 percent respectively for the calibration estimator and the GREG-estimator are negligible. But the bias of the GREG-estimator though negligible is the most biased among the estimators considered. The relative bias for the calibration estimator is relatively smaller than that of the GREG-estimator. The variance for the GREG-estimator is significantly larger than the variance of the calibration estimators, as is indicated by their respective mean square errors in table 4. The average length of the confidence interval for the calibration estimator is significantly smaller than that of the GREG-estimator. The coverage probability of the calibration estimator is also smaller than that of the GREG-estimator. These results showed that there is greater variation in the estimates made by the GREG-estimator than the calibration estimator. In general, the domain calibration estimator is more efficient than the GREG-estimator and the variance reduction is about 50 percent which is consistent with theory as is reflected by the high population correlation between the study variable
that minimized the variance of the calibration estimators as reflected in table 2. The design strata estimates are 19,753.1468 and 4,678.6777 for stratum 1 and stratum 2 respectively. Similarly, the variance estimate is 24,431.8245. Following from the above estimates, we deduced that the design strata estimates sum up to the finite population estimates. Analysis for the comparison of performance of estimators showed that the biases of 0.82 percent and 0.96 percent respectively for the calibration estimator and the GREG-estimator are negligible. But the bias of the GREG-estimator though negligible is the most biased among the estimators considered. The relative bias for the calibration estimator is relatively smaller than that of the GREG-estimator. The variance for the GREG-estimator is significantly larger than the variance of the calibration estimators, as is indicated by their respective mean square errors in table 4. The average length of the confidence interval for the calibration estimator is significantly smaller than that of the GREG-estimator. The coverage probability of the calibration estimator is also smaller than that of the GREG-estimator. These results showed that there is greater variation in the estimates made by the GREG-estimator than the calibration estimator. In general, the domain calibration estimator is more efficient than the GREG-estimator and the variance reduction is about 50 percent which is consistent with theory as is reflected by the high population correlation between the study variable 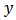 and the auxiliary variable
and the auxiliary variable 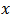 .
.
6. Conclusions
Nonresponse as an aspect in almost every type of sample survey creates problems for estimation which cannot simply be eliminated by increasing sample size. This phenomenon of nonresponse in a sample survey reduces the precision of parameters estimates and increases bias in estimates resulting in larger mean square error, thus ultimately reducing their efficiency.Sample surveys have long been used as cost-effective means for data collection. Such data is used to provide suitable statistics not only for the population targeted by the survey but also for a variety of subpopulations called domains of study. Sample designs and in particular sample sizes are chosen so as to provide reliable estimates for domains of study.One of the main objectives of sample survey is the computation of estimates of means and totals for specific domains of interest. The reliability of the associated estimates depends on the variability of the sample size as well as on the study variables, 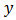 of interest. But budget and other constraints usually prevent the allocation of sufficiently large samples to domains to provide reliable estimates using traditional statistical techniques. This problem of optimal allocation of sample sizes for domain estimation has received less attention than merited in the statistical sample survey theory literature.This paper addressed these problems by proposing calibration estimators for totals of domains of study and developed an approach for finding the best sample design for the domain calibration estimators subject to a cost constraint in the context of stratified random sampling design (STRS) where domains constitute strata in the sampling design to obtain optimal stratum sample sizes that minimized the variances of the proposed domain calibration estimators and reduced the objective function.The efficacy of our proposed calibration estimator was tested through a real data analysis. Five performance criteria, namely; bias (B), relative bias (RB), mean square error (MSE), average length of confidence interval (AL) and coverage probability (CP) were used to compare the relative performances of our proposed domain calibration estimator against the traditional GREG-estimator. Results of the analytical study using real data showed that our proposed calibration estimator is substantially superior to the traditional GREG-estimator with relatively small bias, mean square error and average length of confidence interval.
of interest. But budget and other constraints usually prevent the allocation of sufficiently large samples to domains to provide reliable estimates using traditional statistical techniques. This problem of optimal allocation of sample sizes for domain estimation has received less attention than merited in the statistical sample survey theory literature.This paper addressed these problems by proposing calibration estimators for totals of domains of study and developed an approach for finding the best sample design for the domain calibration estimators subject to a cost constraint in the context of stratified random sampling design (STRS) where domains constitute strata in the sampling design to obtain optimal stratum sample sizes that minimized the variances of the proposed domain calibration estimators and reduced the objective function.The efficacy of our proposed calibration estimator was tested through a real data analysis. Five performance criteria, namely; bias (B), relative bias (RB), mean square error (MSE), average length of confidence interval (AL) and coverage probability (CP) were used to compare the relative performances of our proposed domain calibration estimator against the traditional GREG-estimator. Results of the analytical study using real data showed that our proposed calibration estimator is substantially superior to the traditional GREG-estimator with relatively small bias, mean square error and average length of confidence interval.
References
| [1] | M. D. Bankier, Power allocation: determining sample sizes for subnational areas. The American Statistician 12 (1988), pp. 174-177. |
| [2] | C. M. Cassell, C. E. Sarndal and J. H. Wretman, Some results on generalized difference estimation and generalized regression estimation for finite populations. Biometrika 63 (1976) pp. 615-620. |
| [3] | W.G. Cochran, Sampling Techniques, Wiley and Sons, New York, 1977. |
| [4] | J. C. Deville and C. E. Sarndal, Calibration Estimators in Survey Sampling, Journal of the American Statistical Association, 87 (1992), pp. 376-382. |
| [5] | V.M. Estavao and C.E. Sarndal, Survey estimates by calibration on complex auxiliary information, International Statistical Review, 74 (2006), pp. 127-147. |
| [6] | P. J. Farrell and S. Singh, Model-assisted higher order calibration of estimators of variance, Aust. and New Zealand Journal of Statistics, 47 (2005), pp. 375-383. |
| [7] | W. Gamrot, Estimation of a domain total under nonresponse using double sampling. Statistics in Transition, 7 (2006), pp. 831-840. |
| [8] | D. G. Horvitz and D. J. Thompson, A generalization of sampling without replacement from a finite universe. Journal of the American Statistical Association, 47 (1952), pp. 663-687. |
| [9] | P.S. Kott, Using calibration weighting to adjust for nonresponse and coverage errors. Survey Methodology, 32 (2006), pp. 133-142. |
| [10] | G. E. Montanari and M. G. Ranalli, Nonparametric model calibration estimation in survey sampling, Journal of the American Statistical Association, 100 (2005), pp. 1429-1442. |
| [11] | S. Singh, Survey statistician celebrate golden jubilee year- 2003 of the linear regression estimator, Metrika 2006 pp.1-18. |
| [12] | Singh, Calibrated empirical likelihood estimation using a displacement function: Sir R. A. Fisher’s Honest Balance. INTERFACE Pasadena, CA, USA. 2006. |
| [13] | C. Wu and R. R. Sitter, A Model-calibration approach to using complete auxiliary information from survey data, Journal of the American Statistical Association, 96 (2001), pp. 185-193. |

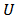 of size
of size 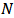 divided into
divided into 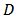 domains;
domains; 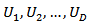 of sizes
of sizes 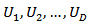 respectively. Domain membership of any population unit is unknown before sampling. It is assumed that domains are quite large[7].The technique of estimation by calibration is based on the idea to use auxiliary information to obtain a better estimate of a population statistic. Consider a finite population
respectively. Domain membership of any population unit is unknown before sampling. It is assumed that domains are quite large[7].The technique of estimation by calibration is based on the idea to use auxiliary information to obtain a better estimate of a population statistic. Consider a finite population 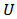 of size
of size 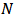 with units labels
with units labels  Let
Let 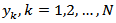 be the study variable and
be the study variable and 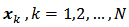 be the
be the 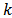 -dimensional vector of auxiliary variables associated with unit
-dimensional vector of auxiliary variables associated with unit 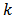 .Suppose we are interested in estimating the domain total
.Suppose we are interested in estimating the domain total 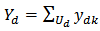 . We draw a sample
. We draw a sample  using a probability sampling design
using a probability sampling design 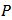 , with probability
, with probability 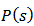 , where the first and second order inclusion probabilities are
, where the first and second order inclusion probabilities are 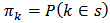 and
and 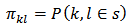 respectively.An estimate of
respectively.An estimate of 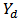 is the Horvitz-Thompson (HT) estimator
is the Horvitz-Thompson (HT) estimator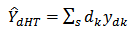
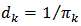 is the sampling weight defined as the inverse of the inclusion probability
is the sampling weight defined as the inverse of the inclusion probability 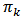 for unit
for unit 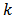 .An attractive property of the HT-estimator is that it is guaranteed to be unbiased regardless of the sampling design
.An attractive property of the HT-estimator is that it is guaranteed to be unbiased regardless of the sampling design 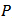 [8]. It variance under
[8]. It variance under 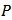 is given as:
is given as: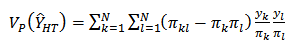
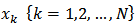 auxiliary variables at unit
auxiliary variables at unit 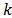 and
and 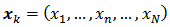 may or may not be known a priori.
may or may not be known a priori. 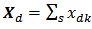 is the domain total for
is the domain total for 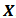 , and is known a priori. Ideally, we would like
, and is known a priori. Ideally, we would like 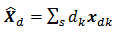
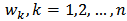 close to
close to 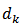 based on a distance function such that
based on a distance function such that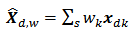
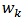 similar to
similar to 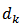 so as to preserve the unbiased property of the HT-estimator. Once
so as to preserve the unbiased property of the HT-estimator. Once 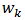 is found, then our propose calibration estimator for
is found, then our propose calibration estimator for 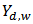 is:
is: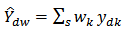
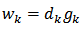 .Thus
.Thus 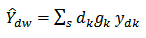
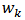 for a given sample
for a given sample 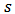 given a distance function. The expectation, variance, and variance estimation of the domain calibration estimator as well as the relationship of the domain calibration estimator to the generalized regression (GREG) estimator is also discussed. In section 3, we discuss the approach for finding the best sample design for the domain calibration estimator using appropriate design weights. Section 4 discusses the approach for the derivation of optimum stratum sample sizes that would minimize the variance of the domain calibration estimator and reduce the objective function under six different criteria. In section 5 we present data analysis and discussion. Section 6 presents the conclusions for the paper.
given a distance function. The expectation, variance, and variance estimation of the domain calibration estimator as well as the relationship of the domain calibration estimator to the generalized regression (GREG) estimator is also discussed. In section 3, we discuss the approach for finding the best sample design for the domain calibration estimator using appropriate design weights. Section 4 discusses the approach for the derivation of optimum stratum sample sizes that would minimize the variance of the domain calibration estimator and reduce the objective function under six different criteria. In section 5 we present data analysis and discussion. Section 6 presents the conclusions for the paper.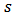 , we want to find
, we want to find 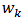 close to
close to 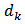 based on a distance function
based on a distance function 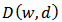 subject to the constraint in equation (4). This is an optimization problem where we wish to minimize
subject to the constraint in equation (4). This is an optimization problem where we wish to minimize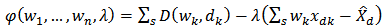
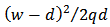 where
where 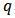 is a tuning parameter that can be manipulated to achieve the optimal minimum of equation (7).However, in practice, it should be noted that the choice of distance function
is a tuning parameter that can be manipulated to achieve the optimal minimum of equation (7).However, in practice, it should be noted that the choice of distance function 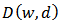 depends on the statistician and the problem considered.
depends on the statistician and the problem considered.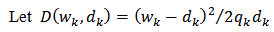
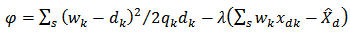
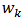 and equating to zero we have
and equating to zero we have 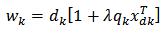
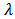 we have
we have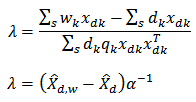
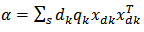 .substituting (11) into (10) we have
.substituting (11) into (10) we have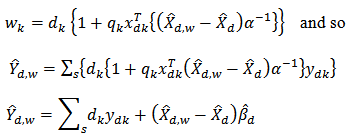
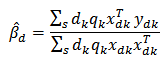 Following from equation (1): That is
Following from equation (1): That is 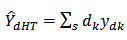 Thus
Thus 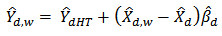
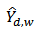 .To find the expectation and variance of
.To find the expectation and variance of 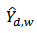 , we use the linearization technique to find an approximation of
, we use the linearization technique to find an approximation of  and
and 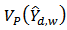 with respect to a probability design
with respect to a probability design 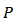 . Let
. Let 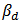 be the population level version of
be the population level version of 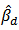 . Then a linear approximation of
. Then a linear approximation of 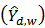 is:
is: 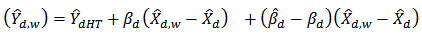
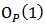 , the second term is of order
, the second term is of order 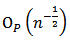 and the last term is of order
and the last term is of order 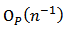 as shown by[4]. Consequently, the last term can be omitted since it is of order
as shown by[4]. Consequently, the last term can be omitted since it is of order 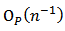 . Thus, we can rewrite (14) as:
. Thus, we can rewrite (14) as: 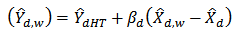
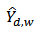 is:
is: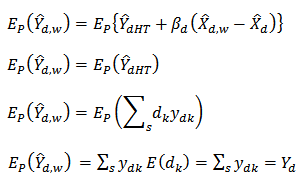
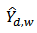 is an approximately design-unbiased estimator of the domain total
is an approximately design-unbiased estimator of the domain total 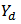 . Note that
. Note that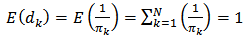 since
since 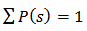 Again using equation (15), the design-based asymptotic variance of
Again using equation (15), the design-based asymptotic variance of 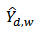 is
is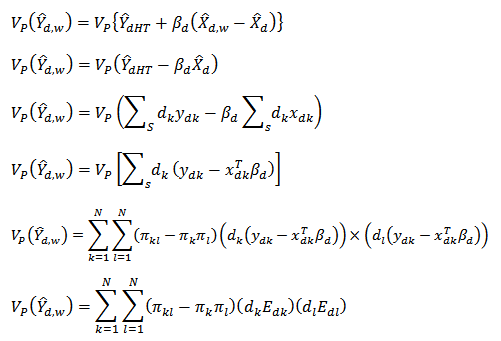
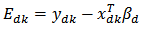 The variance estimator is;
The variance estimator is;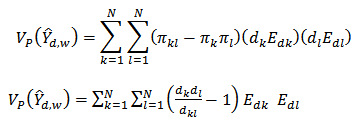
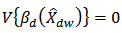 , a consistent and approximate unbiased estimator of variance (18) is:
, a consistent and approximate unbiased estimator of variance (18) is: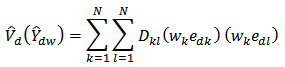 where
where 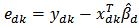 .It should be noted that, it is acceptable to use the design weights
.It should be noted that, it is acceptable to use the design weights 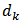 in the variance estimation as in equation (18), but[4] suggest that the calibration weights
in the variance estimation as in equation (18), but[4] suggest that the calibration weights 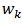 be used in equation (18) as this makes the variance estimator both design-consistent and nearly model unbiased. Moreover, since the calibration estimator is asymptotically equivalent to the GREG-estimator, it can be inferred that calibration estimators are more efficient compared to HT-estimator if there is a strong correlation between
be used in equation (18) as this makes the variance estimator both design-consistent and nearly model unbiased. Moreover, since the calibration estimator is asymptotically equivalent to the GREG-estimator, it can be inferred that calibration estimators are more efficient compared to HT-estimator if there is a strong correlation between 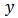 and
and 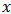 [2].
[2]. 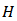 strata and such that
strata and such that 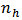 elements are considered from
elements are considered from 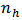 in stratum
in stratum 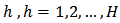 . Then, the design weights needed for the point estimation are
. Then, the design weights needed for the point estimation are 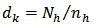 for all
for all 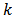 in stratum
in stratum 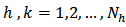 . However, the design weights
. However, the design weights 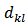 needed for the variance estimation if
needed for the variance estimation if 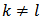 and both
and both 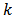 and
and 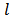 are in different strata, say stratum
are in different strata, say stratum 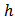 and stratum
and stratum 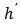 is:
is: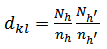
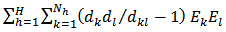 .Then, we have;
.Then, we have;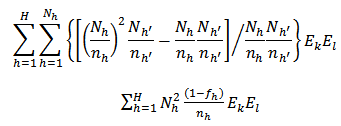
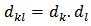 . Consequently, from the following Theorem in stratified sampling design according to[3];Theorem If the samples are drawn independently in different strata,
. Consequently, from the following Theorem in stratified sampling design according to[3];Theorem If the samples are drawn independently in different strata,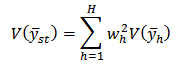 where
where 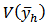 is the variance of
is the variance of 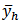 over repeated samples from stratum
over repeated samples from stratum 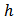 .Since
.Since 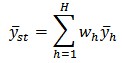
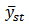 is a linear function of the
is a linear function of the 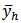 with fixed weights
with fixed weights 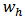 . Hence we may quote the result in statistics for the variance of a linear function
. Hence we may quote the result in statistics for the variance of a linear function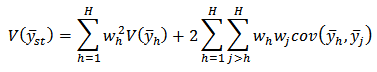 But since samples are drawn independently in different strata, all covariance terms varnish[3 p. 92].We have variance estimator of (18) as:
But since samples are drawn independently in different strata, all covariance terms varnish[3 p. 92].We have variance estimator of (18) as: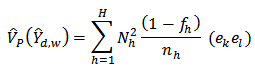
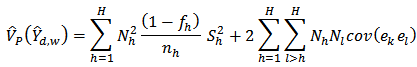
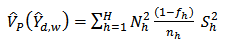
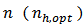 , that minimize the variances of the proposed calibration estimators for a specified cost, or that minimize the cost for a specified variance.Let us consider the simple linear sampling cost function of the form:
, that minimize the variances of the proposed calibration estimators for a specified cost, or that minimize the cost for a specified variance.Let us consider the simple linear sampling cost function of the form: 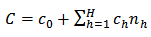
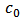 is the overhead cost and
is the overhead cost and 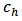 is the cost per unit of obtaining the necessary information in
is the cost per unit of obtaining the necessary information in 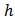 -th stratum. In this paper, we shall consider the following allocation methods: optimum allocation, Neyman allocation, optimal power allocation, Neyman power allocation, square root allocation and Neyman square root allocation.(i) Optimum allocationThe problem of optimum allocation consists in minimizing the sampling variance for a given overall sampling cost of the survey or minimizing the overall sampling cost for specified sampling variance.Let us consider the simple linear sampling cost function of equation (22), the corresponding Lagragian is:
-th stratum. In this paper, we shall consider the following allocation methods: optimum allocation, Neyman allocation, optimal power allocation, Neyman power allocation, square root allocation and Neyman square root allocation.(i) Optimum allocationThe problem of optimum allocation consists in minimizing the sampling variance for a given overall sampling cost of the survey or minimizing the overall sampling cost for specified sampling variance.Let us consider the simple linear sampling cost function of equation (22), the corresponding Lagragian is: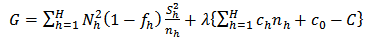
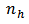 and
and 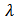 and equating to zero we have respectively
and equating to zero we have respectively 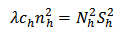 and
and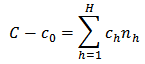 Thus
Thus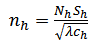
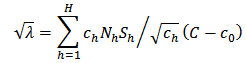 Finally to obtain a solution for
Finally to obtain a solution for 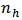 , we substitute for
, we substitute for 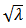 into (24) as follows:
into (24) as follows: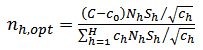
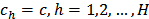 ) , then (25) reduces to
) , then (25) reduces to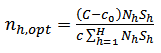
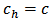 (that is, where the cost per unit is the same in all strata) is called the Neyman allocation.(iii) Optimal power allocationThe power allocation was first considered by[1]. He considered a compromise allocation between equal allocation and Neyman allocation in which the within stratum sample size is proportional to
(that is, where the cost per unit is the same in all strata) is called the Neyman allocation.(iii) Optimal power allocationThe power allocation was first considered by[1]. He considered a compromise allocation between equal allocation and Neyman allocation in which the within stratum sample size is proportional to 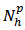 and called it power allocation. Suppose that a stratified random sampling is to be selected. Let
and called it power allocation. Suppose that a stratified random sampling is to be selected. Let 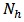 be some measure of size or importance for the
be some measure of size or importance for the 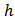 th stratum. It is desired to determine stratum sample sizes
th stratum. It is desired to determine stratum sample sizes 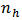 , that the loss function
, that the loss function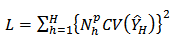
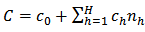 where
where 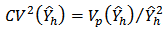 and
and 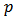 is a constant in the range
is a constant in the range 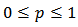 and is called the power of the allocation.Following from our sample design, the loss function is
and is called the power of the allocation.Following from our sample design, the loss function is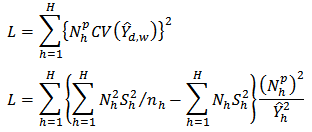 The corresponding lagragian is
The corresponding lagragian is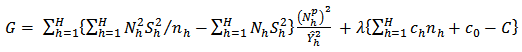
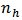 and
and 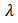 and equating to zero we have
and equating to zero we have 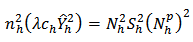 and
and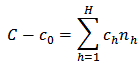 Thus,
Thus,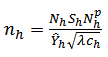
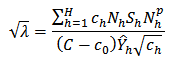 Finally to obtain a solution for
Finally to obtain a solution for 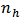 , we substitute for
, we substitute for 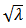 into (29) as follows:
into (29) as follows: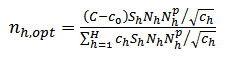
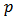 is called the power of the allocation. The choice of
is called the power of the allocation. The choice of 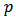 results in significantly different allocations, for example, if the cost per unit is the same across strata (that is,
results in significantly different allocations, for example, if the cost per unit is the same across strata (that is, 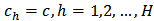 ) and setting
) and setting 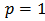 , we obtain the Neyman allocation of (26). Choosing a value of
, we obtain the Neyman allocation of (26). Choosing a value of 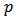 between 0 and 1 can be viewed as a compromise allocation between Neyman allocation and the equal allocation.(iv) Neyman power allocationIf the cost per unit is the same across strata, then;
between 0 and 1 can be viewed as a compromise allocation between Neyman allocation and the equal allocation.(iv) Neyman power allocationIf the cost per unit is the same across strata, then;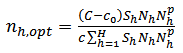
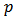 is set to one-half (that is, setting
is set to one-half (that is, setting 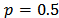 ), we obtain
), we obtain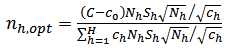
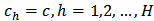 ), and the power of the allocation
), and the power of the allocation 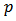 is set to one-half (that is, setting
is set to one-half (that is, setting 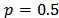 ), then, we obtain what may be called the Neyman square root allocation as:
), then, we obtain what may be called the Neyman square root allocation as: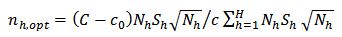
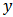 , represents the household expenditure on food and auxiliary variable,
, represents the household expenditure on food and auxiliary variable, 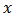 , represents the household income. The statistic of interest is the total cost of food for household and its corresponding estimator for male and female heads of household.The population of household heads was stratified into two strata that constitute the domains; as the male household heads and the female household heads respectively. For the population of individual household heads, we want a separate estimates for male and female household heads defined as two domains of the population. The number of the male household heads and female household heads in the survey are known. We used the calibration estimator for the domain total
, represents the household income. The statistic of interest is the total cost of food for household and its corresponding estimator for male and female heads of household.The population of household heads was stratified into two strata that constitute the domains; as the male household heads and the female household heads respectively. For the population of individual household heads, we want a separate estimates for male and female household heads defined as two domains of the population. The number of the male household heads and female household heads in the survey are known. We used the calibration estimator for the domain total 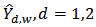 and the following formulation is specified: The number of male household heads,
and the following formulation is specified: The number of male household heads, 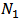 and female household heads,
and female household heads, 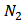 are known and the auxiliary vector has two possible values; namely,
are known and the auxiliary vector has two possible values; namely, 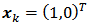 for all male household heads and
for all male household heads and 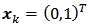 for all female household heads. The population total of the auxiliary vector
for all female household heads. The population total of the auxiliary vector 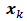 is
is 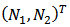 which is also known and
which is also known and 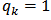 for all
for all 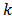 .An assisting model of the form
.An assisting model of the form 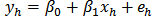 was designed for the calibration estimators, where
was designed for the calibration estimators, where 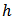 is the number of strata (domains) and
is the number of strata (domains) and 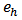 are independently generated by the standard normal distribution.
are independently generated by the standard normal distribution. 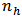 that minimizes the design variance
that minimizes the design variance 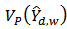 , a population was generated with the following parameters:
, a population was generated with the following parameters: 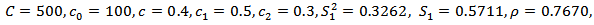
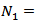
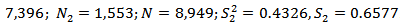 . Table 1 shows the summary of values of
. Table 1 shows the summary of values of  for the six allocation criteria. The variance for the domain calibration estimator using the optimum values of
for the six allocation criteria. The variance for the domain calibration estimator using the optimum values of  from the six different allocation criteria are presented in table 2.
from the six different allocation criteria are presented in table 2.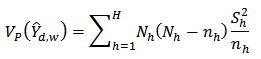 where
where 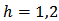 and
and 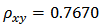 and
and 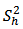 is the stratum variance of the residuals
is the stratum variance of the residuals 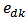 where
where 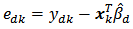 . The optimum value of
. The optimum value of 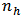 for the Neyman allocation gave the minimum variance. The results of the design variance estimation are presented in table 3.
for the Neyman allocation gave the minimum variance. The results of the design variance estimation are presented in table 3.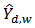 . Let
. Let 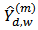 be the estimate of
be the estimate of 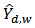 in the
in the 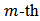 simulation run;
simulation run; 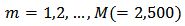 we define
we define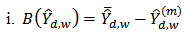 where
where 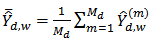
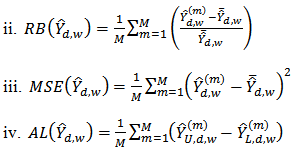 where
where 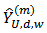 and
and 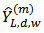 are the upper and lower confidence limit of the corresponding confidence interval.
are the upper and lower confidence limit of the corresponding confidence interval.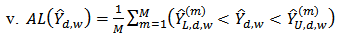 Coverage probability of 95% confidence interval is the ratio of the number of times the true domain total is included in the interval to the total number of runs or the number of replicates. For each estimator of
Coverage probability of 95% confidence interval is the ratio of the number of times the true domain total is included in the interval to the total number of runs or the number of replicates. For each estimator of 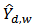 , a 95% confidence interval
, a 95% confidence interval 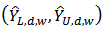 is constructed, where
is constructed, where 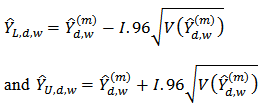 where
where 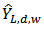 is the lower confidence limit,
is the lower confidence limit, 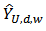 is the upper confidence limit and
is the upper confidence limit and 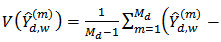
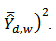 .The analytical study was conducted using the R-statistical package. There were
.The analytical study was conducted using the R-statistical package. There were 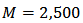 runs in total. For the
runs in total. For the 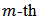 run
run 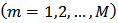 , a Bernoulli sample is drawn where each unit is selected into the sample independently, with inclusion probability
, a Bernoulli sample is drawn where each unit is selected into the sample independently, with inclusion probability 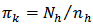 where
where 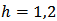 . Following the results of analysis for optimum stratum sample sizes, we fixed
. Following the results of analysis for optimum stratum sample sizes, we fixed 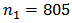 and
and 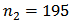 and the corresponding calibration estimators of the domain totals were computed. For simplicity, the tuning parameter
and the corresponding calibration estimators of the domain totals were computed. For simplicity, the tuning parameter 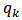 was set to unity
was set to unity 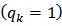 .For each estimator of
.For each estimator of 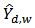 , a 95% confidence interval
, a 95% confidence interval 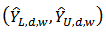 is constructed, where
is constructed, where 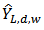 is the lower confidence limit, and
is the lower confidence limit, and 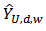 is the upper confidence limit.The results of the analysis are given in table 4.
is the upper confidence limit.The results of the analysis are given in table 4.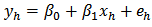 was designed where
was designed where 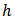 is the number of strata (domains) and
is the number of strata (domains) and 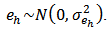 The results of the residual diagnostics showed the
The results of the residual diagnostics showed the 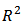 value as 0.588 indicating that the model is significant and that the calibration estimators are unbiased with respect to the sampling design. The correlation between the study variable
value as 0.588 indicating that the model is significant and that the calibration estimators are unbiased with respect to the sampling design. The correlation between the study variable 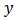 and the auxiliary variable
and the auxiliary variable 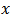 is
is 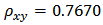 is strong and sufficient implying that the calibration estimators would provide better estimates of the domain totals. The Neyman allocation criterion provides the optimum stratum sample sizes
is strong and sufficient implying that the calibration estimators would provide better estimates of the domain totals. The Neyman allocation criterion provides the optimum stratum sample sizes 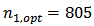 and
and 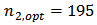 that minimized the variance of the calibration estimators as reflected in table 2. The design strata estimates are 19,753.1468 and 4,678.6777 for stratum 1 and stratum 2 respectively. Similarly, the variance estimate is 24,431.8245. Following from the above estimates, we deduced that the design strata estimates sum up to the finite population estimates. Analysis for the comparison of performance of estimators showed that the biases of 0.82 percent and 0.96 percent respectively for the calibration estimator and the GREG-estimator are negligible. But the bias of the GREG-estimator though negligible is the most biased among the estimators considered. The relative bias for the calibration estimator is relatively smaller than that of the GREG-estimator. The variance for the GREG-estimator is significantly larger than the variance of the calibration estimators, as is indicated by their respective mean square errors in table 4. The average length of the confidence interval for the calibration estimator is significantly smaller than that of the GREG-estimator. The coverage probability of the calibration estimator is also smaller than that of the GREG-estimator. These results showed that there is greater variation in the estimates made by the GREG-estimator than the calibration estimator. In general, the domain calibration estimator is more efficient than the GREG-estimator and the variance reduction is about 50 percent which is consistent with theory as is reflected by the high population correlation between the study variable
that minimized the variance of the calibration estimators as reflected in table 2. The design strata estimates are 19,753.1468 and 4,678.6777 for stratum 1 and stratum 2 respectively. Similarly, the variance estimate is 24,431.8245. Following from the above estimates, we deduced that the design strata estimates sum up to the finite population estimates. Analysis for the comparison of performance of estimators showed that the biases of 0.82 percent and 0.96 percent respectively for the calibration estimator and the GREG-estimator are negligible. But the bias of the GREG-estimator though negligible is the most biased among the estimators considered. The relative bias for the calibration estimator is relatively smaller than that of the GREG-estimator. The variance for the GREG-estimator is significantly larger than the variance of the calibration estimators, as is indicated by their respective mean square errors in table 4. The average length of the confidence interval for the calibration estimator is significantly smaller than that of the GREG-estimator. The coverage probability of the calibration estimator is also smaller than that of the GREG-estimator. These results showed that there is greater variation in the estimates made by the GREG-estimator than the calibration estimator. In general, the domain calibration estimator is more efficient than the GREG-estimator and the variance reduction is about 50 percent which is consistent with theory as is reflected by the high population correlation between the study variable 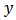 and the auxiliary variable
and the auxiliary variable 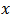 .
.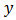 of interest. But budget and other constraints usually prevent the allocation of sufficiently large samples to domains to provide reliable estimates using traditional statistical techniques. This problem of optimal allocation of sample sizes for domain estimation has received less attention than merited in the statistical sample survey theory literature.This paper addressed these problems by proposing calibration estimators for totals of domains of study and developed an approach for finding the best sample design for the domain calibration estimators subject to a cost constraint in the context of stratified random sampling design (STRS) where domains constitute strata in the sampling design to obtain optimal stratum sample sizes that minimized the variances of the proposed domain calibration estimators and reduced the objective function.The efficacy of our proposed calibration estimator was tested through a real data analysis. Five performance criteria, namely; bias (B), relative bias (RB), mean square error (MSE), average length of confidence interval (AL) and coverage probability (CP) were used to compare the relative performances of our proposed domain calibration estimator against the traditional GREG-estimator. Results of the analytical study using real data showed that our proposed calibration estimator is substantially superior to the traditional GREG-estimator with relatively small bias, mean square error and average length of confidence interval.
of interest. But budget and other constraints usually prevent the allocation of sufficiently large samples to domains to provide reliable estimates using traditional statistical techniques. This problem of optimal allocation of sample sizes for domain estimation has received less attention than merited in the statistical sample survey theory literature.This paper addressed these problems by proposing calibration estimators for totals of domains of study and developed an approach for finding the best sample design for the domain calibration estimators subject to a cost constraint in the context of stratified random sampling design (STRS) where domains constitute strata in the sampling design to obtain optimal stratum sample sizes that minimized the variances of the proposed domain calibration estimators and reduced the objective function.The efficacy of our proposed calibration estimator was tested through a real data analysis. Five performance criteria, namely; bias (B), relative bias (RB), mean square error (MSE), average length of confidence interval (AL) and coverage probability (CP) were used to compare the relative performances of our proposed domain calibration estimator against the traditional GREG-estimator. Results of the analytical study using real data showed that our proposed calibration estimator is substantially superior to the traditional GREG-estimator with relatively small bias, mean square error and average length of confidence interval. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML