Navid Feroze1, Muhammad Aslam2
1Department of Mathematics and Statistics, Allama Iqbal Open University, Islamabad, Pakistan
2Department of Statistics, Quaid-i-Azam University, Islamabad, Pakistan
Correspondence to: Navid Feroze, Department of Mathematics and Statistics, Allama Iqbal Open University, Islamabad, Pakistan.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In this paper, the Bayesian analysis of inverse Rayleigh distribution has been considered under singly and doubly type II censored data. The Bayes estimators and corresponding risks have been derived under the assumption of non-informative priors and using symmetric and asymmetric loss functions. The credible intervals have been constructed under the assumption of non-informative priors. The inverse transformation method of simulation has been used for data generation in order to assess and compare the performance of the derived point and interval estimators. The simulation study has been conducted using different sample sizes and various parametric values to analyze the properties of the said estimators.
Keywords:
Bayes Estimators, Squared Error Loss Function (SELF), Quadratic Loss Function (QLF), Weighted Loss Function (WLF), LINEX Loss Function (LLF), Precautionary Loss Function (PLF), Weighted Balanced Loss Function (WBLF), Credible Intervals and Posterior Predictive Distribution
Cite this paper:
Navid Feroze, Muhammad Aslam, "On Posterior Analysis of Inverse Rayleigh Distribution under Singly and Doubly Type II Censored Data", International Journal of Probability and Statistics, Vol. 1 No. 5, 2012, pp. 145-152. doi: 10.5923/j.ijps.20120105.01.
1. Introduction
The inverse Rayleigh distribution is an important life testing distribution. However, it is often not feasible to continue the life testing experiment until the last item has failed. In such situations, the censoring can be a good remedy. There are many developed censoring schemes which can be used for different circumstances. In this study, the two censoring schemes have been compared for estimation of parameter of inverse Rayleigh distribution, under a simulation study using a Bayesian framework.Fermindez et al.[1] obtained the maximum likelihood estimates from type II doubly censored exponential data. Fauzy[2] considered the interval estimation for parameters of exponential distribution under doubly type II censoring. Krishna and Malik[3] presented the reliability estimation in Maxwell distribution under type-II censored data. Kundu and Howlader[4] estimated the inverse Weibull distribution using type II censored data under Bayesian framework. Soliman et al.[5] discussed the Bayesian and non Bayesian estimation of inverse Rayleigh distribution based on lower record values. The Bayes estimators, corresponding risks, interval estimates were derived and evaluated under the assumption of an informative prior. Dey[6] considered Bayesian analysis of the inverse Rayleigh distribution using symmetric and asymmetric loss functions and under a non-informative prior. The Bayes estimators of the reliability function were also obtained.
2. Likelihood Function under Singly and Doubly Type II Censored Data
The probability density function of the inverse Rayleigh distribution is: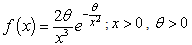 | (1) |
The CDF of the distribution is: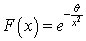 | (2) |
Suppose ‘n’ items are put on a life-testing experiment and only first ‘r’ failure times have been observed, that is, 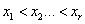 and remaining ‘n – r’ items are still working. Under the assumptions that the lifetimes of the items are independently and identically distributed inverse Rayleigh random variable, the likelihood function of the observed data without the multiplicative constant can be written as:
and remaining ‘n – r’ items are still working. Under the assumptions that the lifetimes of the items are independently and identically distributed inverse Rayleigh random variable, the likelihood function of the observed data without the multiplicative constant can be written as: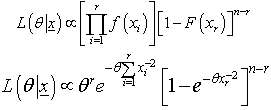 | (3) |
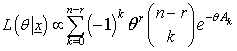 | (4) |
Where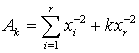 Again, consider a random sample of size ‘n’ from an inverse Rayleigh distribution, and let xr,..., xs be the ordered observations remaining when the ‘r – 1’ smallest observations and the ‘n – s’ largest observations have been censored, The likelihood function for
Again, consider a random sample of size ‘n’ from an inverse Rayleigh distribution, and let xr,..., xs be the ordered observations remaining when the ‘r – 1’ smallest observations and the ‘n – s’ largest observations have been censored, The likelihood function for 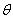 given the Type II doubly censored sample x = (xr,..., xs), is:
given the Type II doubly censored sample x = (xr,..., xs), is: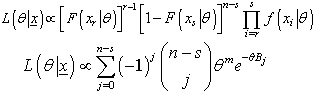 | (5) |
where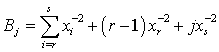 .
.
3. Posterior Distributions for Singly and Doubly Type II Censored Data
The posterior distribution summarizes the current state of known ledge about all the uncertain qualities in a Bayesian analysis. Analytically, the posterior distribution is the product of the prior density and the likelihood. Consider the prior distribution 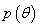 which reflects the prior information before collecting the data
which reflects the prior information before collecting the data 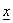 and the likelihood function
and the likelihood function 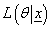 that represents the observed data then the posterior density
that represents the observed data then the posterior density 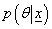 is calculated as proportional to the multiplication of prior distribution and the likelihood function i.e. Posterior density
is calculated as proportional to the multiplication of prior distribution and the likelihood function i.e. Posterior density 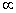 (Prior density)×(Likelihood function)
(Prior density)×(Likelihood function)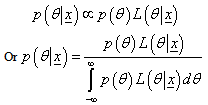 So for the derivation of posterior distribution the specification of the prior distribution is mandatory. The prior distributions can be categorized in two type informative priors and non-informative priors. The informative priors do not always exist. So in case of non availability of the informative priors, the non-informative priors are often used. Among non-informative priors, the uniform and Jeffreys priors have received significant attention. These priors will be assumed for the derivation of posterior distributions.
So for the derivation of posterior distribution the specification of the prior distribution is mandatory. The prior distributions can be categorized in two type informative priors and non-informative priors. The informative priors do not always exist. So in case of non availability of the informative priors, the non-informative priors are often used. Among non-informative priors, the uniform and Jeffreys priors have received significant attention. These priors will be assumed for the derivation of posterior distributions.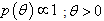 | (6) |
The posterior distribution under the assumption of uniform prior for singly type II censored data is: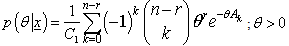 | (7) |
Where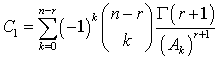 The Jeffreys prior is defined to be:
The Jeffreys prior is defined to be:  ;where
;where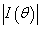 is Fisher Information matrix.Therefore;
is Fisher Information matrix.Therefore; | (8) |
The posterior distribution under the Jeffreys prior for singly type II censored data is: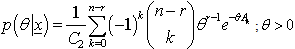 | (9) |
Where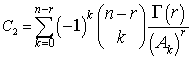 The posterior distribution under the assumption of uniform prior using doubly censored data is:
The posterior distribution under the assumption of uniform prior using doubly censored data is: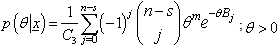 | (10) |
Where 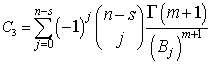 The posterior distribution under the assumption of Jeffreys prior using doubly censored data is:
The posterior distribution under the assumption of Jeffreys prior using doubly censored data is: | (11) |
Where 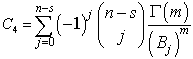
4. Bayes Estimators and Posterior Risks
The Bayes estimators and associated risks under SELF, QLF, WLF, PLF, LLF and WBLF are respectively presented as: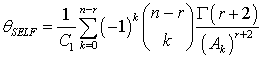 | (12) |
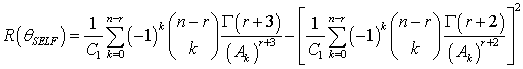 | (13) |
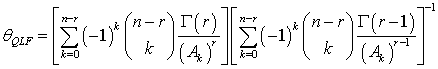 | (14) |
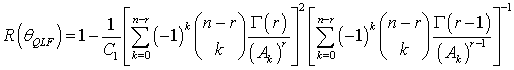 | (15) |
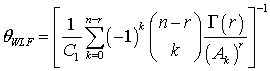 | (16) |
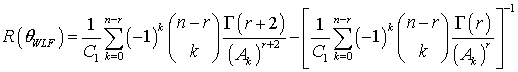 | (17) |
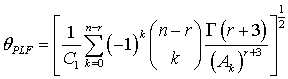 | (18) |
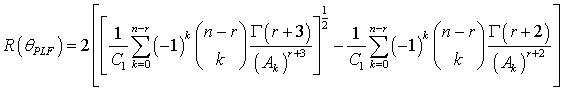 | (19) |
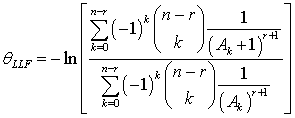 | (20) |
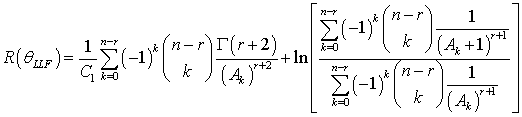 | (21) |
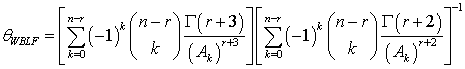 | (22) |
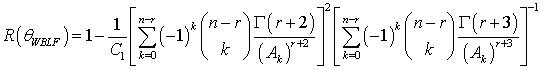 | (23) |
Similarly, the Bayes estimators and posterior risks using other posterior distribution can be obtained.
5. Bayesian Credible Intervals for Singly and Doubly Type II Censored Data
The Bayesian credible intervals for singly and doubly type II censored data under uniform and Jeffreys prior, as discussed by Saleem and Aslam[7], are presented in the following. The credible interval for singly type II censored data under uniform prior is: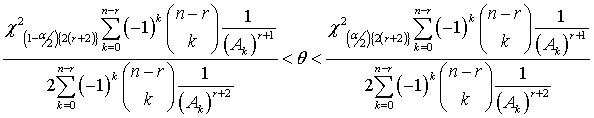 | (24) |
The credible interval for singly type II censored data under Jeffreys prior is: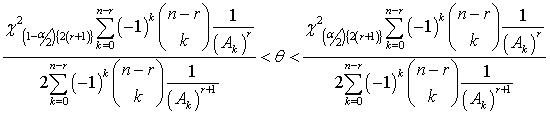 | (25) |
The credible interval for doubly type II censored data under uniform prior is: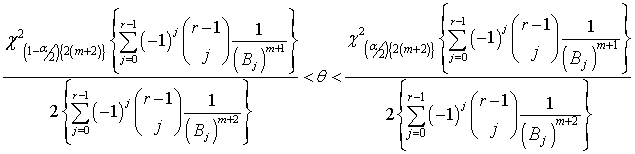 | (26) |
The credible interval for doubly type II censored data under Jeffreys prior is: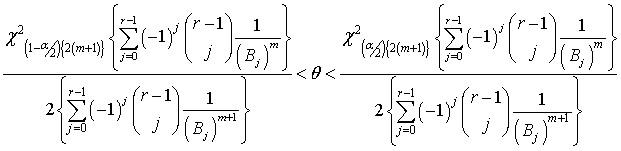 | (27) |
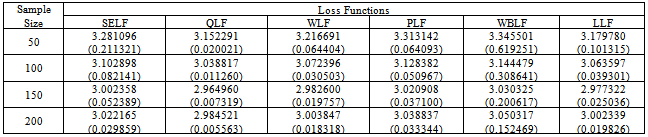
Table 1. The Bayes estimates and risks for singly type II censored data under uniform prior (θ = 3)
 |
| |
|
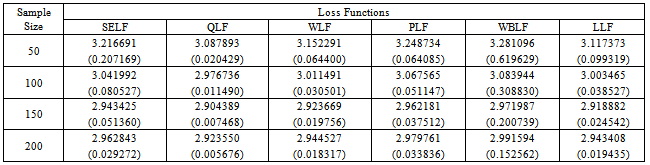
Table 2. The Bayes estimates and risks for singly type II censored data under Jeffreys prior (θ = 3)
 |
| |
|
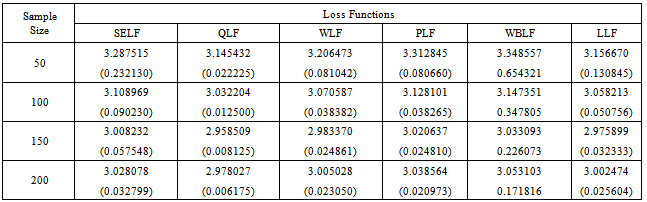
Table 3. The Bayes estimates and risks for doubly type II censored data under uniform prior (θ = 3)
 |
| |
|
Table 4. The Bayes estimates and risks for doubly type II censored data under Jeffreys prior (θ = 3)
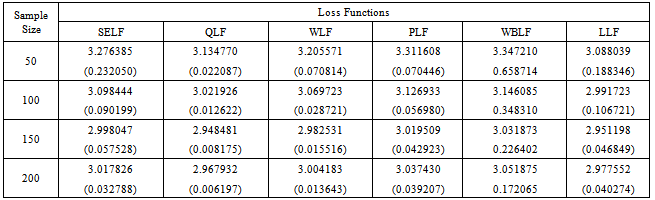 |
| |
|
Table 5. The Bayes estimates and risks for singly type II censored data under uniform prior (θ = 5)
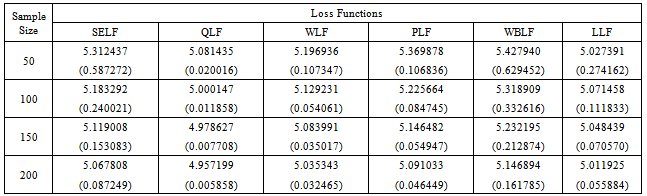 |
| |
|
Table 6. The Bayes estimates and risks for singly type II censored data under Jeffreys prior (θ = 5)
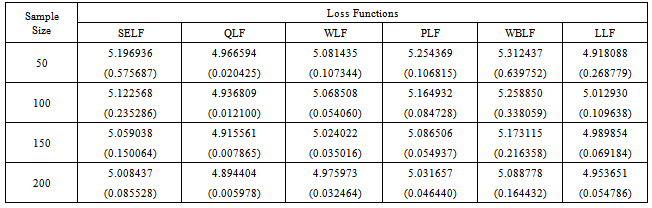 |
| |
|
Table 7. The Bayes estimates and risks for doubly type II censored data under uniform prior (θ = 5)
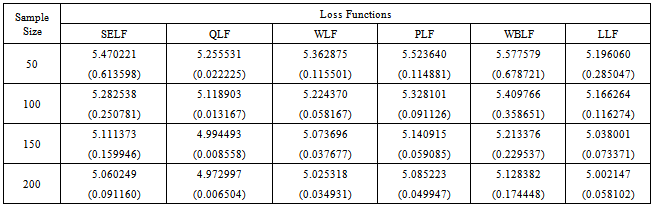 |
| |
|
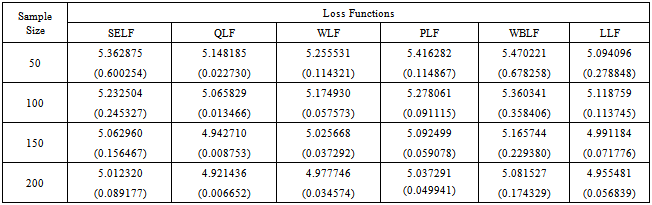
Table 8. The Bayes estimates and risks for doubly type II censored data under Jeffreys prior (θ=5)
 |
| |
|
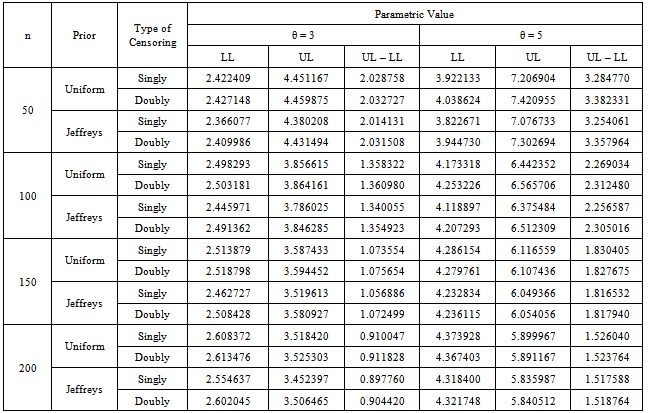
Table 9. The Bayesian credible intervals for singly and doubly type II censored data under uniform and Jeffreys priors
 |
| |
|
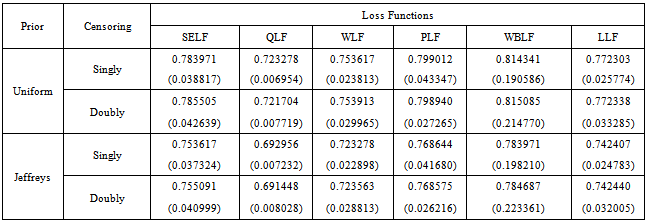
Table 10. The Bayes estimates and risks for singly and doubly type II censored real life data
 |
| |
|
6. Simulation Study
The inverse transformation method of simulation has been used to generate the random data from the distribution. The Bayes estimates and corresponding risks have been calculated using various sample sizes, that is, n = 50, 100, 150 and 200 for. In case of singly type II censoring, the estimation has been done under 20% right censored samples. While for doubly type II censoring, the estimation has been done under 10% left and 10% right censored samples. The results have been replicated to obtain the more representative estimates of the parameter. The risks associated with Bayes estimates have been presented in the parentheses. The above study depicts that the estimated value of the parameter converges to the true value of the parameter by increasing the sample size. The greater values of the parameter impose a negative impact on convergence and performance of the estimates. The estimated value of the parameter under LLF is always lesser than those obtained using other loss functions. The patterns of the estimates, discussed above, are similar under uniform and Jeffreys priors. However, the performance of the Jeffreys prior is better for estimates under SELF, WLF, PLF and LLF. While for estimates under QLF and WBLF, the performance of the uniform prior is better than Jeffreys prior. The results under singly type II censored samples are better than those under doubly type II censored samples. The minimum Bayes risk is associated with estimates under QLF using uniform prior for singly type II censored samples.From the above table it can be assessed that all the intervals contain the true value of the parameter. However, the widths of credible intervals under Jeffreys prior are shorter as compare to those under uniform prior. This property holds for singly and doubly type II censored data. Similarly, the widths of credible intervals under singly type II censored samples are lesser. The width for all credible intervals decreases with increase of sample size. So it can be concluded that Jefferys prior under singly type II censored data can be preferred for interval estimation of the said parameter using Bayesian framework.
7. Real Life Example
Clinical trial designed to access the effectiveness of an antibiotic ointment in relieving pain. The data consist of n = 25 patients. Censoring scheme was chosen as T1 = 0.25, T2 = 0.50 and T3 = 0.75 (in hours).Censored sample of size 19 was observed. (notice that a ”failure” here is actually the time until a patient feels relief from pain)0.554, 0.566, 0.653, 0.665, 0.683, 0.698, 0.786, 0.788, 0.828, 0.829, 0.866, 0.879, 0.881, 0.899, 0.917, 1.037, 1.050, 1.110, 1.138.The calculation based on this sample has been presented in the following table.The real life analysis replicated the patterns and behaviour of the estimates observed under simulation study. The minimum risks have been associated with the estimates under uniform prior using quadratic loss function for singly censored samples.
8. Conclusions
The Bayes estimates and corresponding risks have been evaluated and compared under a simulation study. The simulation study indicates that the performance of the Jeffreys prior is better than uniform with an exception in case of estimates under QLF and WBLF. While the risks associated with estimates under QLF are least for each prior. However, the rate of convergence increases and magnitude of risk decreases with increase in sample size. The inverse pattern is observed for increase in true value of the parameter. On comparing the estimates under singly and doubly type II censored samples, it is found that the estimates using singly type II censored samples are better. The interval estimation also endorse the findings of the point estimation, that is, the credible intervals under Jeffreys prior using singly type II censored samples are having the minimum width. The findings of the real life example are in accordance with the simulation study. Hence for Bayesian analysis of the parameter of inverse Rayleigh distribution, the use of QLF under uniform prior and singly type II censored samples can be preferred.
ACKNOWLEDGEMENTS
Special thanks to referees for their valuable suggestions regarding improvement of the paper.
References
| [1] | A. J. Fermindez, J. I. Bravo, and F. D. Fuentes, “Computing maximum likelihood estimates from Type II doubly censored exponential data”, Statistical Methods & Applications, vol.11, pp. 187-200, 2002. |
| [2] | A. Fauzy, “Interval estimation for parameters of exponential distribution under doubly type II censoring”, J. of Applies Mathematics, vol.10, pp. 71-79, 2004. |
| [3] | H. Krishna, and M. Malik, “Reliability estimation in Maxwell distribution with type-II censored data”, International J. of Quality & Reliability Management, vol.26, pp. 184-195, 2009. |
| [4] | D. Kundu, and H. Howlader, “Bayesian inference and prediction of the inverse Weibull distribution for type-II censored data”, Computational Statistics and Data Analysis, vol.54, pp. 1547-1558, 2010. |
| [5] | A. Soliman, A. E. Amin, and A. A. Aziz, “Estimation and prediction from inverse Rayleigh distribution based on lower record values”, Applied Mathematical Sciences, vol.62, pp. 3057-3066, 2010. |
| [6] | S. Dey, “Bayesian estimation of the parameter and reliability function of an inverse Rayleigh distribution”, Malaysian J. of Mathematical Sciences, vol.6, pp. 113-124, 2012. |
| [7] | M. Saleem, and M. Aslam, “On Bayesian analysis of the Rayleigh survival times under assuming the Rayleigh censor time”, Pak. J. of Statistics, vol.25, pp. 71-82, 2009. |

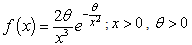
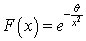
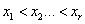 and remaining ‘n – r’ items are still working. Under the assumptions that the lifetimes of the items are independently and identically distributed inverse Rayleigh random variable, the likelihood function of the observed data without the multiplicative constant can be written as:
and remaining ‘n – r’ items are still working. Under the assumptions that the lifetimes of the items are independently and identically distributed inverse Rayleigh random variable, the likelihood function of the observed data without the multiplicative constant can be written as: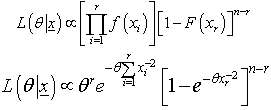
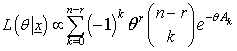
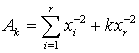 Again, consider a random sample of size ‘n’ from an inverse Rayleigh distribution, and let xr,..., xs be the ordered observations remaining when the ‘r – 1’ smallest observations and the ‘n – s’ largest observations have been censored, The likelihood function for
Again, consider a random sample of size ‘n’ from an inverse Rayleigh distribution, and let xr,..., xs be the ordered observations remaining when the ‘r – 1’ smallest observations and the ‘n – s’ largest observations have been censored, The likelihood function for 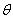 given the Type II doubly censored sample x = (xr,..., xs), is:
given the Type II doubly censored sample x = (xr,..., xs), is: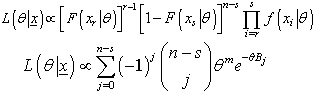
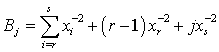 .
.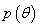 which reflects the prior information before collecting the data
which reflects the prior information before collecting the data 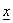 and the likelihood function
and the likelihood function 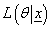 that represents the observed data then the posterior density
that represents the observed data then the posterior density 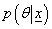 is calculated as proportional to the multiplication of prior distribution and the likelihood function i.e. Posterior density
is calculated as proportional to the multiplication of prior distribution and the likelihood function i.e. Posterior density 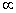 (Prior density)×(Likelihood function)
(Prior density)×(Likelihood function)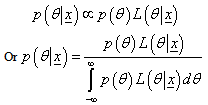 So for the derivation of posterior distribution the specification of the prior distribution is mandatory. The prior distributions can be categorized in two type informative priors and non-informative priors. The informative priors do not always exist. So in case of non availability of the informative priors, the non-informative priors are often used. Among non-informative priors, the uniform and Jeffreys priors have received significant attention. These priors will be assumed for the derivation of posterior distributions.
So for the derivation of posterior distribution the specification of the prior distribution is mandatory. The prior distributions can be categorized in two type informative priors and non-informative priors. The informative priors do not always exist. So in case of non availability of the informative priors, the non-informative priors are often used. Among non-informative priors, the uniform and Jeffreys priors have received significant attention. These priors will be assumed for the derivation of posterior distributions.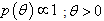
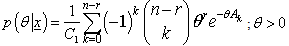
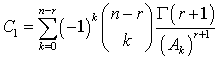 The Jeffreys prior is defined to be:
The Jeffreys prior is defined to be:  ;where
;where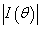 is Fisher Information matrix.Therefore;
is Fisher Information matrix.Therefore;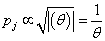
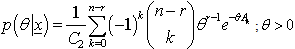
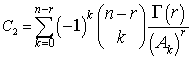 The posterior distribution under the assumption of uniform prior using doubly censored data is:
The posterior distribution under the assumption of uniform prior using doubly censored data is: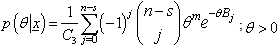
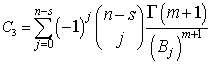 The posterior distribution under the assumption of Jeffreys prior using doubly censored data is:
The posterior distribution under the assumption of Jeffreys prior using doubly censored data is:
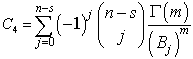
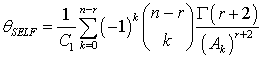
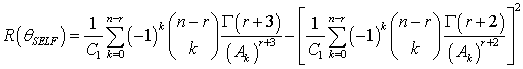
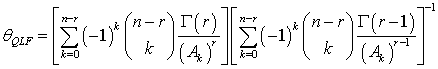
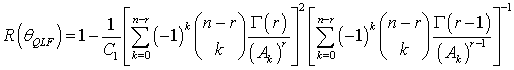
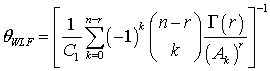
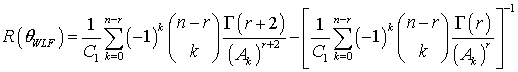
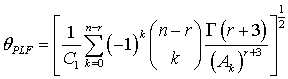
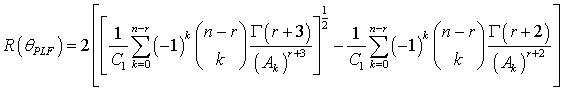
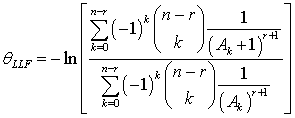
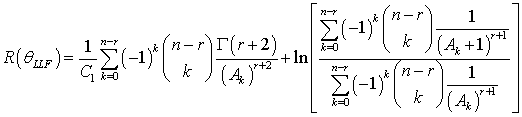
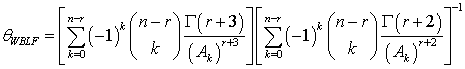
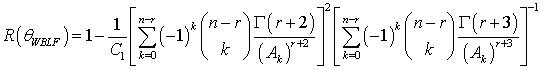
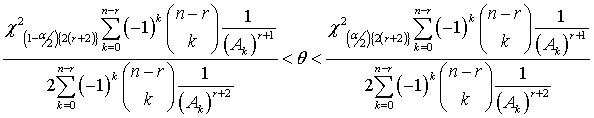
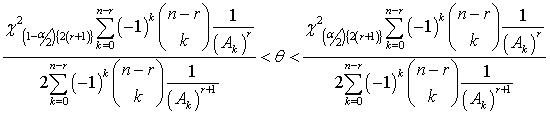

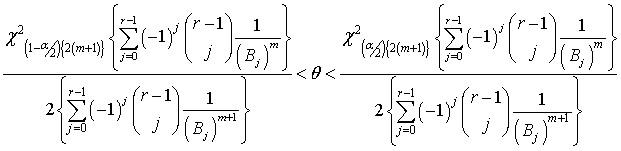
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML








