-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Probability and Statistics
p-ISSN: 2168-4871 e-ISSN: 2168-4863
2012; 1(4): 133-144
doi: 10.5923/j.ijps.20120104.06
A Multivariate Statistical Sampling Technique to Enhance Far Quantile Estimates of Arbitrary Responses
Christian Caillat 1, Eric Carman 2
1Emerging Memory Group, Micron Technology Belgium, Leuven, 3001, Belgium
2Emerging Memory Group, Micron Technology, San-Jose (CA), 95134-5134, USA
Correspondence to: Christian Caillat , Emerging Memory Group, Micron Technology Belgium, Leuven, 3001, Belgium.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
We propose a statistical sampling method, called eXtreme Event Sampling (XES), to compute far quantiles of arbitrary responses of multiple independent random parameters more accurately and efficiently than with Classical Monte-Carlo (CMC). Based on the selective over-sampling of events of low probability of occurrence, the method enables the study of multiple responses at a time, unlike the classical Importance Sampling (IS) techniques, expected to be the best-performing when tuned to a single given response. Though more generic than IS, XES still shows large gains over CMC in both accuracy and sampling efficiency, even for a large number of parameters (up to 27 tested). This article presents the detailed theoretical aspects of XES and an empirical study demonstrating its efficiency in various cases of responses (linear or non-linear), distributions (normal and non-normal) and number of parameters. If the primary target application is the design of semiconductor memory circuits, we believe that the flexibility of the method potentially makes it attractive in other contexts showing similar constraints.
Keywords: Importance Sampling, Monte-Carlo, Statistical Variations, Low Probability Events
Cite this paper: Christian Caillat , Eric Carman , "A Multivariate Statistical Sampling Technique to Enhance Far Quantile Estimates of Arbitrary Responses", International Journal of Probability and Statistics , Vol. 1 No. 4, 2012, pp. 133-144. doi: 10.5923/j.ijps.20120104.06.
Article Outline
1. Introduction
- Strategies for quick and accurate computation of Cumulative Distribution Functions (CDF) and more especially far quantiles is a topic common to a large variety of domains, such as finance, communications, insurance or nuclear physics[1][2], which led researchers to propose a collection of solutions more efficient than the “brute force” of Classical (or “Crude”) Monte-Carlo (CMC). The family of Importance Sampling (IS) strategies is certainly among the most efficient ones to achieve that[3], at least theoretically, since the ideal sampling scheme requires knowing the response (or even better: its density of probability) in order to adjust the sampling to it[1][3]. Indeed, blindly applying an IS strategy such as scaling or translation[3][4], exposes to the risk of getting an increasing variance instead of a decreasing variance of quantile estimates[5]. In the context of microelectronics circuit design, and more particularly semiconductor memories, of primary interest to us, there has been a growing interest in these computation-effective solutions over the past years[6 -9]. The fundamental reason lies in the growing impact of the various sources of statistical fluctuations of unit devices composing the memory cells as technologies progress [10-13] and in the rapid growth of memory capacity, now already entering the 10-100Gb era for standalone memories[14]. In the case of MOSFET transistors, for example, the threshold voltage fluctuation is a well known effect originating from multiple physical sources of randomness[13].If not taken into account properly, these fluctuations are likely to degrade the overall design performance and ultimately compromise the functionality itself, if the failure rate exceeds a critical value (depending on the redundancy scheme used, in the case of memories[15]). Classically, to assess memory design functionality towards cell fluctuations, CMC is performed and various critical signals of the circuit are analyzed (voltages, currents, delays, etc.). Since CMC is CPU intensive and practically ineffective in predicting far quantiles, it is not suitable for Giga-bit arrays. An ideal replacement strategy would not only show significant gain over CMC but be versatile enough to analyze multiple arbitrary signals in a single set of simulation runs, which does not fit well the classical IS strategies, where the sampling is adaptive to a response. Indeed, in the case of multiple responses, applying an IS strategy tuned for a given response to another one, the same above-mentioned risk of a diverging variance exists.For this reason, we recently proposed[16][17] a more generic sampling strategy based on the enhancement of rare events – i.e. with a low probability of occurrence in the parameter space – suitable to any response and that does not require knowing the responses or even deciding beforehand which ones will be analyzed. The proposed method is called eXtreme Event Sampling (XES), as it favors the rare events that are significantly deviating from the nominal parameter conditions for which the circuit is expected to be in its ideal operation region. More specifically, a refined sampling is applied in selected probability ranges, which extends the CDF calculation of a response to far quantiles. In that sense, since XES enhances specific categories of events, it can be considered as an IS scheme and actually shows similar formulas, as we will expose in this article.In a first section, we will detail the theoretical background supporting the construction of the sampling method, including the transformation allowing non-normal parameter distributions to be taken into account. In a second section, we will illustrate the effectiveness of XES through empirical studies for various responses, distributions and number of parameters and finally provide a benchmark of XES to CMC.Definitions:Xki : a vector of k i.i.d. random variables at iteration iR(Xki): response (scalar) of a vector Xkif(.): probability density function (PDF)F(.): cumulative distribution function (CDF)F-1(.): inverse CDFI(T): indicator function yielding 0 if T is false, 1 otherwiseN(µ,σ2): normal distribution of mean µ and variance σ2ξp: p-quantile of a distribution = F-1(p)
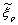 : estimator of ξpWi(.): ith statistical weight of an IS runN: total number of samples in MC or IS runΦ(.): standard normal CDFz: radius of a k-spheren(z): function yielding a number of samples per sphereAll random variables are assumed independent
: estimator of ξpWi(.): ith statistical weight of an IS runN: total number of samples in MC or IS runΦ(.): standard normal CDFz: radius of a k-spheren(z): function yielding a number of samples per sphereAll random variables are assumed independent2. Construction of the Sampling Method
2.1. The Multivariate Normal Distribution
- The lack of information on the responses does not prevent calculating a probability of occurrence of events in a multivariate problem. The idea of XES is to do so in order to over-sample rare events and thus enhance the CDF calculation for far quantiles as compared to a CMC sampling. In order to identify such rare events, we first have to establish the joint probability of a set of random variables (xk).With the assumptions that all input variables are normally distributed and independent, the multivariate joint Probability Density Function (PDF) of a set xk of such variables (xk ~ N(µk,σk2)) reads[18]:
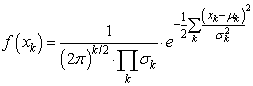 | (1) |
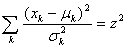 | (2) |
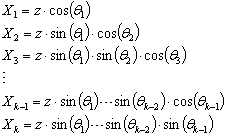 | (3) |
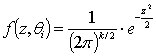 | (4) |
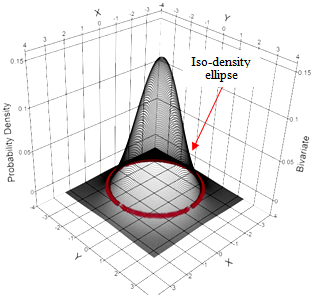 | Figure 1. Example of bivariate probability density function with an iso-density ellipse highlighted. X, Y ~ N(0,1). X/Y scales in standard sigma |
2.2. Marginal PDF on k-Spheres
- Let’s first establish the natural density of samples on a given k-sphere, by calculating the following marginal PDF (pz) of events for a k-sphere of radius z:
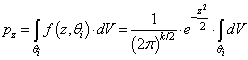 | (5) |
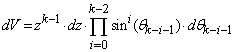 | (6) |
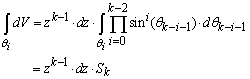 | (7) |
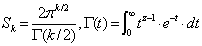 | (8) |
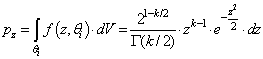 | (9) |
2.3. Empirical CDF Calculation
- Let’s now introduce a function n(z) yielding a number of samples n for a given k-sphere radius z. Since the natural density of samples for a given sphere z is defined by (9), the corrected marginal PDF for a such a sampling plan equals pz/n(z). Taking into account the above and similarly to the classical Monte-Carlo technique[21], we can then compute the empirical probability F(ξ) for a response R(Xk) to be lower than ξ from the following discrete sum (in other words: the discrete CDF of R):
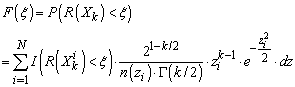 | (10) |
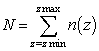 | (11) |
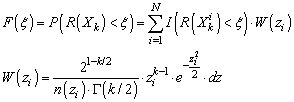 | (12) |
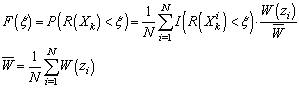 | (13) |
2.4. Uniform Sampling on k-Spheres
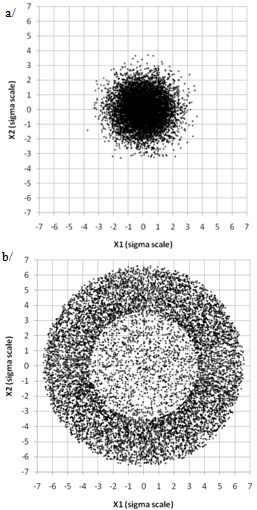
- We implicitly assumed in the above reasoning that the n samples taken on a k-sphere of radius z were equi-probable. In order to respect this condition, we chose to use the following method, introduced by Marsaglia[23], to draw samples over a k-sphere with a uniform spatial distribution:
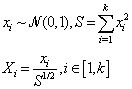 | (14) |
2.5. Sampling Plan: Defining n(z)
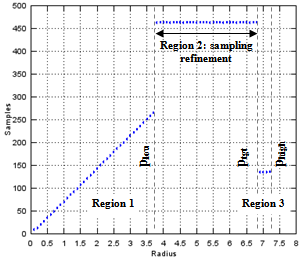
- The last part of the method consists in choosing a number of samples per k-sphere for each radius z.The primary goal of XES being to favor rare events in a selected range of occurrence probability, we first have to compute the CDF of events from the joint PDF (9). The PDF for various k values are illustrated in Figure 2, and (1-CDF) is shown in Figure 3.We stress again here that this represents the probability of a set of events belonging to a given k-sphere to occur, regardless of the actual values of the response, since the response is assumed to be unknown at this stage.
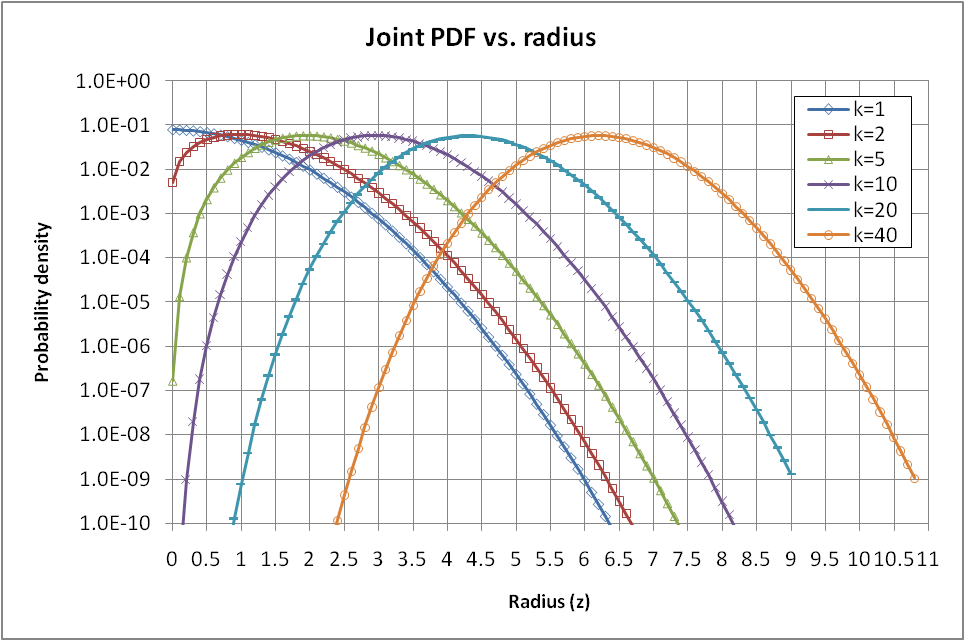 | Figure 2. Joint PDF (9) vs. radius z for various k. Y scale is in log |
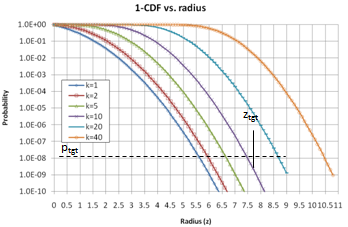 | Figure 3. (1-CDF) vs. radius z for various k. Y scale is in log |
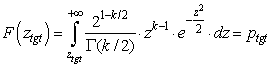 | (15) |
2.6. Actual Coordinates and Non-Normal Distributions
- Up to this point, the random variables are still expressed in a standard normal scale. Therefore, for each variable, a transformation of coordinates from the standard normal distribution to their actual distribution has to be performed before acquiring (or simulating) the responses. For a normal distribution, this is simply achieved by restoring the proper standard deviation (σ) and mean (µ) along the k axes:
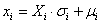 | (16) |
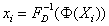 | (17) |
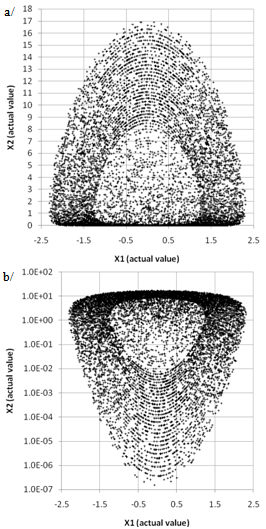 | Figure 6. 2D sampling plan of Figure 5 after transformation of coordinates; X1: N(0,0.35²); X2: Weibull (scale=2,shape=1.5). a/ linear Y-scale; b/ logarithmic Y-scale |
2.7. Confidence Interval, Error Calculation and Gains
- To calculate a confidence interval (CI) on the estimated quantile ξp, we use the classical property of convergence in distribution of quantile error, as described in e.g.[26]:
 | (18) |
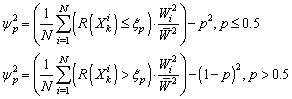 | (19) |
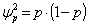 | (20) |
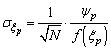 | (21) |
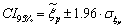 | (22) |
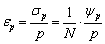 | (23) |
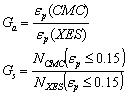 | (24) |
3. Empirical Study
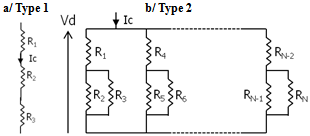
- We implemented the above formulas and sampling scheme in a commercial numerical computing platform in order to evaluate the accuracy and efficiency of the XES method, as we will now illustrate. The examples shown hereafter are built around a series of simple electrical test circuits made of resistors connected in series or in parallel and biased under a constant current Ic (Figure 7). The studied response is a voltage drop (Vd) across the circuit, and the random variables are the resistances. These simple circuits could represent, for example, a memory cell that would be repeated over a memory array and would experience statistical variations of its parameters (here: the resistance value).Since the equivalent resistance of such circuits is calculable, the response has a known analytical formula (Figure 7). In the following examples, this formula is used to calculate the response Vd for each sample and hence reconstruct the CDF; in an actual implementation, a circuit solver would compute the responses.Notes: probabilities in the CDF graphs below are expressed in sigma of the standard normal distribution, except otherwise specified. On such a scale, purely normal distributions show up as a straight line. The parameter dz in (12) is set to a constant value of 0.1 in all the examples below.
3.1. Linear Response
- We will first illustrate XES in the case of a Type 1 circuit (Figure 7 a/) for which the response is linear with respect to the resistances, and for 3 resistors: R1, R2, R3, following normal (section 3.1.1.) or non-normal (section 3.1.2.) distributions.
3.1.1. Normal Distributions
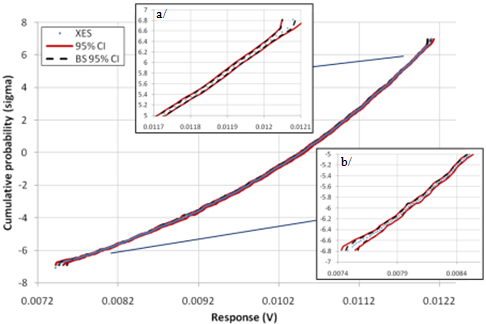
- The resistors are chosen as follows: R1:N(50,0.5²); R2: N(100,10²); R3:N(120,1.5²) – all values in ohm. The number of samples was set to 13,896 for the various plots below. Figure 8 shows the resulting XES CDF for Vd with the plow parameter set to 10-6 and for a targeted probability of 10-9 (assuming the studied population is of 1 billion individuals). Since in this case, the theoretical CDF can also be calculated from the composition of variance[18], we also plotted it in the same graph, in order to check that the two traces were superimposed.The 95% CI was also computed and is shown in Figure 9 together with the CDF for the lower (a/) and upper (b/) part of the CDF. The CI calculated with (22) and from a bootstrap re-sampling gives consistent results. As expected, thanks to the XES strategy, the CI is narrow in the vicinity of the targeted probability, both at +6σ and at -6σ.The relative error on the estimated quantiles (δξ) can also be calculated in this specific case, since the theoretical CDF and hence the true ξp are known:
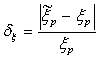 | (25) |
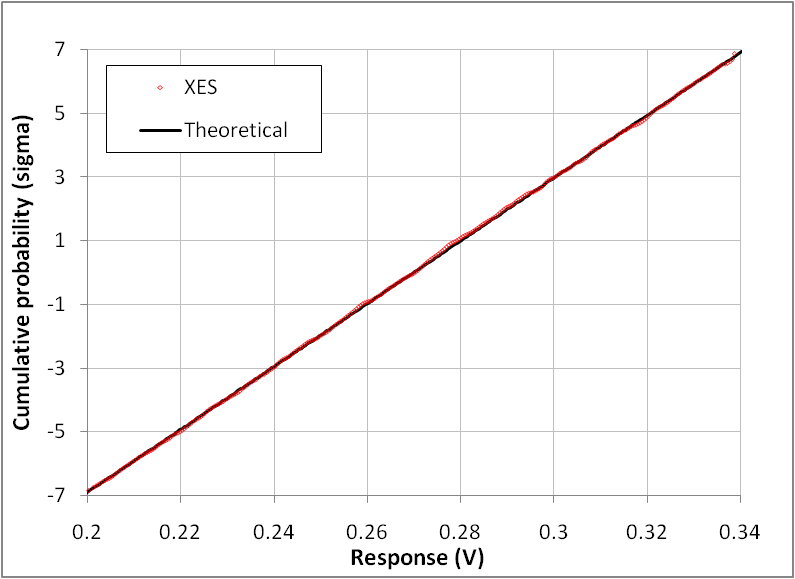 | Figure 8. CDF (sigma scale) of voltage drop (Vd) for 3 resistors / Type 1 circuit. The ptgt parameter is set to 10-9 and plow to 10-6. XES CDF is superimposed to the theoretical straight line |
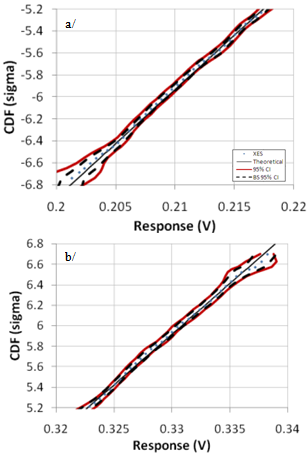 | Figure 9. Detail of a/ lower and b/ upper part of the XES CDF of Vd from Figure 8 as compared to the theoretical straight line; 95% CI calculated from (22) or from BS re-sampling (1000 runs) |
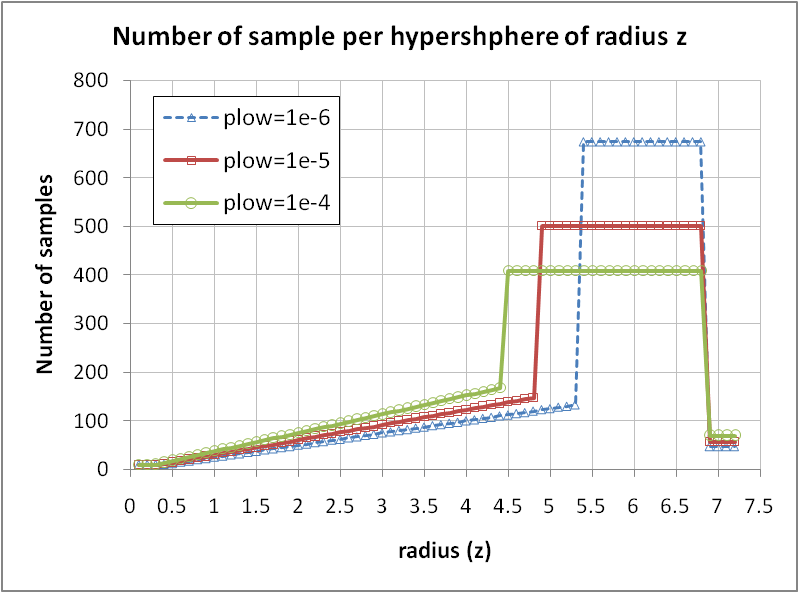 | Figure 10. Sampling plan for various plow, at a constant N=13,896 |
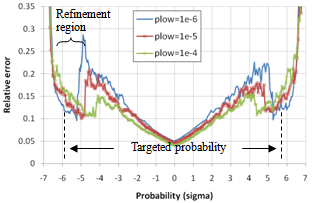 | Figure 11. Relative error εp vs. probability for various plow values at a constant N for CDF of Figure 8. The variations of plow modulate the refinement sampling range and the accuracy in this region |
3.1.2. Non-Normal Distributions
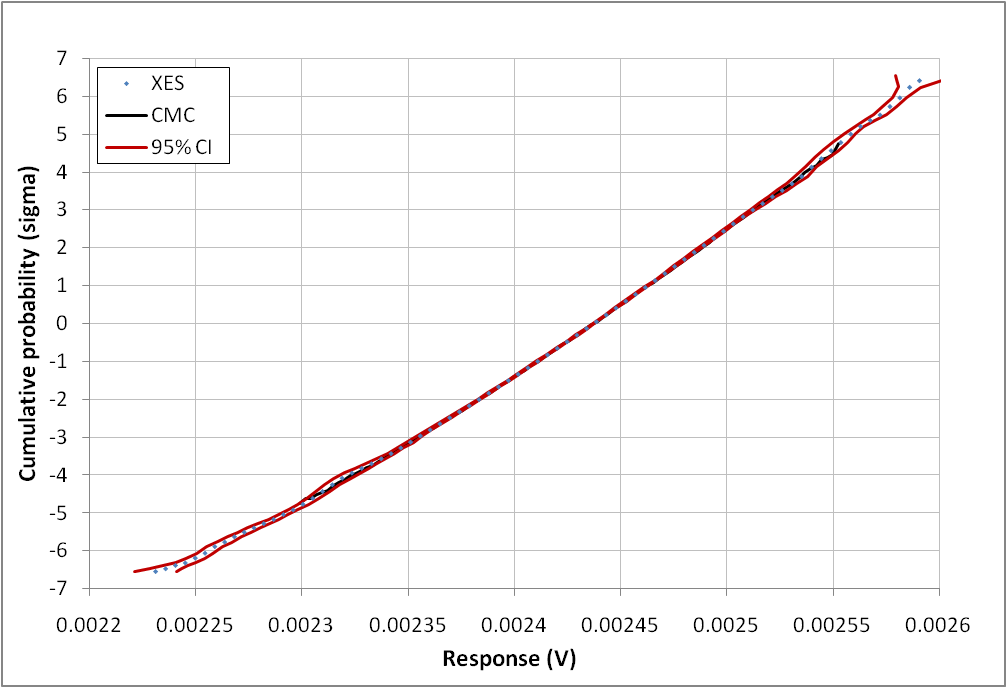
- In this example, the circuit is identical to the previous (3 resistors in series) and resistances are simply changed to 3-parameter Weibull (W) distributions instead of normal, as follows: WR1(scale=1, shape=1.5, location=50), WR2(scale= 1, shape=30, location= 100), WR3(scale=1, shape=4.5, location=120). The values were chosen to yield various PDF asymmetries, as illustrated in Figure 12. The XES parameters are: N=13,872 samples, ptgt=10-9, plow=10-4. The resulting XES CDF is shown in Figure 13 and is superimposed to the CMC trace. The confidence interval in the lower and upper part of the CDF are shown in Figure 14, further illustrating the good accuracy obtained at extreme quantiles even for non normal distributions.
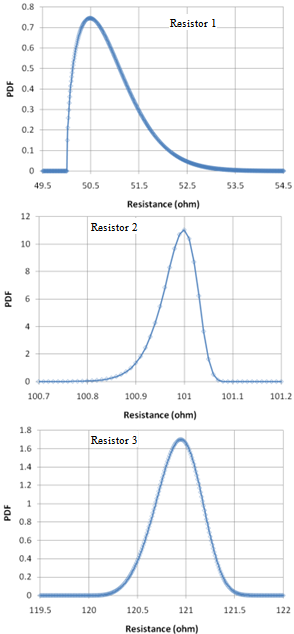 | Figure 12. PDF of the resistances R1, R2 and R3 (Weibull distributions) |
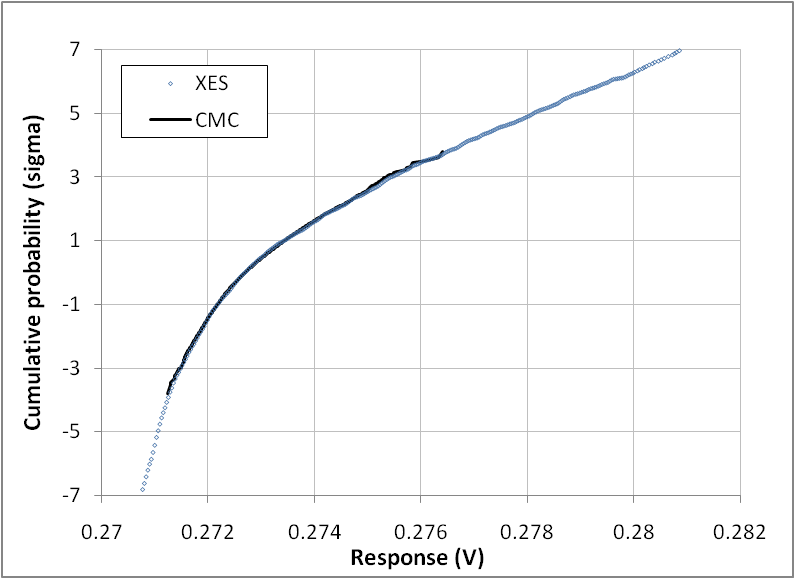 | Figure 13. XES and CMC CDF of the response Vd of 3 resistances following 3-parameter Weibull distributions, Type 1 circuit |
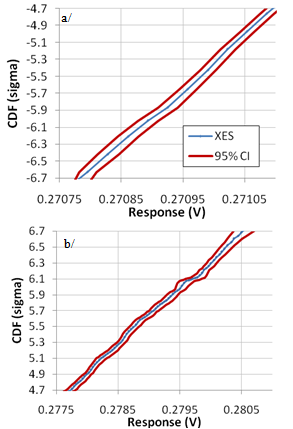 | Figure 14. XES CDF of Vd and 95% Confidence Interval from (22) for a/ lower and b/ upper part of the CDF |
3.2. Non Linear Response
- Considering now a Type 2 circuit and three normally distributed resistances, the resulting response Vd is non-linear, due to the resistors in parallel (Figure 7). In the following example, the resistances are chosen identical to the ones of section 3.1.1. The sampling plan is also similar, with ptgt=10-9, plow=10-5 and N=13,880 samples. The CDF of the response are shown in Figure 15 together with the 95% CI calculated from (22) or with 1000 BS runs. Tight CIs are obtained in the targeted probability range and the two CIs are consistent.
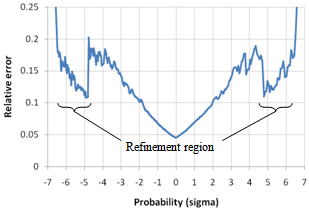 | Figure 16. Relative error εp vs. cumulative probability (sigma scale) |
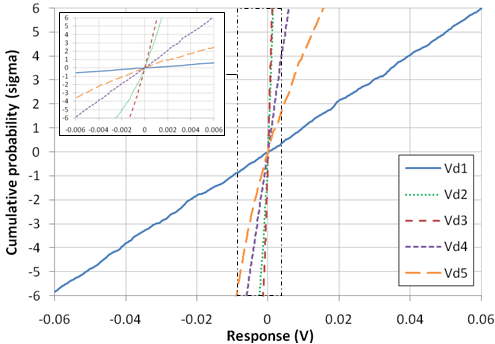
3.3. Multiple Responses, Single Sampling Plan
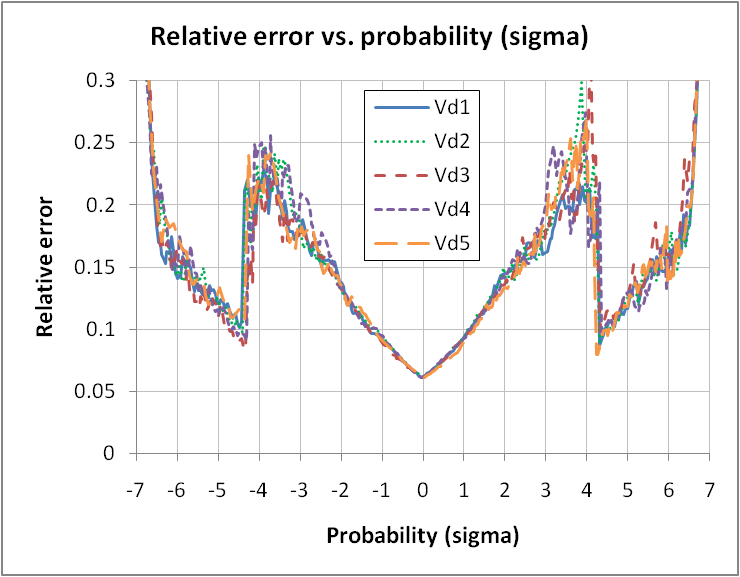 | Figure 18. Relative error εp for the various responses Vd1 to Vd5, single sampling plan, plow, =10-4, ptgt=10-9, N=13,989 |
3.4. Larger Number of Variables (k)
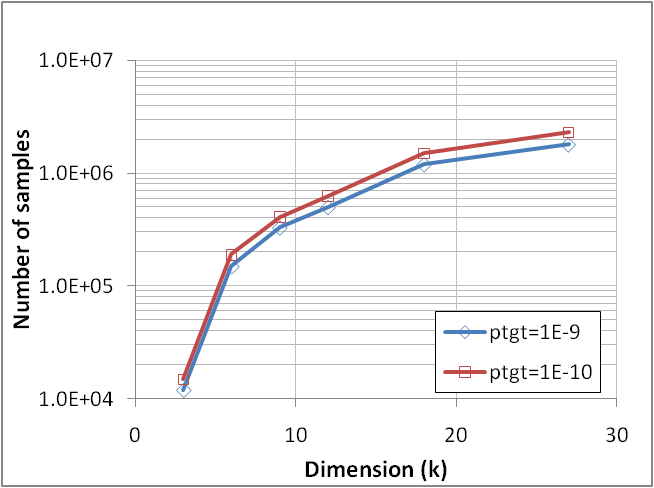
- As mentioned in section 2.5, the area of a k-sphere is growing rapidly with k and z, hence the number of samples required by XES is expected to grow accordingly for far quantiles.We have empirically studied the evolution of the minimal sampling to reach a given relative error (εp<15%) at a target quantile (for both ptgt and its counterpart 1-ptgt), using a simple response (Type 1 circuit) and a growing number of normally distributed variables (k). As graphically illustrated in Figure 19 for two target quantiles (ptgt=10-9 and 10-10), the growth of the number of samples vs. k is indeed fast, especially in the initial range of 3-12 variables.
3.5. Benchmark to CMC
- Based on the previous results, we will now further illustrate the efficiency of XES as k grows by comparing its performances to CMC in term of gain in sampling (Gs) and in accuracy (Ga) as defined in (24).The Tables 1 and 2 below show the gains obtained for ptgt=10-9 and 10-10, respectively, and for various k (up to k=27), considering a response Vd from a Type 1 circuit. The same data are graphically illustrated in Figure 21 and 22, showing that both gains stay quite strong even for 27 variables and further grow as the target quantile is decreasing to ptgt=10-10. It also shows that the gain degradation tends to attenuate as k grows, suggesting that the efficiency of XES over CMC should stay significant for an even larger number of variables.We finally underline that the error on the estimated quantile δξ at ptgt was below 1% for all the XES results of Tables 1 and 2, proving that the method does not introduce significant biases in the far quantile estimates.
| |||||||||||||||||||||||||||||||||
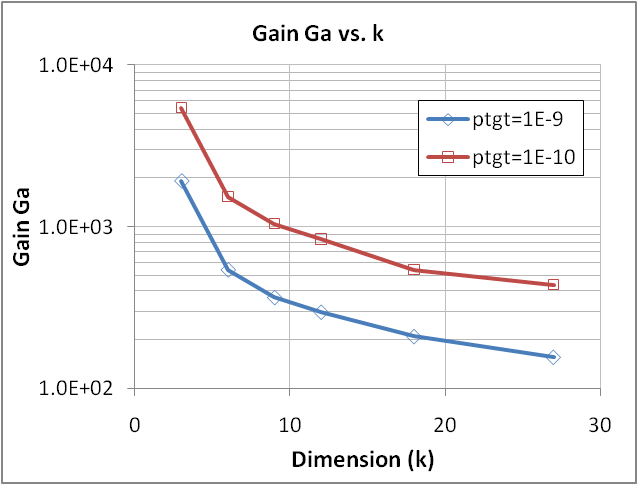 | Figure 21. Gain in accuracy of XES over CMC vs. k for two target quantiles ptgt=10-9 and 10-10 and at a given sampling (see Tables 1 and 2). Response is Vd of a Type 1 Circuit; all variables are normally distributed |
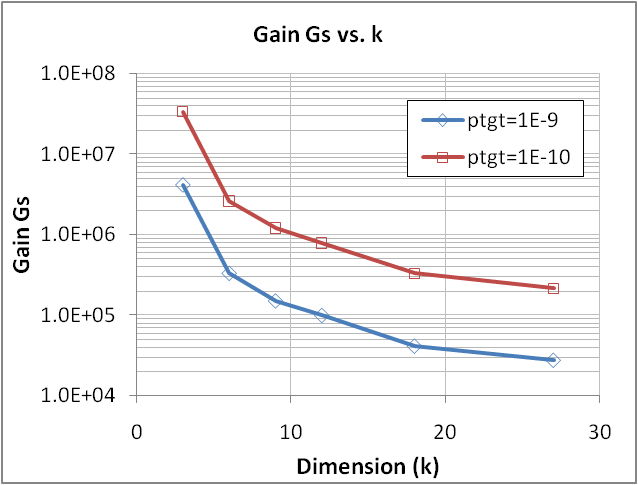 | Figure 22. Gain in sampling of XES over CMC vs. k for two target quantiles ptgt=10-9 and 10-10 and for εp<15%. Response is Vd of a Type 1 Circuit; all variables are normally distributed |
4. Conclusions
- We propose a multivariate sampling method, called XES (eXtreme Event Sampling), as an alternative to CMC and classical IS to compute far quantiles of arbitrary responses. The proposed strategy is similar to an IS scheme, but unlike classical IS techniques, does not require to know the response in advance or to adjust the sampling plan to it. Instead, events of low probability of occurrence are over-sampled in order to enhance far quantiles of responses. As a result, CDF of arbitrary responses can be reconstructed with a good accuracy at extreme quantiles and much more efficiently than CMC, despite the fact the method is generic as compared to an IS approach.The method applies to normally or non-normally distributed parameters and can deal with a large number of variables (up to 27 tested).Thanks to its flexibility, we believe XES is a valuable alternative to classical IS strategies when multiple arbitrary responses are to be studied in a single-pass simulation run (i.e. without adapting the sampling from the responses). Thus, beyond the case of circuit design of interest to us, the method could apply to other domains showing similar constraints.Future developments of the method should include in-depth investigation of the optimal sampling strategy (n(z) function) vs. k, further benchmark including to other IS strategies and finally, implementation of XES in a circuit solver to study real cases.
ACKNOWLEDGEMENTS
- The authors would like to acknowledge Alessandro Calderoni and Andrea Marmiroli (Micron Technology Italy) for their kind support and for valuable discussions and suggestions during the development of the XES method.
References
| [1] | M. Pagano, W. Sandmann, “Efficient Rare Event Simulation - A Tutorial on Importance Sampling”, in Proceedings of the 3rd International Conference on Performance Modelling and Evaluation of Heterogeneous Networks (HetNets), pp.T03/1-38, 2005. Presentation available online: http://netgroup.iet.unipi.it/teaching/prm/2005-06/docs/altro/tutorialIS.pdf. |
| [2] | R. Srinivasan, Importance sampling - Applications in communications and detection, Springer-Verlag, Germany, 2002. |
| [3] | Tim C. Hesterberg, “Advances in Importance Sampling”, PhD dissertation, Stanford University (CA), USA, 1988 (revised 2003). |
| [4] | P.J. Smith, M. Shafi, H. Gao, "Quick simulation: a review of importance sampling techniques in communications systems", IEEE Journal on Selected Areas in Communications, vol.15 no.4, pp.597-613, 1997. |
| [5] | P. Glasserman, Y. Wang, “Counter Examples in Importance Sampling for Large Deviations Probabilities”, Institute of Mathematical Statistics, The Annals of Applied Probability, vol.7, no.3, pp.731-746, 1997. |
| [6] | J. Yeung, H. Mahmoodi, "Robust sense amplifier design under random dopant fluctuations in nano-scale CMOS technologies", in Proceedings of IEEE International SOC Conference, p.261, 2006. |
| [7] | S. Akiyama, T. Sekiguchi, K. Kajigaya, S. Hanzawa, R. Takemura, T. Kawahara, "Concordant memory design using statistical integration for the billions-transistor era", in International Solid-State Circuits Conference Digest, p.466, 2005. |
| [8] | Rouwaida Kanj, Rajiv Joshi, Sani Nassif, “Mixture importance sampling and its application to the analysis of SRAM designs in the presence of rare failure events”, in Proceedings of IEEE Design Automation Conference, pp.69-72, 2006. |
| [9] | H. Nho, S.-S. Yoon, S. Wong, S.-O. Jung, “Statistical simulation methodology for sub-100nm memory design”, IET, Electronics Letters, vol.43, no.16, pp.869-870, 2007. |
| [10] | D. Reid, C. Millar, G. Roy, S. Roy, A. Asenov, "Analysis of threshold voltage distribution due to random dopants: a 100 000-sample 3-D simulation study", IEEE Transaction on Electron Devices, vol.56, no.10, pp.2255-2263, 2009. |
| [11] | P. Magnone, A. Mercha, V. Subramanian, P. Parvais, N. Collaert, M. Dehan, S. Decoutere, G. Groeseneken, J. Benson, T. Merelle, R. J. P. Lander, F. Crupi, C. Pace, "Matching performance of FinFET devices with Fin widths down to 10 nm", IEEE Electron Device Letters, vol.30, no.12, p.1374, 2009. |
| [12] | S. Toriyama, D. Hagishima, K. Matsuzawa, N. Sano," Device simulation of random dopant effects in ultra-small MOSFETs based on advanced physical models", in Proceedings of SISPAD conference, p.111, 2006. |
| [13] | A. Asenov, “3D statistical simulation of intrinsic fluctuations in decanano MOSFETS induced by discrete dopants, oxide thickness fluctuations and LER”, in Proceedings of Simulation of Semiconductor Processes and Devices, pp.162-169,2001; online:http://in4.iue.tuwien.ac.at/pdfs/sispad2001/pdfs/AsenovA_36.pdf. |
| [14] | Overall Roadmap Technology Characteristics Tables, International Technology Roadmap for Semiconductors (ITRS), 2011 edition; online:http://www.itrs.net/Links/2011ITRS/2011Tables/ORTC_2011Tables.xlsm. |
| [15] | I. Koren, C. M. Krishna, Fault-Tolerant Systems, Elsevier, USA, 2007. |
| [16] | C. Caillat, E. Carman, “A fast and accurate statistical sampling technique to predict the impact of device fluctuations on the functionality of large memory arrays”, in Proceeding of the 2011 Micron Technical Seminar (internal Micron publication), pp.36-38, 2012. |
| [17] | C. Caillat, E. Carman, “A Multivariate Statistical Sampling Technique (MuSST) to Assess the Robustness of Very Large Memory Arrays to Local Fluctuations”, unpublished, 2012. |
| [18] | D.P. Bertsekas, J.N. Tsitsiklis, Introduction to Probability, 2nd ed., Athena Scientific, USA, 2008. |
| [19] | L. E. Blumenson, “A Derivation of n-Dimensional Spherical Coordinates”, Mathematical Association of America, The American Mathematical Monthly, vol.67 no.1, pp.63-66, 1960. |
| [20] | D.M.Y. Sommerville, An Introduction to the Geometry of n Dimensions, Dover Publications, USA, 1958. |
| [21] | Harald Niederreiter, Random Number Generation and Quasi-Monte Carlo Methods, Society for Industrial and Applied Mathematics, USA, 1992. |
| [22] | Peter W. Glynn, “Importance Sampling for Monte Carlo Estimation of Quantiles”, in Proceedings of the Second International Workshop on Mathematical Methods in Stochastic Simulation and Experimental Design, pp.180-185, 1996. |
| [23] | G. Marsaglia, "Choosing a point from the surface of a sphere", Institute of Mathematical Statistics, The Annals of Mathematical Statistics, vol.43. no.2, p.645, 1972. |
| [24] | Aruna Sivakumar, Chandra R. Bhat, Giray Ökten, “Simulation Estimation of Mixed Discrete Choice Models Using Randomized Quasi-Monte Carlo Sequences: A Comparison of Alternative Sequences, Scrambling Methods, and Uniform-to-Normal Variate Transformation Techniques”, Transportation Research Board, Transportation Research Record, vol.1921, pp.112-122, 2005. |
| [25] | George Casella, Roger L. Berger, Statistical Inference, 2nd ed., Duxbury Press, USA, 2001. |
| [26] | Fang Chu, Marvin K. Nakayama, “Confidence Intervals for Quantiles and Value-at-Risk when Applying Importance Sampling”, in Proceedings of the 2010 Winter Simulation Conference, pp.2751-2761, 2010. |
| [27] | A. C. Davison, D. V. Hinkley, Bootstrap Methods and their Application, Cambridge University Press, USA, 1997; Shortcourse (Padova University, Italy, 2006) based on the book available at the link:http://www.stat.unipd.it/uploads/File/archivio/20060920141934_20060731132050001_Materiale_Didattico_Davison.pdf. |
| [28] | Bradley Efron, The Jackknife, the Bootstrap, and Other Resampling Plans, Society for Industrial and Applied Mathematics, USA, 1987. Original technical report from the Department of Statistics, Stanford University (CA), USA, 1980 is available online:http://statistics.stanford.edu/~ckirby/techreports/BIO/BIO%2063.pdf. |
| [29] | Paul Glasserman, Sandeep Juneja, “Uniformly Efficient Importance Sampling for the Tail Distribution of Sums of Random Variables”, Journal of Mathematics of Operations Research archive, vol.33, no.1, pp.36-50, 2008. |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML