-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Probability and Statistics
p-ISSN: 2168-4871 e-ISSN: 2168-4863
2012; 1(4): 119-132
doi: 10.5923/j.ijps.20120104.05
On Posterior Analysis of Mixture of Two Components of Gumbel Type II Distribution
Navid Feroze 1, Muhammad Aslam 2
1Department of Mathematics and Statistics, Allama Iqbal Open University, Islamabad, Pakistan
2Department of Statistics, Quaid-i-Azam University, Islamabad, Pakistan
Correspondence to: Navid Feroze , Department of Mathematics and Statistics, Allama Iqbal Open University, Islamabad, Pakistan.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
This paper describes the Bayesian analysis of the parameters of mixture of two components of Gumbel type II distribution. A heterogeneous population has been modeled by means of two components mixture of the Gumbel type II distribution under type I censored data. The Bayes estimators of the said parameters have been derived under the assumption of non-informative priors on the basis of different loss functions. A censored mixture data is simulated by probabilistic mixing for the computational purpose. The comparisons among the estimators have been made in terms of corresponding posterior risks. The posterior predictive distributions and intervals have been derived and evaluated under each prior.
Keywords: Bayes Estimators, Posterior Risks, Mixture Models, Loss Functions
Cite this paper: Navid Feroze , Muhammad Aslam , "On Posterior Analysis of Mixture of Two Components of Gumbel Type II Distribution", International Journal of Probability and Statistics , Vol. 1 No. 4, 2012, pp. 119-132. doi: 10.5923/j.ijps.20120104.05.
Article Outline
1. Introduction
- The Gumbel type II distribution is used to model the extreme events like extreme earthquake, rainfalls, temperature, floods etc. It has another side of applications which deals with life testing experiments. Chechile[1] obtained the posterior distribution assuming that the random sample is taken from the Gumbel distribution using the conjugate prior. Corsini et al.[2] discussed the maximum likelihood (ML) algorithms and Cramer-Rao (CR) bounds for the location and scale parameters of the Gumbel distribution. Mousa[3] obtained the Bayesian estimation for the two parameters of the Gumbel distribution based on record values. Koutsoyiannis and Baloutsos[4] described that the Gumbel distribution has been the prevailing model for quantifying risk associated with extreme rainfall. Rasmussen and Gautam[5] extended the probability weighted moments (PWM) to what is called the generalized method of probability weighted moments (GPWM) because there is no reason why the PWMs provide the most efficient estimators of Gumbel parameters and quantile especially in hydrology. Malinowska and Szynal[6] obtained the Bayes estimators for the two parameters of a Gumbel distribution based on kth lower record values. Nadarajah and Kotz[7] introduced the beta Gumbel (BG) distribution and provided closed-form expressions for the moments, the asymptotic distribution of the extreme order statistics and discussed the maximum likelihood estimation procedure. Miladinovic and Tsokos[8] modified the classical Gumbel probability distribution in order to study the failure times of a given system. Park et al.[9] gave a novel equation for the scale parameter of the Gumbel distribution. Heo and Salas[10] examined the log-Gumbel distribution regarding quantile estimation and confidence intervals of quantiles. Thompson et al.[11] introduced a distributional hypothesis test for left censored Gumbel observations based on the probability plot correlation coefficient (PPCC).The mixture models have received great attention of the analysts in the recent era. These models include finite and infinite number of components that can analyze different datasets. A finite mixture of probability distribution is suitable to study a population categorized in number of subpopulations. A population of lifetimes of certain electrical elements can be classified into number of subpopulations based on causes of failures. The analysis of mixture models under Bayesian framework has developed a significant interest among the statisticians. The authors dealing with Bayesian analysis of mixture models include Saleem and Aslam[12], Saleem et al.[13], Majeed and Aslam[14] and Kazmi et al.[15]. These contributions to the mixture models are the great motivations for the resent study. We considered two component mixture of Gumbel type II distribution. The population of certain items is assumed to be partitioned into two subpopulations. The randomly selected observations from the said population are considered to be a part of one of the above mentioned subpopulations. These subpopulations are assumed to follow the Gumbel type II distribution. Therefore, the two components mixture of Gumbel type II distributions has been proposed to model this population. The observations have been assumed to be right censored. The inverse transformation technique of simulation under a probabilistic mixing has been used to generate data and to evaluate the performance of different estimators.
2. The Model and Likelihood Function
- A density function for mixture of two components densities with mixing weights (p,q) is:
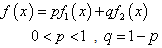 | (1) |
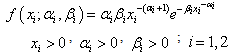 | (2) |
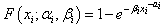 | (3) |
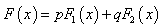 | (4) |
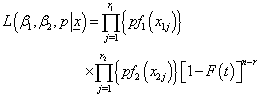 | (5) |
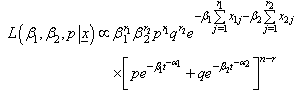 | (6) |
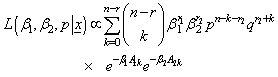 | (7) |
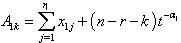 and
and 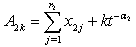
3. The Posterior Analysis under the Assumption of Uniform Prior
- One of the most widely used non-informative priors, proposed by Laplace[16], is a uniform prior. It has been applied to many problems, and often the results are entirely satisfactory. This prior has been used for the posterior estimation. Let
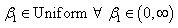 ,
, 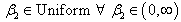 and
and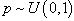 . Assuming independence, these priors result into a joint prior that is proportional to a constant. That joint prior has been used to derive the joint posterior distribution of
. Assuming independence, these priors result into a joint prior that is proportional to a constant. That joint prior has been used to derive the joint posterior distribution of 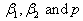 . The marginal distribution for each parameter can be obtained by integrating the joint posterior distribution with respect to nuisance parameters. The joint posterior distribution is:
. The marginal distribution for each parameter can be obtained by integrating the joint posterior distribution with respect to nuisance parameters. The joint posterior distribution is: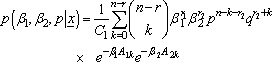 | (8) |
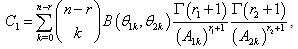
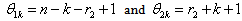 Using the posterior distribution, discussed in (8), the Bayes estimators and posterior risks under different loss functions have been derived and presented in the following.Bayes estimators and associated risks under uniform prior using squared error loss function (SELF) are:
Using the posterior distribution, discussed in (8), the Bayes estimators and posterior risks under different loss functions have been derived and presented in the following.Bayes estimators and associated risks under uniform prior using squared error loss function (SELF) are: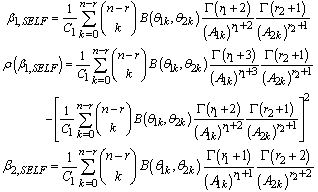
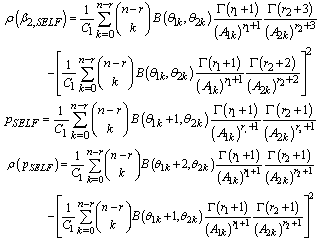 Bayes estimators and risk under uniform prior using quadratic loss function (QLF) are:
Bayes estimators and risk under uniform prior using quadratic loss function (QLF) are: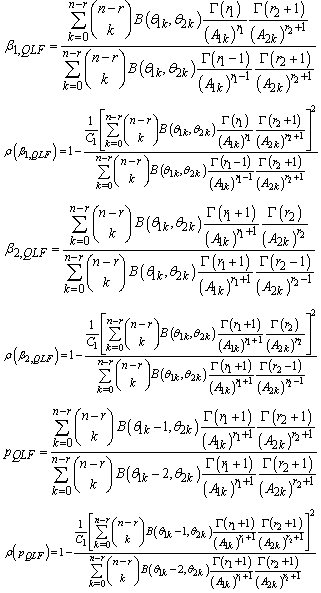 Bayes estimators and risk under uniform prior using weighted loss function (WLF) are:
Bayes estimators and risk under uniform prior using weighted loss function (WLF) are: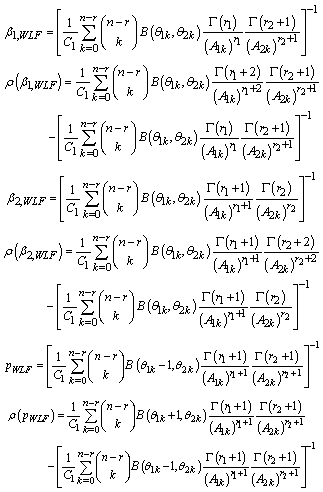 Bayes estimators and risk under uniform prior using precautionary loss function (PLF) are:
Bayes estimators and risk under uniform prior using precautionary loss function (PLF) are: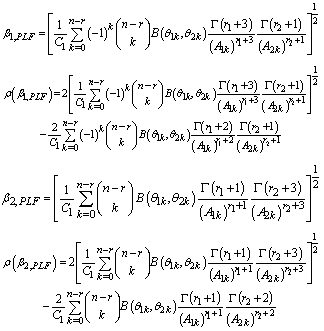
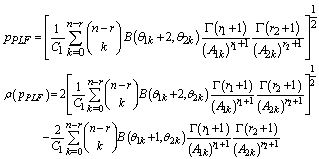
4. The Posterior Analysis under the Assumption of Jeffreys Prior
- Another non-informative prior has been suggested by Jeffreys[17] which is frequently used in situations where one does not have much information about the parameters. This is defined as the distribution of the parameters proportional to the square root of the determinants of the Fisher information matrix i.e.
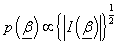 Where
Where 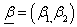 is the vector of parameters and
is the vector of parameters and 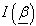 is (2×2) Fisher information matrix, defined as;
is (2×2) Fisher information matrix, defined as;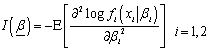 Where
Where 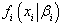 have been defined in (2) and
have been defined in (2) and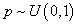 . Assuming independence, the joint prior is obtained as:
. Assuming independence, the joint prior is obtained as: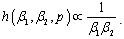 | (9) |
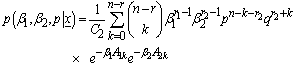 | (10) |
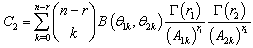 The Bayes estimators and associated posterior risks have been derived under different loss functions using the posterior distribution (10).Bayes estimators and associated risks under Jeffreys prior using squared error loss function (SELF) are:
The Bayes estimators and associated posterior risks have been derived under different loss functions using the posterior distribution (10).Bayes estimators and associated risks under Jeffreys prior using squared error loss function (SELF) are: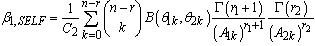
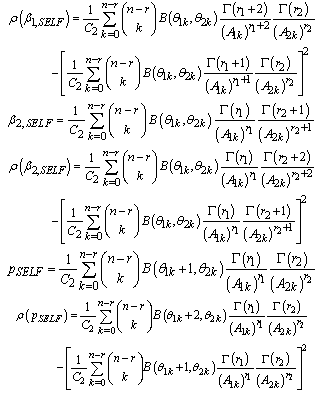 Bayes estimators and risk under Jeffreys prior using quadratic loss function (QLF) are:
Bayes estimators and risk under Jeffreys prior using quadratic loss function (QLF) are: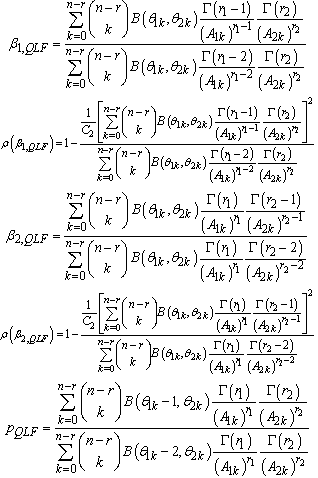
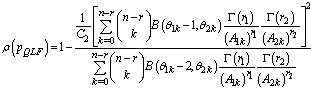 Bayes estimators and risk under Jeffreys prior using weighted loss function (WLF) are:
Bayes estimators and risk under Jeffreys prior using weighted loss function (WLF) are: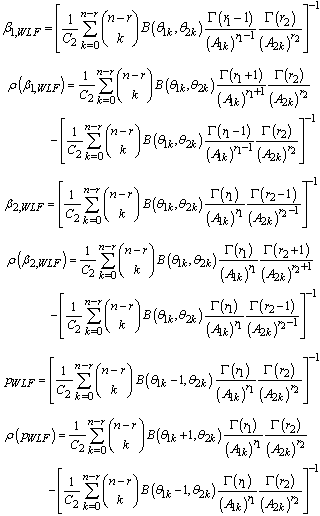 Bayes estimators and risk under Jeffreys prior using precautionary loss function (PLF) are:
Bayes estimators and risk under Jeffreys prior using precautionary loss function (PLF) are: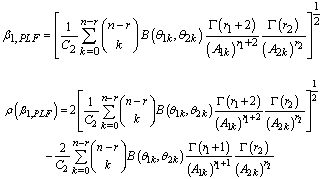
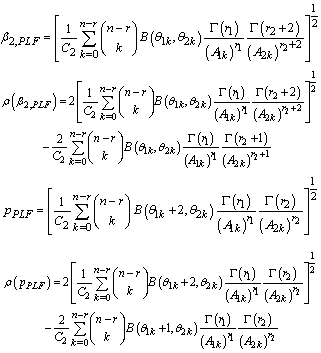
5. Posterior Predictive Distributions and Intervals
- The posterior predictive distributions under uniform and Jeffreys priors are:
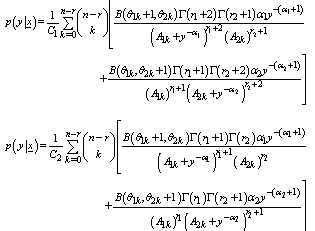 The posterior predictive intervals under uniform prior can be obtained by solving the following two equations respectively.
The posterior predictive intervals under uniform prior can be obtained by solving the following two equations respectively. Where ‘k’ is level of significanceThe posterior predictive intervals under uniform prior can be obtained by solving the following two equations respectively.
Where ‘k’ is level of significanceThe posterior predictive intervals under uniform prior can be obtained by solving the following two equations respectively.
6. Simulation Study
- A simulation study has been conducted to assess and compare the performance of Bayes estimators and to analyse the impact of sample size, mixing weight and magnitude of parametric values on the Bayes estimators. Samples of sizes n = 100, 200, 300, 400 and 500 have been generated by inverse transformation method from two components mixture of Gumbel type II distribution. The parametric values used are:
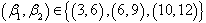 and
and 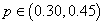 . The probabilistic mixing has been used to generate the mixture data. For each observation a random number has been generated from
. The probabilistic mixing has been used to generate the mixture data. For each observation a random number has been generated from 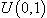 . If
. If 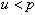 the observation has been randomly taken from first subpopulation and if
the observation has been randomly taken from first subpopulation and if 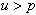 then the observation have been taken from the second subpopulation.The observations above a fixed censoring time T have been assumed to be right censored. Under each combination of parametric values, the choice of censoring time has been made so that the censoring rate in the respective sample has been 20%. As one sample cannot completely describe the behaviour and properties of the Bayes estimators, the results have been replicated 1000 times and the average of results has been presented in the tables below.
then the observation have been taken from the second subpopulation.The observations above a fixed censoring time T have been assumed to be right censored. Under each combination of parametric values, the choice of censoring time has been made so that the censoring rate in the respective sample has been 20%. As one sample cannot completely describe the behaviour and properties of the Bayes estimators, the results have been replicated 1000 times and the average of results has been presented in the tables below.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
7. Analysis under Real Life Data
- The real life data (following Gumbel distribution) regarding monthly wind speed in Cameron Highland from year 2004-2006 presented by Zaharimi et al.[18] is used to illustrate the applicability of the results obtained in previous sections.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
8. Conclusions
- The purpose of the article is to find out the appropriate combination of prior distribution and loss function to estimate the parameters of two-component mixture of Gumbel type II distribution. The parameters have been estimated under the assumption of two non-informative priors and four loss functions (symmetric and asymmetric). The posterior predictive intervals have also been evaluated. From the findings of the study it can be concluded that in order to estimate the said parameters, the use of Jeffreys prior and quadratic loss function can be preferred.
References
| [1] | A. R. Chechile, “Bayesian analysis of Gumbel distributed data”, Communications in Statistics - Theory and Methods, vol.30, no.3, pp. 211-224, 2001. |
| [2] | G. Corsini, F. Gini, M. V. Gerco, et al. “Cramer-Rao bounds and estimation of the parameters of the Gumbel distribution”, IEEE, vol.31, no.3, pp. 1202-1204, 2002. |
| [3] | A. Mousa, “Bayesian estimation, prediction and characterization for the Gumbel model based on records”, Statistics, vol.36, no.1, pp. 58-69, 2002. |
| [4] | D. Koutsoyiannis, and G. Baloutsos, “Analysis of a long record of annual maximum rainfall in Athens, Greece, and design rainfall inferences”, Natural Hazards, vol.22, no.1, pp. 29-48, 2000. |
| [5] | Rasmussen, P. F., and Gautam, N. “Alternative PWM-estimators of the Gumbel distribution. Journal of Hydrology”, vol.280, no.1-4, pp. 265-271, 2003. |
| [6] | I. Malinowka, and D. Szynal, “On characterization of certain distributions of kth lower (upper) record values”, Applied Mathematics and Computation, vol.202, no.1, pp. 338-347, 2008. |
| [7] | S. Nadarajah, and S. Kotz, “The beta Gumbel distribution”, Math. Probab. Eng., vol.10, 323-332, 2004. |
| [8] | B. Miladinovic, and P. C. Tsokos, “Sensitivity of the Bayesian reliability estimates for the modified Gumbel failure model”, International Journal of Reliability, Quality and Safety Engineering (IJRQSE), vol.16(40), pp. 331-341, 2009. |
| [9] | Y. Park, S. Sheetlin, and L. J. Spouge, “Estimating the Gumbel scale parameter for local alignment of random sequences by importance sampling with stopping times”, Ann. Statist., vol.37, no.6A, pp. 3697-3714, 2009. |
| [10] | H. J. Heo, and D. J. Salas, “Estimation of quantiles and confidence intervals for the log-Gumbel distribution”, Stochastic Hydrology and Hydraulics, vol.10, no.3, pp. 187-207, 2010. |
| [11] | E. M. Thompson, J. B. Hewlett, and R. M. Vogel, “The Gumbel hypothesis test for left censored observations using regional earthquake records as an example”, Nat. Hazards Earth Syst. Sci., vol.11, pp. 115-126, 2011. |
| [12] | M. Saleem, and M. Aslam, "Bayesian Analysis of the Two Component Mixture of the Rayleigh Dist. With the Uniform and the Jeffreys Priors", J. of Applied Statistical Science, Vol.16, no.4, pp.105-113, 2008. |
| [13] | M. Saleem, M. Aslam, and P. Economou, "On the Bayesian analysis of the mixture of power function distribution using the complete and the censored sample", Journal of Applied Statistics, vol.37, no.1, pp. 25-40, 2010. |
| [14] | M. Y. Majeed, and M. Aslam, “Bayesian analysis of the two component mixture of inverted exponential distribution under quadratic loss functions”, International Journal of Physical Sciences, vol.7, no.9, pp. 1424-1434, 2012. |
| [15] | S. M. A. Kazmi, M. Aslam, and S. Ali "On the Bayesian estimation for two component mixture of maxwell distribution, Assuming Type I Censored Data", International Journal of Applied Science and Technology (IJAST), vol.2, no.1, pp. 197-218, 2012. |
| [16] | P. S. Laplace, “Theorie analytique des probabilities”, Veuve Courcier Paris, 1812. |
| [17] | H. Jeffreys, “Theory of Probability”, 3rd edn. Oxford University Press, pp. 432, 1961. |
| [18] | A. Zaharimi, S. Najid, and A. Mahir, “Analyzing Malaysian wind speed data using statistical distribution”, Proceedings of the 4th IASME / WSEAS Inter. Conf. on Energy & Environment, Malysia, pp. 363-370, 2009. |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML