J. Subramani 1, S. Balamurali 2
1Department of Statistics, Pondicherry University, R V Nagar, Kalapet, Puducherry, 605 014, India
2Department of Computer Applications, Kalasalingam University, Krishnankoil, 6426 190, Srivilliputhur,Tamilnadu, India
Correspondence to: J. Subramani , Department of Statistics, Pondicherry University, R V Nagar, Kalapet, Puducherry, 605 014, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Control charts, also known as Shewhart charts in statistical process control are the statistical tools used to determine whether a manufacturing process is in a state of statistical control or not. If analysis of the control chart indicates that the process is currently under statistical control (i.e. is stable, with variation only coming from sources common to the process) then no corrections or changes to process control parameters are needed or desirable. In addition, data from the controlled process can be used to predict the future performance of the process with the help of process capability indices. That is, the suitability and the performance of the manufacturing process are assessed in two stage processes namely control charts and process capability indices. This paper deals with the techniques namely, capability based control charts which combines the two stage processes into a single stage process in industrial applications for on line process control. The relative performance of the capability based control charts for variables is assessed with that of existing usual control charts for variables, namely 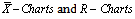 . It is observed that the proposed method is simple to apply and does not warrant any tedious computations both for control charts and for computing process capability indices. For the sake of convenience we have presented the control charts constants for constructing capability based
. It is observed that the proposed method is simple to apply and does not warrant any tedious computations both for control charts and for computing process capability indices. For the sake of convenience we have presented the control charts constants for constructing capability based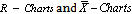 . The proposed method is also illustrated with the help of a numerical example.
. The proposed method is also illustrated with the help of a numerical example.
Keywords:
Control Charts, Industrial Applications, Process Capability Index, Quality Characteristics
Cite this paper:
J. Subramani , S. Balamurali , "Control Charts for Variables with Specified Process Capability Indices", International Journal of Probability and Statistics , Vol. 1 No. 4, 2012, pp. 101-110. doi: 10.5923/j.ijps.20120104.03.
1. Introduction
The present scenario of total quality management demands the effective use of statistical tools for analyzing quality problems and improving the performance of production process. Measuring, monitoring and maintaining several quality characteristics to achieve further improvements are required in every production process. Many of the quality characteristics are measurable in nature and can be expressed in terms of numerical measurement by measuring them using micrometer, vernier calipers etc. For example, length, diameter, weight, pocket width, distance and groove diameter of a shaft are some of the quantifiable quality characteristics encountered during the production of shafts. When dealing with measurable quality characteristics, it is usually necessary to monitor the behaviour of the mean value of the quality characteristics and its variability. To study the behaviour of the production process and to take a necessary action on the process, control charts for variables are very much used which requires to collect random samples from the production process and to compute the estimate of the quality characteristics. Further one has to show that the process is under statistical control before computing the process capability indices. Nowadays process capability analysis is a mandatory requirement and to have a minimum prescribed value for the process capability indices Cp and Cpk to be a supplier for original manufacturing companies, particularly in the field of automobile industries. Process capability indices (PCI) have proliferated in both use and variety during the last three decades. Their widespread and often uncritical use led to improvements in quality. Process capability indices are considered as a practical tool by many advocates of the statistical process control industry. They are used to determine whether the manufacturing process is capable of producing units within the product or process specifications. A capability index is a dimensionless measure based on the process parameters and the process specifications, designed to quantify, in a simple and easily understood way, the performance of the process. Several process capability indices have been developed among which the basic and widely used indices are Cp and Cpk. (see Kane[8]). A detailed review of the process capability indices can be seen in Kotz and Johnson[9]. The process capability indices are unit less measures showing the capability of a manufacturing process whether it is capable of operating within its specifications limits. If the value of the PCI exceeds one, then the process is considered to be satisfactory or capable. However this approach ignores the fact that these PCIs are random variables with distributions. Confidence limits play a major role for the correct interpretation of PCIs. Recently, techniques and tables were developed to construct confidence limits for the process capability indices. These techniques are based on the assumption that the underlying process is normal. Moreover, since many processes can frequently have skewed or heavily tailed distributions. In practice, the interval estimation technique that is free from the assumption of distribution is desirable. The various other properties and the behaviour of process capability indices at different type of distributions were studied by many authors. For example, the 95% confidence limits for the process capability indices Cp and Cpk were constructed by Chou, Owen and Borrego[5]. As their limits on Cpk can produce 97% or 98% lower confidence limits (instead of 95%) making them conservative, an approximation presented by Bissell[4] is recommended. Franklin and Wasserman[6] presented an initial study of the properties of these three bootstrap confidence intervals for Cpk. Franklin and Wasserman[7] constructed the confidence limits for some basic capability indices and examined their behaviors when the underlying process is normal, skewed or heavily tailed distributions. Balamurali andKalyanasundaram[3] constructed bootstrap confidence limits for the capability indices Cp, Cpk and Cpm based on lognormal and chi-squared distributions. Balamurali[2] considered the above capability indices under short run production processes and constructed the confidence limits. However the problems one has to face are the following: There is a considerable time taken for establishing and monitoring the process through control charts for variables; inadequate technical personnel to correctly interpret the outcome of the control charts; unnecessary inventory and delay due to the computation of process capability indices and to take a decision on the process based on the resulting values of process capability indices. Hence it is felt to have an alternative method to achieve the benefit of both control charts for variables and the process capability analysis. As a result we have proposed new type of control charts for variables based on the required process capability indices Cp and Cpk, called as “control charts for variables with specified value for process capability indices”. Further we have presented the control charts constants to construct the proposed control charts and are explained with the help of a numerical example. For a more detailed discussion on the control charts for variables and process capability analysis, the readers are referred to Montgomery[10], Spiring[11], Sarkar and Pal[1], Subramani[12, 13], Subramani and Balamurali[14] and the references cited therein. In this paper, we propose a capability based control chart for on line process control. The relative performance of this control charts for variables is assessed with that of existing usual control charts for variables. It is observed that the proposed method is simple to apply and does not warrant any tedious computations both for control charts and for computing process capability indices. We are also presenting the control charts constants for constructing capability based control charts. The proposed method is also illustrated with a numerical example.
2. Control Charts and Process Capability Analysis
2.1. Usual Method
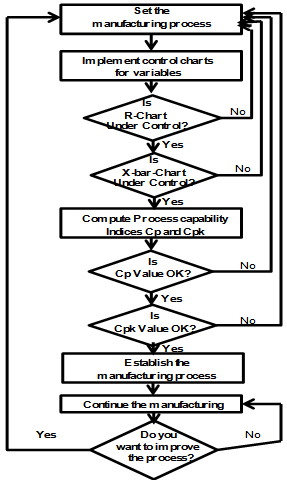 | Figure 1. Present M anufacturing System |
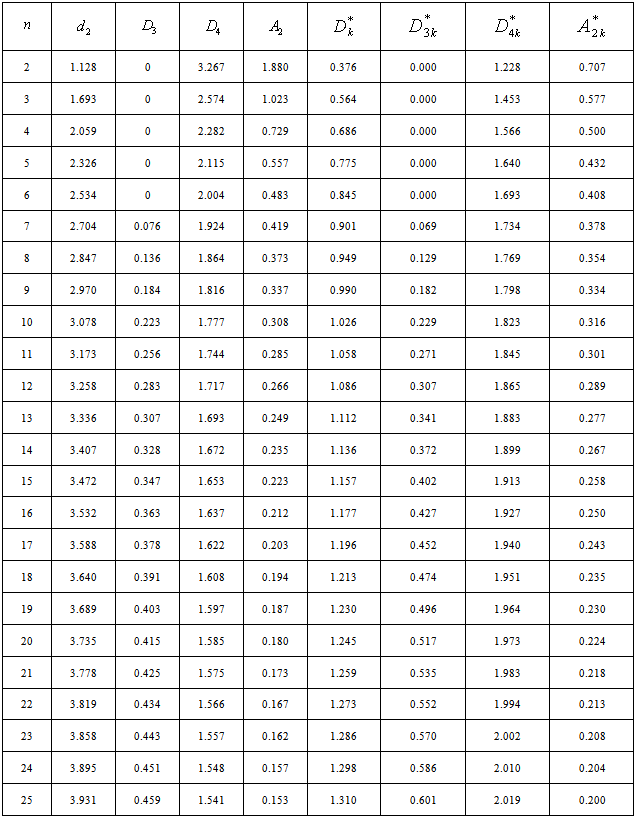
For the sake of convenience to the readers, we have presented the control charts for variables for checking whether the process is under statistical control or not. That is, to take a decision whether the process can be allowed further without making any adjustment or to take corrective actions if any, to bring back the process under statistical control. Once the process has been brought under the state of statistical control by both 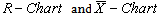 then the process capability indices
then the process capability indices 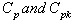 can be computed. If the values of the process capability indices are at the satisfactory level, the process can be allowed further without making any change or adjustment in the process. Otherwise suitable adjustments have to be made so that the process shall satisfy both the requirements of control charts and the process capability indices. The present manufacturing process can be explained in the flow chart as shown in Figure 1. The following are the various computational formulae involved in constructing the control charts and for the computation of process capability indices.
can be computed. If the values of the process capability indices are at the satisfactory level, the process can be allowed further without making any change or adjustment in the process. Otherwise suitable adjustments have to be made so that the process shall satisfy both the requirements of control charts and the process capability indices. The present manufacturing process can be explained in the flow chart as shown in Figure 1. The following are the various computational formulae involved in constructing the control charts and for the computation of process capability indices.
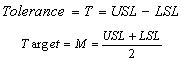 LSL: Lower Specification Limit of the Quality CharacteristicsUSL: Upper Specification Limit of the Quality CharacteristicsWhen the sample size n=5, the values for the control chart constants obtained from the table are as given below:D4 = 2.114, D3 = 0, d2 = 2.326 and A2 = 0.577 The Control limits for constructing
LSL: Lower Specification Limit of the Quality CharacteristicsUSL: Upper Specification Limit of the Quality CharacteristicsWhen the sample size n=5, the values for the control chart constants obtained from the table are as given below:D4 = 2.114, D3 = 0, d2 = 2.326 and A2 = 0.577 The Control limits for constructing  and
and  are as given below:Control limits for
are as given below:Control limits for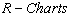 :
: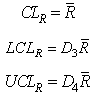 Control limits for
Control limits for 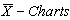 :
: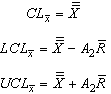
2.2. Proposed Method- Control Charts for Variables with Specified 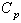 Value
Value
Suppose that a customer wants to have products produced in a process with a specified value for the process capability index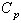 . To achieve this, the manufacturer has to establish a process under statistical control and then the process capability index has to be computed. If the computed value of
. To achieve this, the manufacturer has to establish a process under statistical control and then the process capability index has to be computed. If the computed value of 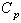 is more than the specified value given by the customer, the process can be run without any adjustment. Otherwise suitable actions have to be taken to meet the required process capability values. The drawback of this method is that the manufacturer has to keep all the produced items in the inventory until the computation of the process capability index and to take a decision on the process based on the process capability index. It is a time consuming procedure as well as requires additional skilled personnel. To avoid this, we have proposed control charts for variables with specified process capability indices. In the proposed method, the process is under statistical control means that it satisfies the required process capability index. Further it is not necessary to compute the process capability indices separately. The proposed manufacturing process can be explained in the flow chart shown in Figure 2.
is more than the specified value given by the customer, the process can be run without any adjustment. Otherwise suitable actions have to be taken to meet the required process capability values. The drawback of this method is that the manufacturer has to keep all the produced items in the inventory until the computation of the process capability index and to take a decision on the process based on the process capability index. It is a time consuming procedure as well as requires additional skilled personnel. To avoid this, we have proposed control charts for variables with specified process capability indices. In the proposed method, the process is under statistical control means that it satisfies the required process capability index. Further it is not necessary to compute the process capability indices separately. The proposed manufacturing process can be explained in the flow chart shown in Figure 2. 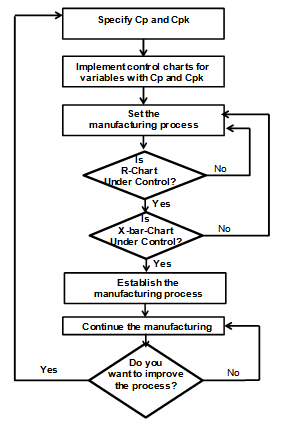 | Figure 2. Present M anufacturing System |
The following are the derivation of various computational formulae involved in constructing the proposed control charts with specified process capability index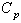 .
.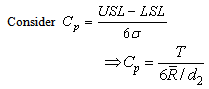 If
If 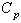 value is given then
value is given then 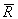 value can be obtained from the above formula as
value can be obtained from the above formula as 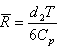
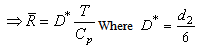 Similarly one can obtain the lower control limit (LCL) and upper control limit (UCL) of the
Similarly one can obtain the lower control limit (LCL) and upper control limit (UCL) of the  as given below:
as given below: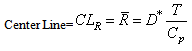
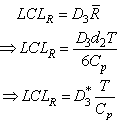
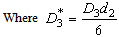
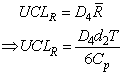 In the similar manner one can compute the control limits to construct
In the similar manner one can compute the control limits to construct 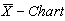 with specified
with specified 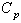 value as given below.
value as given below.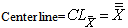 Lower control limit for the proposed
Lower control limit for the proposed 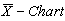 is obtained as given below:
is obtained as given below: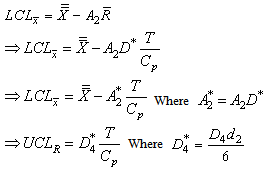 One can use the above control limits to construct
One can use the above control limits to construct 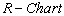 with specified
with specified 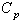 value.Similarly one may obtain the upper control limit for the proposed
value.Similarly one may obtain the upper control limit for the proposed 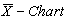 as
as 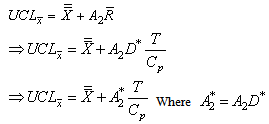
Table 1. Control Charts Constants for specified
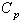 value value
 |
| |
|
Thus the control limits for the control charts with specified  value are as given below:Control limits for proposed
value are as given below:Control limits for proposed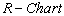 :
: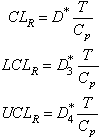 Control limits for proposed
Control limits for proposed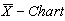 :
: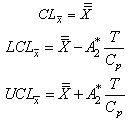 One can use the above control limits to construct the
One can use the above control limits to construct the 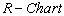 and
and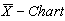 with specified
with specified 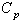 value. For the sample size
value. For the sample size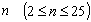 , we have presented the values of the control charts constants
, we have presented the values of the control charts constants 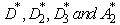 in the Table 1 given below.The advantageous of the proposed control charts is that the observed range values are not required for computing the control limits. Further if the process is under the state of statistical control means that it automatically satisfies the required conditions regarding the values of process capability index
in the Table 1 given below.The advantageous of the proposed control charts is that the observed range values are not required for computing the control limits. Further if the process is under the state of statistical control means that it automatically satisfies the required conditions regarding the values of process capability index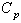 .
.
2.3. Proposed Method- Control Charts for Variables with Specified 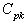 value
value
In the section 2.2, we have introduced a method for constructing control charts for variables with specified value for the process capability index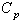 . In the similar manner we have developed a method for constructing control charts for variables with specified value for the process capability index
. In the similar manner we have developed a method for constructing control charts for variables with specified value for the process capability index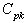 . The following are the derivation of various computational formulae involved in constructing control charts for variables with specified process capability index
. The following are the derivation of various computational formulae involved in constructing control charts for variables with specified process capability index 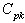
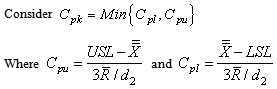 After a little algebra, one can rewrite the
After a little algebra, one can rewrite the 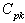 as
as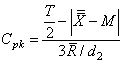 If
If 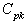 value is given then
value is given then 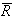 value can be obtained from the above formula as
value can be obtained from the above formula as 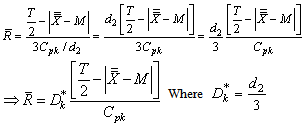 Similarly one can obtain the lower control limit (LCL) and upper control limit (UCL) of the
Similarly one can obtain the lower control limit (LCL) and upper control limit (UCL) of the 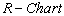 as given below:
as given below: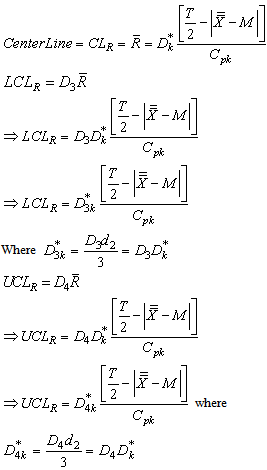 One can use the above control limits to construct
One can use the above control limits to construct 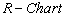 with specified
with specified 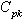 value.In the similar manner one can compute the control limits to construct
value.In the similar manner one can compute the control limits to construct 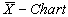 with specified
with specified 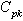 value as given below.
value as given below.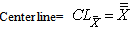 Lower control limit for the proposed
Lower control limit for the proposed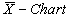 is obtained as given below:
is obtained as given below: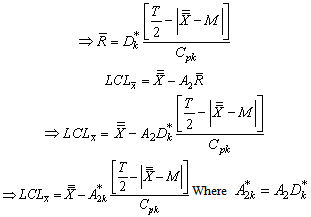 Similarly one may obtain the upper control limit for the proposed
Similarly one may obtain the upper control limit for the proposed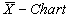 as
as 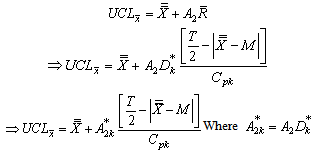 Thus the control limits for the proposed control charts with specified
Thus the control limits for the proposed control charts with specified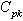 value are as given below:Control limits for
value are as given below:Control limits for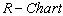 with specified
with specified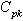 value
value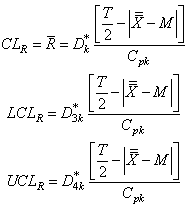 Control limits for the proposed
Control limits for the proposed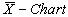 with specified
with specified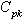 value:
value: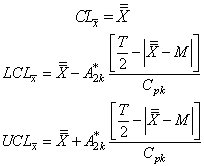 The above control limits can be further simplified by substituting the values of and, which lead to the following two cases:Case 1: When
The above control limits can be further simplified by substituting the values of and, which lead to the following two cases:Case 1: When 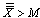 Control limits for
Control limits for with specified
with specified value
value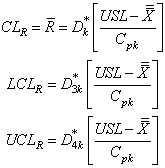 Control limits for the proposed
Control limits for the proposed with specified
with specified value:
value: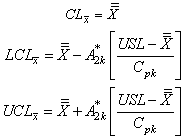
Table 2. Control Charts Constants for specified
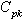 value value
 |
| |
|
Case 2: When 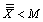 Control limits for
Control limits for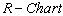 with specified
with specified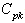 value
value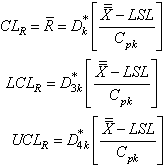 Control limits for the proposed
Control limits for the proposed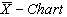 with specified
with specified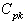 value:
value: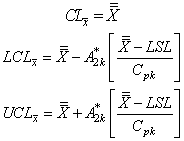 One can use the above control limits to construct the
One can use the above control limits to construct the 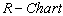 and
and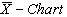 with specified
with specified 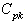 value. For the given sample size
value. For the given sample size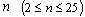 , we have presented the values of the control charts constants
, we have presented the values of the control charts constants 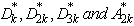 in the Table 2 given below.The advantageous of the proposed control charts with specified
in the Table 2 given below.The advantageous of the proposed control charts with specified 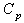 and
and 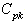 values, is that the observed range values are not required for computing the control limits. Further if the process is under the state of statistical control means that it automatically satisfies the required conditions regarding the values of process capability indices
values, is that the observed range values are not required for computing the control limits. Further if the process is under the state of statistical control means that it automatically satisfies the required conditions regarding the values of process capability indices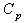 and
and 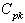 .
.
3. Numerical Example
Consider the data given below in Table 3 is the Example 5.1 (Montgomery[10], page 213). The data is pertaining to the manufacturing of Piston Rings for an automotive engine produced by a forging process. Twenty five samples, each of size five have been taken and the inside diameter is measured. The resulting data together with the sample means and sample range values are given below in Table 3.From the above values we have obtained the following: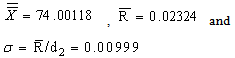 Case 1: Usual Method of Control Charts and the Computation of Process Capability IndicesControl Limits for R-Chart are obtained as:
Case 1: Usual Method of Control Charts and the Computation of Process Capability IndicesControl Limits for R-Chart are obtained as: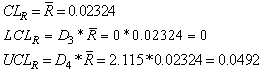 Control Limits for
Control Limits for 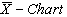 are obtained as:
are obtained as: 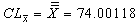
| Table 3. Data of Inside Diameter of Piston Rings (Spec: 74.000±0.05 mm) |
| | Sample Number | x1 | x2 | x3 | x4 | x5 | Sample Mean | Range R | | 1 | 74.030 | 74.002 | 74.019 | 73.992 | 74.008 | 74.0102 | 0.038 | | 2 | 73.995 | 73.992 | 74.001 | 74.011 | 74.004 | 74.0006 | 0.019 | | 3 | 73.988 | 74.024 | 74.021 | 74.005 | 74.002 | 74.0080 | 0.036 | | 4 | 74.002 | 73.996 | 73.993 | 74.015 | 74.009 | 74.0030 | 0.022 | | 5 | 73.992 | 74.007 | 74.015 | 73.989 | 74.014 | 74.0034 | 0.026 | | 6 | 74.009 | 73.994 | 73.997 | 73.985 | 73.993 | 73.9956 | 0.024 | | 7 | 73.995 | 74.006 | 73.994 | 74.000 | 74.005 | 74.0000 | 0.012 | | 8 | 73.985 | 74.003 | 73.993 | 74.015 | 73.988 | 73.9968 | 0.030 | | 9 | 74.008 | 73.995 | 74.009 | 74.005 | 74.004 | 74.0042 | 0.014 | | 10 | 73.998 | 74.000 | 73.990 | 74.007 | 73.995 | 73.9980 | 0.017 | | 11 | 73.994 | 73.998 | 73.994 | 73.995 | 73.990 | 73.9942 | 0.008 | | 12 | 74.004 | 74.000 | 74.007 | 74.000 | 73.996 | 74.0014 | 0.011 | | 13 | 73.983 | 74.002 | 73.998 | 73.997 | 74.012 | 73.9984 | 0.029 | | 14 | 74.006 | 73.967 | 73.994 | 74.000 | 73.984 | 73.9902 | 0.039 | | 15 | 74.012 | 74.014 | 73.998 | 73.999 | 74.007 | 74.0060 | 0.016 | | 16 | 74.000 | 73.984 | 74.005 | 73.998 | 73.996 | 73.9966 | 0.021 | | 17 | 73.994 | 74.012 | 73.986 | 74.005 | 74.007 | 74.0008 | 0.026 | | 18 | 74.006 | 74.010 | 74.018 | 74.003 | 74.000 | 74.0074 | 0.018 | | 19 | 73.984 | 74.002 | 74.003 | 74.005 | 73.997 | 73.9982 | 0.021 | | 20 | 74.000 | 74.010 | 74.013 | 74.020 | 74.003 | 74.0092 | 0.020 | | 21 | 73.982 | 74.001 | 74.015 | 74.005 | 73.996 | 73.9998 | 0.033 | | 22 | 74.004 | 73.999 | 73.990 | 74.006 | 74.009 | 74.0016 | 0.019 | | 23 | 74.010 | 73.989 | 73.990 | 74.009 | 74.014 | 74.0024 | 0.025 | | 24 | 74.015 | 74.008 | 73.993 | 74.000 | 74.010 | 74.0052 | 0.022 | | 25 | 73.982 | 73.984 | 73.995 | 74.017 | 74.013 | 73.9982 | 0.035 | | Average | 74.00118 | 0.02324 |
|
|
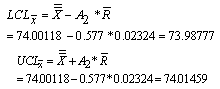 By plotting the control limits, sample ranges and sample means, one may get
By plotting the control limits, sample ranges and sample means, one may get  and
and  as given in Figure 3 and Figure 4. From the
as given in Figure 3 and Figure 4. From the  , we observe that all the plotted sample range values are falling within the control limits. Hence we may conclude that the variations are under control. Similarly from the
, we observe that all the plotted sample range values are falling within the control limits. Hence we may conclude that the variations are under control. Similarly from the , we observe that all the plotted sample means are falling inside the control limits. Hence we may conclude that the averages are also under the statistical control.
, we observe that all the plotted sample means are falling inside the control limits. Hence we may conclude that the averages are also under the statistical control.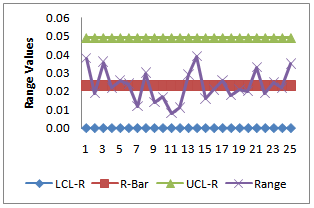 | Figure 3. R-Chart- Usual Method |
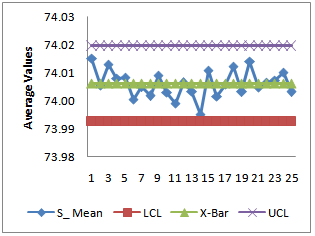 | Figure 4. X-Bar Chart- Usual Method |
The manufacturing capability of a process can normally be evaluated in terms of process capability indices 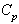 and
and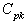 . The process capability indices obtained from the above values are given below:
. The process capability indices obtained from the above values are given below: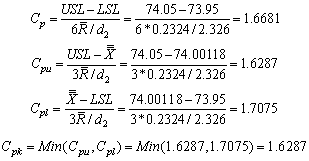 If the customer’s requirement of the process capability index
If the customer’s requirement of the process capability index 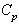 is 1.5, then one may conclude from the above capability indices that the process is an efficient one. However If the customer’s requirement of the process capability index
is 1.5, then one may conclude from the above capability indices that the process is an efficient one. However If the customer’s requirement of the process capability index 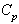 is 2.0, then one may conclude from the above capability indices that the process is not an efficient one and hence the process has to be adjusted so as the resulting process capability index
is 2.0, then one may conclude from the above capability indices that the process is not an efficient one and hence the process has to be adjusted so as the resulting process capability index 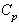 is at least 2.0. Case 2: Control Charts with specified
is at least 2.0. Case 2: Control Charts with specified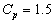 In this case we construct the control limits for the given value of process capability index
In this case we construct the control limits for the given value of process capability index 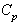 and hence separate computation of the process capability index is not required. Further the proposed control charts states that the process is under the statistical control means that the process satisfies the requirement of the process capability index. Hence one can construct several control limits for different values of process capability index
and hence separate computation of the process capability index is not required. Further the proposed control charts states that the process is under the statistical control means that the process satisfies the requirement of the process capability index. Hence one can construct several control limits for different values of process capability index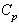 . If any plotted points falls outside the control limits with specified
. If any plotted points falls outside the control limits with specified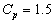 means that the process does not satisfy the required process capability index
means that the process does not satisfy the required process capability index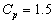 .Let the given process capability index
.Let the given process capability index 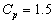 . Then the Control limits for
. Then the Control limits for  with specified
with specified are obtained as given below:
are obtained as given below: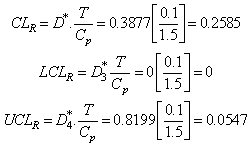 Control limits for
Control limits for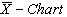 with specified
with specified 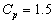
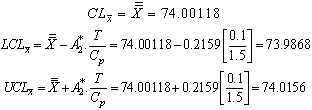 By plotting the control limits, sample ranges and sample means, one may get
By plotting the control limits, sample ranges and sample means, one may get 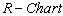 and
and 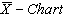 with specified
with specified 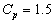 as given in Figure 5 and Figure 6. From the
as given in Figure 5 and Figure 6. From the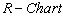 , we observe that all the plotted sample range values are falling within the control limits. Hence we may conclude that the variations are under control. Similarly from the
, we observe that all the plotted sample range values are falling within the control limits. Hence we may conclude that the variations are under control. Similarly from the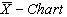 , we observe that all the plotted sample means are falling inside the control limits. Hence we may conclude that the averages are also under the statistical control. Further we conclude that the process capability index for the given process is at least 1.5 and satisfies the customer’s requirements.
, we observe that all the plotted sample means are falling inside the control limits. Hence we may conclude that the averages are also under the statistical control. Further we conclude that the process capability index for the given process is at least 1.5 and satisfies the customer’s requirements.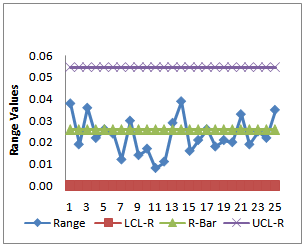 | Figure 5. R- Chart with Specified Cp=1.5 |
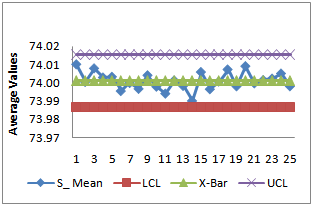 | Figure 6. X-Bar Chart with Specified Cp=1.5 |
Case 3: Control Charts with specified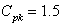 In this case we construct the control limits for the given value of process capability index
In this case we construct the control limits for the given value of process capability index 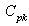 and hence separate computation of the process capability index is not required. Further the proposed control charts states that the process is under the statistical control means, the process satisfies the requirement of the process capability index. Hence one can construct several control limits for different values of process capability index. If any plotted points falls outside the control limits with specified
and hence separate computation of the process capability index is not required. Further the proposed control charts states that the process is under the statistical control means, the process satisfies the requirement of the process capability index. Hence one can construct several control limits for different values of process capability index. If any plotted points falls outside the control limits with specified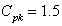 means that the process does not satisfy the required process capability index
means that the process does not satisfy the required process capability index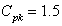 .Let the given process capability index
.Let the given process capability index 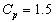 . Further
. Further 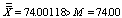 the control limits with specified process capability index
the control limits with specified process capability index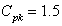 are obtained as given below:Control limits for
are obtained as given below:Control limits for with specifiedvalue
with specifiedvalue Control limits for the proposed
Control limits for the proposed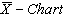 with specified
with specified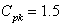 value are obtained as given below:
value are obtained as given below: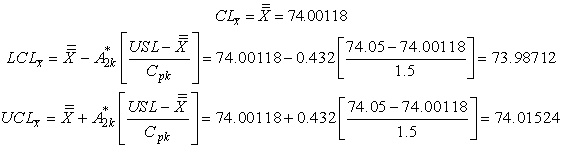
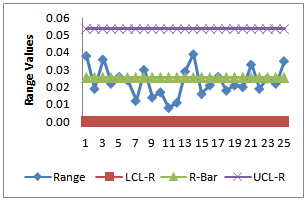 | Figure 7. R-Chart with Specified Cpk=1.5 |
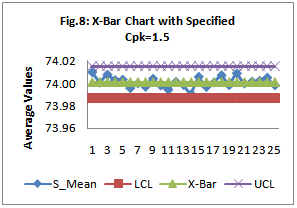 | Figure 8. X-Bar Chart with Specified Cpk=1.5 |
By plotting the control limits, sample ranges and sample means, one may get 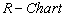 and
and 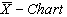 with specified
with specified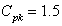 as given in Figure 7 and Figure 8. From the
as given in Figure 7 and Figure 8. From the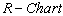 , we observe that all the plotted sample range values are falling within the control limits. Hence we may conclude that the variations are under control. Similarly from the
, we observe that all the plotted sample range values are falling within the control limits. Hence we may conclude that the variations are under control. Similarly from the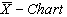 , we observe that all the plotted sample means are falling inside the control limits. Hence we may conclude that the averages are also under the statistical control. Further we conclude that the process capability index
, we observe that all the plotted sample means are falling inside the control limits. Hence we may conclude that the averages are also under the statistical control. Further we conclude that the process capability index 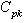 for the given process is at least 1.5 and satisfies the customer’s requirements.
for the given process is at least 1.5 and satisfies the customer’s requirements.
4. Conclusions
In this paper, we have proposed a control chart which is based on the process capability indices Cp and Cpk for on line process control, which have the benefit of the usual control charts and the process capability indices. That is, the proposed control charts combines the two stage controlling mechanism namely, Control Charts and the process capability indices into a single stage controlling mechanism to monitor the process online and to assess the suitability of the manufacturing process. It has been shown that the relative performance of the proposed control charts for variables can be assessed with that of usual variable control charts. It has also been shown that the proposed control chart is simple to apply and does not warrant any tedious computations both for control charts and for computing process capability indices. Moreover, we have also presented tables for the control charts constants for computing the control limits of the capability based control charts. The proposed method has also been illustrated with a numerical example. This study can also be extended to develop control charts based on other process capability indices.
ACKNOWLEDGEMENTS
The authors are thankful to the editor and the referees for their useful comments, which have helped to improve the presentation of the paper.
References
| [1] | Ashok Sarkar and Surajit Pal, “Process Control and Evaluation in the Presence of Systematic Assignable Cause”, Quality Engineering, Vol.10, pp.383-388, 1997 |
| [2] | Balamurali, S, “Bootstrap Confidence Limits for Short Run Capability Indices”, Quality Engineering, Vol.15, pp.643-648, 2003 |
| [3] | Balamurali, S., and Kalyanasundaram, M “BootstrapLower Confidence limits for the Process Capability Indices Cp, Cpk and Cpm ”, International Journal of Quality and Reliability Management, Vol. 19, No.8/9, pp.1088-1097, 2002 |
| [4] | Bissell, A. F. “How Reliable is Your Capability Index?”, Applied Statistics, Vol.39, pp.331-340, 1990 |
| [5] | Chou, Y., Owen, D.B., and Borrego, .A “Lower Confidence Limits on Process Capability Indices”, Journal of Quality Technology, Vol.22, pp.223-229, 1990 |
| [6] | Franklin, L.A., and Wasserman, G.S. “Bootstrap Confidence Interval Estimates of Cpk: An Introduction”, Communications in Statistics - Simulation and Computation, Vol.20, pp.231-242, 1991 |
| [7] | Franklin, L.A., and Wasserman, G.S. “Bootstrap Lower Confidence Limits for Process Capability Indices”, Journal of Quality Technology , Vol.24, No.4, pp.196-210, 1992 |
| [8] | Kane, V. E., “ Process Capability Indices”, Journal of Quality Technology, Vol.18, pp.41-52, Corrigenda pp. 265, 1986 |
| [9] | Kotz, S., and Johnson, N.L. “Process Capability Indices – A Review, 1992-2000”, Journal of Quality Technology, Vol.34, No.1, pp.2-19, 2002 |
| [10] | Montgomery, D.C, Introduction to Statistical Quality Control, Fourth Edition, John Wily, New York, 2001 |
| [11] | Spring, F.A, “Assessing Process Capability in the Presence of Systematic Assignable Cause”, Journal of Quality Technology, Vol.23, pp.125-132, 1991. |
| [12] | Subramani, J, “Application of Systematic Sampling in Process Control, Statistics and Applications,” Journal of Society of Statistics, Computer and Applications, (New Series), 1, 7-17, 2004 |
| [13] | Subramani, J, “Process Control in the Presence of Linear Trend”, Model Assisted Statistical Applications, 5, 272-281, 2010 |
| [14] | Subramani, J, Balamurali S, “On Line Computation of Process Capability Indices”, International Journal of Statistics and Applications, Vol2, no.5, 2012, To appear. |

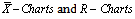 . It is observed that the proposed method is simple to apply and does not warrant any tedious computations both for control charts and for computing process capability indices. For the sake of convenience we have presented the control charts constants for constructing capability based
. It is observed that the proposed method is simple to apply and does not warrant any tedious computations both for control charts and for computing process capability indices. For the sake of convenience we have presented the control charts constants for constructing capability based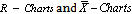 . The proposed method is also illustrated with the help of a numerical example.
. The proposed method is also illustrated with the help of a numerical example.

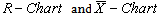 then the process capability indices
then the process capability indices 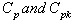 can be computed. If the values of the process capability indices are at the satisfactory level, the process can be allowed further without making any change or adjustment in the process. Otherwise suitable adjustments have to be made so that the process shall satisfy both the requirements of control charts and the process capability indices. The present manufacturing process can be explained in the flow chart as shown in Figure 1. The following are the various computational formulae involved in constructing the control charts and for the computation of process capability indices.
can be computed. If the values of the process capability indices are at the satisfactory level, the process can be allowed further without making any change or adjustment in the process. Otherwise suitable adjustments have to be made so that the process shall satisfy both the requirements of control charts and the process capability indices. The present manufacturing process can be explained in the flow chart as shown in Figure 1. The following are the various computational formulae involved in constructing the control charts and for the computation of process capability indices.
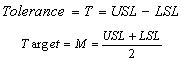 LSL: Lower Specification Limit of the Quality CharacteristicsUSL: Upper Specification Limit of the Quality CharacteristicsWhen the sample size n=5, the values for the control chart constants obtained from the table are as given below:D4 = 2.114, D3 = 0, d2 = 2.326 and A2 = 0.577 The Control limits for constructing
LSL: Lower Specification Limit of the Quality CharacteristicsUSL: Upper Specification Limit of the Quality CharacteristicsWhen the sample size n=5, the values for the control chart constants obtained from the table are as given below:D4 = 2.114, D3 = 0, d2 = 2.326 and A2 = 0.577 The Control limits for constructing 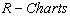 and
and 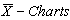 are as given below:Control limits for
are as given below:Control limits for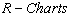 :
: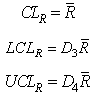 Control limits for
Control limits for 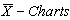 :
: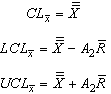
 Value
Value . To achieve this, the manufacturer has to establish a process under statistical control and then the process capability index has to be computed. If the computed value of
. To achieve this, the manufacturer has to establish a process under statistical control and then the process capability index has to be computed. If the computed value of 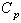 is more than the specified value given by the customer, the process can be run without any adjustment. Otherwise suitable actions have to be taken to meet the required process capability values. The drawback of this method is that the manufacturer has to keep all the produced items in the inventory until the computation of the process capability index and to take a decision on the process based on the process capability index. It is a time consuming procedure as well as requires additional skilled personnel. To avoid this, we have proposed control charts for variables with specified process capability indices. In the proposed method, the process is under statistical control means that it satisfies the required process capability index. Further it is not necessary to compute the process capability indices separately. The proposed manufacturing process can be explained in the flow chart shown in Figure 2.
is more than the specified value given by the customer, the process can be run without any adjustment. Otherwise suitable actions have to be taken to meet the required process capability values. The drawback of this method is that the manufacturer has to keep all the produced items in the inventory until the computation of the process capability index and to take a decision on the process based on the process capability index. It is a time consuming procedure as well as requires additional skilled personnel. To avoid this, we have proposed control charts for variables with specified process capability indices. In the proposed method, the process is under statistical control means that it satisfies the required process capability index. Further it is not necessary to compute the process capability indices separately. The proposed manufacturing process can be explained in the flow chart shown in Figure 2. 
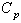 .
.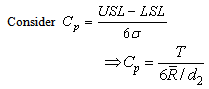 If
If 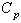 value is given then
value is given then 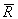 value can be obtained from the above formula as
value can be obtained from the above formula as 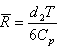
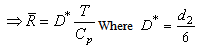 Similarly one can obtain the lower control limit (LCL) and upper control limit (UCL) of the
Similarly one can obtain the lower control limit (LCL) and upper control limit (UCL) of the 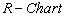 as given below:
as given below: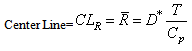
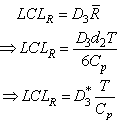
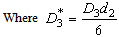
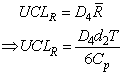 In the similar manner one can compute the control limits to construct
In the similar manner one can compute the control limits to construct 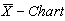 with specified
with specified 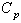 value as given below.
value as given below.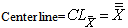 Lower control limit for the proposed
Lower control limit for the proposed 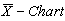 is obtained as given below:
is obtained as given below: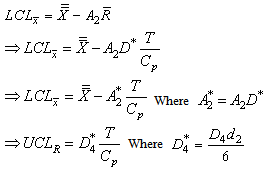 One can use the above control limits to construct
One can use the above control limits to construct 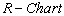 with specified
with specified 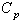 value.Similarly one may obtain the upper control limit for the proposed
value.Similarly one may obtain the upper control limit for the proposed 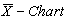 as
as 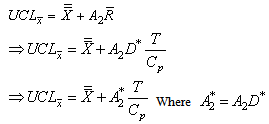
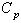 value are as given below:Control limits for proposed
value are as given below:Control limits for proposed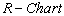 :
: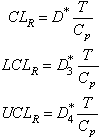 Control limits for proposed
Control limits for proposed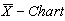 :
: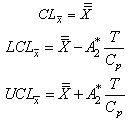 One can use the above control limits to construct the
One can use the above control limits to construct the  and
and with specified
with specified  value. For the sample size
value. For the sample size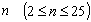 , we have presented the values of the control charts constants
, we have presented the values of the control charts constants 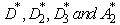 in the Table 1 given below.The advantageous of the proposed control charts is that the observed range values are not required for computing the control limits. Further if the process is under the state of statistical control means that it automatically satisfies the required conditions regarding the values of process capability index
in the Table 1 given below.The advantageous of the proposed control charts is that the observed range values are not required for computing the control limits. Further if the process is under the state of statistical control means that it automatically satisfies the required conditions regarding the values of process capability index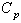 .
. 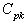 value
value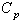 . In the similar manner we have developed a method for constructing control charts for variables with specified value for the process capability index
. In the similar manner we have developed a method for constructing control charts for variables with specified value for the process capability index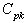 . The following are the derivation of various computational formulae involved in constructing control charts for variables with specified process capability index
. The following are the derivation of various computational formulae involved in constructing control charts for variables with specified process capability index 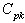
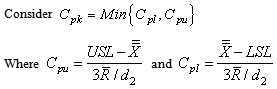 After a little algebra, one can rewrite the
After a little algebra, one can rewrite the 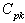 as
as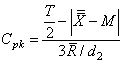 If
If 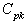 value is given then
value is given then 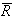 value can be obtained from the above formula as
value can be obtained from the above formula as 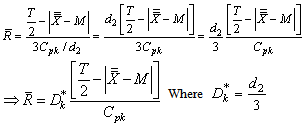 Similarly one can obtain the lower control limit (LCL) and upper control limit (UCL) of the
Similarly one can obtain the lower control limit (LCL) and upper control limit (UCL) of the  as given below:
as given below: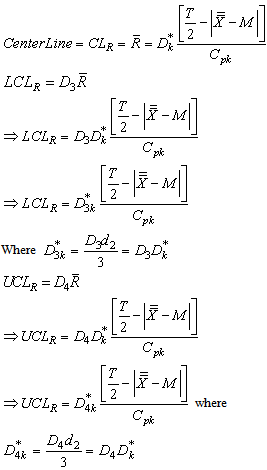 One can use the above control limits to construct
One can use the above control limits to construct  with specified
with specified 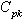 value.In the similar manner one can compute the control limits to construct
value.In the similar manner one can compute the control limits to construct 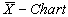 with specified
with specified 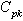 value as given below.
value as given below.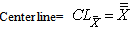 Lower control limit for the proposed
Lower control limit for the proposed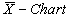 is obtained as given below:
is obtained as given below: Similarly one may obtain the upper control limit for the proposed
Similarly one may obtain the upper control limit for the proposed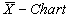 as
as 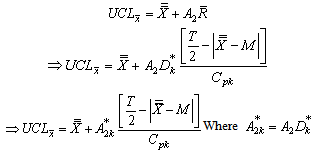 Thus the control limits for the proposed control charts with specified
Thus the control limits for the proposed control charts with specified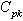 value are as given below:Control limits for
value are as given below:Control limits for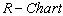 with specified
with specified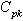 value
value Control limits for the proposed
Control limits for the proposed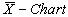 with specified
with specified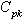 value:
value: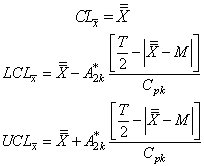 The above control limits can be further simplified by substituting the values of and, which lead to the following two cases:Case 1: When
The above control limits can be further simplified by substituting the values of and, which lead to the following two cases:Case 1: When 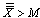 Control limits for
Control limits for with specified
with specified value
value Control limits for the proposed
Control limits for the proposed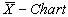 with specified
with specified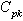 value:
value: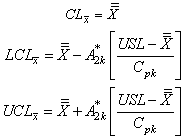
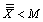 Control limits for
Control limits for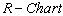 with specified
with specified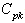 value
value Control limits for the proposed
Control limits for the proposed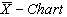 with specified
with specified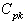 value:
value: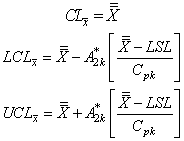 One can use the above control limits to construct the
One can use the above control limits to construct the  and
and with specified
with specified  value. For the given sample size
value. For the given sample size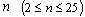 , we have presented the values of the control charts constants
, we have presented the values of the control charts constants 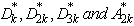 in the Table 2 given below.The advantageous of the proposed control charts with specified
in the Table 2 given below.The advantageous of the proposed control charts with specified 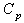 and
and 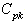 values, is that the observed range values are not required for computing the control limits. Further if the process is under the state of statistical control means that it automatically satisfies the required conditions regarding the values of process capability indices
values, is that the observed range values are not required for computing the control limits. Further if the process is under the state of statistical control means that it automatically satisfies the required conditions regarding the values of process capability indices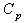 and
and 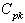 .
.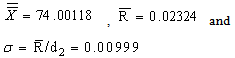 Case 1: Usual Method of Control Charts and the Computation of Process Capability IndicesControl Limits for R-Chart are obtained as:
Case 1: Usual Method of Control Charts and the Computation of Process Capability IndicesControl Limits for R-Chart are obtained as: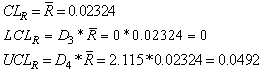 Control Limits for
Control Limits for 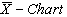 are obtained as:
are obtained as: 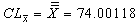
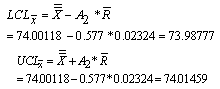 By plotting the control limits, sample ranges and sample means, one may get
By plotting the control limits, sample ranges and sample means, one may get 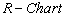 and
and 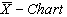 as given in Figure 3 and Figure 4. From the
as given in Figure 3 and Figure 4. From the 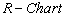 , we observe that all the plotted sample range values are falling within the control limits. Hence we may conclude that the variations are under control. Similarly from the
, we observe that all the plotted sample range values are falling within the control limits. Hence we may conclude that the variations are under control. Similarly from the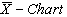 , we observe that all the plotted sample means are falling inside the control limits. Hence we may conclude that the averages are also under the statistical control.
, we observe that all the plotted sample means are falling inside the control limits. Hence we may conclude that the averages are also under the statistical control.

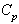 and
and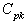 . The process capability indices obtained from the above values are given below:
. The process capability indices obtained from the above values are given below: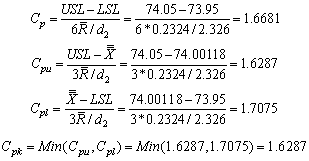 If the customer’s requirement of the process capability index
If the customer’s requirement of the process capability index 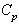 is 1.5, then one may conclude from the above capability indices that the process is an efficient one. However If the customer’s requirement of the process capability index
is 1.5, then one may conclude from the above capability indices that the process is an efficient one. However If the customer’s requirement of the process capability index 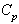 is 2.0, then one may conclude from the above capability indices that the process is not an efficient one and hence the process has to be adjusted so as the resulting process capability index
is 2.0, then one may conclude from the above capability indices that the process is not an efficient one and hence the process has to be adjusted so as the resulting process capability index 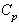 is at least 2.0. Case 2: Control Charts with specified
is at least 2.0. Case 2: Control Charts with specified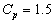 In this case we construct the control limits for the given value of process capability index
In this case we construct the control limits for the given value of process capability index 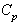 and hence separate computation of the process capability index is not required. Further the proposed control charts states that the process is under the statistical control means that the process satisfies the requirement of the process capability index. Hence one can construct several control limits for different values of process capability index
and hence separate computation of the process capability index is not required. Further the proposed control charts states that the process is under the statistical control means that the process satisfies the requirement of the process capability index. Hence one can construct several control limits for different values of process capability index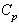 . If any plotted points falls outside the control limits with specified
. If any plotted points falls outside the control limits with specified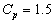 means that the process does not satisfy the required process capability index
means that the process does not satisfy the required process capability index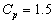 .Let the given process capability index
.Let the given process capability index 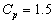 . Then the Control limits for
. Then the Control limits for 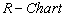 with specified
with specified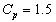 are obtained as given below:
are obtained as given below: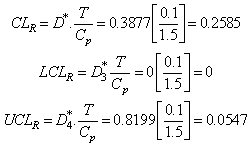 Control limits for
Control limits for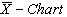 with specified
with specified 
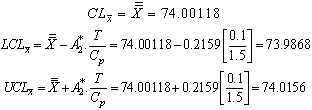 By plotting the control limits, sample ranges and sample means, one may get
By plotting the control limits, sample ranges and sample means, one may get 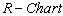 and
and 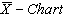 with specified
with specified 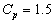 as given in Figure 5 and Figure 6. From the
as given in Figure 5 and Figure 6. From the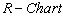 , we observe that all the plotted sample range values are falling within the control limits. Hence we may conclude that the variations are under control. Similarly from the
, we observe that all the plotted sample range values are falling within the control limits. Hence we may conclude that the variations are under control. Similarly from the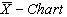 , we observe that all the plotted sample means are falling inside the control limits. Hence we may conclude that the averages are also under the statistical control. Further we conclude that the process capability index for the given process is at least 1.5 and satisfies the customer’s requirements.
, we observe that all the plotted sample means are falling inside the control limits. Hence we may conclude that the averages are also under the statistical control. Further we conclude that the process capability index for the given process is at least 1.5 and satisfies the customer’s requirements.

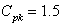 In this case we construct the control limits for the given value of process capability index
In this case we construct the control limits for the given value of process capability index 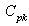 and hence separate computation of the process capability index is not required. Further the proposed control charts states that the process is under the statistical control means, the process satisfies the requirement of the process capability index. Hence one can construct several control limits for different values of process capability index. If any plotted points falls outside the control limits with specified
and hence separate computation of the process capability index is not required. Further the proposed control charts states that the process is under the statistical control means, the process satisfies the requirement of the process capability index. Hence one can construct several control limits for different values of process capability index. If any plotted points falls outside the control limits with specified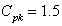 means that the process does not satisfy the required process capability index
means that the process does not satisfy the required process capability index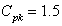 .Let the given process capability index
.Let the given process capability index 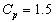 . Further
. Further 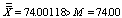 the control limits with specified process capability index
the control limits with specified process capability index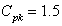 are obtained as given below:Control limits for
are obtained as given below:Control limits for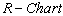 with specifiedvalue
with specifiedvalue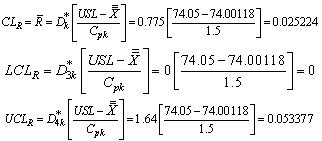 Control limits for the proposed
Control limits for the proposed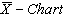 with specified
with specified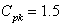 value are obtained as given below:
value are obtained as given below: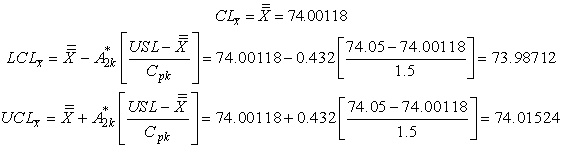


 and
and  with specified
with specified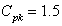 as given in Figure 7 and Figure 8. From the
as given in Figure 7 and Figure 8. From the , we observe that all the plotted sample range values are falling within the control limits. Hence we may conclude that the variations are under control. Similarly from the
, we observe that all the plotted sample range values are falling within the control limits. Hence we may conclude that the variations are under control. Similarly from the , we observe that all the plotted sample means are falling inside the control limits. Hence we may conclude that the averages are also under the statistical control. Further we conclude that the process capability index
, we observe that all the plotted sample means are falling inside the control limits. Hence we may conclude that the averages are also under the statistical control. Further we conclude that the process capability index 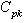 for the given process is at least 1.5 and satisfies the customer’s requirements.
for the given process is at least 1.5 and satisfies the customer’s requirements. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML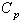 value
value
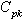 value
value