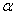Anil Gaur
Department of Statistics, Panjab University, Chandigarh, 160014, India
Correspondence to: Anil Gaur , Department of Statistics, Panjab University, Chandigarh, 160014, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
One of the commonly observed one-factor response patterns in practice is the umbrella ordering in which the response variable increases with an increase in the treatment up to a point, then decreases with further increase in the treatment level. In this article, a nonparametric test for several sample scale problem against umbrella alternative with at least one strict inequality, when peak of the umbrella is known, is proposed using ranked-set data. The proposed statistic has the advantage of not requiring the several distribution functions to have a common median, but rather any common quantile of order  , (not necessarily ½) which is assumed to be known. The proposed test statistic is based on weighted linear combination of statistic proposed by Ozturk and Deshpande[11]. The distribution of the test statistic and optimal weights has been calculated. It is shown that the new test is uniformly more efficient in terms of Pitman asymptotic relative efficiency than its simple random sampling analog and its Mack-Wolfe (Mack and Wolfe (1981)) version as well.
, (not necessarily ½) which is assumed to be known. The proposed test statistic is based on weighted linear combination of statistic proposed by Ozturk and Deshpande[11]. The distribution of the test statistic and optimal weights has been calculated. It is shown that the new test is uniformly more efficient in terms of Pitman asymptotic relative efficiency than its simple random sampling analog and its Mack-Wolfe (Mack and Wolfe (1981)) version as well.
Keywords:
Umbrella Ordering, U-statistic, Test for Scale, Ranked-set Sample
Cite this paper:
Anil Gaur , "A Nonparametric Test for Umbrella Alternate Scale Problem Using Ranked-set Data", International Journal of Probability and Statistics , Vol. 1 No. 4, 2012, pp. 95-100. doi: 10.5923/j.ijps.20120104.02.
1. Introduction
The ranked-set sampling (RSS) approach was first proposed by McIntyre[9] for estimating mean pasture yields. This approach is useful where making measurements on experimental units is either expensive, time-consuming or destructive, but the mechanism for either informally or formally ranking a set of sample units is relatively easy and reliable. RSS utilizes large number of informal measurements for deciding which expensive units should be fully measured. RSS generates a set of observations (data) with smaller sampling variation than for the simple random sampling. Barnett and Moore[1], Kaur, Patil, Sinha, and Taillie[6] and Patil[13] have given eloquent account on the settings where RSS technique has found applications. However, a brief introduction to the concept of RSS for completeness is given below for completeness.Suppose X is a random variable with density function f(x). First, the items in each of k independent random samples of size k from f(x) are separately subjected to ordering on the attribute of interest via some ranking process by visual inspection or based on a concomitant variable. RSS involves selecting one unit among every ranked set consisting of k units for quantification, with the other k-1 units not being investigated further. One may select the unit with rank 1 from the first set, the unit with rank 2 from the second set, and so on, i.e., from the rth sample, r = 1, 2,….., k, the item judged to be the rth smallest is retained and measured. The first cycle is completed when the unit with rank k is selected from the kth set. The selected rank order can be any permutation of 1, 2,….., k based on the type of ranking, whether perfect or imperfect. This entire process is repeated for m independent cycles. Each cycle involves k2 units and among which only k units will be selected for quantification. Finally, the RSS data consists of mk independent observations, with one item retained and measured from each of the mk independent samples. When the judgment ranking is perfect, then the observations retained from the ith cycle are denoted by Xi = X(1)i, ….., X(k)i ; i= 1, 2,….., m, and the entire ranked-set sample is denoted by X1, ..…, Xm = X(1)1, ....., X(k)1 ,….., X(1)m, ....., X(k)m. In case the judgment ranking is not perfect, the round brackets in the subscript are replaced by square brackets. There has been a lot of work on testing for equality of location parameters in ranked-set sampling, but very little work on testing for equality of scale parameters problem. Stokes and Sager[17] were the first researchers to consider a nonparametric setting with RSS data. They developed important properties of the empirical distribution function from a RSS and compared these properties with those of the empirical distribution of a simple random sample. Bohn and Wolfe[2] developed a nonparametric test based on RSS data for testing the difference between two treatments. They compared this procedure with the Mann-Whitney test for simple random sample data. Bohn and Wolfe[3] proposed a the test for ranked-set two-sample location problem under imperfect judgment ranking. Ozturk[10] provided two-sample inference based on the RSS sign statistic. Ozturk and Wolfe[12] proposed an improved ranked-set two-sample Mann-Whitney-Wilcoxon test. Flinger and MacEachern[4] proposed a test for two-sample location problem based on the ranks in the RSS which led to tests for the centers of distributions. Ozturk and Deshpande[11] proposed a test of equality of the scale parameters of the two populations based on RSS. But, to our knowledge, no test of equality of homogeneity of scale parameters against umbrella alternatives based on RSS is available. A nonparametric test for homogeneity of scale parameters against umbrella alternative, with at least one strict inequality has been tackled as a testing problem in the following context. Let
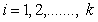 , be independent random samples of size
, be independent random samples of size 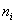 from absolutely continuous cumulative distribution functions
from absolutely continuous cumulative distribution functions 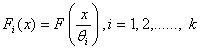 , where
, where 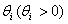 is the scale parameter. It is assumed that these distribution functions have zero as the common quantile of order
is the scale parameter. It is assumed that these distribution functions have zero as the common quantile of order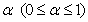 , i.e.,
, i.e., 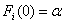 for
for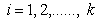 . It is also assumed that
. It is also assumed that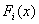 ,
, 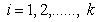 , are identical in all respects except possibly their scale parameters. The hypothesis which is of interest in this paper can be formally stated as follows:
, are identical in all respects except possibly their scale parameters. The hypothesis which is of interest in this paper can be formally stated as follows: 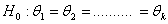 against the umbrella alternative
against the umbrella alternative with at least one strict inequality and h, the peak of the umbrella, is known.For some earlier work on this problem see Gaur et al.[5] and Singh and Liu[16]. Singh and Liu[16] proposed a test statistics for homogeneity of scale parameters against umbrella alternative with at least one strict inequality based isotonic estimator of scale parameter. They also provided one-sided simultaneous confidence intervals for all the ordered pairwise scale ratios, and critical points for two parameter exponential probability distribution. Recently, Gaur et al.[5] provided three test statistics based on linear combination of two-sample U-statistics for testing homogeneity of scale parameters against umbrella alternative, with at least one strict inequality, when the peak of the umbrella, h is known. Gaur et al.[5] test require that the different distribution functions have common quantile of order
with at least one strict inequality and h, the peak of the umbrella, is known.For some earlier work on this problem see Gaur et al.[5] and Singh and Liu[16]. Singh and Liu[16] proposed a test statistics for homogeneity of scale parameters against umbrella alternative with at least one strict inequality based isotonic estimator of scale parameter. They also provided one-sided simultaneous confidence intervals for all the ordered pairwise scale ratios, and critical points for two parameter exponential probability distribution. Recently, Gaur et al.[5] provided three test statistics based on linear combination of two-sample U-statistics for testing homogeneity of scale parameters against umbrella alternative, with at least one strict inequality, when the peak of the umbrella, h is known. Gaur et al.[5] test require that the different distribution functions have common quantile of order 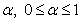 , (not necessarily ½) which is assumed to be known. In this paper, we extend the concept of ranked-set samples to the k-sample scale setting when the scale parameters follow an umbrella pattern, with peak of umbrella, h to be known. The test is given in section 2 and distribution of the test statistic is discussed in section 3. Section 4 is devoted to optimal choice of weights. In section 5, we consider the performance of the proposed test statistic against its simple random sample analog. It is shown that the proposed test has higher Pitman efficiency for the same number of fully measured observations.
, (not necessarily ½) which is assumed to be known. In this paper, we extend the concept of ranked-set samples to the k-sample scale setting when the scale parameters follow an umbrella pattern, with peak of umbrella, h to be known. The test is given in section 2 and distribution of the test statistic is discussed in section 3. Section 4 is devoted to optimal choice of weights. In section 5, we consider the performance of the proposed test statistic against its simple random sample analog. It is shown that the proposed test has higher Pitman efficiency for the same number of fully measured observations.
2. The Proposed Test
To construct a multi-sample umbrella alternative problem, we select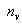 independent ranked-set samples from absolutely continuous distribution
independent ranked-set samples from absolutely continuous distribution 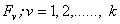 , then apply the ranked-set concept and repeat the process for u cycles, where
, then apply the ranked-set concept and repeat the process for u cycles, where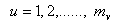 . Let
. Let  ;
; 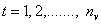 ;
; 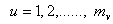 ;
; 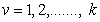 , be k independent ranked-set samples of size nv*mv. We assume that the distribution functions have zero as the common quantile of order
, be k independent ranked-set samples of size nv*mv. We assume that the distribution functions have zero as the common quantile of order  , i.e.,
, i.e.,  for
for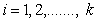 . First we consider the two-sample U-statistic, proposed by Ozturk and Deshpande[11] where the assumption of the common quantile of order
. First we consider the two-sample U-statistic, proposed by Ozturk and Deshpande[11] where the assumption of the common quantile of order 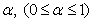 is made and then extend it to the k sample umbrella alternative problem. Define for i< j; i,j=1,2,…,k,
is made and then extend it to the k sample umbrella alternative problem. Define for i< j; i,j=1,2,…,k,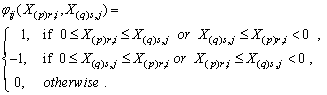 The two-sample U-statistic corresponding to the kernel
The two-sample U-statistic corresponding to the kernel 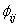 is
is  .The statistic
.The statistic  is obviously a U-statistic (Lehmann[7]) corresponding to the kernel
is obviously a U-statistic (Lehmann[7]) corresponding to the kernel  . It can be seen that the kernel takes non-zero value only when both X(p)r,i’s and X(q)s,j’s have the same sign. For testing
. It can be seen that the kernel takes non-zero value only when both X(p)r,i’s and X(q)s,j’s have the same sign. For testing  against
against , with
, with 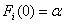 for
for , we propose the test statistics
, we propose the test statistics ,where,
,where, 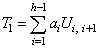 ,
, 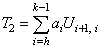 ,where
,where 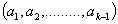 are some real positive constants to be chosen suitably and
are some real positive constants to be chosen suitably and  is the ranked-set two-sample statistic proposed by Ozturk and Deshpande[11]. For each set of values
is the ranked-set two-sample statistic proposed by Ozturk and Deshpande[11]. For each set of values  , we get a distinct member of this class of test statistics. Large values of T are significant for testing
, we get a distinct member of this class of test statistics. Large values of T are significant for testing  against
against 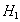 . When
. When 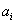 =1, (
=1, (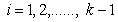 ), we obtain Mack-Wolfe (Mack and Wolfe[8]) version of T as
), we obtain Mack-Wolfe (Mack and Wolfe[8]) version of T as .
.
3. Distribution of the Proposed Test
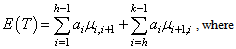 | (3.1) |
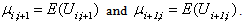 | (3.2) |
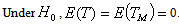 | (3.3) |
Using the results of Lehmann[7], the proof of the following theorem follows from the transformation theorem (see Serfling[15], page 122) immediatelyTheorem 3.1: The asymptotic null distribution of 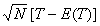 , as
, as 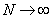 in such a way that
in such a way that  is normal with mean 0 and variance
is normal with mean 0 and variance 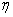 , where
, where 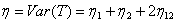 | (3.4) |
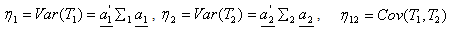 | (3.5) |
 After involved computations, it can be seen that under
After involved computations, it can be seen that under ,
,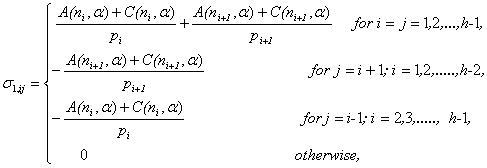 | (3.6) |
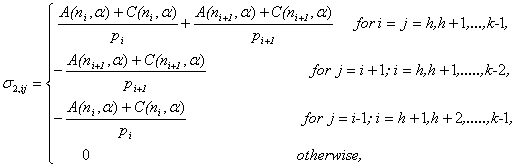 | (3.7) |
where, 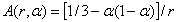 ,
,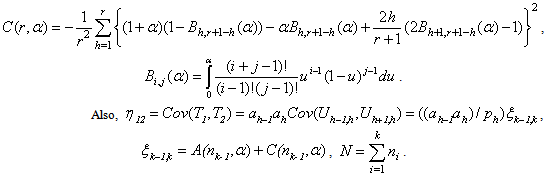 | (3.8) |
In case all the sample sizes are equal i.e., p1= p2=…= pk=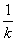 and ni=n , then
and ni=n , then | (3.9) |
 | (3.10) |
 | (3.11) |
Also, substituting (3.5), (3.8), (3.9), (3.10) and (3.11) in (3.4), we get | (3.12) |
Similarly, the asymptotic null distribution of 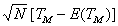 is normal with mean zero and variance
is normal with mean zero and variance  .
.
4. Optimal Choice of Weights
Under the sequence of Pitman alternatives, the square of the efficacy of test T is given by 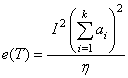 ,where,
,where,  For efficiency comparisons, we consider the equal sample size and equally spaced alternatives of the type
For efficiency comparisons, we consider the equal sample size and equally spaced alternatives of the type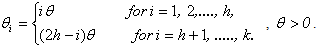 | (4.1) |
Making use of the results due to Rao[14] (page 60) for determining optimal weights, we obtain the optimal weights  for which T has maximum efficiency. For odd k and h=(k+1)/2,
for which T has maximum efficiency. For odd k and h=(k+1)/2,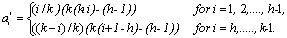 | (4.2) |
The square of the efficacy of tests T with optimal choice of weights in (3.3) is given by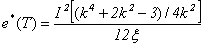 | (4.3) |
And the square of the efficacy of tests 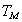 is given by
is given by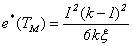 | (4.4) |
5. Asymptotic Relative Efficiencies
In this section, we compute and compare the Pitman asymptotic relative efficiency of T with respect to its Mack-Wolfe version, TM, also with its competitor test (the test A given by Gaur et al.[5]) in simple random sampling. Using Ozturk and Deshpande[11] and Gaur et al.[5], efficacy of test A of Gaur et al.[5], TSRS test under multivariate setting can be given by 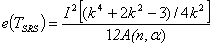 .Then the asymptotic relative efficiency (ARE) of the T test with respect to TSRS test can be computed form the ratio of the Pitman efficacies, and the ARE for different values of n are given in Table 1.
.Then the asymptotic relative efficiency (ARE) of the T test with respect to TSRS test can be computed form the ratio of the Pitman efficacies, and the ARE for different values of n are given in Table 1. 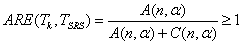 | (5.1) |
Also, 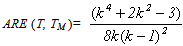 and the values of ARE for different values of k are given in Table 2.It is straight forward that these asymptotic relative efficiencies are independent from underlying distribution F. The inequality in equation (5.1) follows from the fact that
and the values of ARE for different values of k are given in Table 2.It is straight forward that these asymptotic relative efficiencies are independent from underlying distribution F. The inequality in equation (5.1) follows from the fact that  is negative. The asymptotic relative efficiency (ARE) of the T test with respect to TSRS test has been calculated for certain value of n and
is negative. The asymptotic relative efficiency (ARE) of the T test with respect to TSRS test has been calculated for certain value of n and  and presented in Table 1.
and presented in Table 1.
6. Conclusions
The AREs in Table 1 and Table 2, immediately show that test for homogeneity of scale parameters against umbrella alternative based on ranked-set sample, T, is always better than the simple random sample test, TSRS, with respect to pitman efficiency. Also, the proposed test T is better than its Mack-Wolfe version, TM irrespective of underlying distribution. As k increases, the proposed test T become more efficient as compared to its Mack-Wolfe version, TM .| Table 1. ARE of the T with respect to TSRS |
| | n |
| | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | | 2 | 1.139 | 1.195 | 1.099 | 1.028 | 1 | 1.028 | 1.099 | 1.195 | 1.139 | | 3 | 1.589 | 1.386 | 1.242 | 1.142 | 1.103 | 1.142 | 1.242 | 1.386 | 1.589 | | 4 | 1.853 | 1.573 | 1.396 | 1.277 | 1.231 | 1.277 | 1.396 | 1.573 | 1.853 | | 5 | 2.092 | 1.756 | 1.552 | 1.418 | 1.367 | 1.418 | 1.552 | 1.756 | 2.092 | | 6 | 2.319 | 1.934 | 1.708 | 1.561 | 1.506 | 1.561 | 1.708 | 1.934 | 2.319 |
|
|
| Table 2. ARE of T with respect to TM with different values of k |
| | k | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | | ARE(T,TM) | 1.000 | 1.050 | 1.238 | 1.458 | 1.691 | 1.929 | 2.171 | 2.415 | 2.661 |
|
|
References
| [1] | Barnett, V. and Moore, K., 1997. Best linear unbiased estimates in ranked-set sampling with particular reference to imperfect ordering. Journal of Applied Statistics, 24, 697-710. |
| [2] | Bohn, L.L. and Wolfe, D.A., 1992. Nonparametric two-sample procedures for ranked-set samples data. Journal of American Statistical Association, 87, 552-561. |
| [3] | Bohn, L.L. and Wolfe, D.A., 1994. The effect of imperfect judgement rankings on properties of procedures based on the ranked-set samples analogue of the Mann-Whitney-Wilcoxon statistic. Journal of American Statistical Association, 89, 168-176. |
| [4] | Flinger, M.A. and MacEachern, S.N., 2006. Nonparametric two-sample methods for ranked-set sample data. Journal of American Statistical Association, 101, 1107-1118. |
| [5] | Gaur, A., Mahajan, K.K., Arora, S., 2012. New nonparametric tests for testing homogeneity of scale parameters against umbrella alternative. Statistics and Probability Letters, 82, 1681-1689. |
| [6] | Kaur, A., Patil, G.P., Sinha, A.K. and Taillie, C., 1995. Ranked set sampling: an annotated bibliography. Environmental and Ecological Statistics, 2, 25-54. |
| [7] | Lehmann, E.L., 1963. Robust estimation in analysis of variance. Annals of Mathematical Statistics, 34, 957-966. |
| [8] | Mack, G.A. and Wolfe, D.A., 1981. k-sample rank tests for umbrella alternatives. Journal of American Statistical Association, 76, 175-181. |
| [9] | McIntyre, G.A., 1952. A method of unbiased selective sampling using ranked-set sampling. Australian Journal of Agricultural Research, 3, 385-390. |
| [10] | Ozturk, O., 1999.Two-sample inference based on one-sample ranked-set sample sign statistic. Journal of Nonparametric Statistics, 10, 197-212. |
| [11] | Ozturk, O. and Deshpande, J.V., 2004. A new nonparametric test using ranked set data for a two-sample scale problem. Sankhya, 66, 513-527. |
| [12] | Ozturk, O. and Wolfe, D.A., 2000. An improved ranked set two-sample Mann-Whitney-Wilcoxon test. The Canadian Journal of Statistics, 28, 123-135. |
| [13] | Patil, G.P., 1995. Editorial: ranked set sampling. Environmental and Ecological Statistics, 2, 271-285. |
| [14] | Rao, C.R., 1973. Linear Statistical Inference and its applications. Wiley Eastern Ltd. New York. |
| [15] | Serfling, R.J., 1980. Approximation theorems of mathematical statistics. John Wiley, New York. |
| [16] | Singh P., and Liu W., 2006. A test against an umbrella ordered alternative. Computational Statistics and Data Analysis, 51, 1957-1964. |
| [17] | Stokes, S.L. and Sager, T.W., 1988. Characterization of a ranked-set sample with application to estimating distribution functions. Journal of American Statistical Association, 82, 374-381. |

 , (not necessarily ½) which is assumed to be known. The proposed test statistic is based on weighted linear combination of statistic proposed by Ozturk and Deshpande[11]. The distribution of the test statistic and optimal weights has been calculated. It is shown that the new test is uniformly more efficient in terms of Pitman asymptotic relative efficiency than its simple random sampling analog and its Mack-Wolfe (Mack and Wolfe (1981)) version as well.
, (not necessarily ½) which is assumed to be known. The proposed test statistic is based on weighted linear combination of statistic proposed by Ozturk and Deshpande[11]. The distribution of the test statistic and optimal weights has been calculated. It is shown that the new test is uniformly more efficient in terms of Pitman asymptotic relative efficiency than its simple random sampling analog and its Mack-Wolfe (Mack and Wolfe (1981)) version as well.

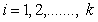 , be independent random samples of size
, be independent random samples of size 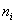 from absolutely continuous cumulative distribution functions
from absolutely continuous cumulative distribution functions 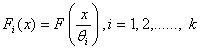 , where
, where 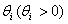 is the scale parameter. It is assumed that these distribution functions have zero as the common quantile of order
is the scale parameter. It is assumed that these distribution functions have zero as the common quantile of order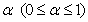 , i.e.,
, i.e., 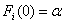 for
for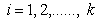 . It is also assumed that
. It is also assumed that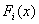 ,
, 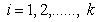 , are identical in all respects except possibly their scale parameters. The hypothesis which is of interest in this paper can be formally stated as follows:
, are identical in all respects except possibly their scale parameters. The hypothesis which is of interest in this paper can be formally stated as follows: 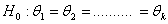 against the umbrella alternative
against the umbrella alternative with at least one strict inequality and h, the peak of the umbrella, is known.For some earlier work on this problem see Gaur et al.[5] and Singh and Liu[16]. Singh and Liu[16] proposed a test statistics for homogeneity of scale parameters against umbrella alternative with at least one strict inequality based isotonic estimator of scale parameter. They also provided one-sided simultaneous confidence intervals for all the ordered pairwise scale ratios, and critical points for two parameter exponential probability distribution. Recently, Gaur et al.[5] provided three test statistics based on linear combination of two-sample U-statistics for testing homogeneity of scale parameters against umbrella alternative, with at least one strict inequality, when the peak of the umbrella, h is known. Gaur et al.[5] test require that the different distribution functions have common quantile of order
with at least one strict inequality and h, the peak of the umbrella, is known.For some earlier work on this problem see Gaur et al.[5] and Singh and Liu[16]. Singh and Liu[16] proposed a test statistics for homogeneity of scale parameters against umbrella alternative with at least one strict inequality based isotonic estimator of scale parameter. They also provided one-sided simultaneous confidence intervals for all the ordered pairwise scale ratios, and critical points for two parameter exponential probability distribution. Recently, Gaur et al.[5] provided three test statistics based on linear combination of two-sample U-statistics for testing homogeneity of scale parameters against umbrella alternative, with at least one strict inequality, when the peak of the umbrella, h is known. Gaur et al.[5] test require that the different distribution functions have common quantile of order 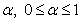 , (not necessarily ½) which is assumed to be known. In this paper, we extend the concept of ranked-set samples to the k-sample scale setting when the scale parameters follow an umbrella pattern, with peak of umbrella, h to be known. The test is given in section 2 and distribution of the test statistic is discussed in section 3. Section 4 is devoted to optimal choice of weights. In section 5, we consider the performance of the proposed test statistic against its simple random sample analog. It is shown that the proposed test has higher Pitman efficiency for the same number of fully measured observations.
, (not necessarily ½) which is assumed to be known. In this paper, we extend the concept of ranked-set samples to the k-sample scale setting when the scale parameters follow an umbrella pattern, with peak of umbrella, h to be known. The test is given in section 2 and distribution of the test statistic is discussed in section 3. Section 4 is devoted to optimal choice of weights. In section 5, we consider the performance of the proposed test statistic against its simple random sample analog. It is shown that the proposed test has higher Pitman efficiency for the same number of fully measured observations. 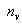 independent ranked-set samples from absolutely continuous distribution
independent ranked-set samples from absolutely continuous distribution 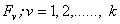 , then apply the ranked-set concept and repeat the process for u cycles, where
, then apply the ranked-set concept and repeat the process for u cycles, where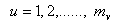 . Let
. Let  ;
; 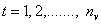 ;
; 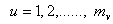 ;
; 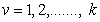 , be k independent ranked-set samples of size nv*mv. We assume that the distribution functions have zero as the common quantile of order
, be k independent ranked-set samples of size nv*mv. We assume that the distribution functions have zero as the common quantile of order  , i.e.,
, i.e.,  for
for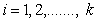 . First we consider the two-sample U-statistic, proposed by Ozturk and Deshpande[11] where the assumption of the common quantile of order
. First we consider the two-sample U-statistic, proposed by Ozturk and Deshpande[11] where the assumption of the common quantile of order 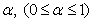 is made and then extend it to the k sample umbrella alternative problem. Define for i< j; i,j=1,2,…,k,
is made and then extend it to the k sample umbrella alternative problem. Define for i< j; i,j=1,2,…,k,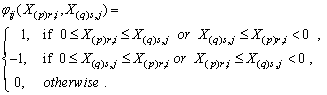 The two-sample U-statistic corresponding to the kernel
The two-sample U-statistic corresponding to the kernel 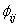 is
is 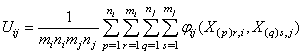 .The statistic
.The statistic  is obviously a U-statistic (Lehmann[7]) corresponding to the kernel
is obviously a U-statistic (Lehmann[7]) corresponding to the kernel  . It can be seen that the kernel takes non-zero value only when both X(p)r,i’s and X(q)s,j’s have the same sign. For testing
. It can be seen that the kernel takes non-zero value only when both X(p)r,i’s and X(q)s,j’s have the same sign. For testing  against
against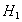 , with
, with 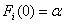 for
for , we propose the test statistics
, we propose the test statistics ,where,
,where, 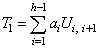 ,
, 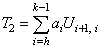 ,where
,where 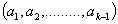 are some real positive constants to be chosen suitably and
are some real positive constants to be chosen suitably and  is the ranked-set two-sample statistic proposed by Ozturk and Deshpande[11]. For each set of values
is the ranked-set two-sample statistic proposed by Ozturk and Deshpande[11]. For each set of values  , we get a distinct member of this class of test statistics. Large values of T are significant for testing
, we get a distinct member of this class of test statistics. Large values of T are significant for testing  against
against 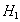 . When
. When 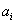 =1, (
=1, (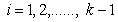 ), we obtain Mack-Wolfe (Mack and Wolfe[8]) version of T as
), we obtain Mack-Wolfe (Mack and Wolfe[8]) version of T as .
.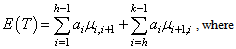
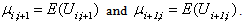
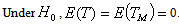
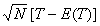 , as
, as 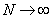 in such a way that
in such a way that  is normal with mean 0 and variance
is normal with mean 0 and variance 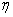 , where
, where 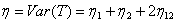
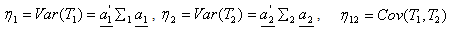
 After involved computations, it can be seen that under
After involved computations, it can be seen that under ,
,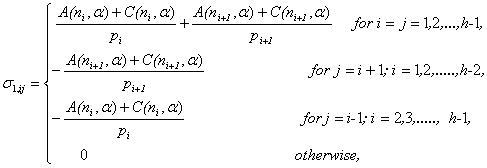
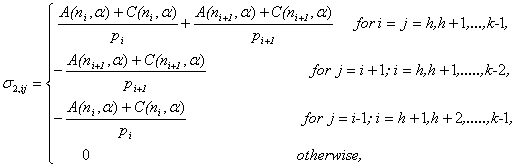
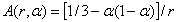 ,
,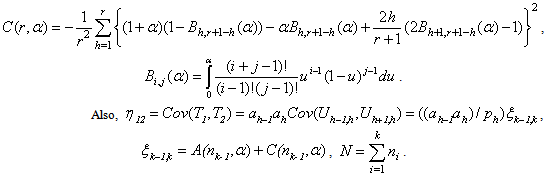
 and ni=n , then
and ni=n , then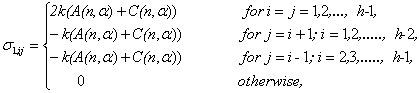
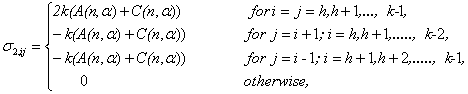
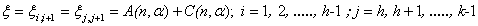
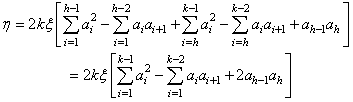
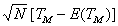 is normal with mean zero and variance
is normal with mean zero and variance  .
.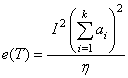 ,where,
,where,  For efficiency comparisons, we consider the equal sample size and equally spaced alternatives of the type
For efficiency comparisons, we consider the equal sample size and equally spaced alternatives of the type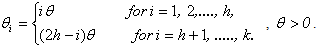
 for which T has maximum efficiency. For odd k and h=(k+1)/2,
for which T has maximum efficiency. For odd k and h=(k+1)/2,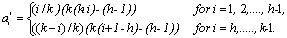
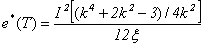
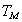 is given by
is given by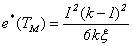
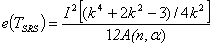 .Then the asymptotic relative efficiency (ARE) of the T test with respect to TSRS test can be computed form the ratio of the Pitman efficacies, and the ARE for different values of n are given in Table 1.
.Then the asymptotic relative efficiency (ARE) of the T test with respect to TSRS test can be computed form the ratio of the Pitman efficacies, and the ARE for different values of n are given in Table 1. 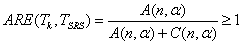
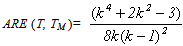 and the values of ARE for different values of k are given in Table 2.It is straight forward that these asymptotic relative efficiencies are independent from underlying distribution F. The inequality in equation (5.1) follows from the fact that
and the values of ARE for different values of k are given in Table 2.It is straight forward that these asymptotic relative efficiencies are independent from underlying distribution F. The inequality in equation (5.1) follows from the fact that  is negative. The asymptotic relative efficiency (ARE) of the T test with respect to TSRS test has been calculated for certain value of n and
is negative. The asymptotic relative efficiency (ARE) of the T test with respect to TSRS test has been calculated for certain value of n and  and presented in Table 1.
and presented in Table 1. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML