Acha Chigozie Kelechi
Department of Statistics Michael Okpara University of Agriculture, Umudike, Abia State, Nigeria
Correspondence to: Acha Chigozie Kelechi , Department of Statistics Michael Okpara University of Agriculture, Umudike, Abia State, Nigeria.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The paper discusses the symmetric balanced incomplete block designs (SBIBD’s) and further verifies whether treatment adjustment in SBIBD is necessary using analysis of variance (ANOVA) method. Fortunately, the data collected for the analysis were in the same group of the balanced incomplete-block designs (BIBD’s), that is, symmetric balance incomplete block design (SBIBD).The ANOVA method is applied differently on the two sets of data arising from the symmetric balanced incomplete block designs (SBIBDs). In this work, the basic interest is to verify empirically whether treatment adjustment is necessary in SBIBDs with data from National Root Crop Research Institute (N.R.C.R.I), Umudike, AbiaState. To achieve this, we considered treatment (not adjusted), treatment (adjusted), and block (adjusted) in the ANOVA method. The study discovered that if ANOVA method is applied on the symmetric balanced incomplete block design (SBIBD) when a treatment is not significant, it turns out to be significant when the same treatment is adjusted. It obvious from the experiments that were carried out that the adjustment of the treatment in SBIBD’s is very necessary when the ANOVA method is applied. Apart from the improvement in the level of significance of the result, the error is also greatly reduced when treatment is adjusted.
Keywords:
Treatments, Blocks, Symmetric, Design, Homogeneity
1. Introduction
The basic concepts of the statistical design of experiments and data analysis were discovered in the early part of the 20th century as a cost effective research design tool to help improve yields in farming. Since then, many types of designs experiments and analysis techniques have been developed to meet the diverse needs of researchers and engineers. One of such experimental designs is called the block design. A block design is a set together with a family of subsets (repeated subsets are allowed at times) whose members are chosen to satisfy some set of properties that are deemed useful for a particular application. These applications come from many areas, including experimental design, finite geometry, software testing, cryptography, and algebraic geometry. Many variations have been examined, but the most intensely studied are the balanced incomplete block designs (BIBDs or 2-designs) which historically were related to statistical issues in the design of experiments, see,[1]. A complete-block design is one of the most widely used designs. It is used when it is possible to run all the treatment combinations in each block. In situations where it is not possible to run all the treatment combinations in each block due to shortage of experimental apparatus or facilities or the physical size of the block, an incomplete-block design is used: see, for example,[2],[3]. A balanced incomplete block design (BIBD) is an experimental design in which t treatments are combined in b blocks of size k, where kTo the best of my knowledge complete block design is widely used by researchers more than the balanced incomplete block designs because the missing data in BIBDs are computed before analysis. Although, classical ANOVA method can be used to analyzed BIBD without computing the missing data see, for example[5],[3],[6]. In this paper, the basic interest is on balanced incomplete design (BIBD’s). Here, the Classical analysis-of-variance method was applied on two sets of SBIBD data. The objective of this study is to check if treatment adjustment in SBIBDs is necessary with respect to their errors.
1.1. Hypothesis
Ho: MSE (SBIBDnot adjusted) = MSE (SBIBDadjusted)
2. Literature
Previous studies on block designs by[7],[8],[9],[2],[10] and[11],[12] and[13] served as guide in this paper. However, this paper briefly discusses symmetric balanced incomplete block design (SBIBD) with respect to their errors using the Classical analysis-of-variance method. The Classical analysis-of-variance method is a statistical method for making simultaneous comparisons between two or more means. This method was differently applied to data collected and was represented in various analysis-of-variance tables. The case study data employed here were obtained from the National Root Crops Research Institute (NRCRI) Umudike, Abia State, Nigeria. The data are on varieties of cassava with different ratios of Nitrogen, Phosphorous and potassium (NPK). The data are secondary data, whose entries are abinito arranged as BIBD by the experimenter.
2.1. Preliminaries
Symmetric balanced incomplete-block design: Here, we assume that there are t treatments and b blocks, see;[14]. In addition, we assume each block contains k treatment each of which occurs r times in the design (or is replicated r times), and that there are N = tr = bk total observations; see, for example[3] Furthermore, the number of times each pair of treatments appears in the same block is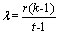 | (1) |
If t = b, the design is said to be symmetric. The parameter 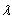 must be an integer. The symmetry property of a design occurs when the row effect and the column effects of the design are interchanged and still the error sum of squares so calculated in each remains the same, see,[3]
must be an integer. The symmetry property of a design occurs when the row effect and the column effects of the design are interchanged and still the error sum of squares so calculated in each remains the same, see,[3]
2.2. The Classical Model
Some existing data sets are evaluated to see if they satisfy the assumption for application of chosen models. There are three conceptual classes of such models in designs:• Fixed-effects models• Random -effects models• Mixed-effects modelsIn this work, fixed effects model is employed. The fixed effect model analysis of variance applies to situations in which the experimenter has subjected his experimental material to several treatments, each of which affects only the mean of the underlying normal distribution of the “response variable”, see,[15].
2.3. The Classical ANOVA
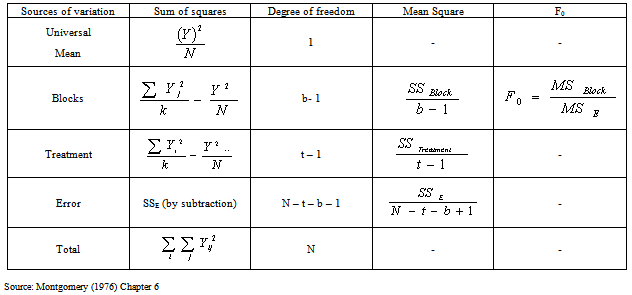
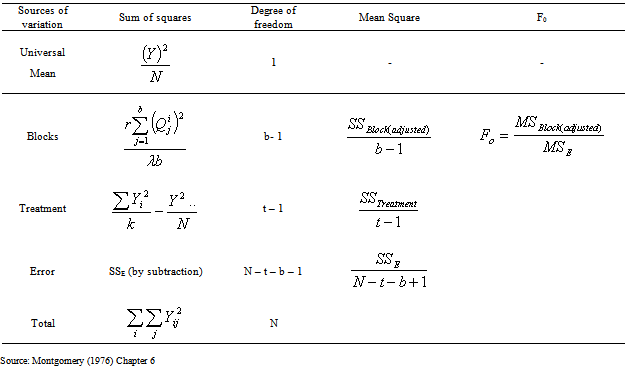
In statistics, analysis of variance is a collection of statistical models and their associated procedures which compare means by splitting the overall observed variance into different parts see.[15].The analysis of variance for classical ANOVA is summarized in [TABLE 1, TABLE 2,TABLE 3]
3. Notations
• MSE (SBIBDadjusted) = Mean square error for the SBIBDadjusted.• MSE (SBIBDnot adjusted) = Mean square error for the SBIBDnot adjusted.• b=block,• r=replication,• k=block size, • t=treatments,• m=number of groups,• 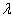 = group of blocks,• N=total,• SS=sum of squares• ANOVA=analysis of variance,• SBIBD=symmetric balanced incomplete block design.
= group of blocks,• N=total,• SS=sum of squares• ANOVA=analysis of variance,• SBIBD=symmetric balanced incomplete block design.Table 1. Analysis of variance for the balanced incomplete block design when treatment is adjusted
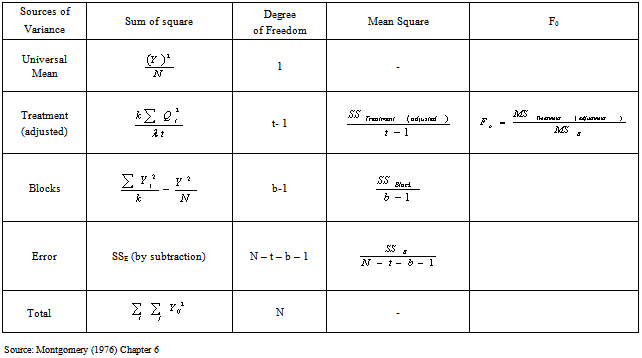 |
| |
|
Table 2. Analysis of Variance for the balanced incomplete block design when treatment is not adjusted
 |
| |
|
Table 3. Analysis of Variance for the Balanced incomplete Block Design when Block is adjusted
 |
| |
|
4. Results of the Experiments
4.1. Experiment 1
| Table 4. Qualitative layout of the experiment 1 |
| | Block 1 | B | C | D | | Block 2 | A | B | C | | Block 3 | A | B | D | | Block 4 | A | C | D |
|
|
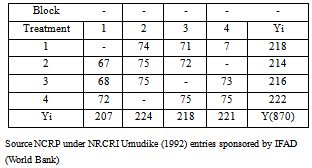
Table 5. Raw data for the analysis of variancefor experiment 1
 |
| |
|
| Table 6. Analysis of variance when treatment and block are not adjusted for experiment 1 |
| | Sources of variation | Sum of square | Degrees freedom | Mean squares | F-ratio | F-test at 0.01 | F-test at 0.05 | | Universal mean | 6.3075 | 1 | | | - | - | | Treatment | 22.75 | 3 | 3.89 | 1.36 | 3.62 | 3.41 | | Block | 55.00 | 3 | 18.33 | - | - | - | | Error | 3.25 | 5 | 2.87 | - | - | - | | Total | 63156 | 12 | - | - | - | - |
|
|
| Table 7. Analysis of variance when block is adjusted for experiment 1 |
| | Sources of variation | Sum of square | Degrees freedom | Mean squares | | Universal mean | 6.3075 | 1 | - | | Treatment | 11.67 | 3 | - | | Block (adjusted) | 66.08 | 3 | 22.03 | | Error | 3.25 | 5 | 0.65 | | Total | 63156 | 12 | - |
|
|
| Table 8. Analysis of variance when treatment is adjusted for experiment 1 |
| | Sources of variation | Sum of square | Degrees freedom | Mean squares | F-ratio | F-test at 0.01 | F-test at 0.05 | | Universal mean | 6.3075 | 1 | - | - | - | - | | Treatment (adjusted) | 22.75 | 3 | 7.58 | 11.66 | 3.62 | 3.41 | | Block | 55.00 | 3 | - | - | - | - | | Error | 3.25 | 5 | 0.65 | - | - | - | | Total | 63156 | 12 | - | - | - | - |
|
|
A balanced incomplete-block design (BIBD) that is symmetric was used to study the yield onfour varieties of cassava with four different rates of NPK. These rates were admitted in addition to the natural manure. The data collected from the experiment are tabulated in the layout of [TABLE 4, TABLE 5]Considering the data in Table 5 for the fertilizer experiment, one notices that it is a balanced incomplete block design with t = b =4, k= r =, 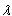 = 2 and N = 12. The analysis of the data in Table 5 is shown in [TABLE 6, TABLE 7, TABLE 8]The analysis of variance in Table 6 shows that Fcal ≤ Ftab at different levels probability, we conclude that the fertilizer applied has no significant effect on the cassava.The balanced incomplete block design in table 7 is symmetric since a = b = 4. However, in Table 8, Fcal ≥ Ftab at different levels of probability, we conclude that the fertilizer applied has a significant effect on the cassava.
= 2 and N = 12. The analysis of the data in Table 5 is shown in [TABLE 6, TABLE 7, TABLE 8]The analysis of variance in Table 6 shows that Fcal ≤ Ftab at different levels probability, we conclude that the fertilizer applied has no significant effect on the cassava.The balanced incomplete block design in table 7 is symmetric since a = b = 4. However, in Table 8, Fcal ≥ Ftab at different levels of probability, we conclude that the fertilizer applied has a significant effect on the cassava.
4.2. Experiment 2
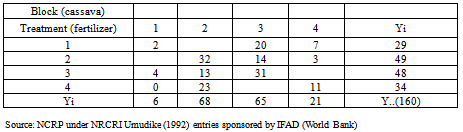
A balanced incomplete-block design (BIBD)that is symmetric was used to study the yield on four varieties of cassava with four different rates of NPK. These rates were administered in addition to the natural manure. The data collected from the experiment are tabulated in the layout of; [TABLE 9, TABLE 10]Table 9 is the qualitative layout of the experiment 2 while table 10 is the raw data for the analysis of-variance for experiment 2.Considering the data in table 10 for the fertilizer experiment, one notices that it is a balanced incomplete block design with the analysis of variance of the data in table 10 is shown in| Table 9. Qualitative layout of the experiment 2 |
| | Block 1 | B | C | D | | Block 2 | A | C | D | | Block 3 | A | B | C | | Block 4 | A | B | D |
|
|
Table 10. Raw data for the analysis of-variance for experiment 2
 |
| |
|
[TABLE 11, TABLE 12, TABLE 13]The analysis of variance in Table 11 shows that 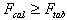 at different levels of probability, we conclude that the fertilizer applied has a significant effect on the cassava.Table 12 is the analysis of variance when block is adjusted for Experiment2. In table 13, Fcal≥Ftab at different levels of probability, we conclude that the fertilizer applied has a significant effect on the cassava.Table14 is the summarized results of the symmetric balanced incomplete block design
at different levels of probability, we conclude that the fertilizer applied has a significant effect on the cassava.Table 12 is the analysis of variance when block is adjusted for Experiment2. In table 13, Fcal≥Ftab at different levels of probability, we conclude that the fertilizer applied has a significant effect on the cassava.Table14 is the summarized results of the symmetric balanced incomplete block design| Table 11. Analysis of variance when treatment and block are not adjusted for experiment 2 |
| | Sources ofVariation | Sum ofsquares | Degree offreedom | MeanSquare | F-ratio | F-test at 0.01 | F-testAt 0.05 | | Universal mean | 2133.33 | 1 | | | | | | Treatment | 975.34 | 3 | 325.11 | 6.05 | 3.62 | 3.41 | | Blocks | 100.67 | 3 | | | | | | Error | 268.66 | 5 | 53.732 | | | | | Total | 3478 | 12 | | | | |
|
|
| Table 12. Analysis of variance when block is adjusted for Experiment2 |
| | Sources of variation | Sum of squares | Degrees of freedom | Mean squares | | Universal mean | 2133.33 | 1 | | | Treatment | 975.34 | 3 | | | Blocks (adjusted) | 6.17 | 3 | | | Error | 363.17 | 5 | 72.63 | | Total | 3478 | 12 | |
|
|
| Table 13. Analysis of variance when treatment is adjusted for experiment 2 |
| | Sources of variation | Sum of square | Degrees freedom | Mean squares | F-ratio | F-test at 0.01 | F-test at 0.05 | | Universal mean | 2133.33 | 1 | - | - | - | - | | Treatment (adjusted) | 880.83 | 3 | 293.61 | 4.04 | 3.62 | 3.41 | | Block | 100.67 | 3 | 18.33 | - | - | - | | Error | 363.17 | 5 | 72.63 | - | - | - | | Total | 3478 | 12 | - | - | - | - |
|
|
| Table14. Summarized results of the symmetric balanced incomplete block design |
| | | EXPERIMENT 1A | EXPERIMENT 1B | | | 0.05 | 0.01 | 0.05 | 0.01 | | TREATMENT(NOT ADJUSTED) | NOT SIGNIFICANT | NOT SIGNIFICANT | SIGNIFICANT | SIGNIFICANT | | TREATMENT (ADJUSTED) | SIGNIFICANT | SIGNIFICANT | SIGNIFICANT | SIGNIFICANT |
|
|
5. Summary and Conclusions
In table 6, when treatment was not adjusted,the F-ratio of 1.36 indicates that the treatment is not significant at 1% and 5%level of significance. But in table 8 where the treatment was adjusted, the F-ratio of 11.66 turns out to be highly significant and the error highly reduced at the same level of significance.Table 7 and table 12 where block is adjusted confirm that the experiments used in this work are symmetric balanced incomplete block designs (SBIBDs) by showing that the error sum of squares for the treatments when adjusted equals the error sum of squares for the blocks when adjusted. Considering the results obtained from table 11(when treatment is not adjusted) and table 13(when treatment is adjusted)both of which are statisticallysignificant at 1% and 5% level of significance but table 13 turns out to be better by minimizing the error.Adjustment of treatments in SBIBD does not only lead to the results being statistically significant but also gives minimum error. It is obvious that treatment adjustment is very necessary in the experiments. In this research work, classical ANOVA method makes insignificant result when treatments are not adjusted to become significant by adjusting the treatments and also reduces error.
SUGGESTION
Further research work can be done on the unsymmetric balanced incomplete block designs (USBIBD’s) to know whether treatment adjustment is necessary.
References
| [1] | On-line: definition of blockde sign: http://en.wikipedia.org/wiki/Blockdesign accessed 6th June 2012. |
| [2] | Acha, C. K. (2010). Impact of Housing and Age of Birds on Egg Production. International Journal of Numerical Mathematics, 5(2):275 – 298. |
| [3] | Montgomery, D.C. (1976). Design and Analysis of Experiments, John Wiley and sons, Inc, New York. |
| [4] | On-line:[4] accessed 6th June 2012 |
| [5] | Gomez. A.K. and Gomez, A.A. (1983). Statistical Procedures for Agricultural Research, John Wiley and Sons, Inc, New York. |
| [6] | Cochran, W.G. and Cox, G.M. (1957). Experimental designs, J. Wiley, New York. |
| [7] | Yates, F. (1936): Incomplete Randomized Blocks, Annals of Eugenics, 7:121-140.Stokes, S.L. (1980). |
| [8] | Bose, R. C. (1939). On the construction of balanced incomplete-block designs, annals of eugenics, 9:353-399. |
| [9] | Fisher, R.A. (1940). An Examination of the Different Possible Solutions of a Problem in Incomplete-Blocks, Annals of Eugenics, 10:52-75. |
| [10] | Bose, R.C. and Nair, K.R. (1939). Partially balanced incomplete-block designs, Ankhya, 4:237-372. |
| [11] | Nair, K.R. and Rao, C.R. (1942). A Note on Partially Balanced Incomplete Block Designs, Science and Culture, 7:568-569. |
| [12] | Street, A.I. and street, D.J (1987): Combinatories of Experimental Design, Oxford University Press, Oxford. |
| [13] | Bose, R. C. (1949). A Note on Fishers inequality for balanced incomplete-block designs, Annals of Math.Stat.20:619-620. |
| [14] | On-line: symmetricdesign;www.answer.com/topic/symmetric-design-mathematics accessed 6th June 2012 |
| [15] | Hill D.H and Williams W.C. (2005). The America heritage dictionary of the English language, file://A:/ Analysis of Variance: Definition and Much More From Answer Com.Htm. |

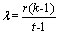
 must be an integer. The symmetry property of a design occurs when the row effect and the column effects of the design are interchanged and still the error sum of squares so calculated in each remains the same, see,[3]
must be an integer. The symmetry property of a design occurs when the row effect and the column effects of the design are interchanged and still the error sum of squares so calculated in each remains the same, see,[3]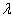 = group of blocks,• N=total,• SS=sum of squares• ANOVA=analysis of variance,• SBIBD=symmetric balanced incomplete block design.
= group of blocks,• N=total,• SS=sum of squares• ANOVA=analysis of variance,• SBIBD=symmetric balanced incomplete block design.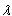 = 2 and N = 12. The analysis of the data in Table 5 is shown in [TABLE 6, TABLE 7, TABLE 8]The analysis of variance in Table 6 shows that Fcal ≤ Ftab at different levels probability, we conclude that the fertilizer applied has no significant effect on the cassava.The balanced incomplete block design in table 7 is symmetric since a = b = 4. However, in Table 8, Fcal ≥ Ftab at different levels of probability, we conclude that the fertilizer applied has a significant effect on the cassava.
= 2 and N = 12. The analysis of the data in Table 5 is shown in [TABLE 6, TABLE 7, TABLE 8]The analysis of variance in Table 6 shows that Fcal ≤ Ftab at different levels probability, we conclude that the fertilizer applied has no significant effect on the cassava.The balanced incomplete block design in table 7 is symmetric since a = b = 4. However, in Table 8, Fcal ≥ Ftab at different levels of probability, we conclude that the fertilizer applied has a significant effect on the cassava.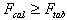 at different levels of probability, we conclude that the fertilizer applied has a significant effect on the cassava.Table 12 is the analysis of variance when block is adjusted for Experiment2. In table 13, Fcal≥Ftab at different levels of probability, we conclude that the fertilizer applied has a significant effect on the cassava.Table14 is the summarized results of the symmetric balanced incomplete block design
at different levels of probability, we conclude that the fertilizer applied has a significant effect on the cassava.Table 12 is the analysis of variance when block is adjusted for Experiment2. In table 13, Fcal≥Ftab at different levels of probability, we conclude that the fertilizer applied has a significant effect on the cassava.Table14 is the summarized results of the symmetric balanced incomplete block design Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML



