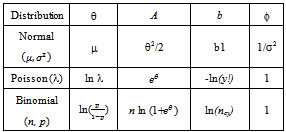-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Probability and Statistics
2012; 1(3): 41-47
doi: 10.5923/j.ijps.20120103.03
Generalized Linear Mixed Models for Longitudinal Data
Ahmed M. Gad , Rasha B. El Kholy
Department of Statistics, Faculty of Economics and Political Science, Cairo University, Cairo, Egypt
Correspondence to: Ahmed M. Gad , Department of Statistics, Faculty of Economics and Political Science, Cairo University, Cairo, Egypt.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
The study of longitudinal data plays a significant role in medicine, epidemiology and social sciences. Typically, the interest is in the dependence of an outcome variable on the covariates. The Generalized Linear Models (GLMs) were proposed to unify the regression approach for a wide variety of discrete and continuous longitudinal data. The responses (outcomes) in longitudinal data are usually correlated. Hence, we need to use an extension of the GLMs that account for such correlation. This can be done by inclusion of random effects in the linear predictor; that is the Generalized Linear Mixed Models (GLMMs) (also called random effects models). The maximum likelihood estimates (MLE) are obtained for the regression parameters of a logit model, when the traditional assumption of normal random effects is relaxed. In this case a more convenient distribution, such as the lognormal distribution, is used. However, adding non-normal random effects to the GLMM considerably complicates the likelihood estimation. So, the direct numerical evaluation techniques (such as Newton - Raphson) become analytically and computationally tedious. To overcome such problems, we propose and develop a Monte Carlo EM (MCEM) algorithm, to obtain the maximum likelihood estimates. The proposed method is illustrated using a simulated data.
Keywords: Generalized Linear Mixed Models, Logistic Regression, Longitudinal Data, Monte Carlo EM Algorithm, Random Effects Model
Article Outline
1. Introduction
- Longitudinal data consist of repeated observations, for the same subject, of an outcome variable. There may be a set of covariates for each subjects. Let
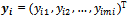 be an
be an 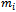 x 1 vector representing the observed sequence of the outcome variable
x 1 vector representing the observed sequence of the outcome variable 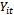 recorded at time t = 1,2, ... ,
recorded at time t = 1,2, ... , 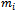 , for the ith subject, i=1,2, ...., n. Also, assume that xij = (xit1, xit2, ..., xitp) is an 1x p vector of p covariates observed at time t. Thus, Xi is an mi x p matrix of covariates corresponding to the ith subject taking the form:
, for the ith subject, i=1,2, ...., n. Also, assume that xij = (xit1, xit2, ..., xitp) is an 1x p vector of p covariates observed at time t. Thus, Xi is an mi x p matrix of covariates corresponding to the ith subject taking the form: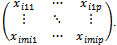 .For simplicity we can assume that mi=m.The primary focus is on the dependence of the outcome on the covariates[3,5]. In other words, we are usually interested in the inference about the regression coefficients, in the usual linear models of the form
.For simplicity we can assume that mi=m.The primary focus is on the dependence of the outcome on the covariates[3,5]. In other words, we are usually interested in the inference about the regression coefficients, in the usual linear models of the form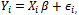 where
where 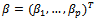 is a p x1 vector of the regression coefficients. It is usually assumed that the errors,
is a p x1 vector of the regression coefficients. It is usually assumed that the errors,  , are independent and identically normally distributed. Therefore, these models are not used in situations when response variables have distributions other than the normal, or even when they are qualitative rather than quantitative. Examples include binary longitudinal data.To solve this problem, Reference[18] introduce the generalized linear models (GLM) as a unified framework to model all types of longitudinal data[13, 15, 24]. These models assume that the distribution of Yit ( i = 1, ..., n, t = 1, 2, ..., m) belongs to the exponential family. The exponential family distributions can be written in the form:
, are independent and identically normally distributed. Therefore, these models are not used in situations when response variables have distributions other than the normal, or even when they are qualitative rather than quantitative. Examples include binary longitudinal data.To solve this problem, Reference[18] introduce the generalized linear models (GLM) as a unified framework to model all types of longitudinal data[13, 15, 24]. These models assume that the distribution of Yit ( i = 1, ..., n, t = 1, 2, ..., m) belongs to the exponential family. The exponential family distributions can be written in the form: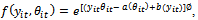 | (1) |
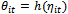 and
and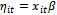 . Also
. Also 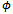 is the scale parameter and it is treated as a nuisance parameter when the main interest is in the regression coefficients[13]. The distribution in Equation (1) is the canonical form and
is the scale parameter and it is treated as a nuisance parameter when the main interest is in the regression coefficients[13]. The distribution in Equation (1) is the canonical form and 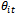 is called the natural parameter of the distribution.The first two moments of
is called the natural parameter of the distribution.The first two moments of 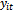 in Equation (1) are given by
in Equation (1) are given by 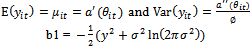 | (2) |
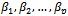 , are equal to some function of the expected value of
, are equal to some function of the expected value of 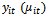 , i. e.,
, i. e., 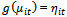 where
where 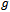 is a monotone and differentiable function called the link function. From Equation (1) and Equation (2), we can write the inverse of the link function as
is a monotone and differentiable function called the link function. From Equation (1) and Equation (2), we can write the inverse of the link function as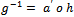 . Note that a link function in which
. Note that a link function in which 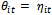 (e.g., h is the identity function) is called the canonical link function. It is sometimes preferred because it often leads to simple interpretable reparametrized models. By looking at θ in Table 1, we can see that the canonical link functions that correspond to the given distributions are the identity (normal distribution), the log (Poisson distribution) and the logit (binomial distribution) functions. Hence, the GLM has three elements:
(e.g., h is the identity function) is called the canonical link function. It is sometimes preferred because it often leads to simple interpretable reparametrized models. By looking at θ in Table 1, we can see that the canonical link functions that correspond to the given distributions are the identity (normal distribution), the log (Poisson distribution) and the logit (binomial distribution) functions. Hence, the GLM has three elements:
|
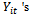 that are assumed to share the same distribution from the exponential family,2. The systematic component which is the explanatory variables that produce the linear predictor
that are assumed to share the same distribution from the exponential family,2. The systematic component which is the explanatory variables that produce the linear predictor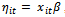 , and3. The link function which is a monotone and differentiable function
, and3. The link function which is a monotone and differentiable function 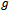 relating the mean
relating the mean 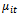 and the linear predictor
and the linear predictor 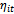 .The aim of this paper is to obtain the maximum likelihoodestimates (MLE) of the regression parameters for the logit model relaxing the normality assumption. In this case the estimation process is cumbersome and intractable. Hence, MCMC techniques could be alternative choice. We propose and develop the Monte Carlo EM (MCEM) algorithm, to obtain the maximum likelihood estimates. The proposed method is illustrated using simulated data.The rest of the paper is organized as follows. In Section 2, we review three distinct approaches to model longitudinal data. Also, we introduce the random effect model. Section 3 discusses several alternatives to maximum likelihood estimation for GLM. The EM algorithm and its variant, namely Monte Carlo EM (MCEM), are described and applied to the random effect model in Section 4. In Section 5, we implement the proposed MCEM algorithm to a simulated binary data. The results obtained from the simulated data are presented in Section 6. Finally, conclusions are given in Section 7.
.The aim of this paper is to obtain the maximum likelihoodestimates (MLE) of the regression parameters for the logit model relaxing the normality assumption. In this case the estimation process is cumbersome and intractable. Hence, MCMC techniques could be alternative choice. We propose and develop the Monte Carlo EM (MCEM) algorithm, to obtain the maximum likelihood estimates. The proposed method is illustrated using simulated data.The rest of the paper is organized as follows. In Section 2, we review three distinct approaches to model longitudinal data. Also, we introduce the random effect model. Section 3 discusses several alternatives to maximum likelihood estimation for GLM. The EM algorithm and its variant, namely Monte Carlo EM (MCEM), are described and applied to the random effect model in Section 4. In Section 5, we implement the proposed MCEM algorithm to a simulated binary data. The results obtained from the simulated data are presented in Section 6. Finally, conclusions are given in Section 7.2. Modeling Longitudinal Data
- There are three distinct strategies for modeling longitudinal data. Each strategy provides different way to model the individual
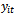 in terms of
in terms of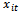 , taking into consideration the possible correlation between the subject’s measurements.
, taking into consideration the possible correlation between the subject’s measurements.2.1. The Marginal Model
- In this approach two models are specified; one for the marginal mean,
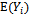 , and the other for the marginal covariance,
, and the other for the marginal covariance, 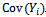 In other words, we assume a known structure for the correlation between a subject'smeasurements. The two more natural generalization of the diagonal covariance matrix (case of uncorrelated measurements) are the uniform and the exponential correlation structures. Modelling the mean and the covariance separately has the advantage of making valid inferences about
In other words, we assume a known structure for the correlation between a subject'smeasurements. The two more natural generalization of the diagonal covariance matrix (case of uncorrelated measurements) are the uniform and the exponential correlation structures. Modelling the mean and the covariance separately has the advantage of making valid inferences about 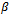 even when an incorrect form of the within-subject correlation structure is assumed.
even when an incorrect form of the within-subject correlation structure is assumed.2.2. The Transition Model
- This approach combines the assumptions about the dependence of
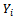 on
on 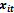 and the correlation among repeated
and the correlation among repeated 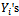 into a single equation. The idea behind this approach is that correlation within subject arises because one response is explicitly caused by others. We can specify a regression model for the conditional expectation,
into a single equation. The idea behind this approach is that correlation within subject arises because one response is explicitly caused by others. We can specify a regression model for the conditional expectation, 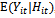 , as an explicit function of
, as an explicit function of 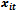 and the other observations on the same subject. The function
and the other observations on the same subject. The function 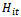 is a function of
is a function of 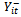 , where
, where 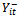 is the set of all observations on the subject i except at time t. For longitudinal data, it is natural to reduce the set
is the set of all observations on the subject i except at time t. For longitudinal data, it is natural to reduce the set 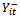 to include only observations prior to time t;
to include only observations prior to time t; 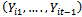 . A well known example of the transition model is the first-order autoregressive model in which
. A well known example of the transition model is the first-order autoregressive model in which 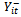 depends on the past history in
depends on the past history in 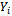 only through the preceding measurement
only through the preceding measurement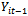 . Note that the covariance matrix for
. Note that the covariance matrix for 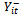 in this case corresponds to the marginal model with exponential correlation structure.
in this case corresponds to the marginal model with exponential correlation structure.2.3. The Random Effects Model
- This model assumes that the correlation among a subject's measurements arises from sharing unobserved variables. That is, there are random effects which represent unobserved factors that are common to all responses for a given subject. These random effects vary across subjects[8].Using the GLM framework, we assume that, conditional on the unobserved variables (
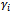 ), we have independent responses from a distribution belongs the exponential family, i.e.,
), we have independent responses from a distribution belongs the exponential family, i.e., 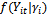 has the form in Equation (1) and the conditional moments are given by
has the form in Equation (1) and the conditional moments are given by 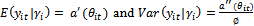 . The general specifications of the generalized linear mixed model (GLMM) are:1. The conditional mean,
. The general specifications of the generalized linear mixed model (GLMM) are:1. The conditional mean, 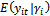 , is modelled by
, is modelled by 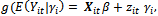 where
where 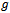 is an appropriate known link function. The
is an appropriate known link function. The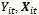 and
and 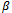 are the outcome variable, the covariates and the regression coefficients vector respectively. The
are the outcome variable, the covariates and the regression coefficients vector respectively. The 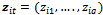 is an 1x q subset of
is an 1x q subset of 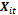 associated with random coefficients and
associated with random coefficients and 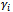 is a q x 1 vector of random effects with mean 0 and variance D.2. The random effects,
is a q x 1 vector of random effects with mean 0 and variance D.2. The random effects, 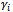 , are independent realizations from a common distribution.3. Given the actual coefficients,
, are independent realizations from a common distribution.3. Given the actual coefficients,  , for a given subject, the repeated observations for that subject are mutually independent.Hence, the GLMM is an extension of GLM that includes random effects in the linear predictor, giving an explicit probability model that explains the origin of the correlations [9,10].Note that for linear model, where the response variable has a normal distribution and the identity link function is used, the random effect model coincides with the marginal model assuming the uniform correlation structure.
, for a given subject, the repeated observations for that subject are mutually independent.Hence, the GLMM is an extension of GLM that includes random effects in the linear predictor, giving an explicit probability model that explains the origin of the correlations [9,10].Note that for linear model, where the response variable has a normal distribution and the identity link function is used, the random effect model coincides with the marginal model assuming the uniform correlation structure.3. Estimation of GLM
- The method of maximum likelihood is the theoretical basis for parameter estimation in GLM. However, in longitudinal data framework, the presence of within subject correlation renders the use of standard maximum likelihood estimation methods to be problematic. The reason behind this problem is that there are no multivariate generalization to non-normal distributions. As a result, Reference[11] introduce the generalized estimating equations (GEE) method. This method does not make use of the underlying multivariate distribution. It uses certain information associated with the marginal distribution rather than the actual likelihood, which is referred to as quasi-likelihood method[1, 12, 13].References[11] and[25] introduce a class of estimating equations to account for correlated measurements of longitudinal data. The GEEs can be thought of as an extension of quasi-likelihood to the case where the variance cannot be fully specified in terms of the mean, but rather additional correlation parameters must be estimated. Several alternative methods for analyzing longitudinal data can be implemented using the GEEs, assuming different designs or structures of the correlation matrix[26, 27]. It is difficult to adapt the GEEs for the GLMM. This is due to the fact that the GEEs work most naturally for models specified marginally, not for the GLMMs which are specified conditionally on the random effects[14]. The GEEs, by themselves, do not help to separate out different sources of variation. In addition, they are not direct technology for best prediction of random effects.The penalized quasi-likelihood (PQL) is another alternative to the maximum likelihood estimation when correlated data are to be incorporated in the GLM. In this approach a penalty function is added to the quasi-likelihood to prevent the random effects from getting too “big”. This method works well for the GLMM when the conditional distribution of the data given the random effects is approximately normal. However, the method can fail badly for distributions that are far from normal[14]. One possible reason for this drawback is the large number ofapproximations needed to solve the integration of the logquasi-likelihood with the additional “penalty” term.As can be seen, the alternatives to ML fail to work well for many of the GLMMs. Therefore, the classical method remains favourable even though incorporating random factors in the linear predictor of the GLM leads to difficult-to-handle likelihoods. To overcome this difficulty, approaches for approximating or calculating and then maximizing the likelihood are explored.
4. Likelihood Function for GLMM
- The GLM often leads to means which are non-linear in parameters, or models with non-normal errors. Also, it leads to missing data or dependence among the responses. This results in a non-quadratic likelihood function in the parameters. Hence, it gives rise to nonlinearity problems in ML estimation[16, 19, 23].Recall the notation for the GLMM from Section 2.3. Let
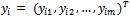 denote the observed data vector of size m for the ith subject. The conditional distribution of
denote the observed data vector of size m for the ith subject. The conditional distribution of 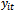 given
given 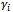 (the random effect vector for the ith subject) follows a GLM of the form in Equation (1) with linear predictor
(the random effect vector for the ith subject) follows a GLM of the form in Equation (1) with linear predictor 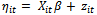
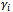 . The vector
. The vector 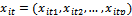 represents the tth row of
represents the tth row of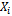 , the model matrix for the fixed effects,
, the model matrix for the fixed effects, 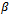 . The
. The 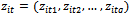 represents the tth row of
represents the tth row of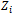 , the model matrix for random effects,
, the model matrix for random effects, 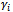 , corresponding to the ith subject.We now formulate the notion of a GLMM:
, corresponding to the ith subject.We now formulate the notion of a GLMM: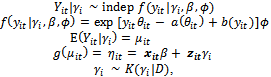 | (4) |
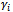 with variance-covariance matrix D.The probability of any response pattern
with variance-covariance matrix D.The probability of any response pattern 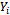 (of size m), conditional on the random effects
(of size m), conditional on the random effects 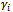 is equal to the product of the probabilities of the observations on each subject, because they are independent given the common random effects.
is equal to the product of the probabilities of the observations on each subject, because they are independent given the common random effects.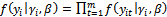 Thus the likelihood function for the parameter
Thus the likelihood function for the parameter 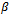 and D can be written as:
and D can be written as: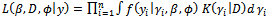 | (5) |
4.1. The EM Algorithm
- The EM algorithm[2] is a method to obtain the ML estimates, in presence of incomplete data, which avoids an explicit calculation of the observed data log-likelihood. The EM algorithm iterates two steps: the E-step and the M-step. In the E-step, the expected value of the log-likelihood of the complete data, given the observed data and the current parameter estimates, is obtained[22]. Thus the computation in the M-step can be easily applied to pseudo-complete data. The observed (incomplete) data likelihood function always increases or stays constant at each iteration of the EM algorithm. For more details see[17].A typical assumption in the GLMM is to consider the random effect,
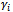 , as missing data. The complete data is then
, as missing data. The complete data is then 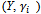 and the complete data likelihood is given by
and the complete data likelihood is given by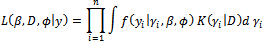 Although the observed data likelihood function in Equation (5) is complicated, the complete data likelihood is relatively simple. In other words, the integration over the random effects in Equation (5) is avoided since the value of (the missing data) will be simulated during the EM algorithm and will be no longer unknown.The log-likelihood is given by
Although the observed data likelihood function in Equation (5) is complicated, the complete data likelihood is relatively simple. In other words, the integration over the random effects in Equation (5) is avoided since the value of (the missing data) will be simulated during the EM algorithm and will be no longer unknown.The log-likelihood is given by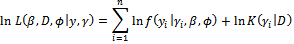 | (6) |
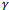 to be the missing data has two advantages. First, upon knowing
to be the missing data has two advantages. First, upon knowing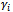 , the
, the 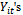 are independent. Second, in the M-step, where the maximization is with respect to the parameters
are independent. Second, in the M-step, where the maximization is with respect to the parameters 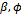 and D, the parameters
and D, the parameters 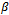 and
and 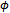 only in the first term of Equation (6). Thus, the M-step with respect to
only in the first term of Equation (6). Thus, the M-step with respect to 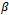 and
and 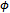 uses only the GLM portion of the likelihood function. So, it is similar to a standard GLM computation assuming that
uses only the GLM portion of the likelihood function. So, it is similar to a standard GLM computation assuming that 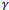 is known. Maximizing with respect to D, in the second term, is just maximum likelihood using the distribution of
is known. Maximizing with respect to D, in the second term, is just maximum likelihood using the distribution of 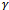 after replacing sufficient statistics (in the case that K(.) belongs to the exponential family) with the conditional expected values.For the GLMM of the form in Equation (4), at the (r + 1) iteration, starting with initial values
after replacing sufficient statistics (in the case that K(.) belongs to the exponential family) with the conditional expected values.For the GLMM of the form in Equation (4), at the (r + 1) iteration, starting with initial values 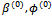 and
and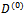 , the EM algorithm follows the steps:1. The E-step (Expectation step)Calculate the expectations with respect to the conditional distribution using the current parameters' value
, the EM algorithm follows the steps:1. The E-step (Expectation step)Calculate the expectations with respect to the conditional distribution using the current parameters' value 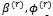 and
and 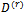 (a)
(a) 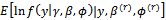 (b)
(b) 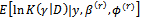 2. The M-step (Maximization step)Find the values(a)
2. The M-step (Maximization step)Find the values(a) 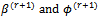 that maximizes 1 (a).(b)
that maximizes 1 (a).(b) 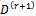 that maximizes 1 (b).If convergence is achieved, then the current values are the MLEs, otherwise increment r = r + 1 and repeat the two steps.
that maximizes 1 (b).If convergence is achieved, then the current values are the MLEs, otherwise increment r = r + 1 and repeat the two steps.4.2. The Monte Carlo EM Algorithm (MCEM)
- In general, the expectations in the E-step above, cannot be obtained in a closed form. So we propose using the Monte Carlo Markov Chains (MCMC) techniques[6, 20, 21]. A random draw from the conditional distribution of
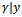 is obtained. Then the required expectations are evaluated via Monte Carlo approximations.The Metropolis-Hastings algorithm can be implemented to draw a sample
is obtained. Then the required expectations are evaluated via Monte Carlo approximations.The Metropolis-Hastings algorithm can be implemented to draw a sample 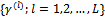 from the conditional distribution of
from the conditional distribution of 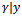 . A candidate value
. A candidate value 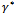 is generated from a proposal distribution Q(.). This potential value is accepted, as opposed to keeping the previous value, by a probability
is generated from a proposal distribution Q(.). This potential value is accepted, as opposed to keeping the previous value, by a probability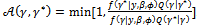 | (7) |
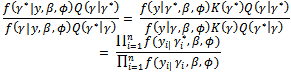 This calculation only involves the conditional distribution of
This calculation only involves the conditional distribution of 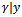 Incorporating the Metropolis algorithm into the EM algorithm, starting from initial values
Incorporating the Metropolis algorithm into the EM algorithm, starting from initial values 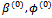 and
and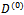 , at iteration (r + 1),1. Generate L values
, at iteration (r + 1),1. Generate L values 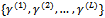 from the conditional distribution
from the conditional distribution 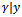 using the Metropolis algorithm and the current parameters' values
using the Metropolis algorithm and the current parameters' values 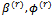 and
and 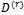 2. The E-step (Expectation step)Calculate the expectations as Monte Carlo estimates(a)
2. The E-step (Expectation step)Calculate the expectations as Monte Carlo estimates(a) 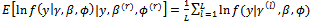 (b)
(b) 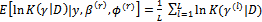 3. The M-step (Maximization step)Find the values (a)
3. The M-step (Maximization step)Find the values (a) 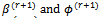 that maximizes 2 (a).(b)
that maximizes 2 (a).(b) 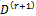 that maximizes 2 (b).If convergence is achieved, then the current values are the MLEs, otherwise increment r = r + 1 and go to step 1.
that maximizes 2 (b).If convergence is achieved, then the current values are the MLEs, otherwise increment r = r + 1 and go to step 1.5. Simulation Study
- The proposed method is evaluated using simulated data set. The response variable is assumed to be binary variable.
5.1. Simulation Setup
- The number of subjects is fixed at 100 subjects and the time points are chosen as 7 occasions. Binary responses
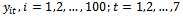 are generated, conditionally on the random effect
are generated, conditionally on the random effect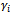 , from a Bernoulli distribution with mean
, from a Bernoulli distribution with mean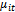 . The random intercept logit model
. The random intercept logit model 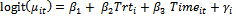 is used.The parameters values are chosen as
is used.The parameters values are chosen as 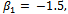
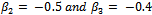 . The binary covariate Trti is set to be 1 for half of the subjects and 0 for the other half. The continuous covariate Time is independently generated from normal distribution with mean vector (0 1 2 3 6 9 12) and standard deviation vector (0 0.1 0.2 0.3 0.5 0.6 0.8). Note that, for each subject i, the 1st value of the Time covariate will always be 0. The random intercepts
. The binary covariate Trti is set to be 1 for half of the subjects and 0 for the other half. The continuous covariate Time is independently generated from normal distribution with mean vector (0 1 2 3 6 9 12) and standard deviation vector (0 0.1 0.2 0.3 0.5 0.6 0.8). Note that, for each subject i, the 1st value of the Time covariate will always be 0. The random intercepts 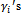 are obtained as
are obtained as 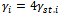 such that
such that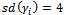 . Standardized random intercepts
. Standardized random intercepts  are generated from lognormal distribution Ln N(0; 1). The lognormal density is chosen to represent a skewed distribution whose support does not cover the whole real line unlike the normal distribution. This setup is the same as in[7] to enable us to compare our results with those in[7].In this case the GLMM in Equation (4) is
are generated from lognormal distribution Ln N(0; 1). The lognormal density is chosen to represent a skewed distribution whose support does not cover the whole real line unlike the normal distribution. This setup is the same as in[7] to enable us to compare our results with those in[7].In this case the GLMM in Equation (4) is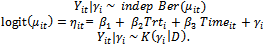 | (8) |
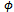 = 1 so it drops out from the calculations. Second, we have a single random effect which is common (has the same value) for all the measurements of each subject. Thus
= 1 so it drops out from the calculations. Second, we have a single random effect which is common (has the same value) for all the measurements of each subject. Thus 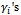 are iid from
are iid from 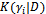 where the variance D is a scalar. Finally, the distribution K(.) will be the lognormal distribution.
where the variance D is a scalar. Finally, the distribution K(.) will be the lognormal distribution.5.2. The Logit-Lognormal Model
- For this model, the probability density function of the random effect is log-normal with parameters a and b,
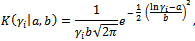 where
where 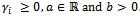 The likelihood function in Equation (5) can be written as:
The likelihood function in Equation (5) can be written as: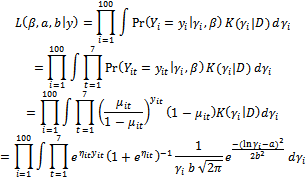 Hence, the log-likelihood is given as:
Hence, the log-likelihood is given as: We apply the MCEM algorithm introduced in Section 4.2. Starting from initial values
We apply the MCEM algorithm introduced in Section 4.2. Starting from initial values 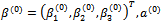 and
and 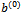 at iteration (r+1), the algorithm proceeds as:1. For each subject i, generate L values
at iteration (r+1), the algorithm proceeds as:1. For each subject i, generate L values 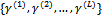 from
from 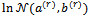 using the Metropolis algorithm with probability of acceptance as in Equation (7) given by
using the Metropolis algorithm with probability of acceptance as in Equation (7) given by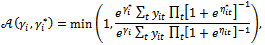 where
where 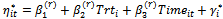 and
and 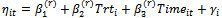 2. The E-StepCalculate the expectations as Monte Carlo estimates(a)
2. The E-StepCalculate the expectations as Monte Carlo estimates(a) 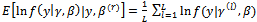
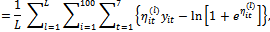 where
where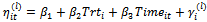 (b)
(b) 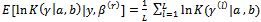
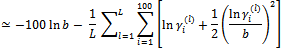 Note that
Note that 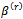 do not show explicitly in this step but they already used in Step 1 to generate the L values of
do not show explicitly in this step but they already used in Step 1 to generate the L values of 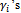 3. The M-stepFind the values (a)
3. The M-stepFind the values (a) 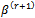 that maximizes 2 (a).(b)
that maximizes 2 (a).(b) 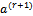 and
and 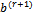 that maximizes 2 (b) to use them for the calculation of the standard deviation
that maximizes 2 (b) to use them for the calculation of the standard deviation 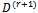 If convergence is achieved, then the current values are the MLEs, otherwise increment r = r + 1 and return to step 1.
If convergence is achieved, then the current values are the MLEs, otherwise increment r = r + 1 and return to step 1.5.3. Simulation Results
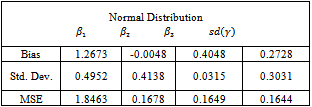
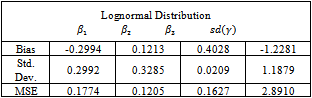
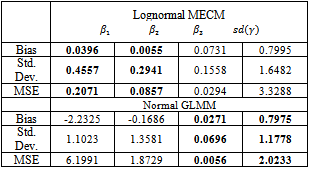
- The algorithm described above is implemented using the MATLAB package. Fifty data sets were generated according to the setup in Section 5.1. The random effect was simulated from a lognormal distribution. Then each data set is analysed using the Metropolis EM (MEM) algorithm twice. First, under the normality assumption of the random effects. Second, assuming that the random effects belong to the lognormal distribution. Summaries of the results are given in Tables 2 and 3. Note that Bias, Std. Dev. and MSE are the average bias, standard deviation and mean squared error of the estimates respectively.
|
|
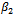 is more biased but this is compensated with smaller variance resulting in a lower value of the MSE. On the other hand, the estimate for the standard deviation of the random effect is better for the normal model than the lognormal model.It is clear that there is only a small improvement concerning the estimate of
is more biased but this is compensated with smaller variance resulting in a lower value of the MSE. On the other hand, the estimate for the standard deviation of the random effect is better for the normal model than the lognormal model.It is clear that there is only a small improvement concerning the estimate of 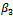 when using the logormal MEM. The bias for
when using the logormal MEM. The bias for 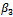 is large when using either, normal or lognormal MEM, it is 100% of the true value of the parameter. Therefore, we turn to a modified MEM (MECM) to improve the results. The modification is in the M-step where the parameter vector
is large when using either, normal or lognormal MEM, it is 100% of the true value of the parameter. Therefore, we turn to a modified MEM (MECM) to improve the results. The modification is in the M-step where the parameter vector 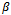 is divided into two subsets;
is divided into two subsets; 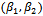 and (
and (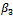 ). The maximization of the Monte Carlo expectations calculated in the preceding E-step is replaced by a conditional maximization. In other words, we first calculate
). The maximization of the Monte Carlo expectations calculated in the preceding E-step is replaced by a conditional maximization. In other words, we first calculate 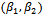 that maximize the expectation while
that maximize the expectation while 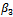 is held fixed. Next, we substitute the maximization arguments for
is held fixed. Next, we substitute the maximization arguments for 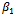 and
and 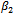 in the expectation function and find the value of
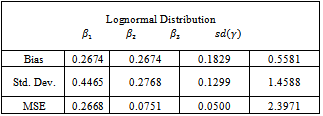
in the expectation function and find the value of 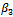 that maximizes the function. We repeat this conditional maximization twice. The results obtained for 50 data sets are summarized in Table 4.
that maximizes the function. We repeat this conditional maximization twice. The results obtained for 50 data sets are summarized in Table 4.
|
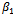 and the bias is considerably lower for
and the bias is considerably lower for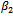 ,
, 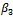 and the standard deviation of the random effect
and the standard deviation of the random effect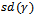 . On the other hand, the estimates for
. On the other hand, the estimates for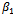 ,
, 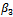 and
and 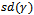 become more variable.
become more variable.
|
 and
and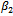 . Results for
. Results for 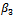 are good for both lognormal MECM and normal GLMM models, however, the latter gives better values. Finally, MECM algorithm produces more variable estimates for
are good for both lognormal MECM and normal GLMM models, however, the latter gives better values. Finally, MECM algorithm produces more variable estimates for 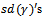 resulting in a higher value for MSE.
resulting in a higher value for MSE.6. Conclusions
- In this paper, we developed a Monte Carlo EM algorithm to estimate regression parameters for a logit model with lognormal random effects. The proposed method was applied to simulated binary data. A modified M-step was used to improve the results but a trade off between small values for bias and small variability must be made. In general, the obtained results are acceptable when comparing the MEM estimates to those calculated using the normal GLMM. Further work is to apply the proposed method to larger data sets. We can develop the MEM to logit model with different distribution for the random effect, namely, gamma distribution which is a natural conjugate for the binary data. This work is under investigation now.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML