1. Introduction

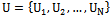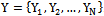Consider a finite population of N distinct and identifiable units. Let Y be a real variable with value Y_i measured on giving a vector . The problem is to estimate the population mean on the basis of a random sample selected from the population U and / or its variance . When there is no additional information on the auxiliary variable available, the simplest estimator of population mean is the simple random sample mean without replacement. However if an auxiliary variable X closely related to the study variable Y is available then one can use Ratio or Regression estimators to improve the performance of the estimator of the study variable. In this paper, we consider the problem of estimation of the population variance and use the auxiliary information to improve the efficiency of the estimator of population variance .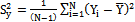

Estimation of population variance is considered by Isaki[10] where ratio and regression estimators are proposed. Prasad and Singh[14] have considered a ratio type estimator for estimation of population variance by improving Isaki's estimator[10] with respect to bias and precision. Arcos et al.[14] have introduced another ratio type estimator, whichhas also improved the Isaki's estimator[10], which is almost unbiased and more precise than the other estimators.

Before discussing further about the traditional ratio type variance estimator, modified ratio type variance estimators and the proposed modified ratio type variance estimator, the notations to be used in this paper are described below:

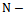Population size

Sample size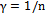

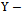Study variable

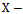Auxiliary variable

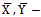Population means

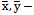Sample means

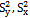Population variances

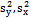Sample variances

Coefficient of variations

Coefficient of correlation

Bias of the estimator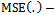

Mean squared error of the estimator

Ratio type variance estimator of

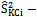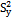
Existing modified ratio type variance estimator of

Proposed modified ratio type variance estimator of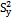

Isaki[10] suggested a ratio type variance estimator for the population variance 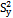when the population variance 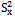of the auxiliary variable X is known together with its bias and mean squared error as given below:

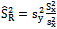(1)

Table 1. Existing modified ratio type variance estimators with their biases, mean squared errors

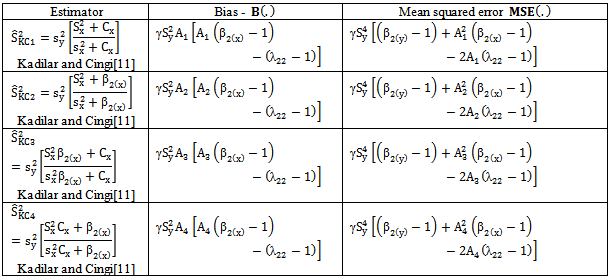
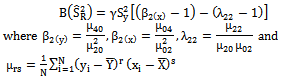The Ratio type variance estimator given in (1) is used to improve the precision of the estimate of the population variance compared to simple random sampling when there exists a positive correlation between X and Y. Further improvements are also achieved on the classical ratio estimator by introducing a number of modified ratio estimators with the use of known parameters like, Co-efficient of Variation and Co-efficient of Kurtosis. The problem of constructing efficient estimators for the population variance has been widely discussed by various authors such as Das and Tripathi[7], Isaki[10], Singh et al.[17,19], Agarwal and Sithapit[1], Garcia and Cebrain[8], Arcos et al.[4], Ahmed et al.[2], Al-Jararha and Al-Haj Ebrahem[3], Bhushan[5], Prasad and Singh[14], Reddy[15], Singh and Chaudhary[16], Upadhyaya and Singh[23], Wolter[24], Kadilar and Cingi[11,12] and Gupta and Shabbir[9].

Motivated by Sisodia and Dwivedi[20], Singh et al.[18] and Upadhyaya and Singh[22], Kadilar and Cingi[11] suggested four ratio type variance estimators using known values of Co-efficient of variation C_X and Co-efficient of Kurtosis 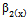of an auxiliary variable X together with their biases and mean squared errors as given in the Table 1:

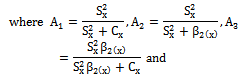The modified ratio type variance estimators discussed above are biased but have minimum mean squared errors compared to the traditional ratio type variance estimator. The list of estimators given in Table 1 uses the known values of the parameters like and their linear combinations. Subramani and Kumarapandiyan[21] used the known value of the population median M_d of the auxiliary variable to improve the ratio estimators in estimation of population mean. Further we know that the value of median is unaffected and robustness by the extreme values or the presence of outliers in the population values unlike the other parameters like the variance, coefficient of variation and coefficient of kurtosis. The above discussed points have motivated us to introduce a modified ratio type variance estimator using the known value of the population median of the auxiliary variable. As a result, it is observed that the proposed estimator performs better than the traditional ratio type variance estimator as well as the existing modified ratio type variance estimators listed in Table 1. The materials of the present study are arranged as given below. The proposed estimator with known population median is presented in section 2 where as the conditions in which the proposed estimator performs better than the existing estimators are derived in section 3. The performances of the proposed and the existing estimators are assessed for certain natural populations in section 4 and the conclusion is presented in section 5.

2. Proposed Estimator

As we stated earlier one can always improve the performance of the estimator of the study variable by using the known population parameters of the auxiliary variable, which are positively correlated with that of study variable. In this section we have suggested a modified ratio type variance estimator using the population median of the auxiliary variable.

The proposed modified ratio type variance estimator for population variance 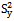is defined as

(2)

is the population median of the auxiliary variable X.

The bias and mean squared error of 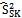=to the first degree of approximation are derived and given below:

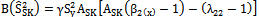(3)

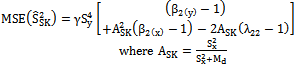(4)

3. Efficiency Comparison of Proposed Estimator

As we mentioned earlier the bias and mean squared error of the traditional ratio type variance estimator are given below:

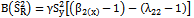(5)

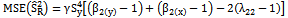(6)

For want of space; for the sake of convenience to the readers and for the ease of comparisons, the biases, the mean squared errors and the constants of the modified ratio type variance estimators given in Table 1 are represented in single class as given below:

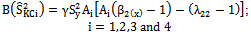(7)

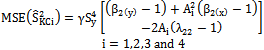(8)

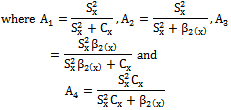The bias and mean squared error of the proposed modified ratio type variance estimator are given below:

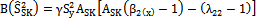(9)

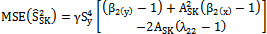(10)

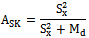From the expressions given in (6) and (10) we have derived the condition for which the proposed estimator is more efficient than the traditional ratio type variance estimator and it is given below:

(11)

From the expressions given in (8) and (10) we have derived the conditions for which the proposed estimator is more efficient than the existing modified ratio type variance estimators given in Table 1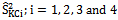, and are given below:

(12)

4. Numerical Study

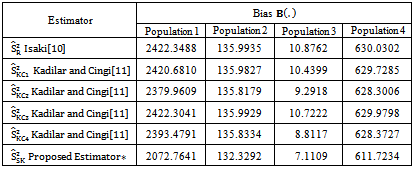
The performance of the proposed modified ratio type variance estimator is assessed with that of traditional ratio type estimator and existing modified ratio type variance estimators listed in Table 1 for certain natural populations. The populations 1 and 2 are the real data set taken from the Report on Waste 2004 drew up by the Italian bureau for the environment protection-APAT. Data and reports are available in the following website address http://www.osservatorionazionalerifiuti.it[25]. In the data set, for each of the Italian provinces, three variables are considered: the total amount (tons) of recyclable-waste collection in Italy in 2003(Y), the total amount of recyclable-waste collection in Italy in 2002(X₁) and the number of inhabitants in 2003(X₂). The population 3 is taken from Murthy[13] given in page 228 and population 4 is taken from Cochran[6] given in page 152. The population parameters and the constants computed from the above populations are given below:

Table 2. Parameters and Constants of the Populations

The biases and mean squared errors of the existing and proposed modified ratio type variance estimator for the populations given above are given in the following Tables:

Table 3. Biases of the existing and proposed modified ratio type variance estimators

Table 4. Mean squared error of the existing and proposed modified ratio type variance estimators

From the values of Table 3, it is observed that the bias of the proposed modified ratio type variance estimator is less than the biases of the traditional and existing modified ratio type variance estimators. Similarly from the values of Table 4, it is observed that the mean squared error of the proposed modified ratio type variance estimator is less than the mean squared errors of the traditional and existing modified ratio type variance estimators.

5. Conclusions

In this paper we have proposed a modified ratio type variance estimator using known value of Median of the auxiliary variable. The bias and mean squared error of the proposed modified ratio type variance estimator are obtained and compared with that of traditional ratio type variance estimator and existing modified ratio type variance estimators. Further we have derived the conditions for which the proposed estimator is more efficient than the traditional and existing estimators. We have also assessed the performances of the proposed estimator for some known populations. It is observed that the bias and mean squared error of the proposed estimator are less than the biases and mean squared errors of the traditional and existing estimators for certain known populations. Hence we strongly recommend that the proposed modified ratio type variance estimator may be preferred over the traditional ratio type variance estimator and existing modified ratio type variance estimators for the use of practical applications.

ACKNOWLEDGEMENTS

The authors record their gratitude to the editor and the reviewer for their constructive comments, which have improved the presentation of the paper. The second author wishes to record his gratitude and thanks to the Vice Chancellor, Pondicherry University for the financial assistance to carry out this research work through the University Fellowship.