Nursidik Yulianto1, 2, Bambang Widiyatmoko2, Purnomo Sidi Priambodo1
1Department of Electrical Engineering, Universitas Indonesia (UI), Depok, Indonesia
2Research Center for Physics, Indonesian Institute of Sciences (LIPI), South Tangerang, Indonesia
Correspondence to: Purnomo Sidi Priambodo, Department of Electrical Engineering, Universitas Indonesia (UI), Depok, Indonesia.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Semiconductor laser can be implemented in various fields, such as for telecommunication, radar, spectroscopy and sensor. Specialized for radar application, laser can be applied to generate microwave with heterodyne technique by mixing two laser sources. In this application, the quality of the laser wavelength stability is crucial in order to generate stability desired microwave source. In some studies it has been reported that the change of temperature causes the wavelength changes linearly. In our experiment, it is proven that the increase in temperature causes a shift in the peak wavelength toward the long wavelength laser typical of 0.094 nm/°C. Theoretically, it is shown that the wavelength shift caused by the thermal expansion on the laser grating period. In addition to the shift in wavelength, it is also shown that the increase in temperature causes a decrease in the optical power at the laser output. From the experiments of mixing two lasers that we have conducted, it was found that the tunability factor of laser beat frequency versus temperature is 10.35 GHz/°C. In this paper we show that the beat frequency of the result of mixing two laser diodes can be tuned by varying the temperature of one laser by varying Peltier temperature and laser injection current and let the other laser constant.
Keywords:
Microwave generation, Optical wave mixing, Wavelength shift, DFB laser, Temperature effect
Cite this paper: Nursidik Yulianto, Bambang Widiyatmoko, Purnomo Sidi Priambodo, Temperature Effect towards DFB Laser Wavelength on Microwave Generation Based on Two Optical Wave Mixing, International Journal of Optoelectronic Engineering, Vol. 5 No. 2, 2015, pp. 21-27. doi: 10.5923/j.ijoe.20150502.01.
1. Introduction
The invention of the laser in the end of 1950s was first demonstrated by Theodore Maiman [1] and subsequently in 1962, the development of semiconductor lasers [2] was a milestone in the progress of photonics technology and its use in a variety of modern applications, namely telecommunications [3], radar [4], spectroscopy [5] and sensor [6]. Specialized in radar technology that works in the Gigahertz frequency range, which was originally developed by the generator technology based on klystron tube [7], currently being developed by utilizing a laser that has the character of a relatively better coherence and lower power consumption.A light, small, portable radar device with low power consumption is needed both for military and civil aviation [8]. In the process, the laser as a high-frequency oscillator is used as a microwave generator, by mixing two laser light with a frequency adjacent to generate a beat frequency in the order of Gigahertz [9]. The main advantages of microwave generator that is based on mixing the two lasers as RF radar applications are low power consumption and is more portable than the method that uses klystron or Negative resistance Diode (NDR).Besides those two advantages, the method of generation RF mixing two laser-based radar has a weakness, which is wavelength and output intensity of the semiconductor laser changes due to the changes in environmental temperature of the laser. Due to radar applications which require a stable source transmitter on the wavelength and output intensity, the temperature stability of laser is very essential. Keeping the temperature of the laser in order to keep it stable is a crucial factor. It requires an automatic control method for stabilizing the difference between the two laser wavelengths by controlling the temperature of the second laser. It is necessary for the characterization of temperature as a major tunability factor of laser wavelength to be used in the RF generator Radar. Moreover, the increase in temperature causes an increase in phonon radiation that resulted in decreasing the intensity of the laser output power.The effect of temperature change on the laser wavelength becomes fundamental for generating a tunable microwave source by using mixing two identical laser diodes technique. By varying peak wavelength of one of both lasers, it is expected to generate a tunable beat. In this experiment the effect of laser temperature change due to varying Peltier temperature and laser injection current to vary the output microwave wavelength is subject to be discussed.
2. Photonic and Microwave Wavelength Shift Analysis
Semiconductor laser used in this study is the type InGaAsP DFB laser with a wavelength range that can be tuned in area of C band. DFB lasers are widely used as a semiconductor laser that can reach operating single-longitudinal-mode, i.e. lasers with peak wavelength single-mode or also known as Bragg wavelength λB [10]. To achieve a single-longitudinal mode operation, laser is designed to use a distributed Bragg reflector gratings structure, which is placed on the active waveguide (WG) layer surface. The gratings functions to disrupt the evanescent wave of the fundamental mode in the active layer laser and acts as a mirror of Fabry Perot laser configuration. This technicque is more effective and efficient than using Fabry Perot double coating mirror configuration to produce a single mode wavelength output as shown in Figure 1 below.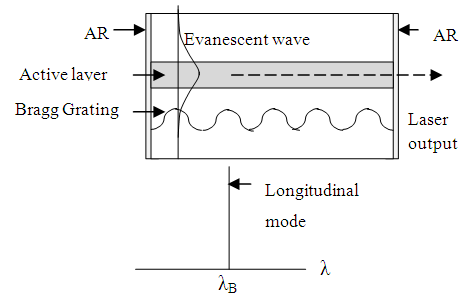 | Figure 1. Architecture Scheme of DFB laser [13, 18] |
As shown on Figure 1, Laser DFB has a grating layer structure on the active WG layer structure, where the optical grating has a period to select the reflected wavelength. This grating acts as a distributed filter, which only allows one longitudinal cavity modes (called λB Bragg wavelength) that will propagate back and forth [10]. The grating layer interacts directly with the evanescent mode of the single mode in the WG active layer. Optical grating performs a very efficient and effective distributed reflection, then it is named as distributed feedback laser.The relation between grating period Λ and output laser wavelength is written by the following equation [14]: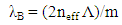 | (1) |
Where m is a positive integer that describes the grating order, λB is the Bragg wavelength and neff is the effective refractive index when the lasing mode in the active layer [11]. For InGaAsP DFB laser operating at λ = 1550 nm, requires the value Λ of about 220 nm when using a first order Bragg diffraction (m = 1) and neff of 3.6 at a temperature of 300 K [12, 14, 16].One way to adjust the wavelength shift DFB laser is by performing temperature variation. A temperature change causes a thermal expansion change on the grating period of laser cavity. Furthermore, it causes change of the DFB laser wavelength output. Typically, the experiments show the average semiconductor has a resonant wavelength shift of about 1 Ǻ/K [11]. The effect of wavelength change due to index refraction change is not reported, because of very small effect.In this paper, the technique to generate microwave carrier is conducted by mixing two DFB laser sources, which are detected by high speed photodetector (HSPD). The HSPD output is microwave beat frequency of the mixing. The microwave output signal resulted from mixing two DFB laser wave can be written as following [19, 20]: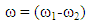 | (2) |
where ω1 and ω2 are optical frequencies of DFB first laser and second laser respectively. Polarization matching becomes a crucial problem for superposition wave such as in this two light-wave mixing. Hence, it is mandatory requirement that the two light waves should be in polarization match. In the case of this experiment where mixing two light waves by using fiber optical coupler, it requires to use Polarizaton Maintenance Fiber (PMF).In order to obtain a stable GHz microwave carrier at a certain frequency, it is required a temperature system to control a frequency deviation between those two laser sources.One laser is dedicated as a reference (constant) optical frequency (ω1) and the second one is varied by controlling its temperature. The temperature of DFB laser control system in this experiment include controller, peltier, thermistor and photodiode (PD) as shown in Figure 2 below. 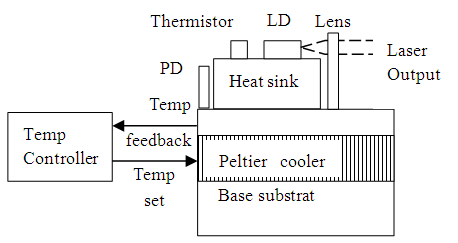 | Figure 2. Schematic laser diode laser device using a thermoelectric cooler for tenability [15] |
As shown on Figure 2, Laser temperature is controlled by a device called Peltier. Peltier works like a heat pump. It is directly controlled electronically by the control system. Laser Diode (LD) Wavelength will be shifted due to grating periode thermal expansion. Laser temperature is monitored by thermistor and its intensityis measured by PD [17]. Those two are feedback to the system control. As the result, by varying the temperature, the wavelength of one laser can be shifted and the microwave beat frequency can be tuned.
3. Experimental Results and Discussion
In variable microwave generation applications, one of the mixing lasers should be stable and the other one varied as required. Both lasers have identical characteristic and technical properties. It is required to obtain the wavelength-temperature slope (dλB/dT) of wavelength with respect to temperature shifts. The coefficient value is the slope as result of measurement plot from laser wavelength with respect to temperature, as shown in the following explanation.DFB laser temperature is controlled by laser driver and varying the setting temperature value (Tset) between 30 and 47oC at a fixed injection current (Iinj) that is equal to 20-mA out of maximum injection current 40-mA. The spectral wavelength is read by using the Optical Spectrum Analyzer (OSA) as shown in Figure 3 below.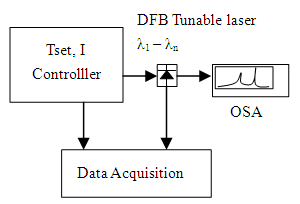 | Figure 3. Diagram laser testing wavelength by temperature controller |
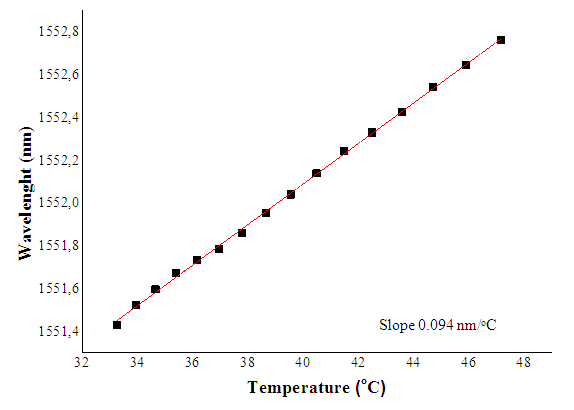 | Figure 4. Wavelength variation versus laser temperature |
Wavelength with respect to temperature is shown in Figure 4, The graph shows a relatively linear relation. The experimental result shows that the slope in Figure 4 is 0.094 nm/°C or 0.94 Ǻ/K. This slope is called wavelength-temperature slope (dλB/dT). It can be seen from Eq. 1 that increasing laser temperature will cause thermal grating period expansion. In temperature variation region from 30 to 47°C, the refractive index of the resonant mode (neff) is relatively constant, hence the deviation can be ignored. Then, based on Eq. 1, the deviation of Bragg wavelength (dλB) due to grating period deviation (dΛ) can be written as following: 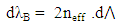 | (2) |
where d⋀ depends on laser temperature deviation dT. This relationship in DFB laser is written: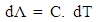 | (3) |
where C is a ratio that indicates the grating period expansion in nm due to increasing laser temperature per °C. In order to obtain relationship between C-ratio and wavelength-temperature slope (dλB/dT), Eq. 3 is plugged in to Eq. 2, and results in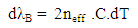 | (4) |
and finally,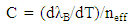 | (5) |
Eq.5 shows that for typical laser, where neff = 3.6 and wavelength-temperature slope (dλB/dT) = 0.094 nm/°C, will have grating period expansion ratio C of 0.014 nm/°C.Increasing laser temperature does not only cause wavelength shift to the longer part, but also lowering its output intensity as well [13]. The experiment result is shown on Figure 5 below: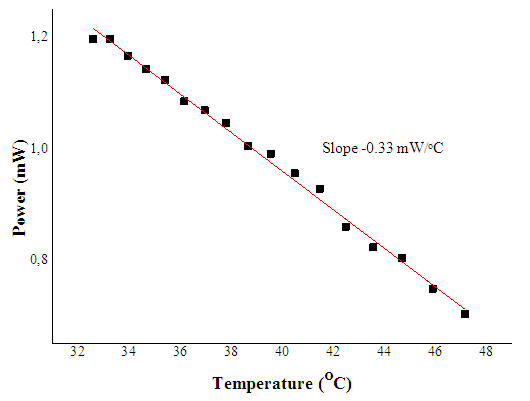 | Figure 5. Optical power laser output with respect to increasing the laser temperature |
The graph shows a relatively linear relation. The experimental result shows that the slope in Figure 5 is -0.033 mW/°C. Our hypothesis is that it occurs as the effect of increasing phonon that results in reducing number of output photon. The temperature of the laser is mainly influenced by the injection current to the DFB laser system and the heating Peltier component. From the experiment, injection current is varied from 10 to 40-mA at temperature constant of 40.5°C. As the output, the laser power increased by 1.10-mW/mA. Hence, laser output power is varied due to variation of Peltier operational temperature and laser injection current. The effect of injection current to the temperature laser has been observed. From experiment, it is shown a linear relation between laser temperature and injection current as 0.006°C /mA. Based on this value, we can obtain the relation between laser wavelength and the laser injection current variation which is defined as 0.00056-nm/mA.In microwave generation by mixing two laser technique, one laser source is set as a reference light source with a fixed wavelength and the second as a tunable laser. Heterodyne technique is used in this experiment to measure beat frequency of the mixed lasers. Microwave generation scheme is as shown in Figure 6.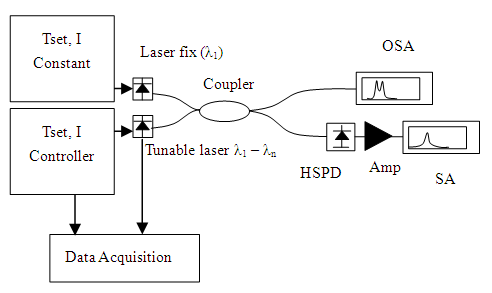 | Figure 6. Microwave generation scheme use heterodyne technique |
Mixing two optical waves are detected by high speed phcotodetector, and the output is frequency deviation (microwave) from both signals. When one of the laser wavelength is shifted by temperature, then the microwave frequency deviation can be varied as shown in Eq. 2. It means microwave can be tuned by varying one of laser temperature.The experiment of mixing two single mode lasers with the equal properties and output 0.05 mW is setup by setting one laser as a reference wavelength and the second laser as a tunable wavelength. The results of beat frequency reads by OSA, can be seen in Figure 7 below. Figure 7(a) shows several optical wavelengths with different deviations reads by Optical Spectrum Analyzer (OSA). Figure 7(b) shows the expected microwave frequency variations due to different mixing optical wavelengths reads by Signal Analyzer (SA).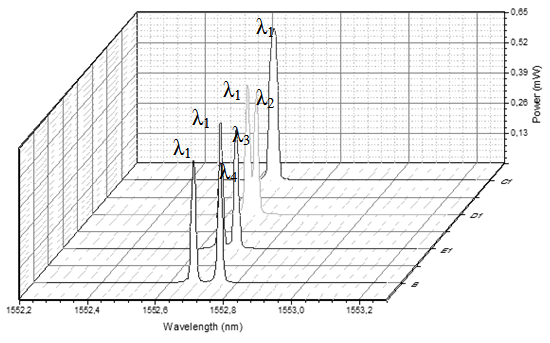 | Figure 7(a). Mixing two optical wavelength sources |
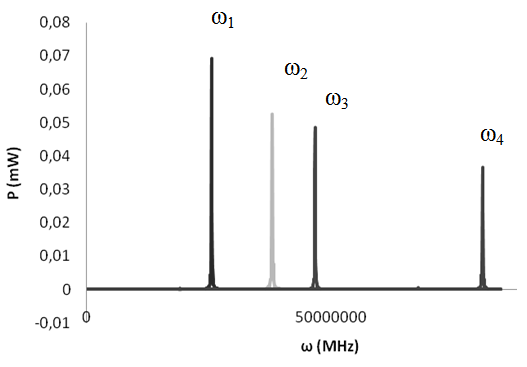 | Figure 7(b). The expected microwave outputs |
When temperature deviation of both laser is made higher, it makes wavelength deviation from both laser increased, then results in higher microwave beat frequency output. However, in the other hand, the increasing one of laser temperature affecting to decrease the laser power output. This results in lowering microwave output power. This condition is shown clearly in Figure 7(b), where the higher microwave frequency corresponds to lower output power.Our last experiment shows the results of controlling temperature deviation from both lasers in microwave generation by mixing optical-waves configuration. Reference laser is set at 40.5°C and power 0.05 mW and the second laser at the beginning is set at equal power and temperature. By varying the second laser temperature deviation in the range from 0 to 2.3°C, it results in microwave output frequency range from 0 to 23.8 GHz, as shown in Figure 8. It means microwave frequency can be tuned at 10.35 GHz/°C laser temperature deviation.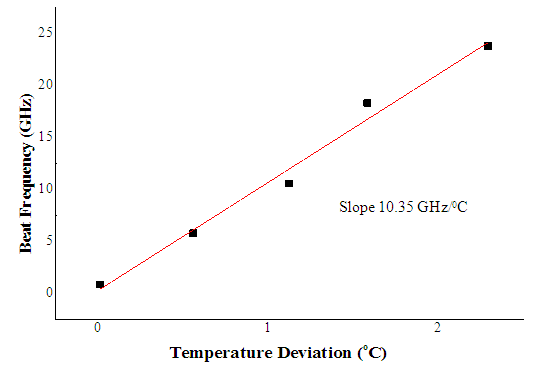 | Figure 8. The output beat frequency versus temperature deviation (at starting temperature of 40.5°C and output power 0.05mW) |
Figure 8 and Figure 9 show that the generated microwave can be influenced by both temperatures due to Peltier control and injection current (Iinj), respectively. In this paper we develop that we can control the generated microwave frequency by controlling: Peltier temperature, laser injection current or both together.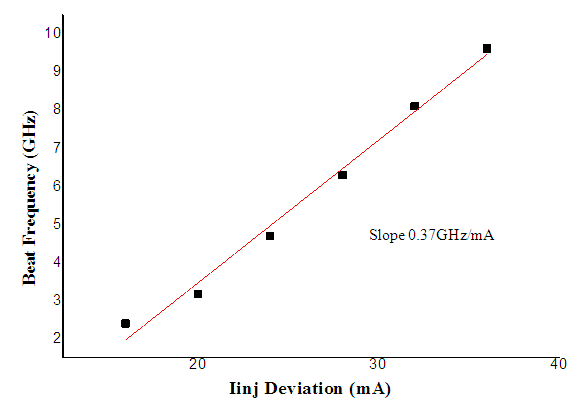 | Figure 9. The output beat frequency versus laser injection current (Iinj) deviation (at starting temperature of 40.5°C and injection current 20 mA) |
In this experiment, by varying peltier temperature, we obtain the tunability factor of 10.35 GHz/°C. Moreover, we obtain a more detail tunability factor as we control the laser wavelength by the varying laser injection current, which reaches 0.374 GHz/mA. This result shows us that temperature control is a fundamental factor for microwave frequency tunability where we can obtain 25 GHz by varying the temperature 2.5°C. In other case, the injection current control is more sensitive and adjustable for microwave frequency generation, eventough it can be only adjusted into a maximum injection current of 40-mA. The stability from two ways tunability can see in Figure 10 below.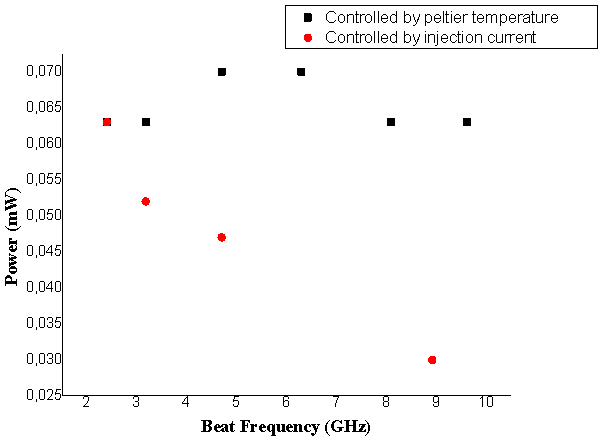 | Figure 10. Power stability of microwave frequency tuned by temperature deviation 0-9°C and injection current deviation 0-10 mA |
Varying the laser wavelength by adjusting the laser injection current will produce more stable microwave output power frequency than if the laser temperature is varied by peltier control. Both of the phenomena compensate each other in controlling generated microwave frequency more output power stable.
4. Conclusions
From the experiment, we are able to conclude that for typical DFB laser, output wavelength shift due to increasing temperature is about 0.094 nm/°C shifted to the longer wavelength and it corresponds to grating period expansion of 0.014 nm/°C. However, the increasing laser temperature affects to decrease the laser power output by 0.033 mW/°C. This condition causes microwave generation technique based on mixing two optical waves will have lower power output in corresponds to the effort to increase microwave frequency as shown in Figure 7(b). Furthermore, by varying the second laser temperature deviation in the range from 0 to 2.3°C, it results in microwave output frequency range from 0 to 23.8 GHz, as shown in Figure 8. It means microwave frequency can be tuned at 10.35 GHz/°C laser temperature deviation and injection current of 0.37 GHz/mA. For thefuture application, we recommend to apply electronics control system to keep the microwave frequency and its power out stable.
References
| [1] | Bertolotti, Mario. The history of the laser. CRC press, 2004. |
| [2] | Dupuis, Russell D. "Special issue papers: An introduction to the development of the semiconductor laser." IEEE Journal of Quantum Electronics 23.6 (1987). |
| [3] | Matsumura, Atsushi, and Takashi Kato. "Development of DFB lasers for CWDM applications." SEI Technical Review-English Edition- 63 (2006): 3. |
| [4] | Henderson, Sammy W., et al. "Coherent laser radar at 2 μm using solid-state lasers." Geoscience and Remote Sensing, IEEE Transactions on 31.1 (1993): 4-15. |
| [5] | Johnstone, Walter, et al. "Tunable diode laser spectroscopy for industrial process applications: System characterization in conventional and new approaches." Sensors Journal, IEEE 8.7 (2008): 1079-1088. |
| [6] | Guan, Bai-Ou, et al. "Polarimetric heterodyning fiber grating laser sensors." Journal of Lightwave Technology 30.8 (2012): 1097-1112. |
| [7] | Kinross-Wright, John, and John Plato. "Klystron station for the advanced free electron laser." Power Modulator Symposium, 1994., Twenty-First International. IEEE, 1994. |
| [8] | Evans, E. D. "Radar systems and technologies for Navy air and missile defense." Radar Conference, 2000. The Record of the IEEE 2000 International. IEEE, 2000. |
| [9] | Wake, David, Claudio R. Lima, and Phillip A. Davies. "Optical generation of millimeter-wave signals for fiber-radio systems using a dual-mode DFB semiconductor laser." Microwave Theory and Techniques, IEEE Transactions on 43.9 (1995): 2270-2276. |
| [10] | Ghafouri-Shiraz, H. Distributed feedback laser diodes and optical tunable filters. John Wiley & Sons, 2004. |
| [11] | Singh, Jasprit. Optoelectronics: An introduction to materials and devices. McGraw-Hill College, 1996. |
| [12] | Rosencher, Emmanuel, and Borge Vinter. Optoelectronics. Cambridge University Press, 2002. |
| [13] | Farsad, E., et al. "Experimental parametric investigation of temperature effects on 60W-QCW diode laser." World Acad. Sci. Eng. Technol 59 (2011): 1190-1196. |
| [14] | Gerd Keiser’s. Optical Fiber Communications. 4ed., Copyright © The McGraw-Hill Companies, Inc. |
| [15] | Blouin, Leonard T., Frank I. Marcus, and Louis Lampe. "Assessment of effects of a radiofrequency energy field and thermistor location in an electrode catheter on the accuracy of temperature measurement." Pacing and Clinical Electrophysiology 14.5 (1991): 807-813. |
| [16] | Bennett, Brian R., Richard A. Soref, and Jesus A. del Alamo. "Carrier-induced change in refractive index of InP, GaAs and InGaAsP." Quantum Electronics, IEEE Journal of 26.1 (1990): 113-122. |
| [17] | Hayashi, Tsuyoshi, Kenji Sato, and Satoshi Sekine. "Thermal interaction in a distributed-feedback laser diode (DFB LD) array module." Lightwave Technology, Journal of 11.3 (1993): 442-447. |
| [18] | Kitamura, M., et al. "Low-threshold and high temperature single-longitudinal-mode operation of 1.55 μm-band DFB-DC-PBH LDs." Electronics Letters 20.14 (1984): 595-596. |
| [19] | Hirose, Akira, and Karl Erik Lonngren. Introduction to wave phenomena. Wiley-Interscience, 1985. |
| [20] | Jianping Yao, Microwave Photonics : Photonis Generation of Microwave and Millimeter-Wave Signals, IJMOT Vol. 5 No.1, January 2010, 16-21. |


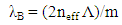
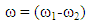



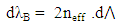
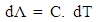
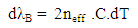
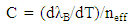







 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML