| [1] | K. J. Blow, D. Wood, “Stability and compression of pulses in soliton laser,” IEEE J. Quantum Electron. QE-22 (1986) 1109-1116. |
| [2] | U. Osterberg and W. Margulis: XIV int. quant. electr. conf. IQEC ’86, Tech. Digest., San Francisco, 1986, p. 102. |
| [3] | R. H. Stolen “Non-linear properties of fibres, in S. E. Miller and A. G. Chynoweth (Eds.) ‘Optical fibre communications’ (Academic Press, 1979). |
| [4] | R. Y. Chiao, E. Garmire and C. H. Townes, “Self-trapping of optical beams”, Phys. Rev. Lett. 13 (1964) 479-482, Erratum, ibid, 14 (1965) 1056. |
| [5] | P. L. Kelly, “Self-focusing of optical beams”, Phys. Rev. Lett 15 (1965) 1005-1008. |
| [6] | P. L. Baldeck, F. Raccah and R. Alfanro, “Observation of self-focusing in optical fibres with picosecond pulses” Optics. Lett. 12 (1987) 588-589. |
| [7] | S. W. Allison, G. T. Gillies, D. W. Magnuson, and T. S. Pagano, “Pulsed laser damage to optical fibers,” Appl. Opt. 24 (1985) 3140-3145. |
| [8] | R. Kashyap and K. J. Blow, “Observation of catastrophic self-propelled self-focusing in optical fibres,” Electron. Lett. 24 (1988) 47-49. |
| [9] | 1. D. P. Hand and P. St. J. Russell, “Solitary thermal shock waves and optical damage in optical fibers: the fiber fuse,” Opt. Lett. 13 (1988) 767-769. |
| [10] | T. J. Driscoll, J. M. Calo, and N. M. Lawandy, “Explaining the optical fuse,” Opt. Lett. 16 (1991) 1046-1048. |
| [11] | D. D. Davis, S. C. Mettler, and D. G. DiGiovanni, “A comparative evaluation of fiber fuse models,” Proc. SPIE Laser-Induced Damage Opt. Mater. 2966 (1997) 592–606. |
| [12] | R. M. Percival, E. S. R. Sikora, and R. Wyatt, “Catastrophic damage and accelerated ageing in bent fibres caused by high optical powers,” Electron. Lett. 36 (2000) 414-416. |
| [13] | 6. R. M. Atkins, P. G. Simpkins, and A. D. Yablon, “Track of a fiber fuse: a Rayleigh instability in optical waveguides,” Opt. Lett. 28 (2003) 974-976. |
| [14] | R. Kashyp and I. Blowk, “Spectacular demonstration of catastrophic failure in long lengths of optical fiber via selfpropelled self-focusing” 8th National Quantum Electronics Conference, Session PD7, Univ. of St Andrews, 21-25 Sept. 1987. |
| [15] | B. V. Hunter, K. H. Leong, C. B. Miller, J. F. Golden, R. D. Glesias, and P. J. Laverty, “Understanding high-power fiber-optic laser beam delivery,” J. Laser Appl. 8 (1996) 307-316. |
| [16] | X. Sun, J. Li, A. Hokansson, “Study of optical fiber damage under tight bend with high optical power at 2140 nm,” Conference Proceedings of SPIE vol. 6433 (2007). |
| [17] | L. Prigent, J. -P. Hamaide, “Measurement of fiber nonlinear Kerr coefficient by four-wave mixing,” IEEE Photon. Technol. Lett. 5 (1993) 1092–1095. |
| [18] | A. Boskovic, S. V. Chernikov, J. R. Taylor, L. Gruner-Nielsen, O. A. Levring, “Direct continuous-wave measurement of n2 in various types of telecommunication fiber at 1.55 µm,” Opt. Lett. 21 (1996) 1966–1968. |
| [19] | K. Nakajima, T. Omae, M. Ohashi, “Conditions for measuring nonlinear refractive index n2 of various singlemode fibres using CW SPM method,” IEEE Proc. Optoelectron. 148 (2001) 209–214. |
| [20] | J.-C. Antona, S. Bigo, S. Kosmalski, “Nonlinear index measurements of various fibre types over C + L bands using four-wave mixing,” in: Proc. of 27th European Conference on Optical Communications, Amsterdam, The Netherlands, 2001, pp. 270–271. |
| [21] | Y. Namihira, K. Miyagi, K. Kaneshima, M. Tadakuma, C. Vinegoni, G. Pietra, K. Kawanami, “A comparison of six techniques for nonlinear coefficient measurements of various single mode optical fibers,” in: Technical Digest of the 12th Symposium on Optical Fiber Measurement, Boulder, CO, USA, 2002. |
| [22] | A. Lamminpää, T. Niemi, E. Ikonen, P. Marttila, H. Ludvigsen, “Effects of dispersion on nonlinearity measurement of optical fibers,” Opt. Fiber Technol. 11 (2005) 278–285. |
| [23] | J. Fatome, S. Pitois, G. Millot, “Measurement of nonlinear and chromatic dispersion parameters of optical fibers using modulation instability,” Opt. Fiber Technol. 12 (2006) 243–250. |
| [24] | D. Milam, and M. J. Weber, “Measurement of nonlinear refractive index coefficients using time resolved interferometry: Application to optical materials for high power neodymium lasers,” J. Appl. Phys. 47 (1976) 2499-2501. |
| [25] | R. C. Miller, “Optical second harmonic generation in piezoelectric crystals,” Appl. Phys. Lett. 5 (1964) 17–19. |
| [26] | E. M. Vogel, M. J. Weber, and D. M. Krol, "Nonlinear optical phenomena in glass," Phys. Chem. Glasses 32 (1991) 231-254. |
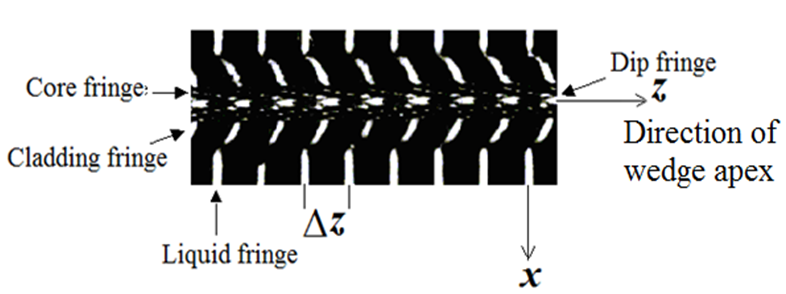
| [27] | H. A. El-Hennawi, F. El-Diasty, H. El-Ghandoor, and M. A. Soliman, “Multiple-beam interference fringes applied to investigate the index profile of the optical fiber dip,” Opt. Quant. Electron. 43 (2012) 35–48. |
| [28] | F. El-Diasty, “Characterization of optical fibers by two- and multiple-beam interferometry,” Opt. Laser Eng. 46 (2008) 291-305. |
| [29] | N. Barakat, H. A. El-Hennawi, and F. El-Diasty, "Multiple-beam interference fringes applied to GRIN optical waveguides to examine fiber formation." Appl. Opt. 27 (1988) 5090-5094. |
| [30] | I. P. Kaminow, H. M. Presby, J. B. MacChesney, P. B. O’Connor, “Ternary fiber glass composition for minimum modal dispersion over a range of wavelength,” Technical Digest Optical Fiber Transmission II, Opt. Soc. Am. PD5-1 (1977). |
| [31] | T. Kato, Y. Suetsugu, M. Nishimura, “Estimation of nonlinear refractive index in various silica-based glasses for optical fibers,” Opt. Lett. 20 (1995) 2279-2281. |
| [32] | F. A. Abdel Wahab, F. El-Diasty, M. Abdel-Baki, “Dispersion dependence of second-order refractive index and complex third-order optical susceptibility in oxide glasses,” Phys. Lett. A 373 (2009) 3355-3360. |

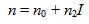
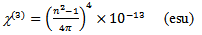
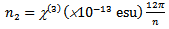
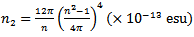
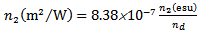
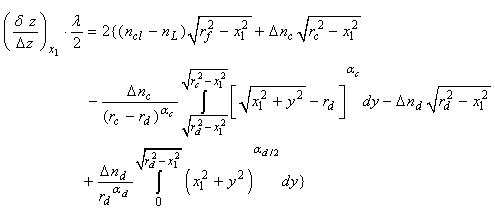
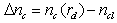 and αc is a shaping parameter controlling the shape of the core index profile. Also,
and αc is a shaping parameter controlling the shape of the core index profile. Also, 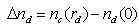 and αd is a parameter controlling the shape of the dip index profile.
and αd is a parameter controlling the shape of the dip index profile. 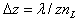 is the fringe spacing in the liquid region and δz is the fringe shift in the fiber region, where λ is the wavelength.
is the fringe spacing in the liquid region and δz is the fringe shift in the fiber region, where λ is the wavelength.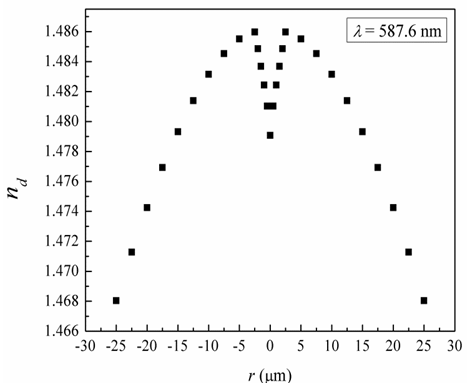
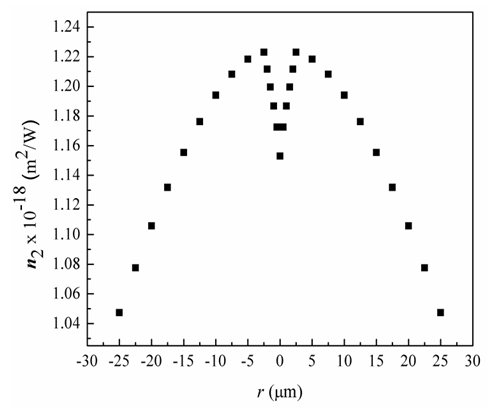
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML