-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Optoelectronic Engineering
2012; 2(4): 18-25
doi: 10.5923/j.ijoe.20120204.01
Spectral Efficient Coding Schemes in Optical Communications
T. H. Lotz , W. Sauer-Greff , R. Urbansky
University of Kaiserslautern, Department of Electrical and Computer Engineering, Kaiserslautern, 67663, Germany
Correspondence to: T. H. Lotz , University of Kaiserslautern, Department of Electrical and Computer Engineering, Kaiserslautern, 67663, Germany.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Achieving high spectral efficiency in optical transmissions has recently attracted much attention, aiming to satisfy the ever increasing demand for high data rates in optical fiber communications. Therefore, strong Forward Error Correction (FEC) coding in combination with multilevel modulation schemes is mandatory to approach the channel capacity of the transmission link. In this paper we give design rules on the joint optimization of coding and signal constellations under practical considerations. We give trade-offs between spectral efficiency and hardware complexity, by comparing coding schemes using capacity achieving constellations with bit-interleaved coded modulation and iterative decoding (BICM-ID) against applying conventional square quadrature amplitude modulation (QAM) constellations but employing powerful low complexity low-density parity-check (LDPC) codes. Both schemes are suitable for optical single carrier (SC) and optical orthogonal frequency-division multiplexing (OFDM) transmission systems, where we consider the latter one in this paper, due to well-studied equalization techniques in wireless communications. We numerically study the performance of different coded modulation formats in optical OFDM transmission, showing that for a fiber optical transmission link of 960 km reach the net spectral efficiency can be increased by ≈0.4 bit/s/Hz to 8.61 bit/s/Hz at a post FEC BER of <10-15 by using coded optimized constellations instead of coded 64-QAM.In this paper we propose a high spectral efficient coded modulation scheme for implementation in future optical communication systems operating at data rates beyond 400 Gb/s. In detail, we adapt the “Turbo Principle” to BICM-ID[8] and combine it with a high-rate outer algebraic code to obtain a post-FEC BER <10-15, which is a typical demand in optical transponders. Furthermore we give simple design principles for the design of BICM-ID based on the extrinsic information transfer (EXIT) chart analysis[9]. The optical channel is considered to be weakly-nonlinear. Therefore the proposed techniques are also applicable for single-carrier transmission; however we consider OFDM since it appears to be more appropriate for the high order modulation formats and efficient equalization algorithms that are well established in wireless communications.
Keywords: Coherent Communications, Optical OFDM, Bit-Interleaved Coded Modulation and Iterative BICM-ID, Spectral Efficiency, Capacity Approaching Constellations (IPM)
Article Outline
1. Introduction
- Over the last decade there has been an exponential growth of bandwidth-intensive services such as video on demand, cloud storage and social networking which require large volumes of data to be transmitted over long distances. Based on current trends, this growth is likewise to continue, driving the need to increase transmission capacity. Ongoing commercial developments with data rates of 100 Gbit/s in the standardized 50 GHz wavelength-division multiplexing (WDM) grid consider polarization division multiplexed quadrature phase shift keying (PDM-QPSK) as the most suitable modulation format[1]. This allows a per polarization spectral efficiency of up to 2.0 bit/s/Hz. Next generation systems will need to supply data rates beyond 400 Gbit/s. Therefore it is necessary to exploit the channel capacity of the fiber up to its theoretical limit. The most effective method to increase the spectral efficiency of any communication system is to employ larger modulation formats[2]. However, in order to approach channel capacity the constellation itself needs to be modified with respect to information theory. In[3] the design principles of capacity achieving circular constellations, based on iterative polar quantization (IPQ), are proposed. For higher modulation formats the robustness to noise is degraded, claiming the need for powerful FEC coding schemes, relying on the “Turbo Principle”[4]. The combination of iterative polar modulation (IPM) and LPDC codes have already been a matter of investigation in[5], using multilevel coding (MLC) and iterative multistage decoding[6], but omitting complexity considerations, investigations on the available channel capacity and error floor evaluations. To cope with the non-linear channel effects and dispersion, we consider OFDM in combination with multiple-input multiple output polarization multiplexed equalization to be most appropriate, as it offers high spectral efficiency and needs only simple computation operations for equalization[7]. The remainder of the paper is organized as follows: In Section 2 the design principles of capacity achieving constellations are derived. In Section 3, the investigated optical OFDM system is introduced and the available channel capacity for different modulation formats is estimated. The basic coded modulation scheme, namely BICM-ID, is reviewed in Section 4. Design principles for BICM-ID with IPQ signal constellations, using recursive systematic convolutional (RSC) codes and square signal constellations, using LDPC codes, are given in Sections 5 and 6. We conclude our paper in Section 7.
2. Design of Capacity Approaching Constellations by Means of Iterative Polar Quantization
- In order to exploit the available channel capacity up to its theoretical limit the signal distribution needs to comply with the channel characteristics. In additive white Gaussian noise (AWGN) channels, such as thermal and amplified spontaneous emission (ASE) noise dominated channels, a Gaussian source provides the maximum shaping gain value.A Gaussian distribution at the channel input can be realized by different strategies. One considers shaping, first proposed in[10] by Gallager, where it is shown that optimal coding for the Gaussian channel is utilized by grouping bits from a binary code, where the larger group is assigned to the less probable points in the constellation, and the smaller to the more frequent[11]. In this concept the basis constellation A is square; shaping is performed by additional shaping encoders and decoders. A hardware complexity considering design of this approach is proposed in[11], but is hardly feasible for high data rates.Therefore we consider a different strategy to provide a Gaussian source, by applying non-uniform signal constellations, which comply with the channel characteristics. Design principles of capacity achieving constellations are proposed in[3]. In order to provide Gaussian signaling at the input of the system, we optimize the signal constellation A by minimizing the quantization mean square error (QMSE) of a Gaussian information source by means of IPQ. The constellation points of the obtained constellation are distributed over the circles of radii determined by a Rayleigh distribution[3]. The idea of using a Rayleigh distribution p(r) originates from the fact that the envelope r of a two-dimensional Gaussian distribution is Rayleigh distributed. Let Nr denote the number of circles in the constellation and Lj denote the number of constellation points per circle of radius mj; j ∈ {1,2,...,Nr}. Then the optimum number of constellation points at the jth circle for a 2M-ary signal set is determined by minimizing the QMSE
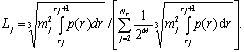 | (1) |
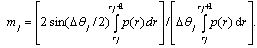 | (2) |
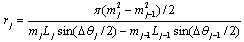 | (3) |
| ||||||||||||||||||||||||||||||||||||||
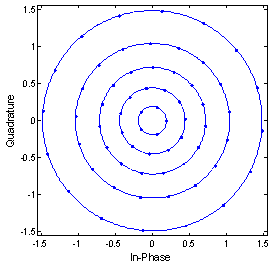 | Figure 1. The 64-IPM signal constellation |
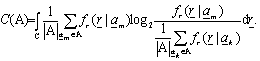 | (4) |
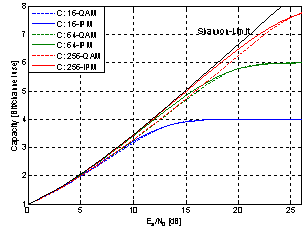 | Figure 2. Channel capacities for different IPM and square QAM modulations |
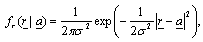 | (5) |
3. The Optical OFDM System and Channel Capacity Estimation
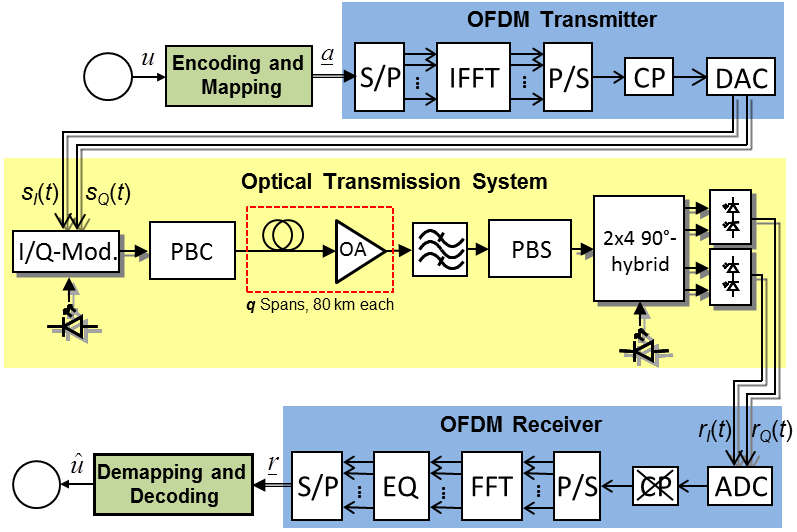 | Figure 3. The optical OFDM communication system |
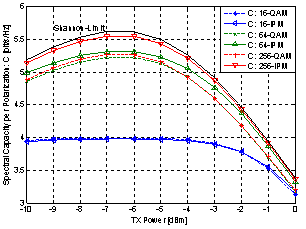 | Figure 4. Capacities of different modulation formats after 960 km SSMF transmission |
4. Advanced Spectral Efficient Coding in Optical Communications
- In classical non-coherent optical communication systems, operating at data rates up to 10 Gb/s, no powerful FEC coding is required, since in the systems a pre-FEC BER of <10-4 is obtained and a post-FEC BER of only <10-12 is demanded. Hence the algebraic Reed-Solomon (RS) (255, 239) code, supplying a net coding gain (NCG) of 5.62 dB at a pre-FEC BER of 1.8∙10-4 for a post-FEC BER 10-12 is the most used code in these systems[14].But when higher data rates are claimed, more powerful coding schemes need to be considered. In today’s systems with 40 Gbit/s differential phase-shift keying, enhanced FEC (EFEC) coding, as recommend by the ITU in[15], is utilized by the concatenation of the Bose-Chaudhuri- Hocguenghem (BCH) (3860, 3824) code and the BCH (2040, 1930) code, using iterative decoding. The BCH (3860, 3824) + BCH (2040, 1930) concatenated code has a code overhead of 6.69 %. After three iterations this code achieves a NCG of 8.99 dB at a pre-FEC BER of 3.15∙10-3 and a post-FEC BER of 10-15. If iterative decoding is to be avoided the ITU recommends the RS (2720, 2550) code with a NCG of 8 dB at a pre-FEC BER of 1.1∙10-3[15]. All of these codes are binary linear cyclic codes, with decoders processing hard decision values of the received output bit stream. So these schemes are most suitable for low BER, but when coherent modulation formats beyond QPSK are employed and approaching the Shannon limit is desired, soft decision decoding is inevitable.A straightforward approach to combine multilevel signaling and coding is BICM-ID, which can be considered the simplest approach to achieve high spectral efficiency while providing a low decoder complexity[2]. However, coding schemes relying on the Turbo Principle may run into an error floor, which is several decades higher than the desired post-FEC BER of 10-15. Therefore, we apply BICM-ID for inner coding and concatenate it with a high-rate outer code to remove residual errors. The proposed coding scheme is depicted in Figure 5.
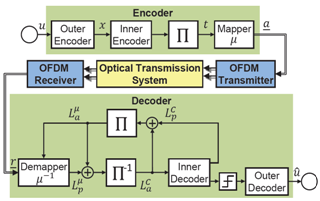 | Figure 5. Proposed concatenated iterative soft-demapping and decoding scheme |
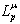 . In the first iteration these a posteriori LLR values
. In the first iteration these a posteriori LLR values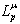 are deinterleaved and soft-in/soft-out decoded in a symbol-by-symbol a posteriori probability (APP) estimator; a BCJR[16] or LDPC decoder[10] depending on the used encoder. The output of the decoder delivers the APP LLR
are deinterleaved and soft-in/soft-out decoded in a symbol-by-symbol a posteriori probability (APP) estimator; a BCJR[16] or LDPC decoder[10] depending on the used encoder. The output of the decoder delivers the APP LLR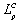 . For iterative decoding it is necessary to exchange extrinsic information between the soft-demapper and the decoder only. So the soft-input LLR values of the coded bits for the soft-demapper consist of interleaved a posteriori LLR of the decoder without the a-priori information,
. For iterative decoding it is necessary to exchange extrinsic information between the soft-demapper and the decoder only. So the soft-input LLR values of the coded bits for the soft-demapper consist of interleaved a posteriori LLR of the decoder without the a-priori information, 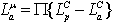 . Respectively, the a-priori LLR for the BCJR decoder are computed as the deinterleaved extrinsic LLR of the soft-demapper,
. Respectively, the a-priori LLR for the BCJR decoder are computed as the deinterleaved extrinsic LLR of the soft-demapper, 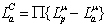 .The decoder performs bitwise soft-input processing, thus the demapper extracts a soft value for each coded bit t0,1,..,M-1 of a 2M-ary complex channel symbol r .When a-priori information is available, the soft-demapper calculates the APP LLR
.The decoder performs bitwise soft-input processing, thus the demapper extracts a soft value for each coded bit t0,1,..,M-1 of a 2M-ary complex channel symbol r .When a-priori information is available, the soft-demapper calculates the APP LLR 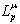 of bit k computes to[9]
of bit k computes to[9]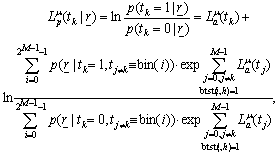 | (6) |
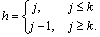 | (7) |
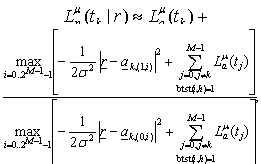 | (8) |
5. Design of BICM-ID for IPM
- In this section we discuss the design of BICM-ID, using a 64-IPM signal constellation and RSC codes. We restricted the use of LDPC codes and utilized RSC codes, since they offer a greater degree of freedom in design for coded modulation, when the code rate is high. As denoted above, residual errors are removed by an outer RS (2720, 2550) code. In order to design the BICM-ID scheme towards proper convergence and to acquire a post-FEC BER below the threshold BER of the outer RS code of 1.1∙10-3, we use the EXIT chart analysis, which is a powerful tool to visualize the flow of extrinsic information between the soft-demapper and decoder[9]. In the EXIT chart analysis, the mutual information (MI) of the decoder/demapper is plotted versus its a-priori input, i.e. the MI of the demapper/decoder. If an optimum demapper/decoder is used, the knowledge of the MI contained in the a-priori information is sufficient to derive the MI of the decoder/demapper. Denoting the encoder/demapper input by Xa and the corresponding extrinsic decoder/demapper output by Xe, the MI I(Xe;Xa) calculates to
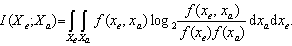 | (9) |
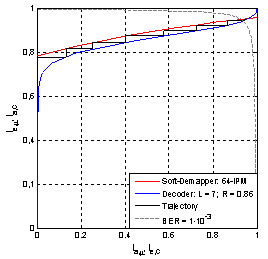 | Figure 6. EXIT chart for the designed 64-IPM signal constellation and RSC code at a fiber per-channel launch power of -7 dBm after 960 km SSMF transmission |
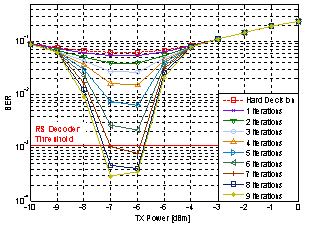 | Figure 7. BER vs. per-channel input power at the decoder output of the designed coded 64-IPM scheme after 960 km SSMF transmission |
6. Coded Modulation with LDPC Codes
- For optical transponders processing at data rates beyond 400 Gbit/s, another potential candidate for strong soft-decision-based FEC in BICM-ID are LDPC codes, which are linear codes defined by the sparse parity-check matrix invented by Gallager[10]. They allow for an iterative decoding procedure, denoted as belief propagation or sum-product algorithm, where extrinsic information is exchanged between variable nodes, corresponding to information and redundancy bits, and check nodes, representing the parity check equations. The edges between them are given by the parity-check matrix. An LDPC codes is specified by two degree distributions λ(x) and ρ(x), where
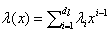 and
and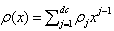 . λi is the fraction of edges that belong to degree-i variable nodes, ρj is the fraction of edges that belong to degree-j check nodes, dl is the maximum variable node degree, and dc is the maximum check node degree. LDPC codes are expected to exhibit superior error-correcting performance close to the Shannon limit, which implies a flat LDPC decoder EXIT function in the EXIT chart analysis.
. λi is the fraction of edges that belong to degree-i variable nodes, ρj is the fraction of edges that belong to degree-j check nodes, dl is the maximum variable node degree, and dc is the maximum check node degree. LDPC codes are expected to exhibit superior error-correcting performance close to the Shannon limit, which implies a flat LDPC decoder EXIT function in the EXIT chart analysis.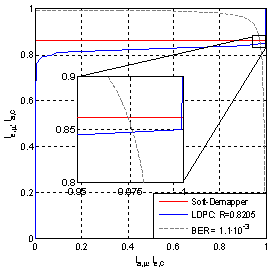 | Figure 8. EXIT chart for the designed 64-QAM signal constellation and LDPC code at a fiber per-channel launch power of -7 dBm after 960 km SSMF transmission |
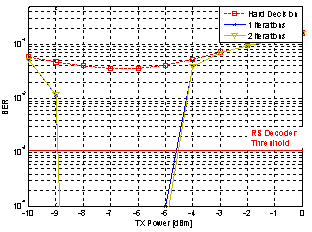 | Figure 9. BER vs. per-channel input power at the decoder output of the designed coded 64-QAM scheme after 960 km SSMF transmission |
7. Conclusions
- In this paper we presented a simple, but spectral highly efficient coding scheme for optical OFDM-based communications, relying on the concatenation of BICM-ID with a high-rate outer code to obtain a post-FEC BER < 10-15. Further, we provided design principles of capacity approaching constellations and showed how to jointly optimize mapping and coding for a proper convergence of the iteration loop.We demonstrate that non-uniform constellations based on IPQ outperform conventional square signal constellations. In order to compare the performance of IPM versus QAM towards BER performance we developed different coding schemes, showing that in both cases an overall post-FEC BER < 10-15 is achievable, but, when using coded 64-IPM a spectral efficiency of 8.64 bit/s/Hz in both states of polarization after 960 km SSMF transmission could be obtained, which is ≈0.4 bit/s/Hz greater compared to coded 64-QAM.However for a practical implementation we suggest coded modulation schemes, based on QAM constellations and LDPC codes, to be more appropriate, since they are implementable more efficiently in hardware to operate at high data rates. Disregarding the loss in spectral efficiency due to OFDM pilots duration and guard interval, this coding scheme is able to approach the Shannon limit by 1.85 bit/s/Hz in both states of polarization.
ACKNOWLEDGEMENTS
- This work was supported by the German Research Foundation (DFG) under grant UR 75/3-1.
References
| [1] | R. Nagarajan, D. Lambert, M. Kato, V. Lal, G. Goldfarb, J. Rahn, et. al.‚ "10 Channel, 100Gbit/s per Channel, Dual Polarization, Coherent QPSK, Monolithic InP Receiver Photonic Integrated Circuit", in Proc. OFC/NFOEC, OML7, San Diego, CA, USA, 2011. |
| [2] | T. Lotz, W. Sauer-Greff and R. Urbansky, "Capacity Approaching Coded Modulation in Optical Communications," Proc. 13th International Conference on Transparent Optical Networks (ICTON), Stockholm, Sweden 2011. |
| [3] | Z. H. Peric, I. B. Djordjevic, S. M. Bogosavljevic and M. C. Stefanovic, "Design of Signal Constellations for Gaussian Channel by Iterative Polar Quantization," in Proc. 9th Mediterranean Electrotechnical Conference 2, pp. 866-869, 18-20 May 1998; Tel-Aviv, Israel. |
| [4] | C. Berrou, A. Glavieux, and P. Thitimajshima, "Near Shannon limit error correcting coding and decoding: Turbo-Codes," Proc. IEEE ICC, pp. 1064–1070, 1993. |
| [5] | I. B. Djordjevic, H. G. Batshon, L. Xu and T. Wang, "Coded Polarization-Multiplexed Iterative Polar Modulation (PM-IPM) for Beyond 400 Gb/s Serial Optical Transmission," in Proc. OFC/NFOEC, OMK2, San Diego, CA, USA, 2010. |
| [6] | I. B. Djordjevic, M. Arabaci, and L. Minkov, "Next Generation FEC for High-Capacity Communication in Optical Transport Networks," J. Lightw. Technol. 27, 3518-3530 (2009). |
| [7] | X. Liu, S. Chandrasekhar, Z. Benyuan, P. J. Winzer, A. H. Gnauck, D.W. Peckham, "448-Gb/s Reduced-Guard-Interval CO-OFDM Transmission Over 2000 km of Ultra-Large-Area Fiber and Five 80-GHz-Grid ROADMs," Journal of Lightwave Technology, 2011 |
| [8] | S. ten Brink, J. Speidel and R.-H. Yan, "Iterative Demapping and Decoding for Multilevel Modulation," Proc. IEEE GLOBECOM, 1998. |
| [9] | S. ten Brink, "Convergence Behavior of Iteratively Decoded Parallel Concatenated Codes," IEEE Trans. Commun., vol. 49, 2001. |
| [10] | R. G. Gallager, Information Theory and Reliable Communication, New York: Wiley, 1968. |
| [11] | D. Raphaeli and A. Gurevitz, "Constellation Shaping for Pragmatic Turbo-Coded Modulation with High Spectral Efficiency," IEEE Trans. Commun., vol. 52, p. 341345, 2004. |
| [12] | H. G. Batshon, I. B. Djordjevic, L. Xu and T. Wang, "Iterative Polar Quantization-Based Modulation to Achieve Channel Capacity in Ultrahigh-Speed Optical Communication Systems," IEEE Photonics Journal, vol. 2, 2010. |
| [13] | M. Mayrock and H. Haunstein, "Spectral Efficiency Limitation by Fiber Non-linearity in Optical OFDM Transmission Systems, " in Proceedings of 14th International OFDM Workshop, Hamburg, Germany, September 2009. |
| [14] | M. Mayrock, "Analysis and Compensation of Non-linear Signal Distortion in Optical OFDM," 15th International OFDM-Workshop, pp. 56–60, 2010. |
| [15] | International Telecommunication Union, "Interfaces for the Optical Transport Network," Telecommunication Standardization Sector, G.709, 2003. |
| [16] | International Telecommunication Union, "Forward error correction for high bit-rate DWDM submarine systems," Telecommunication Standardization Sector, G.975.1, 2004. |
| [17] | L. Bahl, J. Cocke, F Jelinek and J. Raviv, "Optimal Decoding of Linear Codes for Minimizing Symbol Error Rate, " IEEE Trans. Inf. Theory, vol. 20, 1974. |
| [18] | S.-Y. Chung, R.J. Richardson, and R.L. Urbanke, "Analysis of sum-product decoding of low-density parity-check codes using a Gaussian approximation," IEEE Trans. Inf. Theory, vol. 47, 2001. |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML