1. Introduction

The development of free electron lasers allowed the achievement of laser generation with wavelengths between 3 and 20 μm. Clinical tests showed that laser generation with a wavelength of 6.45 μm is the most applicable in the medical practice for the treatment of bone and soft tissue and provides the best subsequent recovery. This wavelength is widely applicable in biology. Free electron lasers, due to their price and design, cannot be mass produced and are not commercially attractive. This raises the question of the development of other laser generation sources at this wavelength, as alternatives to free electron lasers. One of the possible solutions is the development of strontium vapour lasers (atom and ion transfers) with generation at several wavelengths in the infrared spectrum - 2.06, 2.20, 2.69, 2.92, 3.01, 3.07, and 6.45 μm. Due to its acceptable price, compact size, and easy operation, the strontium laser successfully competes with free electron lasers, generating at the same wavelength. For this reason, the design and development of the strontium laser continues to be of interest[1,8]. The strontium atom actively affects the laser tube -quartz or ceramic - causing its destruction. The typical service periodis several tens of hours. These difficulties posed by pure strontium limit the subsequent development of this type of laser. The laser based on strontium bromide (SrBr₂), which replaces metal strontium, is an alternative to strontium atom and ion lasers. It solves the problem with the chemical destruction of the laser tube caused by metal strontium. In [4] for the first time a laser based on SrBr₂ excited by a nanosecond pulsed longitudinal discharge was reported. In [5, 6] a significantly improved version of this device with laser output power of 2.4 W was presented, and in[7, 8] the laser output power reaches 4.27 W, with 90% of the generation at the 6.45 μm line. The obtained results are comparable with those of a metal strontium laser. Research in this field focuses on the development of SrBr₂ based laser sources with higher output power. This would widen the range of their applications. When working towards extending the service life and improving the reliability of the devices, the analysis of the physical processes occurring in the active laser volume and determining the degree of influence of all independent parameters on the output characteristics of the laser device (output laser power, laser efficiency, service life of the laser tube, laser generation deterioration within the course of service, etc.) are of crucial importance.

The development of purely experimental research has long had limitations. These are related to the huge volume and the ever higher costs of experimental labour. The advances in modelling and automation of engineering research are ever more necessary in order to increase the efficiency of the process of designing new laser sources. The so called structural or micro modelling is the most commonly used in the field of gas lasers and metal compound vapour lasers. The physical object is assigned some internal structure or pattern. The macro behaviour of the object is a consequence of the collective micro behaviour of all these particles. Differential equations, systems of differential equations or other relationship formulas which reflect the physical laws and processes, occurring in the active laser volume, are used to describe the physical system mathematically. The so-called phenomenological or macro modelling is an alternative to this type of research. In this case the composition and the processes within the actual physical system are not examined. Based only on experimental data and using statistical techniques, it is possible to analyse the condition and predict the behaviour of the object under investigation. Similar statistical techniques are widely used in economics, sociology, political science, marketing, management, etc. In the field of gas lasers and metal vapour laser they are still not widely utilized. For the first time, these techniques were used for a metal bromide vapour laser, generating in the visible and ultraviolet spectrum[9-14]. For strontium metal vapour lasers and the SrBr₂ vapour laser such investigations have not been carried out. In this article, on the base of known experimental data some statistical parametric techniques (factor and regression analysis) will be used for the first time for experiment laser design planning. Problems related to the performance of filtering and extremal experiment will be solved.

The objectives of this paper are: (i) to estimate the degree of influence of each input independent parameter on laser output power; (ii) to establish a parametric regression dependence between the output power and the input data; (iii) to estimate and predict the behaviour of the laser system by using the obtained models for existing and future experiments.

The statistical investigation has been conducted using the SPSS software package[15].

2. Problem Setup and Subject of Study

The subject of investigation is a strontium dibromide vapour laser which is an original Bulgarian design and is being developed at the Laboratory of Metal Vapour Lasers at the Institute of Solid State Physics of the Bulgarian Academy of Sciences, Sofia[5-8].

A conceptual schematic of the laser is given in Figure 1. The laser tube is made out entirely of quartz. A thermo- chemically resistant inner tube of Аl₂О₃ has been inserted into the active laser volume because of the high temperature (over 1000℃). Laser output power, denoted by Pout has been selected as a dependent output characteristic (response variable). We will investigate the relationship between laser output power Pout, W and 7 input independent variables: 1) Diameter D1, mm of the outer (quartz) tube (inner size); 2) Diameter D2, mm of the inner (ceramic) tube (inner size); 3) La, cm - distance between the two electrodes; 4) Cequi, pF - equivalent capacity of the condensation battery; 5) Pin2, KW - electric power supplied to the active volume taking into account 50% supply losses; 6) PRF, KHz - pulse repetition frequency of the electrical supply; 7) Pne, torr - pressure of the neon buffer gas.

The study is carried out for n=167 known experiment data for two type of SrBr₂ lasers[5-8].

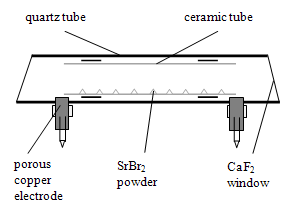Figure 1. Schematic diagram of the examined strontium bromide vapour laser

3. Factor Analysis

Factor analysis (FA) is a statistical technique intended for transforming sets of correlating variables into a new set of non-correlating artificial variables or factors, which describe as best as possible the general variation of the input data[16]. This technique also allows for a reduction in the number of initial variables by grouping those which correlate with each other into a common factor and the division of non- correlating ones into different factors. Mathematically this is achieved by reducing the dimensionality of the initial space through the set up of a new basis of artificial grouping variables (factors). Factors can be orthogonal or oblique.

The main goal of FA is to establish the number of factors k, which is significantly dependent on the strength of correlation between the predictor variables. In order to further differentiate the association of the predictors with one or another factor, an additional transformation of the factors is carried out using the so called factor rotation.

The first step in factor analysis is the calculation of the correlation matrix of the standardized input variables. For our data it is shown in Table 1.

This matrix shows the degree of correlation of each of the 7 variables with the response variable of the system Pout. In accordance with the factor analysis technique[16] when the absolute value of the correlation coefficient between two quantities is more than 0.5, it is considered that they are correlated. If this value is over 0.7 and more the correlation is strong, and between 0.3 and 0.5 the correlation is average. Under 0.3, the correlation is considered weak.

Table 1. Correlation matrix of all initial variables and the output power Pout Correlation D1_mm D2_mm La_cm Cequi_pF Pin2_KW PRF_KHz Pne_torr Pout_W D1_mm 1.000 -1.000 -1.000 -0.370 -0.875 0.373 -0.647 -0.965 D2_mm -1.000 1.000 1.000 0.370 0.875 -0.373 0.647 0.965 La_cm -1.000 1.000 1.000 0.370 0.875 -0.373 0.647 0.965 Cequi_pF -0.370 0.370 0.370 1.000 0.285 -0.282 0.381 0.243 Pin2_KW -0.875 0.875 0.875 0.285 1.000 -0.263 0.566 0.918 PRF_KHz 0.373 -0.373 -0.373 -0.282 -0.263 1.000 -0.074 -0.320 Pne_torr -0.647 0.647 0.647 0.381 0.566 -0.074 1.000 0.566 Pout_W -0.965 0.965 0.965 0.243 0.918 -0.320 0.566 1.000

The results shown in Table 1 lead to the conclusion that the quantities D1, D2, La, Pin2 and Pne correlate strong with the output power Pout. Two independent variables are weakly correlated with Pout. These are PRF and Cequi. Certain optimum value intervals have been determined for these based on the accumulated experiment experience. In future experiments it is sufficient to have the values of these two quantities within the established intervals as this would not influence significantly laser output power Pout.

In Table 1 it is also observed the availability of a mutual correlation between many of the input variables. Moreover, D1, D2 and La are collinear. To this reason a direct application of multivariate regression is not acceptable. To overcome the problem with multicollinearity, we carry out a factor analysis.

The second step is the grouping of the 7 physical variables into groups (factors). The variables in each group (factor) must be strongly correlated and between the quantities in different factors there must be a weak correlation (or lack thereof), i.e. factors need to be linearly independent from one another. In this study we used the method of principal component analysis (PCA) for obtaining 7 possible orthogonal factors (components), by determining its relative percentage in total variance of data. The values of its corresponding eigenvalues of the correlation matrix are given in Table 2, column Total.

Table 2. Total Variance Explained in Factor Analysis with All Predictors and Four Factors. Extraction Method: Principal Component Analysis Component Initial Eigenvalues Extraction Sums of Squared Loadings Extraction Sums of Squared Loadings Total % of Variance Cumulative % Total % of Variance Cumulative % 1 4.617 65.955 65.955 4.617 65.955 65.955 2 0.985 14.069 80.024 0.985 14.069 80.024 3 0.829 11.837 91.861 0.829 11.837 91.861 4 0.400 5.716 97.577 0.400 5.716 97.577 5 0.170 2.423 100.000 6 5E-15 7E-15 100.000 7 2E-15 3E-15 100.000

The third step in factor analysis is to choose a subset of factors from the extracted components that accounts relatively high in the total variance of data. The components with lower influence can be ignored. This way the dimensionality of the initial space of the input variables will be reduced. Factor analysis does not provide a formal technique which determines the number of factors explicitly. Usually, for technical data the number of factors must account for the predominant part of the experiment sample, say over 90-95%. The results in Table 2 show that three factors cumilate 91.86% of data and four factors cumulate 97.58% of the total sample. We take 4 factors for our analysis.

It must be noted, that the use of components with corresponding eigenvalues less than 1 is a well known statistical fact[17].

At the next step of factor analysis we carried out the rotation of factors by the varimax method. The loadings of input variables in the rotated matrix are shown in Table 3 (the loadings in varimax can be between -1 and 1). The loadings less than 0.5 are omitted as statistically unsignificant[14,18]. We obtain the following four factors:

(1)

From Table 3 it is seen that the four factors (1) are well separated. As they are generated by the method of Principal Component Analysis, they are also orthogonal each to other. The first 4 variables are grouped together and load very high on the first factor F1. This is explained by the physical processes occurring in the laser source. The loading of D1 is negative, so its reduction will result in an increase of Pout, while the increase of D1, La and Pin2 will increase Pout. In future experiments the quantities from the first factor need to be changed together (D1 in the opposite direction) since this way they can be treated as a single variable. The other factors F2, F3, and F4 contain single variables.

Table 3. Rotated Component Matrix with Four Factors. Extraction Method: Principal Component Analysis. Rotation Method: Varimax Variables Factors F1 F2 F3 F4 D1 -0.926 D2 0.926 La 0.926 Pin2 0.921 Pne 0.882 Cequi 0.965 PRF 0.970

The rotated factors (1) account for 52.5%, 15.2%, 15.1%, and 14.8% of total variance of data, respectively.

In this manner, from a total of 7 independent input variables we obtain 4 independent factor variables, which explain over 97.6% of data and undoubtedly allow the reduction of the amount of experiment planning for this type of lasers.

4. Principal Component Regression

Usually, multivariate regression analysis is used to construct models which give explicit relationship between several independent variables (predictors or regressors) 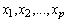and one (or more) dependent on these variables (response) 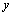. In this case, we are looking for a functional relationship 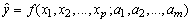which expresses the influence of individual independent variables on the dependent one. The latter is called a regression model or a regression equation of relative to 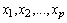, and 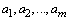are the regression coefficients (parameters).

When the mutual multivariate distribution of all variables is normal, the regression equation can be linear relative to the regression coefficients and has the following form:

Regression equation (2) for our data cannot directly include the seven initial variables D1, D2, La, Pin2, PFR, Cequi and Pne as predictors, because they are multicollinear (see Table 1). To overcome this problem we apply a particular type of multivariate regression called principal component regression (PCR)[14,17-18]. This method constructs empirical models using factor variables as predictors. In our case, the obtained four factor variables (1) can be used, since these are orthogonal and form four main basis vectors representing 97.6% of all data. The linear model will take the form

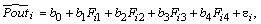(3)

Three different methods for determining the regression coefficients in (3) were applied, namely: linear, stepwise, and backward linear regression. The models obtained through the three methods are identical.

Table 4. Coefficients of the Principal Component Regression Model with Using Factor Variables (1) Model Unstandardized Coefficients t Sig. B Std. Error Beta (Constant) 3.068 0.014 219.284 0.000 F1 0.991 0.014 0.961 70.640 0.000 F2 -0.133 0.014 -0.129 -9.498 0.000 F3 0.035 0.014 0.034 2.519 0.013 F4 0.177 0.014 0.172 12.633 0.000

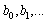The resulting model coefficients of PCR are given in Table 4. The first column is the list of the constant and the four variables participating in the analysis. Column B contains the calculated non-standardized coefficients Column Beta shows the standardized coefficients. The coefficients have been obtained with a very good standard error of 0.014. The t- statistics of the coefficients and their statistical significance are also given. In this case, the coefficients are statistically significant at usual level 0.05 (Sig. <0.05).

With the help of the calculated coefficients from Table 4, the linear regression models for laser efficiency Pout can be written down in the following form:

For the standardized values, the model is:

The obtained regression coefficients in (4) indicate the degree of influence of the four factors (respectively of the grouped variables) on laser generation (output laser power). Equation (5) shows the relative degree of influence of the factors on Pout. It can be concluded that the first factor F1, grouping D1, D2, La, and Pin2, has more influence than the other factors. The overall statistical significance of the model at 0.05 level is Sig.= 0.000.

Therefore, the model (4)-(5) can be used for an approximate representation of laser output power Pout.

The basic parameters of the quality of the model fit are as follows: the coefficient of multiple regression is R=0.985 and the coefficient of determination is R²=0.970. The latter signifies that the model accounts for 97% of the total variance of the sample. This value is high, for this reason, it can be concluded that the model fits the data well. The other important parameter is the standard error of estimate, which is 0.18078 and is acceptable. Figure 2 shows the experiment values of the output laser power Pout versus the predicted values, calculated by the model (4).

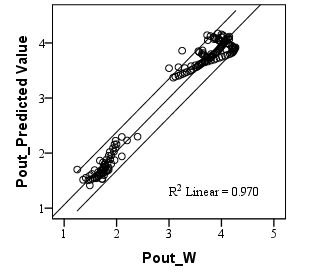Figure 2. Comparison of the experimental values of the output laser power Pout and predicted values, obtained by regression model (4) with a 5% two sided error interval

5. Physical Interpretation of the Obtained Results

The results from the factor and regression analysis indicate that the physical quantities, included in the first factor F1 are significant for the behaviour of the laser source. The geometric parameters and the supplied electric power are significant in determining laser output power. These have a high degree of influence on the distribution of the intensity of the electric field, the energy of the electrons, and the temperature profile of the neutral gas. All of this is decisive for the processes of populating the upper laser levels and laser generation. The quantity D1 is entered with a negative sign, which means that during the development of new laser sources with new geometric design, the outer diameter of the tube must be reduced. This is a crucial result which can be obtained only using the tools of statistical analysis of the real experimental data. In our opinion, the reason for this dependence is the ineffective temperature profile in the active volume of existing laser sources. An increase of the inner diameter and a reduction of the outer one would allow for changes in the process of cooling of the active laser volume. In this way, the achieved temperature field would provide more favourable conditions for the population of upper laser levels and would improve laser output power.

6. Predicting Laser Output Power

In this paragraph, we will predict the behaviour of a new laser source with new parameters of the 7 input laser variables.

The prediction will be carried out using the following procedure:

1. We enlarge the initial sample by appending a new case with 7 supposed values for the seven basic variables. The value for Pout in this last case is left empty.

2. The factor analysis procedure is performed once again with this enlarged data sample. The goal is to determine the new factors, which include the factor values for the last case.

3. We repeat the procedure of principal component regression. The new coefficients of equations (4) and (5) are determined.

4. The new predicted value of Pout is determined with the help of equation similar to (4) and the obtained factor variables.

Some of the results of the upper procedure are given in Table 5.

Columns 2-8 contain data of selected cases for input laser variables. Column 9 shows three actual measured power outputs. Column 10 presents the calculated values for given cases obtained using modelling equations of type (2). Column 11 presents the relative error for the predicted laser output power with respect to the experiment. It is limited not more of 7-8% (see also Figure 2.). Column 12 shows the increase of laser output power compared to the maximum measured Pout = 4.27 W, row V3, column 9.

The first 3 rows, numbered V1, V2, and V3 show the examples of real experiment data and the corresponding predictions with the help of equation (2). The following 7 rows numbered 1-7 present predictions for new variants of cases of laser sources, obtained by the procedure, described in the beginning of this section. The predictions adhere to the requirement that the values of variables D1 and PRF is to be reduced and not increased.

7. Analysis of Predicted Results

We will base our analysis on the Table 6. Experiment V3, where laser output power Pout = 4.27 W is the highest, is used for comparison. Column 1 represents the corresponding cases from Table 5. The active laser volume V, cm³ (for tube diameter D2 and length La) is calculated in column 3 (see also Table 5). Column 4 indicates the supplied power per unit length (PL=Pin2/La, W/cm) and column 5 - the supplied electric power per unit volume (Pv=Pin2/V, W/cm³).

Table 5. Evaluation and Prediction of Output Laser Power Pout Case D1_mm D2_mm La_cm Cequi_pF Pin2_KW PRF_KHz Pne_torr Pout_W Pout Predicted, W % % 1 2 3 4 5 6 7 8 9 10 11 12 V1 46.0 19.8 98 632.3 0.96 19 44.7 3.74 3.66 2.14 - V2 46.0 19.8 98 793.1 1.05 19 48.7 3.80 3.75 2.32 - V3 46.0 19.8 98 632.3 1.05 19 44.7 4.27 3.92 8.20 - 1 45.5 20.1 98 632.3 1 19 45 - 4.06 - -4.92 2 45.0 20.5 98 632.3 1.1 9 46 - 4.63 - 8.43 3 44.5 21.0 100 632.3 1.1 19 46 - 5.02 - 17.56 4 44.0 21.0 102 632.3 1.1 18 47 - 5.19 - 21.55 5 43.5 22.0 102 632.3 1.11 18 48 - 5.67 - 32.79 6 43.0 22.5 103 650.0 1.125 17 49 - 6.02 - 40.98 7 42.5 22.5 104 650.0 1.15 17 50 - 6.26 - 46.60

The predicted results confirm the strong influence of the studied quantities from the first factor F1. Laser output power is heavily dependent on the geometric design of the laser tube. With the increase of the active volume (increment of D2 and La) and the increase of the supplied electric power, Pin2 laser generation also increases. Columns 4 and 5 are particularly interesting. These show that with respect to the quantity PL, its predicted variation fluctuates around the experimental value from V3 - 10.71 W/cm. Apparently, this quantity is close to the optimum. The results in column 5 lead to the conclusion that in planning future experiments the supplied electric power per unit volume must be lower than the quantity from V3, which is 3.48 W/cm³. It appears the actual laser tube is burdened by electric power, which is not optimal.

Table 6. Behavior of Some Important Indirect Variables, Characterized the Output Laser Power Case Pin2, W V, cm3 PL, W/cm Pv, V/cm3 1 2 3 4 5 V3 1050 301.8 10.71 3.48 1 1000 311.0 10.20 3.22 2 1100 323.5 11.22 3.40 3 1100 346.4 11.00 3.18 4 1100 353.3 10.78 3.11 5 1100 387.7 10.88 2.86 6 1125 409.5 10.92 2.75 7 1150 413.5 11.06 2.78

When developing new laser sources, it needs to be taken into account that the outer diameter D1 needs to be reduced. In our opinion, this would improve the thermal balance of the new laser device. It would reduce the thermo-chemical deterioration of the active substance, increase the physical service life of the laser tube, and improve the total efficiency of the laser source.

8. Conclusions

For the first time, statistical techniques allowing the solution of partial problems related to the planning of the experiment have been applied for a SrBr₂ laser. With the help of factor and principal component regression analysis, a filtering experiment has been carried out, which allowed for the reduction of the 7 input real independent quantities by grouping them in new 4 artificial variables (factors). This way the engineering work and the related costs connected with experimentation can be significantly reduced. A partial extremal future experiment has been carried out, allowing the prediction of the behaviour of the laser source and the establishment of optimum values for the independent variables relevant for the development of new devices. Further theoretical study is planned to improve the obtained results by using nonparametric statistical techniques for constructing nonlinear and locally nonlinear models of the SrBr₂ lasers.

ACKNOWLEDGEMENTS

This paper is performed with the partial support of the Scientific Research Department of Plovdiv University –NPD, project NI11-FMI-004.