1. Introduction

As our modern life is becoming faster day by day, in the current decade, scientific and engineering problems are specially confined in a particular area to attain the reliable, faithful and high speed performances in computation[1-3,5] and communication[4,6]. Unfortunately, the VLSI technology, so far is being used, cannot beat this challenge. Electrons have a limited speed. So, this technology is already in a saturated state from both the aspects – size and speed. Moreover, our venture for the advancement of this technology creates new problems like hot carriers, electromagnetic interference, short channel effects etc. These factors endanger the device reliability.

Presently, in fewer fields, electronic devices are replaced by electro-optical (OE) devices[6,11]. This technology tem- porarily overcomes some physical problems. But the previous limitations still exist as electronic parts are still there in those hybrid components.

In the above circumstances, there is a way-out to replace the traditional circuits with all-optical ones[2-3,7,15-17]. Photonics is the future of technology. In the last few years, light, as signal carrier, has already established its validity in various all-optical operations[1-3,5-7,9,11,15-23]. Among many other techniques, non linear material (NLM) has been established its validity as optical switching devices[1-3,5,9]. All-optical signal processing technologies by non-linear material based directional switch are considered as a possible long-term route in the evolution of current telecommunication network and ultra high-speed signal processing[10-17].

The all optical implementation of various subtraction schemes[5] have been studied by taking the complement of the subtrahend and adding it to the minuend. The schemes for optical implementation of subtractors using Semiconductor Optical Amplifier (SOA)[6] and electro-optic- modulators (EOM)[11] have been attempted. The paper presents a scheme for the implementation of all optical Parallel Subtractor (PS)[10] by Half Subtractor (HS) and Full Subtractor (FS)[15] with logic circuits in direct manner [8,10], as done with paper and pencil, by nonlinear optical material based switching mechanism, in such a way that will obey the truth table[8,10,15]. By this method, each subtrahend bit of the number is subtracted from its corresponding significant minuend bit to get DIFFERENCE bit including the case of BORROW bit, as in conventional electronics. Our proposed circuits are very much reliable because they follow the basic principle of subtraction operation. An ALU of dream goal, an optical computer, can be implemented including this scheme.

2. All-optical Switching Behaviour of Nonlinear Material and its Use as All-optical Gates

The phenomenon photorefractivity[13-17] of some non- linear optical material is used in nonlinear all-optical intensity switching mechanism. The photorefractive effect, where the refractive index changes induced by a light field when the crystal is subjected to intense laser radiation, defocusing and scattering of the light, is observed, as a result of an inhomogeneous change in the refractive index. It is also found that these changes still prevail even after the light is switched off, but it could be erased by strong, uniform illumination [14].The refractive index of some nonlinear materials (NLM) such as carbon disulfide, pure silica, potassium dihydrophosphate (KDP), (KH₂PO₄) crystal etc. varies linearly with the intensity of the light incident on it. The refractive index (n) of such isotropic dielectric non-crystalline media can be put into an equation as in (1).

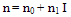(1)

Here n₀ is the linear term, n₁ is the nonlinear correction term and I is the intensity of the incident light beam on the material.

We can implement the switching mechanism with such nonlinear material by taking an interface between two media of which one is a linear material (LM), whose refractive index n₀ is independent of the intensity of light and the other is aforesaid NLM. A laser beam, highly intense polarized light, preferably pulse laser of intensity I_1, is allowed to fall on the interface from linear to nonlinear part in a particular direction XO (incidence angle θ₁) as depicted in Figure 1. The refracted beam from the NLM follows the path OZ. But when another higher intense laser beam of intensity I₂ (I₂> I₁) is made to incident along XO, after refraction from the NLM the light passes through OY direction (angle of refraction θ₂). The deviation of refractive angle for different incident light intensity I₁ and I₂ is < ZOY = Δθ₂. Thus the combination of LM and NLM may act nicely as a directional all-optical switch. This is the unit block of our proposed subtraction circuit.

Figure 1. Intensity switching of optical nonlinear material

In the expression of refractive index in (1), n₀ is linear term and n₁ is the nonlinear correction term. For carbon disulfide (CS₂)[2,3,12] n₀ = 1.63, n₁ = 514×10^-20 m²/W. and for fused silicon dioxide[2,3,12] (SiO₂) n₀ = 1.458, n₁ = 2.7×10^-20 m²/W. If we use CS₂ and SiO₂ as nonlinear materials and the pulse laser of intensity I = 2×10¹⁸ W/m² as a source, we can estimate the deviations of light in two cases as given in Table 1.

The logic gates[2-3,5,15-17] are implemented in optics using NLM by taking the presence of light signal as 1 and the absence of it as 0. The implementation of such logic gates can be done by using some femtosecond laser pulses and 1-mm-thick potassium dihydrophosphate crystal at the pick intensity of 0.6 TW/cm² and duration of 60 fs[3-4,15-17]

2.1. All Optical NOT Gate

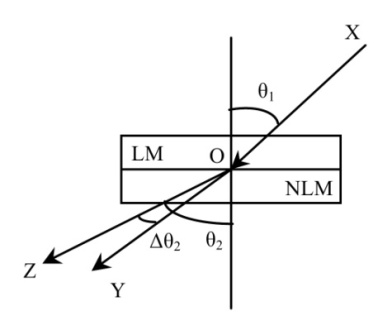
To implement an all optical NOT gate using non-linear material a constant intensity pulse laser source (CILS) is used as shown in Figure 2. It is also called probe beam. Here P₁ is taken as input beam. A detector is placed at P₂ will detect the output beam after refraction. If P₁ is absent, the light will follow a path OP₂ and will be detected by the detector due to presence of CILS. But if P₁ is present, after refraction, the light will follow a path other than OP₂, may be OP₃, and the detector will not detect any light signal. Thus the system acts as optical NOT gate.

Figure 2. All-optical NOT gate

2.2. All-optical Ex-OR Gate

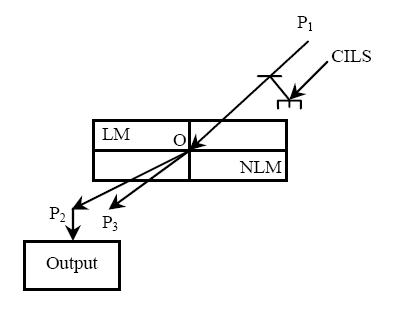
The two inputs all-optical XOR gate using NLM is shown in Figure 3. Here V1 and V2 are two input channels. A detector is placed at V3 gives the output. When only one input channel carries light signal, the light beam after refraction will detect by the detector at V3, unless not.

Figure 3. All-optical EX-OR gate

Table 1. Estimation of the Deviation of Pulsed Laser Light when Passing Through Carbon Disulfide (CS2) and Silicon Dioxide (SiO2) Material Angle of Incidence (θ1) Incident light intensity n(= n0 + n1 I) Angle of refraction (θ2) Deviation(Δθ2 = θ′2 - θ′′2) carbon disulfide (CS2) 45 deg I=2×1018 W/m2 11.91 3.404 deg = θ′2 1.578 deg 45 deg 2I 22.19 1.827 deg= θ′′2 silicondi-oxide (SiO2) 45 deg I=2×1018 W/m2 1.512 27.883 deg= θ′2 1.041 deg 45 deg 2I 1.566 27.842 deg= θ′′2

2.3. All Optical AND Gate

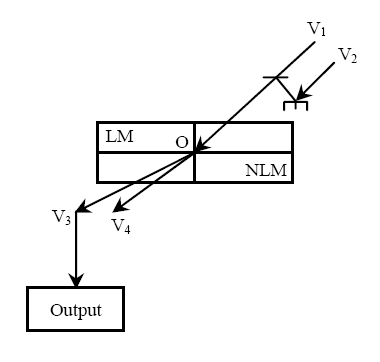
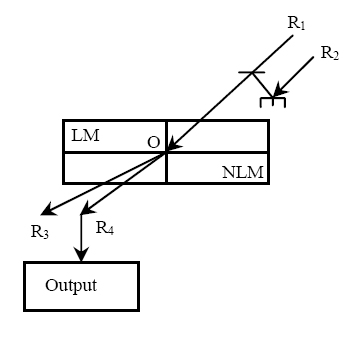
The two inputs all-optical AND gate using NLM is shown in Figure 4. Here R₁ and R₂ are two input channels. A detector is placed at R₄ gives the output. Now when both the channels carry light signal, the light beam after refraction one can get light at the detector (situated at R₄), unless not.

Figure 4. All-optical two-input AND gate

Figure 5. All optical three-input one-or-all circuit

2.4. All Optical Three-input One-or-all Circuit

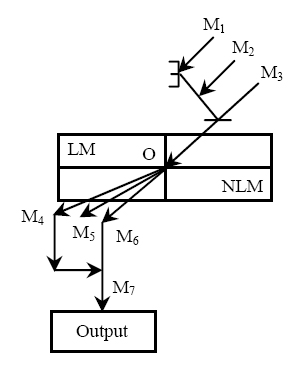
The all-optical three-input one-or-all circuit using NLM is shown in Figure 5. Here M₁, M₂ and M₃ are three input channels. A detector is placed at M₇ gives the output. Now when any one of the input channels carries light signal, the light beam after refraction will detected by the detector at M₇ and there will be light at M₇ if all the inputs have light also The output remains dark for all other combinations of input states.

2.5. All Optical Three-input Two-or-all Circuit

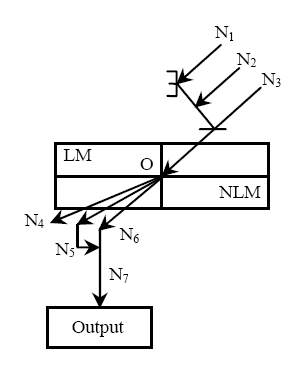
The all-optical three-input two-or-all circuit using NLM is described in Figure 6. Here N₁, N₂ and N₃ are three input channels. A detector is placed at N₇ gives the output. Now when any two or all of the input channels carry light signal, the light beam after refraction will detected by the detector at M₇, unless not.

Figure 6. All optical three-input two-or-all circuit

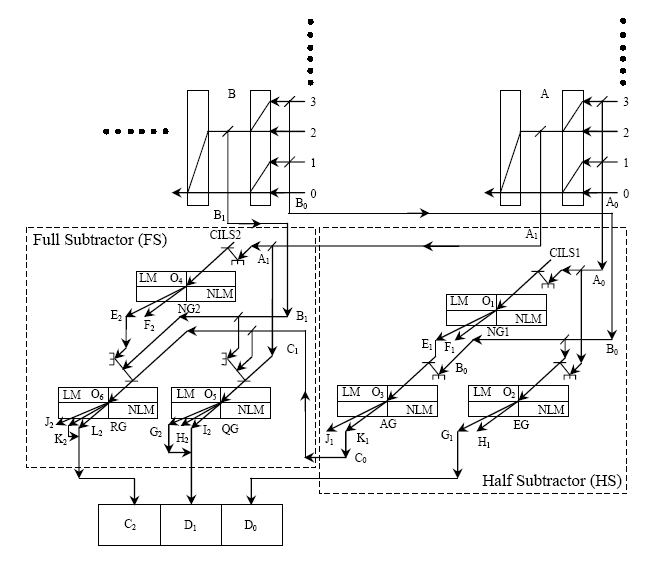Figure 7. All-optical parallel subtraction schem using NLM as switch

3. All-Optical Parallel Subtractor

We design an all-optical binary subtraction scheme capable of subtraction between two multibit data in parallel. The system is shown in the Figure 7. Tree architectures[1,5,9] A and B are used to convert a decimal value into its respective binary value, A₁A₀ and B₁B₀ respectively. Here B₁B₀ is to be subtracted from A₁A₀. One 1-bit full subtractor[15] and one 1-bit half subtractor[15] system are combined to obtain a general all optical parallel subtraction. For half subtractor system[15] A₀ and B₀ are the two inputs. The outputs are taken from D₀ (DIFFERENCE) and C₀ (BORROW). The all optical half subtractor is constructed by three all optical logic gates. NG1, EG and AG are the optical NOT gate, two-input EX-OR gate and two-input AND gate respectively. The truth table of an all-optical half subtractor is given in Table 2[8,10,15]. For full subtractor[15], the inputs are A₁, B₁ and C₁ (= C₀ BORROW from previous half subtractor). The outputs are from D₁ (DIFFERENCE) and C₂ (BORROW). The all optical full subtractor is implemented with an all optical NOT gate (NG2), a three-input one_or_all circuit (QG) and a three-input two_or_all circuit (RG). The truth table of an all-optical full subtractor is set in Table 3 [8,10,15]. The final output result is C₂D₁D₀. This is the binary output of (A₁A₀ – B₁B₀).Let us consider an example for subtracting 3 from 2. We take A = 2 and B = 3. The binary equivalent of A = 2 is A₁A₀ = 10 and the binary equivalent of B = 3 is B₁B₀ = 11.

Table 2. Truth Table of All-optical Half Subtractor Inputs Outputs A0 B0 C0 D0 0 0 0 0 0 1 1 1 1 0 0 1 1 1 0 0

For half subtractor, the inputs are A₀ = 0 and B₀ = 1. The outputs will be DIFFERENCE = 1 and BORROW = 1, which means D₀ =C₀ = 1. Now the inputs of the full subtractor are A₁ = 1, B₁ = 1 and C₁ = 1 (from half subtractor BORROW). The output will be DIFFERENCE = 1 and BORROW = 1 which means D₁ = 1 and C₂ = 1.

The final result will be C₂D₁D₀ = 111 which comes from the subtraction of 11(3) from 10(2) when a 1 has been borrowed from the next stage. And then 10 – 11 becomes 110(6) – 11(3) which gives D₁D₀ = 11(3). The C₂ = 1 represents that 1 has to be deducted from next bit of the minuend.

For parallel subtraction of two different strings of multibit (more than 2 bits) binary number we need more expanded trees for decimal number to equivalent binary number conversion. And then, we also require additional full subtractors. The dots in the Figure 7 are representing such elevations.

All-optical parallel subtractor can subtract decimal or binary optical numbers in parallel. In our scheme we use all optical intensity switchs in designing the all optical parallel subtractor. In our design the light beam which is fed back is coming from the output of O₁ and O₄ switches. Again the concept used here to design these all optical switches (O₁ and O₄) has an advantage. Whenever the outputs of these all optical switches (O₁ and O₄) are assumed to be at ‘1’ state, the source of that ‘1’ state are the constant intensity pulse laser sources (CILS) used as probe beams. So in each feedback arrangement described in our scheme similar intense light beam is fed back. In this way the reduction of intensity by using beam splitter will not affect the non-linear response of the device. The light sources are so chosen that each input beam intensity is in the range of intensity which is detected as ‘1’ by the detector after refraction.

Table 3. Truth Table of All_optical Full Subtractor Inputs Outputs An Bn Cn-1 Cn Dn 0 0 0 0 0 0 0 1 1 1 0 1 0 1 1 0 1 1 1 0 1 0 0 0 1 1 0 1 0 0 1 1 0 0 0 1 1 1 1 1

4. Conclusions

Our proposed circuits are very much reliable because they follow the basic principle of subtraction operation. The light signals that are severally used, bended and the feedback light signals from the outputs are made by mirrors and beam splitters to make the circuits simple. As the circuit is purely all-optical in nature and very simple, one can obtain the speed of operation far more than THz limit[2,3,12-24]. This subtraction scheme should be the first step on our dream way to all-optical Arithmetic Unit. The entire scheme should perform properly using suitable nonlinear material[2,3, 12-17,24]. Essentially inputs should be chosen properly for proper function of the system.

ACKNOWLEDGEMENTS

The authors want to acknowledge Professor Sourangshu Mukhopadhyay of the for his valuable suggestions.