-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Networks and Communications
p-ISSN: 2168-4936 e-ISSN: 2168-4944
2021; 11(1): 1-16
doi:10.5923/j.ijnc.20211101.01
Received: Jun. 10, 2021; Accepted: Jun. 25, 2021; Published: Jul. 26, 2021

Performance of Coherent Optical Networks Incorporating Kramers-Kronig Direct-Detection Receivers Part I: Double Sideband Transmission
Zainab H. Hasan, Raad S. Fyath
Department of Computer Engineering, Al-Nahrain University, Baghdad, Iraq
Correspondence to: Raad S. Fyath, Department of Computer Engineering, Al-Nahrain University, Baghdad, Iraq.
| Email: |  |
Copyright © 2021 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Recently, direct-detection (DD) technique, which does not use a local laser, has been proposed to retrieve the phase of the coherently modulated optical signal from the photocurrent at the receiver side. This technique uses Hilbert transform-based Kramers-Kronig (KK) algorithm and has been mostly investigated for less than 100 Gbps optical networks. The aim of this paper is to design and performance investigate KK-based coherent optical networks operating with 200 Gbps and beyond data rates under double-sideband transmission. A carrier-assisted coherent optical network configurations supported by KK-based DD technique is designed using VPIphotonics ver.11 software. The configuration uses two lasers at the transmitter side, one is modulated by the information (message) while the second one is used as an assisted optical carrier. Configuration II uses only one laser where the information is embedded in its field using a single-sideband modulation. Virtual assisted optical carrier is generated by making the message modulates radio frequency (RF) subcarrier before using optical modulation. The configuration is designed to support single-polarization (SP) 16-QAM signaling with 200 and 400 Gbps bit rates. The designs are then extended for dual-polarization (DP) multiplexing to support 400 and 800 Gbps networks. The effect of various design and system parameters on the transmission and bit error rate characteristics are investigated. The simulation results show that the configuration can support maximum reach of 440 and 428 km for SP 200 and 400 Gbps, respectively.
Keywords: Kramers-Kronig (KK), Direct-detection (DD), Single-polarization (SP), Dual-polarization (DP)
Cite this paper: Zainab H. Hasan, Raad S. Fyath, Performance of Coherent Optical Networks Incorporating Kramers-Kronig Direct-Detection Receivers Part I: Double Sideband Transmission, International Journal of Networks and Communications, Vol. 11 No. 1, 2021, pp. 1-16. doi: 10.5923/j.ijnc.20211101.01.
Article Outline
1. Introduction
- Recently, there is increasing data traffic demand to support high-capacity services related to internet-of-things (IoT), 5G and beyond networks, and advanced TV technology [1]. Optical networks can be redesigned using advanced modulation techniques to support the high-capacity demand [2] but the challenge is how to design low-cost receiver at the user end. Low-cost optical networks and communication systems relay on intensity modulation (IM)/direct-detection (DD) technique [3]. In this technique, the digital data (information) modulates the intensity of the optical carrier (laser output) while a single photodiode (PD)-based receiver is used to recover the data back at the user end. Direct-detection scheme does not require a local oscillator (LO), i.e., a local laser, at the receiver side which makes the detection process to be low cost. Unfortunately, IM/DD technique does not support high bit rate-transmission distance product. To increase the capacity of optical networks, coherent modulation techniques should be used in the transmitter side [4]. In this technique, the input digital data modulates the phase or phase and amplitude of the electrical field of the optical carrier. Coherent detection is required at the receiver side to recover the data. Here, the fields of received optical signal and LO laser are mixed before incident on the PD to achieve high-efficient optical-to-electrical conversion. The LO laser should operate synchronously in frequency or frequency and phase relative to the unmodulated laser at the transmitter side. This makes coherent-detection receiver is more cost and least robust than DD counterpart.Recently, the concept of coherent modulation/direct-detection (CM/DD) optical networks has been introduced. In these networks, coherent modulation is used at the transmitter side to increase the transmission capacity while a DD scheme is implemented at the receiver side to achieve low-cost, high-robust detection [5]. The idea is to use Kramers-Kronig (KK) algorithm which can retrieve the phase information from the photocurrent using Hilbert transform [6]. This opens an active research field to address the transmission performance and effect of system impairments for coherent modulation/KK-based DD optical networks, especially when high-bit rate (100 Gbps and beyond) is transmitted per optical carrier [7]. This topic is addressed in this work for 200-800 Gbps single-channel transmission. It is worth to mention here that multiplexing techniques such as wavelength-division multiplexing (WDM) can also be used here to support high-capacity transmission in KK-based optical networks.
2. Related Works
- In 2016, Mecozzi et al. [8] proposed a direct-detection coherent receiver that combines the advantages of coherent transmission and the cost effectiveness of direct detection. The operation principle of the proposed receiver is based on the KK relations, while its implementation requires transmitting a CW signal at one edge of the information-carrying signal. Numerical investigation was performed for many cases including the transmission of 24 GBaud 16 QAM modulated signal, with raised-cosine pulse shaping having 0.05 roll-off factor, over 100 km standard single mode fiber (SSMF). The results show that KK receiver scheme allows digital post compensation of linear propagation impairments. Further, the proposed receiver was found to be favorably compared to existing schemes in terms of power consumption and is optimal in terms of spectral efficiency. In 2017, Hoang et al. [9] proposed four-dimensional (4D) modulation with DD employing a novel Stokes vector KK transceiver. It was shown that employing a Stokes vector receiver, transmitting a digital carrier and using KK detection offers an effective way to derotate polarization multiplexed complex double sideband signal without using a local oscillator at the receiver. The feasibility of digital polarization demultiplexing was experimentally demonstrated, and the impact of system parameters and configurations including carrier-to-signal-power ratio (CSPR), guard band of the digital carrier, oversampling ratio and real multiple-input multiple-output (MIMO) scheme was experimentally investigated. With 60 GBaud DP 16QAM signals, the authors reported the first single wavelength 480 Gb/s (net bit rate 400 Gb/s) transmission over 80km fiber in C-band. In 2018, Chen et al. [10] reviewed in detail experimental demonstrations of KK-based DD systems with high spectral efficiencies, high per-carrier interface rates, and 100-km reach. SP and DP versions of KK-based receiver were demonstrated. Discrete multitone (DMT) transmission with a line rate of 220-Gbps over a 100-km SSMF link without optical dispersion management was demonstrated using a 63-GHz bandwidth single-diode KK receive. Further, a 4-channel DP WDM 100-km SSMF transmission based on DP-KK receivers was investigated experimentally. The 24-GBaud 32-QAM channels were asymmetrically placed on a 37.5-GHz channel grid and the achieved spectral efficiency was 5.3 bits/s/Hz In 2019, Yi et al [11] investigated the performance of low-complexity heterodyne optical coherent receivers with a single PD per polarization. Two techniques were used to compare signal-signal beat interference (SSBI) mitigation: firstly, using a high power local oscillator and, secondly, employing the KK digital linearization scheme. Numerical investigation was performed to address the impact of SSBI and LO relative intensity noise (RIN) on the performance of such coherent transceivers. The results indicate that, in the case of a RIN-free LO laser, a strong LO is effective in mitigating SSBI and achieves a similar performance to that of the KK algorithm. However, the required increase in LO-to-signal power ratio (LOSPR) is significant. For example, a 20 dB higher optimum LOSPR was observed in the 28 GBaud DP 16-QAM system at an optical CSPR of 22 dB. The drawback of using such a high LOSPR is the increased penalty due to RIN-LO beating terms. In 2019, Bo and Kim [12] presented a detailed comparison between the conventional and upsampling-free (US-F) KK algorithms through numerical simulations. They stated that a technical challenge associated with the implementation of a conventional KK receiver is the high sampling rate DSP. Since nonlinear operations (such as logarithm and exponential functions) included in the conventional KK algorithm broaden the signal spectrum significantly, digital upsampling (US) is required at the beginning of DSP. To solve this problem, the authors proposed and demonstrated a new KK algorithm operates without the digital US. In this US-F algorithm, the exponential function is removed by expressing the complex signal in the Cartesian form (i.e., real plus imaginary) and replacing the logarithm function with its mathematical approximation. The performance of the both KK receivers were examined using orthogonal frequency-division multiplexing (OFDM) and Nyquist SCM signals formatted in 16-QAM and 64-QAM. The results show that the US-F KK algorithm reduces the complexity and power consumption by a factor of 7 to 10, in comparison with the conventional algorithm at the expense of small sensitivity penalties. The sensitivity penalties incurred by using the US-F KK algorithm (with respect to the conventional algorithm) are less than 1 dB for 16-QAM OFDM and Nyquist SCM signals. In 2021, Deb and Cartledge [13] investigated the use of the KK receiver for dispersion compensation in a DD system based on a directly-modulated laser. They showed the validity of the KK receiver by considering a linear contribution to the optical phase arising from a numerical solution of the laser rate equations as a frequency shift of the optical spectrum. The modulated optical signal can then meet the minimum-phase condition required by the KK algorithm. A system model was presented based on the direct modulation of a 10 Gbps laser with 16-QAM subcarrier modulation. The principle was demonstrated in simulation by transmitting an optically filtered optically filtered vestigial sideband (VSB) 53.5 Gbps16-QAM SCM signal over 65 km of unamplified SSMF. After DD of the VSB signal, the KK algorithm was employed to reconstruct the minimum-phase representation for the received amplitude. Dispersion compensation was applied after DD with a KK receiver. In addition, the impact of the optical filter parameters and receiver sampling rate on system performance were investigated. In 2021, van der Heide [5] introduced a flexible, software-defined real-time multi-modulation format receiver implemented on an off-the-shelf general-purpose graphics processing unit (GPU). They showed the potential for massive parallel processing provided by a GPU to recover directly-detected M-PAM signals and M-QAM signals with KK-Based detection. The flexible receiver architecture was used to receive and process in real time 2 GBaud optical signals using 2-PAM, 4-PAM, 8-PAM, and 16-PAM modulation, 1 GBaud 4-QAM, 16-QAM, and 64-QAM modulation. Experimental performance evaluation was shown for back-to-back transmission. In addition, performance was evaluated after transmission over 91 km field-deployed optical fiber and reconfigurable optical add-drop multiplexers (ROADMs). Continuous real-time transmission revealed stable performance despite the varying environment of installed fiber. These results indicate the potential of massive parallel processing provided by GPUs for low-cost flexible optical links for a range of modulation formats.It is clear from this literature survey that most of the work was reported for a single-polarization (SP) KK receiver-based optical networks with less than 100 Gbps data rate per single channel. It is interesting to address the performance of such networks for higher-bite rate SP transmission (for example, 200 and 40Gbps). Further, one can redesign the system using DP multiplexing to double the transmission bit rate. The effect of system parameters needs to be investigated for these advanced systems. These issues are considered in this work.
3. Concepts and Principles of Operation Kramers-Kronig Receiver-Based Optical Networks
- Kramers-Kronig (KK) receiver combines the advantages of coherent detection with simple direct detection [14]. This receiver is capable of detecting the complex-valued electrical field of the signal using single photodiode-detection scheme without incorporating local laser. The operation algorithm of this receiver is based on Hilbert transform and has the capability of retrieving the phase information from the directly-detection intensity waveforms. The system uses a single-ended PD supported by digital signal processing (DSP) to detect the QAM symbols sent by the transmitter side. A reference carrier is added to the signal which is needed for coherent down-conversion. This carrier is usually added to the signal spectrum of the transmitter and placed in the vicinity, but outside the spectrum of the data signal [15]. Note that adding the carrier at transmitter side ensures that both reference carrier and signal will suffer the same level of polarization effect introduced by the fiber during transmission. Thus polarization controller is not needed at the receiver side if both carrier and data signal have the same state of polarization at the transmitter side.The KK receiver offers many advantages over conventional DD receivers. Among these advantages are (i) The DD scheme adopted in KK receiver enables data recovery from received optical QAM symbols without using a local laser. This leads to low-cost and robust detection scheme while reserving the advantages of coherent modulator [8]. (ii) This receiver enables single-sideband (SSB) DD transmission [16]. Direct-detection systems may use SSB-QAM subcarrier modulation (SCM) including orthogonal frequency-division multiplexing (OFDM) to achieve high-spectral efficiency. Further, SSB transmission reduces the effect of fiber dispersion on the transmitted signal quality.(iii) The KK receiver reduces the effect of signal-signal beat interference (SSBI) originated by the square-law characteristics of the PD, where the generated photocurrent is proportional to the square of the incident field amplitude [8, 17]. Careful design of this receiver leads to SSBI cancellation [18].(iv) The SSBI can be cancelled completely without using a large carrier-to-signal power ratio (CSPR) which is usually adopted by other SSBI cancellation techniques [14]. In term of receiver sensitivity, the KK receiver outperforms DD receivers incorporating other SSBI cancellation techniques. (v) Since KK receiver has inherently coherent-like detection mechanism which enables it to detect complex valued electric techniques developed for coherent detection can be used here [14]. For example, DSP based algorithms can be used to compensate electronically the effect of fiber dispersion and fiber nonlinearity in the electrical domain of KK receiver [19].
3.1. Hilbert Transform and Analytic Signal
- Recall that the operation of KK detection scheme is based on Hilbert transform. This subsection introduces the main concepts of this transform and states briefly its relation with “analytic signal”. The explanation is based heavily on Ref. [20].Hilbert transform is an allpass linear filtering process which shifts the phase of its input signal by -90° for all positive-frequency component (i.e., +90° phase shift for all negative frequency components). The impulse and frequency response of this filter can be expressed, respectively, as [20]
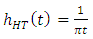 | (1a) |
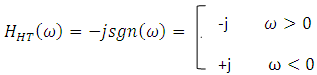 | (1b) |
 for all positive and negative frequencies.Analytic signal is defined as a signal which has no negative-frequency components. The real and imaginary parts of this signal are related by Hilbert transform. Let sa(t) is a complex analytic signal given by
for all positive and negative frequencies.Analytic signal is defined as a signal which has no negative-frequency components. The real and imaginary parts of this signal are related by Hilbert transform. Let sa(t) is a complex analytic signal given by 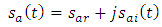 | (2a) |
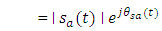 | (2b) |
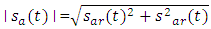 | (2c) |
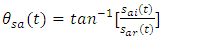 | (2d) |
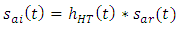 | (3a) |
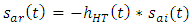 | (3b) |
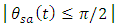 and therefore uniquely defined [21]. Applying the natural logarithm for both sides of eqn. (2b) yields
and therefore uniquely defined [21]. Applying the natural logarithm for both sides of eqn. (2b) yields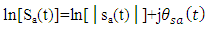 | (4) |
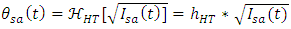 | (5) |
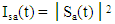 is the signal intensity and
is the signal intensity and  is the Hilbert transform. It is clear from eqn. (5) that the phase information of an analytic signal can be recovered from its intensity if the signal has minimum phase characteristic [19].
is the Hilbert transform. It is clear from eqn. (5) that the phase information of an analytic signal can be recovered from its intensity if the signal has minimum phase characteristic [19].3.2. Operation Principles of Kramers-Kronig Receiver
- This subsection presents briefly the main concepts related to the operation of optical KK receiver. Let the transmitter generates optical data (signal) whose electric field is expressed by
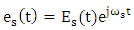 | (6) |
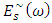 is the Fourier transform (FT) of Es(t). The frequency-shift property of FT states
is the Fourier transform (FT) of Es(t). The frequency-shift property of FT states 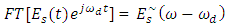 | (7) |
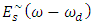 is symmetric around ω = ωd compared with ω = 0 for
is symmetric around ω = ωd compared with ω = 0 for 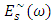 . If one chooses ωd to be positive and satisfy condition ωd ≥ Bme, then the spectrum
. If one chooses ωd to be positive and satisfy condition ωd ≥ Bme, then the spectrum 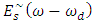 exists only for positive frequencies. This condition implies that
exists only for positive frequencies. This condition implies that 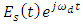 is an analytic signal.Return back to eqn. (7) and assume that the transmitter superimposes this complex data with a copolarized reference optical carrier whose electric field is given by
is an analytic signal.Return back to eqn. (7) and assume that the transmitter superimposes this complex data with a copolarized reference optical carrier whose electric field is given by 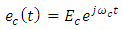 | (8) |
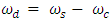 | (9) |
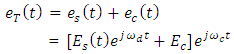 | (10) |
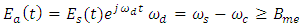 | (11) |
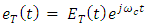 | (12a) |
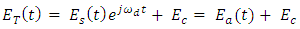 | (12b) |
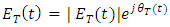 is an analytic signal. When
is an analytic signal. When 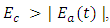 the waveform
the waveform 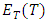 is a minimum –phase signal where its phase
is a minimum –phase signal where its phase 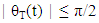 and therefore, unequal defined. Applying the natural algorithm for both sides of eqn. (12b) yields
and therefore, unequal defined. Applying the natural algorithm for both sides of eqn. (12b) yields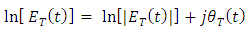 | (13a) |
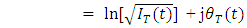 | (13b) |
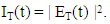 Note that the signal ln[ET(t)] is an analytic signal and therefore, its phase θT(t) is connected to its part,
Note that the signal ln[ET(t)] is an analytic signal and therefore, its phase θT(t) is connected to its part, 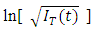 by the Hilbert transform given in eqn. (3a)
by the Hilbert transform given in eqn. (3a)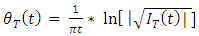 | (14) |
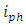 is produces by the PD is proportional to the square of the incident field envelope [15]
is produces by the PD is proportional to the square of the incident field envelope [15]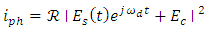 | (15) |
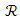 is the PD respectively measured in A/W. Equation (15) indicates that the photocurrent consists of three components, namely the contributions of signal-signal mixing
is the PD respectively measured in A/W. Equation (15) indicates that the photocurrent consists of three components, namely the contributions of signal-signal mixing 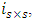 carrier-carrier mixing
carrier-carrier mixing 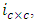 and signal carrier mixing
and signal carrier mixing 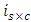
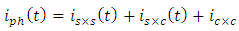 | (16) |
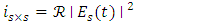 | (17a) |
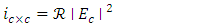 | (17b) |
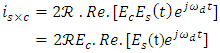 | (17c) |
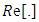 denotes the real part of the parameter. Note that
denotes the real part of the parameter. Note that 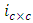 is a DC current since Ec is constant amplitude [8,17].
is a DC current since Ec is constant amplitude [8,17].4. Design and Concepts of KK Receiver-Based Optical Networks
- This section presents design concepts and performance investigation of point-to-point single-polarization (SP) coherent optical network incorporating KK-based receiver for direct detection. The design concepts are applied for two 16-QAM systems operating with 200 and 400 Gbps bit rates. The transmission performance and effect of impairments are investigated for both systems. The results are used as a guideline to design and investigate the performance of two dual-polarization (DP) 16-QAM systems operating with 400 and 800 Gbps bit rates. All the networks reported in this work are designed and performance investigated using VPIphotonics ver.11 software. A bit error rate (BER) threshold BERth of 3.8X10-3, which corresponds to 7% hard decision (HD) forward error correcting (FEC) code, is used to estimate the maximum reach of the designed transmission systems.
4.1. Single-Polarization System Under Investigation
- This subsection focuses on the design concepts of a point-to-point SP KK receiver-based coherent optical network. The system is designed and implemented in VPIphotonics environment and the support introduced by KK algorithm is introduced here.
4.1.1. System Description and Design Issues
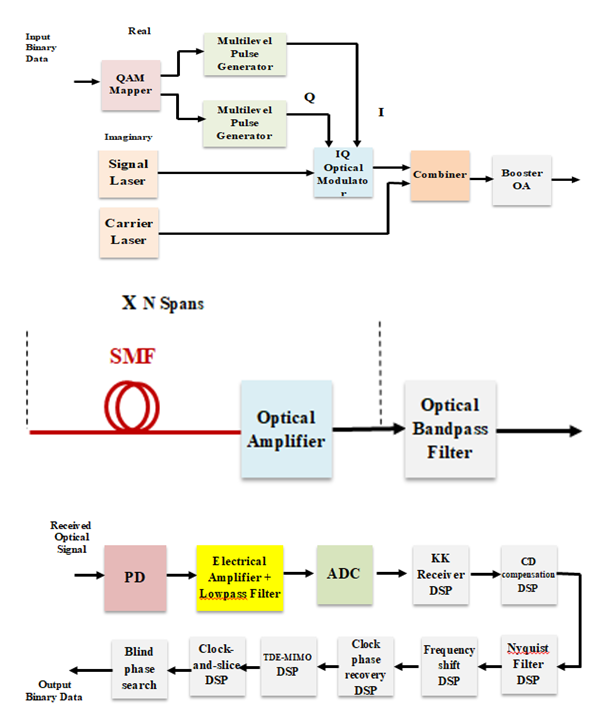
- Figure 1 shows the block diagram of the designed SP coherent modulation/direct detection optical network. The system consists of three main parts, coherent optical transmitter, fiber transmission link, and KK-based DD optical receiver.
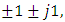
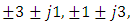 and
and 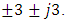 The real and imaginary values of the mapper output are used to control two multilevel electric pulse generators (in-phase (I) and quadrature (Q) PAMs, respectively). The output of these two pulse generators are used to intensity modulate the I and Q components of the signal laser field (i.e., cosωst and
The real and imaginary values of the mapper output are used to control two multilevel electric pulse generators (in-phase (I) and quadrature (Q) PAMs, respectively). The output of these two pulse generators are used to intensity modulate the I and Q components of the signal laser field (i.e., cosωst and 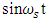 components). The generated modulated optical signal is added with a CW component produced by the carrier laser. The combined optical signal is amplified using a booster optical amplifier (OA) before launched to the fiber link.Each of the electrical pulse generator produces square-root raised cosine spectral shaping pulses to ensure zero intersymbol interference (ISI) at the receiver detection process. The bandwidth of these pulses (i.e., electrical message bandwidth) is given by
components). The generated modulated optical signal is added with a CW component produced by the carrier laser. The combined optical signal is amplified using a booster optical amplifier (OA) before launched to the fiber link.Each of the electrical pulse generator produces square-root raised cosine spectral shaping pulses to ensure zero intersymbol interference (ISI) at the receiver detection process. The bandwidth of these pulses (i.e., electrical message bandwidth) is given by 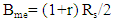 | (18) |
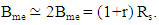 The frequency of the CW carrier laser 𝑓c is selected to yield a field component lying just outside the spectrum of the modulated optical signal
The frequency of the CW carrier laser 𝑓c is selected to yield a field component lying just outside the spectrum of the modulated optical signal 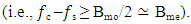 b- Transmission Link (Fig. 1b)The transmission link consists of multispan single-mode fiber (SMF). An optical amplifier is inserted at the end of each span to compensate the corresponding fiber loss. The gain of the amplifier in decibels GdB = αLs where α is the fiber loss in dB/km and Ls is the span length in km. An optical bandpass filter (OBPF) is inserted at the end of the transmission link to reduce the amount of amplified spontaneous emission noise (associated with the optical amplifiers) that incidents on the photodiode at the receiver side. The OBPF should have a sufficient bandwidth to pass the spectrum of the hybrid optical signal (i.e., modulated optical signal plus the inserted carrier). The low and high cutoff frequencies of this filter, 𝑓L and 𝑓h, are approximately estimated as 𝑓L = 𝑓s ― Bme = 𝑓s ― Bmo/2 and 𝑓h > 𝑓c = 𝑓s + ∆𝑓 where ∆𝑓 is frequency difference between the carrier and signal data lasers and should be chosen to be ≥ Bmo/2 ≃ Bme, see Fig. 2.
b- Transmission Link (Fig. 1b)The transmission link consists of multispan single-mode fiber (SMF). An optical amplifier is inserted at the end of each span to compensate the corresponding fiber loss. The gain of the amplifier in decibels GdB = αLs where α is the fiber loss in dB/km and Ls is the span length in km. An optical bandpass filter (OBPF) is inserted at the end of the transmission link to reduce the amount of amplified spontaneous emission noise (associated with the optical amplifiers) that incidents on the photodiode at the receiver side. The OBPF should have a sufficient bandwidth to pass the spectrum of the hybrid optical signal (i.e., modulated optical signal plus the inserted carrier). The low and high cutoff frequencies of this filter, 𝑓L and 𝑓h, are approximately estimated as 𝑓L = 𝑓s ― Bme = 𝑓s ― Bmo/2 and 𝑓h > 𝑓c = 𝑓s + ∆𝑓 where ∆𝑓 is frequency difference between the carrier and signal data lasers and should be chosen to be ≥ Bmo/2 ≃ Bme, see Fig. 2. 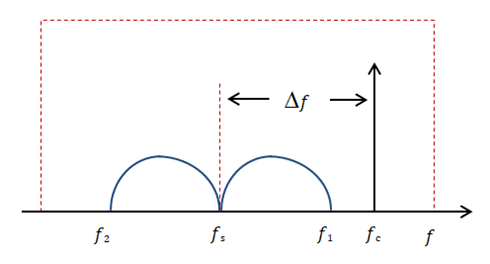 | Figure 2. Spectral requirement for the optical passband filter |
 𝑓2 = 𝑓s - BmeTo simplify the design of the OBPF, the central frequency and bandwidth of the OBPF are set, respectively, to 𝑓s and > 2Δ𝑓. This makes the OBPF parameters adapt the used lasers frequencies 𝑓s and 𝑓c.c- Optical Receiver (Fig. 1c) The optical receiver uses DD process supported by KK algorithm to extract the data from the received coherently modulated optical signal without using a local laser. The received optical signal is applied to a photodiode (PD) to produce the photocurrent. This current will pass through a series of analog and digital signal processing to recover the information data. First, the photocurrent is amplified using a low-noise electronic amplifier and then pass through a lowpass filter to extract the electrical message spectrum. The filtered photocurrent is then applied to analog-to-digital converter (ADC) to produce a digital signal suitable for the next processing (DSP) units. The DSP units perform the following functioni- Kramers- Kronig receiver algorithm.ii- Fiber chromatic dispersion (CD) compensation.iii- Nyquist-Filter shaping.iv- Frequency shift offset.v- Clock phase recovery.vi- Time delay estimation (TDE)-Multiple-input multiple-output (MIMO).vii- Clock-and-slice.viii- Blind phase search.These DSP units are available in VPIphotonics ver.11 library.
𝑓2 = 𝑓s - BmeTo simplify the design of the OBPF, the central frequency and bandwidth of the OBPF are set, respectively, to 𝑓s and > 2Δ𝑓. This makes the OBPF parameters adapt the used lasers frequencies 𝑓s and 𝑓c.c- Optical Receiver (Fig. 1c) The optical receiver uses DD process supported by KK algorithm to extract the data from the received coherently modulated optical signal without using a local laser. The received optical signal is applied to a photodiode (PD) to produce the photocurrent. This current will pass through a series of analog and digital signal processing to recover the information data. First, the photocurrent is amplified using a low-noise electronic amplifier and then pass through a lowpass filter to extract the electrical message spectrum. The filtered photocurrent is then applied to analog-to-digital converter (ADC) to produce a digital signal suitable for the next processing (DSP) units. The DSP units perform the following functioni- Kramers- Kronig receiver algorithm.ii- Fiber chromatic dispersion (CD) compensation.iii- Nyquist-Filter shaping.iv- Frequency shift offset.v- Clock phase recovery.vi- Time delay estimation (TDE)-Multiple-input multiple-output (MIMO).vii- Clock-and-slice.viii- Blind phase search.These DSP units are available in VPIphotonics ver.11 library.4.1.2. Kramers-Kronig Algorithm
- The KK algorithm is implemented in the receiver to retrieve the phase information from the photocurrent through Hilbert transform. The electric field of the optical signal incident on the PD can be expressed by
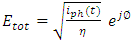 | (18) |
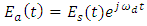 where
where 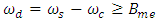
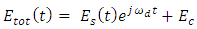 | (19) |
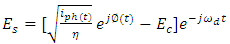 | (20) |
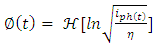 | (21) |
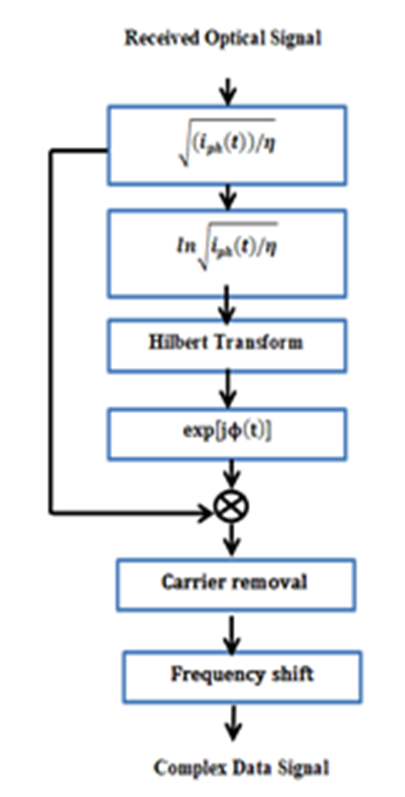 | Figure 3. Schematic diagram of Kramers-Kronig receiver |
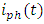 .(ii) Apply Hilbert transform to
.(ii) Apply Hilbert transform to 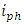 in order to estimate the phase information Ø(t). (Eqn 21). (iii) Calculate Etot(t) using the values of
in order to estimate the phase information Ø(t). (Eqn 21). (iii) Calculate Etot(t) using the values of 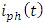 and Ø(t). (Eqn.18)(iv) Remove the reference carrier from Etot(t). (Eqn. 20)(v) Shift the resulting signal from the intermediate frequency ωd to the baseband.
and Ø(t). (Eqn.18)(iv) Remove the reference carrier from Etot(t). (Eqn. 20)(v) Shift the resulting signal from the intermediate frequency ωd to the baseband.4.2. Simulation Results for SP KK-Based Optical Networks
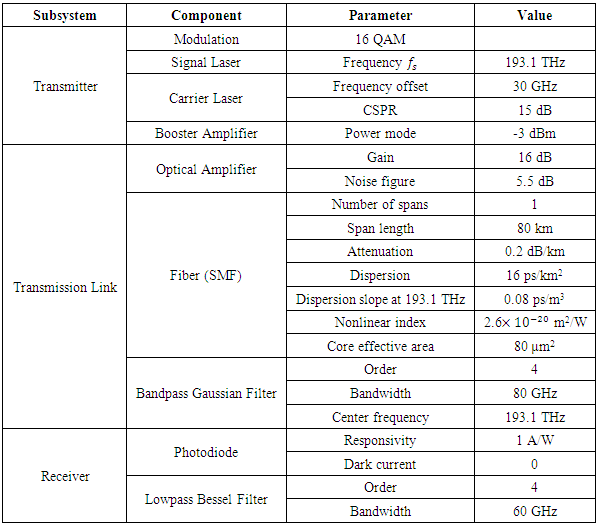
- This subsection presents simulation results to assess the transmission performance of SP 16-QAM point-to-point coherent optical networks incorporating KK-based DD receiver. The results are reported for two systems operating with a bit rate of 200 and 400 Gbps and implemented in VPIphotonics environment to support C band operation (𝑓s = 193.1 THz, i.e., λ ≃ 1550 nm). Unless otherwise stated, the main system parameters values used in the simulation are listed in Table 1. The transmission link consists of multispan, each span has 80 km SMF followed by a 16 dB OA to compensate the span loss of 0.2 dB/km.
|
4.2.1. Performance of 200 Gbps 16-QAM System
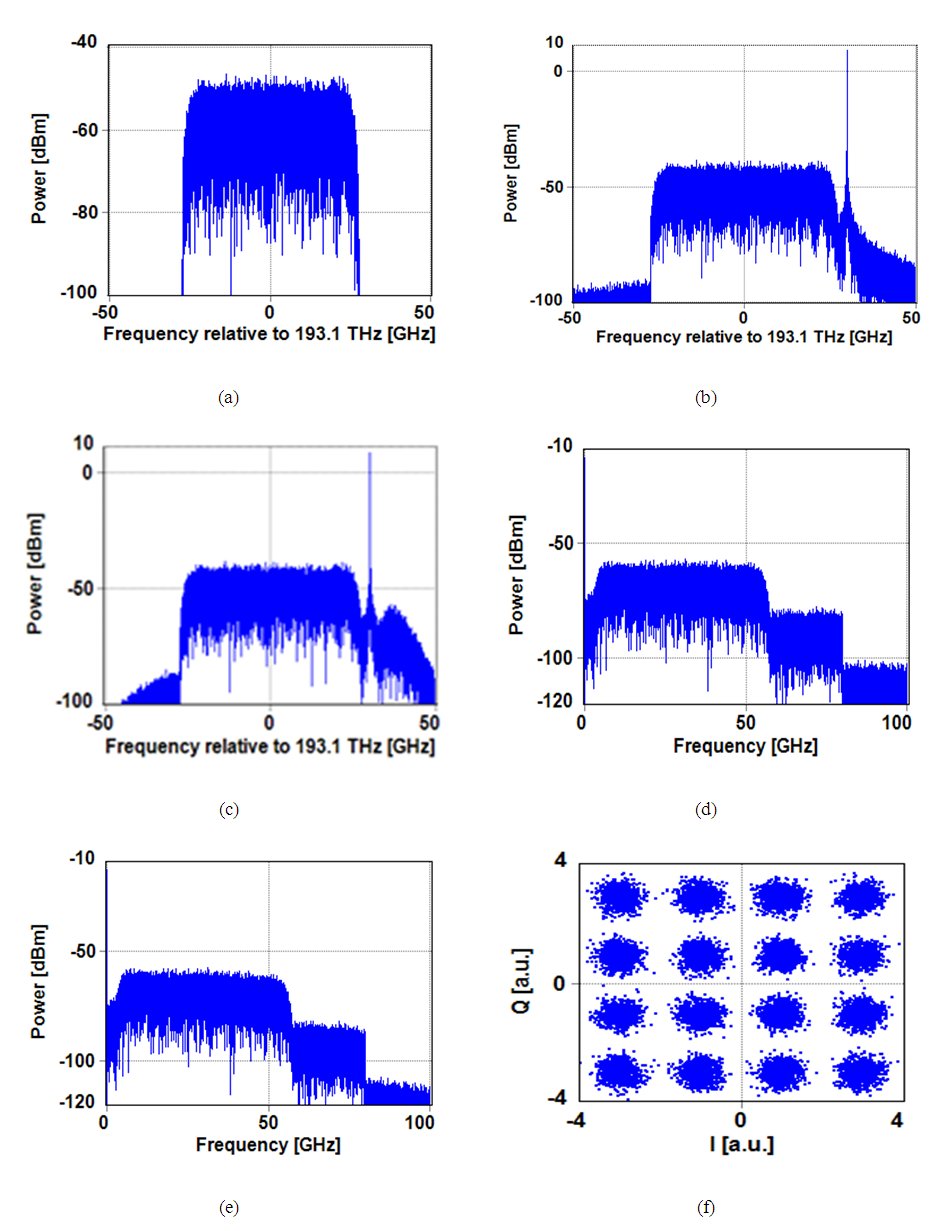
- Figures 4a-e show the signals spectra at different points of the 200 Gbps 16-QAM system. The corresponding receiver constellation diagram (at the output of the DSP) is presented in Fig. 4f. The parameters values used to obtain these results are single-span link (span length Lspan= 80 km), RCF roll-off r = 0.1, signal power launched to the fiber Ps = -3dBm, carrier-to-signal power ratio CSPR = 15 dB, carrier frequency offset Δ𝑓 = 30 GHz, and bandwidth of the OBPF = 80 GHz.It is clear from Fig. 4a that the modulated optical signal has approximately a -3 dB bandwidth of 27.5 GHz (Bmo= (1+r)Rs, where Rs= 25 GSps is the sampling rate). Thus choosing Δ𝑓 = 30 GHz ensures that the carrier component is placed outside the modulated optical signal spectrum. Note also that the received constellation diagram (Fig. 4f) is clear yielding low BER (BER= 4.7X10-5 < BERth).
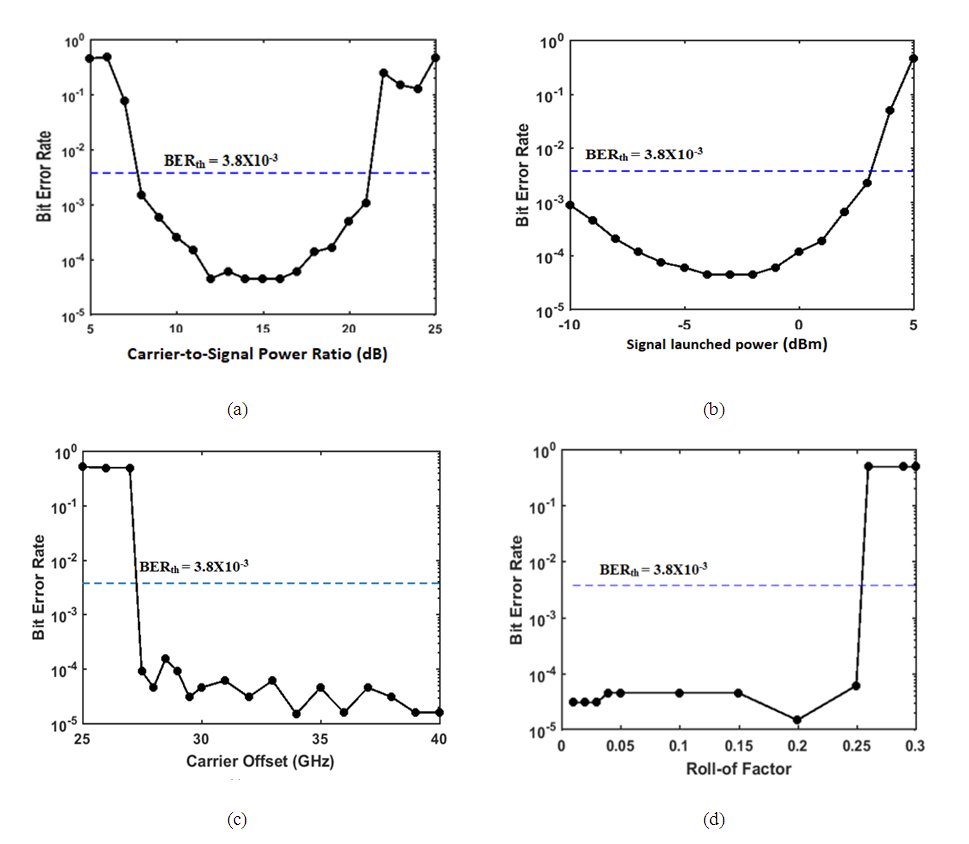 | Figure 5. Variation of BER of SP 200 Gbps 16-QAM system with (a) Carrier-to-signal power ratio. (b) Signal launched power. (c) Carrier offset. (d) Roll-off factor |
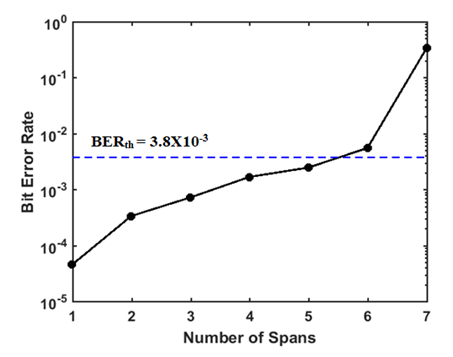 | Figure 6. Variation of BER of SP 200 Gbps 16-QAM with transmission distance |
4.2.2. Performance of 400 Gbps 16-QAM System
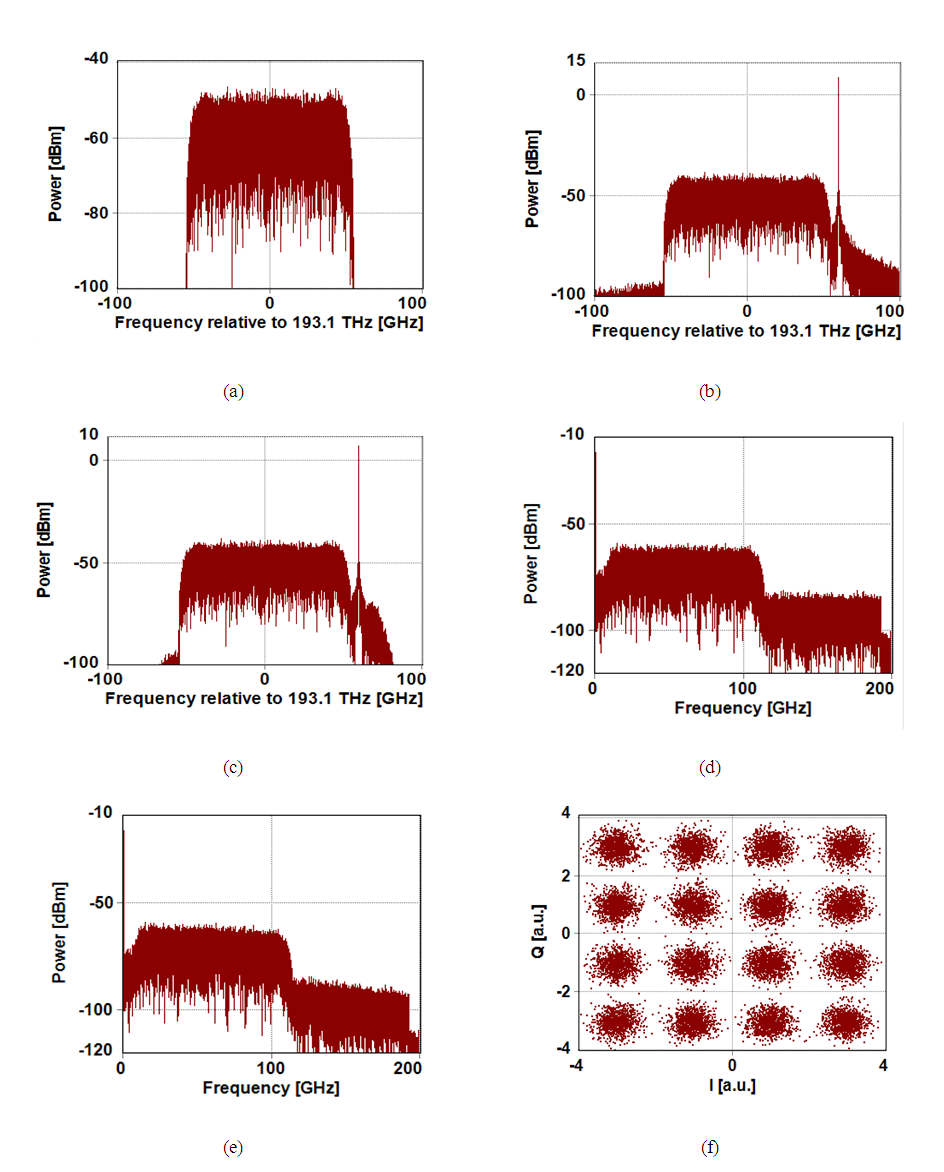
- The investigation reported in subsection 4.2 are repeated here for 400 Gbps 16-QAM system and the results are shown in Figs. 7 and 8. The signal spectra at different points of the system are depicted in Figs. 7a-e assuming L = 80 km, r = 0.1, Ps = -3 dBm, CSPR = 15 dB, and ∆𝑓 = 60 GHz. The -3 dB bandwidth of the modulated optical signal is around 55 GHz as shown in Fig. 6a which corresponds to (1+r) Rs where Rs=50 GSps. The received constellation diagram is shown in Fig. 3-7f which yields a BER of 4.7X10-5 (< BERth = 3.8X10-3). The parametric study is shown in Fig. 3-8 and has been used to select the following design parameters: CSPR = 15 dB, Ps = -3 dBm, ∆𝑓 = 60 GHz and r = 0.1. The variation of BER with transmission distance is illustrated in Fig. 3-9. Note that the maximum reach is 428 km when the achieved BER equals to the threshold value of 3.8X10-3.
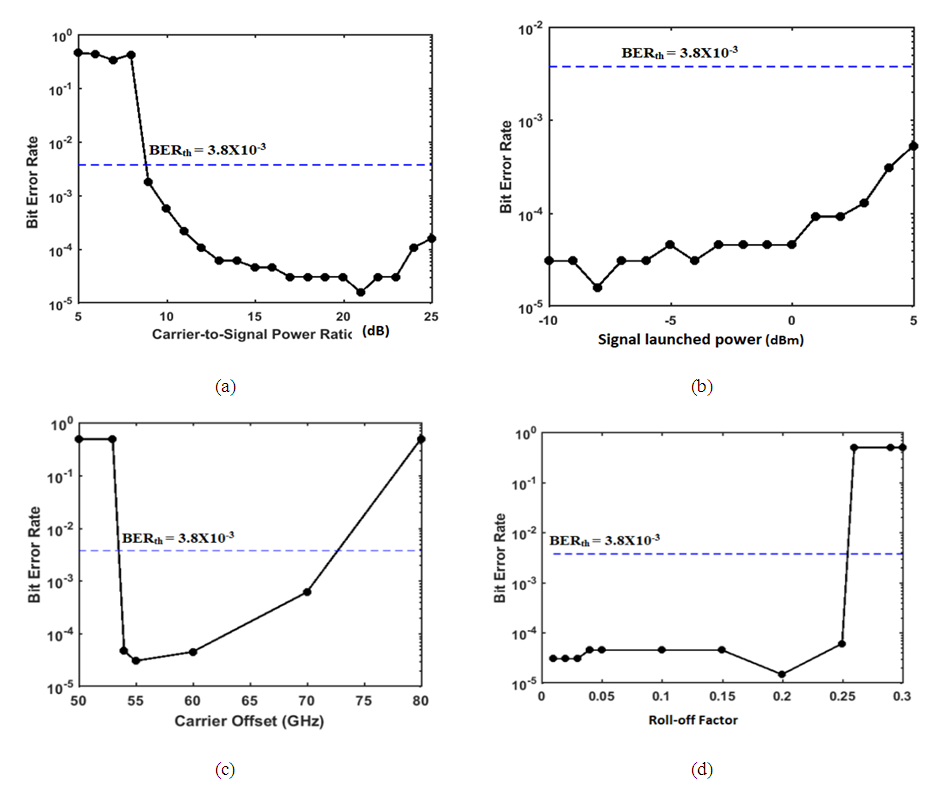 | Figure 8. Variation of BER of 400 Gbps 16-QAM with (a) Carrier-to-signal power ratio (dB). (b) Signal launched power. (dBm). (c) Carrier offset (GHz). (d) Roll-off factor |
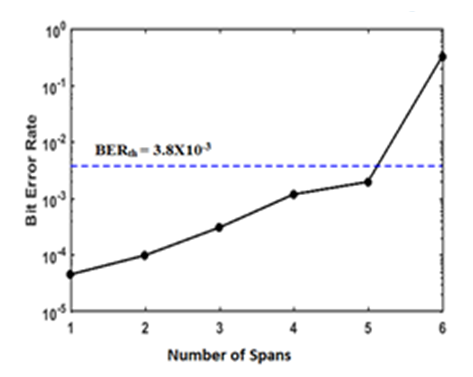 | Figure 9. Variation of BER of SP 400 Gbps 16-QAM with transmission distance |
4.3. Design of Dual-Polarization KK Receiver-based System
- Dual polarization (DP) technique is an efficient way to double the transmitted bit rate by multiplexing two half-bit rate quadrature SP systems into the optical fiber link. This technique can be considered as a two-channel polarization multiplexing where the speeds of used electronics and electrical-to-optical (and vice versa) converters are less than that used in an equivalent single-channel system. This subsection presents design configuration for DP coherent modulation KK-based DD optical communication system. Two 16-QAM systems are designed in Figure 10 shows a block diagram for the designed DP KK receiver-based system. The system consists of two identical subsystems sharing the same optical channel (fiber link) and designed to operate with two perpendicular polarization states TE and TM (or X and Y). Each subsystem consists of an optical modulator to generate the "modulated optical signal + carrier" and DD optical receiver incorporating KK algorithm. The signal and carrier lasers fields are polarized at 45° to ensure that each field has equal TE and TM components. A polarization combiner acts as a multiplexer at the transmitter side while a polarization splitter is used at the receiver side for demultiplexing purpose.
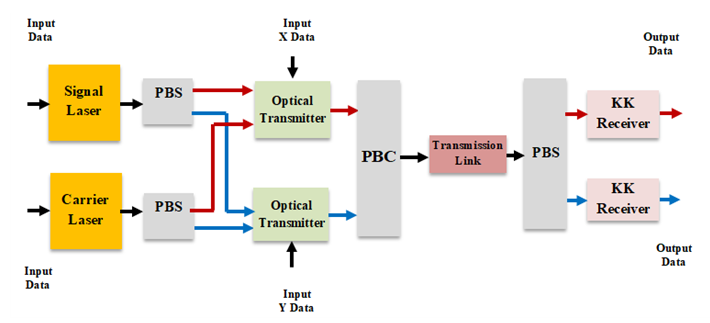 | Figure 10. Block diagram for the dual-polarization designed KK receiver-based systems.PBS: Polarization beam splitter PBC: Polarization beam combiner |
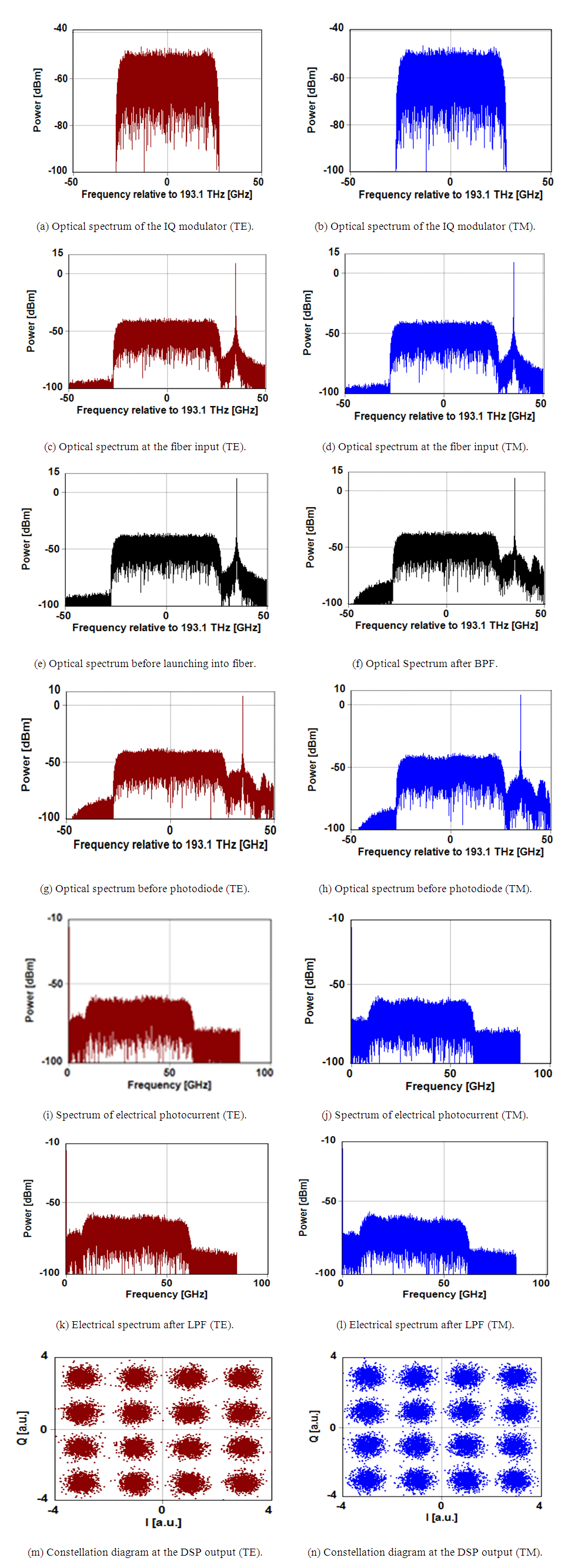 | Figure 11. Spectra and constellation diagrams of DP 400 Gbps 16-QAM system |
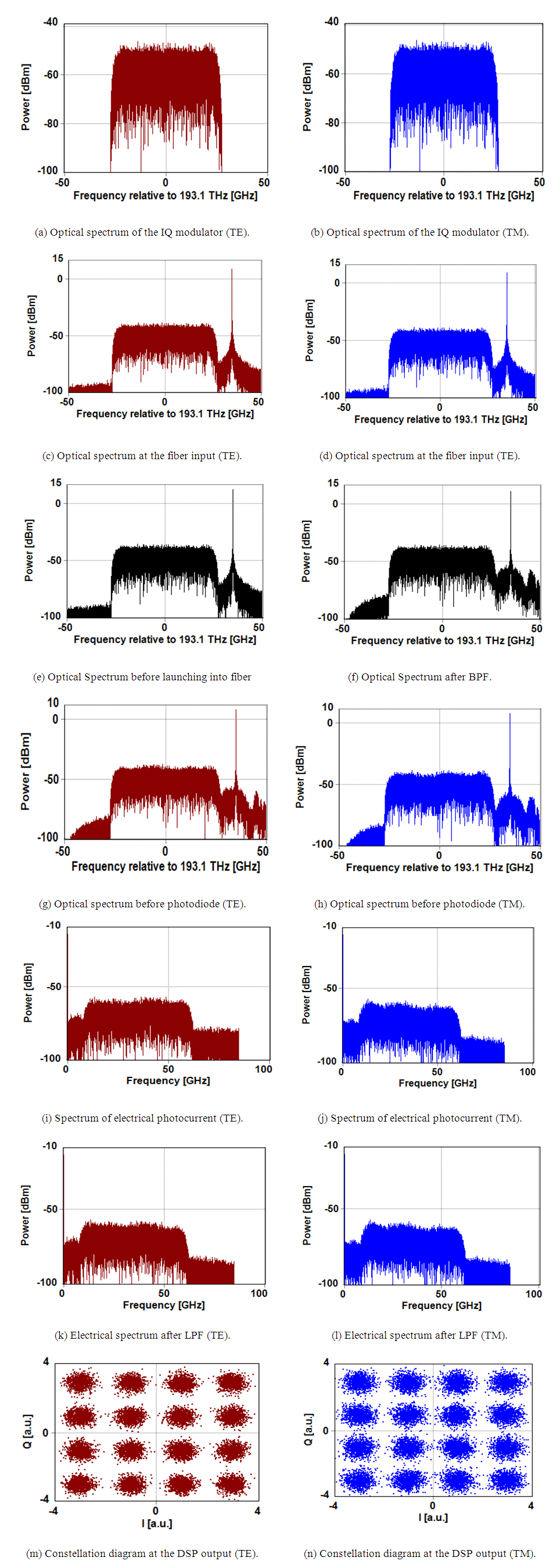 | Figure 12. Spectra and constellation diagrams of the DP 800 Gbps 16-QAM system |
5. Conclusions
- A point-to-point optical network configuration has been designed using coherent modulation/direct detection schemes to support single-polarization (SP) 200 and 400 Gbps 16-QAM signaling. The design has been modified to double the transmission bit rates (400 and 800 Gbps) using dual-polarization (DP) multiplexing technique. The configuration uses two lasers at the transmitter side and Kramers-Kronig algorithm to retrieve the complex phase of the received optical signal data from the photocurrent using Hilbert transform in addition to implementing DSP-based electronic chromatic dispersion at the receiver side. The main conclusions drawn for this study are (i) The configuration supports the transmission of SP 400 Gbps 16-QAM (DP 800 Gbps 16-QAM) signal over more than 100 km SSMF. (ii) The KK-based receiver offers efficient direct-detection process for double-sideband coherent-modulated optical signals operating at these high-bit rates.(iii) The configuration offers 440 and 428 km maximum reach for SP 16-QAM signals operating with 200 and 400 Gbps data rates, respectively.(iv) There is an optimum value for the carrier-to-signal power ratio, CSPRopt, of 15 dB when 200 and 400 Gbps SP 16-QAM signals are transmitted over a single span (80 km) of SSMF, respectively.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML