-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Networks and Communications
p-ISSN: 2168-4936 e-ISSN: 2168-4944
2013; 3(2): 39-44
doi:10.5923/j.ijnc.20130302.01
Analysis on the Algebraic Decoding of the (31, 16, 7) QR Code by Using IFBM Algorithm
Hung-Peng Lee
Department of Computer Science and Information Engineering, Fortune Institute of Technology, Kaohsiung, 83160, Taiwan
Correspondence to: Hung-Peng Lee, Department of Computer Science and Information Engineering, Fortune Institute of Technology, Kaohsiung, 83160, Taiwan.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
An analysis on the algebraic decoding of the (31, 16, 7) quadratic residue (QR) code with reducible generator polynomial that uses the inverse-free Berlekamp-Massey (IFBM) algorithm to determine the error-locator polynomial is presented in this paper. The primary known syndrome S1 will be equal to zero for some weight-3 error patterns. However, the zero S1 does not cause a decoding failure while using the IFBM algorithm to determine the error-locator polynomial. Two examples with detailed step-by-step analysis show the decoding procedure.
Keywords: Quadratic Residue Code, Algebraic Decoding Algorithm, Inverse-Free Berlekamp-Massey Algorithm, Error Pattern, Syndrome
Cite this paper: Hung-Peng Lee, Analysis on the Algebraic Decoding of the (31, 16, 7) QR Code by Using IFBM Algorithm, International Journal of Networks and Communications, Vol. 3 No. 2, 2013, pp. 39-44. doi: 10.5923/j.ijnc.20130302.01.
Article Outline
1. Introduction
- The well-known QR codes, introduced by Prange[1] in 1957, are cyclic BCH codes with code rates greater than or equal to one-half. In addition, the codes generally have large minimum distances so that most of the known QR codes are the best-known codes. The code augmented by a parity bit, for example, the (24, 12, 8) QR code was utilized to provide error control on the Voyager deep-space mission[2].In the past decades, several decoding techniques have been developed to decode the binary QR codes. The ADAs most used to decode the QR codes are the Newton identities with either Sylvester resultants[3-7,12-13,15] or Gröbner bases[16] , or inverse-free Berlekamp-Massey (IFBM) algorithm[8-11,14] to determine the error-locator polynomial. Among them, the ADA of the (31, 16, 7) QR code[5,12,14,15] with the reducible polynomial can correct up to three errors in the finite field GF(25), because the error-correcting capability of the code is
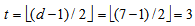 errors, where
errors, where 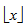 denotes the greatest integer less than or equal to x, and d = 7 is the minimum Hamming distance of the code. In[5,12,15], the Newton identities are applied to determine the coefficients of the error-locator polynomials. In[14], the IFBM algorithm[18] is applied to determine the error-locator polynomial of the received sequence. Finally, the Chien search algorithm[19] is applied to find the roots of the error-locator polynomial.In[15], the decoding algorithm is very complicated because the syndrome S7 = 0. However, the IFBM does not use the syndrome S7 to determine the error-locator polynomial of the (31, 16, 7) QR code. For the QR codes with irreducible generator polynomial, the primary known syndrome S1 cannot be equal to zero, because the zero S1 denotes that the received word has no errors in the transmission channel. Besides, S1 = 0 means that the power (mod codelength n) of S1 are all zero; that is, S2 = (S1)2 = 0, S4 = (S1)4 = 0, …. For the (89, 45, 17) QR code with reducible generator polynomial in the finite field GF(211), the IFBM algorithm can be used to determine the error-locator polynomial while the syndrome S1 = 0[20]. Similarly, for the (31, 16, 7) QR code with reducible generator polynomial in the finite field GF(25), the zero primary known syndromes, S1 = 0 and S5 = 0, do not cause a decoding failure in decoding weight-3 error patterns while using the IFBM algorithm to determine the error-locator polynomial. The analysis of two examples on the weight-3 error patterns shows the fact.The rest parts of this paper are organized as follows: The background of systematic (31, 16, 7) QR codes is briefly given in Section 2. The analysis on the zero primary known syndromes for the weight-3 error patterns is presented in Section 3. Finally, this paper concludes with a brief summary in Section 4.
denotes the greatest integer less than or equal to x, and d = 7 is the minimum Hamming distance of the code. In[5,12,15], the Newton identities are applied to determine the coefficients of the error-locator polynomials. In[14], the IFBM algorithm[18] is applied to determine the error-locator polynomial of the received sequence. Finally, the Chien search algorithm[19] is applied to find the roots of the error-locator polynomial.In[15], the decoding algorithm is very complicated because the syndrome S7 = 0. However, the IFBM does not use the syndrome S7 to determine the error-locator polynomial of the (31, 16, 7) QR code. For the QR codes with irreducible generator polynomial, the primary known syndrome S1 cannot be equal to zero, because the zero S1 denotes that the received word has no errors in the transmission channel. Besides, S1 = 0 means that the power (mod codelength n) of S1 are all zero; that is, S2 = (S1)2 = 0, S4 = (S1)4 = 0, …. For the (89, 45, 17) QR code with reducible generator polynomial in the finite field GF(211), the IFBM algorithm can be used to determine the error-locator polynomial while the syndrome S1 = 0[20]. Similarly, for the (31, 16, 7) QR code with reducible generator polynomial in the finite field GF(25), the zero primary known syndromes, S1 = 0 and S5 = 0, do not cause a decoding failure in decoding weight-3 error patterns while using the IFBM algorithm to determine the error-locator polynomial. The analysis of two examples on the weight-3 error patterns shows the fact.The rest parts of this paper are organized as follows: The background of systematic (31, 16, 7) QR codes is briefly given in Section 2. The analysis on the zero primary known syndromes for the weight-3 error patterns is presented in Section 3. Finally, this paper concludes with a brief summary in Section 4.2. Background of the Binary (31, 16, 7) QR Code
- The codeword of the binary (n, k, d) QR code is defined algebraically as a multiple of its generator polynomial g(x) with coefficients in GF(2). Let the length of the code n be a prime number of the form n = 8m ± 1, where m is a positive integer and m be the smallest positive integer such that 2m ≡ 1 (mod n). Thus, GF(2m) is the extension field of GF(2). Also, let k = (n+1)/2 be the message length and d be the minimum Hamming distance or Hamming weight of the code. The generator polynomial as a cyclic code is given by
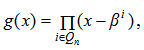 | (1) |
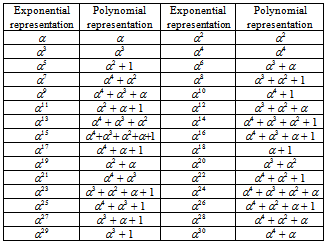
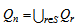 relating Qn to the cyclotomic cosets, modulo n.Let an element α GF(25) be a root of the primitive polynomial p(x) = x5 + x2 + 1. Then, α generates the multiplicative group of nonzero elements in GF(25). Also, let an element β = αu, where u = (2m – 1)/n = (25 – 1)/31 = 1, is a primitive 31th root of unity in GF(25); that is, β = α. The all 31 roots of x31 – 1 = 0 are shown in Table 1.
relating Qn to the cyclotomic cosets, modulo n.Let an element α GF(25) be a root of the primitive polynomial p(x) = x5 + x2 + 1. Then, α generates the multiplicative group of nonzero elements in GF(25). Also, let an element β = αu, where u = (2m – 1)/n = (25 – 1)/31 = 1, is a primitive 31th root of unity in GF(25); that is, β = α. The all 31 roots of x31 – 1 = 0 are shown in Table 1.
|
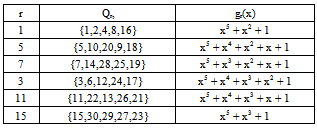
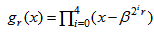 . Therefore, the six cyclotomic cosets Qr and their corresponding minimal polynomials are shown in Table 2.
. Therefore, the six cyclotomic cosets Qr and their corresponding minimal polynomials are shown in Table 2.
|
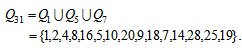 | (2) |
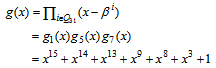 | (3) |
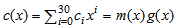 , where ci ∈ GF(2) for 0 ≤ i ≤ 30, and m(x) = m15x15 + + m1x + m0 denotes information polynomial, where mi ∈ GF(2) for 0 ≤ i ≤ 15. In such a representation, this type of codeword is called the non-systematic encoding. In practice, the encoding procedure is often implemented by the use of systematic encoding. Let p(x) = p14x14 + + p1x + p0 be the parity-check polynomial, where pi ∈ GF(2) for 0 ≤ i ≤ 14. Also, let m(x)xn-k divide by g(x), then we get the following identity:
, where ci ∈ GF(2) for 0 ≤ i ≤ 30, and m(x) = m15x15 + + m1x + m0 denotes information polynomial, where mi ∈ GF(2) for 0 ≤ i ≤ 15. In such a representation, this type of codeword is called the non-systematic encoding. In practice, the encoding procedure is often implemented by the use of systematic encoding. Let p(x) = p14x14 + + p1x + p0 be the parity-check polynomial, where pi ∈ GF(2) for 0 ≤ i ≤ 14. Also, let m(x)xn-k divide by g(x), then we get the following identity: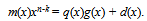 | (4) |
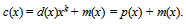 | (5) |
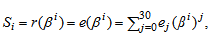 | (6) |
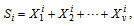 where
where 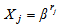 for 1 ≤ j ≤ v are called the error locators. Assuming that v errors occur, the classical error-locator polynomial L(x) is defined by
for 1 ≤ j ≤ v are called the error locators. Assuming that v errors occur, the classical error-locator polynomial L(x) is defined by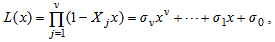 | (7) |
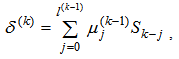 | (8) |
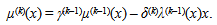 | (9) |
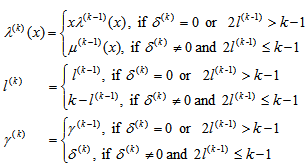 | (10) |
3. Analysis on the Zero Primary Known Syndromes for the Weight-3 Error Patterns
- The ADA given in[14] used the IFBM algorithm to determine the error-locator polynomial. In order to use the IFBM algorithm, the consecutive syndromes, Si for 1 ≤ i ≤ 6, need to be computed first. Among them, there are two unknown syndromes S3, and S6, where S6 can be computed from the square of S3. The determination of the unknown syndrome S3 is computed from (17) of[12].For the (31, 16, 7) QR code, a C++ program shows that there are 155 weight-3 error patterns will cause the primary known syndromes and the primary unknown syndromes to be equal to zero; however, they are not simultaneous equal to zero. The zero primary known syndromes do not cause a decoding failure while using the IFBM algorithm to determine the error-locator polynomial. The following example shows the decoding procedure.
3.1. The Case of Primary Known Syndrome S1 = 0
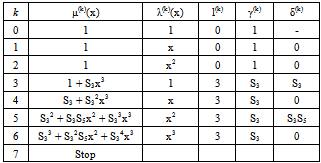
- Example 1:If m(x) = x7, by (4) and (5), then the systematic codeword is c(x) = x30 + x29 + x27 + x26 + x25 + x20 + x19 + x7. If there is a weight-3 error pattern e(x) = x18 + x + 1 occurred in the transmission channel, then the received word becomes r(x) = x30 + x29 + x27 + x26 + x25 + x20 + x19 + x18 + x7 + x + 1.The syndromes S1 = 0, S2 = 0, S4 = 0, and S5 = α30 are computed by (6), respectively, and the syndromes S3 = α19 and S6 = S32 = α7 are computed by (17) in[12]. Next, the IFBM algorithm is applied to obtain the error-locator polynomial. The decoding procedure is described as follows:Define initial value as follows: k = 0, μ(0)(x) = 1, λ(0)(x)=1, l(0) = 0, γ(0) = 1.Set k = k + 1 = 0 + 1 = 1. By (8), compute
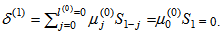 By (9), compute μ(1)(x) = γ(0)μ(0)(x) – δ(1)λ(0)(x)•x = 1∙1 – 0∙1∙x = 1.The condition in (10) is δ(1) = 0. Compute λ(1)(x) = xλ(0)(x) = x, l(1) = l(0) = 0, and γ(1) =γ(0) = 1, respectively. Go to step 2.Set k = k + 1 = 1 + 1 = 2. By (8), compute
By (9), compute μ(1)(x) = γ(0)μ(0)(x) – δ(1)λ(0)(x)•x = 1∙1 – 0∙1∙x = 1.The condition in (10) is δ(1) = 0. Compute λ(1)(x) = xλ(0)(x) = x, l(1) = l(0) = 0, and γ(1) =γ(0) = 1, respectively. Go to step 2.Set k = k + 1 = 1 + 1 = 2. By (8), compute 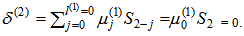 By (9), compute μ(2)(x) = γ(1)μ(1)(x) – δ(2)λ(1)(x)x = 0∙1 – 0∙1∙x = 1.The condition in (10) is δ(2) = 0. Compute λ(2)(x) = xλ(1)(x) = xx = x2, l(2) = l(1) = 0, and γ(2) = γ(1) = 1, respectively. Go to step 2.Set k = k + 1 = 2 + 1 = 3. By (8), compute
By (9), compute μ(2)(x) = γ(1)μ(1)(x) – δ(2)λ(1)(x)x = 0∙1 – 0∙1∙x = 1.The condition in (10) is δ(2) = 0. Compute λ(2)(x) = xλ(1)(x) = xx = x2, l(2) = l(1) = 0, and γ(2) = γ(1) = 1, respectively. Go to step 2.Set k = k + 1 = 2 + 1 = 3. By (8), compute 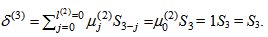 By (9), compute μ(3)(x) = γ(2)μ(2)(x) – δ(3)λ(2)(x)•x = 1∙1 – S3∙x2∙x = 1 + S3x3.The conditions in (10) are δ(3) = S3 ≠ 0 and 2l(2) = 0 ≤ k – 1 = 3 – 1 = 2. Compute λ(3)(x) = μ(2)(x) = 1, l(3) = k - l(2) = 3 – 0 = 3, and γ(3) = δ(3) = S3, respectively. Go to step 2.Set k = k + 1 = 3 + 1 = 4. By (8), compute.By (9), compute μ(4)(x) = γ(3)μ(3)(x) – δ(4)λ(3)(x)•x = S3(1 – S3x3) = S3 + S32x3.The condition in (10) is δ(4) = 0. Compute λ(4)(x) = x•1 = x, l(4) = l(3) = 3, and γ(4) = γ(3) = S3, respectively. Go to step 2.Set k = k + 1 = 4 + 1 = 5. By (8), compute
By (9), compute μ(3)(x) = γ(2)μ(2)(x) – δ(3)λ(2)(x)•x = 1∙1 – S3∙x2∙x = 1 + S3x3.The conditions in (10) are δ(3) = S3 ≠ 0 and 2l(2) = 0 ≤ k – 1 = 3 – 1 = 2. Compute λ(3)(x) = μ(2)(x) = 1, l(3) = k - l(2) = 3 – 0 = 3, and γ(3) = δ(3) = S3, respectively. Go to step 2.Set k = k + 1 = 3 + 1 = 4. By (8), compute.By (9), compute μ(4)(x) = γ(3)μ(3)(x) – δ(4)λ(3)(x)•x = S3(1 – S3x3) = S3 + S32x3.The condition in (10) is δ(4) = 0. Compute λ(4)(x) = x•1 = x, l(4) = l(3) = 3, and γ(4) = γ(3) = S3, respectively. Go to step 2.Set k = k + 1 = 4 + 1 = 5. By (8), compute 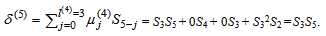 By (9), compute the error-locator polynomial of degree 3, μ(5)(x) = γ(4)μ(4)(x) – δ(5)λ(4)(x)•x = S3(S3 + S32x3) – (S3S5)xx = S32 + S3S5x2 + S33x3.The condition in (10) is 2l(k-1) = 2l(4) = 6 > k – 1 = 5 – 1 = 4. Compute λ(5)(x) = xλ(4)(x) = xx = x2, l(5) = l(4) = 3, and γ(5) = γ(4) = S3, respectively. Go to step 2.Set k = k + 1 = 5 + 1 = 6. By (8), compute
By (9), compute the error-locator polynomial of degree 3, μ(5)(x) = γ(4)μ(4)(x) – δ(5)λ(4)(x)•x = S3(S3 + S32x3) – (S3S5)xx = S32 + S3S5x2 + S33x3.The condition in (10) is 2l(k-1) = 2l(4) = 6 > k – 1 = 5 – 1 = 4. Compute λ(5)(x) = xλ(4)(x) = xx = x2, l(5) = l(4) = 3, and γ(5) = γ(4) = S3, respectively. Go to step 2.Set k = k + 1 = 5 + 1 = 6. By (8), compute 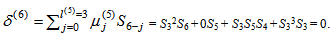 By (9), compute the error-locator polynomial of degree 3, μ(6)(x) = γ(5)μ(5)(x) – δ(6)λ(5)(x)x = S3(S32 + S3S5x2 + S33x3) = S33 + S32S5x2 + S34x3.The condition in (10) is δ(6) = 0, compute λ(6)(x) = xλ(5)(x) = xx2 = x3, l(6) = l(5) = 3, and γ(6) = γ(5) = S3, respectively. Go to step 2.Set k = k + 1 = 6 + 1 = 7. Since k = 7 > 2t = 6, go to stop.The above decoding procedure is simplified in Table 3.
By (9), compute the error-locator polynomial of degree 3, μ(6)(x) = γ(5)μ(5)(x) – δ(6)λ(5)(x)x = S3(S32 + S3S5x2 + S33x3) = S33 + S32S5x2 + S34x3.The condition in (10) is δ(6) = 0, compute λ(6)(x) = xλ(5)(x) = xx2 = x3, l(6) = l(5) = 3, and γ(6) = γ(5) = S3, respectively. Go to step 2.Set k = k + 1 = 6 + 1 = 7. Since k = 7 > 2t = 6, go to stop.The above decoding procedure is simplified in Table 3.
|
3.2. The Case of Primary Known Syndrome S5 = 0
- Example 2:If m(x) = x7, by (4) and (5), then the systematic codeword is c(x) = x30 + x29 + x27 + x26 + x25 + x20 + x19 + x7. If there is a weight-3 error pattern e(x) = x19 + x + 1 occurred in the transmission channel, then the received word becomes r(x) = x30 + x29 + x27 + x26 + x25 + x20 + x7 + x + 1.The known syndromes S1 = α5, S2 = α10, S4 = α20, and S5 = 0 are computed by (6), respectively, and the known syndromes S3 = α24 and S6 = α17 are computed by (17) in[12]. Next, the IFBM algorithm is applied to obtain the error-locator polynomial. The decoding procedure is described as follows:Define initial value as follows: k = 0, μ(0)(x) = 1, λ(0)(x)=1, l(0) = 0, γ(0) = 1.Set k = k + 1 = 0 + 1 = 1. By (8), compute
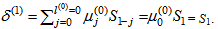 By (9), compute μ(1)(x) = γ(0)μ(0)(x) – δ(1)λ(0)(x)•x = 1∙1 – S1∙1∙x = 1 + S1x.By (10), the conditions δ(1) = S1 ≠ 0 and 2l(0) = 2∙0 = 0 ≤ k – 1 = 1 – 1 = 0 are satisfied. Then compute λ(1)(x) = μ(0)(x) = 1, l(1) = k – l(0) = 1 – 0 = 1, and γ(1) = δ(1) = S1, respectively. Go to step 2.Set k = k + 1 = 1 + 1 = 2. By (8), compute
By (9), compute μ(1)(x) = γ(0)μ(0)(x) – δ(1)λ(0)(x)•x = 1∙1 – S1∙1∙x = 1 + S1x.By (10), the conditions δ(1) = S1 ≠ 0 and 2l(0) = 2∙0 = 0 ≤ k – 1 = 1 – 1 = 0 are satisfied. Then compute λ(1)(x) = μ(0)(x) = 1, l(1) = k – l(0) = 1 – 0 = 1, and γ(1) = δ(1) = S1, respectively. Go to step 2.Set k = k + 1 = 1 + 1 = 2. By (8), compute 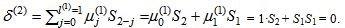 By (9), compute μ(2)(x) = γ(1)μ(1)(x) – δ(2)λ(1)(x)x = S1(1 + S1x) – 0∙1∙x = S1 + S12x.By (10), the condition δ(2) = 0 is satisfied. Then compute λ(2)(x) = xλ(1)(x) = x, l(2) = l(1) = 1, and γ(2) = γ(1) = S1, respectively. Go to step 2.Set k = k + 1 = 2 + 1 = 3. By (8), compute
By (9), compute μ(2)(x) = γ(1)μ(1)(x) – δ(2)λ(1)(x)x = S1(1 + S1x) – 0∙1∙x = S1 + S12x.By (10), the condition δ(2) = 0 is satisfied. Then compute λ(2)(x) = xλ(1)(x) = x, l(2) = l(1) = 1, and γ(2) = γ(1) = S1, respectively. Go to step 2.Set k = k + 1 = 2 + 1 = 3. By (8), compute 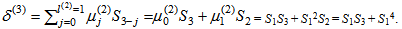 By (9), compute μ(3)(x) = γ(2)μ(2)(x) – δ(3)λ(2)(x)•x = S1(S1 + S12x) – (S1S3 + S14)∙x∙x = S12 + S13x +(S1S3 + S14)x2.By (10), the conditions δ(3) ≠ 0 and is 2l(2) = 2 ≤ k – 1 = 3 – 1 = 2. Compute λ(3)(x) = μ(2)(x) = S1 + S12x, l(3) = k – l(2) = 3 – 1 = 2, and γ(3) = δ(3) = S1S3 + S14, respectively. Go to step 2.Set k = k + 1 = 3 + 1 = 4. By (8), compute.
By (9), compute μ(3)(x) = γ(2)μ(2)(x) – δ(3)λ(2)(x)•x = S1(S1 + S12x) – (S1S3 + S14)∙x∙x = S12 + S13x +(S1S3 + S14)x2.By (10), the conditions δ(3) ≠ 0 and is 2l(2) = 2 ≤ k – 1 = 3 – 1 = 2. Compute λ(3)(x) = μ(2)(x) = S1 + S12x, l(3) = k – l(2) = 3 – 1 = 2, and γ(3) = δ(3) = S1S3 + S14, respectively. Go to step 2.Set k = k + 1 = 3 + 1 = 4. By (8), compute. 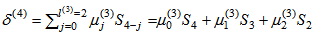 = S12S4 + S13S3 + (S1S3 + S14)S2 = 0.By (9), compute μ(4)(x) = γ(3)μ(3)(x) – δ(4)λ(3)(x)•x = (S1S3 + S14)( S12 + S13x +(S1S3 + S14)x2) – 0(S1 + S12x)x = (S13S3 + S16) + (S17 + S14S3)x + (S12S32 + S18)x2.By (10), the condition in is δ(4) = 0 is satisfied. Then compute λ(4)(x) = xλ(3)(x) = x(S1 + S12x) = S1x + S12x2, l(4) = l(3) = 2, and γ(4) = γ(3) = S1S3 + S14, respectively. Go to step 2.
= S12S4 + S13S3 + (S1S3 + S14)S2 = 0.By (9), compute μ(4)(x) = γ(3)μ(3)(x) – δ(4)λ(3)(x)•x = (S1S3 + S14)( S12 + S13x +(S1S3 + S14)x2) – 0(S1 + S12x)x = (S13S3 + S16) + (S17 + S14S3)x + (S12S32 + S18)x2.By (10), the condition in is δ(4) = 0 is satisfied. Then compute λ(4)(x) = xλ(3)(x) = x(S1 + S12x) = S1x + S12x2, l(4) = l(3) = 2, and γ(4) = γ(3) = S1S3 + S14, respectively. Go to step 2.
|
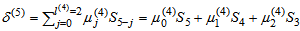 = (S13S3 + S16)0 + (S17 + S14S3)S4 + (S12S32 + S18)S3 = S111 + S12S33.By (9), compute μ(5)(x) = γ(4)μ(4)(x) – δ(5)λ(4)(x)•x = (S1S3 + S14)((S13S3 + S16) + (S17 + S14S3)x + (S12S32 + S18)x2) – (S111 + S12S33)(S1x + S12x2)x = (S110 + S14S32) + (S111 + S15S32)x + (S16S32 + S19S3)x2 + (S113 + S14S33)x3.By (10), the conditions δ(4) ≠ 0 and 2l(k-1) = 2l(4) = 4 ≤ k – 1 = 5 – 1 = 4 are satisfied. Then compute λ(5)(x) = μ(4)(x) = (S13S3 + S16) + (S17 + S14S3)x + (S12S32 + S18)x2, l(5) = k – l(4) = 5 – 2 = 3, and γ(5) = δ(5) = S111 + S12S33, respectively. Go to step 2.Set k = k + 1 = 5 + 1 = 6. By (8), compute δ(6) =
= (S13S3 + S16)0 + (S17 + S14S3)S4 + (S12S32 + S18)S3 = S111 + S12S33.By (9), compute μ(5)(x) = γ(4)μ(4)(x) – δ(5)λ(4)(x)•x = (S1S3 + S14)((S13S3 + S16) + (S17 + S14S3)x + (S12S32 + S18)x2) – (S111 + S12S33)(S1x + S12x2)x = (S110 + S14S32) + (S111 + S15S32)x + (S16S32 + S19S3)x2 + (S113 + S14S33)x3.By (10), the conditions δ(4) ≠ 0 and 2l(k-1) = 2l(4) = 4 ≤ k – 1 = 5 – 1 = 4 are satisfied. Then compute λ(5)(x) = μ(4)(x) = (S13S3 + S16) + (S17 + S14S3)x + (S12S32 + S18)x2, l(5) = k – l(4) = 5 – 2 = 3, and γ(5) = δ(5) = S111 + S12S33, respectively. Go to step 2.Set k = k + 1 = 5 + 1 = 6. By (8), compute δ(6) = 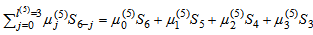 = (S110 + S14S32)S6 + (S111 + S15S32)S5 + (S16S32 + S19S3)S4 + (S113 + S14S33)S3 = 0.By (9), compute the error-locator polynomial of degree 3, μ(6)(x) = γ(5)μ(5)(x) – δ(6)λ(5)(x)x = (S111 + S12S33)( (S110 + S14S32) + (S111 + S15S32)x + (S16S32 + S19S3)x2 + (S113 + S14S33)x3) – 0((S13S3 + S16) + (S17 + S14S3)x + (S12S32 + S18)x2)x = (S121 + S16S35 + S112S33 + S115S32) + (S122 + S116S32 + S113S33 + S17S35)x + (S120S3 + S117S32 + S111S34 + S18S35)x2 + (S124 + S16S36)x3.By (10), the condition δ(6) = 0 is satisfied. Then compute λ(6)(x) = xλ(5)(x) = x((S13S3 + S16) + (S17 + S14S3)x + (S12S32 + S18)x2) = (S13S3 + S16)x + (S17 + S14S3)x2 + (S12S32 + S18)x3, l(6) = l(5) = 3, and γ(6) = γ(5) = S111 + S12S33, respectively. Go to step 2.Set k = k + 1 = 6 + 1 = 7. Since k = 7 > 2t = 6, go to stop.The above decoding procedure is simplified in Table 4. When k = 6, one obtains the error-locator polynomial μ(6)(x) = L(x) = (S121 + S16S35 + S112S33 + S115S32) + (S122 + S116S32 + S113S33 + S17S35)x + (S120S3 + S117S32 + S111S34 + S18S35)x2 + (S124 + S16S36)x3, which means that μ(6)(x) has three roots. By applying Chien search algorithm, the roots of L(x) are exactly the inverse of the three error locators {0, 1, 19}. For example, the third error locator is α19, and the reciprocal of α19 is α12. Substituting α12 into L(x), then the error-locator polynomial L(α12) = ((α5)21 + (α5)6(α24)5 + (α5)12(α24)3 + (α5)15(α24)2) + ((α5)22 + (α5)16(α24)2 + (α5)13(α24)3 + (α5)7(α24)5)α12 + ((α5)20(α24) + (α5)17(α24)2 + (α5)11(α24)4 + (α5)8(α24)5)(α12)2 + ((α5)24 + (α5)6(α24)6)(α12)3 = α12 + α26 + α8 + α30 + (α17 + α4 + α13 + 1)α12 + (1 + α9 + α27 + α5)α24 + (α27 + α19)α5 = α12 + α26 + α8 + α30 + α29 + α16 + α25 + α12 + α24 + α2 + α20 + α29 + α + α24 = 0. Similarly, the first and the second error locators are α0 = 1 and α, then we obtain L(1) = 0 and L(α30) = 0, respectively. A C++ program shows that the total 155 weight-3 error patterns with S5 = 0 can be corrected.For the primary known syndrome S7, there are also 155 weight-3 error patterns are equal to zero. However, the IFBM algorithm does not use S7 to decode the weight-3 error patterns.
= (S110 + S14S32)S6 + (S111 + S15S32)S5 + (S16S32 + S19S3)S4 + (S113 + S14S33)S3 = 0.By (9), compute the error-locator polynomial of degree 3, μ(6)(x) = γ(5)μ(5)(x) – δ(6)λ(5)(x)x = (S111 + S12S33)( (S110 + S14S32) + (S111 + S15S32)x + (S16S32 + S19S3)x2 + (S113 + S14S33)x3) – 0((S13S3 + S16) + (S17 + S14S3)x + (S12S32 + S18)x2)x = (S121 + S16S35 + S112S33 + S115S32) + (S122 + S116S32 + S113S33 + S17S35)x + (S120S3 + S117S32 + S111S34 + S18S35)x2 + (S124 + S16S36)x3.By (10), the condition δ(6) = 0 is satisfied. Then compute λ(6)(x) = xλ(5)(x) = x((S13S3 + S16) + (S17 + S14S3)x + (S12S32 + S18)x2) = (S13S3 + S16)x + (S17 + S14S3)x2 + (S12S32 + S18)x3, l(6) = l(5) = 3, and γ(6) = γ(5) = S111 + S12S33, respectively. Go to step 2.Set k = k + 1 = 6 + 1 = 7. Since k = 7 > 2t = 6, go to stop.The above decoding procedure is simplified in Table 4. When k = 6, one obtains the error-locator polynomial μ(6)(x) = L(x) = (S121 + S16S35 + S112S33 + S115S32) + (S122 + S116S32 + S113S33 + S17S35)x + (S120S3 + S117S32 + S111S34 + S18S35)x2 + (S124 + S16S36)x3, which means that μ(6)(x) has three roots. By applying Chien search algorithm, the roots of L(x) are exactly the inverse of the three error locators {0, 1, 19}. For example, the third error locator is α19, and the reciprocal of α19 is α12. Substituting α12 into L(x), then the error-locator polynomial L(α12) = ((α5)21 + (α5)6(α24)5 + (α5)12(α24)3 + (α5)15(α24)2) + ((α5)22 + (α5)16(α24)2 + (α5)13(α24)3 + (α5)7(α24)5)α12 + ((α5)20(α24) + (α5)17(α24)2 + (α5)11(α24)4 + (α5)8(α24)5)(α12)2 + ((α5)24 + (α5)6(α24)6)(α12)3 = α12 + α26 + α8 + α30 + (α17 + α4 + α13 + 1)α12 + (1 + α9 + α27 + α5)α24 + (α27 + α19)α5 = α12 + α26 + α8 + α30 + α29 + α16 + α25 + α12 + α24 + α2 + α20 + α29 + α + α24 = 0. Similarly, the first and the second error locators are α0 = 1 and α, then we obtain L(1) = 0 and L(α30) = 0, respectively. A C++ program shows that the total 155 weight-3 error patterns with S5 = 0 can be corrected.For the primary known syndrome S7, there are also 155 weight-3 error patterns are equal to zero. However, the IFBM algorithm does not use S7 to decode the weight-3 error patterns.4. Conclusions
- For the QR codes with irreducible generator polynomial, the primary known syndrome S1 cannot be equal to zero while the IFBM algorithm is used to determine the error-locator polynomial. In this paper, two examples with detailed step-by-step analysis show that the IFBM algorithm can obtain an valid error-locator polynomial for the (31, 16, 7) QR code with reducible generator polynomial in GF(25). However, the determination of the error-locator polynomial by using the IFBM is time-consuming. An efficient condition may be added in the IFBM to reduce the decoding time in the future.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML