Manfred Schneps-Schneppe 1, Janis Sedols 2
1Ventspils University College, Ventspils International Radio Astronomy Centre Inzenieru st 101, Ventspils, LV-3601, Latvia
2Institute of Mathematics and Computer Science, University of Latvia, Raina boulevard 29, Riga, LV-1459, Latvia
Correspondence to: Manfred Schneps-Schneppe , Ventspils University College, Ventspils International Radio Astronomy Centre Inzenieru st 101, Ventspils, LV-3601, Latvia.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
We use parallels between the older telephone switches and the multi-skill call centers. We compare different call center routing policies at low and high call rates λ. By numerical results it is shown that a call center with equally distributed skills is preferable compared to traditional grading-type design. The strong proof is given by expansion of call loss probabilities in powers of λ and of 1/λ, respectively. The proof draws on one excellent V. Benes’s paper (from Bell Labs). The main conclusion leads to a new principle for call center design: from throughput point of view a multi-skill call center with equally distributed skills is preferable compared to traditional grading-type design.
Keywords:
Call Center, Skill Based Routing, Teletraffic; Limited Availability, Asymptotic Expansion for Loss Probability
1. Introduction
In a typical call center, the arriving calls are classified in different types, according to the required technical skill to answer the call, the language, importance of the call, etc. Agents are also classified in skill groups according to the subset of call types they can handle. Calls arrive at random according to some stochastic process. When a call arrives, it may be assigned immediately to an agent that can handle it (if there is one available) or it may be put in a queue (usually one queue per call type). When an agent becomes available, the agent may be assigned a call from one of the queues, or may remain idle (e.g., waiting for more important calls). All these assignments are made according to some routing policy that often incorporates priority rules for the calls and agents. Calls waiting in a queue may abandon after a random patience time. Those subscribers who abandon waiting may call again later, although those retrials are rarely modelled in practice, usually because of lack of sufficient data. Callers who received service may also call again for a number of reasons; these are called returns.In the (degenerate) special case where each agent has a single skill, we have several single queues in parallel. If each agent has all skills, then we have a single skill set and a single queue. The system is obviously easier to analyse in these extreme cases. With all agents having all skills, the system is also more efficient (smaller waiting times, fewer abandonment). Agents with more skills are also more expensive; their salaries depend on their skill sets. Thus, forlarge volume of call types, it makes sense to select a number of single-skill agents (specialists) to handle most of the load. A small number of agents with two or more skills can cover the fluctuations in the proportion of calls of each type in the arriving load.The multi-skill call center is far too complex to be available for strong mathematical analysis. The state of research into solving skill-based routing problems is still in its infancy. A special case where two classes of calls are served by a single pool of cross-trained agents is studied in[1] and multi-skill centers in[2]. For a literature survey on asymptotic heavy-traffic regimes we refer to[3,4]. The excellent survey of multi-skill call centers contains paper[5]. As initial point for our study we use paper[6]. There the authors consider routing and scheduling problems under the assumption that there is no queuing, assuming that queued calls are blocked, or, equivalently, that queued calls abandon waiting right away, which result in the so called blocked calls cleared discipline.The paper is organized as follows. Section 2 contains numerical examples for simple multi-skill call center models. These models take into account the structure of the call center and method used for routing of calls. The results have shown that a call center with equally distributed skills is preferable comparing to the traditional grading-type design. Section 3 contains a short version of mathematical proof on call loss probabilities at low and high call rates. The proof uses one excellent V. Benes's paper[7] from Bell Labs. In Section 4 we apply these results to compare the structures of call centres at low and high call rates. Section 5 contains a discussion on the basis of numerical examples looking for future research.The paper is a version of our previous paper[8] extended basically for tutorial purposes, namely: the simple numerical examples are given in Section 2, numerical results – for unsolved issues in Section 5, and some additional detail – proving the theorems.
2. Numerical Examples
Calls from different skill classes are offered to the call center according to a Poisson process with rate λ. The agents in the center are grouped according to their heterogeneous skill sets that determine the classes of calls that they can serve. Each agent group serves calls with independent and equally exponentially distributed service times equal to one (for simplicity). We consider a call center with no buffers in the system, so that every arriving call either has to be routed immediately or has to be blocked and is lost. The objective in the system is to calculate the call lost probability.Example 1. Markov process for the simpliest two-skill call center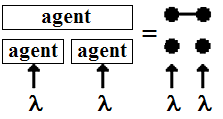 | Figure 1. Two-skill call center with 3 agents |
Fig 1 displays the simplest two-skill center model: 2 skills and 3 agents, two of them are individualists (single skill) available for calls as the first choice and one generalist (2-skill agent) available for calls as the second choice. To calculate the call lost probability we build Markov process having 8 states as shown in the state diagram (Fig 2). (Busy agents are given in black.)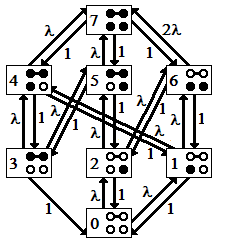 | Figure 2. State diagram and Markov process intensities |
Markov process stationary state probabilities pi, i = 0,…, 7 are defined by the equations:2λ p0=p1+p2+p3(2λ+1)p1=λp0+p4+p6(2λ+1)p2=λp0+p5+p6(2λ+1)p3=p4+p5(λ+2)p4=λp3+λp1+p7(λ+2)p5=λp3+λp2+p7(2λ+2)p6=λp1+λp2+p73p7=λp4+λp5+2λp6p0+p1+…+p7=1By solving the system we get the call loss probability π (pictured in Fig 3):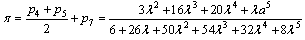
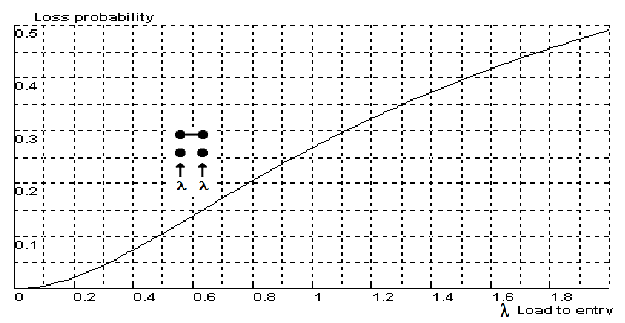 | Figure 3. Two-skill call center loss probability |
Discussion. Let us compare now the just above studied call center model (Fig 1 and Fig 4a) with two others: a similar one (Fig 4b) but by opposite choice of agents – generalist is considered as the first choice and one more in which each agent has both skills (Fig 4c). As Fig 5 shows, the minimum call loss is in the case of full availability system (Fig 4c), and the corresponding loss probability is defined by Erlang formula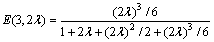 The above studied scheme (Fig 1) is in the middle and the scheme with generalist as the first choice (Fig 4b) gives the largest call loss.
The above studied scheme (Fig 1) is in the middle and the scheme with generalist as the first choice (Fig 4b) gives the largest call loss.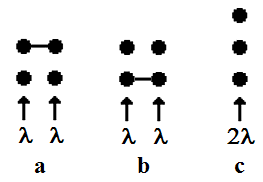 | Figure 4. Three simple call center models |
 | Figure 5. Loss probability: three simple call center models |
Example 2. Grading-type center vs center with equally distributed skillsLet us start with a historical remark. Up to 50 years ago one of the authors (the first one) in his young student age had a chance to deliver the numerical results for the two schemes shown in Fig. 6 at the Kolmogorov’s applied probability seminar at Moscow State University. These schemes relate to so called step-by-step telephone exchanges. The results have surprised Andrey Kolmogorov, namely: in his opinion, in the case of limited access of switch outlets the optimal scheme should be in the form of grading (Fig. 6a). But…this statement, as it turned out, is true only for low call rate. In the case of high call rate, the optimal one is the scheme with equally distributed outlets as in Fig. 6b. In terms of call center, both these schemes are 4-skill centers with 6 agents, and each skill call rate is equal to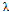 .Traditionally, there are two types of agents in a call center: individualists (handling calls of one type) and generalists (handling calls of any type). Figure 6a corresponds to the traditional scheme: there are 4 agents who handle calls of one type (from different 4 skills) and 2 agents who are generalists. Every callflow has access to 3 agents, and the calls are looking for idle agent from below (as arrays show). We show that it is advantageous to reject the traditional scheme and switch to a scheme with the same number of different skills for any agent (as is shown in Fig. 6b). These results were included in our paper[9].Figure 7 depicts the loss probability curves for these two schemes. And what is surprising? Beginning with a loss probability as low as 0.25 (less than 1%), it is advantageous to use the equally distributed scheme where any agent is received by two type calls. The advantage occurs at as low total call rate as 0.73 (i.e. there is less than one call in the whole system) and the agents are busy only 0.73/6 = 12% of the time. Therefore, the traditional grading-type call centers could be recommended when call rates are very low.
.Traditionally, there are two types of agents in a call center: individualists (handling calls of one type) and generalists (handling calls of any type). Figure 6a corresponds to the traditional scheme: there are 4 agents who handle calls of one type (from different 4 skills) and 2 agents who are generalists. Every callflow has access to 3 agents, and the calls are looking for idle agent from below (as arrays show). We show that it is advantageous to reject the traditional scheme and switch to a scheme with the same number of different skills for any agent (as is shown in Fig. 6b). These results were included in our paper[9].Figure 7 depicts the loss probability curves for these two schemes. And what is surprising? Beginning with a loss probability as low as 0.25 (less than 1%), it is advantageous to use the equally distributed scheme where any agent is received by two type calls. The advantage occurs at as low total call rate as 0.73 (i.e. there is less than one call in the whole system) and the agents are busy only 0.73/6 = 12% of the time. Therefore, the traditional grading-type call centers could be recommended when call rates are very low.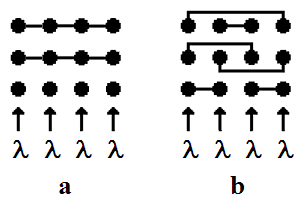 | Figure 6. Two multi-skill call center schemes: a) grading-type, b) with equally distributed skills |
3. Expansion of Loss Probability in Powers of λ and 1/λ
As we have shown above by numerical analysis, the classical grading-type call centers are preferable for low call flows only. At call loss around 1%, the loss probability curves are cross, and more preferable are the schemes with uniformly distributed skills among the agents. Now we go to the strong mathematical analysis of this phenomenon.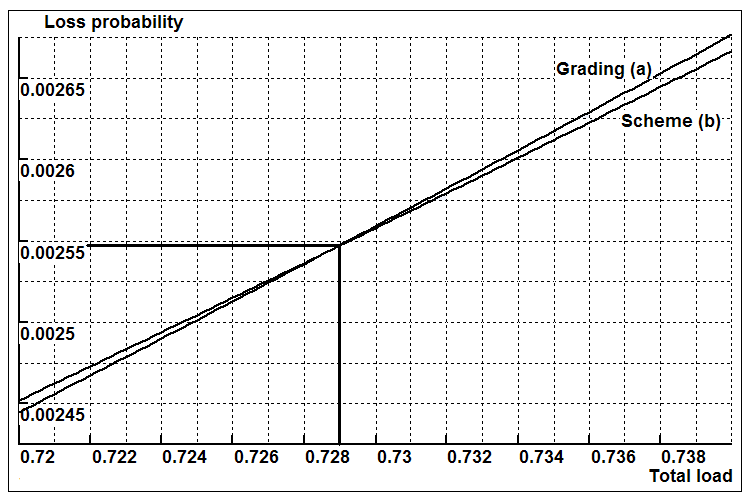 | Figure 7. Comparison of call center routing policy: grading (a) is preferable for low rates only, but as load grows the scheme (b) becomes preferable |
For simplicity of formulas, we consider rectangular-type call centers with parameters: n – skills (call flows), d – number of available agents for each call flow, v – total number of agents. Therefore, the call center has n*d skill-points divided into v groups (among v agents). The call center serves n Poisson call flows (each of rate λ), the holding time is exponentially distributed (with parameter equal to one, for simplicity of formulas). If all d agents available to some call flow are busy, the call is lost. We describe the call processing by means of Markov process with a state set S of 2v states. If x is a state, the notation 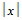 will denote the number of calls in progress in state x – the number of busy lines in state x.We define the levels
will denote the number of calls in progress in state x – the number of busy lines in state x.We define the levels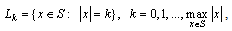 as the sets of states in which a specified number of calls is in progress. The {Lk} form a partition of S,
as the sets of states in which a specified number of calls is in progress. The {Lk} form a partition of S,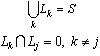 .The “neighbours” of a state x are just those states which can be reached from x by adding or removing one call. These neighbours y of x can be divided into two sets according as y > x or y < x; so we are led to defineAx = set of neighbours above x = set of states accessible from x by adding a call ,Bx = set of neighbours below x = set of states accessible from x by removing one call (see Fig 8).To describe how routes are assigned to calls, we introduce a routing matrix R = (rxy), where rxy – number of the call flows (each flow of separate skill) which move the system from state x to state y, s(x) – number of call flows having at least one idle agent in state x. Obviously,
.The “neighbours” of a state x are just those states which can be reached from x by adding or removing one call. These neighbours y of x can be divided into two sets according as y > x or y < x; so we are led to defineAx = set of neighbours above x = set of states accessible from x by adding a call ,Bx = set of neighbours below x = set of states accessible from x by removing one call (see Fig 8).To describe how routes are assigned to calls, we introduce a routing matrix R = (rxy), where rxy – number of the call flows (each flow of separate skill) which move the system from state x to state y, s(x) – number of call flows having at least one idle agent in state x. Obviously, 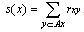 ,rx – element of matrix R in│x│ degree having indexes (0, x). Obviously, rx means the number of paths to move from state 0 to state x by means of incoming calls only.
,rx – element of matrix R in│x│ degree having indexes (0, x). Obviously, rx means the number of paths to move from state 0 to state x by means of incoming calls only.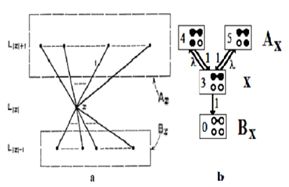 | Figure 8. A state x and sets Ax, Bx in the state diagram: a) common view, b) example from Fig. 2 |
For the purpose of defining a Markov stochastic process it is convenient and customary to collect the assumptions introduced above in a matrix of transition rates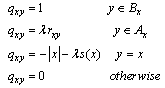 We get the state probabilities px as the solution of linear algebraic system
We get the state probabilities px as the solution of linear algebraic system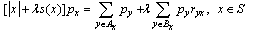 and probability of call loss is equal
and probability of call loss is equal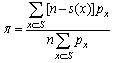 In order to study the optimal call center design principles we apply to the expansion of call loss probability in powers of λ (Theorem 1) and in powers of 1/λ (Theorem 2). As mentioned above, we consider rectangular-type call center with parameters: n – skills (call flows), d – number of available agents for each call flow, v – total number of agents.Theorem 1[9]. Expansion of loss probability in powers ofIf the sequence {cm (x), m ≥ 0, x from S} is defined by
In order to study the optimal call center design principles we apply to the expansion of call loss probability in powers of λ (Theorem 1) and in powers of 1/λ (Theorem 2). As mentioned above, we consider rectangular-type call center with parameters: n – skills (call flows), d – number of available agents for each call flow, v – total number of agents.Theorem 1[9]. Expansion of loss probability in powers ofIf the sequence {cm (x), m ≥ 0, x from S} is defined by 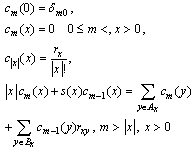 and
and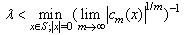 then the asymptotic expansion of call loss probability in powers of λ is available at point of λ= 0, and the members not equal to 0 are of power not less than λd .According to this theorem for x> 0 we have expansion
then the asymptotic expansion of call loss probability in powers of λ is available at point of λ= 0, and the members not equal to 0 are of power not less than λd .According to this theorem for x> 0 we have expansion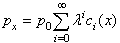 and the call loss probability is equal to
and the call loss probability is equal to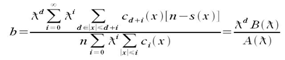 Theorem 2[10]. Expansion of loss probability in powers of 1/λ.If the sequence {dm (x),
Theorem 2[10]. Expansion of loss probability in powers of 1/λ.If the sequence {dm (x),  } is defined by
} is defined by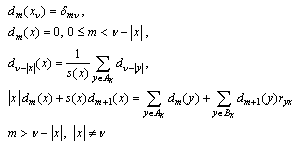 and
and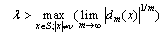 then the asymptotic expansion of call loss probability in powers of
then the asymptotic expansion of call loss probability in powers of 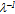 is available at point of
is available at point of 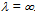 According to this theorem we have the expansion
According to this theorem we have the expansion 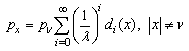 Call loss probability is equal to
Call loss probability is equal to 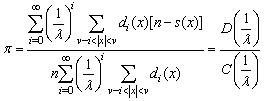 and according to Taylor series
and according to Taylor series 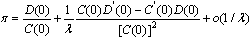 The four first expansion terms are defined by
The four first expansion terms are defined by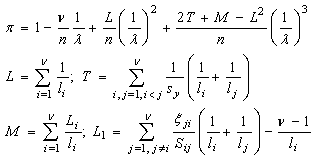 where li – the total number of agents with i-skills,sij – the number of skills for which at least one agent is available in state when only agents i and j are free,
where li – the total number of agents with i-skills,sij – the number of skills for which at least one agent is available in state when only agents i and j are free,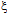 ji – the number of skills (part of sij) from which calls are coming to agent j when only agents i and j are free.
ji – the number of skills (part of sij) from which calls are coming to agent j when only agents i and j are free.
4. On New Principle of Call Center Design
Let us continue with one more historical remark. To a large extent, our paper is based on the results of a study of a distinguished mathematician of Bell Laboratories V.E. Benes[7, 11] who carried out a research on so called crossbar telephone switches. Theorem 3 given below follows Benes’s paper[7] from 1963. This paper contains formulas for expansion of loss probability in powers of 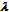 . A little later, in 1965 we developed the same type results for step-by-step telephone switches[10] using expansion of loss probability in powers of
. A little later, in 1965 we developed the same type results for step-by-step telephone switches[10] using expansion of loss probability in powers of 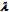 and in powers of 1/
and in powers of 1/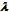 . Benes paper[11] from 1966 contains a similar expansion in powers of 1/
. Benes paper[11] from 1966 contains a similar expansion in powers of 1/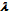 . And in this context it is worthy to mention Benes words[11]. He has written: “The question has arisen whether there are examples of pairs of networks, with the same number of crosspoints, the first of which is better than the second at one value of
. And in this context it is worthy to mention Benes words[11]. He has written: “The question has arisen whether there are examples of pairs of networks, with the same number of crosspoints, the first of which is better than the second at one value of 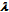 , while the second is better than the first at another value of
, while the second is better than the first at another value of 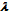 ”. The same type of problem was a goal of our studies[10] – only for another telephone exchange generation – step-by-step switches.Theorem 3[10]. On optimality of grading-type call center at
”. The same type of problem was a goal of our studies[10] – only for another telephone exchange generation – step-by-step switches.Theorem 3[10]. On optimality of grading-type call center at 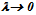 At
At 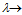 0 and given rectangular-type call center with parameters: n – skills (call flows), v – total number of agents, d – number of available agents for each call flow, the optimal call center design should follow the principles:1). The skill-field (n, d, v) is divided (as possible) in skill-sets with 1 and n skill-points (it means that each agent has 1 or n skills), and individualists are available earlier than generalists,2). If the above requirement could not be fulfilled, then skill-sets with another skill-points are available after individualists and before generalists.The idea for proof. The proof is based on Theorem 1. The coefficients cm(x) are related to the number of calls, moving system from state 0 to state x. For example, c│x│(x) = rx /│x│! (rx means the number of paths to move from state 0 to state x by incoming calls only) and the first term in the expansion at
0 and given rectangular-type call center with parameters: n – skills (call flows), v – total number of agents, d – number of available agents for each call flow, the optimal call center design should follow the principles:1). The skill-field (n, d, v) is divided (as possible) in skill-sets with 1 and n skill-points (it means that each agent has 1 or n skills), and individualists are available earlier than generalists,2). If the above requirement could not be fulfilled, then skill-sets with another skill-points are available after individualists and before generalists.The idea for proof. The proof is based on Theorem 1. The coefficients cm(x) are related to the number of calls, moving system from state 0 to state x. For example, c│x│(x) = rx /│x│! (rx means the number of paths to move from state 0 to state x by incoming calls only) and the first term in the expansion at 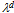 is equal to
is equal to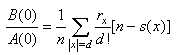 Therefore, the first choice agents should be individualists. The proof follows from the analysis of the next terms.Theorem 4[10]. On optimality of equally distributed skill-points at
Therefore, the first choice agents should be individualists. The proof follows from the analysis of the next terms.Theorem 4[10]. On optimality of equally distributed skill-points at 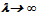 At
At 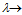 ∞ and given rectangular-type call center with parameters: n – skills (call flows), v – total number of agents, d – number of available agents for each call flow, the optimal call center design should follow the principles:1). The skill-field (n, d, v) is divided between agents with r or r+1 skills, where r =[nd/v] ([ ] denotes the whole part),2). Agents with r skills are available earlier than agents with r+1 skills,3). Each agent has equal (as possible) number of different skills with each of the other agents.Idea for proof. The proof is based on Theorem 3. The first two terms in expansion of loss probability in powers of
∞ and given rectangular-type call center with parameters: n – skills (call flows), v – total number of agents, d – number of available agents for each call flow, the optimal call center design should follow the principles:1). The skill-field (n, d, v) is divided between agents with r or r+1 skills, where r =[nd/v] ([ ] denotes the whole part),2). Agents with r skills are available earlier than agents with r+1 skills,3). Each agent has equal (as possible) number of different skills with each of the other agents.Idea for proof. The proof is based on Theorem 3. The first two terms in expansion of loss probability in powers of 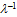 don’t give any information on the scheme structure. The third term at power
don’t give any information on the scheme structure. The third term at power 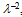 , equal to L/n, gets minimum value when
, equal to L/n, gets minimum value when 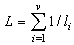 takes minimum value. According to definition
takes minimum value. According to definition 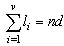 where li are integer numbers, therefore they should be (as possible) equal i.e. equal to[nd/v] or[nd/v] + 1. From that the requirement 1 of Theorem 4 follows. Let’s prove the requirement 3 for particular case when nd/v is an integer, i.e. equal r. Then
where li are integer numbers, therefore they should be (as possible) equal i.e. equal to[nd/v] or[nd/v] + 1. From that the requirement 1 of Theorem 4 follows. Let’s prove the requirement 3 for particular case when nd/v is an integer, i.e. equal r. Then 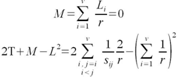 and we need to minimize the first sum. If we denote the number of common inlets for lines i and j by qij then
and we need to minimize the first sum. If we denote the number of common inlets for lines i and j by qij then 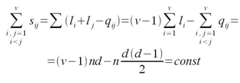 This sum takes minimum value when all sij are equal (as possible). It means that each skill-set has equal (as possible) number of different skills with each of the other skill-sets, and the requirement 3 for particular case is proved necessary.
This sum takes minimum value when all sij are equal (as possible). It means that each skill-set has equal (as possible) number of different skills with each of the other skill-sets, and the requirement 3 for particular case is proved necessary.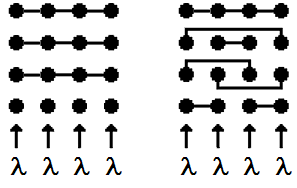 | Figure 9. The call centers (of Fig 6) expanded by one additional agent-generalist |
5. Discussion
To make clear the advantage of equally distributed skills solution, we shall give some additional numerical examples as a basis for future study.Example 3. Universal agents influenceIn Fig. 9, the two previous schemes are shown but with one more agent-generalist added as the last choice. It shows strong influence: the loss curves are crossing at total traffic of only 0.105 and when the loss probability is 0.23 × 10–9, i.e., almost zero. This means that it is reasonable to have more universal agents in reserve, but apply the equally distributed scheme.Example 4. Agents number doublingThe other possible variant of modification is the doubling of the agents number in each of the six groups that were shown in Fig. 6. This way we will get two schemes with 12 agents in each (Fig. 10). The solution of the system of 212 equations shows that the pattern almost does not change: the loss curves are crossind if the losses are 0.0032 (instead of 0.0025 in Fig. 6). However, this result may be achieved under total traffic of 3.65, which constitutes 31% of the agent’s workload, i.e., less than a third of the time. Generally, the overall picture shows no changes: the scheme with equally distributed skills among the agents is practically preferable at any load.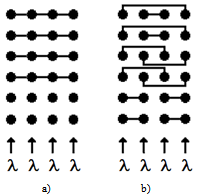 | Figure 10. Doubled agent groups (in comparing to Fig 6a and 6b) |
Example 5. Waiting space influenceObviously, use of waiting places always reduces call losses: due to waiting places the loss curves are moved to the right. What is more interesting: due to waiting places the preference of equally distributed agent skills grows.| Table 1. The crosspoint of loss curves for schemes 6a and 6c with waiting places |
| | Number of waiting places | Total load | Loss probability crosspoint | | 0 | 0.72855 | 0.2542 x 10-2 | | 1 | 0.6427 | 0.9424 x 10-4 | | 2 | 0.616 | 0.4091 x 10-5 |
|
|
The calculation shows that the waiting spaces increase the advantage of equally distributed schemes (Table 1). The absence of waiting spaces corresponds to the initial case in Fig. 6; i.e. the curves cross when the losses are 0.25%. Adding one waiting space for every call flow moves the concurrence point to 0.94 × 10–4, and, if there are two waiting spaces, the curves cross even earlier when the losses are 0.41 × 10–5 only.Example 6. One unsolved problemSee examples (Fig. 11) of three almost same call centers but with different agent access policy. The above studied scheme 11a and two similar schemes 11b and 11c are depicted, but there is a slight difference in the calls assignment, which should provide, in our opinion, more even distribution and higher performance. However, this change worsens the scheme’s traffic capacity (Table 2): the initial scheme 11a remains the most preferable, scheme 11c is the second, and scheme 11b is the third. This is hard to explain, and additional research is required. Seems it depennds on the correlation between call flows.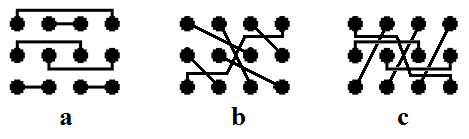 | Figure 11. Unexplained effect of call flow correlation. |
| Table 2. Comparison of schemes with equally distributed skill-points but different access policy |
| | Total traffic | Loss probability | | Fig. 11a | Fig. 11b | Fig. 11c | | 410.250,0625 | 0.673150.189030.66143×10-20.92525×10-4 | 0.673200.192840.91470×10-20.18718×10-3 | 0.673190.192230.85695×10-20.15925×10-3 |
|
|
6. Conclusions
Numerical analysis of simple multi-skill call centers proposes a new principle for call center design: from throughput point of view, a multi-skill call center with equally distributed skills is preferable compared to traditional grading-type design. The strong proof is given by expansion of call loss probabilities in powers of call rate λ and of 1/λ, respectively.
References
| [1] | Bhulai S. and Koole G. A queueing model for call blending in call centers. IEEE Transactions on Automatic Control, 2003, 48: 1434–1438. |
| [2] | Gurvich I., Armony M., and Mandelbaum A. Service level differentation in call centers with fully _exible servers. Management Science , 2008, 54: 279–294. |
| [3] | Koole G. and Mandelbaum A. Queueing models of call centers: an introduction. Annals of Operations Research, 2002, 113: 41–59. |
| [4] | Gans N., Koole G., and Mandelbaum A. Telephone call centers: tutorial, review, and research prospects. Manufacturing and Service Operations Management, 5: 79–141, 2003. |
| [5] | Bhulai S. Dynamic routing policies for multi-skill call centers. Prob in Eng and Inf Sc 23 (1), 75–99, 2009. |
| [6] | Koole G. and Talim J. Exponential approximation of multi-skill call centers architecture. In Proceedings of QNETs 2000, pages 23/1–10, 2000. |
| [7] | Benes V.E. Markov processes representing traffic in connecting networks. Bell System Techn. J., 1963, 42, 6, 2795–2838. |
| [8] | Schneps-Schneppe M., and Sedols J. Multi-Skill Call Center as a Grading from “Old” telephony. In S. Balandin et al. (Eds) Smart Spaces and Next Generation Wired/Wireless networking. LNCS 5764, pp. 154-167, 2009. |
| [9] | Schneps-Schneppe M. New principles of limited availability scheme design, Elektrosviaz, Nr 7, 1963, 40-46 (in Russian). |
| [10] | Sedol J., and Schneps-Schneppe M. Some qualitative study of limited availability schemes, Problemy peredachi informatsii, 1, Nr 2 (1965), 88–94 (in Russian). |
| [11] | Benes V.E. Some examples of comparisons of connecting networks. Bell System Techn. J., 45, 10, 1966, 1829–1935. |

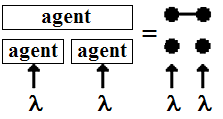

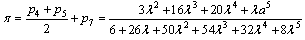

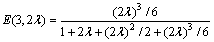 The above studied scheme (Fig 1) is in the middle and the scheme with generalist as the first choice (Fig 4b) gives the largest call loss.
The above studied scheme (Fig 1) is in the middle and the scheme with generalist as the first choice (Fig 4b) gives the largest call loss.

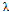 .Traditionally, there are two types of agents in a call center: individualists (handling calls of one type) and generalists (handling calls of any type). Figure 6a corresponds to the traditional scheme: there are 4 agents who handle calls of one type (from different 4 skills) and 2 agents who are generalists. Every callflow has access to 3 agents, and the calls are looking for idle agent from below (as arrays show). We show that it is advantageous to reject the traditional scheme and switch to a scheme with the same number of different skills for any agent (as is shown in Fig. 6b). These results were included in our paper[9].Figure 7 depicts the loss probability curves for these two schemes. And what is surprising? Beginning with a loss probability as low as 0.25 (less than 1%), it is advantageous to use the equally distributed scheme where any agent is received by two type calls. The advantage occurs at as low total call rate as 0.73 (i.e. there is less than one call in the whole system) and the agents are busy only 0.73/6 = 12% of the time. Therefore, the traditional grading-type call centers could be recommended when call rates are very low.
.Traditionally, there are two types of agents in a call center: individualists (handling calls of one type) and generalists (handling calls of any type). Figure 6a corresponds to the traditional scheme: there are 4 agents who handle calls of one type (from different 4 skills) and 2 agents who are generalists. Every callflow has access to 3 agents, and the calls are looking for idle agent from below (as arrays show). We show that it is advantageous to reject the traditional scheme and switch to a scheme with the same number of different skills for any agent (as is shown in Fig. 6b). These results were included in our paper[9].Figure 7 depicts the loss probability curves for these two schemes. And what is surprising? Beginning with a loss probability as low as 0.25 (less than 1%), it is advantageous to use the equally distributed scheme where any agent is received by two type calls. The advantage occurs at as low total call rate as 0.73 (i.e. there is less than one call in the whole system) and the agents are busy only 0.73/6 = 12% of the time. Therefore, the traditional grading-type call centers could be recommended when call rates are very low.

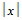 will denote the number of calls in progress in state x – the number of busy lines in state x.We define the levels
will denote the number of calls in progress in state x – the number of busy lines in state x.We define the levels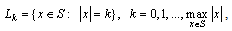 as the sets of states in which a specified number of calls is in progress. The {Lk} form a partition of S,
as the sets of states in which a specified number of calls is in progress. The {Lk} form a partition of S,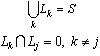 .The “neighbours” of a state x are just those states which can be reached from x by adding or removing one call. These neighbours y of x can be divided into two sets according as y > x or y < x; so we are led to defineAx = set of neighbours above x = set of states accessible from x by adding a call ,Bx = set of neighbours below x = set of states accessible from x by removing one call (see Fig 8).To describe how routes are assigned to calls, we introduce a routing matrix R = (rxy), where rxy – number of the call flows (each flow of separate skill) which move the system from state x to state y, s(x) – number of call flows having at least one idle agent in state x. Obviously,
.The “neighbours” of a state x are just those states which can be reached from x by adding or removing one call. These neighbours y of x can be divided into two sets according as y > x or y < x; so we are led to defineAx = set of neighbours above x = set of states accessible from x by adding a call ,Bx = set of neighbours below x = set of states accessible from x by removing one call (see Fig 8).To describe how routes are assigned to calls, we introduce a routing matrix R = (rxy), where rxy – number of the call flows (each flow of separate skill) which move the system from state x to state y, s(x) – number of call flows having at least one idle agent in state x. Obviously, 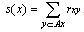 ,rx – element of matrix R in│x│ degree having indexes (0, x). Obviously, rx means the number of paths to move from state 0 to state x by means of incoming calls only.
,rx – element of matrix R in│x│ degree having indexes (0, x). Obviously, rx means the number of paths to move from state 0 to state x by means of incoming calls only.
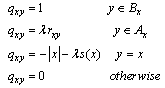 We get the state probabilities px as the solution of linear algebraic system
We get the state probabilities px as the solution of linear algebraic system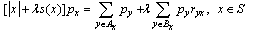 and probability of call loss is equal
and probability of call loss is equal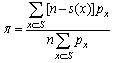 In order to study the optimal call center design principles we apply to the expansion of call loss probability in powers of λ (Theorem 1) and in powers of 1/λ (Theorem 2). As mentioned above, we consider rectangular-type call center with parameters: n – skills (call flows), d – number of available agents for each call flow, v – total number of agents.Theorem 1[9]. Expansion of loss probability in powers ofIf the sequence {cm (x), m ≥ 0, x from S} is defined by
In order to study the optimal call center design principles we apply to the expansion of call loss probability in powers of λ (Theorem 1) and in powers of 1/λ (Theorem 2). As mentioned above, we consider rectangular-type call center with parameters: n – skills (call flows), d – number of available agents for each call flow, v – total number of agents.Theorem 1[9]. Expansion of loss probability in powers ofIf the sequence {cm (x), m ≥ 0, x from S} is defined by 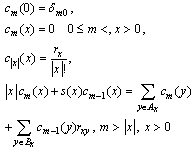 and
and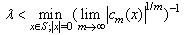 then the asymptotic expansion of call loss probability in powers of λ is available at point of λ= 0, and the members not equal to 0 are of power not less than λd .According to this theorem for x> 0 we have expansion
then the asymptotic expansion of call loss probability in powers of λ is available at point of λ= 0, and the members not equal to 0 are of power not less than λd .According to this theorem for x> 0 we have expansion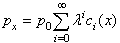 and the call loss probability is equal to
and the call loss probability is equal to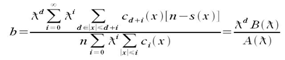 Theorem 2[10]. Expansion of loss probability in powers of 1/λ.If the sequence {dm (x),
Theorem 2[10]. Expansion of loss probability in powers of 1/λ.If the sequence {dm (x), 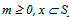 } is defined by
} is defined by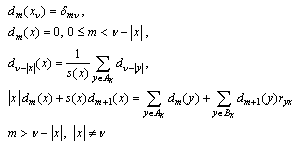 and
and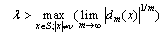 then the asymptotic expansion of call loss probability in powers of
then the asymptotic expansion of call loss probability in powers of 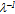 is available at point of
is available at point of 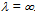 According to this theorem we have the expansion
According to this theorem we have the expansion 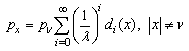 Call loss probability is equal to
Call loss probability is equal to 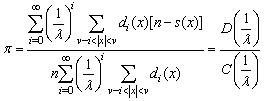 and according to Taylor series
and according to Taylor series 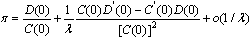 The four first expansion terms are defined by
The four first expansion terms are defined by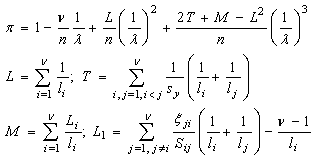 where li – the total number of agents with i-skills,sij – the number of skills for which at least one agent is available in state when only agents i and j are free,
where li – the total number of agents with i-skills,sij – the number of skills for which at least one agent is available in state when only agents i and j are free,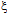 ji – the number of skills (part of sij) from which calls are coming to agent j when only agents i and j are free.
ji – the number of skills (part of sij) from which calls are coming to agent j when only agents i and j are free.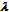 . A little later, in 1965 we developed the same type results for step-by-step telephone switches[10] using expansion of loss probability in powers of
. A little later, in 1965 we developed the same type results for step-by-step telephone switches[10] using expansion of loss probability in powers of 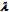 and in powers of 1/
and in powers of 1/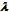 . Benes paper[11] from 1966 contains a similar expansion in powers of 1/
. Benes paper[11] from 1966 contains a similar expansion in powers of 1/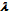 . And in this context it is worthy to mention Benes words[11]. He has written: “The question has arisen whether there are examples of pairs of networks, with the same number of crosspoints, the first of which is better than the second at one value of
. And in this context it is worthy to mention Benes words[11]. He has written: “The question has arisen whether there are examples of pairs of networks, with the same number of crosspoints, the first of which is better than the second at one value of 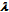 , while the second is better than the first at another value of
, while the second is better than the first at another value of 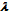 ”. The same type of problem was a goal of our studies[10] – only for another telephone exchange generation – step-by-step switches.Theorem 3[10]. On optimality of grading-type call center at
”. The same type of problem was a goal of our studies[10] – only for another telephone exchange generation – step-by-step switches.Theorem 3[10]. On optimality of grading-type call center at 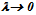 At
At 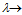 0 and given rectangular-type call center with parameters: n – skills (call flows), v – total number of agents, d – number of available agents for each call flow, the optimal call center design should follow the principles:1). The skill-field (n, d, v) is divided (as possible) in skill-sets with 1 and n skill-points (it means that each agent has 1 or n skills), and individualists are available earlier than generalists,2). If the above requirement could not be fulfilled, then skill-sets with another skill-points are available after individualists and before generalists.The idea for proof. The proof is based on Theorem 1. The coefficients cm(x) are related to the number of calls, moving system from state 0 to state x. For example, c│x│(x) = rx /│x│! (rx means the number of paths to move from state 0 to state x by incoming calls only) and the first term in the expansion at
0 and given rectangular-type call center with parameters: n – skills (call flows), v – total number of agents, d – number of available agents for each call flow, the optimal call center design should follow the principles:1). The skill-field (n, d, v) is divided (as possible) in skill-sets with 1 and n skill-points (it means that each agent has 1 or n skills), and individualists are available earlier than generalists,2). If the above requirement could not be fulfilled, then skill-sets with another skill-points are available after individualists and before generalists.The idea for proof. The proof is based on Theorem 1. The coefficients cm(x) are related to the number of calls, moving system from state 0 to state x. For example, c│x│(x) = rx /│x│! (rx means the number of paths to move from state 0 to state x by incoming calls only) and the first term in the expansion at 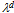 is equal to
is equal to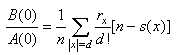 Therefore, the first choice agents should be individualists. The proof follows from the analysis of the next terms.Theorem 4[10]. On optimality of equally distributed skill-points at
Therefore, the first choice agents should be individualists. The proof follows from the analysis of the next terms.Theorem 4[10]. On optimality of equally distributed skill-points at 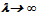 At
At 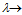 ∞ and given rectangular-type call center with parameters: n – skills (call flows), v – total number of agents, d – number of available agents for each call flow, the optimal call center design should follow the principles:1). The skill-field (n, d, v) is divided between agents with r or r+1 skills, where r =[nd/v] ([ ] denotes the whole part),2). Agents with r skills are available earlier than agents with r+1 skills,3). Each agent has equal (as possible) number of different skills with each of the other agents.Idea for proof. The proof is based on Theorem 3. The first two terms in expansion of loss probability in powers of
∞ and given rectangular-type call center with parameters: n – skills (call flows), v – total number of agents, d – number of available agents for each call flow, the optimal call center design should follow the principles:1). The skill-field (n, d, v) is divided between agents with r or r+1 skills, where r =[nd/v] ([ ] denotes the whole part),2). Agents with r skills are available earlier than agents with r+1 skills,3). Each agent has equal (as possible) number of different skills with each of the other agents.Idea for proof. The proof is based on Theorem 3. The first two terms in expansion of loss probability in powers of 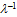 don’t give any information on the scheme structure. The third term at power
don’t give any information on the scheme structure. The third term at power 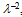 , equal to L/n, gets minimum value when
, equal to L/n, gets minimum value when 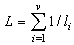 takes minimum value. According to definition
takes minimum value. According to definition 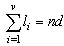 where li are integer numbers, therefore they should be (as possible) equal i.e. equal to[nd/v] or[nd/v] + 1. From that the requirement 1 of Theorem 4 follows. Let’s prove the requirement 3 for particular case when nd/v is an integer, i.e. equal r. Then
where li are integer numbers, therefore they should be (as possible) equal i.e. equal to[nd/v] or[nd/v] + 1. From that the requirement 1 of Theorem 4 follows. Let’s prove the requirement 3 for particular case when nd/v is an integer, i.e. equal r. Then 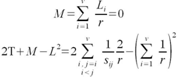 and we need to minimize the first sum. If we denote the number of common inlets for lines i and j by qij then
and we need to minimize the first sum. If we denote the number of common inlets for lines i and j by qij then 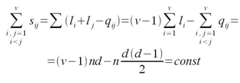 This sum takes minimum value when all sij are equal (as possible). It means that each skill-set has equal (as possible) number of different skills with each of the other skill-sets, and the requirement 3 for particular case is proved necessary.
This sum takes minimum value when all sij are equal (as possible). It means that each skill-set has equal (as possible) number of different skills with each of the other skill-sets, and the requirement 3 for particular case is proved necessary.


 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML