1. Introduction

With the increased demand for wireless communication systems a promised Quality of Service (QoS) is required in a satisfactory manner, to manage the incoming new calls and handoff calls more efficiently. In wireless and cellular communication systems, handoff is an important aspect due to the mobility of devices and it directly affects the quality of service. It is the mechanism that transfers an ongoing call from one cell to another as a user moves through the coverage area of a cellular system. The capacity of all cellular systems is limited, so handoff should be utilized in the most efficient way[1-3]. Various performance issues are analysed for different call admission control (CAC) models in the past[4-6].

In cellular mobile networks handoff is an important feature since it is the means through which the continuity of a call is maintained when a mobile moves from one cell area to another. The large amount of radio resources used for handoffs and the effect of handoff techniques on system interference, user satisfaction level and capacity create a demand for efficient handoff techniques. When the handover rate of the system increases, the probability of an ongoing call to be dropped due to a lack of free channel is high.

The probability of new call blocking and the probability of a handoff dropping is same in non prioritized scheme[7]. Handover prioritization schemes result in a decrease of handoff dropping and in an increase of new call blockingprobability, that is, it reduces the total number of admitted traffic. The concept of these strategies is to reserve a number of channels called guard channels exclusively for handovers[8].

However, from the user’s point of view, dropping of an ongoing call is less desirable than blocking of a new call attempt. But fractional guard channel (FGC) scheme reserves a non-integral number of guard channels for handoff calls by accepting new calls with some probability that depends on the current channel occupancy[3].

During communication a mobile device always remains within the range of at least one base station (BS). Due to the limited spectrum, cellular systems distribute smaller cells in order to achieve high system capacity. Since each handover requires from the network management to reroute the call to the new BS, the number of the expected handovers increases. To meet the demands for higher capacity the smaller cells are deployed. When a MS moves away from the BS, the received signal strength decreases, and when it gets lower than a threshold level, the handoff procedure is initiated. Handoff decision is based on received signal strengths (RSS) from current BS and neighbouring base stations (BSs).

Mobile station (MS) moving from one BS 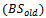to another BS 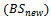is shown in Figure 1. It is assumed that the signal is averaged over time, so that rapid fluctuations due to the multipath nature of the radio environment can be eliminated. The mean signal strength of 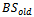decreases as the MS moves away from it. Similarly, the mean signal strength of 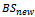increases as the MS approaches it. MS measures the signal strengths from surrounding BSs and interference levels on all channels. A handoff can be initiated if the signal strength of the serving BS is lower than that of another BS by a certain threshold. The call is dropped if the received signal strength from the current BS falls below the receiver threshold level prior to the mobile being assigned a channel in the target cell[9]. As the number of handoffs increases, dropping probability also increases. Several handoff techniques have been proposed and implemented in various cellular networks[10-13].

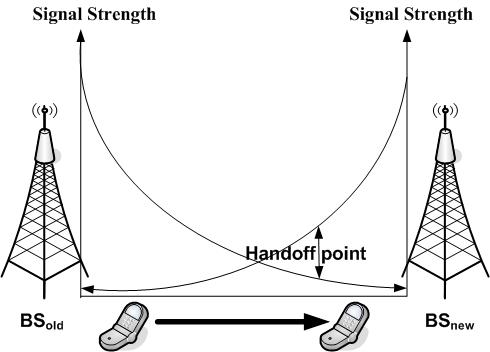Figure 1. Signal level versus handoff point

Based on received signal strength indication (RSSI) and bit error rate (BER) of local BS and other BS Hand over margin is decided. The MS breaks its old link and access the new BS which is called as break before make handover. This kind of network assigned handoff decision is known as mobile-assisted handoff (MAHO)[14, 15]. The handoff time between handoff decision and execution is approximately one second. 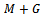The scheme accepts good quality signal with availability of channels exclusively for handoff calls in the adjacent cell[16]. The queuing handoff priority scheme that handles the channels reserved for handoff calls depending on the current status of the queue effectively reduces forced termination, at the expense of increased new call blocking probability[17].

It is not possible to always maintain a good signal quality when handoff takes place in a wireless mobile system. Mobile Controlled Handoff (MCHO) extends the role of the MS by giving overall control to it. It provides the opportunity to the MS for choosing good signal BS out of all received signals from surrounding BSs. MS measures the signal strengths from surrounding BSs and interference levels on all channels. A handoff can be initiated if the signal strength of the serving BS is lower than that of another BS by a certain threshold. This type of handoff has a short reaction time. In MCHO technology, MS made decision of handoff based on signal quality received and reaction time is very low. Good quality signal calls are received and served successfully while poor signal quality calls are dropped or handed over to other BSs.

In this paper, we focus our attention in a generic communication network that guarantees seamless mobility to its customers. We proposed two analytical model where handoff calls handle based on its signal quality and re-handoff of low quality signal calls are taken care. A channel assignment scheme, called fractional guard channel (FGC) admits new calls with probability 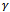when the channel occupancy is more than or equal toC. These new calls compensate free channels raised due to dropped handoff calls. In proposed model I preference is given to incoming handoff calls. The cell stops providing channels to the incoming handoff calls if all the channels are occupied. When the channel occupancy is more than or equal to threshold C , new calls are accepted with acceptance probability. Model II allocates available channels to the incoming handoff calls from general pool along with the incoming new calls on first-come, first-served (FCFS) basis. After threshold C , new calls are accepted with acceptance probability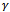. The poor signal quality incoming handoff calls are re-handed off to other BSs. The objective is to decrease the probability of dropping of a call due to low quality signal and make a trade-off between new and handoff calls so that all the channels efficiently used.

The rest of the paper is structured as follows. Section 2 contains description and analysis of proposed Mode I and its computational aspects. Analysis of proposed Model II is given in section 3. Computational experiences with verity of numerical results in the form of graphs are discussed in section 4. Final section 5 concludes the paper.

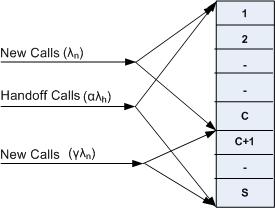Figure 2. System model

2. Description and Analysis of the Proposed Model I

The system with homogenous cells is considered in the proposed model I. Each cell is having S number of channels and we focus our attention on a single cell, which we call the reference cell. A new call is generated in the reference cell when a mobile user of the reference cell makes a call. When a mobile user holding a channel enters the handoff area of the reference cell from a neighbouring cell, a handoff request is generated. In this model, the new call rate is uniformly distributed over the mobile service area. If the handoff attempt finds all channels in the target cell are filled, it is dropped. The system model for the reference cell is shown in Figure 2.

The total number of channels S of a reference cell are contributed for new call and handoff call in three different patterns. All the handoff calls are accepted till a free channel is available and dropped if all S channels are busy. New calls are accepted up to a threshold channel C.

To balance the number of new and handoff call service, the proposed model accepts new calls with probability 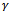after C channels. If all the S channels are busy, new calls are also blocked.

The analysis in[5] presumes that a handoff call always has an acceptable signal quality. In real practice, however, there may be a small probability that such calls do not have adequate signal quality. In such situations, a channel will be allocated to a handoff call, but such a call cannot be sustained by the new BS due to poor signal quality. Let 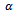be the probability that a handoff call is of good signal and let 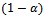be the probability of receiving a poor quality handoff call that is immediately dropped for bad quality signal. The proposed model for varying signal quality (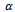) reduces new call blocking probability by accepting new calls with probability 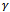when the channel occupancy is more than or equal to C .

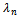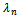We assume that both new and handoff call attempts are generated according to a Poisson process with mean rates and, respectively. The effective incoming call traffic rate up to C channel is 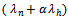, since any poor- signal-quality handoff call is immediately dropped. An incoming-call traffic rate from C to S channel capacity is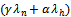. After S all new call and handoff call traffic are blocked. Calls under progress in a cell are either completed or blocked. We assume the channel holding time to have an exponential distribution with mean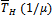. We define 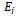as the state of the base station when j is the number of channels used in the cell. The state transition diagram for this traffic model is shown in Figure 3.

Let 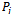represent the steady state probability that the base station is in state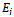. Using the birth-death processes, the

probability distribution 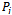is found to be

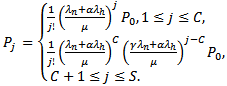Using normalization condition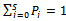, an expression for 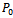is obtained as

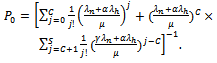Various performance characteristics of particular interest are the fraction of new call attempts which are blocked, completed and handoff call dropped due to unavailability of free channel. The dropping probability of handoff call is given by

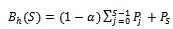(1)

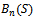If chances for a mobile to cross a cell boundary during call duration are small then the probability of blocking is the major indication of system traffic performance. The blocking probability of a new call is the sum of the probabilities that the state number of the base station is larger than or equal to C. Hence

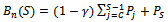(2)

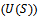The channel utilization is defined as the ratio of the expected value of the channels occupied by calls to the capacity of the system. Thus, the channel utilization can be given as

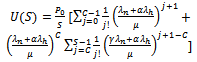(3)

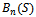Another measure of system performance is a weighted sum of and 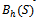which is called cost function, and it can be expressed as

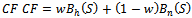(4)

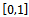where w is within the interval and indicates the relative importance of blocking and dropping probabilities. The cost function is an empirical measuring way of systems quality of service. The dropping probability 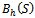is more important than blocking probability 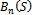from the user’s point of view, so w must be within the interval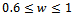

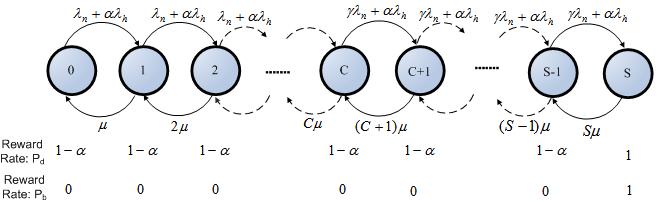Figure 3. State transition diagram

2.1. Computational Aspects

When the number of channels S is large in cellular networks, using the dropping and blocking probabilities directly numerical difficulties arises in the computations. In this subsection, we show numerically stable methods of computation that avoids the computation of factorials and large power of loads. We establish all computations based on recursive relations.

Let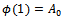, and compute

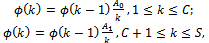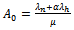where and.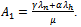

Then let, and compute

This computation is more stable than the direct use of equation (1). The numerator and denominator above can become very large for large values of 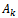and S , leading to overflow. A better recursion is the following:

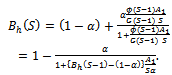Now, let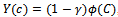, then compute

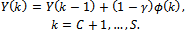In this case, the computation is more stable than the direct use of equation (2) and a better recursion is the following:

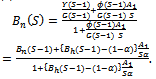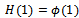Let and compute

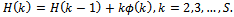Using recursive formula the computation of the channel utilization factor (3) is more stable. The recursion of the channel utilization factor (3) is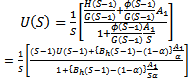

3. Description and Analysis of the Proposed Model II

The network service provider goal is to maximize the revenue by improving network resource utilization, which is usually associated with minimizing the handoff dropping while keeping the new call blocking probability below a certain threshold. The proposed model II captures the situation wherein a poor signal quality handoff is not immediately dropped as in the proposed model I. Instead, such a call can be re-handed off to some other better serving BSs. Performance analysis of this scheme is carried out by using two dimensional Markov model that incorporates poor-signal quality handoff calls as shown in Figure 4.

Each state is labelled as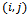, where 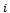denotes the number of poor signal quality handoff calls being handled, and 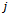denotes the number of good signal quality ongoing calls. For more improvement of the probability of handoff dropping, we reserved a fractional amount of channels for the handoff calls to have more priority than the new calls which implies the decreasing of the probability of handoff dropping. The reservation of fractional number of channels will balance the handoff dropping probability and the new calls blocking probability.

The proposed model II assumes a homogeneous cellular environment where each cell equipped with S number of channels. Out of S channels 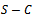number of channels are utilized for both handoff calls and new calls and rest of the channels use a fractional guard channel policy to accept new calls along with handoff calls that is, 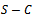channels accept new calls with probability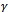. Arrival of new and handoff calls are assumed to be exponentially distributed with rate 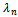and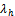, respectively. A call entering to the system is either handled or leave the system due to poor signal quality with probability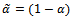. The call completion time and handoff time, are assumed to be exponentially distributed with rate 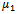and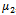, respectively. The total time spent by a call is also assumed to be exponentially distributed with rate.

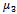Since poor signal call in a cell is also random variable having exponential distribution and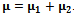. The time spent by a poor quality handoff quality handoff calls need to re-handed off quickly so it is assumed that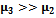. The network performance will be improved due to the using of the two dimensional Markov model, that is, the new of handoff dropping decrease.

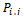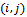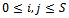Let represent the steady state probability that the base station is in state. For and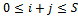, the state probabilities are given by

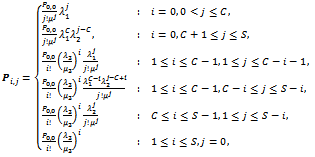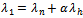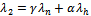where,  and.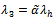

Using the normalization equation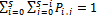, the value of 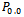can be computed as

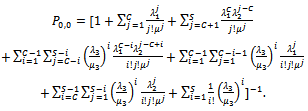We can compute the new call blocking probability (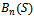) and handoff call dropping probability (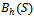) after computing the steady-state probabilities for various states. The blocking probability of new calls, 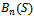, can be derived as

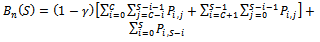The dropping probability of handoff call, that is, the call departs the handoff region before it can be assigned a channel is given by

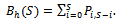The channel utilization (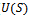) can be given as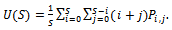

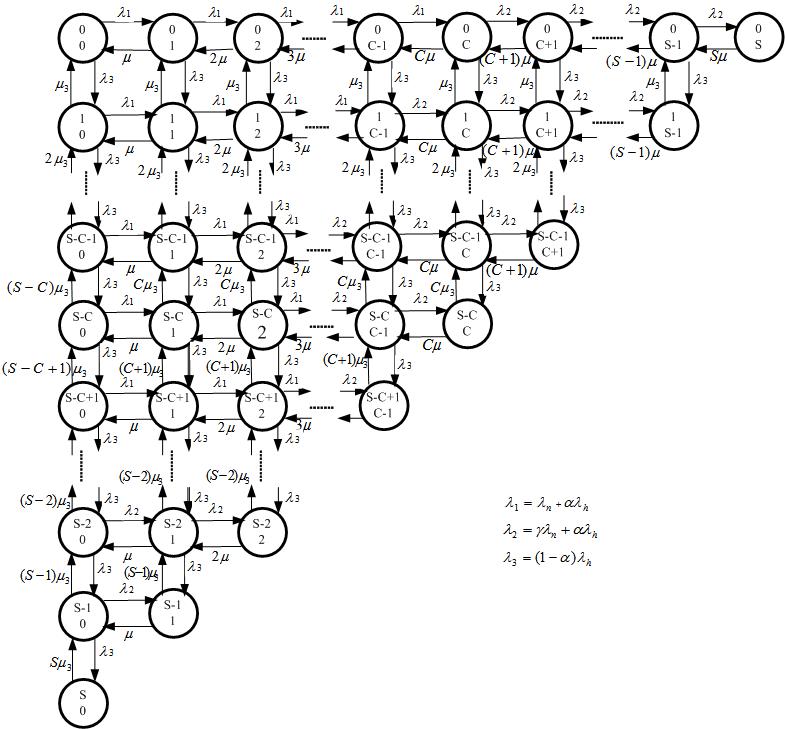Figure 4. State transition diagram

4. Numerical Results

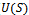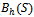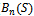In this section, we present the numerical analysis of both the models to investigate the impact on performance of the parameters and comparisons with conventional channel reservation schemes. The performance is evaluated numerically for both the models in terms of channel utilization, dropping and blocking probabilities, and, respectively. The parameters for Figures 5 to 8 are taken as 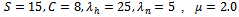and model I is under consideration.

Figures 5 and 6 present the new call blocking probability (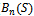)and the handoff call dropping probability (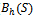), respectively, as a function of signal quality (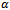) for various values of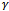. It can be observed that the blocking probability increases with increase of signal quality of handoff calls for all values of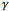, but it is smaller in large value of 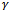as compared to small value of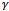. The dropping probability seems to be insensitive of the 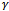for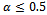, that is, all curves go through the same point. This can be explained by the fact that, as the poor signal quality handoff call increases, such calls are dropped immediately. On dropping such calls released channels may be used for new incoming calls, thereby reducing the new call blocking probability. It is important to note that decrease in blocking probability is compensated by very little increase in dropping probability. Hence, by choosing proper value of 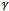and 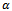we can optimize both the new call blocking probability and the handoff call dropping probability.

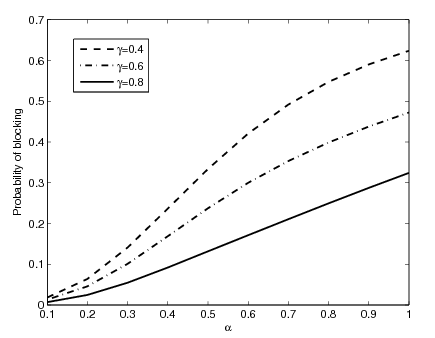Figure 5. Impact of on blocking probability

Figures 7 and 8 depict the new call blocking probability 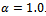and handoff dropping probability, respectively, under channel sizes S . For various values of C , the blocking and dropping probabilities are evaluated when It can be seen that with the increase of channel size S both blocking and dropping probabilities decreases, as more channels are available. When the threshold C is small, the new call blocking probability is significantly more than the dropping probability, which is quite small. By increasing the value of C , the dropping probability increases, while the blocking probability decreases. The choice of C is made so as to properly trade-off between these two performance metrics.

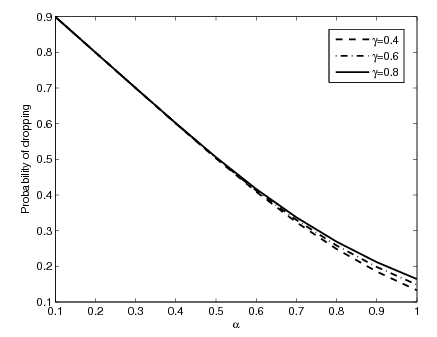Figure 6. Impact of on dropping probability

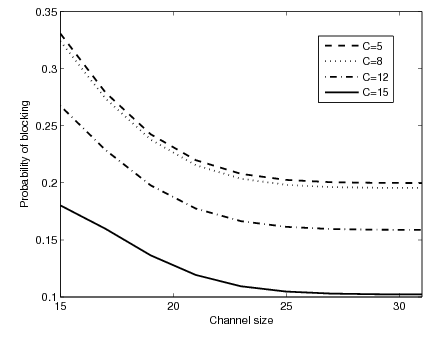Figure 7. Effect of channel size on blocking probability

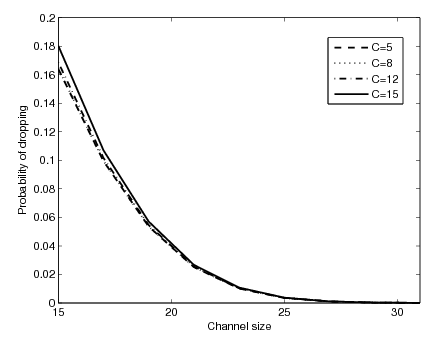Figure 8. Effect of channel size on dropping probability

Figure 9 illustrates impact of on handoff call dropping probability for various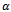. We choose the following set of parameters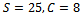, , 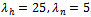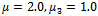and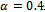. It can be observed that as 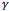increases the dropping probability (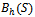) increases mono-tonically. Because the new calls being accepted more in numbers as the value of 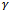increases, which leaves few channels available for handoff calls. It is also observed that with increase of 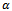the dropping probability decreases. As the new calls are facilitated by accepting with probability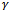, blocking probability decreases. Hence, by choosing the value of 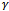appropriately a better performance result can be achieved for various signal quality handoff calls.

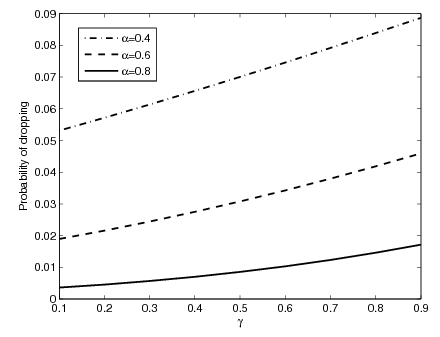Figure 9. Probability of dropping versus

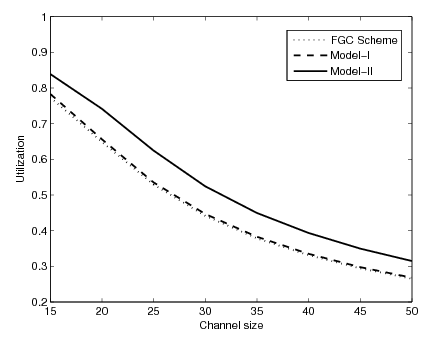Figure 10. Channel size versus utilization

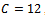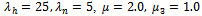Figure 10 shows the behaviour of channel utilization as a function of channel size for various channel allocation schemes. The system parameters are taken as, and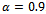. It can be seen that as channel size increases utilization decreases for all the schemes. As channel size increases more channels are available, which results in decrease in channel utilization. As expected, the proposed model II gives maximum channel utilization as compared to proposed model I and FGC scheme. Hence to utilize channels efficiently we can setup an admissible number of channels in the cell.

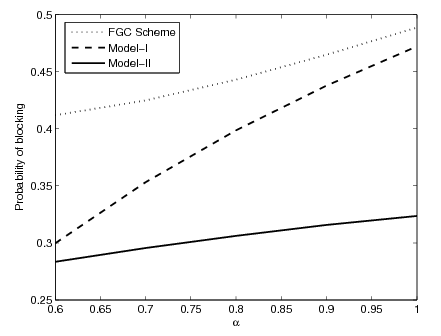Figure 11. Impact of α on blocking probability

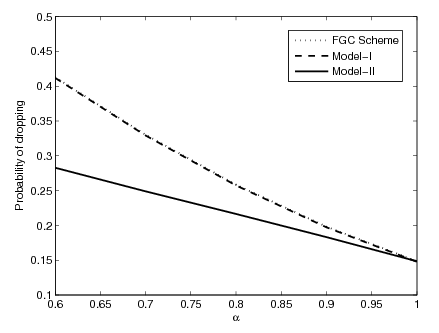Figure 12. Impact of α on dropping probability

Figures 11 and 12 show the effect of on blocking and dropping probabilities for various channel allocation schemes. We choose the system parameters as 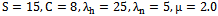and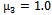. Both the new call blocking and handoff call dropping probabilities jointly accounts for the user satisfaction or dissatisfaction. Since dropping an active call is usually more annoying to the user than blocking a new call. It can be seen that for all models blocking probability increases with increase of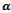. This is due to more acceptances of good signal quality handoff calls. For the model I and FGC scheme, dropping probability is invariant with respect to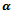. However, for the model II as 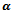increases dropping probability decreases. This is due to the fact that the increased value of 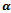implies fewer handoff calls being dropped immediately, which leaves fewer channels available for accepting new calls, thus increasing blocking probability. For the model II, the increased value of 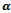implies fewer handoff calls being dropped or re-handed off. Furthermore, as 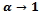the dropping probability for all schemes converges to the same minimum value. It can be seen that as handoff signal quality increases the dropping probability decreases monotonically. We observed that proposed model II gives a lower dropping probability due to re-handoff of low signal quality handoff calls. When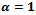, the dropping probability of all the models meet at a point. We can conclude that proposed model II is an efficient channel allocation mechanism, by lowering dropping as well as blocking probability.

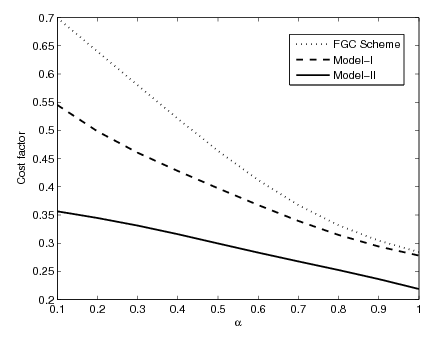Figure 13. Impact of on cost factor

In order to deduce the best utilization of the resources of a cell, on the part of the subscribers, it is necessary to introduce an appropriate cost function. In Figure 13, the cost function for various channel allocation schemes is illustrated. We observe that the cost factor decreases as the signal quality increases. In most of the cases, dropping probability is of more importance than blocking probability, thus, the common values for this parameter is . 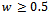For each of the schemes we have chosen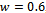, that is, more importance given to handover calls. We can note that the model II satisfies best our demands. The handoff dropping is more significant than new call blocking probability, because interruption of handoff calls upsets customers much more than blocking of new calls. As the model II utilizes the maximum resources, thus minimizes the cost function. Hence we can setup an admissible new call acceptance probability and the sufficient good signal quality in the system in order to have lower cost factor.

4. Conclusions

In this paper, we proposed two channel allocation schemes that handle the channels based on signal quality of handoff calls. We developed and analysed an efficient handoff scheme using mobile controlled handoff and fractional guard channel techniques, where MS measures the signal strength from surrounding BSs and interference levels on all channels for re-handoff decision. Performance analysis such as utilization, blocking and dropping probabilities as a function of channel size as well as the signal quality of the handoff calls is computed. It is shown that, by taking into account both the signal quality and the availability of free channels for processing a handoff call, the proposed schemes are able to deliver better performance.

Model II is based on the argument that instead of dropping poor signal quality handoff calls it is better to re-handoff such calls to some other BSs. It is seen that the blocking probability of new calls reduced significantly by accepting new calls with probability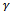. A better performance results can be achieved for various signal quality handoff calls by choosing the new call acceptance probability appropriately. The analysis carried out in this paper shows that ignoring the effects of poor signal quality handoff calls leads to exasperating in performance. It is concluded that the proposed model II outperforms other proposed model I and FGC scheme.