1. Introduction

New customer-oriented applications and triple play services are rapidly pushing the development of telecommunications. As a result, there is an increasing demand for network bandwidth and quality of service[1]. An optical network based on the WDM (Wavelength Division Multiplexing) technique is considered as a very promising approach for developing future large bandwidth networks. A WDM optical network consists of nodes interconnected by optical fibers, which transfer optical signals at different wavelengths, the so-called lightpaths. These networks are deployed mainly as backbone networks for nationwide or global coverage. The nodes in these networks actually represent the access stations for different LAN networks. The future of optical WDM networks are all-optical networks, where the lightpath is routed from the source node to the destination node without undergoing optical-electrical-optical (O/E/O) conversion at any intermediate node, which means that the signal remains in the optical domain.

However, in the current phase, these networks are facing many technical difficulties[2-6]. One of them is the problem of overcoming the physical impairments introduced by long-haul fibers and cascading optical components such as erbium-doped fiber amplifiers (EDFA) and optical crossconnects (OXC). Contributing factors include opticalnoise, chromatic dispersion, polarization mode dispersion, nonlinear effects and crosstalk. Thus,there is a maximum transparent reach limit for optical signals. In order to go beyond the limit, signal regeneration must reamplify, reshape, and retime the optical signals (so called 3R-regeneration). The regeneration is helpful in improving signal quality, so that a lightpath is able to travel farther before the signal reaches its destination. In principle, the regeneration can be accomplished purely in the optical domain. However, regeneration in the electronic domain, which converts an optical signal into electronic format and then uses the electronic signal to modulate an optical laser, is currently the most reliable technique[3,4]. But, the cost of wavelength converters is still very high and significant for the network financial budget[7]. That is why it is necessary to reach some kind of trade-off.

An all-optical network is also called a transparent optical network. The opposite is an opaque optical network. The opaque network employs 3R-regeneration at every intermediate node in order to regenerate the signal and to improve transmission quality. Since electronic regeneration is very expensive to implement on every node in the network and there is a very high increase in power dissipation in the system, a translucent optical network is proposed as a trade-off between transparent and opaque optical networks and a practical approach to strike a balance between them. The translucent optical network is based on the concept of having a relatively small number of strategically chosen opaque (i.e. electronic) nodes where regeneration and wavelength conversion is possible, whereas all other nodes are transparent switch nodes where signals remain in the optical domain[3].

The second problem of WDM networks concerns the routing and wavelength assignment (RWA) process, which consists of two different underlying problems: routing and wavelength assignment. In wavelength-routed networks data are transferred along lightpaths established between the source node and the destination node. A lightpath in a WDM network is created if and only if there is an available route and available wavelength. Both steps must succeed for a lightpath to be established. This involves routing and signaling to reserve a wavelength on each link along the selected path[8]. A lightpath connection request may be blocked on the path because there is no wavelength available on any of the links along the selected path. In order to get really optimal solutions, it is necessary to solve both problems. That is why an efficient and swift RWA algorithm must be implemented bearing in mind the objective that all network resources are optimally utilized. The selection of the route must be such that all the traffic is evenly balanced between all network resources.

The third problem is related to the blocking probability. When the traffic load is excessive, the blocking probability is very high. To prevent these situations when some link is fully utilized and there are no resources to provide service over that link, the alternative path which will avoid that link must be found. But, if the alternative route does not provide the solution this could be handled by dividing the nodes of the WDM network into several groups according to the priority. The LAN network connected to the node that has a higher priority will be given advantage during the process of reserving network resources over the LAN network that has a lower priority. All traffic for which the resources have not been found during routing and wavelength assignment can be multiplexed over the same wavelength using some of the next generation SONET/SDH technologies[9]. In this way, the probability of blocking will be much lower. The drawback of this solution is that a lower bit stream will be offered to some of the low priority nodes. In other words, some of the sessions will not be blocked, but they will have a lower bandwidth.

This paper deals with all the above mentioned problems that WDM networks are facing today. We propose an efficient routing and wavelength assignment heuristic, which at the same time, minimizes the blocking probability of lightpaths in the WDM network and selects the route for a given physical topology in such a manner that all traffic is evenly balanced between all network resources. For all traffic that has a lower priority and for which the RWA algorithm did not find the path, we propose traffic multiplexing which will prevent blocking of lightpaths. To our best knowledge, this is the first research work in investigating routing and wavelength assignment for optical WDM networks together, which optimizes quality of service and capital expenditure of networks based on the distributed Dijkstra sparse placement routing algorithm, first-fit wavelength reservation and traffic multiplexing.

In[10] the multihop routing and wavelength assignment algorithm is applied, but signal degradation in the system and traffic multiplexing is not considered. Reference[11] proposes a graph transformation method for performing RWA in networks with sharable wavelength conversion. Given a network with N nodes and W wavelengths, they formed an auxiliary graph with 2NW vertices in which each vertex represented entering or exiting the node on a given wavelength channel. The RWA was performed by use of Dijkstra’s algorithm to find the shortest path through the auxiliary graph. In[12] it is proposed that RWA could be divided in three separate steps: routing, selection of regeneration sites and wavelength assignment. The RWA problem is also analyzed in[7], but only for transparent optical networks. The wavelength assignment scheme that improves the blocking probability of WDM networks that use limited-range wavelength converters is analyzed in[13]. The sparse electronic placement algorithm is discussed in [2, 5] in which a number of opaque nodes used for regeneration are sparsely placed in the network. Reference[3] gives an excessive overview of recent studies regarding translucent optical networks.

The rest of this paper is organized as follows: in Section 2, we describe the network and switch architecture of translucent optical networks; in Section 3, a description of the routing and wavelength assignment algorithm is made. We address the statement of the problem in Section 4, present the numerical results of the simulation in Section 5 and give conclusions in the last section.

2. Network and Switch Architecture

Optical networks, in which each node routes some lightpaths transparently, while others go through optical-electrical-optical 3R-regeneration, are known as translucent. The sparse placement algorithm defines at which node in the network to place an electronic core capable of 3R-regeneration. The placement should provide for all physical impairments in the lightpath to be compensated and for all traffic in the network to be balanced. A translucent WDM optical network consists of a number of nodes interconnected by fiber links. Each of the links is capable of carrying W wavelengths. Long fiber links may be interspersed with inline optical amplifiers (e.g. EDFA). We assume that two adjacent nodes are connected with one pair of unidirectional fibers to provide the bi-directional connectivity.

A lightpath starts from the source node transmitter and terminates at the destination node receiver. The sparse regeneration node model allows all-optical switching in all nodes, while some of the nodes in the network are 3R-regeneration capable. When a lightpath is routed through intermediate regenerators at these regeneration capable nodes, it is divided into several fragments by the O/E/O regeneration. This process is planned in such a manner that the node receives the optical signal having the power sufficient for accurate decision.

The RWA algorithms and simulation processes are applied in this paper on the following two broadly used topologies of the optical networks[4,5,16]: 15-node/21-link Pacific Bell network topology and 24-node/43-link USANET network topology.

Translucent networks with sparsely placed opaque nodes contain two types of nodes, opaque and transparent. Opaque nodes can regenerate optical signals and convert wavelengths electronically, while transparent ones have the optical switching function only. At the opaque node, all arriving signals are detected and processed in the electronic domain. This node can also perform wavelength conversion, because it applies the switched outgoing signal to a new laser source. On the contrary, the all-optical transparent node provides a purely optical switching function for incoming optical signals, but cannot perform signal 3R-regeneration. Sparse regeneration uses the O/E/O regeneration resources sparsely distributed in the network.

Each network node consists of an optical core (optical crossconnect - OXC) and an access station. An OXC consists of multiplexers, optical switches, input/output amplifiers, taps and demultiplexers. Optical transmitters and receivers are in an access station. Opaque nodes are assigned a number of optional electronic processing modules (electronic core). At each node, the wavelengths of the incoming fiber links are demultiplexed and switched in the OXC, and then multiplexed onto the outgoing fiber links[3, 4]. In case of a regeneration capable node, the signal is sent to the electronic core where all input optical signals are converted to the electronic form, then processed at the 3R-regeneration unit (retiming, reshaping, reamplification), and finally converted back to optical signals, which is the end of the regeneration process.

The electronic switch is also capable of multiplexing the traffic from different nodes. The traffic is buffered, segmented and packed into payloads. The payloads from different clients may be multiplexed using either a sequential round-robin method or a queuing schedule[9]. The multiplexing method choice depends on the size of client frames and on the frequency of arrival. Round-robin is typically used when client frames to be multiplexed are almost synchronous and preferably of the same length. A queuing schedule is used when client frames are asynchronous, there is substantial variability in frame length, and there is a random arrival of packets. In such cases, the incoming client frames need to be buffered, retimed to reduce jitter, and then multiplexed. One of the benefits, but also weaknesses of the queuing schedule is that it requires a buffer length with margin and an intelligent scheduler algorithm.

3. Routing and Wavelength Assignment

Formally, the RWA problem can be stated as follows: given a set of lightpaths that need to be established within the network, and given a constraint on the number of wavelengths (fiber capacity constraint), determine the routes over which these lightpaths should be set up and also determine the wavelengths which should be assigned to these lightpaths so that the maximum number of lightpaths is established[14]. While the shortest path routes (according to distance, available resources, or by some other criteria) may often be preferable, this choice may sometimes have to be sacrificed in order to allow more lightpaths to be set up. In general, good RWA algorithms allow several alternate routes for each lightpath that needs to be established. Lightpath sessions that cannot be set up due to constraints on routes and wavelengths are said to be blocked. That is why it is very important to implement the routing algorithm which will find the shortest path route according to several criteria, but also several alternate routes in case that resources on the shortest path are already reserved.

RWA of lightpaths in optical networks is usually done in two steps. The first step tries to find a route between the node pair, and the second assigns wavelengths for links of the route. The literature suggests different solutions, with separate or simultaneous handling of these steps.. One approach is to route all connections first, and then assign wavelengths to them as a separate step. With this strategy, it is possible to have no available wavelengths for the found route. Another approach is to combine the steps so that routing is tied to a particular wavelength. This latter approach is typically accomplished by starting with a particular wavelength and reducing the network topology to only those links on which this wavelength is available. The routing algorithm is then run on this pruned topology. If a suitable route cannot be found, another wavelength is chosen and the process is run through again for the matching topology. With this combined approach, a free wavelength is guaranteed for any found route[12]. In this paper, we have applied the combination of the first and second approach: we start with separate steps first, but if we find insufficient network recourses we tie the routing algorithm to the wavelength assignment in order to find an alternate solution.

3.1. Routing Algorithm

The purpose of the routing algorithm is to select an appropriate route from source to destination among all existing routes in the network. If there is more than one choice in selecting the route, the controller can select the route according to some heuristics, such as the shortest path routing, load balancing routing, etc. We used both criteria in the routing algorithm.

Given that a lightpath is t be set up between a source node and a destination node, we consider the distributed Dijkstra’s shortest cost (weight) path algorithm to be capable of determining the best route with a carefully chosen way to assign a cost to each link[15]. For the problem under consideration, the overall objective is to optimize the balance between the lightpath lengths and the efficient usage of the network traffic capacities.

For each lightpath demand, we assign a weight 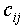to each network link (i, j), which is defined as:

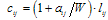(1)

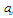where and W denote the number of currently available and the number of total wavelengths on the link (i, j), respectively, and 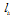is the physical link length in kilometers[4].

As we have previously emphasized, the longer an optical signal travels over a transparent path (path without opaque nodes) and the more switching nodes the signal passes through, the higher the signal quality degradation is. Therefore, in the paper[6, 16] it is proposed to use two parameters described as follows: Lhop is the acceptable maximum transparent path length (there are no opaque or regeneration nodes on the route) measured in hops (the number of intermediate nodes passed through) and Llen is the acceptable maximum geographical transparent length of the optical signal in kilometers. If the length of the route is larger than the length Llen or the service signal travels more hops than Lhop, the end receiver will not detect the service signal. Then, the lightpath should be regenerated at intermediate nodes.

On the other hand, if we use only this criterion, some of the links in the network will suffer from excessive traffic, and some other links will occupy only a small proportion of the bandwidth. In order to utilize the network efficiently, we take the number of currently occupied paths as the current cost (weight) of the link, and for any additional path transported by that link the weight is increased by the factor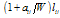. The route for a new lightpath is the least weight route between the source–destination node pair. In other words, this algorithm attempts to even out the utilization of links in the network and the lightpath distance. The selection of nodes which will be capable of performing O/E/O conversion is made based on the following two criteria: destination signal quality and uniform traffic distribution across the network. The obtained result is a translucent optical network[16].

3.2. Wavelength Assignment

The simplest wavelength-routed networks assign one wavelength to all links of the connection between the source node and the destination node. This requirement is known as the wavelength continuity constraint. This constraint can be avoided by use of wavelength converters at intermediate nodes. A wavelength converter is a device that converts the input wavelength λi into a different output wavelength, λo. In wavelength-routed networks with wavelength converters, a lightpath can be established even if there is no common wavelength on all links along the path. This approach can improve the blocking probability and the efficient utilization of wavelengths[13]. That is why we have used the wavelength converters in the opaque nodes of the optical network for improving the blocking probability.

There are several wavelength assignment heuristics that have been proposed in the literature: Random, First-Fit, Least-Used, Most-Used, Min-Product, Least Loaded, Wavelength Reservation, etc[14]. These heuristics can be implemented and combined with different routing schemes. There are schemes which attempt to reduce the overall blocking probability for new connections and there are some which aim to reduce the blocking probability for connections that traverse more than one link. In this paper we use a combination of First-Fit and Wavelength Reservation assignment heuristics.

In the First-Fit wavelength assignment heuristic all wavelengths are numbered. When searching for available wavelengths, a lower numbered wavelength is considered before a higher numbered wavelength. The first available wavelength is then selected. The computation cost of this scheme is low because there is no need to search the entire wavelength space for each route[17]. In the Wavelength Reservation heuristic a given wavelength on a specified link is reserved for the traffic stream, usually a multihop stream. For example, in Fig. 2, the wavelength λ1 on the link (8,9) may be reserved only for the connection from node 6 to node 10 (it has priority over the connection between nodes 8 and 9); thus, a connection request from node 8 to node 9 cannot be set up on λ1 on link (8,9). In this case the alternate route must be found for connection between nodes 6 and 10. This scheme reduces the blocking for multihop traffic.

In this paper we have combined the two schemes. We have taken the following algorithm: λi (1≤i≤W) is assigned to the lightpath if the following conditions are fulfilled: λi is available along the selected route, total transparent path length is shorter than the transparent length Llen, number of transparent nodes on the lightpath is less than Lhop and the route is not reserved for a higher priority connection. If some of the conditions are not satisfied, another route is searched for.

4. Problem Statement

The optical network is represented by an oriented multigraph G(V,E) with a node set V = {n1 ,n2,…,nN} and an arc–edge set E = {l1 ,l2 ,…,lL} labeled with the geographical fiber link distance, where each edge is associated with a two directional fiber. Throughout the paper, we assume that all fiber links have the same capacity, i.e. the number W of available wavelengths. The multihop routing and wavelength assignment algorithm with minimum blocking rate (mul_RWA_min_BP) which we propose in this paper works as follows.

For each connection request from source to destination, we attempt to establish a lightpath, i.e. a sequence of wavelength subpaths. In each subpath we can assign the same wavelength and the set of subpaths define a path from source to destination, subject to the following set of constraints[10]: (i) collision-avoidance constraints, i.e. two different lightpaths using the same fiber must have distinct wavelengths; (ii) fiber capacity constraints, i.e. the number of lightpaths using the same fiber should not exceed the capacity of the fiber defined by the maximum number of wavelengths per fiber; (iii) hop constraints, i.e. no more than Lhop transparent nodes should be on the path; (iv) length constraints, i.e. the transparent path should not be longer than Llen in kilometers.

Distributed Dijkstra algorithm provides an optical network with the necessary number of nodes capable of performing O/E/O conversion, with routes between any two nodes[16]. For the first pair in the sequence of priority nodes, the chosen route is observed and every link of the chosen route is searched for the same available wavelength. The algorithm proceeds by checking the wavelength number 1, followed by number 2 and, finally W. If the wavelength is available, the algorithm reserves it. Otherwise, the algorithm returns and finds the last opaque node in the route, and reserves the first available wavelength between that node and the destination. But, if it is still unable to find an available wavelength, it goes further back to the next opaque node and reserves an available wavelength between these two opaque nodes, repeating the procedure until it reaches the source. If, at any point of the route, it is unable to find an available wavelength which would enable the task fulfillment, the algorithm is interrupted. Once the algorithm is interrupted, the link for which no available resources have been found in order to perform the connection is removed from the network (by setting the link price to infinity) and Dijkstra algorithm is set off once again to determine a new route. Once the route is determined, the whole procedure starts all over again, i.e. the same available wavelength is looked for throughout the route, and so forth. If enough available resources cannot be found in this route either, another link is removed from the network and the Dijkstra algorithm called for once again. Such procedure is repeated until a route with sufficient resources is found or until the Dijkstra algorithm reports that there are no available routes between the two nodes.

If there are no available routes between the two nodes, we return to the initial route and observe whether the source and destination are opaque nodes. If so, the signal is multiplexed and packed together with other signals over the same wavelength. If not, the opaque nodes closest to the source and destination are searched for and, if there is an available wavelength to connect the source and destination with these two nodes, multiplexing is performed between the two nodes. If this is not possible, then the source and/or destination are identified as opaque nodes. The procedure is also repeated for other nodes in the network. This way it is possible to have a higher number of nodes with O/E/O conversion than in the translucent network, but still lower than in the opaque network. Multiplexing is performed only for lower priority traffic. In this way, the quality of service is increased since there is no blocking, but the available flow decreases for each multiplexed session.

A dedicated program was developed in order to realize the mul_RWA_min_BP algorithm. It consists of the procedures and functions described as follows:

INPUT parameters: the network G(V,E); the number of wavelengths W; the maximum length in hops Lhop; the maximum length in kilometers Llen; the matrix T=(Tsd) where Tsd is the number of connections from ns (source) to nd (destination); the list of nodes whose ingoing and outgoing traffic has priority towards the rest of the nodes.

The set S defines the overall set of connection requests induced by the T matrix. Let N be the number of nodes and L be the number of links in the network. We also use the following notation: p is a cursor on the current node, where s is a source node, d is a destination node and e designates the node with the O/E/O capabilities, (i,j) defines the link between the nodes i and j and 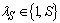defines the numeration of the current lightpath session.

Function D.D.S.P_ALGORITHM runs the Distributed Dijkstra Sparse Placement Routing Algorithm which is described in detail in[16]. The output of this function is twofold. First one are the lightpaths between every source-destination pair in the network as a result of the distributed Dijkstra algorithm. The other one are the nodes that should be equipped with O/E/O converters in order to satisfy the length and hop constraints, defined by parameters Llen and Lhop.

The INITIALIZATION procedure takes the following input: the paths and the nodes obtained as output of the D.D.S.P.R_ALGORITHM, the traffic matrix T and the list of priority nodes. It also initializes the index λs to the value of 1.

The LIGHT_SELECT procedure checks whether the path obtained by the D.D.S.P.R_ALGORITHM has available lightpaths with minimal conversions at intermediate nodes. It starts with the first lambda and then follows the path from source node to the destination node reserving this first lambda. If the first lambda in some link on lightpath have previously been reserved by some other lightpath, the procedure continues with the second lambda. A lambda that is available on the whole path is reserved and the procedure is terminated, otherwise zero is returned to indicate that this procedure has failed.

If the procedure returns zero, the cursor is placed on the first opaque node on the path and the same procedure is run again but now just on the rest of the path from this opaque node until destination node. If this procedure returns zero again these steps are repeated if there are additional O/E/O converters on the path.

In case the final result of the LIGHT_SELECT procedure is zero, the REMOVE_LINK function is run. For the link (i,j) on the path where all wavelengths are reserved we put .

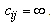The PATH_λs_EXIST procedure checks whether the function D.D.S.P.R_ALGORITHM has found the path for the session λs.

The OPAQUE_NODE_SELECTION function is run if there is no path for the session λs and the source and destination have no conversion capabilities. If there is no nodes on the path having O/E/O converters the source and destination node are selected to have 3R regenerators. Otherwise one additional node has to be selected so that path has available lightpaths with minimal conversions. This is done through several iterations. If the source node has O/E/O converters the other node is selected on the path between the node closest to the source node which also has O/E/O converters and the destination node. If the destination node has O/E/O converters the other node is selected on the path between the node closest to the destination node which also has O/E/O converters and the source node. If both source and destination node has no O/E/O converters and there are such nodes on the path the traffic is multiplexed between two selected nodes which assures that there will be minimal conversions.

The RESERVATION function reserves all lambdas on the path, as the result of the LIGHT_SELECT procedure which finds available lambdas on the path.

The MUX function multiplexes the traffic between two chosen nodes with O/E/O capabilities on the path and packs them with all other multiplexed traffic between the node pairs from other sessions.

The OUTPUT parameters are: blocking probability for the sessions in the matrix T, number and arrangement of opaque nodes in the network, network utilization (percentage of used wavelengths in the links), percentage of the sessions that have been multiplexed.

The complete algorithm is summarized in Figure 1.

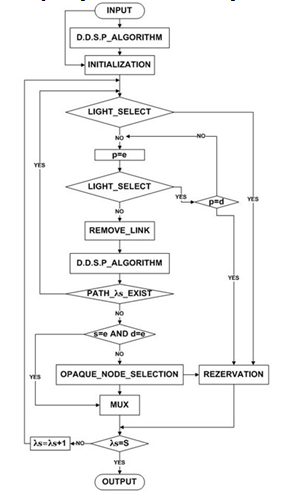Figure 1. Flow chart of the mul_RWA_min_BP heuristic

The upper bound of the standard Dijkstra algorithm computation complexity is O(N2) at worst[11] and the D.D.S.P_ALGORITHM computation complexity can be improved to O(L+NlogN). Since this algorithm can be run several times during the mul_RWA_min_BP heuristic, the computational complexity and running times are of the order of O(L2+N·L·logN), which can be very time consuming for large numbers of N and L.

5. Numeric Results

No heuristic can be validated until it is supported by practical results. In order to demonstrate the proposed algorithm performance, we made a simulation. Not being able to find a suitable simulator that could support our routing problem, we designed and developed a simulator to implement routing and wavelength assignment in optical transport networks. The simulator was developed in Java language. All experiments were conducted on a 3 GHz PC with 4G RAM. The simulator accepts input parameters such as the number of nodes in the network, link information with associated weight, number of wavelengths per fiber, maximum transparent length measured in hops, maximum transparent geographical length in kilometers and traffic matrix with a number of sessions between every pair of nodes. The outputs of the simulator are the number and placement of opaque nodes, the utilization, the number of successfully connected sessions and the number of sessions that have to be multiplexed with other traffic.

All these input parameters can be initialized before running simulations to obtain results for a given selection of parameters. Permutation routing was used in order to find out the sample source-destination pairs in which every node in the network acts as the source for every other node in the network. The total number of source-destination pairs in permutation routing depends on the number of nodes. Extensive simulations are then carried out for each combination of parameters of interest and the obtained results are presented.

In this section, we conduct four cases of simulation experiments in order to measure the network performance under different input settings. We study the following four cases: transparent optical network, translucent optical network, translucent optical non-blocking network, opaque optical network. The translucent optical network is obtained as a result of the D.D.S.P_ALGORITHM and the translucent optical non-blocking network as a result of the mul_RWA_min_BP heuristic. In order to compare these 4 cases we apply two network topologies: Pacific Bell network topology and USANET network topology. We use the following data range for the parameters: Lhop: 3 ÷ 4 hops; W: 1 ÷ 256 wavelengths; Llen: 2,000 ÷ 5,000 km; traffic matrix: 50 ÷ 400 sessions per iteration.

The simulator outputs are compared in order to evaluate the proposed algorithms. To investigate the effectiveness of the proposed wavelength-assignment algorithm, we created a network simulation in which the lightpath requests arrive with a previously defined number of requested sessions between two nodes. The number of requested sessions are placed in the matrix T. New matrix is created for every iteration following the rule with probability of session appearances. Let the Pij(n) represents the probability that between nodes i and j there are n requested sessions in matrix T. We use the following values: Pij(0)=0.6, Pij(1)=0.35, Pij(2)=0.04, Pij(3)=0.007 Pij(n>3)=0.003, for every pair (i,j).

All these probabilities had discrepancies of ±10% during the process, and 10,000 iterations were performed for each input parameter instance. As discussed earlier, the goal is to have a less expensive network, evenly balanced network traffic, low blocking probability and prioritized traffic regarding the source-destination pair. The general results for all cases are as follows.

Table 1 gives the number of opaque nodes of the Pacific bell network for all four optical network configuration types. The number of nodes with O/E/O properties changes significantly with the change in number of wavelengths, so higher values of parameter W bring significant savings in equipping the network with additional electronic devices for signal conversion and processing. If W = 16, as many as 65% nodes can be completely transparent for signals in the optical domain.

Table 1. Number of Opaque Pacific Bell Network Nodes for Ls = 3000km w opaque non-blocking translucent translucent transparent 1 15 15 5 0 8 15 10 5 0 16 15 5 5 0

Figure 2 shows the session blocking probability for all four network configuration types depending on the number of wavelengths, for the Pacific bell network. It is obvious that the non-blocking translucent network shows the best performance, having no blocked sessions, while other network types have the negligibly small blocking probability only when W reaches 16. This results from the search for alternate paths, and if there are no free resources in that case, the sessions are multiplexed. The proposed algorithm has much greater results in regard with the quality of service compared with the algorithm in[16] because none of the requested sessions are not blocked. But on the other side some of the sessions must have reduced bit rate due to the multiplexed traffic.

Figure 3 shows the dependence of the session blocking probability on the number of requested sessions expressed through the matrix T, for the case of the Pacific bell network. The number of requested sessions is shown in decimal notation since it represents the average value for 10,000 iterations. Simulation results show that, unlike other network types, the non-blocking translucent networks has no blocked sessions regardless of the network traffic increase. The proposed heuristic proved to be immune to the quantity of traffic generated within the Pacific bell network.

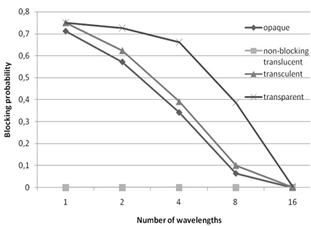Figure 2. Session blocking probability for the Pacific bell network as a function of the number of wavelengths. Llen = 3000km, Lhop = 3, average number of requested sessions is 97

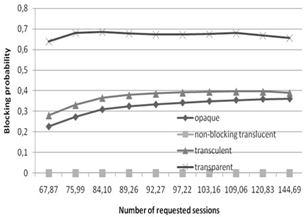Figure 3. Pacific bell network session blocking probability as a function of the average number of requested sessions. Llen = 3000km, Lhop = 3, W = 4

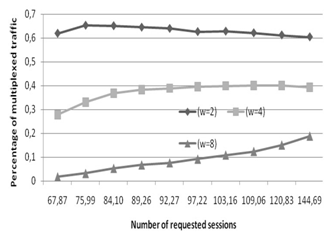Figure 4. Percentage of multiplexed traffic for non-blocking translucent heuristic for the Pacific bell network as a function of the number of requested sessions. Llen = 3000km, Lhop = 3

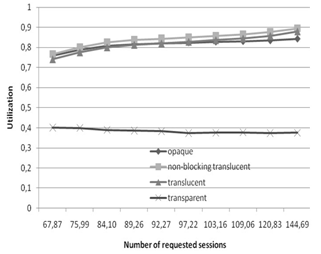Figure 5. Pacific bell network resource utilization as a function of the average number of requested sessions. Llen = 3000km, Lhop = 3, W = 4

Table 2 gives the number of opaque nodes for the USANET network for all four optical network configuration types. For higher values of the parameter W there is a certain saving in equipping the network with additional electronic devices for signal conversion and processing. If W = 64, as many as 70% nodes can be completely transparent for signals in the optical domain.

Table 2. Number of Opaque USANET Network Nodes for Ls = 3000km w opaque non-blocking translucent translucent transparent 1 24 24 13 0 16 24 21 10 0 24 24 19 10 0 32 24 16 10 0 64 24 7 7 0 128 24 6 6 0

Figure 6 shows the session blocking probability for all four network configuration types depending on the number of wavelengths. It is obvious that the non-blocking translucent network again shows the best performance, having no blocked sessions, while other network types have the negligibly small blocking probability only when W reaches 24.

Figure 7 shows the dependence of the session blocking probability on the number of requested sessions expressed through the matrix T, for the case of the USANET network. The number of requested sessions is expressed through average value of 10,000 iterations. The simulation results show that the non-blocking translucent heuristic has no blocked sessions regardless of the increase in network traffic. The proposed heuristic proved to be immune to the quantity of traffic generated within the USANET network as well.

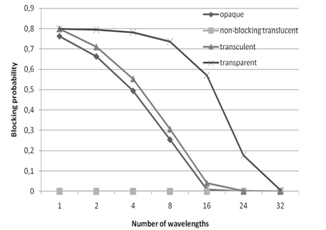Figure 6. Session blocking probability for the USANET network as a function of the number of wavelengths. Llen = 3000km, Lhop = 3, average number of requested sessions 255

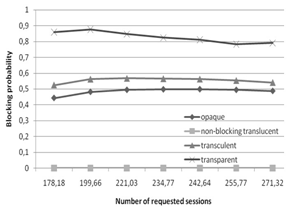Figure 7. USANET network session blocking probability as a function of the average number of requested sessions. Llen = 3000km, Lhop = 3, W = 4

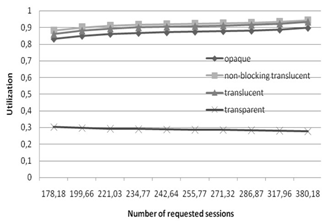Figure 8. USANET network resource utilization as a function of the average number of requested sessions. Llen = 3000km, Lhop = 3, W = 4

6. Conclusions

In this paper, we study a non-blocking translucent wavelength routed optical network architecture that effectively overcomes the signal quality degradation in a fully transparent network, while using much less wavelength-convertible 3R O/E/O regenerators than a fully opaque network, while improving blocking probability compared to a traditional translucent network. We study the problem of finding the shortest and alternative paths in the RWA algorithm and multiplexing the sessions in WDM optical networks. These nodes are selected and the routing assignment is done by applying the distributed Dijkstra algorithm. The novelty lies in optimizing the process of analyzing the signal quality degradation, network load balancing, number of opaque nodes and quality of service.

The comparison of the proposed RWA heuristic with other commonly used strategies in terms of blocking probability and network utilization is presented. The simulation results show that the proposed heuristic has no blocking sessions compared with other best algorithms. Our numerical simulation demonstrates that, for larger number of wavelengths, it is sufficient to equip no more than 30% of nodes with electronic 3R-regeneration capability. Our results further show that network performances can be improved by increasing the number of wavelengths. Accordingly, we show through simulation that the proposed algorithm gives very good results for small and medium sized networks. Since the complexity of the problem is relatively high for large networks (more than 30 nodes), we need to apply additional relaxations.