1. Introduction

Since Dassios[5], Harrison[7] and Paulsen[15], several models for Risk Analysis had been established, but there are no connections to the CAPM, Sharpe[16]. As was pointed out by Dassios[5], these processes should provide a standard theory for studying applications in insurance risk theory. The Poisson arrival condition will be relaxed to a general renewal arrival process, Karatzas[10]. The service payment model will follow the replacement model in Gihman[6]. The analysis of integral representation will be given by Moriconi[14], the properties of which were subsequently investigated by Lintner[11]. In this paper, relevant facts that affect the probability of ruin can be mapped to Network Security System so that people can determine the stability of Network Systems. The models for the corruption of an event can be viewed as the stage of Network Security Risk, using the parameters to determine its stability.

2. Stochastic Risk Model

Let 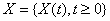be a stochastic process with stationary, independent increments, finite variance, and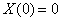. We call this as gain process. Given a positive y of initial stable values and a positive stable rate, we define the stable process by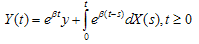

(2.1)

Let be a Poisson process with arrival rate λ, and let 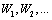be independent and identically distributed random variables with distribution F. Let c be a finite

constant, take

Let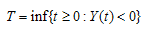

Call T the time of ruin and r(.) the probability of ruin, then

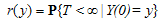(2.2)

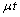Assume that the process X is defined on a probability space and has stationary, independent increments with E[X(t)] = and Var[X(t)]=, where and.

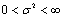Let 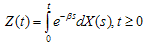, then

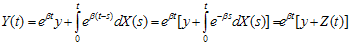Theorem:

We have

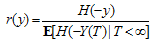(2.3)

where H is the distribution function of.

The proof of the theorem had been done properly in Harrison[7].

3. Stable Rate Determines System Stability

As the stable rate 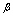increases, the ruin function r(.) will get smaller. This fact can say a lot about the way to control stability of systems. The chance of being intruded will be smaller if the stable rate is raised or higher.

For the characteristic function of X(t) we have

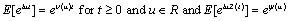Where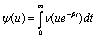

From[6], the representation can be

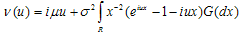(3.1)

where G is a probability distribution in R.

Suppose

The exponential function is

then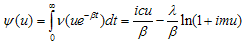

(3.2)

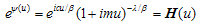Invert H then

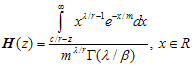(3.3)

with is the Gamma function

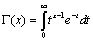
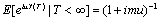
The probability of ruin is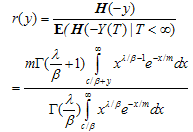

(3.4)

Suppose now that (m > 0),

with F (x) = 1 for x > 0. We obtain

Similarly, take the inversion, we have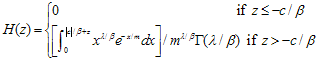

4. Some Problems in Network Security Risk

From (2.1) and (2.2), we can remodel the parameters as components in Network such as traffic channels, systems, encryption processes. The probability of ruin in this environment will represent for the stability and risk of network security components.

Theorem 4.1

Assume 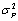= 0. Let and consider the equation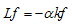

(4.1)

Where

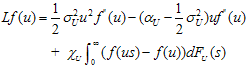(4.2)

Let y (u) and z(u) be solutions of (4.1) with and 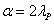respectively, and such that 0 < y (u), z (u) < 1. Assume:

(B1) if 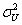> 0, then

Otherwise it is sufficient that

(B2)

then

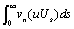Proof. Let X (u) = exp{}, then since k is real,

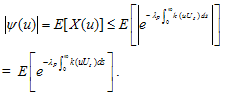and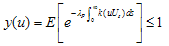

is the solution of (4.1) with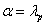. For some constant c,

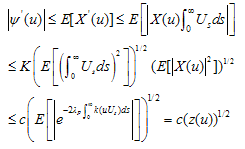Since by. Then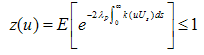

5. Conclusions

In this paper, ideas of mapping to Network Security Risk had been presented for the important applications of System Security Risk so that companies can use to evaluate the System Security stability.

The applications of Stochastic Ruin Models will be useful for System Intrusions, to prevent attacks. By using appropriate parameters for the environment, the models for Network Security Risk play important role for Homeland Security, to make decisions for kinds of secure system implementations. Further investigations on the applications on the particular devices for Network Security systems will be studied in the future.