-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Networks and Communications
p-ISSN: 2168-4936 e-ISSN: 2168-4944
2011; 1(1): 18-22
doi: 10.5923/j.ijnc.20110101.04
Fading Channel with Orthogonal Multi-carrier Code Division Multiple Access Signal
Issam Trrad 1, Amjad Hindi 1, Ziad Sobih 2
1Department of Electrical Engineering, Jadara University, Irbid, 21110, Jordan
2Department of Electrical Engineering, Isra University, Amman, 11622, Jordan
Correspondence to: Ziad Sobih , Department of Electrical Engineering, Isra University, Amman, 11622, Jordan.
| Email: | 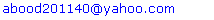 |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
The wireless industry is currently undergoing a major transition from second generation (2G) to third generation (3G) wireless technologies, and the increasing demands for communication services require higher transmission rates that further stimulates the demand on wideband technologies depicted in the form of code division multiple access (CDMA) on one hand. Also, as the privacy is a prime issue in modern communications therefore the carriers orthogonality is a fundamental concept for a sustainable development of the communications sector. This paper attempts to assess wireless communications channels and propose techniques to improve the performance of modern wireless communications. Hence from a strategic perspective, an analytical study into the performance of Group Orthogonal Multi Carrier Code Division Multiple Access (GO-MC-CDMA) in which subcarriers assigned to users which are orthogonal to other groups, the channel bandwidth is the main theme of this paper; from which the problems that may affect the communications link are high lighted and measures to counterbalance and alleviate multipath fading are proposed and investigated. Such measures are: Space diversity combining techniques and minimum – mean square error, and interference cancellation and detection are considered in this research. As a result of this research it can be stipulated that subcarriers grouping does reduce Multi-User-Interference (MUI) between frequency groups thus enhance the performance of MC-CDMA system in the mission of meeting newly emerging wideband communications services, such as video conference and others.
Keywords: Fading Channel, Code Division Multiple Access (CDMA), Multi User Interference, Additive White Gaussian Noise, Frequency Division Multiple Access, Multiuser Orthogonal Frequency Division Multiplexing (M-OFDM)
Cite this paper: Issam Trrad , Amjad Hindi , Ziad Sobih , "Fading Channel with Orthogonal Multi-carrier Code Division Multiple Access Signal", International Journal of Networks and Communications, Vol. 1 No. 1, 2011, pp. 18-22. doi: 10.5923/j.ijnc.20110101.04.
Article Outline
1. Introduction
- OFDM is a robust scheme to frequency selective fading, however, it has several disadvantages such as difficulty in subcarrier synchronization and sensitivity to frequency offset and nonlinear amplification, which result from the fact that it is composed of a number of subcarriers with their overlapping power spectra and exhibits a non-constant nature in its envelope. However, the combination of OFDM signaling and CDMA scheme has one major advantage that it can lower the symbol rate in each subcarrier so that a longer symbol duration makes it easier to quasi-synchronize the transmissions. The Multicarrier CDMA schemes are categorized mainly into two groups: One spreads the original data stream using a given spreading code, and then modulates a different subcarrier with each chip (in a sense that the spreading operation is in the frequency domain), and other spreads the serial-to-parallel (S/P); converted data streams using a given spreading code, and then modulates a different subcarrier with each of the data stream (the spreading operation in this is in the time domain); similar to a normal direct sequence code division multiple access (DS-CDMA) scheme[1]. In order to exploit the maximum possible channel diversity while being able to accommodate dynamic load changes, a group orthogonal multi carrier code division multiple access (GO-MC-CDMA) scheme is developed. This scheme does not require complex code assignment operations. The set of subcarriers is partitioned into groups, and the users who are assigned subcarriers of the same group are separated using spreading codes. Furthermore, it can be seen that grouping the subcarriers together will help the user to achieve full multipath diversity which is essential for the mitigation of the multipath effects. Also the users in each group are immune to interference from other groups, hence explains the name of this scheme, as group orthogonal MC-CDMA.
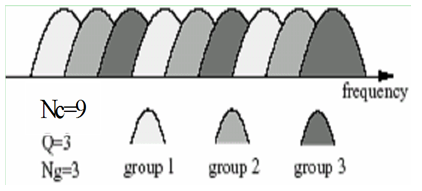
2. System Model
- In this section a complete modeling of the above system is presented. A symbol-spread case is considered, where each active user transmits only one symbol over a block of Nc chips, the symbol period is
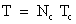 . The entire available bandwidth is utilized with Nc subcarriers that are spaced by 1/T apart. If fi denotes the ith column of the Fast Fourier Transform (FFT) matrix FNc, then fi* is the ith digital subcarrier. The Nc subcarriers are partitioned into Ng groups with each group having Q = Nc/Ng subcarriers. A user chooses a specific group of subcarriers to transmit its information bearing symbols; and Q users share Q subcarriers per group, which ensures no spectral efficiency loss[2]. The system model of GO-MC-CDMA is illustrated in the block diagram of Figure 1. Let Sn,m( i ) be the information bearing symbol of user m in the nth group transmitted during the time interval [iT, (i + 1)T)]. A Q × 1 spreading code cm is used to spread Sn,m(i) to the Q subcarriers of the nth group. the Q × Q matrix is defined as C:= [c0, c1, . . . , cQ−1], whose columns consist of Q spreading codes of the nth group. The spreading code matrix C does not have to be identical for different groups. But since there is no MUI between users of different groups by design, the same code matrix is chosen for all groups. C is designed such that, all user codes are linearly independent, with |cq(i)|2 = 1/Q,
. The entire available bandwidth is utilized with Nc subcarriers that are spaced by 1/T apart. If fi denotes the ith column of the Fast Fourier Transform (FFT) matrix FNc, then fi* is the ith digital subcarrier. The Nc subcarriers are partitioned into Ng groups with each group having Q = Nc/Ng subcarriers. A user chooses a specific group of subcarriers to transmit its information bearing symbols; and Q users share Q subcarriers per group, which ensures no spectral efficiency loss[2]. The system model of GO-MC-CDMA is illustrated in the block diagram of Figure 1. Let Sn,m( i ) be the information bearing symbol of user m in the nth group transmitted during the time interval [iT, (i + 1)T)]. A Q × 1 spreading code cm is used to spread Sn,m(i) to the Q subcarriers of the nth group. the Q × Q matrix is defined as C:= [c0, c1, . . . , cQ−1], whose columns consist of Q spreading codes of the nth group. The spreading code matrix C does not have to be identical for different groups. But since there is no MUI between users of different groups by design, the same code matrix is chosen for all groups. C is designed such that, all user codes are linearly independent, with |cq(i)|2 = 1/Q,  q, i = 1, . . . , Q , where cq(i) is the ith entry of cq. This design condition is satisfied when cq is a scaled binary code e.g., Walsh-Hadamard or Gold Code or, any constant modulus complex field code.
q, i = 1, . . . , Q , where cq(i) is the ith entry of cq. This design condition is satisfied when cq is a scaled binary code e.g., Walsh-Hadamard or Gold Code or, any constant modulus complex field code.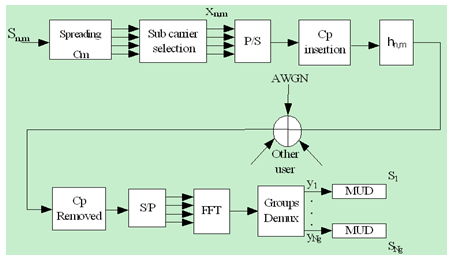 | Figure 1. System model of GO-MC-CDMA |
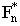 comprise of the Q digital subcarriers of the nth group, while any Q subcarriers can be assigned to a group of users, then if a set of equi-spaced subcarriers is selected, the following matrix is obtained:
comprise of the Q digital subcarriers of the nth group, while any Q subcarriers can be assigned to a group of users, then if a set of equi-spaced subcarriers is selected, the following matrix is obtained: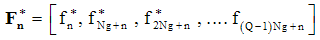 | (1) |
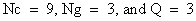 . Where The Nc×1 signal vector of user m in the nth group during the ith block, modulated on Q subcarriers, may be expressed as
. Where The Nc×1 signal vector of user m in the nth group during the ith block, modulated on Q subcarriers, may be expressed as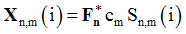 | (2) |
 | Figure 2. Equi-spaced group subcarrier assignment |
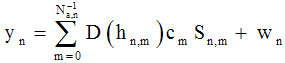 | (3) |
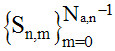 in the nth group. In order to reduce the loss in bandwidth and power efficiency due to CP, the block spreading approach can be incorporated, where K >1 symbols are transmitted per user per block. The KNc subcarriers are used to transmit a total of KNc symbols per block without increasing signal bandwidth. The subcarriers are partitioned into Ng = KNc/Q groups. Each user is assigned to K groups, and transmits one symbol in each group. At the receiver, using the K input-output Equation (2), the K symbols are detected of the same user independently. This block spreading of GO-MC-CDMA avoids ISI among symbols from the same user, which facilitates the accommodation of the dynamic load changes in the system to improve the performance at low load[2].
in the nth group. In order to reduce the loss in bandwidth and power efficiency due to CP, the block spreading approach can be incorporated, where K >1 symbols are transmitted per user per block. The KNc subcarriers are used to transmit a total of KNc symbols per block without increasing signal bandwidth. The subcarriers are partitioned into Ng = KNc/Q groups. Each user is assigned to K groups, and transmits one symbol in each group. At the receiver, using the K input-output Equation (2), the K symbols are detected of the same user independently. This block spreading of GO-MC-CDMA avoids ISI among symbols from the same user, which facilitates the accommodation of the dynamic load changes in the system to improve the performance at low load[2].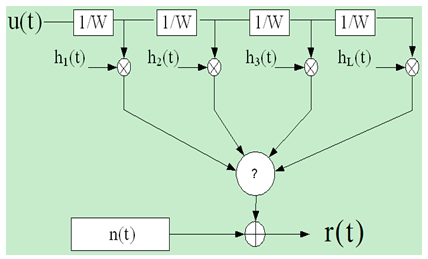 | Figure 3. Tapped delay line model of frequency selective channel |
3. Fading Channel Model
- The tapped delay line is shown in Figure 3. The time variant tap weights {hp(n)} are zero mean complex valued stationary Gaussian random process, and they correspond to the L different delays τ = pTm , where p=1,2,…L. For all practical purposes, the channel tapped delay line model can be truncated at L = [TmW]+1 taps ,where Tm is a total multipath delay spread and W is the signal bandwidth. Then, the noisy received signal can be expressed in the form [3]:
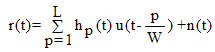 | (4) |
4. Space Diversity Technique and Simulation Results
- Figure 4 shows the configuration of a two-branch diversity system. Both branches are weighted by their respective instantaneous voltage-to-noise ratios, the branches are then co-phased prior to summing in order to ensure that all branches are added in phase for maximum diversity gain. The summed signals are used as the received signals, connected then to the demodulator.
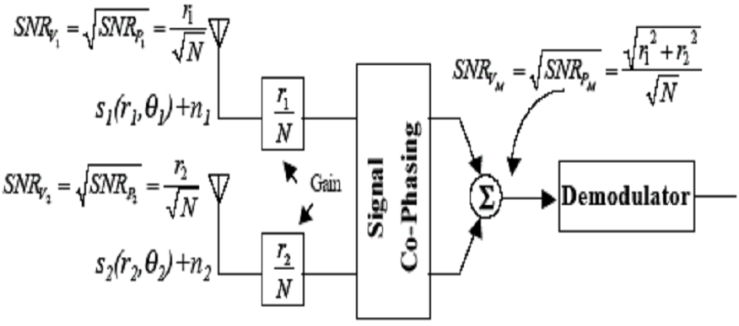 | Figure 4. Block diagram of a two-branch maximal ratio combiner for equal noise powers |
5. Conclusions
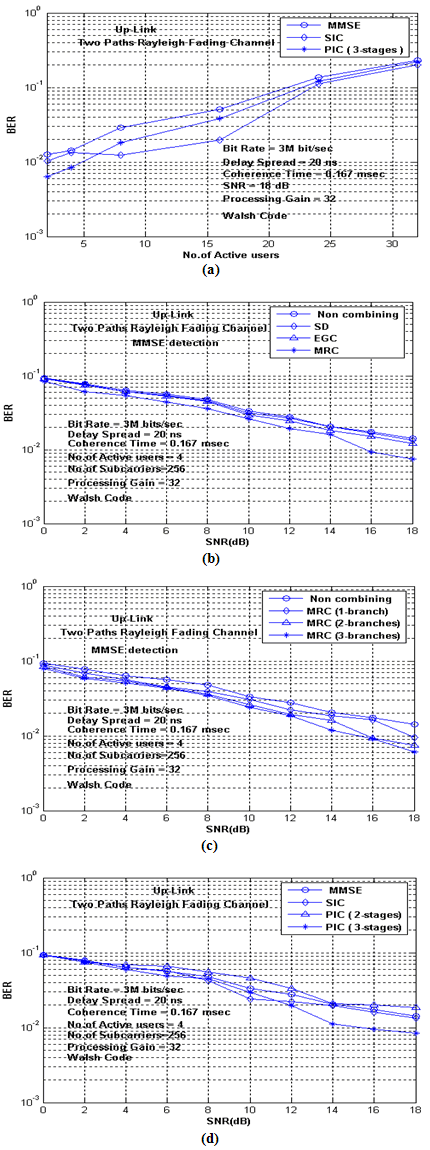
- Maximal ratio combining (MRC) takes better advantage of all the diversity branches in the system. A special case of MRC is presented in the next section. MRC always performs better than either selection diversity or equal gain combining EGC because it is an optimum combiner. The information on all channels is used with this technique to get a more reliable received signal[5]. For high number of active users, SIC detector is efficient because the number of stages is equal to the number of active users, but the time delay between the users is very high. PIC detector also has a good result when the number of active users is increased, and it becomes more complex for design. This criterion is shown in Figure 5a. Figure 5b shows the advantage of using different diversity combining techniques to improve bit error rate in GO-MC-CDMA system. The SD and EGC combining improve the bit error rate slightly as compared with non combining system.MRC technique gives better BER performance as compared with SD and EGC combining diversity techniques, but it is more complex in the design.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML