1. Introduction

The combination of high strength and good toughness for high strength low alloy (HSLA) steels is achieved through the generation of fine ferrite grain sizes through application of controlled thermo-mechanical processing (TMP) schedules[1]. Steel grades amenable to this treatment will contain small amounts of some or all of Al, Ti, V, Mo and, especially, Nb in combination with C and N[2]. For a hot deformed and recrystallised (fully or partially) HSLA steel, the strength level is largely determined by the mode or average grain size (through the Hall-Petch relationship); toughness, however, is much more dependent on the population of larger grains in the grain size distribution. The grain size distributions are usually characterised as a log-normal distribution for full recrystallisation with the maximum grain size being 2 – 3 times that of the mean / mode[3]. This is a notable effect for unimodal grain size distributions, but bimodal grain size distributions the mixture of coarse and fine grains (banded or in patches) results in increased scatter in toughness values, although the strength levels are similar[4].

Niobium is the most potent microalloying addition for austenite grain size control through both solute drag and strain-induced precipitation (SIP) effects. During solidification, however, niobium shows a strong tendency to segregate into the liquid phase and its low diffusivity in austenite means that it will remain segregated through most of the TMP schedule resulting in spatial variations in the degree of retardation of recrystallisation.

In order to avoid low or scattered toughness values, then the grain size distribution during hot deformation needs to be controlled. In selecting TMP schedules then one on the more widely used predictive schemes is that of Dutta and Sellars (DS)[5]. The following equations are used to predict static recrystallisation and precipitation start time according to 5 % recrystallisation (R_s) and 5 % precipitation (P_s) based on classical nucleation theory.

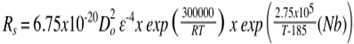
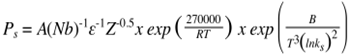where[Nb] is the amount of Nb in solution in austenite; ε is applied strain; T (K) is the deformation temperature; k_s is the supersaturation ratio; D₀ is the austenite grain size at the start of deformation; and Z is Zener-Holloman parameter.

This model was developed from experimental data based on deformation testing of steels with Nb contents between 0.03 - 0.045 wt %, starting prior austenite grain sizes of 100 – 450 μm and using a strain of 0.3[5]. However, unimodal grain sizes are assumed along with a uniform Nb concentration. Earlier studies on a 0.46 wt % Nb steel that had been homogenised for 4 days at 1225°C[6] showed that the DS equations using the parameters above overestimated the proportion of recrystallisation for a 10 s hold after 0.3 strain. The agreement, however, improved when grain size classes were used rather than just the average grain size.

The generality of this approach to dealing with grain size distributions and how chemical heterogeneities are dealt with is the subject of this paper.

2. Materials and Experimental Procedure

The material used in this work was a 290 mm thick continuously cast slab of composition: 0.10 C, 1.51 Mn, 0.32 Si, 0.017 P, 0.005 S, 0.046 Nb, 0.002 Ti, 0.006 V, 0.045 Al and 0.008 N; all wt %. Specimens of size 10 x 15 x 20 mm (machined from the ¼ thickness position of the slab) from the slab were tested in the as-cast state and after being homogenised at 1225 ºC for 4 days under vacuum and slowly cooled at a rate of 3 ºC/min to remove the Nb segregation. The details of selection of homogenisation temperature and time have been discussed elsewhere[7]. The homogenised and segregated specimens were sealed inside silica tubing under a partial Ar atmosphere and reheated to 1150 or 1225°C, soaked for 1 hour and then quenched (tube intact) into water to represent a commercial reheating temperature and time (to dissolve Nb-rich precipitates); quenching was used to preserve the Nb in solution prior to deformation trials. Thermo-Calc software (version Q) was used to determine the equilbrium Nb content in solution at 1150 / 1225ºC in the homogenised condition. The reheated specimens were subjected to plane strain compressive deformation in a Gleeble 3500 over a range of temperatures (975°C to 1075°C) and 0.3 strain being held at the chosen deformation temperatures for a range of times (4 to 10 s) at a strain rate of 10 s^-1 after solutionising at 1150 or 1225°C for 5 minutes.

Samples after reheating and Gleeble simulation were sectioned along their mid-thickness (normal to the compression axis) and mounted in Bakelite. The samples were metallographically polished to a 0.05 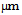SiO₂ finish and etched in saturated aqueous picric acid solution at 60ºC to reveal the prior austenite grain structures. The heat-treated and deformed specimens were examined in a Leica DMRX microscope equipped with KS300 image analysis software. Quantitative determination of austenite grain size in terms of equivalent circle diameter (ECD) was carried out measuring about 1500 grains in terms of individual grain area and ECD (obtained directly from the KS300 software) to determine grain size distributions as an area fraction against size.

3. Results and Discussion

For homogenised material single hit Gleeble tests showed that the fully recrystallised grains showed a distribution that could not be modelled using equation of the type: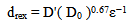where drex is the average recrystallised grain size, D₀ the average starting austenite grain size and D’ a constant with values quoted between 0.66 and 1.86. Inspection of the prior austenite grain size distributions for reheated(un-recrystallised) and fully recrystallised samples, Figures 1 and 2, shows that a good fit could be achieved by merely halving the original grain size on recrystallisation. This amounts to limiting recrystallisation to the formation of two recrystallised grains per deformed austenite grain on average and so may limit this approach to a certain range of starting austenite grains.

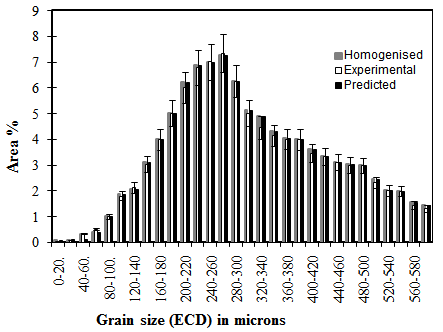Figure 1. Prior austenite grain size distribution for re-heated, homogenised sample

The good agreement between the predicted and experimental distributions in Figures 1 and 2 was obtained when the recrystallising grains were treated as separate classes, i.e. the Dutta-Sellars equations were applied to each 20 m class, using the median size value as D₀ and then determining the fraction of that grain glass that had recrystallised under the thermomechanical simulation conditions. The fraction that had recrystallised was transferred to the class half the size of the original one, whilst the unrecrystallised fraction was left in the original class.

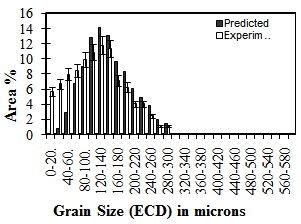Figure 2. Prior austenite grain size distributions (predicted and measured) for a fully recrystallised, homogenised sample

This approach leads to good reproduction of grain size distributions but also a good fit with the recrystallised fractions, Table 1.

Table 1. Predicted (grain class approach) and measured volume fractions of recrystallised grains as a function of deformation temperature Deformation T (°C) Measured recrystallisation % Predicted recrystallisation % 1075 100 93 1050 72 73 1025 42 44 1010 19 17 990 10 8 975 0 0

In the homogenised samples, all grains will have the bulk composition, particularly[Nb], which appears in the Dutta-Sellars equations. When dealing with segregated samples then the composition of the grains will vary depending on whether the grains are in solute-rich or solute-depleted regions of the material. The as-cast structure of the slab has been previously reported[7, 8]; the low[Ti] value in this steel meant that the amount of coarse TiN formed was low so that Nb(C,N) precipitated throughout the austenite grains on cooling rather than primarily on pre-existing TiN. This allowed energy dispersive X-ray spectroscopy (EDS) to be used to determine[Nb], especially in the solute-rich areas. The composition profile for Nb was found to be a ‘top-hat’ with very consistent[Nb] in solute-rich and solute-depleted regions and a very steep change in composition between them. This indicated that, for this steel, the solute-rich and solute-depleted regions could be considered as behaving as material of different composition, uniform within each region (solute-rich and solute-depleted). The EDS analysis also revealed that around 25 % of the as-cast structure for this steel was solute-rich. In other HSLA steels with higher[Ti] then most Nb(C,N) is present as larger caps on the TiN particles so that EDS analysis only reveals detectable[Nb] at the TiN particles.

The average secondary dendrite arm spacing for this slab was 250 , which corresponds to a cooling rate of 0.182 K s^-1. Microsegregation in this system was modelled using a Clyne-Kurz[9] approach. This is based on mass balance and back diffusion of carbon during solidification of the steel to give a solidified fraction, f_s , as a function of temperature, T: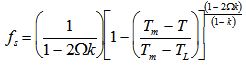

where T_m is the melting temperature of pure iron, T_L is the alloy liquidus temperature, k is the equilibrium partition coefficient and is the solidification factor given by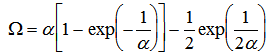

where 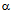is a function of the secondary dendrite arm spacing (SDAS), 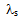, local solidification time, t_f, and solute diffusivity in the solid phase, D_s:

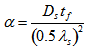The assumptions made are that the first appearance of austenite via the peritectic transformation would form a low-diffusivity layer that would prevent further atomic migration between the dendrite and the interdendritic liquid. On this basis, the solute-depleted fraction would be the integrated fraction solidified by the start of the peritectic transformation; the dominant role of [C] on this transformation meant that the equilibrium value for the peritectic start temperature as predicted from Thermo-Calc was used to define the undercooling temperature range over which the dendrites solidified. Carbon diffusion in ferrite was also used for determination of D_s.

The fractions of solute-rich and solute-depleted determined this way deviated from the equilibrium values at the peritectic start temperature, but Thermo-Calc was used to establish the mass balance between delta-ferrite and liquid that would give these volume fractions (noting that the segregation profiles determined experimentally were top-hat functions). This method gives reasonable agreement between prediction and experiment, Table 2, and has been extended to steels with 0.04 – 0.1 wt % C and 0.019 – 0.094 wt % Nb, all of which involved the peritectic transfiormation during their solidification sequences.

The results shown in Table 2 show reasonable agreement with optical and scanning electron microscopy determination of the solute-rich and solute-depleted fractions, although differences of up to 6 % are observed. These differences may become significant when modelling a commercial multi-pass hot rolling schedule and cross-diffusion effects are being investigated using EDS mapping techniques in order to improve the fit between model and experiment.

Table 2. Predicted and measured solute-rich volume % for a range of C-Nb steels Alloy Predicted Measured 0.052 Nb – 0.06 C 7.6 8.3 0.046 Nb – 0.1 C 20.0 25.0 0.094 Nb – 0.04 C 22.0 28.0 0.019 Nb – 0.1 C 22.0 16.0

The modelling approach is also being expanded to deal with alloys solidifying without involving the peritectic transformation.

In applying the class-based Dutta-Sellars equations to segregated samples then the grain distributions need to be assigned a composition representative of solute-rich or solute-poor regions. For a unimodal grain size distribution, e.g. for re-heating at 1225°C, then each grain size classification is assigned equally to solute-rich and solute-depleted. In this steel then 25 % of the grains in each grain size classification are assumed to have a[Nb] value representative of solute-rich material and 75 % a value representative of solute-depleted, Figure 3.

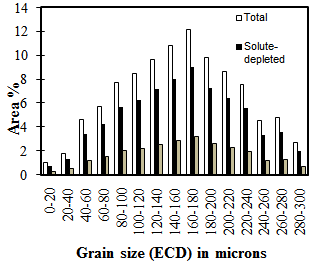Figure 3. Separation of grain size classes into solute-rich and solute-depleted for unimodal grain size distribution (re-heated to 1225°C)

When reheating to 1150°C, the situation is more complex as the resulting prior austenite grain size distribution is bimodal. EDS analysis of the coarse and fine grained regions in this distribution indicated that fine grains were observed in both solute-rich and solute-depleted material, but the coarse grained regions were exclusively solute-depleted. On this basis the coarse grains were assigned a[Nb] value representative of solute-depleted material, whilst the fine grained classes were split into solute-rich (33%) and solute-depleted (67%); the percentages taking into account the amount of solute-depleted material assigned to the coarse grain classes, Figure 4.

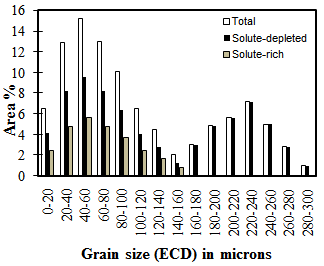Figure 4. Separation of grain size classes into solute-rich and solute-depleted for bimodal grain size distribution (re-heated to 1150°C)

Taking segregation into account results in a number of effects. Firstly the partial recrystallisation range of temperatures is broadened on recrystallisation precipitation time temperature (RPTT) plots compared with an homogenised alloy. This can be predicted using this modification to the original Dutta-Sellars equations and so identifies processing windows at risk of developing bimodal grain structures, Figure 5.

Using the grain size class modification and the differing compositions allowed the grain size distributions to be determined as for the homogenised alloys. Although the fit is good it is not as good as in the homogenised case and this requires further work. Despite this the agreement between the recrystallised fraction predicted using differing compositions for the different grain classes was much better than when an average[Nb] value was used. The discrepancy for the use of an average[Nb] value was generally an underestimate by 30 – 50 %; this came down to an overestimate of 3 – 13 % when the different[Nb] values were used.

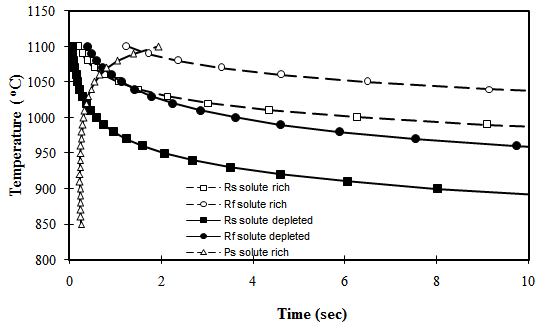Figure 5. Separation of recrystallisation start (square symbols) and finish (circular symbols) temperatures for solute–rich (solid symbols) and solute-depleted (open symbols) in a segregated steel sample

4. Conclusions and Further Work

The use of grain sizes classes instead of an average grain size gives better fit between a Dutta-Sellars-based prediction and experimentally determined recrystallisation fractions in an homogenised sample.

In a segregated steel sample, the use of different[Nb] in the modified Dutta-Sellars approach results in improved prediction of the amount of recrystallisation although the fit for grain size distributions is not as good as that seen for the homogenised case.

For steels solidifying via a peritectic transformation then a Clyne-Kurz approach gives reasonable prediction for the fraction of solute-rich material

The modelling approach is being improved by addressing the fit of grain size distributions; the effects of grain size on stored energy; variations in strain and composition; and solidification without the peritectic.

ACKNOWLEDGEMENTS

The authors wish to thank the support of the School of Metallurgy and Materials at the University of Birmingham and Tata Steel Europe and the results generated by Debalay Chakrabarti, Amrita Kundu and Dayue Zhang.